Exact and Paraxial Broadband Airy Wave Packets in Free Space and a Temporally Dispersive Medium

Abstract

A question of physical importance is whether finite-energy spatiotemporally localized (i.e., pulsed) generalizations of monochromatic accelerating Airy beams are feasible. For luminal solutions, this question has been answered within the framework of paraxial geometry. The time-diffraction technique that has been motivated by the Lorentz invariance of the equation governing the narrow angular spectrum and narrowband temporal spectrum paraxial approximation has been used to derive finite-energy spatiotemporally confined subluminal, luminal, and superluminal Airy wave packets. The goal in this article is to provide novel exact finite-energy broadband spatio-temporally localized Airy solutions (a) to the scalar wave equation in free space; (b) in a dielectric medium moving at its phase velocity; and (c) in a lossless second-order temporally dispersive medium. Such solutions can be useful in practical applications involving broadband (few-cycle) wave packets.

1. Introduction

The Airy beam (propagating along the z-axis)

$$\Psi \left(x,z\right)=e^{-\frac{1}{12}\left(2a+i\frac{z}{k}\right)\left(2a^2-6x-4ia\frac{z}{k}+\frac{z^2}{k^2}\right)}Ai\left(x+ia\frac{z}{k}-\frac{z^2}{k^2}\right)\hspace{0.17em};\hspace{0.33em}k=\omega /c$$

is a remarkable finite-energy solution to the paraxial equation

$$i\frac{\partial }{\partial z}\Psi \left(x,z\right)+\frac{c}{2\omega }\frac{{\partial }^2}{\partial x^2}\Psi \left(x,z\right).$$

It was first introduced analytically by Siviloglou and Christodoulides [1] and subsequently demonstrated experimentally by Siviloglou, Broky, Dogariu, and Christodoulides [2]. Their work was motivated by the infinite-energy nonspreading accelerating Airy solution to the quantum mechanical Schrödinger equation introduced by Berry and Balazs [3]. The Airy beam is slowly diffracting while bending laterally along a parabolic path even though its centroid is constant, it can perform ballistic dynamics akin to those of projectiles moving under the action of gravity, and it is self-healing, that is, it regenerates when part of the “generating” aperture is obstructed; this is due to the reinforcement of the main lobe by the side lobes. Due to these desirable properties of the Airy beam, as well as other types of beams that have been advanced recently, applications have been found in beam focusing, particle manipulation, biomedical imaging, and material processing.

An important question of physical interest is whether spatiotemporally localized (i.e., pulsed) versions of Airy beams are feasible. Space–time paraxial solutions based on the narrow angular spectrum obey the pulsed beam equation

$$\left(\frac{{\partial }^2}{\partial x^2}-\frac{2}{c}\frac{{\partial }^2}{\partial \tau \partial z}\right)u\left(x,z,t\right)=0;\hspace{0.33em}\tau =t-z/c.$$

For luminal solutions, this question has been answered affirmatively by Saari [4], Valdmann, Piksarv, Valta-Lukner, and Saari [5], and Kaganovsky and Heyman [6] within the framework of paraxial geometry.

More recently, work on nonluminal spatiotemporally confined Airy wave packets has appeared in the literature [7,8,9]. However, the Airy solution is intimately related to a parabolic equation. Only for luminal spatiotemporally localized wave solutions to the scalar wave equation can such an association be made. For this reason, subluminal and superluminal spatiotemporally confined Airy solutions to the wave equation do not exist. As a special case, broadband subluminal and superluminal spatiotemporally localized Airy wave packets based only on the narrow angular spectrum paraxial approximation do not exist. The time-diffraction technique introduced by Porras [10,11] recently has been motivated by Besieris and Shaarawi [12] in terms of the Lorentz invariance of the equation governing the narrow angular spectrum and narrowband temporal paraxial approximation $u\left(x,z,t\right)=\exp \left(i{\omega }_0\tau \right)\varphi \left(x,z,t\right),$ with

$$i\left(\frac{\partial }{\partial z}+\frac{1}{c}\frac{\partial }{\partial t}\right)\varphi \left(x,z,t\right)-\frac{1}{2k_0}\frac{{\partial }^2}{\partial x^2}\varphi \left(x,z,t\right);\hspace{0.33em}{k}_0\equiv {\omega }_0/c,$$

where ${\omega }_0$ is the carrier frequency. This approximation has been used to derive finite-energy spatiotemporally confined subluminal, luminal, and superluminal Airy wave packets.

The goal in this article is to provide novel exact finite-energy broadband spatiotemporally localized Airy solutions (a) to the scalar wave equation in free space; (b) in a dielectric medium moving at its phase velocity; and (c) in a lossless second-order temporally dispersive medium. Such solutions can be useful in practical applications involving broadband (few-cycle) wave packets.

2. Finite-Energy (3 + 1)D Spatiotemporally Localized Airy Splash Mode Solution of the Scalar Wave Equation in Free Space

Consider the $\left(3+1\right)D$ scalar wave equation in free space, viz.,

$$\left(\frac{{\partial }^2}{\partial X^2}+\frac{{\partial }^2}{\partial Y^2}+\frac{{\partial }^2}{\partial Z^2}-\frac{{\partial }^2}{\partial T^2}\right)\Psi \left(X,Y,Z,T\right)=0,$$

(1)

written in terms of the nondimensional variables $X=x/x_0,\hspace{0.33em}\hspace{0.33em}Y=y/x_0,\hspace{0.33em}\hspace{0.33em}Z=z/x_0,$ and $T=ct/x_0.$ The introduction of the characteristic variables ${\Lambda }_{\pm }=Z\mp T$ changes the derivatives with respect to Z and T as follows:

$$\frac{\partial }{\partial Z}=\frac{\partial }{\partial {\Lambda }_{+}}+\frac{\partial }{\partial {\Lambda }_{-}},\hspace{0.33em}\hspace{0.33em}\frac{\partial }{\partial T}=-\frac{\partial }{\partial {\Lambda }_{+}}+\frac{\partial }{\partial {\Lambda }_{-}}.$$

Therefore,

$$\frac{{\partial }^2}{\partial Z^2}-\frac{{\partial }^2}{\partial T^2}={\left(\frac{\partial }{\partial {\Lambda }_{+}}+\frac{\partial }{\partial {\Lambda }_{-}}\right)}^2-{\left(-\frac{\partial }{\partial {\Lambda }_{+}}+\frac{\partial }{\partial {\Lambda }_{-}}\right)}^2=4\frac{{\partial }^2}{\partial {\Lambda }_{+}\partial {\Lambda }_{-}},$$

and Equation (1) changes to

$$\left(\frac{{\partial }^2}{\partial X^2}+\frac{{\partial }^2}{\partial Y^2}+4\frac{{\partial }^2}{\partial {\Lambda }_{+}\partial {\Lambda }_{-}}\right)\Psi \left(X,Y,{\Lambda }_{+},{\Lambda }_{-}\right)=0.$$

(2)

A specific solution of this equation is the infinite-energy accelerating Airy wave packet

$$\Psi \left(X,{\Lambda }_{+},{\Lambda }_{-}\right)=\exp \left[i{\Lambda }_{-}\right]e^{-i\frac{1}{24}{\Lambda }_{+}\left(-6X+\frac{1}{4}{\Lambda }_{+}^2\right)}Ai\left(X-\frac{1}{16}{\Lambda }_{+}^2\right).$$

(3)

This wavefunction moves in a parabolic trajectory along the characteristic variable ${\Lambda }_{+}$.

In 1910, Bateman [13,14] discovered a transformation, more general than a conformal change in the metric, which could be used to transform solutions of Maxwell equations into similar ones. In the case of the scalar wave equation, the Bateman transformation in $\left(3+1\right)D$ assumes the form

$${\Psi }_1\left(X,Y,{\Lambda }_{+},{\Lambda }_{-}\right)=\frac{1}{{\Lambda }_{-}}\Psi \left[\frac{X}{{\Lambda }_{-}},\frac{Y}{{\Lambda }_{-}},-\frac{1}{{\Lambda }_{-}},\frac{X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}}{\hspace{0.17em}{\Lambda }_{-}}\right].$$

(4)

The function ${\Psi }_1\left(X,Y,{\Lambda }_{+},{\Lambda }_{-}\right)$ also obeys the scalar wave Equation (2).

The Bateman transformation is applied twice to the solution given in Equation (3). These two sequential operations result in the following new solution to Equation (2):

$$\begin{array}{l}{\Psi }_2\left(X,Y,{\Lambda }_{+},{\Lambda }_{-}\right)=\frac{1}{X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}}Ai\left[-\frac{{\Lambda }_{+}^2-16X\left(X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}\right)}{16{\left(X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}\right)}^2}\right]\\ \times \exp \left[-i\frac{-{\Lambda }_{+}^3+24X{\Lambda }_{+}\left(X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}\right)+96{\Lambda }_{-}{\left(X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}\right)}^2}{96{\left(X^2+Y^2+{\Lambda }_{+}{\Lambda }_{-}\right)}^3}\right].\end{array}$$

(5)

Next, this expression is complexified by means of the changes ${\Lambda }_{+}\to {\Lambda }_{+}-i{a}_1,\hspace{0.17em}\hspace{0.17em}{\Lambda }_{-}\to {\Lambda }_{-}+i{a}_2,$ where $a_{1,2}$ are two positive parameters. Consequently, one obtains

$${\psi }_2\left(R,\varphi ,{\Lambda }_{+,}{\Lambda }_{-,};\hspace{0.17em}{a}_1,a_2\right)=B^{-1}\exp \left(-i\frac{Q}{96B^3}\right)Ai\left[\frac{{\left(a_1+i{\Lambda }_{+}\right)}^2+BR\cos \varphi }{16B^2}\right];$$

(6)

with the exponent $Q$ given as

$$\begin{array}{l}Q=-i{\left(a_1+i{\Lambda }_{+}\right)}^3-i24R\cos \varphi \left(a_1+i{\Lambda }_{+}\right)B+i96\left(a_2-i{\Lambda }_{-}\right)B^2,\\ B=R^2+\left(a_1+i{\Lambda }_{+}\right)\left(a_2-i{\Lambda }_{-}\right)\end{array}$$

(7)

in cylindrical coordinates $\left(X=R\cos \varphi ,\hspace{0.33em}Y=R\sin \varphi \right).$ This is a finite-energy $\left(3+1\right)D$ spatiotemporally localized luminal wave packet belonging to the class of splash modes studied by Ziolkowski [15]. It will be referred to as the Airy splash mode.

The free positive parameters $a_1$ and $a_2$ entering the solution given in Equation (7) are critical. As discussed originally by Ziolkowski ([15]; see also [16]), their presence ensures finite energy. Their relative values measure the size of the forward and backward wave components. Only when $a_1>>a_2$, the backward components are minimized, and the solution is almost undistorted. This is further explained in [17], where it is shown that very close replicas of localized waves, such as the one in Equation (6), can be launched causally from apertures constructed based on the Huygens principle.

Figure 1 shows surface plots of the intensity of Airy splash mode versus ${\Lambda }_{+}$ and $X$ for various values of $T$; the latter is defined by the relationship ${\Lambda }_{-}={\Lambda }_{+}+2T.$ The parameters $a_1$ and $a_2$ have the values $8\times {10}^{-2}$ and $10,$ respectively. The wave packet is relatively undistorted because $a_1>>a_2$.

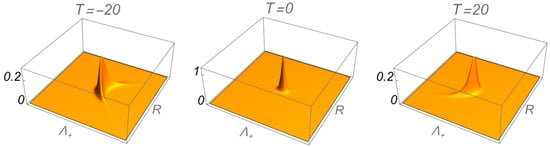
Figure 1. Surface plots of the modulus of ${\psi }_2\left(R,\pi /4,{\Lambda }_{+},{\Lambda }_{-}\right)$ versus ${\Lambda }_{+}\in \left[-4\times {10}^{-1},4\times {10}^{-1}\right]$ and $R\in \left[-6,6\right]$ for three values of $T,$ with the latter defined by the relationship ${\Lambda }_{-}={\Lambda }_{+}+2T.$ The parameters $a_1$ and $a_2$ have the values $8\times {10}^{-2}$ and $10,$ respectively, with the speed of light in vacuum normalized to unity.

The finite-energy wavefunction $U_2^{+}\left(X,Y,{\Lambda }_{+},Z\right)={\Psi }_2\left(X,Y,{\Lambda }_{+},2Z;\hspace{0.33em}{a}_1,a_2\right)$ obeys the paraxial forward pulsed beam equation

$$\left(\frac{{\partial }^2}{\partial X^2}+\frac{{\partial }^2}{\partial Y^2}+\frac{{\partial }^2}{\partial {\Lambda }_{+}\partial Z}\right)U_2^{+}\left(X,Y,{\Lambda }_{+},Z\right)=0.$$

(8)

The transition from Equations (3) to (6) is effected by means of the modified complexification ${\Lambda }_{+}\to {\Lambda }_{+}-i{a}_1,\hspace{0.33em}{\Lambda }_{-}\to 2Z+i{a}_2.$ As a result, one obtains broadband splash mode-type spatiotemporally localized wave solutions to the paraxial equation.

3. Finite-Energy Accelerating Spatiotemporally Localized Airy Wave Packet Solution to the Scalar Equation in Free Space

A solution to Equation (2) is sought in the form

$$\psi \left(X,{\Lambda }_{+},{\Lambda }_{-};\beta \right)=\exp \left(i\beta {\Lambda }_{-}\right)\phi \left(X,{\Lambda }_{+};\beta \right).$$

Then, $\phi \left(X,{\Lambda }_{-};\beta \right)$ is governed by the parabolic equation

$$\left(i4\beta \frac{\partial }{\partial {\Lambda }_{+}}+\frac{{\partial }^2}{\partial X^2}\right)\phi \left(X,{\Lambda }_{+};\beta \right)=0$$

(9)

A solution to this equation is the “accelerating beam”

$$\begin{array}{ll}\phi \left(X,{\Lambda }_{-};\beta \right)& =\exp \left[-\frac{1}{12}\left(2a+i{\Lambda }_{+}\right)\left(2a^2-6\sqrt{2\beta }X-i4a{\Lambda }_{+}+{\Lambda }_{+}^2\right)\right]\\ & \times Ai\left(\sqrt{2\beta }X+ia{\Lambda }_{+}-\frac{{\Lambda }_{+}^2}{4}\right).\end{array}$$

(10)

With $a$ a small positive parameter and ${\Lambda }_{+}$ replaced by $Z,$ $\phi \left(X,Z\right)$ is essentially the finite-energy monochromatic paraxial accelerating Airy beam solution introduced by Siviloglou and Christodoulides [1]. In contrast, $\psi \left(X,{\Lambda }_{+},{\Lambda }_{-};\beta \right)=\exp \left(i\beta {\Lambda }_{-}\right)\phi \left(X,{\Lambda }_{+};\beta \right)$ is not a finite-energy solution to the scalar wave equation. To achieve a finite-energy spatiotemporal solution, an appropriate superposition over the free parameter $\beta$ of the form

$$\psi \left(X,{\Lambda }_{+},{\Lambda }_{-}\right)={\displaystyle \int d\beta }F\left(\beta \right)\exp \left(i\beta {\Lambda }_{-}\right)\phi \left(X,{\Lambda }_{+};\beta \right)$$

(11)

must be undertaken. Such a superposition can be brought to the form

$$\begin{array}{lll}\hfill \psi \left(X,{\Lambda }_{+},{\Lambda }_{-}\right)& =\hfill & Q{\displaystyle {\int }_{-\infty }^{\infty }d\sigma }\exp \left(-{\sigma }^2\right)Ai\left[A\left(\frac{B}{A}-\sigma \right)\right];\hfill \\ \hfill Q& \hfill =& \hfill \frac{1}{\sqrt{a_1-i{\Lambda }_{-}}}\exp [-\frac{1}{6\sqrt{2}}b\left(2a^2-i4a{\Lambda }_{+}+{\Lambda }_{+}^2\right)]\exp \left[\frac{1}{4}{b}^2\frac{X^2}{a_1-i{\Lambda }_{-}}\right],\\ \hfill \mathrm{A}& =\hfill & \frac{\sqrt{a_1-i{\Lambda }_{-}}}{\sqrt{2}X},\hspace{0.33em}b=\sqrt{2}\left(a+i\frac{{\Lambda }_{+}}{2}\right),\hfill \\ \hfill B& =\hfill & \frac{ia{\Lambda }_{+}-\frac{{\Lambda }_{+}^2}{4}+b\frac{X^2}{\sqrt{2\left(a_1-i{\Lambda }_{-}\right)}}}{A}.\hfill \end{array}$$

(12)

where $a_1$ is a positive free parameter. The integral in Equation (12) is an Airy transform [18]. It can be carried out explicitly, yielding the finite-energy accelerating spatiotemporal Airy wave packet

$$\psi \left(X,{\Lambda }_{+},{\Lambda }_{-}\right)=Q\exp \left[\frac{1}{4A^3}\left(B+\frac{1}{24A^3}\right)\right]Ai\left(\frac{B}{A}+\frac{1}{16A^4}\right).$$

(13)

Figure 2 shows surface plots of the modulus square of the Airy wave packet versus ${\Lambda }_{+}$ and $X$ for various values of $T,$ with the latter defined by the relationship ${\Lambda }_{-}={\Lambda }_{+}+2T.$ The parameters $a$ and $a_1$ have the values $5\times {10}^{-2}$ and $100,$ respectively.

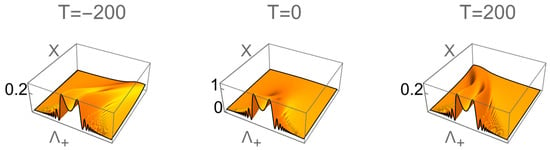
Figure 2. Surface plots of the modulus of $\psi \left(X,{\Lambda }_{+},{\Lambda }_{-}\right)$ versus ${\Lambda }_{+}\in \left[-10,10\right]$ and $X\in \left[0,60\right]$ for three values of $T,$ with the latter defined by the relationship ${\Lambda }_{-}={\Lambda }_{+}+2T.$ The parameters $a$ and $a_1$ have the values $5\times {10}^{-2}$ and 100, respectively, with the speed of light in vacuum normalized to unity.

The finite-energy wavefunction $U_2^{+}\left(X,{\Lambda }_{+},Z\right)\equiv {\Psi }_2\left(X,{\Lambda }_{+},2Z;\hspace{0.17em}\hspace{0.17em}{a}_1,a_2\right)$ obeys the paraxial forward pulsed beam equation (cf. Equation (8)) if the replacement ${\Lambda }_{-}\to 2Z$ is made in Equation (13). As mentioned previously, one then obtains a broadband spatiotemporally localized accelerating Airy solution to the paraxial equation.

4. Finite-Energy Accelerating Broadband Airy Wave Packet Solution in the Presence of Temporal Dispersion

4.1. Basic Equation

For a physically convenient central radian frequency ${\omega }_0$, the real field $u(\overrightarrow{r},t),$ describing electromagnetic wave propagation in a linear, homogeneous, transparent, dispersive medium if polarization is neglected, is expressed as follows:

$$u(\overrightarrow{r},t)=\phi (\overrightarrow{r},t)\hspace{0.17em}\exp \left[-i{\omega }_0\left(t-z/v_{ph}\right)\right]\hspace{0.17em}+cc,\hspace{0.33em}z\ge 0.$$

(14)

Here, $\phi (\overrightarrow{r},t)$ is a complex-valued envelope function and $v_{ph}={\omega }_0/\beta ({\omega }_0)$ denotes the phase speed in the medium defined in terms of the real wave number computed at the central frequency. For pulses as short as a single optical period $T_0=2\pi /{\omega }_0,$ and within the framework of the paraxial approximation, the envelope function obeys the following equation [19,20,21]:

$$\left(1+i\frac{{\beta }_1}{{\beta }_0}\frac{\partial }{\partial \tau }\right)\frac{\partial }{\partial z}\phi \left(\overrightarrow{r},\tau \right)-\left(1+i\frac{{\beta }_1}{{\beta }_0}\frac{\partial }{\partial \tau }\right)iD\left(-i\frac{\partial }{\partial \tau }\right)\hspace{0.33em}\phi \left(\overrightarrow{r},\tau \right)-\frac{i}{2{\beta }_0}{\nabla }_t^2\phi \left(\overrightarrow{r},\tau \right)=0.$$

(15)

Here, ${\nabla }_{\perp }^2$ denotes the transverse (with respect to $z$) Laplacian operator and $\hspace{0.33em}\tau =t-(z/v_{gr})$ corresponds to a moving reference frame, defined in terms of the group speed $v_{gr}=1/{\beta }_1;\hspace{0.33em}\hspace{0.33em}{\beta }_1\equiv {\left.d\beta (\omega )/d\omega \right|}_{\omega ={\omega }_0}$. The operator $D$ is given by the expression

$$D\left(-i\frac{\partial }{\partial \tau }\right)={\displaystyle \sum _{m=2}^{\infty }\frac{{\beta }_m}{m!}}{\left(-i\frac{\partial }{\partial \tau }\right)}^m;\hspace{0.33em}\hspace{0.17em}{\beta }_m=\frac{d^m}{d{\omega }^m}{\left.\beta (\omega )\right|}_{\omega ={\omega }_0}.$$

(16)

In the sequel, only the first term in the series will be retained. This approximation results in the equation

$$\left(1+i\frac{{\beta }_1}{{\beta }_0}\frac{\partial }{\partial \tau }\right)\frac{\partial }{\partial z}\phi \left(\overrightarrow{r},\tau \right)-\left(1+i\frac{{\beta }_1}{{\beta }_0}\frac{\partial }{\partial \tau }\right)\left(-i\frac{{\beta }_2}{2}\frac{{\partial }^2}{\partial {\tau }^2}\right)\hspace{0.33em}\phi \left(\overrightarrow{r},\tau \right)-\frac{i}{2{\beta }_0}{\nabla }_t^2\phi \left(\overrightarrow{r},\tau \right)=0.$$

(17)

Here, $\hspace{0.33em}\hspace{0.33em}{\beta }_2\equiv {\left.d^2\beta (\omega )/d^2\omega \right|}_{\omega ={\omega }_0}$ is the second-order index of dispersion. It is positive for normal dispersion and negative for anomalous dispersion.

4.2. Accelerating Airy Solution

A solution to Equation (17) is sought in the form $\phi \left(\overrightarrow{r},\tau \right)=\tilde{\phi }\left(\overrightarrow{r},\Omega \right)\exp \left(-i\hspace{0.17em}\tau \hspace{0.17em}\Omega \right).$ Furthermore, with $\tilde{\phi }\left(\overrightarrow{r},\Omega \right)=\tilde{\psi }\left(\overrightarrow{r},\Omega \right)\exp \left[i{\beta }_2{\Omega }^{2}z/2\right],$ one obtains the parabolic equation

$$\left[i{\beta }_0\left(1+\frac{{\beta }_1}{{\beta }_0}\Omega \right)\frac{\partial }{\partial z}+\frac{1}{2}{\nabla }_t^2\right]\tilde{\psi }\left(\overrightarrow{r},\Omega \right)=0.$$

(18)

The azimuthally asymmetric expression

$$\tilde{\psi }\left(\rho ,\varphi ,z;\Omega \right)=\exp \left(im\varphi \right)\frac{{\rho }^m}{{\left(a_1+i\hspace{0.17em}z\right)}^{m+1}}\exp \left[-\left({\beta }_0+{\beta }_1\Omega \right)\frac{{\rho }^2}{2\left(a_1+i\hspace{0.17em}z\right)}\right],$$

(19)

with $a_1$ as a positive parameter, satisfies the paraxial Equation (18). A spatiotemporal solution to Equation (17) can be derived by means of the superposition

$$\begin{array}{ll}\phi \left(\rho ,\varphi ,z,\tau \right)& =\exp \left(im\varphi \right)\frac{{\rho }^m}{{\left(a_1+i\hspace{0.17em}z\right)}^{m+1}}\exp \left[-{\beta }_0\frac{{\rho }^2}{2\left(a_1+i\hspace{0.17em}z\right)}\right]\\ & \times {\displaystyle {\int }_{-\infty }^{\infty }d\Omega }\exp \left[-i\Omega \left(\tau -i{\beta }_1\frac{{\rho }^2}{2\left(a_1+i\hspace{0.17em}z\right)}\right)\right] \exp \left[i\frac{{\beta }_2}{2}{\Omega }^{2}z\right]F\left(\Omega \right).\end{array}$$

(20)

A large class of solutions can be obtained by using different spectra $F\left(\Omega \right)$. Choosing the spectrum $F\left(\Omega \right)=\exp \left(-a_2{\beta }_2{\Omega }^2/2\right)\exp \left(i\hspace{0.17em}{\Omega }^3/3\right);\hspace{0.33em}{a}_2>0,$ results in the solution

$$\begin{array}{ll}\phi \left(\rho ,\varphi ,z,\tau \right)& =\exp \left(im\varphi \right)\frac{{\rho }^m}{{\left(a_1+i\hspace{0.17em}z\right)}^{m+1}}\exp \left[-{\beta }_0\frac{{\rho }^2}{2\left(a_1+i\hspace{0.17em}z\right)}\right]\\ & \times \exp \left[-i\frac{{\beta }_2}{2}\left(i{a}_2+\hspace{0.17em}z\right)\left(\frac{2}{3}{\left(i{a}_2+\hspace{0.17em}z\right)}^2{\beta }_2^2/4-i{\beta }_1\frac{{\rho }^2}{a_1+i\hspace{0.17em}z}+\tau \right)\right]\\ & \times Ai\left[-{\beta }_2^2{\left(i{a}_2+\hspace{0.17em}z\right)}^2/4+i{\beta }_1\frac{{\rho }^2}{a_1+i\hspace{0.17em}z}-\tau \right].\end{array}$$

(21)

This is a finite-energy accelerating Airy–Gaussian wave packet. Figure 3 shows the intensity versus $\tau$ and $\rho$ at $z=0$ for $m=0$. Figure 4 shows surface plots of the modulus of the azimuthally symmetric wave packet versus $\tau$ and $z$ for three values of $\rho$.

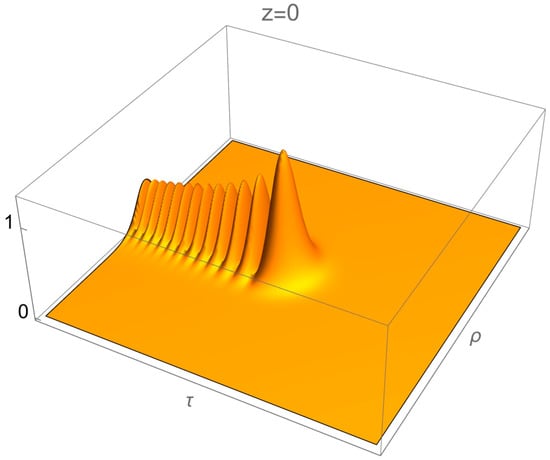
Figure 3. Surface plot of the modulus of $\phi \left(\rho ,\tau \right)$ versus $\tau \in \left[-15,15\right]$ and $\rho \in \left[-10,10\right]$ for $z=0$ and $m=0$.

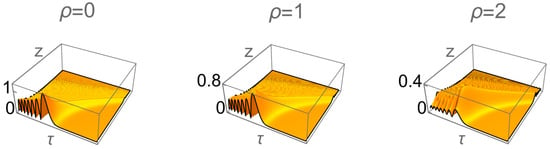
Figure 4. Surface plot of the modulus of the azimuthally symmetric wave packet versus $\tau \in \left[-10,15\right]$ and $z\in \left[0,80\right]$ for three values of $\rho .$ The dimensionless parameters are as follows: $a_1=10,\hspace{0.33em}{a}_2=2,\hspace{0.33em}{\beta }_0=5,$ ${\beta }_1=1,$ and ${\beta }_2={10}^{-1}$.

5. Finite-Energy Accelerating Broadband Airy Wave Packet Solution in a Dielectric Moving at Its Phase Velocity

An equation arising in the case of a dielectric medium moving at its phase velocity is given by [22]:

$$\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}-\frac{2}{v_0}\frac{{\partial }^2}{\partial t\partial z}-\frac{1+{\beta }^2}{v_0^2}\frac{{\partial }^2}{\partial t^2}\right)u\left(x,y,z,t\right)=0.$$

(22)

Here, $v_0$ denotes the phase speed, and $\beta =v_0/c<1$ and $u\left(x,y,z,t\right)$ stand for the longitudinal components $E_z$ and $H_z$ in the absence of sources. On the other hand, the equation of acoustic pressure under conditions of uniform flow is given as follows:

$$\left[{\nabla }^2-\frac{1}{u_0^2}{\left(\frac{\partial }{\partial t}+\overrightarrow{u}\cdot \nabla \right)}^2\right]p\left(\overrightarrow{r},t\right)=0.$$

(23)

Here, $u_0$ is the speed of sound in the rest frame of the medium and $\overrightarrow{u}$ is the uniform velocity of the background flow. In the special case where $\overrightarrow{u}=u{\overrightarrow{a}}_z$ and $u=u_0,$ the resulting equation for the acoustic pressure is isomorphic to Equation (24).

Assuming independence on the transverse variable $y$ in Equation (22), the ansatz

$$u\left(x,z,t\right)=\varphi (x,z)\exp \left[i\omega \frac{1+{\beta }^2}{2v_0}\left(z-\frac{2v_0}{1+{\beta }^2}t\right)\right]$$

(24)

gives rise to the equation

$$\left(i\frac{\omega }{v_0}\frac{\partial }{\partial z}+\frac{1}{2}\frac{{\partial }^2}{\partial x^2}\right)\varphi \left(x,z\right)=0.$$

(25)

This is an exact parabolic equation, in contradistinction to the paraxial approximation of the Helmholtz equation associated with the temporal Fourier transform of the ordinary scalar wave equation. In addition to the well-known beam solutions of the usual paraxial equation, Equation (25) has the following “accelerating” one [1]:

$$\begin{array}{ll}g\left(x,z\right)& =\exp \left[-\frac{1}{12}\left(2a+iz\right)\left(2a^2-i4az+z^2-6x\sqrt{\omega /v_0}\right)\right]\\ & \times Ai\left(x\sqrt{\omega /v_0}-\frac{z^2}{4}+iaz\right).\end{array}$$

(26)

Here, $Ai\left(\cdot \right)$ denotes the Airy function and the positive parameter $a$ ensures finite energy for the monochromatic solution. The beam follows a parabolic trajectory upon propagation.

Finite-energy broadband pulse solutions can be obtained by using the solution (26) together with the ansatz (24) and undertaking a superposition with respect to the frequency $\omega$ (see, e.g., Ref. [22]). A specific spatiotemporal broadband solution is given as follows:

$$\begin{array}{l}u\left(x,z,t\right)=\frac{1}{\sqrt{a_1-iz}}\exp \left[\frac{b^2{x}^2}{4\left(a_1-iz\right)}\right]\exp \left[\frac{1}{4A^2}\left(Y+\frac{1}{24A^4}\right)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} \times Ai\left[Y+\frac{1}{16A^4}\right];\\ Y=\frac{b{x}^2}{\sqrt{2}\left(a_1-iz\right)}-\frac{z^2}{4}+iaz;\\ A=\frac{\sqrt{a_1-i\eta }}{2x};\hspace{0.33em}b=\sqrt{2}\left(a+i\frac{z}{2}\right);\\ \eta =\left(1+{\beta }^2\right)\left(z-\frac{2v_0}{1+{\beta }^2}t\right).\end{array}$$

(27)

Figure 5 shows surface plots of the modulus of the wave packet versus $\tau =t-z\left(1+{\beta }^2\right)/\left(2v_0\right)$ and $x$ for four values of $z$.

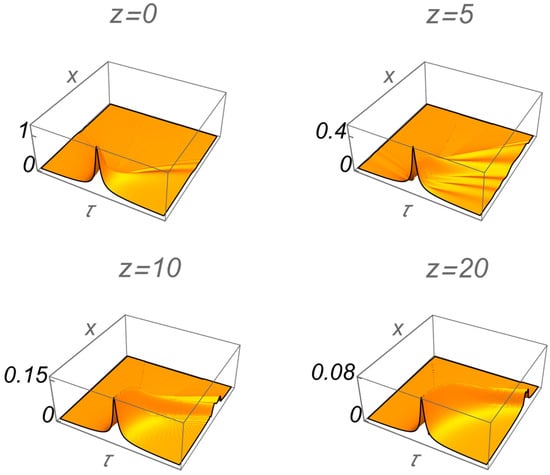
Figure 5. Plot of the modulus of $u\left(x,z,t\right)$ versus $\tau =t-z\left(1+{\beta }^2\right)/\left(2v_0\right) \in \left[-2\times {10}^{-1},2\times {10}^{-1}\right]$ and $x\in \left[0,4\right]$ for four values of $z.$ The parameter values are $a=5\times {10}^{-2},\hspace{0.33em}{a}_1={10}^{-2}$ and $v_0=0.9,$ with the speed of light in vacuum normalized to unity.

6. Concluding Remarks

In this article, four distinct novel finite-energy broadband spatiotemporally confined Airy-type solutions have been presented.

In Section 2, one starts with a solution to the scalar wave equation in the form of an Airy pulse obeying the parabolic equation along one of the characteristic variables of the scalar wave equation, multiplied by a plane wave involving the second characteristic variable. Two sequential applications of the Bateman conformal transformation result in a finite-energy broadband splash mode-type spatiotemporally localized Airy solution to the scalar wave equation in free space. A different exact broadband solution to the scalar wave equation in free space is derived in Section 3. On starts with an infinite energy solution consisting of the product of a plane wave involving one of the characteristic variables of the scalar wave equation and a variant of the Siviloglou–Christodoulides Airy solution obeying the parabolic equation along the second characteristic variable. Several solutions of this form have appeared in the literature (see, e.g., [23]). What distinguishes our work is that an integration over a free parameter entering the solution and the use of the Airy transform yields a different type of a finite-energy broadband spatiotemporally localized Airy solution to the scalar wave equation in free space.

Different types of Airy solutions in the presence of second-order temporal dispersion have appeared in the literature [24,25]. The simplest is the analog of the monochromatic Airy beam involving the axial variable $z$ and the transverse variable $x$. The former involves the axial variable $z$ and the “transverse” variable $\tau =t-z/v_g$, where $v_g$ denotes the group velocity. Another separable solution is of the form $\psi \left(x,y,z,\tau \right)=\varphi \left(z,\tau \right)u\left(x,y\right).$ The $\left(3+1\right)D$ symplectic (non-separable) novel solution of Equation (17) in cylindrical coordinates given in Equation (21) of Section 4 is much more complicated. It is a finite-energy paraxial broadband localized Airy solution.

In Section 5, broadband finite-energy spatiotemporally localized Airy solutions are presented to equations arising in two different physical settings: (a) in the case of a dielectric medium moving at its phase velocity and (b) for acoustic pressure under conditions of uniform flow.