The Determination of the Sensitivity of Refractive Index Sensors
Abstract
1. Introduction
2. Theory
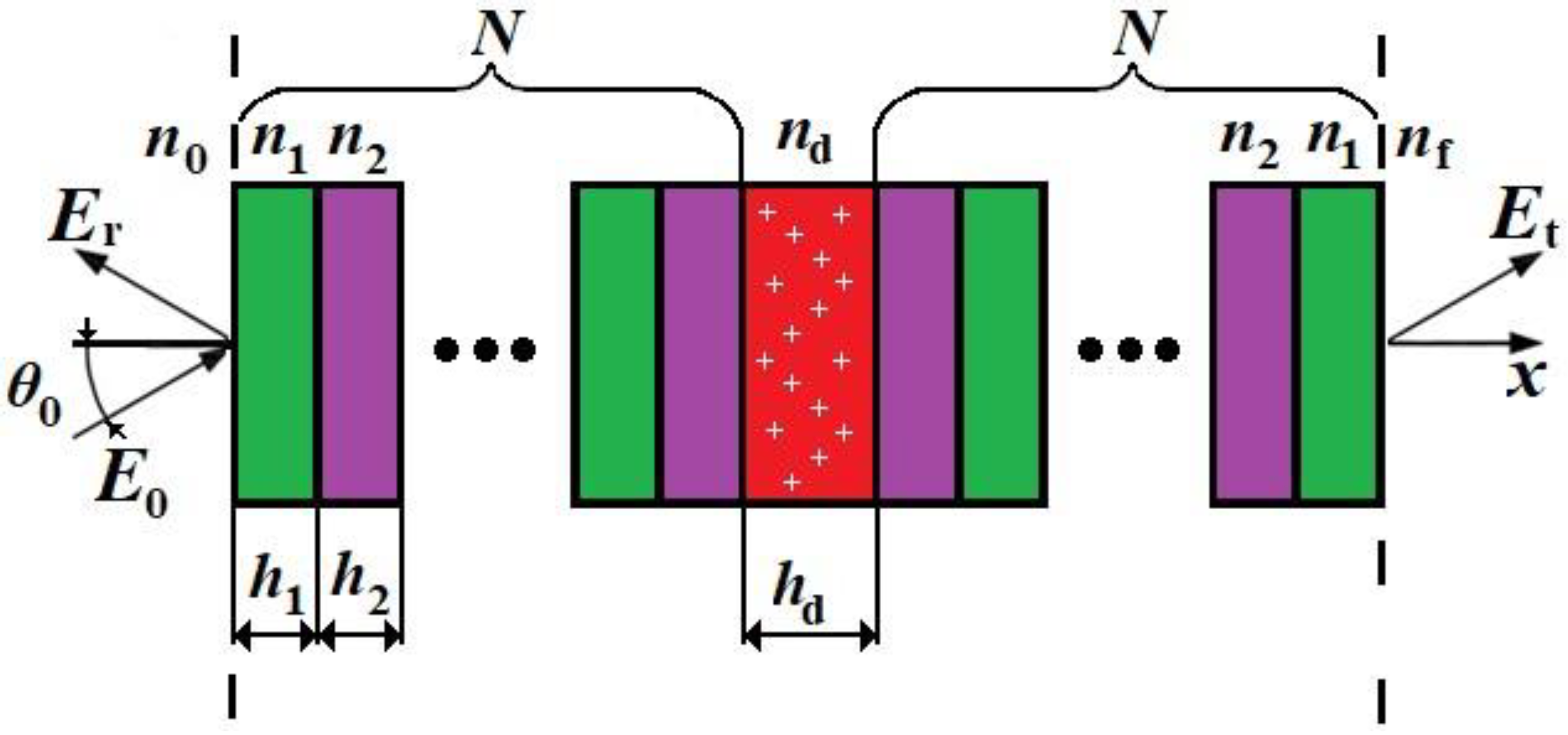
2.1. Model of the Refractive Index Sensor
2.2. Principal Operating Mechanism of the Sensor
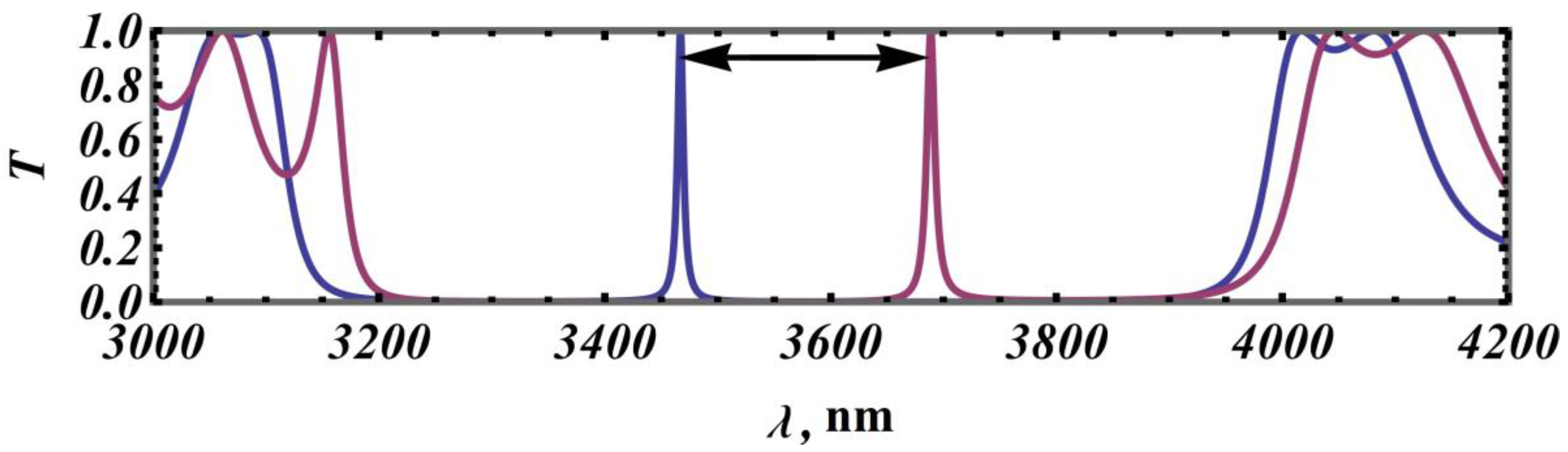
2.3. Absolute and Relative Sensitivities
2.4. Optical Sensor Resolution
3. Results and Discussion
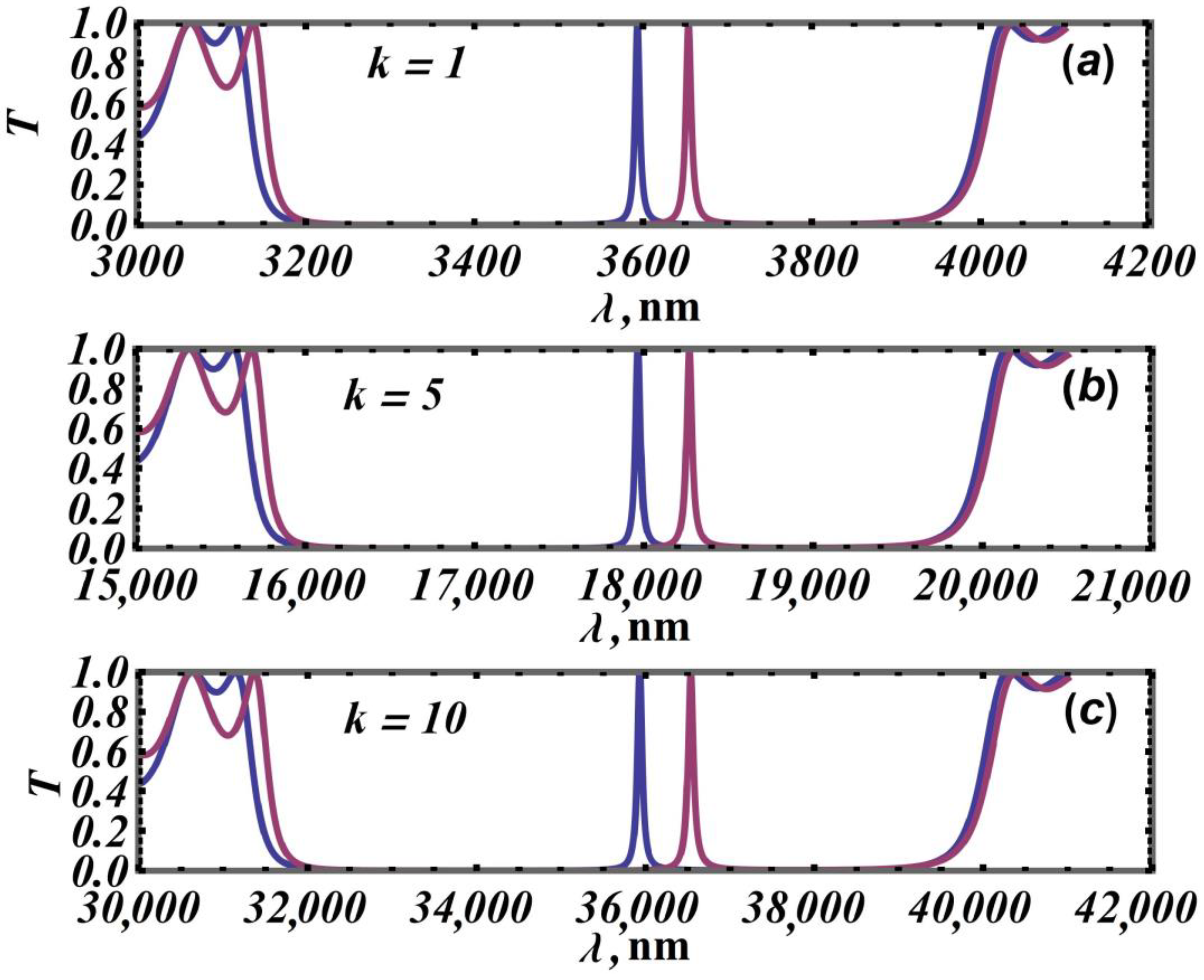
3.1. Comparing Absolute to Relative Sensitivity
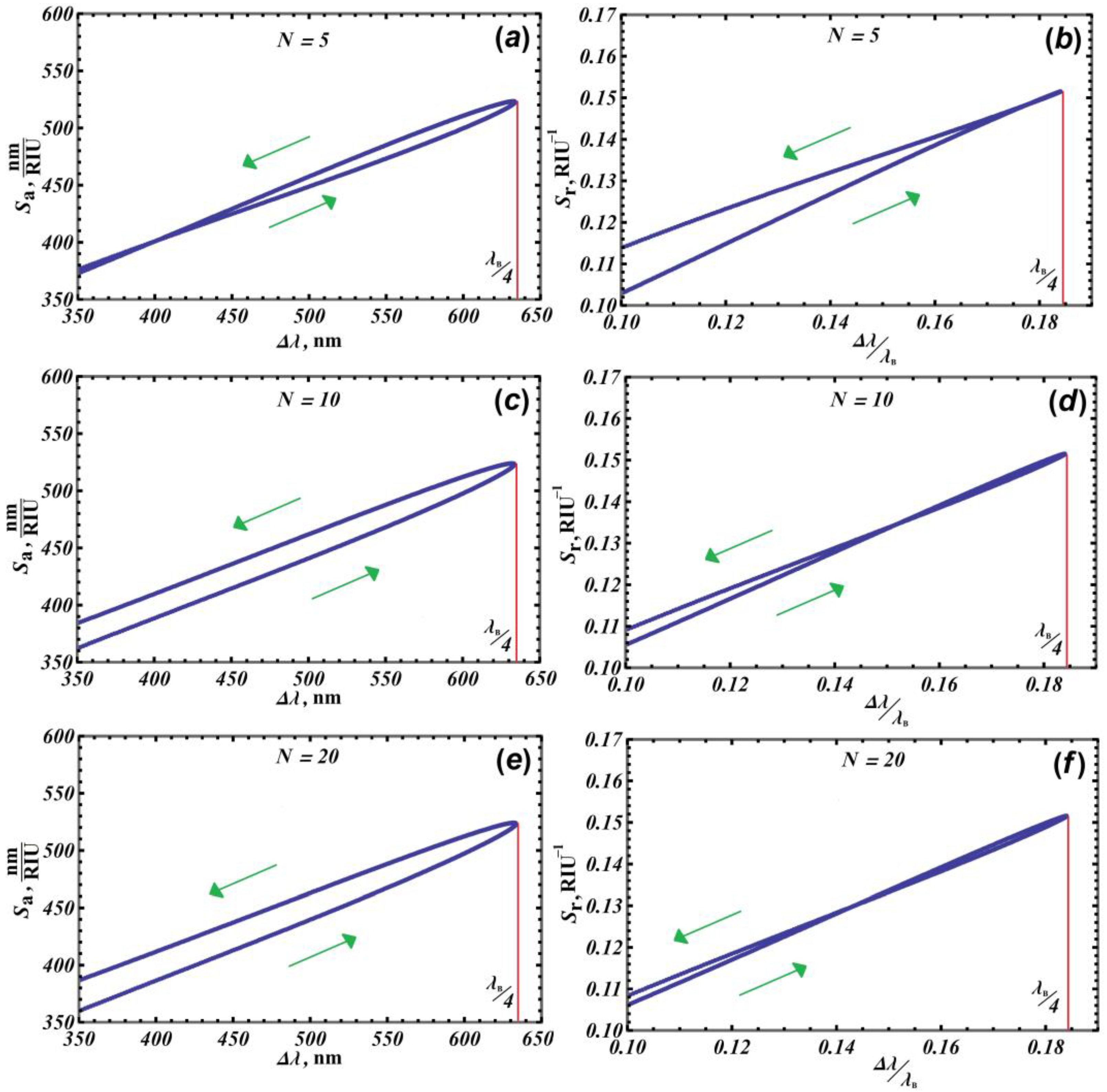
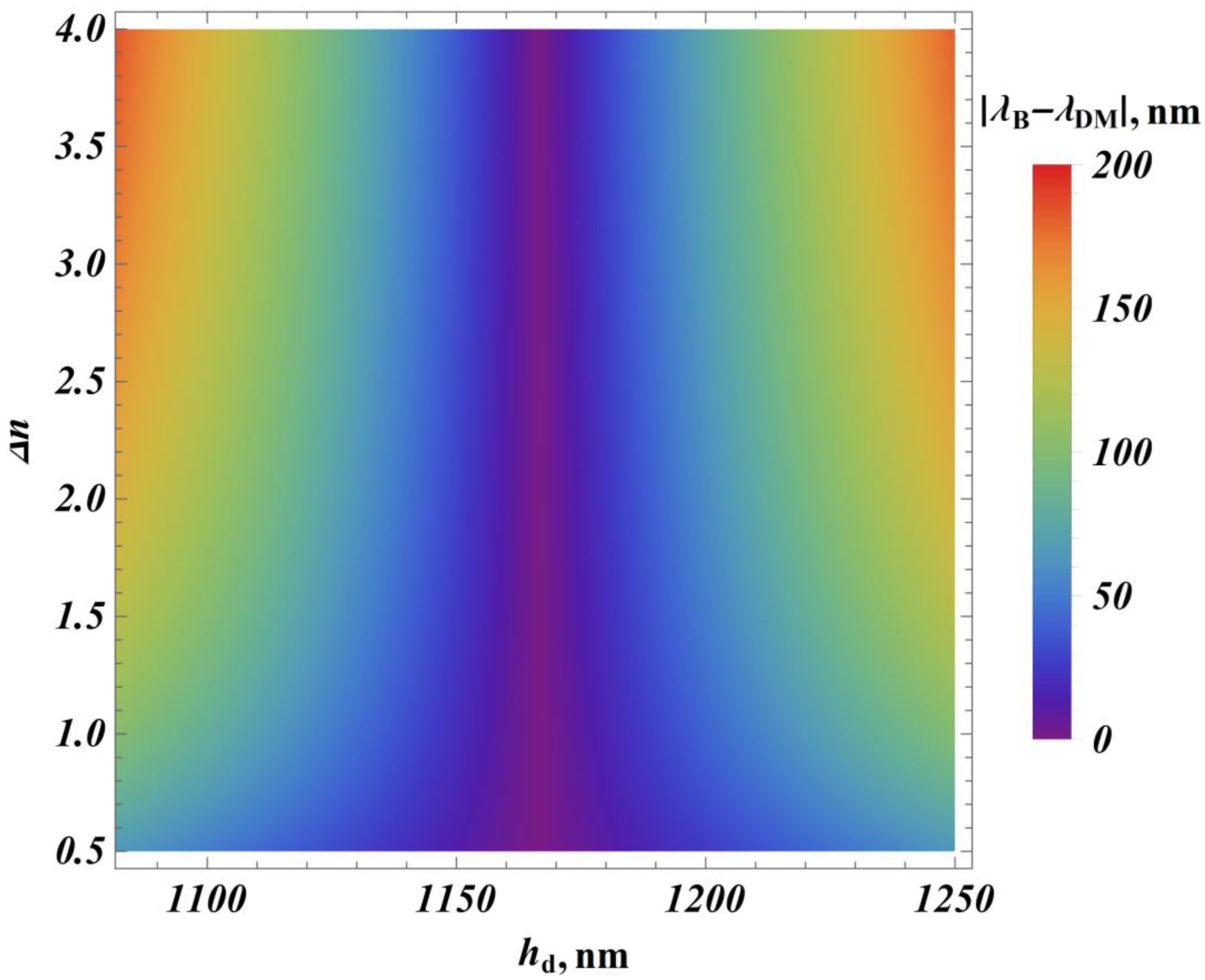
3.2. Convenient Parameters for Optimizing the Sensitivity of a Sensor Based on 1D PCs with Defects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santos, J.L.; Faramarz, F. Handbook of Optical Sensors; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ferreira, M.F.; Castro-Camus, E.; Ottaway, D.J.; López-Higuera, J.M.; Feng, X.; Jin, W.; Jeong, Y.; Picqué, N.; Tong, L.; Reinhard, B.M.; et al. Roadmap on optical sensors. J. Opt. 2017, 19, 083001. [Google Scholar] [CrossRef] [PubMed]
- Tong, L. Micro/nanofibre optical sensors: Challenges and prospects. Sensors 2018, 18, 903. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.D. A review of recent developments in fiber optic sensor technology. Opt. Fiber Technol. 1996, 2, 291–317. [Google Scholar] [CrossRef]
- Grattan, K.T.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Ma, S.; Xu, Y.; Pang, Y.; Zhao, X.; Li, Y.; Qin, Z.; Liu, Z.; Lu, P.; Bao, X. Optical Fiber Sensors for High-Temperature Monitoring: A Review. Sensors 2022, 22, 5722. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, G.; Kumar, S.; Marques, C.; Min, R.; Li, X. Recent advancements in resonant fiber optic gyro—A review. IEEE Sens. J. 2022, 22, 3195502. [Google Scholar] [CrossRef]
- Chai, H.; Zheng, Z.; Liu, K.; Xu, J.; Wu, K.; Luo, Y.; Liao, H.; Debliquy, M.; Zhang, C. Stability of metal oxide semiconductor gas sensors: A review. IEEE Sens. J. 2022, 22, 5470–5481. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tu, L.; Zhang, T.; Wang, L. A review of building detection from very high resolution optical remote sensing images. GISci. Remote Sens. 2022, 59, 1199–1225. [Google Scholar] [CrossRef]
- Jayawickrema, U.M.N.; Herath, H.M.; Hettiarachchi, N.K.; Sooriyaarachchi, H.P.; Epaarachchi, J.A. Fibre-optic sensor and deep learning-based structural health monitoring systems for civil structures: A review. Measurement 2022, 199, 111543. [Google Scholar] [CrossRef]
- Efimov, I.M.; Vanyushkin, N.A.; Gevorgyan, A.H.; Golik, S.S. Optical biosensor based on a photonic crystal with a defective layer designed to determine the concentration of SARS-CoV-2 in water. Phys. Scr. 2022, 97, 055506. [Google Scholar] [CrossRef]
- Luan, E.; Shoman, H.; Ratner, D.M.; Cheung, K.C.; Chrostowski, L. Silicon Photonic Biosensors Using Label-Free Detection. Sensors 2018, 18, 3519. [Google Scholar] [CrossRef] [PubMed]
- Dutta, H.S.; Goyal, A.K.; Srivastava, V.; Pal, S. Coupling light in photonic crystal waveguides: A review. Photonics Nanostruct. Fundam. Appl. 2016, 20, 41–58. [Google Scholar] [CrossRef]
- Dutta, H.S.; Suchandan, P. Design of a highly sensitive photonic crystal waveguide platform for refractive index based biosensing. Opt. Quantum Electron. 2013, 45, 907–917. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Ahmed, M. Ultra-high sensitive 1D porous silicon photonic crystal sensor based on the coupling of Tamm/Fano resonances in the mid-infrared region. Sci. Rep. 2019, 9, 6973. [Google Scholar] [CrossRef] [PubMed]
- Abdol, S.O.; Babak, A. Novel biosensors based on Weyl semimetals. Phys. Scr. 2022, 97, 125502. [Google Scholar] [CrossRef]
- El Beheiry, M.; Liu, V.; Fan, S.; Levi, O. Sensitivity enhancement in photonic crystal slab biosensors. Opt. Express 2010, 18, 22702–22714. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Fan, C.; Zhu, K.; Wu, J.; Qi, X.; Sun, Y.; Xiao, S.; Jiang, H.; Chen, H. Tailoring electromagnetic responses in a coupled-grating system with combined modulation of near-field and far-field couplings. Phys. Rev. B 2022, 105, 245417. [Google Scholar] [CrossRef]
- Bijalwan, A.; Bipin, K.S. Analysis of one-dimensional photonic crystal based sensor for detection of blood plasma and cancer cells. Optik 2021, 226, 165994. [Google Scholar] [CrossRef]
- Dinodiya, S.; Anami, B. Biosensor Based on One-Dimensional Photonic Crystal for Poliovirus Detection. In Advancement in Materials, Manufacturing and Energy Engineering; Springer Nature: Berlin, Germany, 2021; Volume 1. [Google Scholar]
- Miyan, H.; Agrahari, R.; Gowre, S.K.; Mahto, M.; Jain, P.K. Computational study of a compact and high sensitive photonic crystal for cancer cells detection. IEEE Sens. J. 2022, 22, 3298–3305. [Google Scholar] [CrossRef]
- Oskoui, A.; Shojaei, S.S.; Abdollahipour, B. Polarization dependent light propagation in WTe 2 multilayer structure. Sci. Rep. 2023, 13, 13169. [Google Scholar] [CrossRef]
- Suthar, B.; Anami, B. Enhanced optical sensor for waterborne bacteria-based photonic crystal using graded thickness index. Appl. Nanosci. 2023, 13, 5399–5406. [Google Scholar] [CrossRef]
- Olyaee, S.; Samira, N. A high-quality factor and wide measurement range biosensor based on photonic crystal nanocavity resonator. Sens. Lett. 2013, 11, 483–488. [Google Scholar] [CrossRef]
- Efimov, I.M.; Vanyushkin, N.A.; Golik, S.S.; Gevorgyan, A.H. Sensor with enhanced performance based on photonic crystal with a defect layer. Comput. Opt. 2023, 47, 572–579. [Google Scholar] [CrossRef]
- Efimov, I.M.; Vanyushkin, N.A.; Gevorgyan, A.H. Peculiarities of the Electromagnetic Field Distribution Inside a 1D Photonic Crystal with a Defect Layer. Bull. Russ. Acad. Sci. Phys. 2022, 86 (Suppl. S1), S60–S65. [Google Scholar] [CrossRef]
- Al-Dossari, M.; Awasthi, S.K.; Mohamed, A.M.; Abd El-Gawaad, N.S.; Sabra, W.; Aly, A.H. Bio-alcohol sensor based on one-dimensional photonic crystals for detection of organic materials in wastewater. Materials 2022, 15, 4012. [Google Scholar] [CrossRef] [PubMed]
- Edappadikkunnummal, S.; Chembra Vasudevan, R.; Dinesh, S.; Thomas, S.; Desai, N.R.; Kaniyarakkal, S. Detection of Hemoglobin Concentration Based on Defective One-Dimensional Photonic Crystals. Photonics 2022, 9, 660. [Google Scholar] [CrossRef]
- Hu, J.; Daoxin, D. Cascaded-ring optical sensor with enhanced sensitivity by using suspended Si-nanowires. IEEE Photonics Technol. Lett. 2011, 23, 842–844. [Google Scholar]
- Baraket, Z.; Osswa, S.; Mounir, K. Design of magnetic field direction’s sensor based on a 1D tunable magneto-photonic crystal. Opt. Quantum Electron. 2022, 54, 637. [Google Scholar] [CrossRef]
- Daher, M.G.; Jaroszewicz, Z.; Zyoud, S.H.; Panda, A.; Hasane Ahammad, S.K.; Abd-Elnaby, M.; Eid, M.M.; Rashed, A.N. Design of a novel detector based on photonic crystal nanostructure for ultra-high performance detection of cells with diabetes. Opt. Quantum Electron. 2022, 54, 701. [Google Scholar] [CrossRef]
- Almawgani, A.H.; Daher, M.G.; Taya, S.A.; Mashagbeh, M.; Colak, I. Optical detection of fat concentration in milk using MXene-based surface plasmon resonance structure. Biosensors 2022, 12, 535. [Google Scholar] [CrossRef]
- Yupapin, P.; Trabelsi, Y.; Vigneswaran, D.; Taya, S.A.; Daher, M.G.; Colak, I. Ultra-high-sensitive sensor based on surface plasmon resonance structure having Si and graphene layers for the detection of chikungunya virus. Plasmonics 2022, 17, 1315–1321. [Google Scholar] [CrossRef]
- Almawgani, A.H.; Daher, M.G.; Taya, S.A.; Colak, I.; Patel, S.K.; Ramahi, O.M. Highly sensitive nano-biosensor based on a binary photonic crystal for cancer cell detection. Opt. Quantum Electron. 2022, 54, 554. [Google Scholar] [CrossRef]
- Taya, S.A.; Daher, M.G.; Colak, I.; Ramahi, O.M. Highly sensitive nano-sensor based on a binary photonic crystal for the detection of mycobacterium tuberculosis bacteria. J. Mater. Sci. Mater. Electron. 2021, 32, 28406–28416. [Google Scholar] [CrossRef]
- Panda, A.; Pukhrambam, P.D.; Wu, F.; Belhadj, W. Graphene-based 1D defective photonic crystal biosensor for real-time detection of cancer cells. Eur. Phys. J. Plus 2021, 136, 809. [Google Scholar] [CrossRef]
- Khani, S.; Hayati, M. Optical biosensors using plasmonic and photonic crystal band-gap structures for the detection of basal cell cancer. Sci. Rep. 2022, 12, 5246. [Google Scholar] [CrossRef] [PubMed]
- Winn, J.; Fink, Y.; Fan, S.; Joannopoulos, J.D. Omnidirectional reflection from a one-dimensional photonic crystal. Opt. Lett. 1998, 23, 1573–1575. [Google Scholar] [CrossRef] [PubMed]
- Vinogradov, A.; Dorofeenko, A.V.; Erokhin, S.G.; Inoue, M.; Lisyansky, A.A.; Merzlikin, A.M.; Granovsky, A.B. Surface state peculiarities in one-dimensional photonic crystal interfaces. Phys. Rev. B 2006, 74, 045128. [Google Scholar] [CrossRef]
- Wu, F.; Lu, G.; Guo, Z.; Jiang, H.; Xue, C.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Redshift gaps in one-dimensional photonic crystals containing hyperbolic metamaterials. Phys. Rev. Appl. 2018, 10, 064022. [Google Scholar] [CrossRef]
- Wu, F.; Liu, T.; Xiao, S. Polarization-sensitive photonic bandgaps in hybrid one-dimensional photonic crystals composed of all-dielectric elliptical metamaterials and isotropic dielectrics. Appl. Opt. 2023, 62, 706–713. [Google Scholar] [CrossRef]
- Joannopoulos, J.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995; 305p. [Google Scholar]
- Yeh, P. Optical Waves in Layered Media; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Vanyushkin, N.A.; Gevorgyan, A.H.; Golik, S.S. Scattering of a plane wave by an inhomogeneous 1D dielectric layer with gradient refractive index. Opt. Mater. 2022, 127, 112306. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef]
- Yao, J. Optoelectronic oscillators for high speed and high-resolution optical sensing. J. Light. Technol. 2017, 35, 3489–3497. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface micro/nano-optical sensors: Principles and applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef]
- Van de Velde, F.; Knutsen, S.H.; Usov, A.I.; Rollema, H.S.; Cerezo, A.S. 1H and 13C high resolution NMR spectroscopy of carrageenans: Application in research and industry. Trends Food Sci. Technol. 2002, 13, 73–92. [Google Scholar] [CrossRef]
- Wang, K.; Vincent, M. High-resolution photoelectron spectroscopy of molecules. Annu. Rev. Phys. Chem. 1995, 46, 275–304. [Google Scholar] [CrossRef][Green Version]
- Vanyushkin, N.A.; Gevorgyan, A.H.; Golik, S.S. Approximation of one-dimensional rugate photonic crystals using symmetric ternary photonic crystals. Optik 2021, 242, 167343. [Google Scholar] [CrossRef]

| Article | |||
|---|---|---|---|
| 1020 | 5293 | 0.1927 | [11] |
| 80 | 5295 | 0.0151 | |
| 347 | 1004 | 0.3456 | |
| 710 | 2026 | 0.3504 | |
| 260 | 1560 | 0.1667 | [14] |
| 197 | 1600 | 0.1231 | |
| 198 | 1620 | 0.1222 | |
| 173 | 1640 | 0.1055 | |
| 80 | 1800 | 0.0444 | |
| 5018 | 7299 | 0.6875 | [15] |
| 5092 | 7299 | 0.6977 | |
| 5031 | 7293 | 0.6899 | |
| 5013 | 7335 | 0.6834 | |
| 500 | 523 | 0.9560 | [27] |
| 496 | 533 | 0.9316 | |
| 490 | 541 | 0.9058 | |
| 487 | 547 | 0.8897 | |
| 475 | 557 | 0.8520 | |
| 454 | 577 | 0.7875 | |
| 405 | 611 | 0.6639 | |
| 145 | 764 | 0.1891 | [28] |
| 144 | 766 | 0.1881 | |
| 144 | 769 | 0.1879 | |
| 144 | 773 | 0.1863 | |
| 1300 | 1530 | 0.8497 | [29] |
| 515 | 1550 | 0.3322 |
| , nm | |||
|---|---|---|---|
| 1 | 3500 | 440.33 | 0.1258074 |
| 2 | 7000 | 880.65 | |
| 3 | 10,500 | 1320.98 | |
| 4 | 14,000 | 1761.30 | |
| 5 | 17,500 | 2201.63 | |
| 10 | 35,000 | 4403.26 |
| 1 | 440.33 | 680.83 | 0.1258074 | 3.5 | 0.002 |
| 2 | 880.65 | 340.42 | 7.0 | ||
| 5 | 2201.63 | 136.17 | 17.5 | ||
| 10 | 4403.26 | 68.08 | 35.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efimov, I.M.; Vanyushkin, N.A.; Gevorgyan, A.H. The Determination of the Sensitivity of Refractive Index Sensors. Photonics 2024, 11, 56. https://doi.org/10.3390/photonics11010056
Efimov IM, Vanyushkin NA, Gevorgyan AH. The Determination of the Sensitivity of Refractive Index Sensors. Photonics. 2024; 11(1):56. https://doi.org/10.3390/photonics11010056
Chicago/Turabian StyleEfimov, Ilya M., Nikolay A. Vanyushkin, and Ashot H. Gevorgyan. 2024. "The Determination of the Sensitivity of Refractive Index Sensors" Photonics 11, no. 1: 56. https://doi.org/10.3390/photonics11010056
APA StyleEfimov, I. M., Vanyushkin, N. A., & Gevorgyan, A. H. (2024). The Determination of the Sensitivity of Refractive Index Sensors. Photonics, 11(1), 56. https://doi.org/10.3390/photonics11010056





