Abstract
The great success of artificial intelligence (AI) calls for higher-performance computing accelerators, and optical neural networks (ONNs) with the advantages of high speed and low power consumption have become competitive candidates. However, most of the reported ONN architectures have demonstrated simple MNIST handwritten digit classification tasks due to relatively low precision. A microring resonator (MRR) weight bank can achieve a high-precision weight matrix and can increase computing density with the assistance of wavelength division multiplexing (WDM) technology offered by dissipative Kerr soliton (DKS) microcomb sources. Here, we implement a car plate recognition task based on an optical convolutional neural network (CNN). An integrated DKS microcomb was used to drive an MRR weight-bank-based photonic processor, and the computing precision of one optical convolution operation could reach 7 bits. The first convolutional layer was realized in the optical domain, and the remaining layers were performed in the electrical domain. Totally, the optoelectronic computing system (OCS) could achieve a comparable performance with a 64-bit digital computer for character classification. The error distribution obtained from the experiment was used to emulate the optical convolution operation of other layers. The probabilities of the softmax layer were slightly degraded, and the robustness of the CNN was reduced, but the recognition results were still acceptable. This work explores an MRR weight-bank-based OCS driven by a soliton microcomb to realize a real-life neural network task for the first time and provides a promising computational acceleration scheme for complex AI tasks.
1. Introduction
In recent years, the rapid development of artificial intelligence (AI) has achieved remarkable success [1,2] and has brought automatic driving, face recognition, and medical diagnosis into reality [3,4,5,6]. In order to meet the strict requirements of practical applications such as autonomous driving, a system needs to have faster response speeds to make robust decisions and lower power consumption to provide longer battery life [7]. Currently, traditional electronic chips still dominate the computing field, such as graphics processing units (GPUs), application-specific integrated circuits (ASICs), neural network processing units (NPUs), and so on [8,9,10]. However, Moore’s Law is facing failure [11], and the transistor size of electronic chips is approaching the physical limit. Improving chip integration and performance through semiconductor technology is still difficult to meet the growing computing needs.
Light has the inherent nature of low power consumption, low latency, large bandwidth, and high parallelism [12]. The modulation rate of a silicon photonic integrated circuit is several times higher than the clock frequency of an electronic processor, which can significantly improve computing speed. Furthermore, silicon photonic technology is compatible with existing standard complementary metal oxide semiconductor (CMOS) manufacturing, which makes optical neural networks (ONNs) on silicon very competitive and promising accelerator candidates in the post-Moore era [13]. However, since neural network layers are connected by synaptic weights, errors accumulate when noisy signals propagate from one layer to the next, and the computing precision determines the scale of a deep neural network [14,15]. Recently, ONNs have made significant progress in high computing speed, high computing power, and large-scale integration [16,17,18,19,20,21,22], but the precision of most of them is typically about 5 bits, which restricts their application to only simple MNIST handwritten digit classification tasks [23,24,25] and others like these. Therefore, ONNs still face challenges in handling advanced AI applications, such as real-life computer vision tasks.
MRR arrays based on “broadcast-and-weight” architectures can generate a real-valued matrix [21,26] and have been proved to perform multiply-accumulation calculations more efficiently than traditional electronics [27,28,29]. Compared with the Mach–Zehnder interferometer (MZI) mesh and diffractive neural network, whose precision is susceptible to fabrication error [30,31,32,33,34,35], an MRR weight bank can achieve higher computing precision. MRR synapse was recently reported to achieve a 9-bit precision [15], which heralds it potential to handle advanced AI tasks. In addition, MRR weight banks have the merit to improve parallel information-processing capability through wavelength division multiplexing technology [21]. Recently, an optoelectronic computing system (OCS) based on wavelength division multiplexing has successfully demonstrated parallel optical convolution operations using Kerr microcombs that generate equidistant optical frequency lines as the multiwavelength source [21,36]. Therefore, using an optical frequency comb to drive an MRR weight-bank-based OCS is expected to greatly improve computing density.
On the other hand, convolutional neural networks (CNNs) inspired by the biological visual cortex system have a strong ability to extract features and are widely used in image recognition, language processing, and other fields [37,38]. Car plate recognition is an important part of autonomous driving, and it should have higher prediction accuracy and robustness using a CNN [39,40].
Here, combining the advantages of a microcomb-driven MRR array and CNNs, we propose and experimentally demonstrate a microcomb-driven optical convolution scheme to realize Chinese car plate recognition. An integrated Kerr soliton microcomb drives an MRR weight-bank-based photonic processor to perform convolution operations, and the computing precision of one optical convolution operation reaches 7 bits. Experimentally, the mathematical operation of the first convolutional layer is realized through optical convolution, and other operations are performed in the electrical domain. We experimentally tested 10 car plates, and the recognition results of the OCS are highly consistent with those of 64-bit computers. Even when the statistical error of the optical convolution is counted into the rest of the convolution layers for 10 car plate samples, the classification results of the softmax layer are acceptable with tiny degradation. This manifests an essential step forward in promoting optical computing for complex real-life tasks.
2. Principle and Device Design
Figure 1 schematically illustrates the principle of car plate recognition using optical convolution kernels. Figure 1a depicts a simplified model structure diagram of the CNN employed in our experiments. It included two convolutional layers, one pooling layer, and two fully connected layers. The input image was a matrix with a size of 18 18. The two convolutional layers had 16 and 72 convolution kernels, respectively, and the size of these convolution kernels was 3 3. Followed by the downsampling pooling layer were the fully connected layer and the output layer. The output layer had 34 neurons, which were the basis of the classification results of the car plate characters. The first convolutional layer marked by the red box was implemented in the optical domain. In order to convert the convolution into matrix-vector multiplication, the input image data needed to be specifically encoded. The encoding rules are shown in Figure 1b. We took out all three columns of data corresponding to the convolution window (it can be seen as the convolution window sliding down), then slid one stride horizontally to the next position, took out the data in the same way, and stacked them behind the data taken out in the previous step, repeating the above steps until the last sliding position. This rule adapted to the computing method of the matrix kernel and improved the data utilization efficiency. The image data were encoded as input vectors and loaded to a modulator, the weight matrix of the convolution kernel was loaded to an MRR weight bank as a matrix kernel, and the multiplication results detected with a balanced photodetector (BPD) were reconstructed as an output feature map of the convolution layer. The reconstruction rule of the convolution result was to sum all the elements in the k-th diagonal of the matrix multiplication result as the convolution result, whose index was the (k + 1)-th row of each column (the main diagonal of k = 0). The reconstruction rule could be expressed as follows:
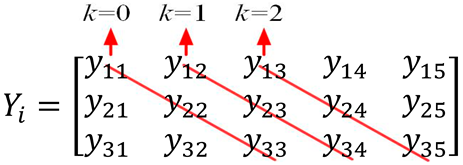 where is the matrix product corresponding to the i-th column of the convolution results. Figure 1c shows a schematic diagram of the experimental setup for convolution operation in a real-valued domain, which mainly included three parts: optical frequency comb generation, data loading control, and optical power detection. An on-chip microcomb pumped with a continuous-wave tunable laser served as the multichannel optical source. Combs matched with the microring resonant peak were regrouped with a wavelength division demultiplexer, and the modulated comb lines flowed to the MRR weight bank through the wavelength division multiplexer. A customed field-programmable gate array (FPGA) transformed the input vector and matrix weights into voltages applied to an intensity modulator and MRR array via a digital-to-analog conversion circuit, which could achieve programmable voltages with 16-bit resolution to manipulate the precise movement of the microring spectrum. The differential optical power of the through port (THRU) and drop port (DROP) of the MRR weight bank was detected using the BPD, and the electrical signal was transmitted to the FPGA for weight evaluation.
where is the matrix product corresponding to the i-th column of the convolution results. Figure 1c shows a schematic diagram of the experimental setup for convolution operation in a real-valued domain, which mainly included three parts: optical frequency comb generation, data loading control, and optical power detection. An on-chip microcomb pumped with a continuous-wave tunable laser served as the multichannel optical source. Combs matched with the microring resonant peak were regrouped with a wavelength division demultiplexer, and the modulated comb lines flowed to the MRR weight bank through the wavelength division multiplexer. A customed field-programmable gate array (FPGA) transformed the input vector and matrix weights into voltages applied to an intensity modulator and MRR array via a digital-to-analog conversion circuit, which could achieve programmable voltages with 16-bit resolution to manipulate the precise movement of the microring spectrum. The differential optical power of the through port (THRU) and drop port (DROP) of the MRR weight bank was detected using the BPD, and the electrical signal was transmitted to the FPGA for weight evaluation.

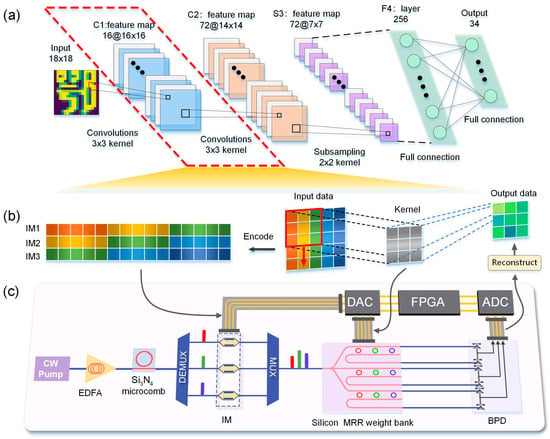
Figure 1.
Schematic of the principle of car plate recognition using optical convolution kernels. (a) Simplified model structure diagram of the CNN employed in our experiments. (b) Encoding rules of the input image and a sketch of the convolution principle. (c) Conceptual schematic of the experimental setup for the convolution operation. A DKS microcomb served as the multiwavelength source and was pumped using a continuous-wave (CW) laser.
To generate a dissipative Kerr soliton (DKS) microcomb that could offer hundreds of equally spaced frequency lines, an integrated MRR with a free spectral range (FSR) of 100 GHz and a loaded Q-factor of above 5 was utilized, as shown in the upper part of Figure 2a. The generation of the DKS was based on the dual balance between Kerr nonlinearity and cavity dispersion, as well as parametric gain and loss [41,42]. A continuous-wave tunable laser was used to generate pump light, which was amplified with an erbium-doped fiber amplifier and then launched into a silicon nitride MRR. The auxiliary-laser-heating approach was adopted. Firstly, the auxiliary light launched from the opposite direction was frequency-tuned to the blue-detuned region close to the resonance peak. Subsequently, the wavelength of the pump light was scanned to keep the cavity in thermal equilibrium, the pump light smoothly entered the red-detuned regime from the blue-detuned regime, and the Kerr microcomb evolved from a chaotic state to a dissipative soliton state. Finally, by fine tuning the wavelength of the pump light, a stable single-soliton frequency comb with a smooth envelope was generated. Figure 2c shows the optical spectrum of a single DKS microcomb with a spacing of 100 GHz.
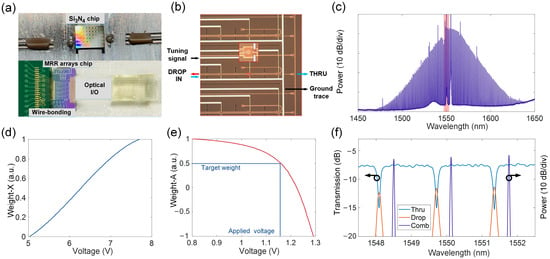
Figure 2.
Characterization results of MRR weight bank and Kerr microcomb. (a) Upper: picture of the packaged microcomb chip. Lower: photo of the packaged MRR array chip with periphery circuits. (b) Micrograph of the microring weight bank and detailed zoom-in micrograph of an individual microring. (c) Measured spectrum of a single DKS comb state with 100-GHz spacing. (d,e) are the optical responses of the modulator and microring to the voltage. (f) Measured optical spectrum of one row of microrings at the THRU and DROP ports and 3 comb lines selected from a single-soliton frequency comb.
The lower part of Figure 2a shows a packaged MRR array chip and peripheral circuits. The device was fabricated on a silicon-on-insulator (SOI) wafer with 220 nm of top silicon and 2 μm of buried oxide substrate. Both wirebonding and vertical grating coupling were already packaged for electrical and optical input/output (I/O). A thermo-electric cooler (TEC) was equipped below the integrated MRR weight bank to keep the environmental temperature stable. A micrograph of the MRR weight bank and the detailed zoom-in micrograph of an individual MRR are shown in Figure 2b. The weight bank consisted of 9 MRRs in an add/drop configuration in which the radius of the rings in each row was designed to be gradually varied to avoid resonance peak collision. To precisely control kernel weight, thermo-optic phase shifters made of TiN heaters were implemented to tune the resonances of the MRRs. For the 3 3 MRR weight bank, three comb lines were used in the experiment, corresponding to the resonant peaks in the spectrum. The resonant peaks of one row of MRRs and the selected comb lines measured using an optical spectrum analyzer (OSA) are shown in Figure 2f. The MRRs could be independently configured by employing thermal isolation trenches between each microring of the MRR arrays to minimize the thermal cross-talk. To realize the matrix multiplication operation, it was necessary to obtain the precise response of the system to the voltage, which consisted of two steps: first, establishing the mapping lookup table between the modulator voltage and the input vector; and second, building the mapping lookup table between the MRR voltage and the kernel weight. The three channels were opened independently in turn, and a modulator voltage sweep program applied to a high-precision voltage source was developed and implemented to achieve calibration of the input vector. As the voltage increased within an appropriate range, the input vector could be normalized to an interval [0, 1], as shown in Figure 2d. Then, a normalized one-valued voltage was applied to the modulator to fix the power of the input light, and the voltage of each MRR was scanned to achieve the calibration of the kernel weight so that the optical power difference between the through port and the drop port could be normalized to an interval [–1, 1]. The MRR weight–voltage (W–V) lookup table is shown in Figure 2e.
3. Results
We successfully implemented car plate recognition using an OCS based on a silicon MRR weight bank driven by DKS microcombs, and the optical recognition results of seven characters per car plate were comparable to those of a 64-bit computer. On the basis of the characteristics of Chinese license plate characters, the first character, the second character, and the remaining five characters of a car plate need to be divided into three categories. The datasets of these three categories were a dataset containing 31 Chinese characters, a dataset containing 26 letters, and a dataset containing 24 letters (excluding I and O) with 10 numbers. The entire dataset was split into training (24,000 pictures) and testing sets (6000 pictures). The groups of weight data were trained using the same CNN model for three categories of characters. The CNN used in our experiments was pretrained using a computer to obtain the weight data of each layer of neurons. In the inference process, the first convolutional layer was implemented in the optical domain, and the feature map obtained from the experiment was sent to other subsequent layers executed in the electrical domain. The MRR performed the linear part of the convolutional layer, and the nonlinear activation function processing was performed using the computer. Taking into account the characteristics of the hardware, the convolution operation was transformed into third-order matrix-vector multiplication with specific encoding rules. The gray-scale values of the character pictures were normalized as the input vector datastream and loaded to the intensity modulator, and the weights of 16 convolution kernels were extracted as matrix kernels and matched to the MRR weight bank. Then, the optical convolution results were sent to the computer after being received by the BPD. It can be seen that there was almost no difference between the optical feature map obtained through the experiment and the feature map obtained using the digital computer (see Figure 3a,b). However, since it was analog computing, in fact, there were small errors between the experimentally obtained feature map and the computer feature map, and the error distribution of each pixel position of the feature map is presented in Figure 3c.
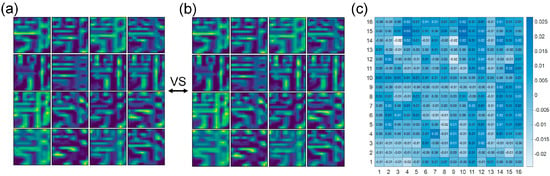
Figure 3.
Comparison between the optical feature map and the electrical feature map. (a) and (b) are the 16 feature maps obtained using optical convolution and digital computer, respectively. (c) The error distribution of each pixel position between the electrical feature map and optical feature map.
To quantify the statistical distribution of computing errors, we performed a statistical analysis on the errors of the 16 feature maps. Figure 4a exhibits the computing precision of the convolutional layer, where the horizontal axis is the theoretical calculation value, and the vertical axis is the experimental measurement value. The bit precision was estimated using the standard deviation of the computing error and then converted to the expression of bit precision with a revised equation from Ref. [15]:
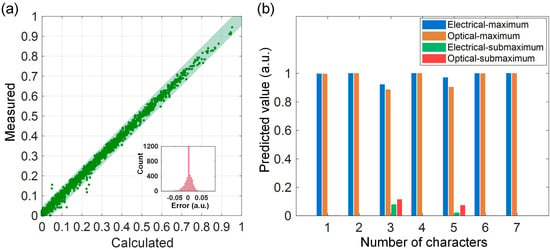
Figure 4.
Experimental error analysis. (a) Quantitative statistical analysis of computing error. The scatter plot shows a 7-bit precision. (b) Comparison of the maximum and submaximum probabilities of the softmax layer for optical computing and electrical computing.
We observed that the sample scatter points were tightly concentrated on the diagonal and distributed in the light green area, which indicates a 7-bit computing precision (the closer the sample scatter points were distributed along the diagonal, the higher the computing precision). The pink inset graph shows the frequency histogram of the error. In order to explore the impact of computing error on character classification results, we compared the per-category probabilities of the softmax output layer inferred from the experimental data with the theoretical calculated results. The softmax layer contained 34 classification outputs, among which the output of the maximum probability category was almost absolutely dominant compared with other outputs. Therefore, we only extracted the maximum and submaximum outputs among the 34 outputs. These two could already represent all the useful information of the classification results when the classification was correct. Figure 4b shows the classification probabilities of seven pictures of the first car plate in Figure 5a, in which the blue and green bars are the maximum and submaximum probabilities of the corresponding classification output of the electronically calculated softmax layer, while the orange and red bars are the counterparts obtained with optical computing. The comparison results show that the maximum value of the optical computing was basically close to that of the electrical computing, which indicates that the error induced by the optical convolution of the first convolutional layer did not cause classification errors. In fact, this error only had a slight impact on a few pictures whose maximum values and submaximum values of the softmax layer were in the same order of magnitude in theoretical calculation but had no effect on pictures whose maximum values were close to one and whose submaximum values were several orders of magnitude smaller or even negligible.
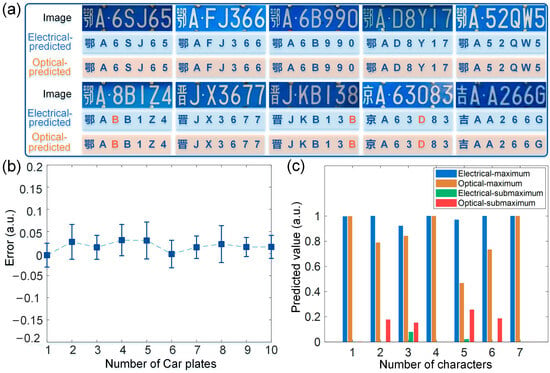
Figure 5.
Experimental results of 10 Chinese car plates and simulation of optical convolution. (a) Computer recognition results of 10 Chinese car plates and corresponding optical convolution inference results. (b) The statistical distribution of computing errors for 10 car plates. (c) Comparison of the maximum and submaximum probabilities of the softmax layer after simulating the second convolutional layer calculated using a photonic processor with the theoretical maximum and submaximum probabilities.
In the experiment, we recognized 10 car plates in total, and the computer recognition results of these 10 car plates are shown in Figure 5a, corresponding to the light blue box. The CNN had a high correct rate, and only three characters marked in dark orange were misrecognized (note that the recognition accuracy of the electrical CNN model was above 95%). For these 10 car plate pictures, the classification results of the optical convolution in the light orange box were the same as those of the computer. Figure 5b shows the statistical distribution of computing errors for these 10 car plates, that is, the standard deviation and mean value of each car plate. The results indicate that the average computing errors of all the characters of each car plate were within the range of 0.05. The hundreds of thousands of sets of error data used during the experiment with the 10 car plates were statistically analyzed as a whole, and the average error of one convolution operation was calculated to be 0.016 with a standard deviation of 0.0342. To simulate the second convolutional layer calculated with the photonic CNN processor, we introduced the ideal Gaussian noise conforming to this error distribution into the forward-propagation calculation of the second convolutional layer so that the classification results of all the convolutional layers executed using optical convolution could be estimated. Figure 5c shows the comparison of the estimated maximum and submaximum probabilities with the ideal ones, and the analysis rules were consistent with the previous ones. It can be seen that the estimated classification results of the softmax layer were slightly degraded. The output of the maximum probability category decreased, and the probability of the second maximum increased significantly, which means that the errors introduced by the second layer reduced the robustness of the CNN, posing a potential risk of misclassification. Nevertheless, the classification results of most images were still correct, which illustrates that the classification result of all the convolutional layers executed using optical computing was acceptable. From the experimental and simulation results, we observed that the performance of the OCS was comparable to that of a 64-bit computer in computer vision tasks based on a CNN. This work verifies the feasibility of optical computing in practical applications and also shows that it has promising applications for other real-world, more complex AI tasks.
4. Discussion
In general, the computing precision of ONNs has rarely been considered compared to computing speed and energy consumption. Thanks to a 7-bit precision, we successfully verified a car plate recognition task using an MRR weight-bank-based OCS. Compared with previous simple MNIST dataset classification tasks, we took a big step toward practicality. In the future, the computing precision can be further improved by optimizing devices or employing more advanced techniques and, hopefully, implementing more complex neural network tasks in real-world scenarios. Since optical computing is analog computing, system noise is inevitable due to the actual values represented by the nonideal devices deviating from the ideal ones. In fact, the main factors that limit the further improvement of the computing precision in the OCS include the instability of the light source power, the poor consistency of the modulator, the cross-talk of the MRRs, the environment fluctuation, and the detection noise of the photodetector. Precise MRR control is still a challenge due to fabrication variance. The static resonance peaks of each MRR are not ideally distributed in the spectrum or even overlap, and a reference voltage needs to be applied to make it redshift to a suitable position. Despite the use of TEC temperature control and thermal isolation trenches, once the applied voltage is too high, thermal cross-talk still occurs. In order to precisely control an MRR, we can employ more advanced manufacturing processes, as well as optimize the design of photonic devices to reduce loss and obtain higher spectral uniformity. For other factors, we can minimize the error caused by system noise using more sophisticated experimental equipment.
Higher computing speed and computing density are the mainstream pursuits of optical computing. Assuming our OCS operates at a 100-GHz photodetection rate, the computation speed is approximately 0.9 TOPS. The system in this study still has great potential for improvement in terms of integration and computing speed. A superior integration technique provides a realistic basis for fully integrated systems [43]. One can integrate a modulator on the chip to reduce the footprint and improve the integration of a system. Thermo-optic modulators can be replaced by ultra-high-speed electro-optic integrated modulators on SOI platforms or thin-film lithium niobate platforms to greatly enhance computing speed [44,45]. Moreover, an MRR is rationally designed so that the next FSR resonance peak of the MRR can match the comb line of the Kerr microcomb, and an MRR weight bank can be upgraded to a tensor core with higher parallelism to further improve the computing density.
This work demonstrated that convergence of optics and electronics is required for an OCS to achieve more complex neural network tasks. Thanks to the recent significant progress in the hybrid integration of photonic chips and electronic circuits [46], it is expected that digital control circuits and silicon-based platform photonic devices will be monolithically integrated in the future. A monolithic system combines the high speed and large bandwidth of photonic computing with the flexibility of electronic computing and could constitute a high-performance OCS with more compactness and more energy efficiency to complete complex practical AI tasks, such as autonomous driving, medical diagnosis, and real-time video recognition [47].
5. Conclusions
In summary, we successfully demonstrated optical convolution-based car plate recognition using an MRR weight-bank-based photonic processor driven by an on-chip Kerr soliton microcomb source. The precision of one optical convolution operation reached 7 bits, and the car plate recognition results of the OCS were comparable to those of electronic computers. Using the error distribution obtained from a large amount of experimental data, the optical computing of subsequent convolutional layers with the same error was simulated, and the simulated classification results were also acceptable. This is the first time that car plate recognition, a complex, real-life application, has been realized with an optical CNN chip. Our work provides a feasible scheme with great potential for an MRR weight-bank-based OCS driven by a microcomb to realize complex neural network tasks.
Author Contributions
Conceptualization, Z.H. and J.C.; methodology, Z.H., J.C. and X.L.; resources, H.Z. and J.D.; data curation, Z.H.; writing—original draft preparation, Z.H. and B.W.; writing—review and editing, J.D.; supervision, X.Z.; funding acquisition, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Key Research and Development Project of China (2022YFB2804200), the National Natural Science Foundation of China (U21A20511), and the Innovation Project of Optics Valley Laboratory (Grant No. OVL2021BG001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, S.; Giles, C.L.; Ah Chung, T.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Ribeiro, A.H.; Ribeiro, M.H.; Paixão, G.M.M.; Oliveira, D.M.; Gomes, P.R.; Canazart, J.A.; Ferreira, M.P.S.; Andersson, C.R.; Macfarlane, P.W.; Meira, W., Jr.; et al. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat. Commun. 2020, 11, 1760. [Google Scholar] [CrossRef]
- Yuan, B.; Yang, D.; Rothberg, B.E.G.; Chang, H.; Xu, T. Unsupervised and supervised learning with neural network for human transcriptome analysis and cancer diagnosis. Sci. Rep. 2020, 10, 19106. [Google Scholar] [CrossRef]
- Wetzstein, G.; Ozcan, A.; Gigan, S.; Fan, S.; Englund, D.; Soljačić, M.; Denz, C.; Miller, D.A.B.; Psaltis, D. Inference in artificial intelligence with deep optics and photonics. Nature 2020, 588, 39–47. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Zhou, H.; Dong, J.; Cheng, J.; Dong, W.; Huang, C.; Shen, Y.; Zhang, Q.; Gu, M.; Qian, C.; Chen, H.; et al. Photonic matrix multiplication lights up photonic accelerator and beyond. Light Sci. Appl. 2022, 11, 30. [Google Scholar] [CrossRef]
- Moons, B.; Verhelst, M. An Energy-Efficient Precision-Scalable ConvNet Processor in 40-nm CMOS. IEEE J. Solid-State Circuits 2017, 52, 903–914. [Google Scholar] [CrossRef]
- Waldrop, M.M. The chips are down for Moore’s law. Nature 2016, 530, 144–147. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Zhou, H.; Dong, J. Photonic Matrix Computing: From Fundamentals to Applications. Nanomaterials 2021, 11, 1683. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Bilodeau, S.; Lima, T.F.d.; Tait, A.N.; Ma, P.Y.; Blow, E.C.; Jha, A.; Peng, H.-T.; Shastri, B.J.; Prucnal, P.R. Demonstration of scalable microring weight bank control for large-scale photonic integrated circuits. APL Photonics 2020, 5, 040803. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, C.; Peng, H.-T.; Bilodeau, S.; Jha, A.; Blow, E.; de Lima, T.F.; Shastri, B.J.; Prucnal, P. Silicon microring synapses enable photonic deep learning beyond 9-bit precision. Optica 2022, 9, 579–584. [Google Scholar] [CrossRef]
- Wu, C.; Yu, H.; Lee, S.; Peng, R.; Takeuchi, I.; Li, M. Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 2021, 12, 96. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Ashtiani, F.; Geers, A.J.; Aflatouni, F. An on-chip photonic deep neural network for image classification. Nature 2022, 606, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Wang, J.; Yi, S.; Zou, W. High-order tensor flow processing using integrated photonic circuits. Nat. Commun. 2022, 13, 7970. [Google Scholar] [CrossRef]
- Zhu, H.H.; Zou, J.; Zhang, H.; Shi, Y.Z.; Luo, S.B.; Wang, N.; Cai, H.; Wan, L.X.; Wang, B.; Jiang, X.D.; et al. Space-efficient optical computing with an integrated chip diffractive neural network. Nat. Commun. 2022, 13, 1044. [Google Scholar] [CrossRef]
- Bai, B.; Yang, Q.; Shu, H.; Chang, L.; Yang, F.; Shen, B.; Tao, Z.; Wang, J.; Xu, S.; Xie, W.; et al. Microcomb-based integrated photonic processing unit. Nat. Commun. 2023, 14, 66. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Fujisawa, S.; de Lima, T.F.; Tait, A.N.; Blow, E.C.; Tian, Y.; Bilodeau, S.; Jha, A.; Yaman, F.; Peng, H.-T.; et al. A silicon photonic–electronic neural network for fibre nonlinearity compensation. Nat. Electron. 2021, 4, 837–844. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Shu, H.; Zhang, Z.; Yi, S.; Bai, B.; Wang, X.; Liu, J.; Zou, W. Optical coherent dot-product chip for sophisticated deep learning regression. Light Sci. Appl. 2021, 10, 221. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Zou, W.; Wang, J.; Wang, R.; Chen, J. High-accuracy optical convolution unit architecture for convolutional neural networks by cascaded acousto-optical modulator arrays: Erratum. Opt. Express 2020, 28, 21854. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Hu, Y.; Ou, X.; Li, X.; Lai, J.; Liu, N.; Cheng, X.; Pan, A.; Duan, H. Metasurface-enabled on-chip multiplexed diffractive neural networks in the visible. Light Sci. Appl. 2022, 11, 158. [Google Scholar] [CrossRef]
- Cheng, J.; He, Z.; Guo, Y.; Wu, B.; Zhou, H.; Chen, T.; Wu, Y.; Xu, W.; Dong, J.; Zhang, X. Self-calibrating microring synapse with dual-wavelength synchronization. Photonics Res. 2023, 11, 347–356. [Google Scholar] [CrossRef]
- Bangari, V.; Marquez, B.A.; Miller, H.; Tait, A.N.; Nahmias, M.A.; Lima, T.F.d.; Peng, H.T.; Prucnal, P.R.; Shastri, B.J. Digital Electronics and Analog Photonics for Convolutional Neural Networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–13. [Google Scholar] [CrossRef]
- Yang, L.; Ji, R.; Zhang, L.; Ding, J.; Xu, Q. On-chip CMOS-compatible optical signal processor. Opt. Express 2012, 20, 13560–13565. [Google Scholar] [CrossRef]
- Cheng, J.; Zhao, Y.; Zhang, W.; Zhou, H.; Huang, D.; Zhu, Q.; Guo, Y.; Xu, B.; Dong, J.; Zhang, X. A small microring array that performs large complex-valued matrix-vector multiplication. Front. Optoelectron. 2022, 15, 15. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Englund, D.; Soljacic, M. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, Y.; Wang, X.; Gao, D.; Dong, J.; Zhang, X. Self-Configuring and Reconfigurable Silicon Photonic Signal Processor. ACS Photonics 2020, 7, 792–799. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Hamerly, R.; Englund, D. Hardware error correction for programmable photonics. Optica 2021, 8, 1247–1255. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Liu, C.; Ma, Q.; Luo, Z.J.; Hong, Q.R.; Xiao, Q.; Zhang, H.C.; Miao, L.; Yu, W.M.; Cheng, Q.; Li, L.; et al. A programmable diffractive deep neural network based on a digital-coding metasurface array. Nat. Electron. 2022, 5, 113–122. [Google Scholar] [CrossRef]
- Fu, T.; Zang, Y.; Huang, Y.; Du, Z.; Huang, H.; Hu, C.; Chen, M.; Yang, S.; Chen, H. Photonic machine learning with on-chip diffractive optics. Nat. Commun. 2023, 14, 70. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Du, S.; Ibrahim, M.; Shehata, M.; Badawy, W. Automatic License Plate Recognition (ALPR): A State-of-the-Art Review. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 311–325. [Google Scholar] [CrossRef]
- Yujie, L.; He, H. Car plate character recognition using a convolutional neural network with shared hidden layers. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 638–643. [Google Scholar]
- Zhou, H.; Geng, Y.; Cui, W.; Huang, S.-W.; Zhou, Q.; Qiu, K.; Wei Wong, C. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities. Light Sci. Appl. 2019, 8, 50. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, B.; Wen, Q.; Qin, J.; Geng, Y.; Zhou, Q.; Deng, G.; Qiu, K.; Zhou, H. Low-noise amplification of dissipative Kerr soliton microcomb lines via optical injection locking lasers. Chin. Opt. Lett. 2021, 19, 121401. [Google Scholar] [CrossRef]
- Chang, L.; Liu, S.; Bowers, J.E. Integrated optical frequency comb technologies. Nat. Photonics 2022, 16, 95–108. [Google Scholar] [CrossRef]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Xiao, X.; Yu, S. Silicon intensity Mach–Zehnder modulator for single lane 100 Gb/s applications. Photonics Res. 2018, 6, 109. [Google Scholar] [CrossRef]
- Atabaki, A.H.; Moazeni, S.; Pavanello, F.; Gevorgyan, H.; Notaros, J.; Alloatti, L.; Wade, M.T.; Sun, C.; Kruger, S.A.; Meng, H.; et al. Integrating photonics with silicon nanoelectronics for the next generation of systems on a chip. Nature 2018, 556, 349–354. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).