Development and Calibration of a Vertical High-Speed Mueller Matrix Ellipsometer
Abstract
:1. Introduction
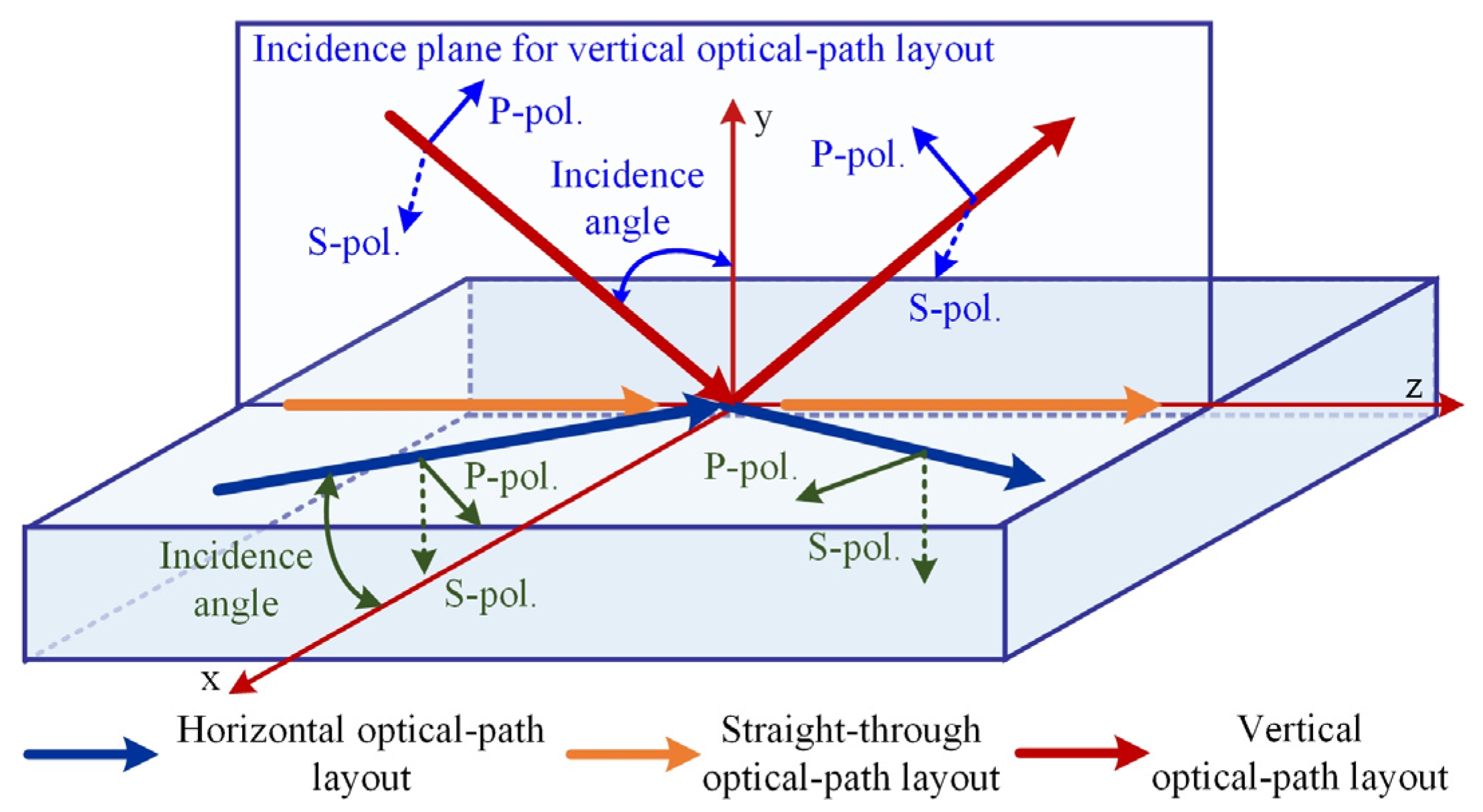
2. Instrument Prototype
3. Calibration Method
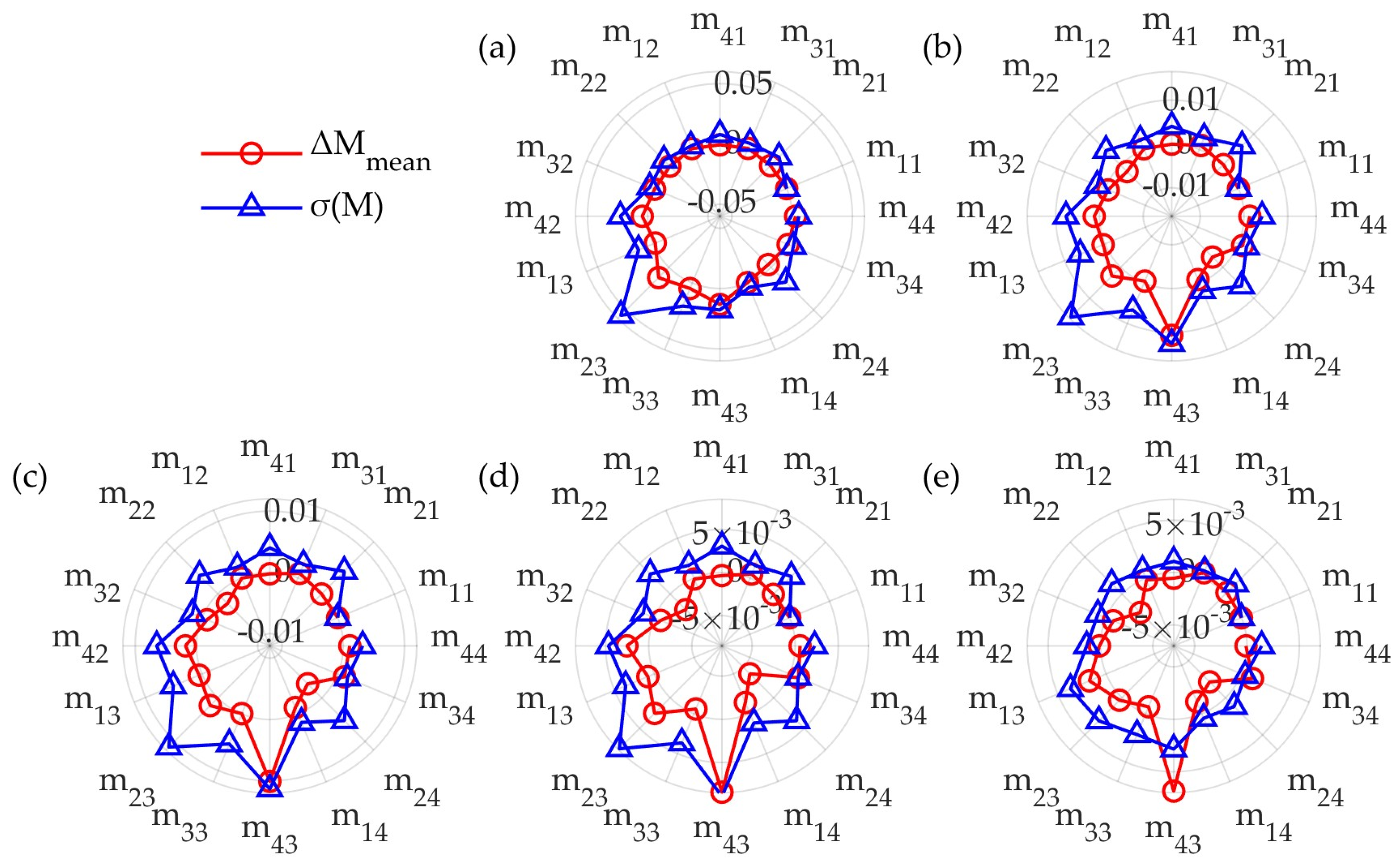
4. Results and Discussion
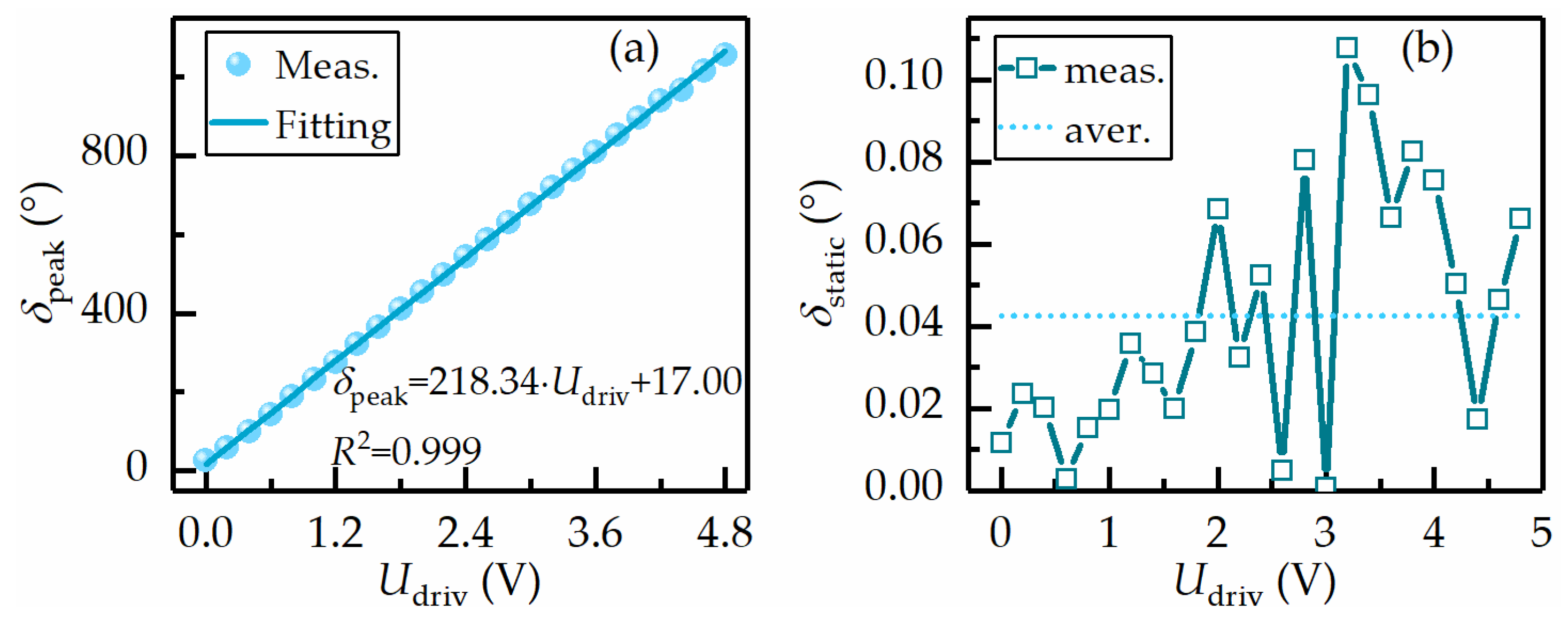
4.1. Calibration of PSA and PSG Module
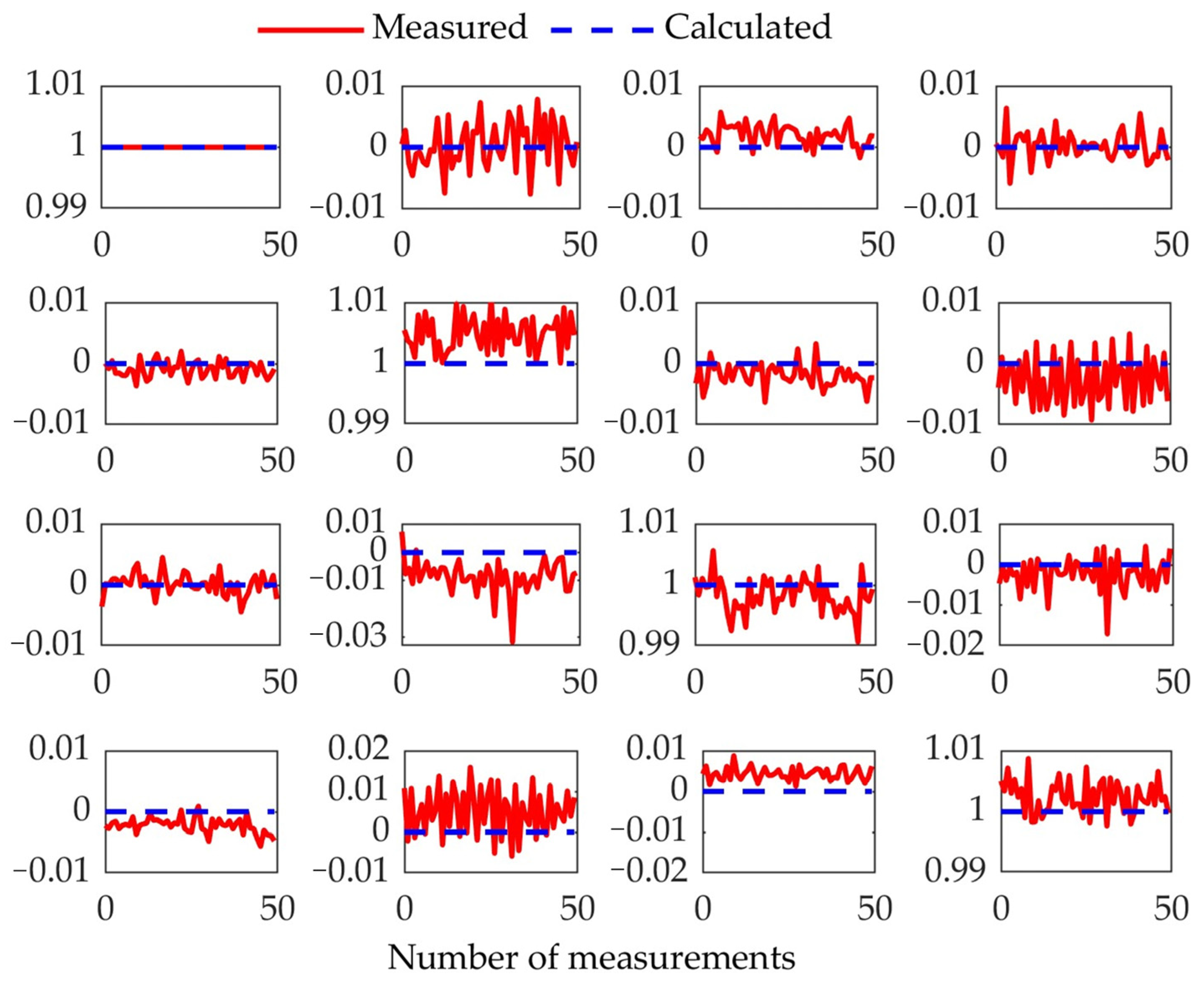
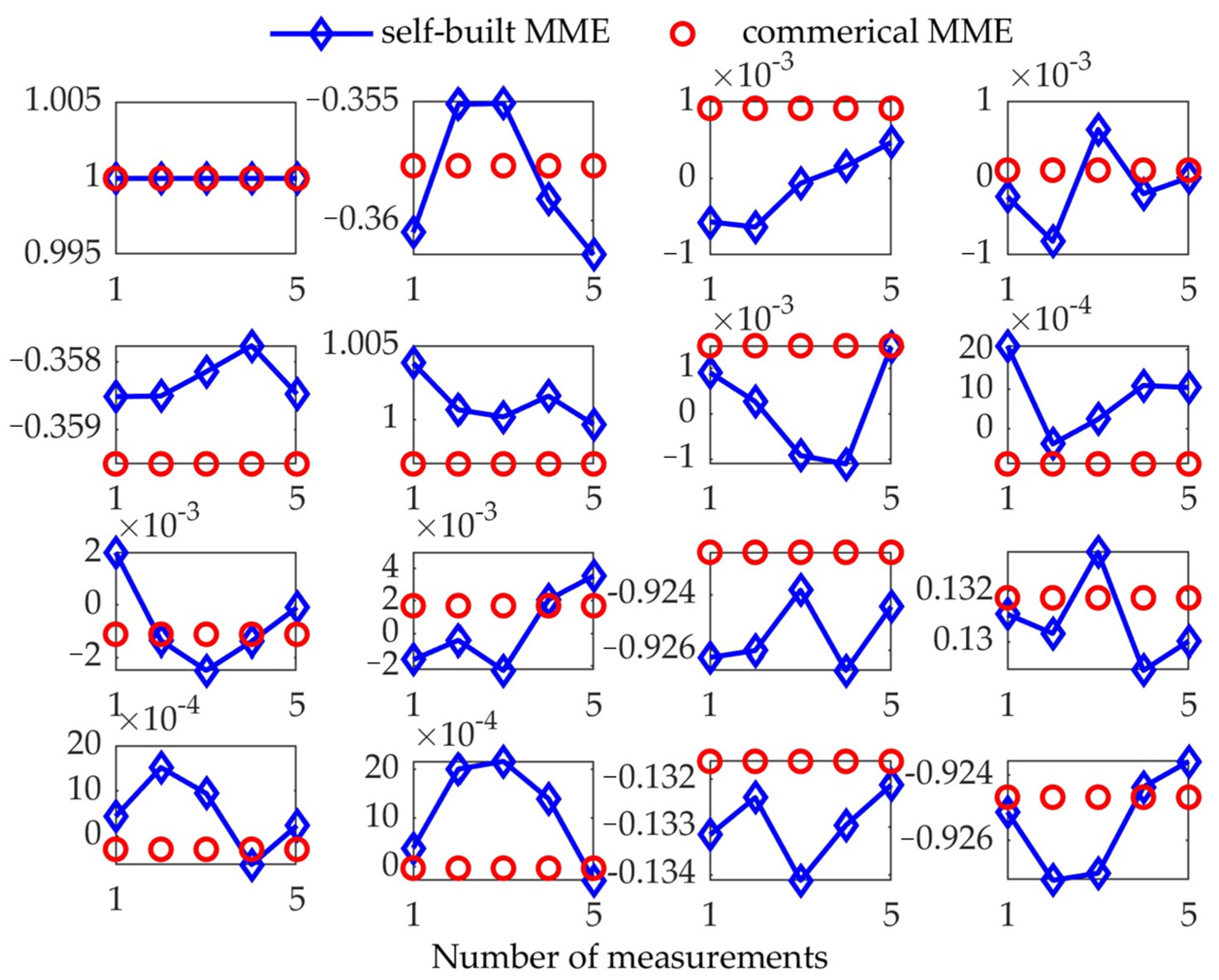
4.2. Measurement Performance of the Vertical Instrument
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benjamin, I. Reaction dynamics at liquid interfaces. Annu. Rev. Phys. Chem. 2015, 66, 165–188. [Google Scholar] [CrossRef] [PubMed]
- Ferrera, M.; Magnozzi, M.; Bisio, F.; Canepa, M. Temperature-dependent permittivity of silver and implications for thermoplasmonics. Phys. Rev. Mater. 2019, 3, 105201. [Google Scholar] [CrossRef]
- Magnozzi, M.; Ferrera, M.; Mattera, L.; Canepa, M.; Bisio, F. Plasmonics of Au nanoparticles in a hot thermodynamic bath. Nanoscale 2019, 11, 1140–1146. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Yang, J.; Zhang, S.; Liu, L. Role of electron-phonon coupling in finite-temperature dielectric functions of Au, Ag, Cu. Phys. Rev. B 2017, 96, 115154. [Google Scholar] [CrossRef]
- Manukyan, K.V.; Avetisyan, A.G.; Shuck, C.E.; Chatilyan, H.A.; Rouvimov, S.; Kharatyan, S.L.; Mukasyan, A.S. Nickel oxide reduction by hydrogen: Kinetics and structural transformations. J. Phys. Chem. C 2015, 119, 16131–16138. [Google Scholar] [CrossRef]
- Vendelbo, S.B.; Elkjær, C.F.; Falsig, H.; Puspitasari, I.; Dona, P.; Mele, L.; Morana, B.; Nelissen, B.J.; van Rijn, R.; Creemeer, J.F.; et al. Visualization of oscillatory behaviour of Pt nanoparticles catalysing CO oxidation. Nat. Mater. 2014, 13, 884–890. [Google Scholar] [CrossRef]
- Yu, J.; Yuan, W.; Yang, H.; Xu, Q.; Wang, Y.; Zhang, Z. Fast gas-solid reaction kinetics of nanoparticles unveiled by millisecond in situ electron diffraction at ambient pressure. Angew. Chem. Int. Ed. 2018, 57, 11344–11348. [Google Scholar] [CrossRef]
- Raeburn, J.; Cardoso, A.Z.; Adams, D. The importance of the self-assembly process to control mechanical properties of low molecular weight hydrogels. Chem. Soc. Rev. 2013, 42, 5143–5156. [Google Scholar] [CrossRef]
- Jiang, H.; Peng, H.; Chen, G.; Gu, H.; Chen, X.; Liao, Y.; Liu, S.; Xie, X. Nondestructive investigation on the nanocomposite ordering upon holography using Mueller matrix ellipsometry. Eur. Polym. J. 2019, 110, 123–129. [Google Scholar] [CrossRef]
- Gillmer, S.R.; Yu, X.; Wang, C.; Ellis, J.D. Robust high-dynamic-range optical roll sensing. Opt. Lett. 2015, 40, 2497–2500. [Google Scholar] [CrossRef]
- Saito, Y.; Arai, Y.; Gao, W. Detection of three-axis angles by an optical sensor. Sens. Actuator. A Phys. 2009, 150, 175–183. [Google Scholar] [CrossRef]
- Long, D.A.; Reschovsky, B.J.; LeBrun, T.W.; Gorman, J.J.; Hodges, J.T.; Plusquellic, D.F.; Stroud, J.R. High dynamic range electro-optic dual-comb interrogation of optomechanical sensors. Opt. Lett. 2022, 47, 4223–4326. [Google Scholar] [CrossRef] [PubMed]
- Bag, A.; Neugebauer, M.; Mick, U.; Christiansen, S.; Schulz, S.A.; Banzer, P. Towards fully integrated photonic displacement sensors. Nat. Commun. 2020, 11, 2915. [Google Scholar] [CrossRef]
- Petkovšek, R.; Petelin, J.; Možina, J.; Bammer, F. Fast ellipsometric measurements based on a single crystal photoelastic modulator. Opt. Express 2010, 18, 21410–21418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, L.; Yi, A.; Gu, H.; Chen, X.; Jiang, H.; Liu, S. Dynamic modulation performance of ferroelectric liquid crystal polarization rotators and Mueller matrix polarimeter optimization. Front. Mech. Eng. 2020, 15, 256–264. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.; Zhu, J.; Jiang, H.; Liu, S. Femtosecond laser induced damaging inside fused silica observed by a single-pulse ultrafast measurement system. Opt. Express 2022, 30, 26111–26119. [Google Scholar] [CrossRef]
- Barroo, C.; Wang, Z.; Schlögl, R.; Willinger, M. Imaging the dynamics of catalysed surface reactions by in situ scanning electron microscopy. Nat. Catal. 2020, 3, 30–39. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, C.; Lin, Q. Entropy analysis and grey cluster analysis of multiple indexes of 5 kinds of genuine medicinal materials. Sci. Rep. 2022, 12, 6618. [Google Scholar] [CrossRef]
- Wehrenberg, C.E.; McGonegle, D.; Bolme, C.; Higginbotham, A.; Lazicki, A.; Lee, H.J.; Nagler, B.; Park, H.-S.; Remington, B.A.; Rudd, R.E.; et al. In situ X-ray diffraction measurement of shock-wave-driven twinning and lattice dynamics. Nature 2017, 550, 496–499. [Google Scholar] [CrossRef]
- Chen, X.; Gu, H.; Liu, J.; Chen, C.; Liu, S. Advanced Mueller matrix ellipsometry: Instrumentation and emerging applications. Sci. China Technol. Sc. 2022, 65, 2007–2030. [Google Scholar] [CrossRef]
- Bian, S.; Cui, C.; Arteaga, O. Mueller matrix ellipsometer based on discrete-angle rotating Fresnel rhomb compensators. Appl. Opt. 2021, 60, 4964–4971. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Chen, X.; Zhang, C. Development of a broadband Mueller matrix ellipsometer as a powerful tool for nanostructure metrology. Thin Solid Films 2015, 584, 176–185. [Google Scholar] [CrossRef]
- Atalar, O.; Van Laer, R.; Safavi-Naeini, A.H.; Arbabian, A. Longitudinal piezoelectric resonant photoelastic modulator for efficient intensity modulation at megahertz frequencies. Nat. Commun. 2022, 13, 1526. [Google Scholar] [CrossRef] [PubMed]
- López-Téllez, J.M.; Bruce, N.C. Mueller-matrix polarimeter using analysis of the nonlinear voltage–retardance relationship for liquid-crystal variable retarders. Appl. Opt. 2014, 53, 5359–5366. [Google Scholar] [CrossRef] [PubMed]
- Marco, D.; López-Morales, G.; Sanchez-López, M.M.; Lizana, Á.; Moreno, I.; Campos, J. Customized depolarization spatial patterns with dynamic retardance functions. Sci. Rep. 2021, 11, 9415. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Jiang, H.; Gu, H.; Chen, X.; Liu, S. High-speed Mueller matrix ellipsometer with microsecond temporal resolution. Opt. Express 2020, 28, 10873–10887. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, H.; Gu, H.; Chen, X.; Liu, S. Attitude metrology based on the field-of-view effect of birefringence using high-speed polarimetry. Opt. Lett. 2020, 45, 2074–2077. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.; Zhong, Z.; Gu, H.; Chen, X.; Jiang, H.; Liu, S. Measurement configuration optimization for dynamic metrology using Stokes polarimetry. Meas. Sci. Technol. 2018, 29, 054010. [Google Scholar] [CrossRef]
- Arteaga, O.; Freudenthal, J.; Wang, B.; Kahr, B. Mueller matrix polarimetry with four photoelastic modulators: Theory and calibration. Appl. Opt. 2012, 51, 6805–6817. [Google Scholar] [CrossRef]
- Fujiwara, H. Spectroscopic Ellipsometry Principles and Applications; John Wiley & Sons, Ltd.: Chichester, UK, 2007; pp. 52–79. [Google Scholar]
- Zhang, S.; Gu, H.; Liu, J.; Jiang, H.; Chen, X.; Zhang, C.; Liu, S. Characterization of beam splitters in the calibration of a six-channel Stokes polarimeter. J. Opt. 2018, 20, 125606. [Google Scholar] [CrossRef]
- Ehrstein, J.; Richter, C.; Chandler-Horowitz, D.; Vogel, E.; Young, C.; Shah, S.; Maher, D.; Foran, B.; Hung, P.Y.; Diebold, A. A comparison of thickness values for very thin SiO2 films by using ellipsometric, capacitance-voltage, and HRTEM measurements. J. Electrochem. Soc. 2006, 153, F12–F19. [Google Scholar] [CrossRef]
- Herzinger, C.M.; Johs, B.; McGahan, W.A.; Woollam, J.A. Ellipsometric determination of optical constants for silicon and thermally grown silicon dioxide via a multi-sample, multi-wavelength, multi-angle investigation. J. Appl. Phys. 1998, 83, 3323–3336. [Google Scholar] [CrossRef]
- Ramirez-Atencia, C.; Bello-Orgaz, G.; R-Moreno, M.D.; Camacho, D. Solving complex multi-UAV mission planning problems using multi-objective genetic algorithms. Soft Comput. 2017, 21, 4883–4900. [Google Scholar] [CrossRef]


| Specification | δpeak (°) | f (kHz) | φ (°) | δstatic (°) | θPEM (°) |
|---|---|---|---|---|---|
| II/FS42LR | 1056.7 | 42.05 | 260.9 | 0.043 | −0.34 |
| II/FS60LR | 1078.8 | 59.64 | 129.9 | 0.036 | 44.82 |
| Nominal Value (nm) | Measured Value (nm) | Reference Value (nm) | Deviation (nm) | Relative Deviation |
|---|---|---|---|---|
| 1.70 | 1.84 ± 0.62 | 1.69 ± 0.01 | 0.15 | 8.15% |
| 18.00 | 17.86 ± 0.23 | 18.10 ± 0.02 | −0.24 | 1.34% |
| 25.00 | 25.13 ± 0.13 | 25.31 ± 0.02 | −0.18 | 0.72% |
| 31.00 | 31.42 ± 0.32 | 30.72 ± 0.04 | 0.72 | 2.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, S.; Deng, B.; Li, L.; Gu, H.; Zhu, J.; Jiang, H.; Liu, S. Development and Calibration of a Vertical High-Speed Mueller Matrix Ellipsometer. Photonics 2023, 10, 1064. https://doi.org/10.3390/photonics10091064
Liu J, Zhang S, Deng B, Li L, Gu H, Zhu J, Jiang H, Liu S. Development and Calibration of a Vertical High-Speed Mueller Matrix Ellipsometer. Photonics. 2023; 10(9):1064. https://doi.org/10.3390/photonics10091064
Chicago/Turabian StyleLiu, Jiamin, Song Zhang, Bowen Deng, Lei Li, Honggang Gu, Jinlong Zhu, Hao Jiang, and Shiyuan Liu. 2023. "Development and Calibration of a Vertical High-Speed Mueller Matrix Ellipsometer" Photonics 10, no. 9: 1064. https://doi.org/10.3390/photonics10091064
APA StyleLiu, J., Zhang, S., Deng, B., Li, L., Gu, H., Zhu, J., Jiang, H., & Liu, S. (2023). Development and Calibration of a Vertical High-Speed Mueller Matrix Ellipsometer. Photonics, 10(9), 1064. https://doi.org/10.3390/photonics10091064





