Abstract
The analysis reported in this paper shows that the homogeneous sensitivity of both fundamental rib waveguide modes, HE00 and EH00, can slightly exceed the sensitivity of the optimized parent slab waveguide. The most crucial difference in the behavior of these two polarizations is that the sensitivity of the HE00 mode is the maximum for strip waveguides. In contrast, the sensitivity of the EH00 mode can either decrease monotonically or not-monotonically with increasing rib height or behave like a homogeneous sensitivity characteristic of the slab waveguide’s EH0 mode. The second important conclusion comes from comparing the sensitivity characteristics with the distributions of the fundamental mode’s optical power. Namely, the homogeneous sensitivity of the rib waveguide is at the maximum if, due to a slight variance in the cover refractive index, a variation in the weighted optical power carried by the mode is the maximum.
1. Introduction
Rib waveguides play a fundamental role in planar integrated optical circuits (PICs) fabricated based on key material systems which include SOI (silicon on insulator) [1], InP/InGaAsP [2], AlGaAs-on-insulator [3], Si3N4/SiO2 [4], a-Al2O3/SiO2 [5], SiO2-TiO2/BK7 glass [6,7], and Ge-on-insulator [8]. This work concerns the silica-titania material platform. It is composed of SiO2-TiO2 waveguide films deposited on BK7 glass substrates. This platform has several advantages over mainstream material platforms and related technologies (i.e., SOI, Si3N4, and InP). They are discussed in the papers [9,10,11], where designs of integrated optics devices using the silica-titania material platform are proposed and discussed. Let us consider PICs used in constructing optical chemical and biochemical sensors [12] that rely on the principle of evanescent wave spectroscopy [13]. They include evanescent wave transducers. If those transducers integrate planar interferometers [14,15], specific requirements regarding the rib waveguides involved in their design can be formulated. In particular, rib waveguides should be in single mode to achieve high interferometric contrast [16] and have high homogeneous sensitivity. The latter quantity is a metric for measuring variations of guided mode effective refractive indices rendered by slight variations of the refractive index of a medium covering the waveguide [17]. The magnitude of homogeneous sensitivity depends on the magnitude and uniformity of the waveguide’s refractive index and morphological parameters. It is well-established that the homogeneous sensitivity of slab waveguides, for a given polarization, has a single maximum if considered a function of the waveguide film thickness [17]. The paper [18] demonstrated that waveguides characterized by uniform refractive index profiles have higher homogeneous sensitivity than those with gradient-index refractive index profiles. Moreover, homogeneous sensitivity increases with increased refractive index contrast on an interface between the waveguide and the cover. Assuming, therefore, that refractive indices of the rib waveguide and the substrate are determined by the given material system, the homogeneous sensitivity can be maximized by the careful selection of rib waveguide morphological parameters, namely: a parent slab thickness H, rib width w, and rib height t. Given this, one can see that for a given polarization, there is only one parent slab of optimum thickness Hm, which can serve as a reference for a whole family of rib waveguides described by H, w, and t. Their homogeneous sensitivity values can be normalized by dividing them by the sensitivity of the optimized parent slab.
The influence of morphological parameters of rib waveguides on their homogeneous sensitivity is discussed in papers [19,20]. However, the analysis presented in those papers concerns SOI, SiOxNy (silicon oxynitride), and Si3N4 rib waveguides and does not consider the single-mode operation range. Moreover, it was carried in a limited range of morphological parameters, where the results obtained using the FEM (finite element method) and the EIM (effective index method) are compatible. These papers calculated homogeneous sensitivity from the waveguiding film’s mode power flux and analytical equations derived from the EIM. The EIM only allows the correct derivation of modal field distributions if the mode is strongly confined to the rib [21]. In this respect, it is to be noted that such a mode is weakly sensitive to variations of the cover refractive index.
This article presents the results of the study on the relation between a rib waveguide single-mode operation regime and their homogeneous sensitivity in terms of characteristics of effective indices and homogeneous sensitivity as a function of their morphological parameters: H, w, and t. This work continues the analysis presented in our previous conference paper [22]. Nevertheless, we believe the results presented here are novel in two aspects. First, the research in this paper was carried out concerning the complete single-mode propagation condition described in the work [23]. Secondly, characteristics of homogeneous sensitivity are discussed concerning the distribution of waveguide mode optical power among a substrate, cover, and waveguide film. The literature has a well-established view that homogeneous sensitivity is the maximum if the fraction of optical power carried in the cover is maximized [19,24]. The presented results show that this is not the case considering rib waveguides. Based on the calculated characteristics of homogeneous sensitivity as a function of rib height, we have shown that homogeneous sensitivity is the maximum if the difference of weighted optical power carried by the mode is the maximum. The weights are refractive indices of the rib waveguide’s cover, waveguide film, and substrate. The magnitude of the effective refractive index increases if the fraction of optical power carried in a medium having the highest refractive index increases. Typically, the waveguide film is such a medium. Given that the magnitude of the homogeneous sensitivity depends on the variation of the effective refractive index, our assumption is proper. That is because, due to the change in the cover refractive index, the distribution of the modal field changes, resulting in a modified distribution of optical power among the cover, waveguide film, and substrate, which have different refractive indices. A similar approach was adopted for the calculation of the rib waveguide’s effective refractive indices by P.C. Kendall [25], who proposed weighting a value of the effective refractive indices by the magnitude of optical power in the rib waveguide’s layers—a substrate, waveguide film, and cover.
2. Structure and Methods
Schematic diagrams of the structures being investigated in this work are presented in Figure 1. The slab waveguide comprises a silica-titania film deposited on a BK7 glass substrate. This film considered infinite along the axis x is characterized by a thickness of d. Except for a strip area, the rib waveguide is fabricated from the parent slab through its partial or full thinning. As a result, a rib is formed. It is assumed that the rib’s walls are vertical. A rib is characterized by width w and height t. An analysis was carried out for the wavelength λ = 635 nm. However, in the case of the slab waveguides, the analysis was also carried out for λ = 1550 nm. This was carried out to compare the homogenous sensitivity of slab waveguides based on the SiO2-TiO2/BK7 material platform to those based on the SOI and Si3N4/SiO2 platforms. The equations describing the refractive index chromatic dispersion of Si, SiO2, and Si3N4 can be found in [26,27,28], respectively. The refractive indices of the silica-titania film nf, BK7 glass substrate ns, and cover nc for λ = 635 nm are the same as those assumed in our paper on the single mode condition [19]. They are: nf = 1.8186, ns = 1.5150, and nc = 1.3320. Their values for λ = 1550 nm are nf = 1.7595, ns = 1.5006, and nc = 1.3160.
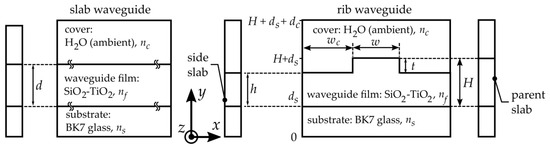
Figure 1.
Schematic view of investigated slab and rib waveguides. Description of symbols: d—slab waveguide thickness, dc and ds—substrate and cover layer thickness in a computational window, ws—the distance between rib sidewalls and vertical boundaries of the computational window, H—parent slab thickness, h—side-slab thickness, w—rib width, t—rib height, nf—refractive index of the waveguide film, ns and nc—refractive indices of the substrate and cover, and x, y, z—coordinate system axes.
The characteristics of homogeneous sensitivity were derived based on the analysis of effective index (modal) characteristics of rib and slab waveguides. Homogeneous sensitivity is defined by the equation [17]:
where neff is an effective index of a given mode. The derivative (1) was approximated by a difference quotient, assuming that the increase of the cover refractive index is Δnc = 0.001. The effective index characteristics and optical power density, associated with fundamental rib waveguide modes, were calculated using the film mode matching method (FMM) [29] implemented in the FIMMWAVE 6.3 solver from Photon Design®. FMM is a rigorous and semi-analytical method that gives accurate results when applied to vertically walled rib waveguides. The Dirichlet boundary conditions were set on the boundaries of the computational domain, the size of which was selected so that the principal components of HEpq modes (Ex and Hy) and EHpq modes (Ey and Hx) were vanishing at those boundaries. The following values determining that size were adopted: ds = 3 µm, dc = 1 µm, and wc = 4 µm. The value of the parameter (1d)nmode was set to 60.
A schematic diagram presenting successive stages of the reported analysis is shown in Figure 2. Modal characteristics of slab and rib waveguides were calculated as a function of d and t, respectively. A single mode propagation range for the investigated rib waveguides was determined based on the characteristics of two kinds of specific rib height values: tsst and tcff. Namely, basic effective index characteristics of the HE01 and EH01 modes may, at tsst, intersect the corresponding side-slab waveguide characteristics of the modes HE0 and EH0, respectively. If such an intersection occurs, the given first-order rib waveguide mode leaks to the side slab for t < tsst, rendering the rib waveguide single mode in this interval. The second mechanism leading to single-mode propagation is to cut-off first-order modes. For t > tcff, an effective index of the given first-order rib waveguide mode is less than the substrate refractive index. The procedure for determining the single-mode propagation range based on the characteristics of tsst(w) and tcff(w) is described in detail in our previous paper [19]. Effective index characteristics of slab waveguides were calculated using the Effective Index Solver, also implemented in the FIMMWAVE solver.
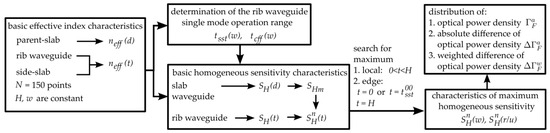
Figure 2.
Schematic diagram of the analysis process. Description of symbols used in this figure: neff—effective refractive index, tsst and tcff—characteristic values of the rib height, and —absolute and normalized homogeneous sensitivity, —homogeneous sensitivity of the optimized parent slab waveguide, and r and u—effective rib width and height. A description of the morphological parameters is given in the caption of Figure 1.
The range of the rib waveguide’s morphological parameter values in which the analysis was carried out is shown in Table 1.

Table 1.
The range of morphological parameter values over which the analysis was carried out. Symbols H, w and t are explained in the caption to Figure 1.
Each basic homogeneous sensitivity characteristic SH(t) was calculated from a pair of neff(t) characteristics. The second characteristic in each pair was calculated for a value of the cover refractive index increased by a factor of Δnc = 0.001. Those characteristics were grouped into sets according to a value of the parent slab thickness H and searched for the presence of maximum values. Such a maximum can be located at the beginning of the interval <0, H>, (t = 0 − parent slab), at its end (t = H), and in the middle of it (local peak). Here, care must be taken if EH modes are being considered. This is because if H is sufficiently low, the EH00 mode can leak from the rib into the side slab (See Figure 1) for t lower than some non-zero value [23]. In that case, is the left boundary of a search interval. The maximum sensitivity values are presented as sets of characteristics. They are functions of rib width w or a parameter defined as the ratio between dimensionless side-slab thickness r and dimensionless rib width u. The parameters u and r, introduced in [30], are given by the following equations:
where the parameter γ depends on polarization, γc,s = 1 for HEpq modes, γc,s = (nc,s/nf)2 for EHpq modes, and k = 2π/λ where λ is a wavelength. The sensitivity values were normalized to the sensitivity of the optimized parent slab because, for each polarization, there is only one value of slab waveguide thickness for which homogeneous sensitivity reaches its maximum.
Finally, the following parameters were determined to determine how the homogeneous sensitivity depends on a distribution of the waveguide mode optical power among the substrate, cover, and waveguide film: filling factor , its difference , and its weighted difference . The first two parameters depend on the considered rib waveguide’s region: the superscript a accepts literals c (cover), f (waveguide film), and s (substrate). The weighted difference measures the change of optical power density for the hole mode. The equation describes the filling factor:
where A is the surface of a given part of the rib waveguide, S is the surface of the computational window, and Pz is the density of optical power defined by the Poynting vector, which has units of W/m2.
is also defined for a given region of the rib waveguide and is described by the equation:
where is the filling factor in the given region of the rib waveguide after increasing the cover refractive index from nc = 1.3320 by Δnc = 0.001. Finally, the weighted difference has the equation:
3. Results
3.1. Parent Slab Waveguide
The characteristics of the homogeneous sensitivity for the parent slab as a function of the waveguide film thickness are presented in Figure 3 and Figure 4. The ones presented in Figure 3b and Figure 4 are for the wavelength λ = 1550 nm. It is well known that if a slab waveguide is single-layered, its characteristics have a single maximum for a specific thickness whose value depends on polarization ( and ) [13]. Those values for the fundamental modes are specified in Table 2.
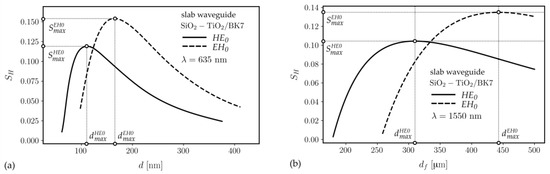
Figure 3.
Homogeneous sensitivity characteristics of the SiO2-TiO2/BK7 slab waveguides for wavelengths λ = 635 nm (a) and λ = 1550 nm (b).
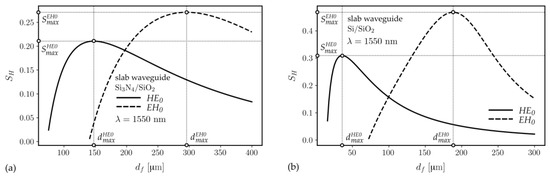
Figure 4.
Homogeneous sensitivity characteristics of the Si3N4/SiO2 (a) and SOI (b) slab waveguides for the wavelength λ = 1550 nm.

Table 2.
Optimized slab waveguide thickness dmax and maximum homogeneous sensitivity Smax of its fundamental modes for the silica-titania platform for the wavelengths 635 nm and 1550 nm and the Si3N4/SiO2 and SOI platforms for the wavelength 1550 nm.
The sensitivity values of the fundamental HE and EH rib waveguide modes are normalized to the maximum sensitivity of the corresponding slab waveguide modes and , respectively. The following equations give the normalized homogenous sensitivity of rib waveguides:
As shown in Table 1, the fundamental slab modes became the most sensitive for significantly different values of the parent slab thickness. For this reason, the characteristics of the rib waveguide’s homogeneous sensitivity were determined in two separate, although partly overlapping, ranges of the parent-slab thickness (see Table 1).
3.2. Rib Waveguide—Fundamental HE Modes
The selected representative characteristics of the HE00 modes (quasi-TE) normalized homogeneous sensitivity are presented in Figure 5. The range of single-mode propagation is distinguished by a bold line format. The character of changes in can be two-fold. The first can be observed on a set of characteristics for a value of the parent slab thickness smaller than dmax. They are presented in Figure 5a. One can see that initially decreases, reaches the local minimum, and finally increases, but the maximum is not achieved for t = H. For each characteristic corresponding with the given value of w, the is maximum for t = 0. In the second case, the value of the parent slab thickness exceeds dmax, increases with t, and reaches its maximum at t = H. The HE00 mode of rib waveguides investigated in this paper acquires maximum homogeneous sensitivity for Ho = 120 [nm], wo = 1.0 [μm], and to = 120 [nm].
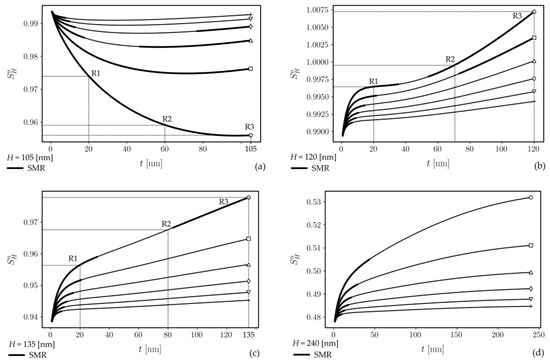
Figure 5.
Normalized homogeneous sensitivity characteristics of HE00 modes for four selected values of the parent slab thickness H: 105 nm (a), 120 nm (b), 135 nm (c), and 240 nm (d). Marker symbols: ○–w = 1.0 [μm], □–w = 1.2 [μm], △–w = 1.4 [μm], ◊–w = 1.6 [μm], ▽–w = 1.8 [μm], and +–w = 2.0 [μm]. The bold line format indicates the single-mode propagation regime (SMR).
The characteristics of homogeneous sensitivity concerning the rib width w for a maximum value of the rib height are presented in Figure 6. Here, the bold line format implies that is the maximum. One can observe that sensitivity reaches the maximum value almost exclusively if t = H. All characteristics in Figure 6 are plotted using the bold line format except for the curve for H = 105 nm. It is also apparent that there are no local maxima of and except for H = 105 nm, which is smaller than optimized thickness dmax for the slab waveguide’s HE0 mode, and that SH is decreasing with the increasing rib width w.
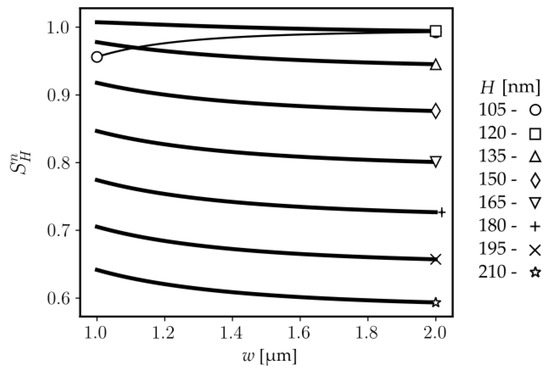
Figure 6.
Normalized homogeneous sensitivity of HE00 modes for t = H. The bold line format is used if the sensitivity reaches the maximum value.
Discussing the rib waveguide sensitivity characteristics concerning their morphological parameters is interesting, given how the optical power is distributed among the substrate, cover, and waveguide film. Three values of the parent slab thickness H were selected, and for each of them, the three values of t were chosen from the appropriate characteristic. They are designated in Figure 5a–c by symbols R1, R2, and R3, respectively. Each corresponds to a rib waveguide with a tuple (H, w, t). The selected parameters are listed in Table 3.

Table 3.
Morphological parameters of the rib waveguides selected for the determination of HE00 modes , , and .
The characteristics of the calculated values of the filling factor and its difference are presented in Figure 7a,b, respectively. One can observe that is not monotonically increasing with the homogeneous sensitivity. In all cases, the optical power is transferred from the substrate to the waveguide film and cover layer—, , and .
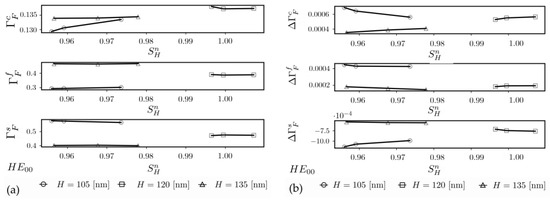
Figure 7.
Characteristic of HE00 modes’ filling factor (a) and its absolute difference (b), both as a function of the normalized homogeneous sensitivity. The superscript a accepts literals c (cover), f (waveguide film), and s (substrate).
The characteristic of the weighted absolute difference of the filling factor is presented in Figure 8. It demonstrates two things. First, they can be either positive or negative. The positive value is obtained for the lowest parent slab thickness H value. This means that the optical power is predominately transferred from the substrate to the waveguide film due to the increase in the cover refractive index and a transformation of the HE00 modal field. For higher values of H, the is negative. It indicates that the optical power more intensively flows to the cover, which has the lowest refractive index. The other conclusion derived from the characteristic of is that its absolute value monotonously increases with the normalized homogeneous sensitivity.
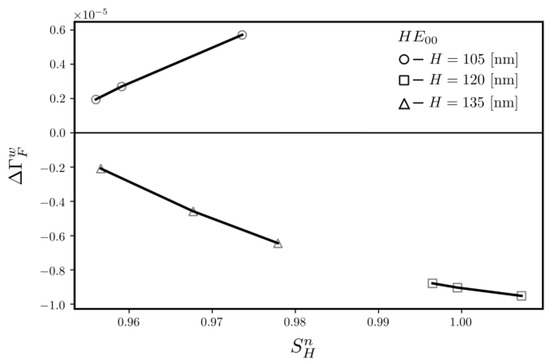
Figure 8.
Characteristic of HE00 modes’ filling factor weighted difference as a function of the normalized homogeneous sensitivity.
3.3. Rib Waveguide—Fundamental HE Modes
The selected representative characteristics of EH00 modes normalized homogeneous sensitivity are presented in Figure 9. The range of single-mode propagation is distinguished by a bold line format. One can observe that characteristics behave differently than those of HE00 modes. As one can observe from Figure 8c,d, they have a single maximum, for some t inside its range of variability, if the parent slab thickness exceeds the optimized thickness dmax for the slab waveguide’s EH0 mode.
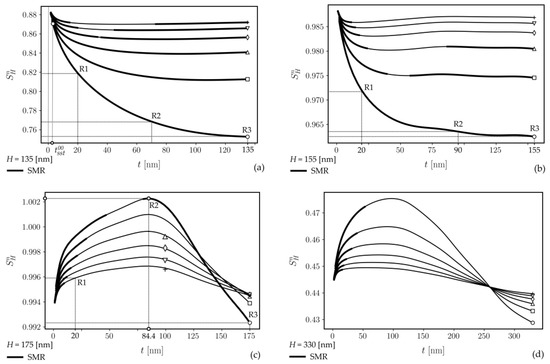
Figure 9.
Normalized homogeneous sensitivity characteristics of EH00 modes for four selected values of the parent slab thickness H: 135 nm (a), 155 nm (b), 175 nm (c), and 330 nm (d). Marker symbols: ○—w = 1.0 [μm], □—w = 1.2 [μm], △—w = 1.4 [μm], ◊—w = 1.6 [μm], ▽—w = 1.8 [μm], and +—w = 2.0 [μm]. The bold line format indicates a single-mode propagation regime (SMR).
The homogeneous sensitivity characteristics of EH00 modes for t = H are presented in Figure 10a. They behave similarly to those obtained for HE00 modes (Figure 6). The only difference is that the rate of decrease is smaller. One can observe that the maximum sensitivity of EH00 modes is predominately reached inside the range of variability of t, i.e., there is a single local maximum. Local maxima of exist only for EH00 modes. Their characteristics, presented in Figure 10b, concern the dimensionless parameter r/u, which reflects the transition from a strip waveguide (low r/u) to the structure tending to the slab waveguide (high r/u). For the given parent slab, the maxima of increase as the rib waveguide structure tends to the slab. The only exception is the characteristic for H = 175 nm on which the global maximum of is obtained. For this value, the maximum of is independent of r/u. The bold line format in Figure 9b implies that is the maximum in the whole range of t variability.
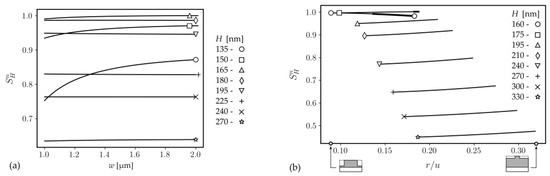
Figure 10.
Normalized homogeneous sensitivity of EH00 modes for t = H (a) and its local maximum concerning dimensionless parameter r/u (b).
The values of , , and have been calculated by the same process as the one used for the HE00 modes. The selected morphological parameters are listed in Table 4.

Table 4.
Morphological parameters of the rib waveguides selected for the determination of EH00 modes , , and .
The characteristics of the calculated values of the filling factor and its difference are presented in Figure 11a,b, respectively. As one can see, similarly as is the case for HE00 modes, is not monotonically increasing with the homogeneous sensitivity, and in all cases, the optical power is transferred from the substrate to the waveguide film and cover layer–, , and .
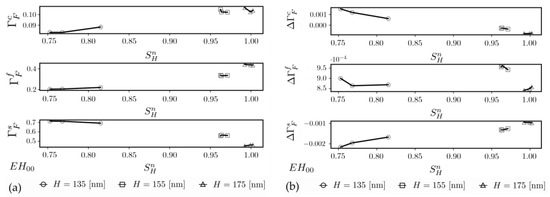
Figure 11.
Characteristics of EH00 modes’ filling factor (a) and its absolute difference (b), both as a function of the normalized homogeneous sensitivity. The superscript a accepts literals c (cover), f (waveguide film), and s (substrate).
The characteristic of the weighted absolute difference of the filling factor is presented in Figure 12. Contrary to the situation observed for HE00 modes (Figure 7), the is positive for all considered values of the parent slab thickness. As one can observe, monotonously increases with the homogeneous sensitivity.
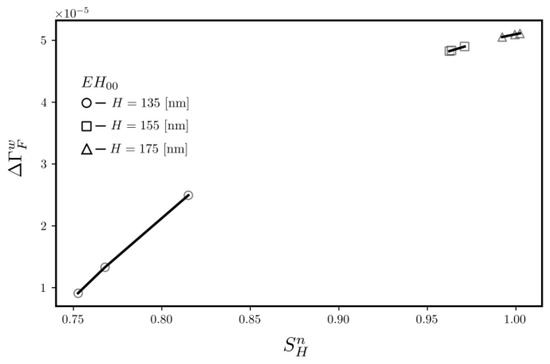
Figure 12.
Characteristic of the weighted difference as a function of the normalized homogeneous sensitivity of EH00 modes.
Regardless of the fabrication technology of rib waveguides, their final opto-geometrical parameters are more or less different than originally assumed. In order to assess how strongly variations of opto-geometrical parameters will influence the homogeneous sensitivity, the following procedure was adapted. One rib waveguide was selected for each fundamental mode. Their parameters are listed in Table 5. For theme, values of base homogeneous sensitivities, were calculated. Subsequently these parameters were individually increased by p percent. This way, the second value was obtained for rib waveguides having one parameter increased. The relative change δSH was calculated using the equation below:

Table 5.
Opto-geometrical parameters and homogeneous sensitivity of rib waveguides selected for assessment of the δSH.
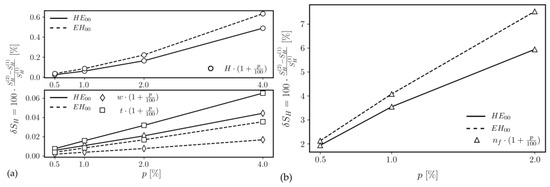
Figure 13.
Characteristics of the relative change of rib waveguide’s homogeneous sensitivity resulting from variations of opto-geometrical parameters: H, w, and t (a) and nf (b). The description of the rib waveguide’s parameters is given in the caption of Figure 1.
The question remains about the uncertainty of homogeneous sensitivity values calculated using a pair of neff(t) characteristics. The following treatment was applied because the uncertainty of effective refractive indices is unknown. Let us consider two characteristic neff(t), one for cover refractive index nc and the second for nc + Δnc. By increasing t tiny, the values of Δneff may be the same, even though both characteristics neff(t), are monotonously decreasing, and should also give varying characteristics of Δneff. However, there are variances between the two levels due to limitations to the accuracy of the neff values of SH. This can be observed in the characteristics presented in Figure 14. The uncertainty of SH read from these characteristics is ΔSH = 1.2×10-4.

Figure 14.
Homogeneous sensitivity of the rib waveguide’s modes HE00 (a) and EH00 (b) in the limited variability range of t. Parameters H and w are given in Table 5.
4. Discussion
As has already been mentioned, the nature of variation of slab waveguide’s homogenous sensitivity SH with the thickness of the waveguide film is well known. Each polarization has one value of the waveguide film thickness maximizing SH. The comparison of maximum achievable homogeneous sensitivities for slab waveguides based on SOI, Si3N4/SiO2, and SiO2-TiO2/BK7 reveals that SOI waveguides are the most sensitive to variations of nc. This results from the fact that the refractive index of silicon nf = 3.4764 is the highest compared to silicon nitride nf = 1.9963 and SiO2-TiO2 nf = 1.7595. However, considering the HE0 mode, one can observe in Figure 4b and read from Table 2 that its maximum sensitivity is reached for a waveguide film with a thickness of only df = 36 nm. Typically, SOI wafers come with epitaxial Si layers of thickness ranging from 200 to 300 nm. The homogeneous sensitivity of the HE0 mode in this range is lower than 0.05.
Considering the variation of rib waveguides SH with the parent slab thickness, it generally has the same character as the slab waveguides. Modes EH00 have a single local maximum, as shown in Figure 10b. In most cases, the subsequent characteristics sharing the same H are well separated. The separation is smaller only for those corresponding with parent slab thickness close to dmax = 165 nm (H = 160 and 175 nm). In the case of the HE00 mode, which does not acquire the maximum for some intermediate rib height , the best thing is to look at the dependence on H when t = H. Considering the variation of SH with t, it can be noted that for rib waveguides whose parent slab thickness is smaller than the thickness of the optimized slab waveguide (H < dmax), an increase in t results in a decrease in SH. The difference between the behavior of HE00 and EH00 modes shows up when the variation of SH with t is considered for H > dmax. The sensitivity of HE00 modes is the maximum for strip waveguides, whereas, in the case of EH00 modes, the maximum is obtained for .
Comparing the characteristics presented in Figure 6 and Figure 10a, we conclude that the character of the relation between the rib’s width and the homogenous sensitivity of the strip waveguide depends on the relation between H and dmax. The SH increases with w if H < dmax and decreases if H > dmax. This relationship is stronger for the HE00 mode.
Homogeneous sensitivity SH is a derivative of the effective refractive index neff concerning the refractive index of the cover nc (1). Assuming the increase of nc is small and constant, homogeneous sensitivity increases with the rise in neff. The magnitude of neff increases with an increasing share of the optical power in the waveguide film, which has the highest refractive index. For this reason, we proposed building a relationship between the weighted filling factor given by (8) and SH. As one can observe, the characteristics , presented in Figure 7 and Figure 11, agree with the assumption that SH is the maximum if a weighted difference of the filling factor is the maximum. As a result of a small increase in Δnc, for both polarizations, the optical power flows from the substrate to the waveguide film and cover (). The magnitude of homogenous sensitivity depends on how much optical power is drawn out from the substrate and how it is further divided between the waveguide film and the cover.
The characteristics of homogenous sensitivity relative change, δSH, resulting from variations of rib waveguide’s opto-geometrical parameters, reveal that δSH is greater than the uncertainty of SH for nf. The rib waveguide’s geometrical parameters shift the results in more minor SH changes. From the point of view of the mentioned material platforms, it poses a challenge for those platforms using multi-compound waveguide films, such as SiO2-TiO2. That is because the refractive index of such films depends on the environmental conditions prevailing during the fabrication process, e.g., humidity.
5. Conclusions
A rib waveguide’s fundamental modes of polarizations, HE and EH, can have higher homogenous sensitivity than the optimized slab waveguide. The values of the maximum increase over relevant sensitivity values for the optimized slab are minimal. And so, in the case of HE0 and HE00 modes, the homogeneous sensitivities of the optimized parent slab and rib waveguide are 0.119 and 0.120, respectively. In the case of the EH0 and HE00 modes, it is 0.154 and 0.155, respectively. The important difference between the magnitude of the response of the HE00 and EH00 mode to a variation of the cover’s refractive index is that the HE00 mode is most sensitive if the rib waveguide becomes a strip waveguide. Suppose the magnitude of SH is essential for the design of some integrated optics structure, which, for other reasons, should be based on strip waveguides. In that case, the HE00 mode may have higher sensitivity. Structures comprising strongly bent waveguides, e.g., ring resonators, may serve as an example. This is because the presence of a sacrificial layer results in high bending losses.
Author Contributions
Conceptualization, C.T.; methodology, C.T.; software, C.T. and P.K.; validation, C.T. and P.K.; formal analysis, C.T. and P.K.; writing—original draft preparation, C.T.; writing—review and editing, C.T. and P.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research was co-financed by the Foundation for Polish Science from the European Regional Development Fund within the project POIR.04.04.00-00-14D6/18 “Hybrid sensor platforms for integrated photonic systems based on ceramic and polymer materials (HYPHa)” (TEAM-NET program).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lipka, T.; Moldenhauer, L.; Müller, J.; Trieu, H.K. Photonic integrated circuit components based on amorphous silicon-on-insulator technology. Photonics Res. 2016, 4, 126–134. [Google Scholar] [CrossRef]
- Swagata, S.; Pradip, D.K.; Pallab, B.; Pranabendu, G. A 1 × 2 polarization-independent power splitter using three-coupled silicon rib waveguides. J. Opt. 2018, 20, 095801. [Google Scholar] [CrossRef]
- Ottaviano, L.; Pu, M.; Semenova, E.; Yvind, K. Low-loss high-confinement waveguides and microring resonators in AlGaAs-on-insulator. Opt. Lett. 2016, 41, 3996–3999. [Google Scholar] [CrossRef] [PubMed]
- Blumenthal, D.J.; Heideman, R.; Geuzebroek, D.; Leinse, A.; Roeloffzen, C. Silicon nitride in silicon photonics. Proc. IEEE 2018, 106, 2209–2231. [Google Scholar] [CrossRef]
- Özden, A.; Demirtas, M.; Ay, F. Polarization insensitive single mode Al2O3 rib waveguide design for applications in active and passive optical waveguides. J. Eur. Opt. Soc.-Rapid 2015, 10, 15005. [Google Scholar] [CrossRef]
- Karasiński, P.; Tyszkiewicz, C.; Rogoziński, R. Optical channel structures based on sol-gel derived waveguide films. Opt. Appl. 2011, XLI, 351–357. [Google Scholar]
- Karasiński, P.; Kaźmierczak, A.; Zięba, M.; Tyszkiewicz, C.; Wojtasik, K.; Kielan, P. Highly Sensitive Sensor Structure Based on Sol-Gel Waveguide Films and Grating Couplers. Electronics 2021, 10, 1389. [Google Scholar] [CrossRef]
- Kang, J.; Takenaka, M.; Takagi, S. Novel Ge waveguide platform on Ge-on-insulator wafer for mid-infrared photonic integrated circuits. Opt. Express 2016, 24, 11855–11864. [Google Scholar] [CrossRef]
- Butt, M.A.; Tyszkiewicz, C.; Karasiński, P.; Zięba, M.; Hlushchenko, D.; Baraniecki, T.; Kazmierczak, A.; Piramidowicz, R.; Guzik, M.; Bachmatiuk, A. Development of a low-cost silica-titania optical platform for integrated photonics applications. Opt. Express 2022, 30, 23678–23694. [Google Scholar] [CrossRef]
- Butt, M.A.; Shahbaz, M.; Kozłowski, Ł.; Kaźmierczak, A.; Piramidowicz, R. Silica-Titania Integrated Photonics Platform-Based 1 × 2 Demultiplexer Utilizing Two Serially Cascaded Racetrack Microrings for 1310 nm and 1550 nm Telecommunication Wavelengths. Photonics 2023, 10, 208. [Google Scholar] [CrossRef]
- Butt, M.A.; Shahbaz, M.; Piramidowicz, R. Racetrack Ring Resonator Integrated with Multimode Interferometer Structure Based on Low-Cost Silica–Titania Platform for Refractive Index Sensing Application. Photonics 2023, 10, 978. [Google Scholar] [CrossRef]
- Kozma, P.; Kehl, F.; Ehrentreich-Förster, E.; Stamm, C.; Bier, F.F. Integrated planar optical waveguide interferometer biosensors: A comparative review. Biosens. Bioelectron. 2014, 58, 287–307. [Google Scholar] [CrossRef]
- Midwinter, J.E. On the use optical waveguide techniques for internal reflection spectroscopy. IEEE J. Quantum Electron. 1971, 7, 339–344. [Google Scholar] [CrossRef]
- Bastos, A.R.; Vicente, C.M.S.; Oliveira-Silva, R.; Silva, N.J.O.; Tacão, M.; da Costa, J.P.; Lima, M.; André, P.S.; Ferreira, R.A.S. Integrated Optical Mach-Zehnder Interferometer Based on Organic-Inorganic Hybrids for Photonics-on-a-Chip Biosensing Applications. Sensors 2018, 18, 840. [Google Scholar] [CrossRef]
- Lo, S.M.; Hu, S.; Gaur, G.; Kostoulas, Y.; Weiss, S.M.; Fauchet, P.M. Photonic crystal microring resonator for label free biosensing. Opt. Express 2017, 25, 7046–7054. [Google Scholar] [CrossRef] [PubMed]
- Leblanc-Hotte, A.; Delisle, J.S.; Lesage, S.; Pete, Y.A. The Importance of Single-Mode Behavior in Silicon-On-Insulator Rib Waveguides With Very Large Cross Section for Resonant Sensing Applications. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 241–248. [Google Scholar] [CrossRef]
- Lukosz, W. Integrated optical chemical and direct biochemical sensor. Sens. Actuators B Chem. 1995, 29, 37–50. [Google Scholar] [CrossRef]
- Karasiński, P. Influence of waveguide parameters on the difference interference in optical planar structure. Opt. Appl. 2002, XXXII, 775–793. [Google Scholar]
- Dell’Olio, F.; Passaro, V.M.N.; De Leonardis, F. Sensitivity analysis of rib waveguides for integrated optical sensors. In Proceedings of the 2nd International Workshop on Advances in Sensors and Interface, Bari, Italy, 26–27 June 2007. [Google Scholar] [CrossRef]
- Dell’Olio, F.; Passaro, V.M.N. Optical sensing by optimized silicon slot waveguides. Opt. Express 2007, 15, 4977–4993. [Google Scholar] [CrossRef]
- Robertson, M.J. Weighted Index Method for Dielectric Waveguide Analysis. In Rib waveguide Theory by the Spectral Index Method; Research Studies Press LTD: Taunton, UK, 1990; Chapter 4.7; pp. 62–65. [Google Scholar]
- Tyszkiewicz, C. Comparison of single mode slab and rib waveguide planar evanescent wave transducers. In Proceedings of the SPIE 11045, Optical Fibers and Their Applications 2018, 110450R, Poland, Naleczow, 20–23 November 2018. [Google Scholar] [CrossRef]
- Tyszkiewicz, C. Complete single mode condition for silica-titania rib waveguides on glass substrates. J. Light. Technol. 2021, 39, 4410–4418. [Google Scholar] [CrossRef]
- Kita, D.M.; Michon, J.; Johnson, S.G.; Hu, J. Are slot and sub-wavelength grating waveguides better than strip waveguides for sensing? Optica 2018, 5, 1046–1054. [Google Scholar] [CrossRef]
- Kendall, P.C.; Adams, M.J.; Ritchie, S.; Robertson, M.J. Theory for calculating approximate values for the propagation constants of an optical rib waveguide by weighting the refractive indices. IEE Proc. A 1987, 134, 699–702. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Li, H.H. Refractive index of silicon and germanium and its wavelength and temperature derivatives. J. Phys. Chem. Ref. Data 1980, 9, 561–658. [Google Scholar] [CrossRef]
- Luke, K.; Okawachi, Y.; Lamont, R.E.M.; Alexander, L.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 40, 4823–4826. [Google Scholar] [CrossRef]
- Sudbo, A.S. Film mode matching: A versatile numerical method for vector mode field calculations in dielectric waveguides. J. Opt. 1993, 2, 211–233. [Google Scholar] [CrossRef]
- Pogossian, S.P.; Vescan, L.; Vonsovici, A. The Single-Mode Condition for Semiconductor Rib Waveguides with Large Cross Section. J. Light. Technol. 1998, 16, 1851–1853. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).