Piston Detection of Optical Sparse Aperture Systems Based on an Improved Phase Diversity Method
Abstract
1. Introduction
2. Theory
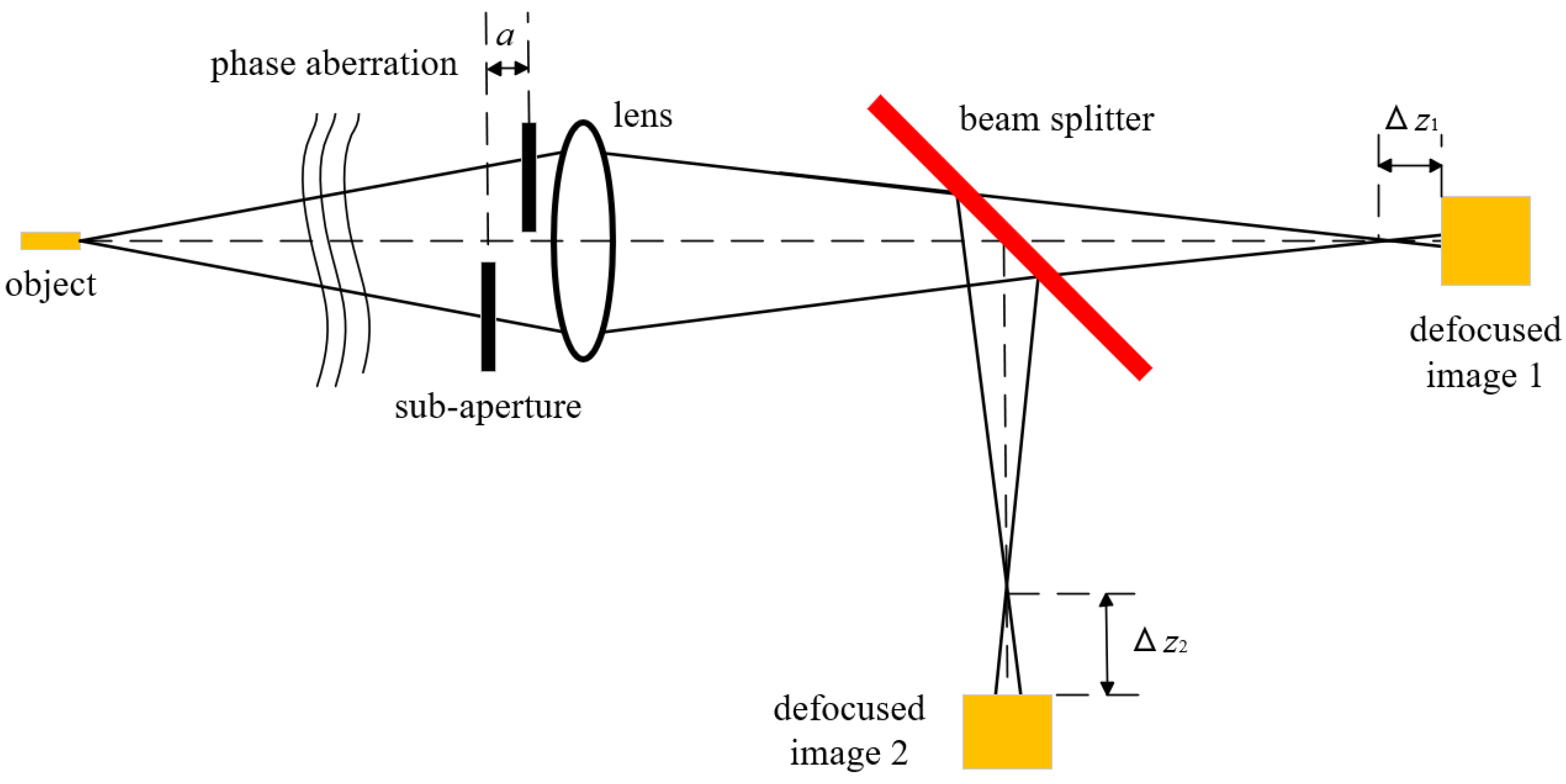
2.1. PD Method Theory
2.2. PSO Theory
2.3. SQP Theory
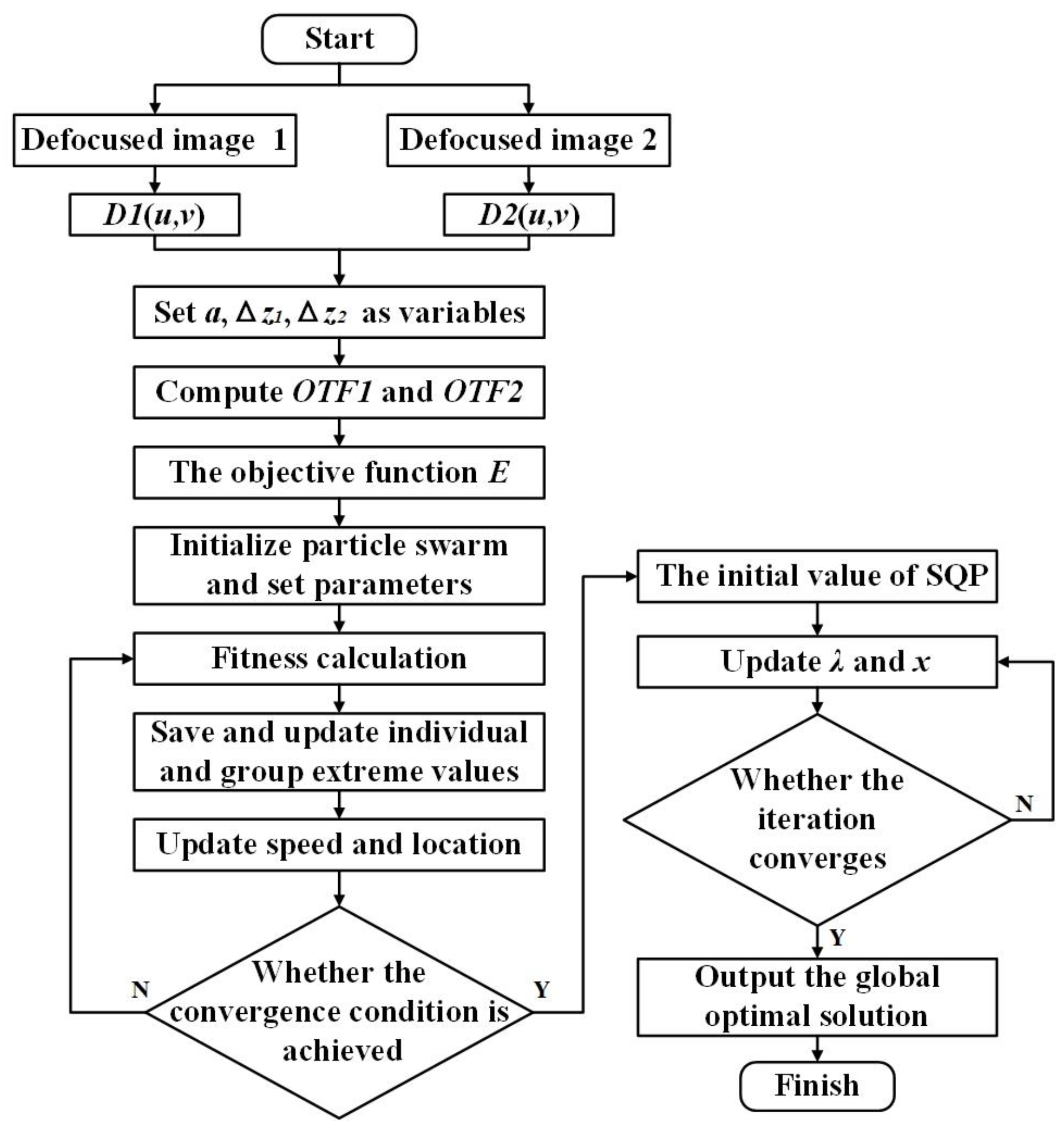
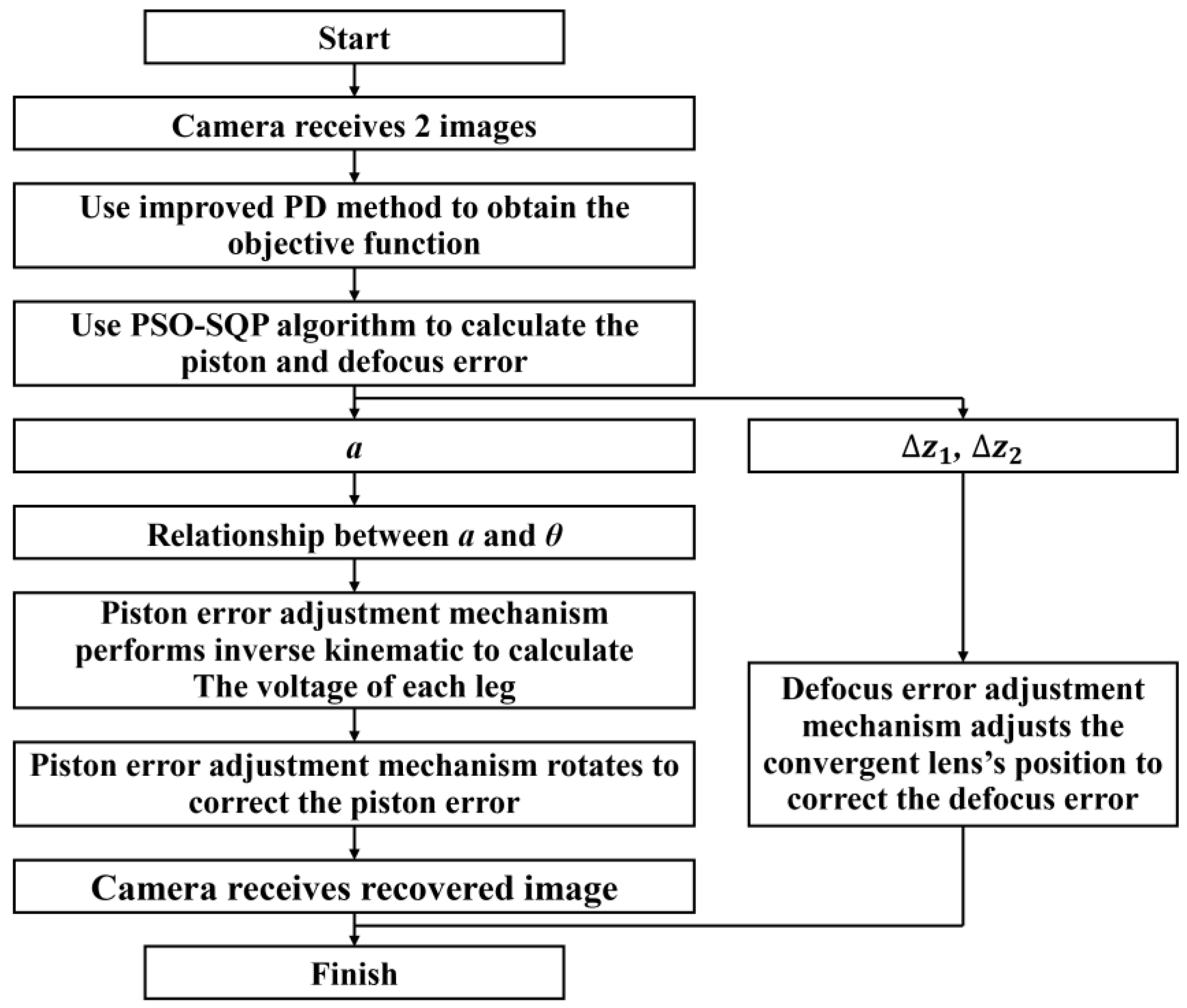
3. Improvements of PD and the Optimization Algorithms
3.1. Improvement of PD
3.2. Improvement of the Optimization Algorithms
4. Simulation
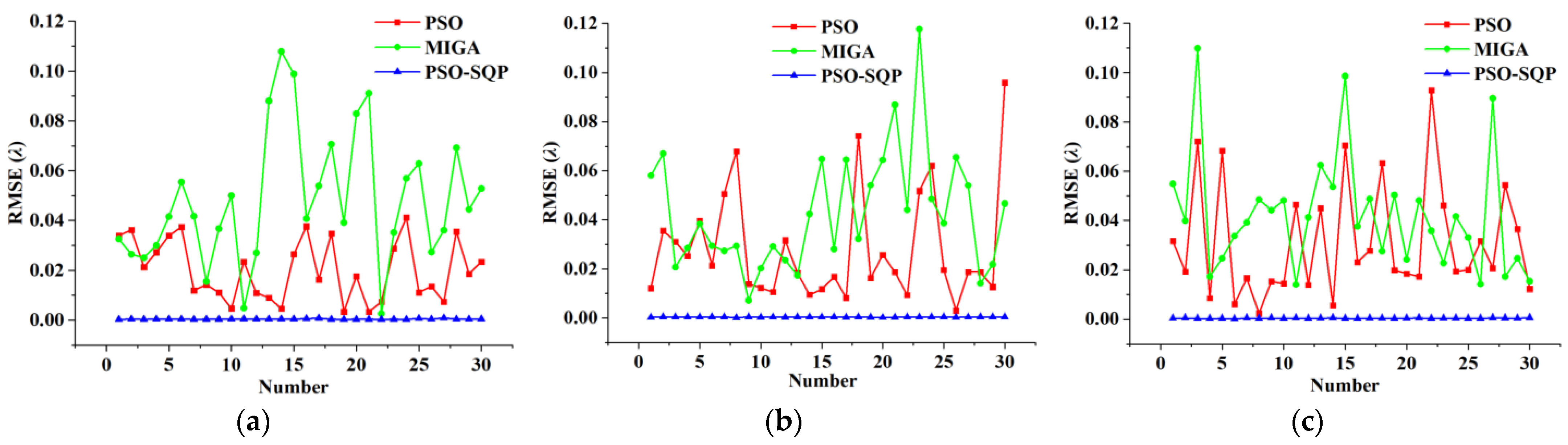
4.1. Piston Detection of Monochromatic Light Conditions
4.2. Piston Detection of Polychromatic Light Conditions
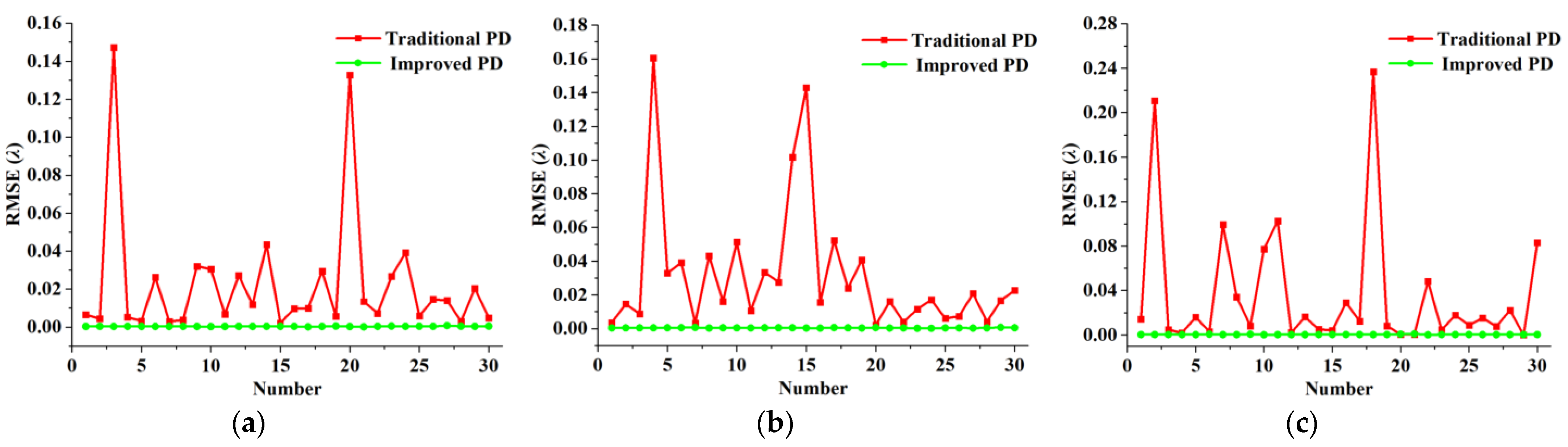
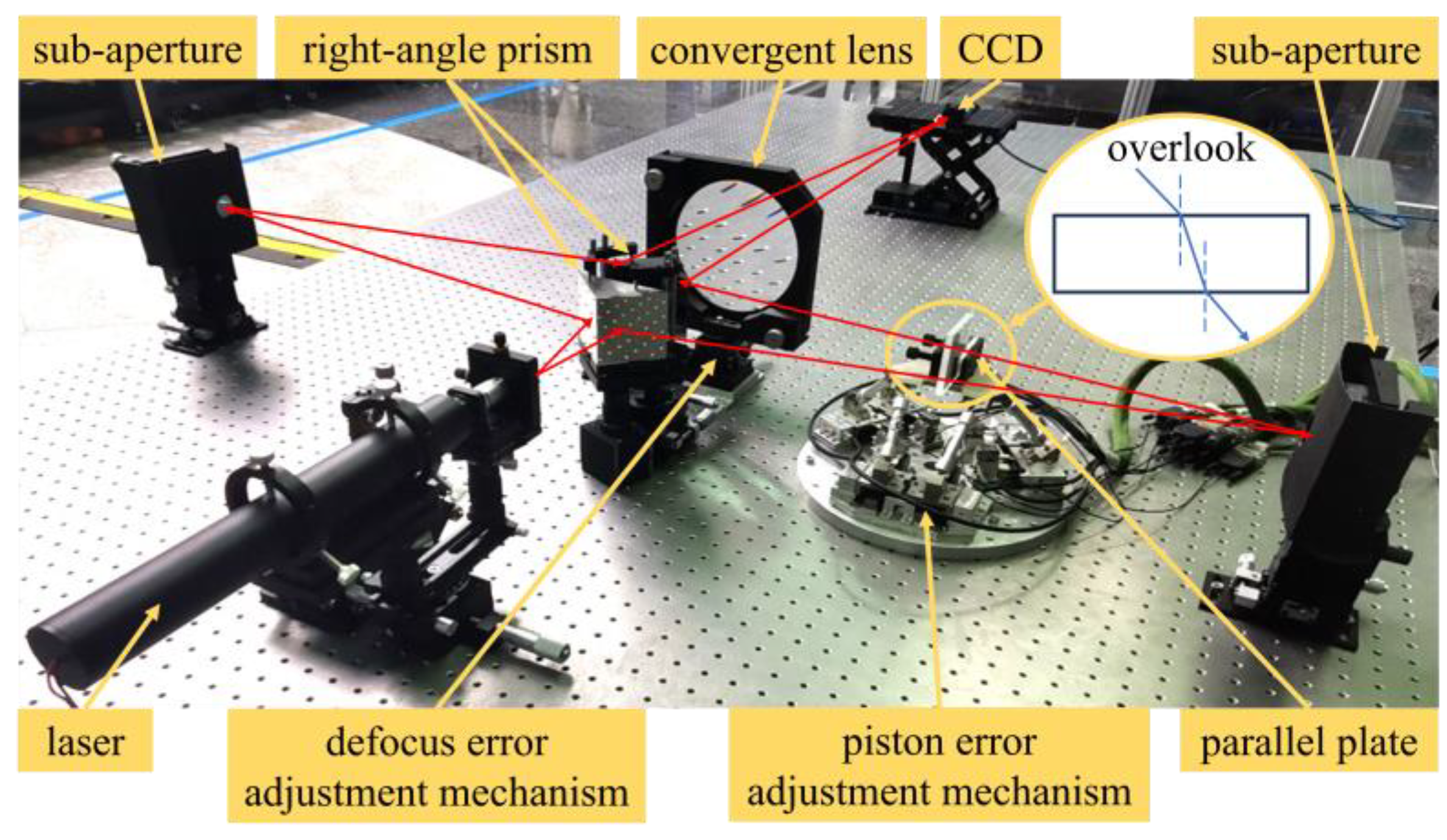
5. Experimental Test
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, L.; Yang, D. Co-phase state detection for segmented mirrors by dual-wavelength optical vortex phase-shifting interferometry. Opt. Express 2022, 30, 14088–14102. [Google Scholar] [CrossRef]
- Aden, B.M.; Marjorie, P.M. Large sparse-aperture space optical systems. Opt. Eng. 2002, 41, 1983–1994. [Google Scholar]
- Wang, D.; Ji, H. Experimental study on imaging and image restoration of optical sparse aperture systems. Opt. Eng. 2007, 46, 103201. [Google Scholar] [CrossRef]
- Gardner, J.P.; Mather, J.C. The James Webb space telescope. Space Sci. Rev. 2006, 123, 485–606. [Google Scholar] [CrossRef]
- Spano, P.; Zerbi, F.M. Challenges in optics for Extremely Large Telescope instrumentation. Astron. Nachr. 2010, 327, 649–673. [Google Scholar] [CrossRef]
- Hill, J.M. The Large Binocular Telescope. Appl. Opt. 2010, 49, D115–D122. [Google Scholar] [CrossRef] [PubMed]
- Trumper, I.; Hallibert, P.A. Optics technology for large-aperture space telescopes: From fabrication to final acceptance tests. Adv. Opt. Photonics 2018, 10, 644–702. [Google Scholar] [CrossRef]
- Li, X.; Yang, X. The piston error recognition technique used in the modified Shack–Hartmann sensor. Opt. Commun. 2021, 501, 127388. [Google Scholar] [CrossRef]
- Larkin, J.E.; Glassman, T.M. Exploring the structure of distant galaxies with adaptive optics on the Keck II Telescope. Publ. Astron. Soc. Pac. 2000, 112, 1526–1531. [Google Scholar] [CrossRef]
- Haffert, S.Y.; Close, L.M. Phasing the Giant Magellan Telescope with the holographic dispersed fringe sensor. J. Astron. Telesc. Inst. 2022, 8, 021513. [Google Scholar] [CrossRef]
- Esposito, S.; Pinna, E. Pyramid sensor for segmented mirror alignment. Opt. Lett. 2005, 30, 2572–2574. [Google Scholar] [CrossRef] [PubMed]
- Deprez, M.; Bellanger, C. Piston and tilt interferometry for segmented wavefront sensing. Opt. Lett. 2016, 41, 1078–1081. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Chan, W.K. A Tip–Tilt and Piston Detection Approach for Segmented Telescopes. Photonics 2020, 8, 3. [Google Scholar] [CrossRef]
- Vievard, S.; Cassaing, F. Large amplitude tip/tilt estimation by geometric diversity for multiple-aperture telescopes. J. Opt. Soc. Am. A 2017, 34, 1272–1284. [Google Scholar] [CrossRef] [PubMed]
- Mourard, D.; Dali, A.W. Group and phase delay sensing for cophasing large optical arrays. Mon. Not. R. Astron. Soc. 2014, 445, 2082. [Google Scholar] [CrossRef][Green Version]
- Simar, J.F.; Stockman, Y. Single-wavelength coarse phasing in segmented telescopes. Appl. Opt. 2015, 54, 1118–1123. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, W. Phasing piston error in segmented telescopes. Opt. Express 2016, 24, 19123–19137. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Zeng, Q. Simultaneous multi-piston measurement method in segmented telescopes. Opt. Express 2017, 25, 24540–24552. [Google Scholar] [CrossRef]
- Xie, Z.; Ma, H. Adaptive piston correction of sparse aperture systems with stochastic parallel gradient descent algorithm. Opt. Express 2018, 26, 9541–9551. [Google Scholar] [CrossRef]
- Lamb, M.P.; Correia, C. Quantifying telescope phase discontinuities external to adaptive optics systems by use of phase diversity and focal plane sharpening. J. Astron. Telesc. Inst. 2017, 3, 039001. [Google Scholar] [CrossRef]
- Li, C.C.; Yan, F.T. Cophasing detection of the segmented diffractive optical elements with the phase diversity method. Opt. Eng. 2022, 61, 123105. [Google Scholar] [CrossRef]
- Campbell, H.I.; Zhang, S. Generalized phase diversity for wave-front sensing. Opt. Lett. 2004, 29, 2707–2709. [Google Scholar] [CrossRef] [PubMed]
- Bolcar, M.R.; Fienup, J.R. Sub-aperture piston phase diversity for segmented and multi-aperture systems. Appl. Opt. 2009, 48, A5. [Google Scholar] [CrossRef] [PubMed]
- Yann, C.M.; Clerc, P.S. Performance evaluation of TRIBES, an adaptive particle swarm optimization algorithm. Swarm Intell. 2009, 3, 149–178. [Google Scholar]
- Sun, Z.B.; Sun, Y.Y. A new trust region-sequential quadratic programming approach for nonlinear systems based on nonlinear model predictive control. Eng. Optim 2019, 51, 1071–1096. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, New York, NY, USA, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Wang, J.; Wang, C. Airfoil shape and angle of attack optimization based on bézier curve and multi-island genetic algorithm. J. Fluid Eng. 2022, 144, 051203. [Google Scholar] [CrossRef]
- Wang, S.M.; Wu, Q.Y. Piston sensing for Golay-6 sparse aperture system with double-defocused sharpness metrics via ResNes-34. Sensors 2022, 22, 9484. [Google Scholar] [CrossRef]






| Design Variables | Group 1 | Group 2 | Group 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a(λ) | Δz1(λ) | Δz2(λ) | a(λ) | Δz1(λ) | Δz2(λ) | a(λ) | Δz1(λ) | Δz2(λ) | |
| Actual co-phase errors | 0.2475 | 0.5647 | 1.0245 | 0.5124 | 0.3575 | 1.2455 | 0.8287 | 0.6325 | 0.9874 |
| Parameter | λ | f | D | l | s | rθ |
|---|---|---|---|---|---|---|
| Unit | nm | mm | mm | mm | μm | ° |
| Value | 632.8 | 815 | 30 | 33 | 1.4 | 0.0024 |
| Methods | Average Value of RMSE (λ) | ||
|---|---|---|---|
| Group 1 | Group 2 | Group 3 | |
| Improved PD based on MIGA | 0.0482 | 0.0427 | 0.0413 |
| Improved PD based on PSO | 0.0202 | 0.0280 | 0.0313 |
| Improved PD based on PSO-SQP | 0.0003 | 0.0003 | 0.0005 |
| Methods | Average Value of RMSE (λ) | ||
|---|---|---|---|
| Group 1 | Group 2 | Group 3 | |
| Traditional PD based on PSO-SQP | 0.0230 | 0.0316 | 0.0365 |
| Improved PD based on PSO-SQP | 0.0003 | 0.0004 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, J.; Liu, T.; Tan, X.; Xu, Z.; Wu, Q. Piston Detection of Optical Sparse Aperture Systems Based on an Improved Phase Diversity Method. Photonics 2023, 10, 1039. https://doi.org/10.3390/photonics10091039
Zhao Y, Li J, Liu T, Tan X, Xu Z, Wu Q. Piston Detection of Optical Sparse Aperture Systems Based on an Improved Phase Diversity Method. Photonics. 2023; 10(9):1039. https://doi.org/10.3390/photonics10091039
Chicago/Turabian StyleZhao, Yang, Jiabiao Li, Tai Liu, Xiangquan Tan, Zhenbang Xu, and Qingwen Wu. 2023. "Piston Detection of Optical Sparse Aperture Systems Based on an Improved Phase Diversity Method" Photonics 10, no. 9: 1039. https://doi.org/10.3390/photonics10091039
APA StyleZhao, Y., Li, J., Liu, T., Tan, X., Xu, Z., & Wu, Q. (2023). Piston Detection of Optical Sparse Aperture Systems Based on an Improved Phase Diversity Method. Photonics, 10(9), 1039. https://doi.org/10.3390/photonics10091039





