Geometric Visualization of the 3D Polarimetric Information of an Arbitrary Electromagnetic Field
Abstract
:1. Introduction
2. Methods
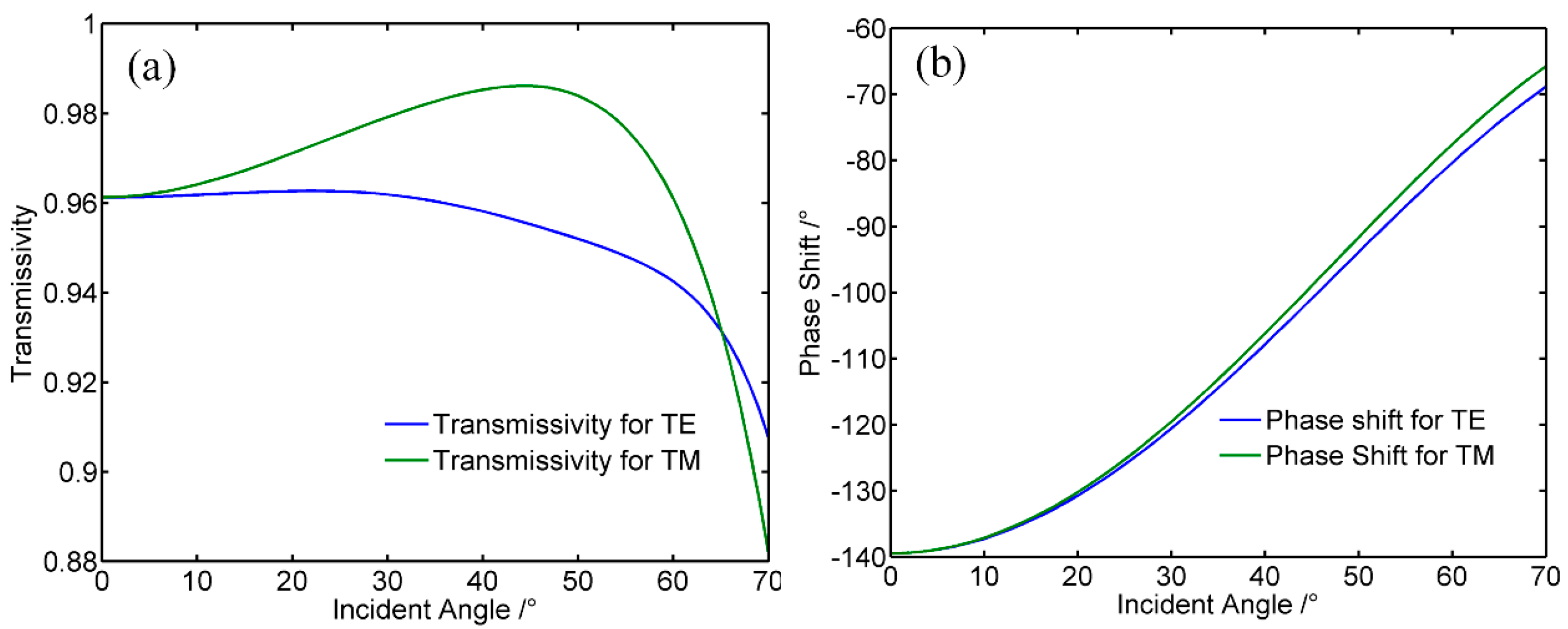
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellis, J.; Dogariu, A.; Ponomarenko, S.; Wolf, E. Degree of polarization of statistically stationary electromagnetic fields. Opt. Commun. 2005, 248, 333–337. [Google Scholar] [CrossRef]
- Dennis, M.R. A three−dimensional degree of polarization based on Rayleigh scattering. J. Opt. Soc. Am. A 2007, 24, 2065–2074. [Google Scholar] [CrossRef] [PubMed]
- Setälä, T.; Lindfors, K.; Friberg, A.T. Degree of polarization for in 3D optical fields generated from a partially polarized plane wave. Opt. Lett. 2009, 34, 3394–3397. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J. Interpretation of the coherency matrix for three−dimensional polarization states. Phys. Rev. A 2014, 90, 043858–043877. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Three−dimensional polarization states of monochromatic light fields. J. Opt. Soc. Am. A 2011, 28, 2279–2285. [Google Scholar] [CrossRef] [PubMed]
- Voipio, T.; Setälä, T.; Shevchenko, A.; Friberg, A.T. Polarization dynamics and polarization time of random three−dimensional electromagnetic fields. Phys. Rev. A 2010, 82, 239–241. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Y.; Liu, Z.; Zhou, J.; Bryanston−Cross, P.J.; Li, Y.; He, W. Three−dimensional polarization algebra for all polarization sensitive optical systems. Opt. Express 2018, 11, 14109–14122. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, C.J.R.; Castello, M.; Diaspro, A. Three−dimensional polarization algebra. J. Opt. Soc. Am. A 2016, 33, 1938–1947. [Google Scholar] [CrossRef] [PubMed]
- Dennis, M.R. Geometric interpretation of the three−dimensional coherence matrix for nonparaxial polarization. J. Opt. A Pure Appl. Opt. 2004, 6, S26–S31. [Google Scholar] [CrossRef]
- Sheppard, C.J. Geometric representation for partial polarization in three dimensions. Opt. Lett. 2012, 37, 2772–2774. [Google Scholar] [CrossRef] [PubMed]
- Samson, J.C. Descriptions of the polarization states of vector processes: Applications to ULF magnetic fields. Geophys. J. R. Astron. Soc. 1973, 34, 403–419. [Google Scholar] [CrossRef]
- Barakat, R. Degree of polarization and the principal idempotents of the coherency matrix. Opt. Commun. 1977, 23, 147–150. [Google Scholar] [CrossRef]
- Setälä, T.; Shevchenko, A.; Kaivola, M.; Friberg, A.T. Degree of polarization for optical near fields. Phys. Rev. 2002, 66, 016615–016622. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J.; Norrman, A.; Friberg, A.T.; Setälä, T. Polarimetric purity and the concept of degree of polarization. Phys. Rev. A 2018, 97, 023838–023842. [Google Scholar] [CrossRef]
- Gil, J.J. Polarimetric characterization of light and media: Physical quantities involved in polarimetric phenomena. Eur. Phys. J. Appl. Phys. 2007, 40, 1–47. [Google Scholar] [CrossRef]
- Gil, J.J.; San José, I. 3D polarimetric purity. Opt. Commun. 2010, 283, 4430–4434. [Google Scholar] [CrossRef]
- Gil, J.J.; Friberg, A.T.; Setälä, T. Structure of polarimetric purity of three−dimensional polarization states. Phys. Rev. A 2017, 95, 053856–053865. [Google Scholar] [CrossRef]
- Ellis, J.; Dogariu, A. Optical polarimetry of random fields. Phys. Rev. Lett. 2005, 95, 203905–203908. [Google Scholar] [CrossRef] [PubMed]
- Leppänen, L.-P.; Friberg, A.T.; Setälä, T. Partial polarization of optical beams and near fields probed with a nanoscatterer. J. Opt. Soc. Am. A 2014, 31, 1627–1635. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetries of Baryons and Mesons, Murray Gell-Mann. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef]

| Stokes Parameters | Physical Meanings |
|---|---|
| s0 | Total intensity |
| s1 | Sum of intensities of ±45° polarized components in x–y plane |
| s2 | Difference in intensities of left/right−handed circular polarized components in x–y plane |
| s3 | Difference in intensities between the x and y polarized components |
| s4 | Sum of intensities of ±45° polarized components in x–z plane |
| s5 | Difference in intensities of left/right−handed circular polarized components in x–z plane |
| s6 | Sum of intensities of ±45° polarized components in y–z plane |
| s7 | Difference in intensities of left/right−handed circular polarized components in y–z plane |
| s8 | Sum of differences in intensities between the x and y polarized components and the z polarized component, respectively. |
| Amplification factor | 100× |
| Numerical aperture (NA) | 1.25 |
| Object height/mm | 0.11 |
| Working wavelength/nm | 486~656 |
| Total length/mm | 315.66 |
| Effective working distance/mm | 0.42 |
| Back working distance/mm | 199.447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, B.; Wei, W.; Zeng, X.; Fu, Y.; Zhao, Y. Geometric Visualization of the 3D Polarimetric Information of an Arbitrary Electromagnetic Field. Photonics 2023, 10, 1040. https://doi.org/10.3390/photonics10091040
Li Y, Li B, Wei W, Zeng X, Fu Y, Zhao Y. Geometric Visualization of the 3D Polarimetric Information of an Arbitrary Electromagnetic Field. Photonics. 2023; 10(9):1040. https://doi.org/10.3390/photonics10091040
Chicago/Turabian StyleLi, Yahong, Bosong Li, Wenhao Wei, Xiangwei Zeng, Yuegang Fu, and Yu Zhao. 2023. "Geometric Visualization of the 3D Polarimetric Information of an Arbitrary Electromagnetic Field" Photonics 10, no. 9: 1040. https://doi.org/10.3390/photonics10091040
APA StyleLi, Y., Li, B., Wei, W., Zeng, X., Fu, Y., & Zhao, Y. (2023). Geometric Visualization of the 3D Polarimetric Information of an Arbitrary Electromagnetic Field. Photonics, 10(9), 1040. https://doi.org/10.3390/photonics10091040





