Anisotropic Purcell Effect and Quantum Interference in Fractal Aggregates of Nanoparticles

Abstract

We study theoretically the emergence of an anisotropic Purcell factor in random two-dimensional fractal aggregates of nanoparticles. These nanoparticles can either be metallic nanoparticles made of silver, which exhibit surface plasmon resonances, or high-index dielectric nanoparticles like silicon, which possess optical Mie resonances. To calculate the spontaneous emission rates of a quantum emitter, we utilize the electromagnetic Green’s tensor within the framework of the coupled-dipole method. Our findings reveal that the Purcell factor exhibits spatial variations, with certain regions, referred to as hot spots, displaying high values for dipoles oriented within the plane of the fractal aggregate, while dipoles oriented vertically to the aggregate have values close to unity. This anisotropy in the Purcell factor leads to significant quantum interference effects in the spontaneous emission paths of multi-level quantum emitters. As a consequence of this quantum interference, we demonstrate the occurrence of population trapping in a V-type quantum emitter embedded within a fractal aggregate of nanoparticles which cannot otherwise take place if the emitter is placed in vacuum.

1. Introduction

The Purcell effect [1] refers to the enhancement of the spontaneous emission rate of an excited quantum emitter in the presence of a resonant electromagnetic environment [2,3]. According to the principles of quantum electrodynamics, when a quantum emitter such as an atom, molecule, or quantum dot interacts with its surrounding electromagnetic field, the emission and absorption processes are modified by the local density of states (LDOS). Near metallic nanoparticles, the LDOS can be greatly enhanced, leading to an increased probability of spontaneous emission. This enhancement arises from the coupling between the emitter and the localized surface plasmons supported by the metallic nanoparticles. The Purcell effect in the vicinity of metallic nanoparticles can be utilized to manipulate and control light–matter interactions at the nanoscale. It enables the enhancement of spontaneous emission rates of nearby quantum emitters, such as fluorescent molecules or quantum dots which is particularly important in the development of efficient light-emitting devices, single-photon sources, and optical sensors [4,5,6,7]. Furthermore, the LDOS enhancement near metallic nanoparticles can be harnessed for enhancing light absorption in photodetectors and solar cells. The increased LDOS improves the absorption efficiency of incident light, leading to enhanced device performance and higher photoconversion efficiency [8,9,10,11]. In addition, the Purcell effect enables sensitive detection and analysis of chemical and biological species. By coupling the analyte molecules with metallic nanoparticles, the LDOS near the nanoparticles can be enhanced, resulting in increased sensitivity of spectroscopic techniques such as surface-enhanced Raman scattering (SERS) and fluorescence spectroscopy, with applications in biosensing, environmental monitoring, and chemical analysis [12,13,14,15]. Foremost, the Purcell effect is of great significance in the field of quantum optics and quantum information processing. It allows for efficient coupling between quantum emitters, such as quantum dots or color centers in diamond [16], and photons, which is crucial for various quantum technologies, including quantum communication, quantum computing, and quantum cryptography [17,18,19,20]. We note that high-index dielectric structures can also result in large Purcell factors [21,22].

The anisotropic Purcell effect refers to the modification of the spontaneous emission rate in a direction-dependent manner. In other words, the emission rate of an excited emitter is altered differently depending on the orientation of its transition dipole moment with respect to the local electromagnetic field. Anisotropic Purcell effects can arise in various scenarios. For example, in plasmonic systems, the presence of anisotropic nanostructures can give rise to localized surface plasmon resonances with different polarizations [23]. The interaction between an emitter and these anisotropic plasmonic resonances can lead to direction-dependent modification of the spontaneous emission rate. Additionally, anisotropic Purcell effects can be observed in photonic crystal structures, where the anisotropy arises from the structure’s periodic arrangement of materials with different refractive indices [24]. In a similar manner, the Purcell effect can be observed in metamaterials [25,26].

Quantum interference (QI) arises when two nearly degenerate excited states of a quantum emitter (QE) undergo spontaneous emission (SE) and interfere as they transition to a common ground state. For QI to occur, the transition dipole moments of the SE pathways should be nonorthogonal, a condition facilitated by the presence of anisotropic Purcell effect [27,28]. Notably, significant differences in the decay rates for orthogonal dipole moments give rise to observable QI [29]. QI in quantum emitters leads to intriguing phenomena in quantum optics, including coherent population trapping [30,31,32], entanglement [33,34,35], lasing without inversion [36,37], narrow spectral lines in resonance fluorescence [28,38,39], optical transparency with slow light [40,41], gain without inversion [42], and enhanced Kerr nonlinearity [43,44,45,46,47].

In the present work, we study the emergence of the (anisotropic) Purcell effect in fractal aggregates of metallic and high-index dielectric nanoparticles. Fractal aggregates of nanoparticles, dielectric or metallic, are structures formed when multiple nanoparticles come together through attractive forces, such as van der Waals interactions or electrostatic forces. These aggregates exhibit a complex, fractal-like geometry, characterized by self-similar patterns at different length scales [48,49]. The fractal nature arises from the iterative process of nanoparticle aggregation [50]. One of the key phenomena associated with fractal aggregates of metallic nanoparticles is the generation and manipulation of surface plasmons. Namely, surface plasmons tend to be localized in small nm sized areas, namely hot spots; this is because the plane running waves are not eigenfunctions of the operator of dilation symmetry that characterizes fractals [51] and therefore fractals cannot support running waves. The precise location and intensity of the “hot spots” depend on various factors, including the size, shape, composition, and arrangement of the nanoparticles within the fractal structure. The positions of the hot spots change chaotically but reproducibly with frequency and/or polarization [52,53,54,55,56,57,58,59,60]. This behavior is reminiscent of that of speckles formed by laser light scattering off a rough surface, although there is a crucial distinction: the scale size of fractal plasmons within the hot spots is on the order of nanometers, contrasting with the micrometer scale typically observed for photons.

In this study, we aim to explore the formation of “hot spots” in the LDOS and therefore in the Purcell effect within fractal clusters of nanoparticles. Our findings reveal a significant enhancement of the Purcell effect, as well as, a strong dependence of the effect on the orientation of the excited dipole moment of the quantum emitter (anisotropic Purcell effect) which leads to the emergence of QI in the emitter. In particular, we show that the emerging degree of QI in fractal aggregates of nanoparticles can lead to optical population trapping in a multi-level quantum emitter residing in a “hot spot” of the aggregate. Our calculations are based on the EM Green’s tensor for a fractal aggregates of nanoparticles obtained via the coupled-dipole method.

2. EM Green’s Tensor in the Coupled-Dipole Method

Generally, the full EM Green’s tensor $\mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime };\omega )$ of an inhomogeneous medium (non-magnetic) characterized by a (relative) spatially and frequency-dependent dielectric function $ϵ(\mathbf{r},\omega )$ is the solution of the wave equation

$$\nabla \times \nabla \times \mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime };\omega )-\frac{ϵ(\mathbf{r},\omega ){\omega }^2}{c^2}\mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime };\omega )={\mathbf{1}}_3·\delta (\mathbf{r},{\mathbf{r}}^{\prime }).$$

(1)

We analyze an ensemble of metal nanoparticles embedded in a uniform medium or vacuum. Our assumption is that the medium is an unbounded, non-dispersive, lossless, and isotropic material with a dielectric constant ${ϵ}_d$ and magnetic permeability $\mu =1$. In this case, the Green’s tensor is the solution of

$$\nabla \times \nabla \times {\mathbf{G}}^0(\mathbf{r},{\mathbf{r}}^{\prime };\omega )-k^2{\mathbf{G}}^0(\mathbf{r},{\mathbf{r}}^{\prime };\omega )={\mathbf{1}}_3·\delta (\mathbf{r},{\mathbf{r}}^{\prime }),$$

(2)

where $k=\frac{\sqrt{{ϵ}_d}\omega }{c}$ is the wavevector inside the material, $\omega$ is the angular frequency of light, c is the vacuum light speed, and ${\mathbf{1}}_3$ is the 3 × 3 unit matrix. By solving the above equation, one finds that the Green’s tensor of the bulk material ${\mathbf{G}}_{ij}^0\left(\omega \right)\left[\equiv {\mathbf{G}}^0({\mathbf{r}}_i,{\mathbf{r}}_j;\omega )\right]$ is

$${\mathbf{G}}_{ij}^0=\frac{e^{ik{r}_{ij}}}{4\pi r_{ij}}\left[\left(1+\frac{ik{r}_{ij}-1}{k^2{r}_{ij}^2}\right)·{\mathbf{1}}_3+\frac{3-3ik{r}_{ij}-k^2{r}_{ij}^2}{k^2{r}_{ij}^2}·\left({\widehat{\mathbf{r}}}_{ij}\otimes {\widehat{\mathbf{r}}}_{ij}\right)\right],$$

(3)

(similar to the electric component of the Green function in free space with $k=k_0=\omega /c$ and $e_d=1$). In the given equation, ${\mathbf{r}}_{ij}={\mathbf{r}}_i-{\mathbf{r}}_j$ represents the vector connecting the ith and jth dipoles, $r_{ij}$ denotes its magnitude, and ${\widehat{\mathbf{r}}}_{ij}$ corresponds to the unit vector aligned with the direction of ${\mathbf{r}}_{ij}$.

In the framework of the coupled-dipole method, the electromagnetic Green’s tensor ${\mathbf{G}}_{ij}\left(\omega \right)\left[\equiv \mathbf{G}({\mathbf{r}}_i,{\mathbf{r}}_j;\omega )\right]$ of a collection of N nanoparticles can be determined by solving the following linear system of $3N$ equations [61]:

$$\sum _k\left[{\delta }_{ik}-\frac{{\omega }^2{ϵ}_d}{c^2}{\alpha }_k\left(\omega \right)·{\mathbf{G}}_{ik}^0\left(\omega \right)\right]·{\mathbf{G}}_{kj}\left(\omega \right)={\mathbf{G}}_{ij}^0\left(\omega \right),$$

(4)

where ${\mathbf{G}}^{\mathbf{0}}$ is the (homogeneous) Green’s tensor of Equation (3), and ${\alpha }_k$ is the polarizability tensor of the kth NP. In the case of small spherical nanoparticles with a radius of S and a relative dielectric permittivity of ${ϵ}_m$, when these nanoparticles are embedded in a material with a relative dielectric permittivity of ${ϵ}_d$, the polarizability without considering photon coupling to the environment can be determined using the Clausius–Mossoti relation

$${\alpha }^0\left(\omega \right)=4\pi {ϵ}_d{S}^3\frac{{ϵ}_m\left(\omega \right)-{ϵ}_d}{{ϵ}_m\left(\omega \right)+2{ϵ}_d}.$$

(5)

A more accurate formula for the polarizability is

$$\alpha \left(\omega \right)=\frac{{\alpha }^0\left(\omega \right)}{1-\frac{i{\alpha }^0\left(\omega \right){\omega }^3\sqrt{{ϵ}_d}}{6\pi c^3}},$$

(6)

where radiation reaction effects are taken into account.

To determine $\mathbf{G}(\mathbf{r},{\mathbf{r}}^{\prime };\omega )$ for a collection of N metallic nanoparticles, the following procedure is employed. When calculating $\mathbf{G}$ for $\mathbf{r}={\mathbf{r}}^{\prime }$, $N+1$ dipoles are created, with the first N representing the metallic nanoparticles in the collection using the polarizabilities described in Equation (6), and the last one being a fictitious dipole placed at $\mathbf{r}={\mathbf{r}}^{\prime }$ with zero polarizability. Similarly, when calculating $\mathbf{G}$ for $\mathbf{r}\ne {\mathbf{r}}^{\prime }$, $N+2$ dipoles are generated, and the last two polarizations are set to zero, representing fictitious dipoles at $\mathbf{r}$ and ${\mathbf{r}}^{\prime }$. Equation (4) is solved using a numerical solver, such as the conjugate gradient method. The imaginary part of the EM Green’s tensor is associated with the directional spontaneous emission rates of a QE via

$${\gamma }_{\alpha }=\frac{1}{2}{d}^2{\omega }^2\mathrm{Im}\left[G_{ii}^{\alpha \alpha }\left(\omega \right)\right],$$

(7)

where i refers to the position ${\mathbf{r}}_i$ of the dipole emitter and $\alpha =x,y,z$. d refers to the dipole moment of the emitter.

3. Results and Discussion

In the present work, our primary objective is to investigate the emergence of the anisotropic Purcell effect in the space among the particles in fractal aggregates of such. In this respect, we investigate the vacuum fluctuations (which cause the spontaneous emission of quantum emitters) in fractal aggregates of nanoparticles, namely the directionality of vacuum fluctuations occurring in the neighbourhood of the fractal aggregate. Since the anisotropic Purcell effect is maximized when there exists a large difference in the spontaneous emission rates between the vertical and tangential orientations of a dipole relative to a material surface [23], we choose to focus on 2D fractal aggregates of nanoparticles, such as that of Figure 1, which consists of 100 nanoparticles. Due to the 2D nature of the aggregate, we expect the realization of a strong anisotropic Purcell effect. The particular configuration shown in Figure 1 exhibits hot spots of the photonic LDOS [62].

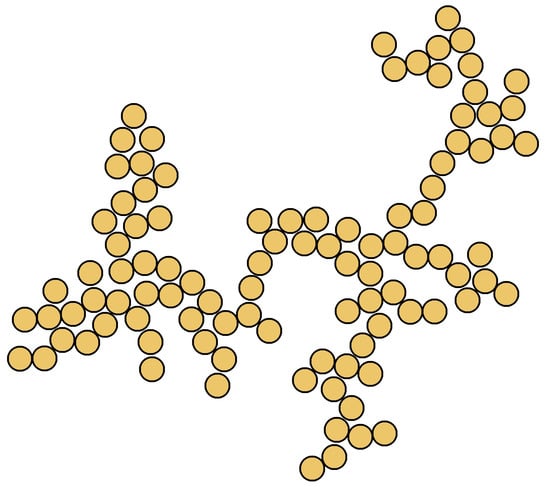
Figure 1. A 2D fractal aggregate of 100 nanoparticles.

To begin with, we assume that the nanoparticles are made of silicon, i.e., dielectric nanoparticles with dielectric constant $ϵ=11.9$. We note that silicon, due to its high dielectric constant, is considered one of the major alternative low-loss materials mimicking the plasmonic response of mainstream noble-metal materials (silver, gold, copper) [63,64,65]. Silicon nanoparticles exhibit Mie resonances resembling the localized surface plasmon resonances and have lower optical losses compared to traditional plasmonic materials, holding promise for applications in sensing, light harvesting, and light–matter interactions due to their compatibility with silicon-based technologies [66]. Similar effects such as those reported below can be observed with fractal aggregates of other types of dielectric nanoparticles such as transition metal dichalcogenide [67] or perovskite nanoparticles [68].

We define the directional (partial) Purcell factor as

$$F_{\alpha }=\frac{{\gamma }_{\alpha }}{{\gamma }_0},$$

(8)

with $\alpha =x,y,z$. ${\gamma }_0$ is the spontaneous emission decay in vacuum. Figure 2 shows the directional Purcell factor $F_{\alpha }$ for frequency $ћ\omega =4.6$ eV, within the $xy$-($z=0$) plane, for the fractal aggregate of Figure 1 wherein the nanoparticles are made of silicon and have a radius $S=10.75$ nm. We note that we only plot $F_{\alpha }$ within a subarea of the entire fractal of Figure 1. Also, we do not include $F_{\alpha }$ within the nanoparticles in our representation, as it lacks practical utility. This is because quantum emitters (QEs) are either attached to the surface of the nanoparticles or positioned around them. We observe remarkably elevated Purcell factors within the inter-nanoparticle region, reaching up to 40 times the decay rate in vacuum (for $F_x$). Notably, we see that $F_x$ and $F_y$ exhibit significantly stronger magnitudes compared to $F_z$, indicating the presence of a robust anisotropic Purcell effect. This observation further confirms the emergence of quantum interference (QI).

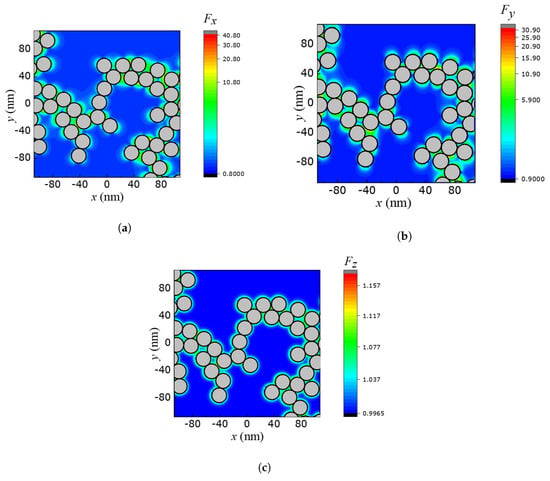
Figure 2. The Purcell factor F in the $xy$-plane ($z=0$) for an x- (a), y- (b) and z- (c) oriented dipole (QE) embedded in a fractal aggregate of silicon nanoparticles with radius $S=10.75$ nm at frequency $ћ\omega =4.2$ eV.

In order to quantify the emergence of QI, we use the degree of QI as

$$p=\frac{F_{\Vert }-F_{\perp }}{F_{\Vert }+F_{\perp }},$$

(9)

where, in our case,

$$\begin{array}{c}\hfill F_{\Vert }=\frac{F_x+F_y}{2}\end{array}$$

(10)

$$\begin{array}{c}\hfill F_{\perp }=F_z.\end{array}$$

(11)

From Figure 3, it is evident that there several areas (“hot spots”) where the degree of QI is highly localized and assumes significantly high (absolute) values. Namely, there are several hot spots where QI exceeds the value of 0.9 and is very close to the theoretical maximum of $p=1$. For this particular frequency ($ћ\omega =4.6$ eV), the maximum value is $p=0.916$, and it occurs at the point $x=-94.7$ nm, $y=6.5$ nm.

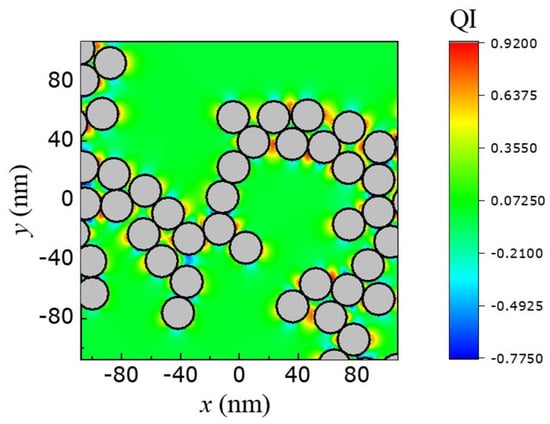
Figure 3. The degree of QI, p, in the $xy$-plane ($z=0$) for a fractal aggregate of silicon nanoparticles with radius $S=10.75$ nm at frequency $ћ\omega =4.6$ eV.

The occurrence of concentrated regions of intense electric field and their associated properties is a distinctive characteristic commonly observed in fractal aggregates composed of nanoparticles. Our observations reveal that the high values of the quantum interference degree (p) arise from the significantly elevated values of $F_{\Vert }$ in comparison to those of $F_{\perp }$, which are close to unity. The amplified values of $F_{\Vert }$, which represent the partial local density of states (LDOS) for dipoles aligned parallel to the fractal cluster’s planes, can be attributed to the fractal geometry. In fractals, localized optical excitations, such as Mie resonances and surface plasmons, tend to be confined to small nanometer-scale areas known as hot spots. This is because the plane running waves do not conform to the eigenfunctions of the dilation symmetry operator that characterizes fractals. Consequently, these excitations in fractals are strongly influenced by the fractal morphology, resulting in the presence of both hot spots (areas with high local fields) and cold spots (areas with low local fields). The spatial distribution of these regions is highly sensitive to the frequency and polarization of the applied field. The positions of the hot spots change chaotically but reproducibly with frequency and/or polarization.

In Figure 4, we show the degree of QI for the same fractal cluster as that of Figure 3 but with silver nanoparticles replacing the silicon ones. The silver nanoparticles have the same size ($S=10.75$ nm) and their EM response is modeled by a Drude-type dielectric function

$$ϵ\left(\omega \right)={ϵ}_{\infty }-\frac{{\omega }_p^2}{\omega (\omega +\mathrm{i}\gamma )},$$

(12)

with ${ϵ}_{\infty }=3.718$, ${\omega }_p=9.716$ eV and $\gamma =0.021$ eV [69]. The plot of Figure 4 is calculated for $ћ\omega =9.1$ eV. We observe that the hot and cold spots appearing in the case of metallic nanoparticles are more intense than the case of the dielectric (Si) ones, possibly due to the fact that the hot (cold) spots emerge from localized surface plasmon resonances rather than Mie resonances. The maximum value of QI is $p=0.958$ and occurs at $x=-99$ nm, $y=94.6$ nm. We note that the results presented in Figure 2, Figure 3 and Figure 4 refer to the case where the nanoparticles of the aggregate are placed in vacuum (air). If the nanoparticles are placed within a dielectric material [70], our results are not affected except from a slight red shift of the frequencies of Figure 2, Figure 3 and Figure 4 where QI is maximized.

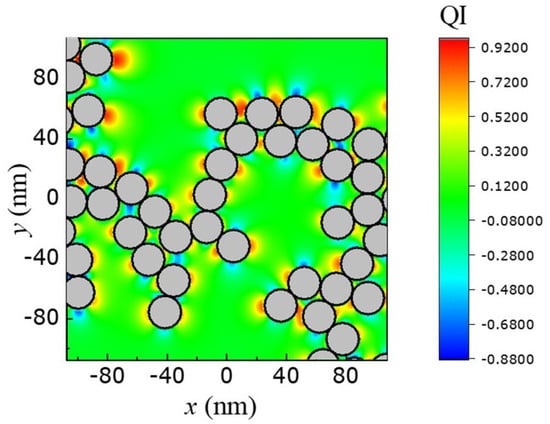
Figure 4. The degree of QI, p, in the $xy$-plane ($z=0$) for a fractal aggregate of silver nanoparticles with radius $S=10.75$ nm at frequency $ћ\omega =9.1$ eV.

In our calculations, we have assumed that the nanoparticles of the fractal aggregate have a radius of around 10 nm. The use of larger nanoparticles would not influence the occurrence of high values of the degree of QI, p. Namely, for the silicon nanoparticles, due to their frequency-independent dielectric function $ϵ=11.9$, the macroscopic Maxwell’s equations possess a scaling property [71] which makes them invariant to a contraction or expansion of the size of the nanoparticles. This means that if we “expand” the silicon nanoparticles by a factor a, we obtain the same plots of Figure 2 and Figure 3 but for frequencies $\omega$/a. However, this scaling property does not exist for metallic nanoparticles whose dielectric function is frequency-dependent and a characteristic length exists which depends on the plasma frequency of the metal (silver, in our case). However, an increase in the size of the silver nanoparticles is not expected to influence the emergence of high values of QI (close to unity) [23,72], although the LDOS is expected to increase with particle size leading to “hotter” LDOS spots in the fractal aggregate.

The most direct application of the presence of an anisotropic Purcell effect is the occurrence of population trapping in a multi-level QE, such as the three-level V-type QE of Figure 5. This V-type system consists of two identical Zeeman sublevels, namely $|2⟩$ and $|3⟩$, along with a single ground state $|1⟩$.

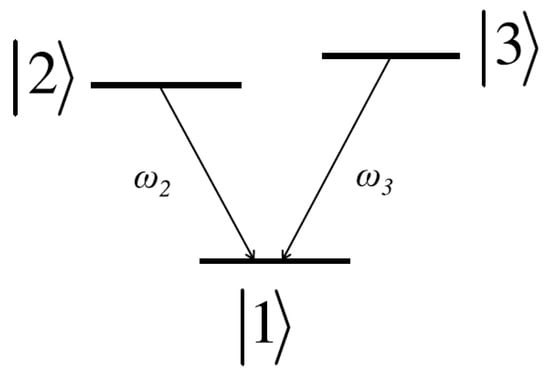
Figure 5. A V-type three-level quantum emitter.

In this model, we assume that the excited levels can undergo spontaneous emission to return to the ground state, while direct transitions between the excited levels are prohibited. By adopting a density-matrix approach and solving the corresponding rate equations in the rotating-wave and Wigner–Weisskopf approximations, the populations of the two excited levels read as [23,72,73,74]

$$\begin{array}{cc}\hfill {\rho }_{22}\left(t\right)& =\frac{1}{4}{(e^{-{\gamma }_{\Vert }t}+e^{-{\gamma }_{\perp }t})}^2\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\rho }_{33}\left(t\right)& =\frac{1}{4}{(e^{-{\gamma }_{\Vert }t}-e^{-{\gamma }_{\perp }t})}^2,\hfill \end{array}$$

(14)

where we assume that only the state $|2⟩$ is initially populated, i.e., we have ${\rho }_{22}\left(0\right)=1$, ${\rho }_{33}\left(0\right)=0$, ${\rho }_{23}\left(0\right)=0$. When QI is not present, $(p=0)$, the population of the state $|2⟩$ evolves exponentially with

$${\rho }_{22}\left(t\right)=e^{-({\gamma }_{\Vert }+{\gamma }_{\perp })t},$$

(15)

and the state $|3⟩$ is not involved in the dynamics, which means

$${\rho }_{33}\left(t\right)=0.$$

(16)

Figure 6 shows the time evolution of the V-type QE of Figure 5 for the maximum QI value occurring for the case of a fractal aggregate of silicon nanoparticles, in which case $p=0.916$. We observe a significant transfer of population to state $|3⟩$ following a rapid initial decay of state $|2⟩$, which is primarily influenced by the decay rate ${\gamma }_{\Vert }$. Subsequently, both states exhibit simultaneous population decay, governed by a decay rate of $2{\gamma }_{\perp }$. Conversely, in the absence of quantum interference (QI), the population of the initially excited state decays exponentially with a rate of ${\gamma }_{\perp }+{\gamma }_{\Vert }$, while the other state remains unexcited. Similar results for the population dynamics are also shown when the QE is embedded within a fractal cluster of silver nanoparticles; see Figure 7. We note, however, that the population excitation of state $|3⟩$ is larger than for the case of the fractal cluster of silicon nanoparticles.

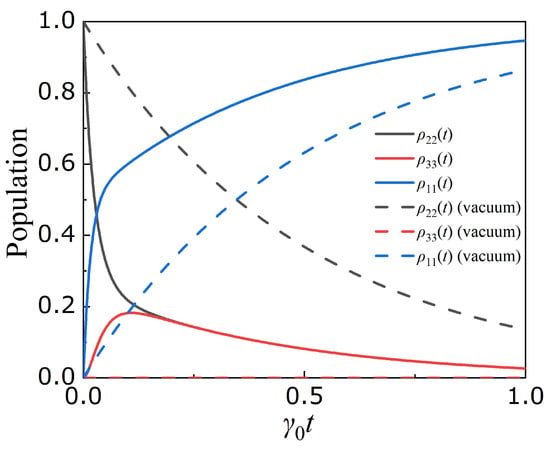
Figure 6. Solid lines: population of states $|1⟩$, $|2⟩$, $|3⟩$ as a function of time when the QE of Figure 5 is embedded in the fractal aggregate of silicon nanoparticles at the point where the maximum QI occurs (see text). In this case, ${\gamma }_{\Vert }=31.98{\gamma }_0$, ${\gamma }_{\perp }=1.12{\gamma }_0$. Broken lines: population of states $|1⟩$, $|2⟩$, $|3⟩$ as a function of time when the QE of Figure 5 is placed in vacuum in which case ${\gamma }_{\Vert }={\gamma }_{\perp }={\gamma }_0$.

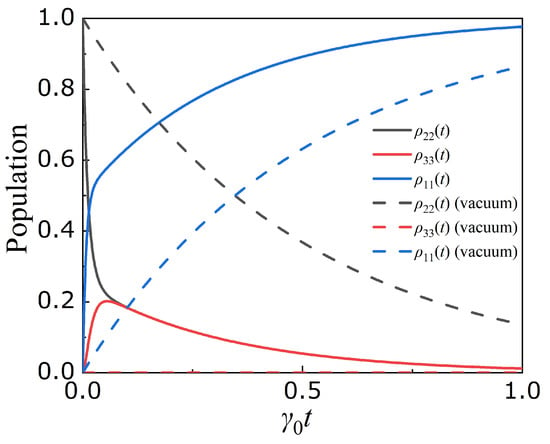
Figure 7. The same as Figure 6 but for a fractal aggregate of silver nanoparticles. Here, ${\gamma }_{\Vert }=70.87{\gamma }_0$, ${\gamma }_{\perp }=1.53{\gamma }_0$.

4. Conclusions

Using calculations involving the electromagnetic Green’s tensor within the coupled-dipole method, we investigated the occurrence of an anisotropic Purcell effect in two-dimensional fractal aggregates containing high-index dielectric nanoparticles as well as metallic nanoparticles. Our findings highlight that the Purcell factor exhibits significant enhancement in localized regions known as hot spots. These hot spots arise from the excitation of localized surface plasmons in aggregates of silver nanoparticles or the excitation of Mie resonances in aggregates of silicon nanoparticles. The presence of these hot spots with high local density of states (LDOS) is a consequence of the scaling properties of fractal structures (dilation symmetry).

We observed that the Purcell factor enhancement primarily occurs for transitions where the dipole moment lies within the plane of the fractal aggregate. In contrast, dipole moments that are perpendicular to the fractal cluster’s plane exhibit a slight deviation from unity, giving rise to the anisotropic Purcell effect. This anisotropic behavior is crucial for the emergence of quantum interference among different spontaneous-emission paths in specific multi-level quantum emitters. Such quantum interference leads to a range of unconventional phenomena in quantum optics, one of which is population trapping.

More specifically, we demonstrated that when a three-level V-type quantum emitter is positioned within the hot spots of either dielectric or metallic fractal clusters, the presence of quantum interference results in unusual population dynamics. These dynamics include non-exponential decay and population in states that would typically remain unoccupied if the emitter were placed in a vacuum environment.