Compact Design for Bi-Polarization Quantum Routers on SOI Platform
Abstract
1. Introduction
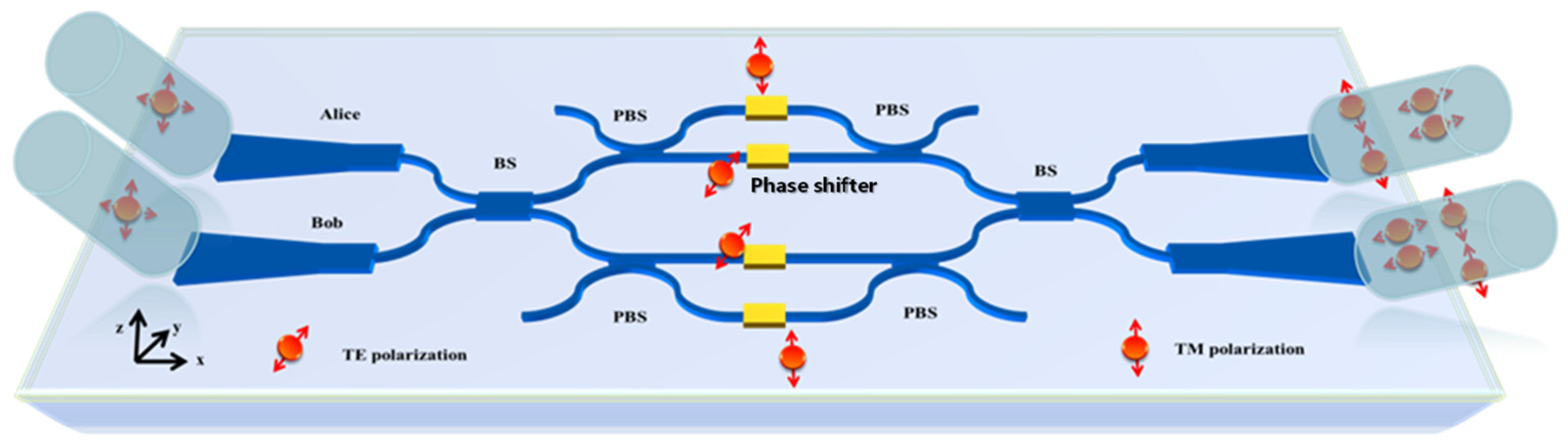
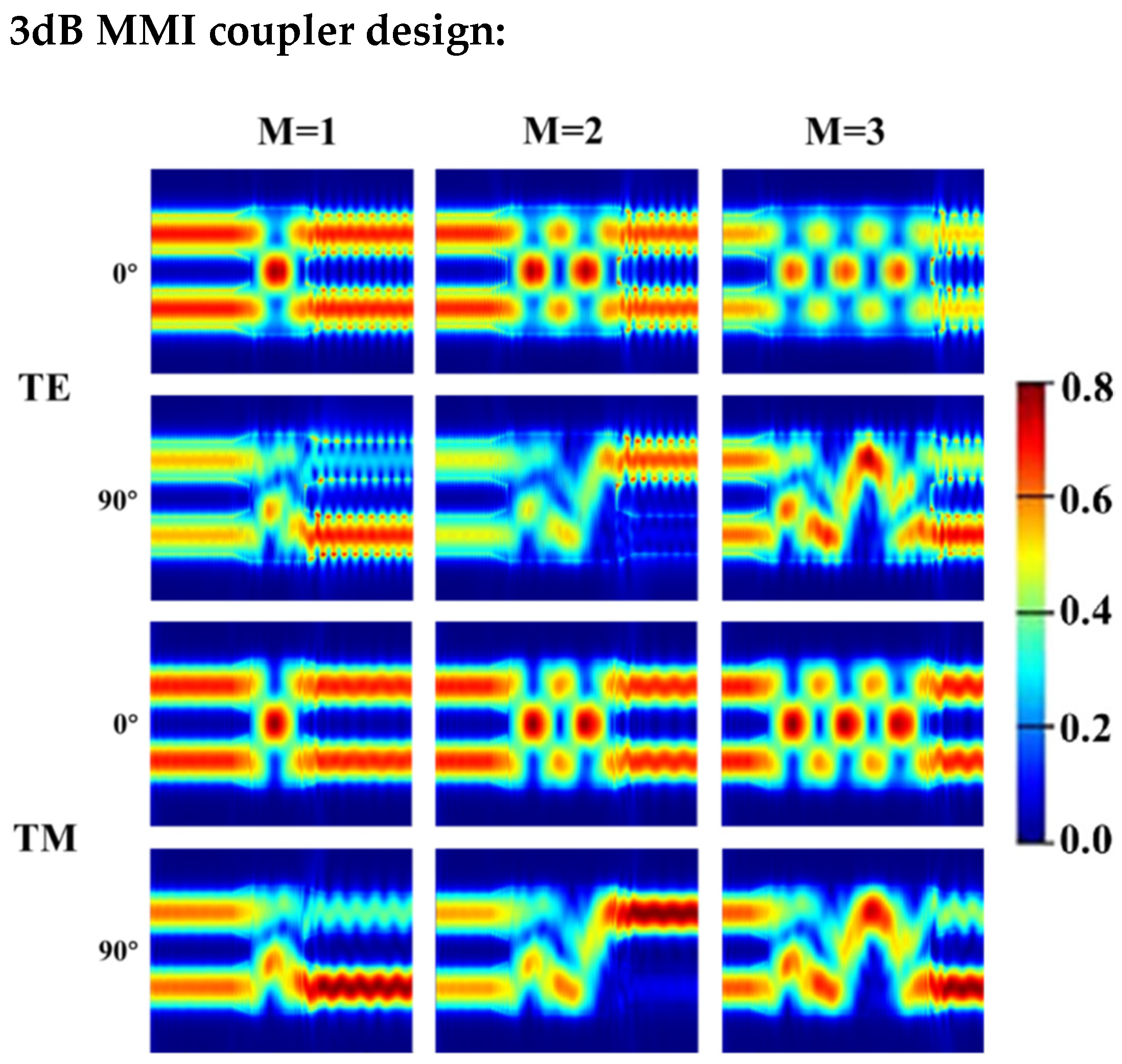
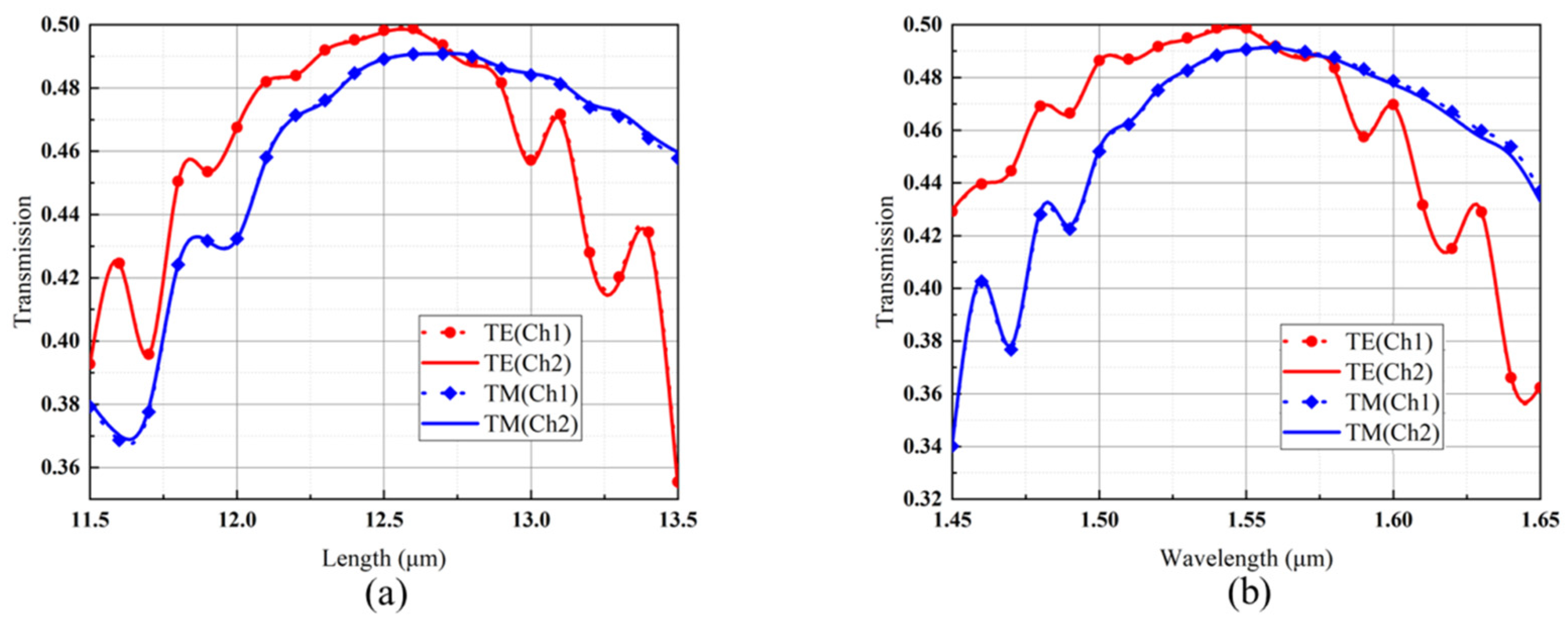
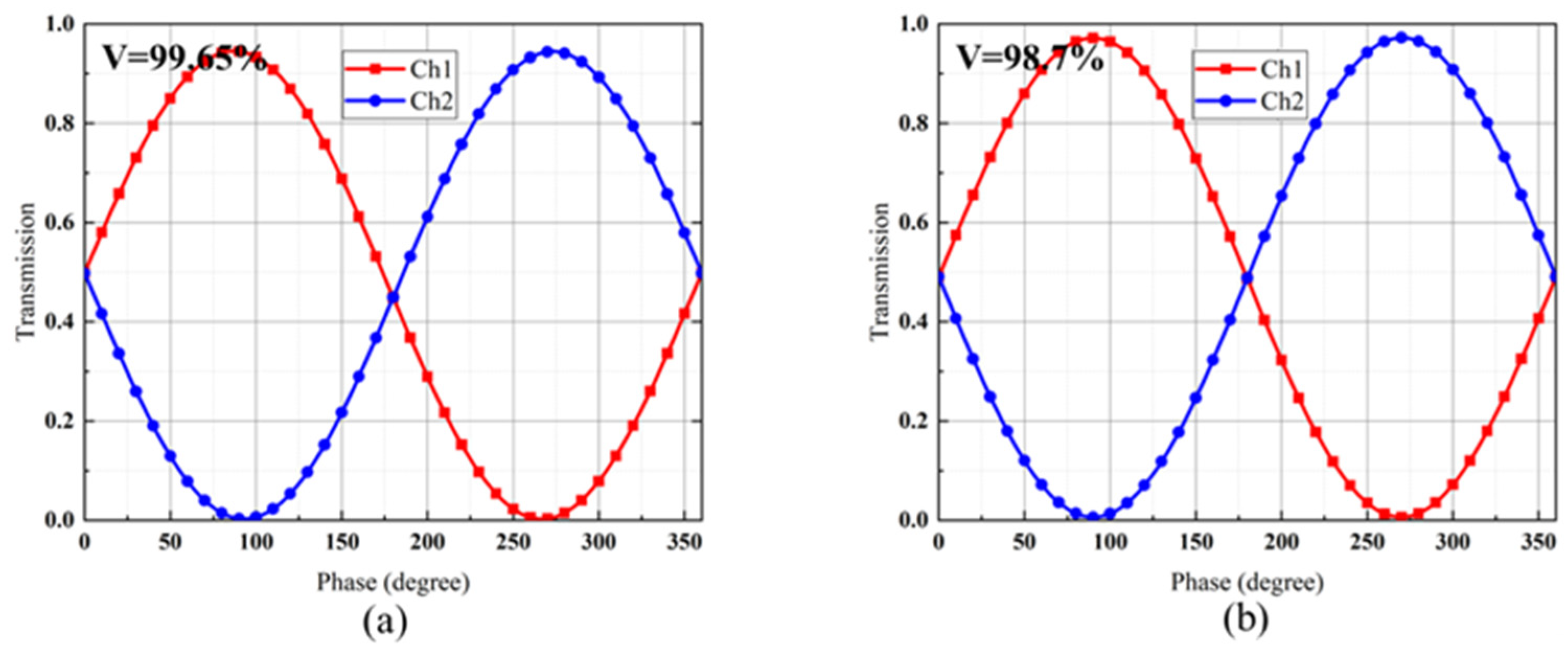
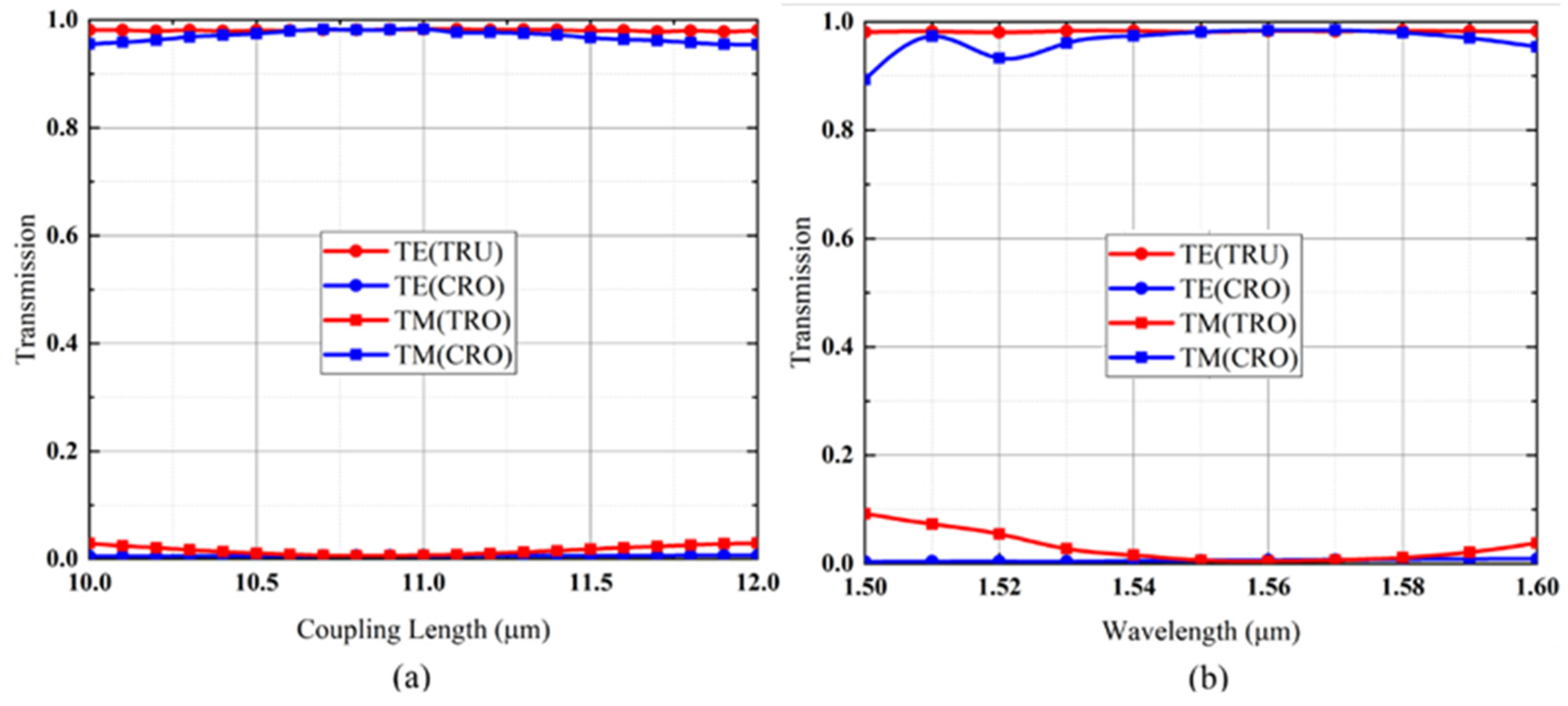
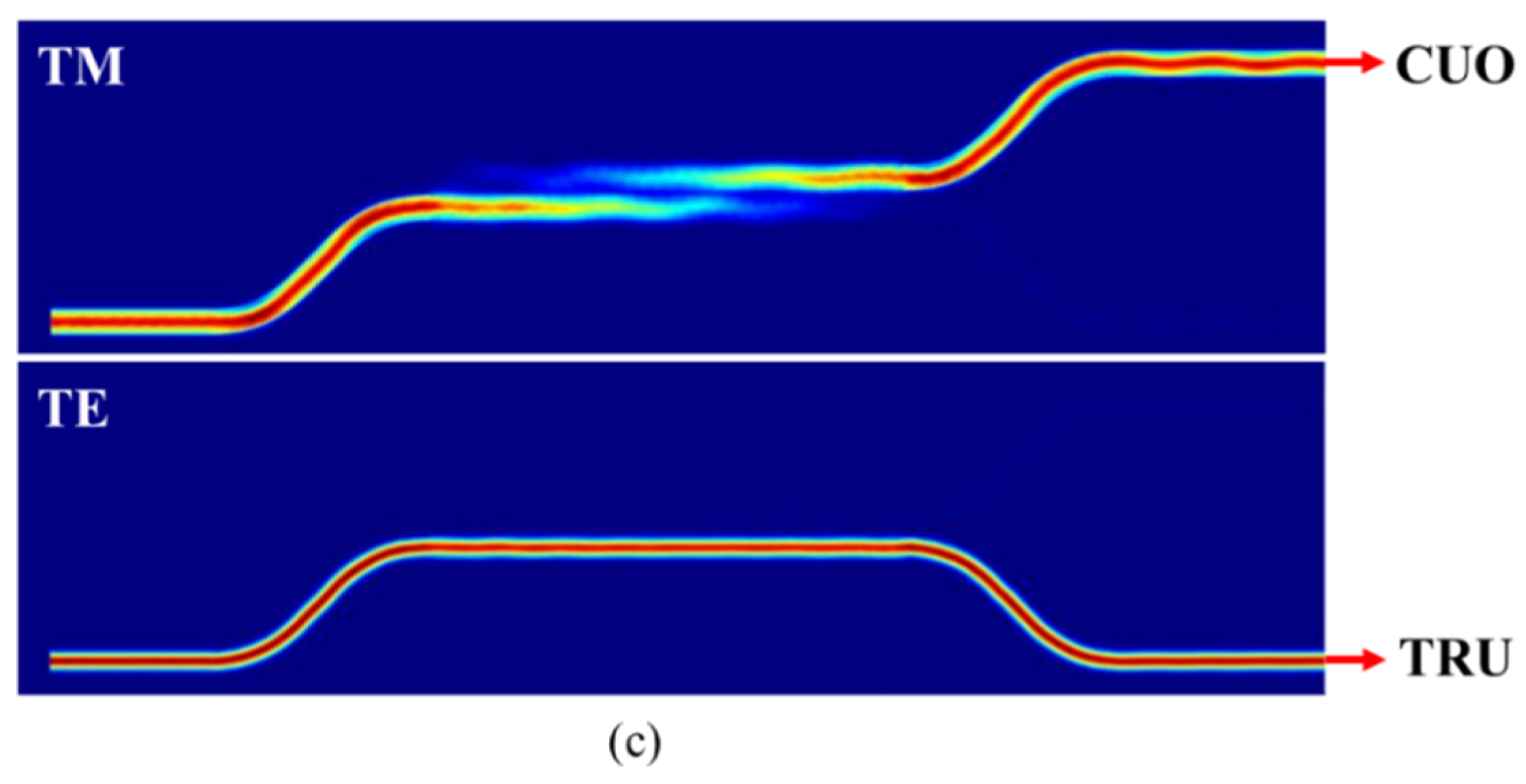
2. Design and Analysis
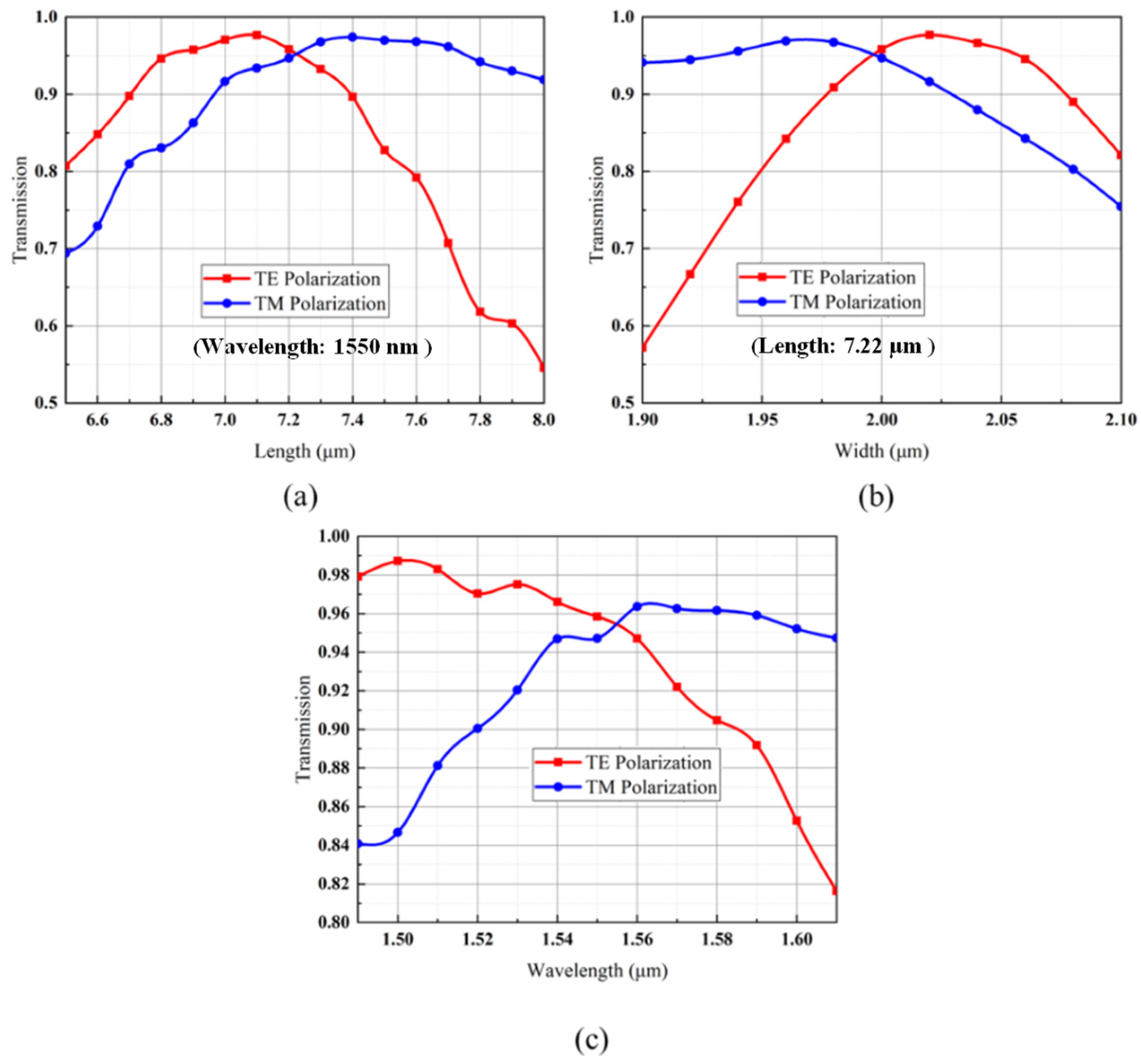
The Polarization Beams Splitters Design
3. Discussion
3.1. Single-Photon State Conversion [33]
3.2. Polarized Entangled Photon Pairs [34]
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacQuarrie, E.R.; Simon, C.; Simmons, S.; Maine, E. The emerging commercial landscape of quantum computing. Nat. Rev. Phys. 2020, 2, 596–598. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 2022, 965, 1–74. [Google Scholar] [CrossRef]
- Stas, P.J.; Huan, Y.Q.; Machielse, B.; Knall, E.N.; Suleymanzade, A.; Pingault, B.; Sutula, M.; Ding, S.W.; Knaut, C.M.; Assumpcao, D.R.; et al. Robust multi-qubit quantum network node with integrated error detection. Science 2022, 378, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.A.; Zhang, Q.; Chen, T.Y.; Cai, W.-Q.; Liao, S.-K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.-G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4600 kilometres. Nature 2021, 589, 214–219. [Google Scholar] [CrossRef]
- Bassoli, R.; Boche, H.; Deppe, C.; Ferrara, R.; Fitzek, F.H.P.; Janssen, G.; Saeedinaeeni, S. Quantum Communication Networks; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- O’Brien, J.L.; Furusawa, A.; Vukovi, J. Photonic quantum technologies. Nat. Photonics 2010, 3, 687–695. [Google Scholar] [CrossRef]
- Wang, M.; Wu, R.; Lin, J.; Zhang, J.; Fang, Z.; Chai, Z.; Cheng, Y. Chemo-mechanical polish lithography: A pathway to low loss large-scale photonic integration on lithium niobate on insulator. Quantum Eng. 2019, 1, e9. [Google Scholar] [CrossRef]
- Wang, R.; Sprengel, S.; Muneeb, M.; Boehm, G.; Baets, R.; Amann, M.-C.; Roelkens, G. 2 μm wavelength range InP-based type-II quantum well photodiodes heterogeneously integrated on silicon photonic integrated circuits. Opt. Express 2015, 23, 26834–26841. [Google Scholar] [CrossRef]
- Poot, M.; Schuck, C.; Ma, X.-S.; Guo, X.; Tang, H.X. Design and characterization of integrated components for SiN photonic quantum circuits. Opt. Express 2016, 24, 6843–6860. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, X.; Zhang, Z.; Guo, K.; Yang, J. Ultra-compact, efficient and high-polarization-extinction-ratio polarization beam splitters based on photonic anisotropic metamaterials. Opt. Express 2022, 30, 538–549. [Google Scholar] [CrossRef]
- Awschalom, D.; Berggren, K.K.; Bernien, H.; Bhave, S.; Carr, L.D.; Davids, P.; Economou, S.E.; Englund, D.; Faraon, A.; Fejer, M.; et al. Development of Quantum Interconnects (QuICs) for Next-Generation Information Technologies. PRX Quantum 2021, 2, 017002. [Google Scholar] [CrossRef]
- Lee, Y.; Bersin, E.; Dahlberg, A.; Wehner, S.; Englund, D. A quantum router architecture for high-fidelity entanglement flows in quantum networks. npj Quantum Inf. 2022, 8, 75. [Google Scholar] [CrossRef]
- Cao, C.; Han, Y.H.; Yi, X.; Yin, P.-P.; Zhang, X.-Y.; Gao, Y.-P.; Fan, L. Implementation of a single-photon fully quantum router with cavity QED and linear optics. Opt. Quantum Electron. 2021, 53, 32. [Google Scholar] [CrossRef]
- Xia, K.; Jelezko, F.; Twamley, J. Quantum routing of single optical photons with a superconducting flux qubit. Phys. Rev. A 2018, 97, 052315. [Google Scholar] [CrossRef]
- Shou, C.; Zhang, Q.; Luo, W.; Huang, G. Photon storage and routing in quantum dots with spin-orbit coupling. Opt. Express 2021, 29, 9772–9785. [Google Scholar] [CrossRef] [PubMed]
- Childress, L.; Hanson, R. Diamond NV centers for quantum computing and quantum networks. Mrs Bull. Mater. Res. Soc. 2013, 38, 134–138. [Google Scholar] [CrossRef]
- Matthews, J.; Politi, A.; Stefanov, A.; O’Brien, J.L. Manipulating multi-photon entanglement in waveguide quantum circuits. Nat. Photonics 2009, 3, 346–350. [Google Scholar] [CrossRef]
- Zhang, G.; Haw, J.Y.; Cai, H.; Xu, F.; Assad, S.M.; Fitzsimons, J.F.; Zhou, X.; Zhang, Y.; Yu, S.; Wu, J.; et al. An integrated silicon photonic chip platform for continuous-variable quantum key distribution. Nat. Photonics 2019, 13, 839–842. [Google Scholar] [CrossRef]
- Kwek, L.C.; Cao, L.; Luo, W.; Wang, Y.; Sun, S.; Wang, X. Chip-based quantum key distribution. AAPPS Bull. 2021, 31, 15. [Google Scholar] [CrossRef]
- Lu, L.; Xia, L.; Chen, Z.; Chen, L.; Yu, T.; Tao, T.; Ma, W.; Pan, Y.; Cai, X.; Lu, Y.; et al. Three-dimensional entanglement on a silicon chip. npj Quantum Inf. 2020, 6, 30. [Google Scholar] [CrossRef]
- Qiang, X.; Loke, T.; Montanaro, A.; Aungskunsiri, K.; Zhou, X.; O’Brien, J.L.; Wang, J.B. Efficient quantum walk on a quantum processor. Nat. Commun. 2016, 7, 11511. [Google Scholar] [CrossRef]
- Zhang, M.; Feng, L.; Li, M.; Chen, Y.; Zhang, L.; He, D.; Guo, G.; Guo, G.; Ren, X.; Dai, D. Supercompact Photonic Quantum Logic Gate on a Silicon Chip. Phys. Rev. Lett. 2021, 126, 130501. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Bacco, D.; Dalgaard, K.; Cai, X.; Zhou, X.; Rottwitt, K. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. npj Quantum Inf. 2017, 3, 25. [Google Scholar] [CrossRef]
- Wang, J.; Bonneau, D.; Villa, M.; Silverstone, J.W.; Santagati, R.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; et al. Chip-to-chip quantum photonic interconnect by path-polarization interconversion. Optica 2016, 3, 407–413. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, Z.; Shrestha, S.; Xu, X.; Liang, J.; Gong, Y.-X.; Bienfang, J.C.; Restelli, A.; Shapiro, J.H.; Wong, F.N.C.; et al. Harnessing high-dimensional hyperentanglement through a biphoton frequency comb. Nat. Photonics 2015, 9, 536. [Google Scholar] [CrossRef]
- Ma, C.; Sacher, W.D.; Tang, Z.; Mikkelsen, J.C.; Yang, Y.; Xu, F.; Thiessen, T.; Lo, H.-K.; Poon, J.K.S. Silicon photonic transmitter for polarization-encoded quantum key distribution. Optica 2016, 3, 1274–1278. [Google Scholar] [CrossRef]
- Zhong, T.; Zhou, H.; Horansky, R.D.; Lee, C.; Verma, V.B.; Lita, A.E.; Restelli, A.; Bienfang, J.C.; Mirin, R.P.; Gerrits, T.; et al. Photon-efficient quantum key distribution using time–energy entanglement with high-dimensional encoding. New J. Phys. 2015, 17, 022002. [Google Scholar] [CrossRef]
- Long, G.L. General quantum interference principle and duality computer. Commun. Theor. Phys. 2006, 45, 825. [Google Scholar]
- Burns, W.K.; Milton, A.F.; Lee, A.B. Optical waveguide parabolic coupling horns. Appl. Phys. Lett. 1977, 30, 28–30. [Google Scholar] [CrossRef]
- Chen, X.F.; Shi, X.D.; Qiu, P.F.; Dai, Z.J.; Yu, Y.; Song, X.X.; Zhang, H.T.; Chen, M.Y.; Ye, Y.X.; Ren, X.D.; et al. Efficient mode converters and filters using asymmetrical directional couplers with subwavelength gratings. Opt. Lett. 2022, 47, 4600–4603. [Google Scholar] [CrossRef]
- Mia, M.B.; Ahmed, S.Z.; Ahmed, I.; Lee, Y.J.; Qi, M.; Kim, S. Exceptional coupling in photonic anisotropic metamaterials for extremely low waveguide crosstalk. Optica 2020, 7, 881–887. [Google Scholar] [CrossRef]
- Simmons, C.; Donaldson, R. Multicore fiber beacon system for reducing back-reflection in satellite quantum key distribution. Opt. Express 2023, 31, 23382–23392. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, D. Time-Correlated Single Photon Counting; Academic press: Cambridge, MA, USA, 2012. [Google Scholar]
- Orieux, A.; Versteegh, M.A.M.; Jöns, K.D.; Ducci, S. Semiconductor devices for entangled photon pair generation: A review. Rep. Prog. Phys. 2017, 80, 076001. [Google Scholar] [CrossRef] [PubMed]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Xue, S.; Wang, Y.; Zhan, J.; Wu, C.; Zhu, P.; Zheng, Q.; Yu, M.; Liu, Y.; et al. Experimental demonstration of quantum transport enhancement using time-reversal symmetry breaking on a silicon photonic chip. Sci. China Phys. Mech. Astron. 2022, 65, 100362. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Z.; Pan, E.; Chen, X.; Song, X.; Zhang, H.; Liang, Y. Compact Design for Bi-Polarization Quantum Routers on SOI Platform. Photonics 2023, 10, 897. https://doi.org/10.3390/photonics10080897
Dai Z, Pan E, Chen X, Song X, Zhang H, Liang Y. Compact Design for Bi-Polarization Quantum Routers on SOI Platform. Photonics. 2023; 10(8):897. https://doi.org/10.3390/photonics10080897
Chicago/Turabian StyleDai, Zijie, Eryi Pan, Xuefeng Chen, Xiaoxian Song, Haiting Zhang, and Ying Liang. 2023. "Compact Design for Bi-Polarization Quantum Routers on SOI Platform" Photonics 10, no. 8: 897. https://doi.org/10.3390/photonics10080897
APA StyleDai, Z., Pan, E., Chen, X., Song, X., Zhang, H., & Liang, Y. (2023). Compact Design for Bi-Polarization Quantum Routers on SOI Platform. Photonics, 10(8), 897. https://doi.org/10.3390/photonics10080897



