Abstract
We numerically investigate the dynamics of a ring consisting of three unidirectionally coupled Erbium-Doped Fiber Lasers (EDLFs) without external pump modulation. The study focuses on the system behavior as the coupling strength is varied, employing a six-dimensional mathematical model that includes three variables for laser intensities and three variables for population inversions of all lasers. Our primary objective is to understand the system evolution towards chaos from a stable equilibrium in the ring, considering the impact of increasing coupling strength. To analyze the system’s behavior, we employ various techniques such as time series analysis, power spectra, Poincaré sections, bifurcation diagrams, and Lyapunov exponents. During the transition to chaos, the system undergoes a Hopf bifurcation and a series of torus bifurcations. An essential aspect of this study is the exploration of a rotating wave propagating along the ring, where the wave nature (periodic, quasiperiodic, or chaotic) depends on the coupling strength. Additionally, we observe the coexistence of periodic and chaotic orbits within a specific range of the coupling strength. However, for very strong coupling, this bistability disappears, resulting in a monostable system with a single limit cycle. This regime exhibits potential for applications that demand short laser pulses with a substantial increase in peak power, reaching nearly 20 times higher levels compared to the continuous mode when the lasers are uncoupled. This discovery holds particular importance for optical communication systems, especially considering the attenuation optical signals experience when transmitted over long distances.
1. Introduction
In recent decades, there have been remarkable advancements in the research and commercialization of fiber lasers. These lasers have undergone revolutionary progress, fueled by their widespread utilization in various fields such as optical communications, optical sensing, laser surgery, nonlinear optics, and optical materials [1,2,3,4,5,6]. Additionally, fiber amplifier technology has emerged as an exceptionally practical platform for industrial applications, primarily due to its compactness, robustness, reliability, and high efficiency. The alignment-free structure and spatial beam profile further enhance its appeal in industrial settings.
Among various types of fiber lasers, erbium-doped fiber lasers (EDFLs) offer several advantages that make them highly suitable for optical communications [7]. The EDFL active medium comprises an optical fiber doped with erbium ions. When the diode-pumped laser light interacts with these erbium ions, it results in high gain and supports a single transverse mode, provided that the fiber parameters are appropriately chosen. First, EDFLs can easily be integrated into optical communication networks due to the compact size of their optical components. Second, the laser wavelength, particularly around 1550 nm, is widely utilized in optical communication systems due to its minimal losses in optical fibers [8]. Third, EDFLs exhibit a diverse range of dynamical behaviors, including period doubling, chaos, and multistability [9,10]. Their dynamics can be controlled and leveraged not only for chaotic communication [2,11] but also for numerous other applications, such as spectral interferometry [12], optical coherence tomography [13], optical sensing [14], optical metrology [15], industrial micromachining [16], LIDAR systems [17], and medicine [18].
Nonlinear effects in fiber lasers are typically considered undesirable due to their potential to disrupt stable laser operation, introduce deviations from a Gaussian pulse shape, and hinder the achievement of a diffraction limit [19]. However, recent studies have revealed that nonlinear effects can be harnessed for certain applications. Consequently, there has been significant research conducted on nonlinear phenomena in EDFLs [19,20,21], with a specific focus on investigating multistability in these laser systems [9,10,22,23,24,25,26].
Multistability characterized by the coexistence of multiple stable states or attractors under a specific parameter set, is a fascinating phenomenon observed in various fields of science, including physics, engineering, chemistry, biology, and medicine (see [27] and references therein). The ability to control multistability enables the selection of desired attractors or the elimination of undesirable ones [28]. In the context, EDFLs subjected to periodic modulation of the laser pump current or cavity losses exhibit the coexistence of up to four periodic attractors. These attractors have different periodicity, with longer periods corresponding to higher pulse energies. For instance, the laser pulse amplitude in the period-5 regime is approximately 50 times higher than that in the period-1 regime [29]. High pulse power fiber lasers have found numerous applications, including in cutting, welding, and surgery, and particularly in optical communications [7], where they enable the long-distance transmission of optical signals without the need for frequent amplification. Recently, by employing selective control of multistability, giant pulses were successfully generated in an array of EDFLs [30].
While the dynamics of a solitary EDFL have been extensively studied [9,10,22,23,24,25], there is still a lack of comprehensive investigation into the dynamics of coupled EDFLs in different coupling configurations. The study of the dynamics of networks of coupled oscillators has garnered significant attention across various scientific disciplines. When multiple oscillators are coupled, the range of potential behaviors becomes more complex, making the analysis of governing equations challenging. Each oscillator may only be connected to a few immediate neighbors [31].
One of the simplest network configurations is a cycle ring of coupled oscillators [32]. The ring dynamics can be highly complex, particularly when the oscillators are coupled unidirectionally, even if the individual uncoupled units exhibit stable equilibrium. Previous works have explored interesting dynamics of ring-coupled oscillators, including chaotic synchronization in three coupled electrical circuits [33], chimera states in nonlocally coupled oscillators [34], and the generation of delays in coupled CMOS inverters [35], among others.
In addition, the ring configuration is particularly attractive because it allows rotating phase waves to propagate along the coupled nodes [36,37,38,39]. Such waves were first found in a ring reactor of reaction–diffusion systems [40,41]. Rotating waves arise when a homogeneous state becomes linearly unstable due to a Hopf bifurcation [42]. Later, Nekorkin and colleagues [43] discovered traveling waves propagating in a ring of coupled bistable phase oscillators with sinusoidal nonlinearity. It should be noted that unidirectional coupling is of particular interest because a signal is transmitted from one subsystem to another without receiving feedback. Moreover, unidirectional rings were explored in coupled electrical circuits based on Chua [44], Lorenz [45,46], and Duffing [47,48] models where rotating waves were also discovered. Transitions from a stable equilibrium through quasiperiodicity to chaos and hyperchaos with respect to the coupling strength were observed in the rings of unidirectionally coupled Lorenz [45,49], Duffing [50], and Rulkov [51] oscillators. The mechanism leading to such transitions was studied in detail in coupled autonomous Duffing oscillators [47,52,53,54].
When studying dynamics in ring-coupled lasers, it is important to acknowledge that previous investigations have predominantly focused on semiconductor lasers [55,56,57]. These studies have demonstrated that when operating in an uncoupled state, semiconductor lasers operate in a continuous-wave regime. However, once the coupling strength surpasses a certain threshold, the lasers transform into an oscillatory state. As the coupling strength further increases, the dynamics follow a route to chaos through a series of Hopf bifurcations, leading to periodic, quasiperiodic, and chaotic oscillations. Within the chaotic range, various synchronization states, ranging from asynchronous behavior to phase synchronization, have been observed.
In this paper, we study, for the first time to our knowledge, the behavior of a ring of EDFLs as the coupling strength is increased, aiming to address the following key questions: What is the route to chaos observed in the EDFL ring? How do the lasers achieve synchronization along this route? By answering these questions, we can gain valuable insights into the collective behavior of coupled EDFLs and make informed decisions regarding optimal laser parameters and configurations for network performance. Since fiber and semiconductor lasers belong to the same class-B lasers [58], we anticipate observing a similar route to chaos in the ring of coupled EDFLs. Through the application of time series analysis, bifurcation diagrams, Poincaré sections, power spectra, and Lyapunov exponents, we demonstrate that while the dynamics of this ring share similarities with other coupled oscillators [50], it also possesses distinctive characteristics inherent to EDFLs.
Long ago, Landau and Hopf discovered a transition to turbulence via a sequence of successive Hopf bifurcations [59,60]. Later, Newhouse, Ruelle, and Takens (NRT) [61] proved that the 3D torus decays into a strange chaotic attractor immediately after the third successive Hopf bifurcation, due to the effect of an arbitrarily small perturbation of the so-called NRT scenario. Although several validations of this effect were verified in a large family of frameworks, little attention was paid to a study of the NRT scenario in optical systems such as lasers, and especially in fiber lasers. Therefore, one of the aims of this work is to analyze this scenario in a cyclic ring of three diffusively coupled EDFLs.
This paper is structured as follows. In Section 2, we present the model of a single EDFL with pump modulation. In Section 3, we introduce the model of a ring of three coupled EDFLs. In Section 4, we investigate the dynamics of the system through the analyses of time series, bifurcation diagrams, Poincaré sections, power spectra, and Lyapunov exponents. Finally, in Section 5, we summarize the main conclusions drawn from our study.
2. Laser Model
To describe the dynamics of diode-pumped EDFLs, we employ the power-balance approach, which accounts for excited state absorption (ESA) in erbium at the 1.5 m wavelength. This approach also considers the averaging of population inversion along the pumped active fiber. By incorporating these factors, the model captures the underlying mechanisms that give rise to intrinsic oscillations in the laser, even in the absence of external modulation, as observed experimentally [10,23].
The balance equations for the intracavity laser power, denoted as P and expressed in units of s (representing the sum of powers of the contra-propagating waves inside the cavity), and the averaged population y of the upper level (referred to as “2” and ranging from 0 to 1 as a dimensionless variable), are derived as follows:
where is the cross-section of the absorption transition from the ground state “1” to the upper state “2”. We suppose that the cross-section of the return stimulated transition is practically the same in magnitude that gives , being the coefficient that stands for the ratio between ESA and ground-state absorption cross-sections at the laser wavelength. is the lifetime of a photon in the cavity ( being the intra-cavity tails of FBG-couplers), is the small-signal absorption of the erbium fiber at the laser wavelength, is the total concentration of erbium ions in the active fiber), is the intra-cavity losses on the threshold ( being the nonresonant fiber loss and R the total reflection coefficient of the FBG-couplers), is the lifetime of erbium ions in the excited state “2”, is the fiber core radius, is the radius of the fundamental fiber mode, and is the factor addressing a match between the laser fundamental mode and erbium-doped core volumes inside the active fiber.
The population of the upper laser level “2” is given as
where is the population of the upper laser level “2”, is the refractive index of a “cold” erbium-doped fiber core, and L is the active fiber length),
is the spontaneous emission into the fundamental laser mode, and the pump power is
where is the pump power at the fiber entrance and is the ratio of absorption coefficients of the erbium fiber at pump wavelength and laser wavelength . We assume that the laser spectrum width is of the erbium luminescence spectral bandwidth. Note that Equations (1) and (2) describe the laser dynamics without external modulation.
The parameters used in our simulations correspond to the real EDFL with an active erbium-doped fiber of cm. Other parameters are , cm, ns, cm, and cm. The last value was measured experimentally and it was a bit higher than cm given by the formula for a step-index single-mode fiber , where the parameter V relates to numerical aperture and as , while the values and result in .
The coefficients characterizing resonant-absorption properties of the erbium-doped fiber at lasing and pumping wavelengths are cm and , respectively, and correspond to direct measurements for heavily doped fiber with erbium concentration of 2300 ppm, cm, cm, , , s [10], , and that yields . Finally, the generation wavelength cm ( J) is measured experimentally, while the maximum reflection coefficients of both FBGs are centered on this wavelength. The pump parameters are the excess over the laser threshold defined as , where the threshold pump power
and the threshold population of the level “2”
with the pump beam radius taken, for simplicity, to be the same as that for generation ().
3. Normalized Equations
To simplify the laser model and generalize it in a dimensionless form, we transform Equations (1) and (2) into the simple form (all parameters and other details can be found in [62]):
where is the laser intensity and is the population inversion with parameters
By numerically solving the system of Equations (8) and (9) using the fourth-order Runge–Kutta method, we generate time series. To simulate the laser dynamics, we utilize parameters that are close to those employed in the experimental study [22]. Specifically, we set the initial pump power to s, resulting in the laser relaxation oscillation frequency , equal to kHz. This frequency is determined from the power spectrum of the damped oscillations presented in Figure 1a. It is evident that solving the laser Equations (8) and (9) leads to a stable fixed point. Although the period of these oscillations is not constant, we determine the dominant frequency in the spectrum shown in Figure 1b, which corresponds to the average frequency of relaxation oscillations. This frequency closely aligns with the laser’s fundamental frequency, and we adopt this value for our simulations.
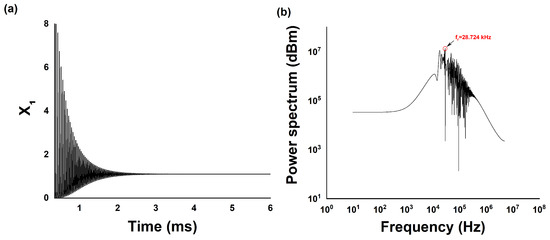
Figure 1.
(a) Time series with relaxation oscillations and (b) power spectrum with relaxation oscillation frequency of EDFL given by Equations (8) and (9).
4. Dynamics of the Ring of Three Unidirectionally Coupled EDFLs
Ring-coupled oscillators can be conceptualized as a recurrent cycle of interactions [63]. Even with just three oscillators, this simple network motif can exhibit thirteen distinct configuration patterns [64], distinguished by various combinations of unidirectional and bidirectional couplings. In this study, our primary focus is on the configuration with unidirectional coupling, as depicted in Figure 2. In this configuration, each laser acts as both a slave and a master oscillator simultaneously. The dynamics of this ring can be mathematically described by two differential equations representing the laser intensity () and the population inversion , given as follows:
with pumping
where k is the coupling coefficient.
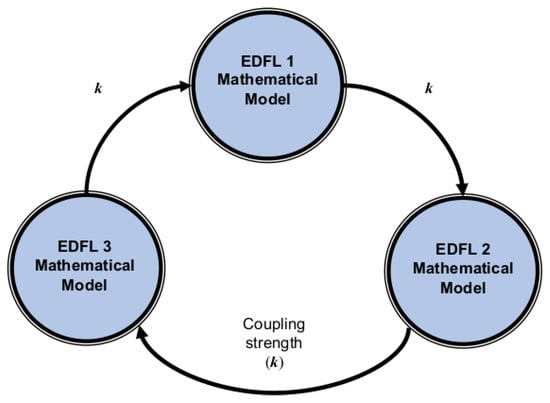
Figure 2.
Schematic diagram of a unidirectional ring of three diffusively coupled EDFLs.
With the ring configuration’s inherent symmetry, the dynamics of each laser within the ring are identical. In Figure 3, we present the bifurcation diagram illustrating the peak amplitude of a single laser () and the largest Lyapunov exponent as functions of the coupling strength k. The bifurcation scenario approaches the Landau route, characterized by the transition from a stable equilibrium to chaos through quasiperiodicity via successive Hopf bifurcations [59,60]. However, another scenario was described by Newhouse, Ruelle, and Takens (the so-called NRT scenario [61]), who found that just after the third Hopf bifurcation, a chaotic attractor appears in the form of a three-dimensional torus. Remarkably, our model described by Equations (10) and (11) exhibits a similar scenario, displaying a transition to hyperchaos as the coupling strength k is increased.
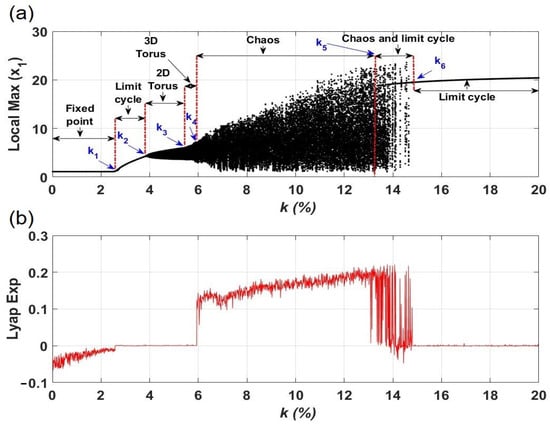
Figure 3.
(a) Bifurcation diagram of the peak intensity (in arbitrary units) and (b) largest Lyapunov exponent as a function of k.
The term represents a diffusive coupling, which refers to the difference in intensities between neighboring lasers. Experimentally, the coupling between adjacent lasers can be realized as follows. First, the laser intensities are measured with photodetectors. Then, the difference between these intensities is multiplied by the desired coupling strength k, and finally the light with the resulting intensity is injected into the neighboring laser.
The time series and Poincaré sections depicted in Figure 4 provide a detailed visualization of the dynamic regimes observed on the route from a stable fixed point to chaos. As the coupling strength is increased from to approximately , the system undergoes a Hopf bifurcation, transforming the equilibrium state (Figure 1) into a limit cycle (Figure 4a). During this transition, the largest Lyapunov exponent approaches zero, indicating the onset of a periodic behavior. This periodic regime persists within a relatively small range of .
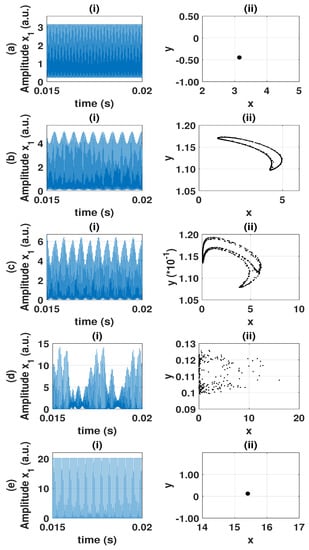
Figure 4.
(i) Time series and (ii) Poincaré sections at (a) (periodic orbit), (b) (2D torus), (c) (3D torus), (d) (chaos), and (e) (periodic orbit).
Subsequently, at , the limit cycle undergoes a transition to a quasiperiodic regime characterized by a two-dimensional (2D) torus, as depicted in Figure 4b. This transition is observed when the second largest Lyapunov exponent approaches zero. It should be noted that within the 2D torus region, the Lyapunov exponent occasionally takes positive values. This occurrence can be attributed to the disparity in step sizes employed by Wolf’s algorithm [65]. However, these positive values are transient, as the Lyapunov exponent returns to zero in subsequent steps.
As the coupling strength further increases, a three-dimensional (3D) torus emerges at (Figure 4c), and the third largest Lyapunov exponent approaches zero. Thus, within the region , the system exhibits a quasiperiodic regime.
At the critical value , the system enters a chaotic regime (Figure 4d), characterized by a positive largest Lyapunov exponent. Another critical point occurs at , where an inverse crisis bifurcation emerges. In this scenario, a stable periodic orbit arises from the initial chaotic regime, resulting in a bistable behavior for the particular value of k, featuring both periodic oscillations and chaos. As the coupling strength continues to increase, a stable limit cycle is once again established at (Figure 4e), as indicated by the return of the largest Lyapunov exponent to zero.
4.1. Rotating Wave
An intriguing phenomenon known as rotating wave occurs at certain values of the coupling strength. This rotating wave arises from the phase difference between neighboring lasers and propagates along the ring structure. In the time series depicted in Figure 4b–d, the rotating wave is evident as a slowly evolving envelope, showcasing periodic, quasiperiodic, or chaotic behavior. It serves as a distinctive dynamical feature of the ring-coupled oscillators.
The existence of a periodic rotating wave was initially discovered in a ring of coupled Chua oscillators [66,67], and later in the rings of coupled Lorenz [49,68] and Duffing oscillators [47,54,69]. The rotating wave operates in a similar manner to external modulation, inducing low-frequency oscillations. When the periodic rotating wave interacts with the local limit cycle of each oscillator, a local 2D torus is formed, resulting in quasiperiodic dynamics (Figure 4c).
As the coupling strength is further increased, the local 2D torus interacts with the quasiperiodic rotating wave, leading to the emergence of a local 3D torus (Figure 4d). With continued increases in the coupling strength, the rotating wave interacts with the local 3D torus and undergoes a transition to chaotic behavior (Figure 4e). Finally, for very strong coupling, the interaction between the rotating wave and the chaotic orbit results in the stabilization of a limit cycle.
The oscillatory regimes are depicted through time series plots in Figure 5 for four distinct coupling strengths: , , , and . In these plots, the only variation among the oscillators lies in their initial phase, resulting in phase shifts at each successive node. Consequently, this leads to the formation of a rotating wave within the cyclic ring. The left column of the figure showcases the two-dimensional time series patterns of the three oscillators, clearly revealing oblique stripes that represent the existence of rotating waves. The inclination of these stripes indicates the propagation of phase waves along the ring of oscillators. The right column of the figure illustrates the phase portraits of the corresponding attractors, which are identical for all oscillators due to the system’s symmetry. Notably, as the coupling strength is increased, the size of the attractor expands. In the right column, the one-dimensional time series of the three lasers are presented, providing further evidence of the rotating wave by depicting the phase difference between the lasers.
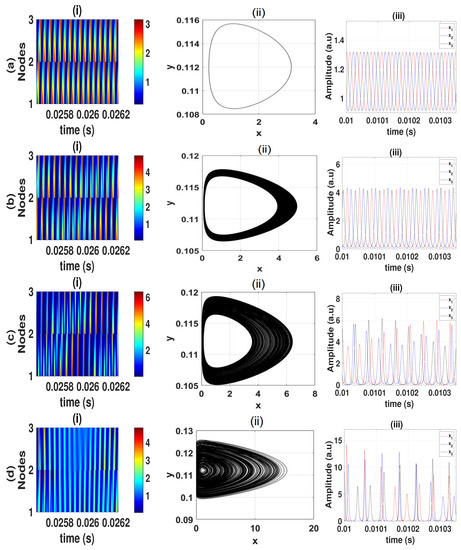
Figure 5.
(i) Rotating wave (ii) phase portraits and (iii) time series for (a) , (b) , (c) , and (d) . The color in the left column indicates the laser intensity.
4.2. Power Spectrum Analysis on the Route to Chaos
Power spectrum analysis utilizing the fast Fourier transform (FFT) is a valuable tool in various scientific and engineering disciplines for investigating system dynamics [70,71]. This analysis complements traditional qualitative and quantitative research techniques in the study of dynamical systems, including Poincaré maps, bifurcation diagrams, and Lyapunov exponents.
In Figure 6, we present a bifurcation diagram showcasing the dominant frequency in the power spectra of as a function of the coupling strength k. Furthermore, in Figure 7, we provide illustrative power spectra for fixed values of k. Upon inspecting the bifurcation diagram depicted in Figure 6, it becomes evident that the first Hopf bifurcation occurs at , signifying the transition from a stationary to a periodic solution. In the power spectrum displayed in Figure 7a, a solitary peak corresponding to the fundamental oscillation frequency emerges.
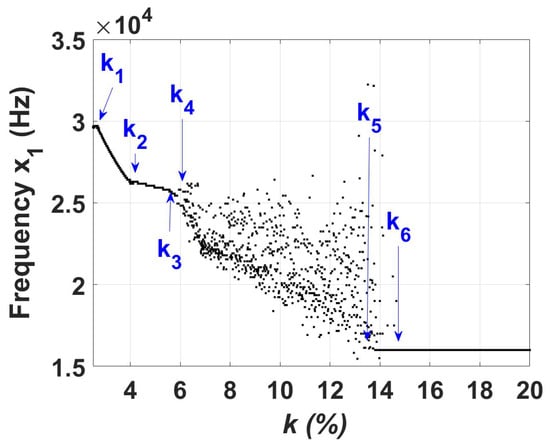
Figure 6.
Bifurcation diagram of the dominant frequency in the power spectra of as a function of the coupling strength k.
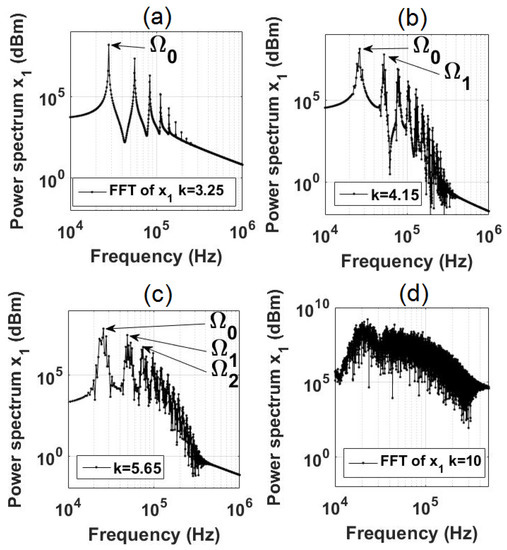
Figure 7.
Power spectra for (a) , kHz (periodic orbit), (b) , kHz, kHz (2D torus), (c) , kHz, kHz, kHz (3D torus), and (d) (chaos).
As the coupling strength is further increased, we encounter the second Hopf bifurcation at , leading to the transformation of the limit cycle into a quasiperiodic solution characterized by two incommensurate frequencies, namely and (refer to Figure 7b). The existence of a 2D torus is observed until the subsequent Hopf bifurcation at , which gives rise to a transition towards a quasiperiodic solution with three frequencies, resulting in a 3D torus. In the power spectrum displayed in Figure 7d, the emergence of a third independent frequency becomes prominent. The dominance of the 3D torus is observed within the interval . While the power spectrum in Figure 7c appears broadband and indicative of chaotic behavior, a comparison between the Poincaré sections in Figure 4c(ii),d(ii) clearly reveals the distinction between the 2D and 3D tori.
A continued increase in the coupling strength k eventually leads to the destruction of the 3D torus, resulting in a direct transition to chaos within the range of . The chaotic response is evident in the power spectrum, displaying numerous frequency peaks that are randomly distributed with varying amplitudes. This type of behavior has been observed in other dynamical systems as well. For instance, Sánchez et al. [49] studied a ring of unidirectionally coupled Lorenz oscillators and observed the transition from a periodic rotating wave to a chaotic rotating wave via quasiperiodicity. Additionally, Borkowski et al. [53] reported the observation of a rotating wave in a ring of seven unidirectionally coupled Duffing oscillators using spectral and bifurcation analyses. These examples highlight the presence of similar phenomena in different dynamical systems.
4.3. Coexistence of Attractors
In the course of the transition from a stable fixed point to chaos, a region of bistability emerges within a narrow range of the coupling strength, specifically . Within this range, two distinct attractors coexist. Figure 8 showcases the phase portraits and corresponding power spectra of these coexisting periodic and chaotic regimes for a specific value of . Recently, a similar phenomenon of multistability was observed in the dynamics of a ring of three fractional-order double-well Duffing oscillators [72]. In that study, the interplay between the fractional order index and coupling strength led to the coexistence of stable fixed points, limit cycles, 2D and 3D tori, as well as chaotic behavior, with the specific outcome depending on the initial conditions.
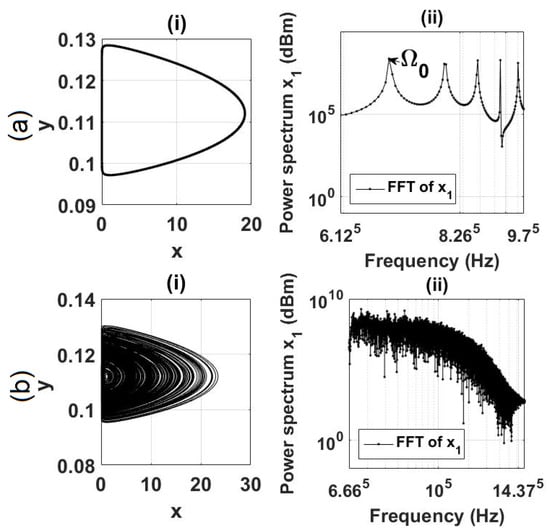
Figure 8.
(i) Phase portraits and (ii) power spectra of coexisting (a) stable limit cycle and (b) chaos at .
In our system, for coupling strengths in the range of , a stable limit cycle coexists with chaos, as depicted in the bifurcation diagram shown in Figure 3. The chaotic and periodic orbits interact with the rotating wave, resulting in the emergence of a monostable limit cycle. This observation bears a resemblance to findings reported in other studies (e.g., [73,74]), where multistability was controlled through a secondary sinusoidal perturbation. In our case, the rotating wave functions analogously to the secondary sinusoidal perturbation, effectively amplifying the laser pulse power. As a result, the lasers operate in a pulsed regime, emitting extremely short pulses with substantial amplitudes. It is important to note that this regime differs fundamentally from traditional Q-switching, which typically requires cavity quality losses, such as an intra-cavity saturable absorber [75,76]. In our case, the pulsed regime arises solely from the increasing coupling strength.
4.4. Synchronization
The rotating waves in the ring of coupled oscillators can be analyzed from the perspective of synchronization. Specifically, phase synchronization between a pair of EDFLs (i and j) can be quantitatively characterized by the difference between their instantaneous phases [64]:
At the same time, identical synchronization between a pair of EDFLs can be determined by the synchronization error
Figure 9 illustrates the synchronization scenarios described by Equations (13) and (14). The plot demonstrates the dependence of time-averaged phase synchronization and average synchronization error on the coupling strength k. It reveals the synchronization pattern transitioning from a stable equilibrium to chaos.
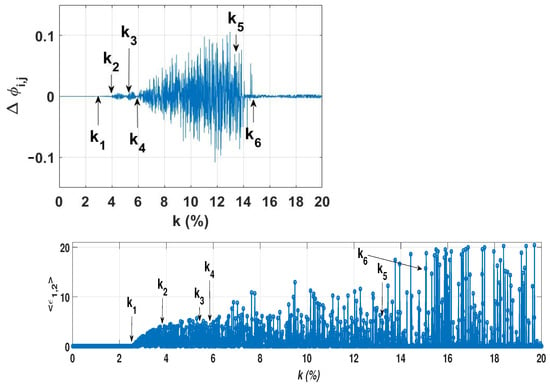
Figure 9.
(Up) Averaged phase synchronization and (down) synchronization error versus coupling strength k.
Within the interval , a stable limit cycle is observed, characterized by phase locking near zero or perfect phase synchronization between the and phases of and , respectively. As the coupling strength is increased, the system enters the ranges of and , where phase locking is lost, and two additional frequencies and emerge, leading to the formation of 2D and 3D tori, respectively. Moving into the range of , phase synchronization is completely lost, resulting in chaotic behavior. Finally, for , the phase locking regime reappears.
Thus, the phase difference between the coupled EDFLs gives rise to the phenomenon of the rotating wave, which propagates along the ring in a periodic, quasiperiodic, or chaotic manner. Consequently, achieving identical synchronization becomes unattainable, as evidenced by the nonzero average synchronization error depicted in Figure 9, down.
5. Conclusions
In this study, we conducted a numerical investigation into the dynamics of a system consisting of three unidirectionally ring-coupled EDFLs as a function of the coupling strength. By employing a six-dimensional mathematical model that accounts for laser intensities and population inversions of all lasers, we extensively examined the system’s behavior on the route from a stable equilibrium to chaos in the ring. Our analysis encompassed various tools including time series analysis, bifurcation diagrams, power spectra, Poincaré sections, and Lyapunov exponents. A key focus of our study was the exploration of the rotating wave propagating along the ring, which exhibited periodic, quasiperiodic, or chaotic behavior depending on the coupling strength.
Furthermore, we made a noteworthy observation regarding the coexistence of periodic and chaotic rotating waves within a specific range of coupling strength. As the coupling strength increased, this bistability ceased to exist, and the system became monostable, characterized by a single limit cycle. We explained this stabilization mechanism as the interaction between the chaotic and periodic orbits with the rotating wave, where the rotating wave acted as a secondary sinusoidal perturbation, leading to the annihilation of the chaotic attractor.
Of particular interest was the significant increase in the peak power of laser pulses due to phase locking under strong coupling conditions. In fact, for coupling strengths exceeding , all EDFLs operated in the pulsed mode, producing very short high-amplitude pulses. This finding has promising implications for applications requiring high-power laser pulses. We achieved a nearly 20-fold increase in peak power compared to the continuous mode observed in the absence of coupling. This outcome holds considerable significance in optical communication, where optical signals experience significant attenuation during propagation along optical fibers. The utilization of optical amplifiers based on the nonlinear properties of EDFLs allows for the generation of sufficiently high power in transmitted optical signals. The coexistence of different pulsed regimes with varying pulse amplitudes, along with the proper control of bistability, offers valuable opportunities for obtaining high-power laser pulses.
It is important to acknowledge the limitations of this study. Our investigation primarily concentrated on the simplest configuration of a three-laser ring, and as such, the conclusions drawn may not directly extrapolate to larger laser networks. However, we hold the belief that certain dynamical characteristics exhibited by our system could potentially extend to larger laser networks, thereby warranting further investigation in future research endeavors.
Author Contributions
J.O.E.d.l.T.: writing—original draft, writing—review and editing, methodology, software, validation, and visualization. J.H.G.-L.: writing—review and editing, resources, and project administration. R.J.-R.: writing—original draft, supervision, funding acquisition, writing—review and editing, and resources. V.A.: writing—review and editing, and resources. G.H.-C.: writing—review and editing, validation, and methodology. A.N.P.: writing—review and editing, visualization, conceptualization, and data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by: Programa Presupuestario F003 CONACYT–MEXICO Convocatoria “Ciencia Básica y/o Ciencia de Frontera. Modalidad: Paradigmas y Controversias de la Ciencia 2022”, under project number: 320597.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
J.O.E.d.l.T. thanks CONACYT for financial support (CVU-854990). R.J.-R. thanks CONACYT for financial support, project No. 320597.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Digonnet, M.J. Rare-Earth-Doped Fiber Lasers and Amplifiers, Revised and Expanded. CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Luo, L.; Chu, P. Optical secure communications with chaotic erbium-doped fiber lasers. J. Opt. Soc. Am. B 1998, 15, 2524–2530. [Google Scholar] [CrossRef]
- Shay, T.; Duarte, F. Tunable Fiber Lasers. In Tunable Laser Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 179–196. [Google Scholar]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; García-López, J.H.; Kazantsev, V.B. Optical fiber synaptic sensor. Opt. Lasers Eng. 2011, 49, 736–742. [Google Scholar] [CrossRef]
- Mary, R.; Choudhury, D.; Kar, A.K. Applications of fiber lasers for the development of compact photonic devices. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 72–84. [Google Scholar] [CrossRef]
- Zhao, L.; Li, D.; Li, L.; Wang, X.; Geng, Y.; Shen, D.; Su, L. Route to larger pulse energy in ultrafast fiber lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1–9. [Google Scholar] [CrossRef]
- Zervas, M.N.; Codemard, C.A. High power fiber lasers: A review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 219–241. [Google Scholar] [CrossRef]
- Castillo-Guzmán, A.; Anzueto-Sánchez, G.; Selvas-Aguilar, R.; Estudillo-Ayala, J.; Rojas-Laguna, R.; May-Arrioja, D.; Martínez-Ríos, A. Erbium-doped tunable fiber laser. In Proceedings of the Laser Beam Shaping IX, International Society for Optics and Photonics, San Diego, CA, USA, 11–12 August 2008; Volume 7062, p. 70620Y. [Google Scholar]
- Saucedo-Solorio, J.M.; Pisarchik, A.N.; Kir’yanov, A.V.; Aboites, V. Generalized multistability in a fiber laser with modulated losses. J. Opt. Soc. Am. B 2003, 20, 490–496. [Google Scholar] [CrossRef]
- Reategui, R.; Kir’yanov, A.V.; Pisarchik, A.N.; Barmenkov, Y.O.; Il’ychev, N.N. Experimental study and modeling of coexisting attractors and bifurcations in an erbium-doped fiber laser with diode-pump modulation. Laser Phys. 2004, 14, 1277–1281. [Google Scholar]
- Ke, J.; Yi, L.; Xia, G.; Hu, W. Chaotic optical communications over 100-km fiber transmission at 30-Gb/s bit rate. Opt. Lett. 2018, 43, 1323–1326. [Google Scholar] [CrossRef]
- Keren, S.; Horowitz, M. Interrogation of fiber gratings by use of low-coherence spectral interferometry of noiselike pulses. Opt. Lett. 2001, 26, 328–330. [Google Scholar] [CrossRef]
- Lim, H.; Jiang, Y.; Wang, Y.; Huang, Y.C.; Chen, Z.; Wise, F.W. Ultrahigh-resolution optical coherence tomography with a fiber laser source at 1 μm. Opt. Lett. 2005, 30, 1171–1173. [Google Scholar] [CrossRef]
- Wu, Q.; Okabe, Y.; Sun, J. Investigation of dynamic properties of erbium fiber laser for ultrasonic sensing. Opt. Express 2014, 22, 8405–8419. [Google Scholar] [CrossRef]
- Droste, S.; Ycas, G.; Washburn, B.R.; Coddington, I.; Newbury, N.R. Optical frequency comb generation based on erbium fiber lasers. Nanophotonics 2016, 5, 196–213. [Google Scholar] [CrossRef]
- Kraus, M.; Ahmed, M.A.; Michalowski, A.; Voss, A.; Weber, R.; Graf, T. Microdrilling in steel using ultrashort pulsed laser beams with radial and azimuthal polarization. Opt. Express 2010, 18, 22305–22313. [Google Scholar] [CrossRef]
- Philippov, V.; Codemard, C.; Jeong, Y.; Alegria, C.; Sahu, J.K.; Nilsson, J.; Pearson, G.N. High-energy in-fiber pulse amplification for coherent lidar applications. Opt. Lett. 2004, 29, 2590–2592. [Google Scholar] [CrossRef]
- Morin, F.; Druon, F.; Hanna, M.; Georges, P. Microjoule femtosecond fiber laser at 1.6 μm for corneal surgery applications. Opt. Lett. 2009, 34, 1991–1993. [Google Scholar] [CrossRef]
- Sanchez, F.; Le Boudec, P.; François, P.L.; Stephan, G. Effects of ion pairs on the dynamics of erbium-doped fiber lasers. Phys. Rev. A 1993, 48, 2220. [Google Scholar] [CrossRef]
- Colin, S.; Contesse, E.; Le Boudec, P.; Stephan, G.; Sanchez, F. Evidence of a saturable-absorption effect in heavily erbium-doped fibers. Opt. Lett. 1996, 21, 1987–1989. [Google Scholar] [CrossRef]
- Rangel-Rojo, R.; Mohebi, M. Study of the onset of self-pulsing behaviour in an Er-doped fibre laser. Opt. Commun. 1997, 137, 98–102. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Barmenkov, Y.O.; Kir’yanov, A.V. Experimental characterization of the bifurcation structure in an erbium-doped fiber laser with pump modulation. IEEE J. Quantum Electron. 2003, 39, 1567–1571. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: Theory and experiment. J. Opt. Soc. Am. B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Barmenkov, Y.O. Locking of self-oscillation frequency by pump modulation in an erbium-doped fiber laser. Opt. Commun. 2005, 254, 128–137. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.N.; Barmenkov, Y.O. Experimental characterization of hopping dynamics in a multistable fiber laser. Phys. Rev. E 2008, 78, 035202. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G.; Taki, M. Rogue waves in a multistable system. Phys. Rev. Lett. 2011, 107, 274101. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Hramov, A.E. Multistability in Physical and Living Systems: Characterization and Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Pisarchik, A.N.; Feudel, U. Control of multistability. Phys. Rep. 2014, 540, 167–218. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; del Valle Hernández, J. Prebifurcation noise amplification in a fiber laser. Phys. Rev. E 2009, 79, 036204. [Google Scholar] [CrossRef] [PubMed]
- Jaimes-Reátegui, R.; Esqueda de la Torre, J.O.; García-López, J.H.; Huerta-Cuellar, G.; Aboites, V.; Pisarchik, A.N. Generation of giant periodic pulses in the array of erbium-doped fiber lasers by controlling multistability. Opt. Commun. 2020, 477, 126355. [Google Scholar] [CrossRef]
- Strogatz, S.H.; Stewart, I. Coupled oscillators and biological synchronization. Sci. Am. 1993, 269, 102–109. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Kyprianidis, I.; Stouboulos, I. Chaotic synchronization of three coupled oscillators with ring connection. Chaos Solitons Fractals 2003, 17, 327–336. [Google Scholar] [CrossRef]
- Abrams, D.M.; Strogatz, S.H. Chimera states in a ring of nonlocally coupled oscillators. Int. J. Bifurcat. Chaos 2006, 16, 21–37. [Google Scholar] [CrossRef]
- Maneatis, J.G.; Horowitz, M.A. Precise delay generation using coupled oscillators. IEEE J. Solid-State Circ. 1993, 28, 1273–1282. [Google Scholar] [CrossRef]
- Ermentrout, G. The behavior of rings of coupled oscillators. J. Math. Biol. 1985, 23, 55–74. [Google Scholar] [CrossRef] [PubMed]
- Keener, J.P. Propagation and its failure in coupled systems of discrete excitable cells. SIAM J. Appl. Math. 1987, 47, 556–572. [Google Scholar] [CrossRef]
- Yamauchi, M.; Wada, M.; Nishio, Y.; Ushida, A. Wave propagation phenomena of phase states in oscillators coupled by inductors as a ladder. IEICE Trans. Fundam. Electron. Comput. Sci. 1999, 82, 2592–2598. [Google Scholar]
- Van der Sande, G.; Soriano, M.C.; Fischer, I.; Mirasso, C.R. Dynamics, correlation scaling, and synchronization behavior in rings of delay-coupled oscillators. Phys. Rev. E 2008, 77, 055202. [Google Scholar] [CrossRef]
- Cohen, D.S.; Neu, J.C.; Rosales, R.R. Rotating spiral wave solutions of reaction-diffusion equations. SIAM J. Appl. Math. 1978, 35, 536–547. [Google Scholar] [CrossRef]
- Noszticzius, Z.; Horsthemke, W.; McCormick, W.; Swinney, H.L.; Tam, W. Sustained chemical waves in an annular gel reactor: A chemical pinwheel. Nature 1987, 329, 619–620. [Google Scholar] [CrossRef]
- Alexander, J. Patterns at primary Hopf bifurcations of a plexus of identical oscillators. SIAM J. Appl. Math. 1986, 46, 199–221. [Google Scholar] [CrossRef]
- Nekorkin, V.I.; Makarov, V.A.; Velarde, M.G. Spatial disorder and waves in a ring chain of bistable oscillators. Int. J. Bifurcat. Chaos 1996, 6, 1845–1858. [Google Scholar] [CrossRef]
- Matias, M.; Pérez-Muñuzuri, V.; Lorenzo, M.; Marino, I.; Pérez-Villar, V. Observation of a fast rotating wave in rings of coupled chaotic oscillators. Phys. Rev. Lett. 1997, 78, 219. [Google Scholar] [CrossRef]
- Sánchez, E.; Matías, M.A. Transition to chaotic rotating waves in arrays of coupled Lorenz oscillators. Int. J. Bifurcat. Chaos 1999, 9, 2335–2343. [Google Scholar] [CrossRef]
- Horikawa, Y. Metastable and chaotic transient rotating waves in a ring of unidirectionally coupled bistable Lorenz systems. Physica D 2013, 261, 8–18. [Google Scholar] [CrossRef]
- Perlikowski, P.; Yanchuk, S.; Wolfrum, M.; Stefanski, A.; Mosiolek, P.; Kapitaniak, T. Routes to complex dynamics in a ring of unidirectionally coupled systems. Chaos 2010, 20, 013111. [Google Scholar] [CrossRef]
- Jaimes-Reátegui, R. Dynamic of Complex System with Parametric Modulation: Duffing Oscillators. Doctoral Dissertation, Centro de Investigaciones en Optica Leon, Leon, Mexico, 2004; pp. 112–119. [Google Scholar]
- Sánchez, E.; Pazó, D.; Matías, M.A. Experimental study of the transitions between synchronous chaos and a periodic rotating wave. Chaos 2006, 16, 033122. [Google Scholar] [CrossRef]
- Barba-Franco, J.; Gallegos, A.; Jaimes-Reátegui, R.; Gerasimova, S.; Pisarchik, A.N. Dynamics of a ring of three unidirectionally coupled Duffing oscillators with time-dependent damping. Europhys. Lett. 2021, 134, 30005. [Google Scholar] [CrossRef]
- Bashkirtseva, I.A.; Ryashko, L.B.; Pisarchik, A.N. Ring of map-based neural oscillators: From order to chaos and back. Chaos Solitons Fractals 2020, 136, 109830. [Google Scholar] [CrossRef]
- Perlikowski, P.; Yanchuk, S.; Wolfrum, M.; Stefanski, A.; Kapitaniak, T. Dynamics of a large ring of unidirectionally coupled Duffing oscillators. In IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design: Proceedings of the IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design, Held Aberdeen, UK, 27–30 July 2010; Springer: Berlin/Heidelberg, Germany, 2013; pp. 63–72. [Google Scholar]
- Borkowski, L.; Stefanski, A. FFT bifurcation analysis of routes to chaos via quasiperiodic solutions. Math. Probl. Eng. 2015, 2015, 367036. [Google Scholar] [CrossRef]
- Borkowski, L.; Perlikowski, P.; Kapitaniak, T.; Stefanski, A. Experimental observation of three-frequency quasiperiodic solution in a ring of unidirectionally coupled oscillators. Phys. Rev. E 2015, 91, 062906. [Google Scholar] [CrossRef] [PubMed]
- Buldú, J.M.; Torrent, M.C.; García-Ojalvo, J.O. Synchronization in semiconductor laser rings. J. Light. Technol. 2007, 25, 1549–1554. [Google Scholar] [CrossRef]
- Gao, Z.C.; Wu, Z.M.; Cao, L.P.; Xia, G.Q. Chaos synchronization of optoelectronic coupled semiconductor lasers ring. Appl. Phys. B 2009, 97, 645–651. [Google Scholar] [CrossRef]
- Arroyo-Almanza, D.A.; Pisarchik, A.N.; Ruiz-Oliveras, F.R. Route to chaos in a ring of three unidirectionally coupled semiconductor lasers. IEEE Photon. Tech. Lett. 2012, 24, 605–607. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Harrison, R.G. Instabilities and Chaos in Quantum Optics; Springer Science & Business Media: Berlin, Germany, 2012; Volume 34. [Google Scholar]
- Landau, L.D. On the problem of turbulence. Dokl. Akad. Nauk USSR 1944, 44, 311. [Google Scholar]
- Hopf, E. A mathematical example displaying features of turbulence. Commun. Pure Appl. Math. 1948, 1, 303–322. [Google Scholar] [CrossRef]
- Newhouse, S.; Ruelle, D.; Takens, F. Occurrence of strange axiom A attractors near quasi periodic flows on Tm, m≧3. Commun. Math. Phys. 1978, 64, 35–40. [Google Scholar] [CrossRef]
- Barba-Franco, J.; Romo-Muñoz, L.; Jaimes-Reátegui, R.; García-López, J.; Huerta-Cuellar, G.; Pisarchik, A.N. Electronic equivalent of a pump-modulated erbium-doped fiber laser. Integration 2023, 89, 106–113. [Google Scholar] [CrossRef]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Pisarchik, A.N.; Del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Matias, M.; Güémez, J.; Pérez-Munuzuri, V.; Marino, I.; Lorenzo, M.; Pérez-Villar, V. Size instabilities in rings of chaotic synchronized systems. Europhys. Lett. 1997, 37, 379. [Google Scholar] [CrossRef]
- Marino, I.; Pérez-Muñuzuri, V.; Pérez-Villar, V.; Sánchez, E.; Matıas, M. Interaction of chaotic rotating waves in coupled rings of chaotic cells. Physica D 1999, 128, 224–235. [Google Scholar] [CrossRef]
- Matías, M.; Güémez, J. Transient periodic rotating waves and fast propagation of synchronization in linear arrays of chaotic systems. Phys. Rev. Lett. 1998, 81, 4124. [Google Scholar] [CrossRef]
- Borkowski, L.; Stefanski, A. Stability of the 3-torus solution in a ring of coupled Duffing oscillators. Eur. Phys. J. Spec. Top. 2020, 229, 2249–2259. [Google Scholar] [CrossRef]
- Krysko, A.; Awrejcewicz, J.; Papkova, I.; Krysko, V. Routes to chaos in continuous mechanical systems: Part 2. Modelling transitions from regular to chaotic dynamics. Chaos Solitons Fractals 2012, 45, 709–720. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, A.; Papkova, I.; Krysko, V. Routes to chaos in continuous mechanical systems. Part 3: The Lyapunov exponents, hyper, hyper-hyper and spatial–temporal chaos. Chaos Solitons Fractals 2012, 45, 721–736. [Google Scholar] [CrossRef]
- Barba-Franco, J.; Gallegos, A.; Jaimes-Reátegui, R.; Pisarchik, A.N. Dynamics of a ring of three fractional-order Duffing oscillators. Chaos Solitons Fractals 2022, 155, 111747. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reategui, R. Control of basins of attraction in a multistable fiber laser. Phys. Lett. A 2009, 374, 228–234. [Google Scholar] [CrossRef]
- Meucci, R.; Marc Ginoux, J.; Mehrabbeik, M.; Jafari, S.; Clinton Sprott, J. Generalized multistability and its control in a laser. Chaos 2022, 32, 083111. [Google Scholar] [CrossRef]
- Pando, C.L.; Meucci, R.; Ciofini, M.; Arecchi, F.T. CO2 laser with modulated losses: Theoretical models and experiments in the chaotic regime. Chaos 1993, 3, 279–285. [Google Scholar] [CrossRef] [PubMed]
- Doedel, E.J.; Pando, C.L. Multiparameter bifurcations and mixed-mode oscillations in Q-switched CO2 lasers. Phys. Rev. E 2014, 89, 052904. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).