Abstract
For the upcoming sixth generation (6G) networks, the application of simultaneous lightwave information and power transfer (SLIPT) in a non-orthogonal multiple access (NOMA) system is a potential solution to improve energy efficiency (EE). In this paper, we propose a novel SLIPT-enabled NOMA multi-user system with power splitting (PS) protocol and investigate the effect of system parameters on EE. In addition, to enhance the energy harvesting and information receiving performance of the proposed system, we build up an optimization framework that aims to maximize the EE of the system by jointly optimizing the power allocation of the users and the PS coefficient. We introduce a two-step particle swarm optimization (PSO) algorithm to solve this problem while satisfying the constraints of maximum transmit power, the minimum achievable data rate, and the minimum harvested energy. The numerical results demonstrate the SLIPT-enabled NOMA system using PSO algorithm has significantly improved up to 3.83 bit/s/J in terms of EE over the traditional orthogonal multiple access (OMA) systems.
1. Introduction
The swift advancement of mobile Internet has resulted in an exponential surge in the number of intelligent terminals, thereby creating a pressing need for reduced system latency and enhanced security access [1]. Concurrently, the battery capacity of network devices is constrained, necessitating a greater emphasis on optimizing the energy consumption of the system. To relieve the pressure of rapid battery consumption and to achieve passive power supply for communication systems, energy harvesting has become a solution to extend the battery operating time. Traditional energy harvesting methods use resources of wind [2] and solar [3], which are less stable due to their dependence on uncontrollable natural resources [4]. Therefore, researchers have proposed simultaneous wireless information and power transfer (SWIPT) in radio frequency (RF) communication [5]. However, traditional RF communication has the disadvantages of scarce spectrum resources and poor security [6]. Hence, there is an urgency for more efficient and secure wireless communication technologies to make up for the shortcomings of RF communication.
Visible light communication (VLC) is recognized as a highly promising technology due to its low cost, abundant spectrum resources, high security, and absence of electromagnetic interference [7]. Based on the vigorous progress of SWIPT, a new framework of simultaneous lightwave information and power transfer (SLIPT) was first proposed in [8]. The SLIPT system is capable of both information receiving and energy harvesting. Due to the high detection sensitivity of the photodiode (PD), PDs are used as receivers in the SLIPT system [9]. Furthermore, the problem of maximizing the sum rate in the downlink visible light communication (VLC) system under minimum rate and harvested energy constraints was also investigated. To extend the achievable communication range, a two-hop underwater optical wireless communication (UOWC) with SLIPT system was presented in [10], which has achieved a higher rate by using relay nodes. The drawbacks of the system, however, are the low photoelectric conversion efficiency of the PD and the inferior ability to harvest energy. In addition, the system using PDs as receivers requires external power to operate, whereas the solar panel can achieve photoelectric conversion without an external power supply. Therefore, a self-powered receiver based on a solar panel was designed and introduced in [11], by which a communication link of Mbps was established, proving that the solar panel can simultaneously realize information receiving and energy harvesting with a lower peak-to-peak amplitude of the received optical signal. For further improving system performance, three effective protocols are discussed in [12] to achieve the separation of signals used for energy harvesting and information detecting in three different domains of time, power and photoelectric converters. The results indicated that the energy harvested from the power domain separation protocol is greater than that of the time-switching protocol. However, it is worth noting that the investigated parameters of the splitting protocols remain constant throughout the evaluation process, which deserves further investigation and potential optimization.
Simultaneously, it is crucial to acknowledge that the capacity of VLC systems faces significant constraints due to the restricted modulation bandwidth of the light-emitting diode (LED) transmitters [13]. Consequently, to accommodate a larger number of users within the VLC system, the implementation of multiple-access techniques becomes imperative. The widely used multiplex access is orthogonal multiple access (OMA), which splits time and frequency domain resources orthogonally [14]. Orthogonal frequency division multiple access (OFDMA) within the OMA scheme is commonly adopted in multi-user systems that achieve higher spectrum efficiency [15]. Nevertheless, since the spectrum is divided, the VLC system with OFDMA scheme has the drawbacks of a limited number of users and low data rate. A promising multiple access is needed to enhance the capacity of VLC system. The non-orthogonal multiple access (NOMA) scheme has garnered considerable attention and interest among researchers with its potential applications and advancements. NOMA allocates power to users based on their channel conditions, which enables multiple users to multiplex in the power domain and exploits entire time and frequency resources. It actively introduces inter-user interference at the transmitter to achieve non-orthogonal splitting of the power domain. Meanwhile, at the receiver, serial interference cancellation (SIC) is used to detect and separate individual user signals [16]. It is observed that NOMA is capable of enhancing the capacity and spectral efficiency of the system whilst satisfying the requirements of multi-user communication [17] through complex design of the receiver, accordingly causing more energy consumption. On this basis, a SLIPT-enabled NOMA scheme for downlink VLC system was proposed in [18], which performed with superior performance compared to the orthogonal multiple access (OMA) scheme. However, optimizing system energy efficiency is rarely addressed in existing studies of SLIPT-enabled NOMA systems.
In this paper, we propose a novel SLIPT-enabled NOMA multi-user system with power-splitting (PS) protocol, which can simultaneously ensure communication and energy harvesting performance for each user. The performance of the proposed system is evaluated by changing fields of view (FoV), number of users and LEDs and consumed power of hardware. Furthermore, we optimize energy efficiency (EE) of the system while satisfying the required achievable data rate and the harvested energy by jointly controlling the power allocation strategy in NOMA and the PS coefficient in SLIPT. In addition, the only EE of the SLIPT-enabled NOMA system is compared with that of SLIPT-enabled OFDMA system.
2. System Model
2.1. Transmitter
The block diagram of the SLIPT-enabled NOMA system is shown in Figure 1. We assume that the maximum number of superposed users on the sub-band is K. At the transmitter, data streams are first modulated. Power domain NOMA is employed on the modulated signals consequently. The total transmit power is limited to . The superposed signal can be expressed as
where and () denote the modulated signal and the allocated power coefficient of the k-th user, respectively. In addition, a DC bias current B is added to the superposition mixture of signal to obtain non-negative transmission signal [19]. The transmitted optical signal is given by
where is the power of LED. In addition, to prevent the LED from producing truncation distortion, input signal needs to be placed within the operating current interval specified for the LED, i.e., [20], where and denote minimum DC bias and maximum DC bias, respectively.
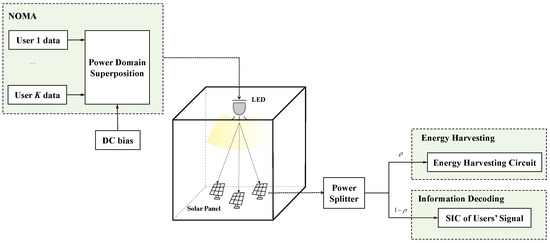
Figure 1.
Block diagram of the proposed SLIPT-enabled NOMA system.
2.2. Channel Model
In the VLC system, the power of the received signal transmitted via a direct path accounts for over 95% of the total power. The line-of-sight (LoS) link is considered in this paper. The channel gain between the LED and the k-th user is denoted by [21]
where is the Lambertian index, is the semi-angle of half power, A is the physical area of the solar panel and is the transmission distance from the LED to the solar panel. and denote radiance angle and incidence angle of k-th user, respectively. is the gain of the optical filter and is set to 1. is the gain of the optical concentrator given by
where n is the refractive index and is set to 1.5. Without loss of generality, it is assumed that the channel gains of users are in order as .
2.3. Receiver
At the receiver, the received optical signal is firstly converted to electrical signal through the solar panel. After photoelectric conversion, the electrical signal of the k-th user at the receiver based on the solar panel can be written as
where is the responsivity in A/W. is created from background shot noise and thermal noise, which can be modeled as additive white Gaussian noise (AWGN) with zero mean and variance . In this paper, we adopt PS protocol to ensure that each user achieves information receiving and energy harvesting simultaneously. Specifically, a power splitter is used to divide the power into and components for energy harvesting and information receiving. For better information receiving, the DC component is first filtered [19]. Successive interference cancellation (SIC) is applied at the receiver to improve the performance since all the users will interfere with each other while sharing the same bandwidth [22]. Channel state information (CSI) is assumed to be perfectly known. Based on the system model proposed before, the signal of the i-th user () is considered as interference with the k-th user. When , there is no interference from other users. Therefore, signal interference noise ratio (SINR) of the k-th user can be expressed as
where is the allocated power to the k-th user. is interference from other neighboring LEDs which can be expressed as
where is the peak amplitude of other LEDs, N is the number of neighboring LEDs. The achievable rate of the k-th user () is given by
where is the bandwidth of the system. Accordingly, the sum rate of the proposed system can be given by
On the other hand, the harvested energy of the k-th user is obtained by [23]
where f denotes the fill factor and is the short-circuit DC current of the k-th user, measured by shutting the solar panel charging circuit, which is given by
where is the DC component that is from neighboring light sources, which can be expressed by
where represents the DC bias of neighboring LEDs and is set to a constant. is the voltage of the k-th user that is measured by opening the solar panel charging circuit and can be written as [24]
where is the thermal voltage and is the dark saturation current. The total power consumption of the system is given by
where is the hardware power consumption.
3. Problem Formulation
The energy efficiency of the system can be defined as the ratio of the sum rate and the total power consumption, which can be written as
The aim of this paper is to maximize the EE of the system while guaranteeing the required achievable data rate and the harvested energy of each user. The optimization problem for EE can be mathematically formulated as
Equation (17) denotes the minimum rate constraint for each user, Equation (18) represents the minimum harvested energy constraint of each user. and denote the minimum rate and the minimum harvested energy, respectively. Equation (19) means that the PS coefficient is constrained to . We first initialize the PS coefficient as . The SINR of the k-th user can be expressed as
Accordingly, the optimization problem can be written as follows
We obtain the optimal power allocation after solving (21)–(23). At this moment, the SINR of k-th user can be expressed as
In this paper, we adopt the two-step particle swarm algorithm (PSO) to jointly optimize and to maximize EE. PSO plays a significant role in solving the resource allocation problem of the communication system [25]. The algorithm is first initialized based on the population size. The position of each particle movement needs to be determined based on its previous position, individual best position and global best position together. Specifically, the particle movement can be referred from the following vector equations [26]
where X represents the position of each particle. n represents the number of iterations, which is considered to be the current state. denotes the current position of the i-th particle. and denote individual optimal position and global optimal position of the population of the i-th particle, respectively. is current velocity of the i-th particle, while is the velocity of the i-th particle at the n+1 moment. The position of the i-th particle at the n+1 moment is denoted by . w is the initialization weight. and are learning factors. and are random numbers obeying uniform distribution. Since the proposed problem is a constrained optimization problem, a method to deal with constraints is required. Therefore, we utilize the penalty method, where the fitness function is based on the objective function of the problem as follows
where is the penalty value, is the i-th constraint of the problem. Regarding the optimization problem with multiple variables in this paper, we can first analyze one variable while regarding the others as constants, then solve the remaining variables. Therefore, we optimize with the fixed in the first step, then optimize with an updated in the second step. and are considered as the moving position of the particles in turn. Each particle judges its performance based on the fitness value function, the number of iterations, and the constraints.
4. Results and Discussions
In this section, numerical results are presented to illustrate how the FoV, number of users, hardware power consumption and number of neighboring LEDs affect the performance of the SLIPT-enabled NOMA system. Considering an indoor area at a height H equipped with N LEDs set on the ceiling, the other simulation parameters are provided in Table 1 unless otherwise specified. In simulation experiments, we considered scenarios with different numbers of users that are sorted in descending order based on channel gains. For cases of four users, a specific user grouping strategy is implemented. The first two users are grouped together and labeled as group , while the remaining two users formed group . Subsequently, a user from is selected and sequentially paired with a user from to ensure that each pair of users maintained a significant difference in channel gains.

Table 1.
Simulation parameters.
In the first simulation, we assume that the number of neighboring LEDs and DC bias mA to investigate the effect of varying FoV on EE is investigated. As shown in Figure 2, when FoV increases in the range of 45–70°, user coverage shrinks and channel quality decreases, but at the cost of deterioration in channel quality. As a result, sum rate decreases and more energy is harvested, resulting in a decrease of EE. At the same time, for a fixed value of FoV, a system with fewer users is able to achieve greater system EE in comparison to a system with a larger number of users. The reason is that the interference between the received signals of the users in the system increases significantly as the number of users increases.
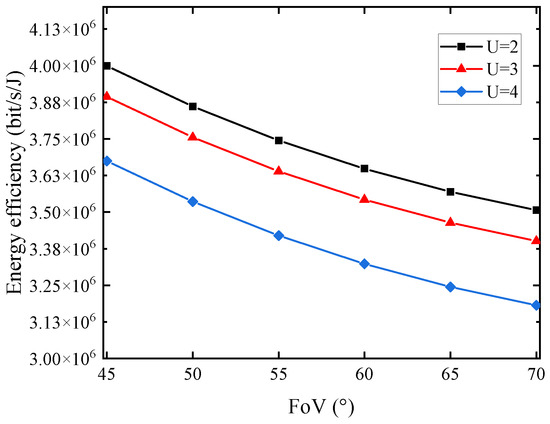
Figure 2.
EE versus FoV with different number of users.
Figure 3 demonstrates EE with varying hardware power consumption and number of users. It is observed that EE decreases with increasing , which is due to an increase in circuit loss, leading to more total energy consumed in the system; however, this has no effect on other factors. From Equation (15), it can be seen that hardware power consumption only incurs an increase in net energy consumption without causing other changes; hence, EE decreases. Furthermore, as the number of users increase, EE decreases, which coincides with the previous simulation results.
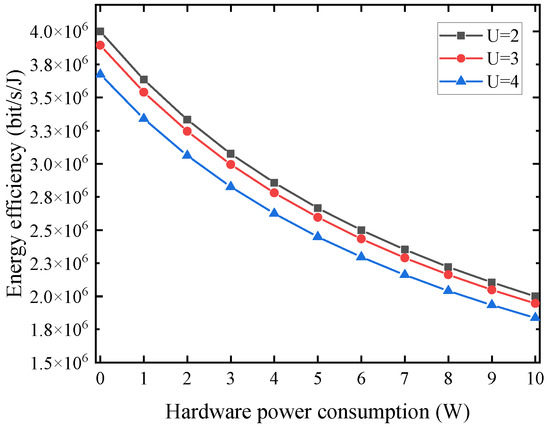
Figure 3.
EE versus hardware power consumption with different number of users.
It can be seen from Figure 4 that there is a negative correlation between the number of neighboring LEDs and EE, meaning that while adding the number of LEDs from zero to ten, the users are affected by more severe interference, resulting in a decrease in sum rate. Although, at the same time that the user can gather energy from the interfering LEDs, the change in the harvested energy is considerably less than the impact caused by the sum rate. The solid line in Figure 4 shows the FoV of 45° while the dashed line indicates the FoV of 55°. It can be seen that the overall EE at the FoV of 55° is less than the EE at the FoV of 45°, which is consistent with the previous results.
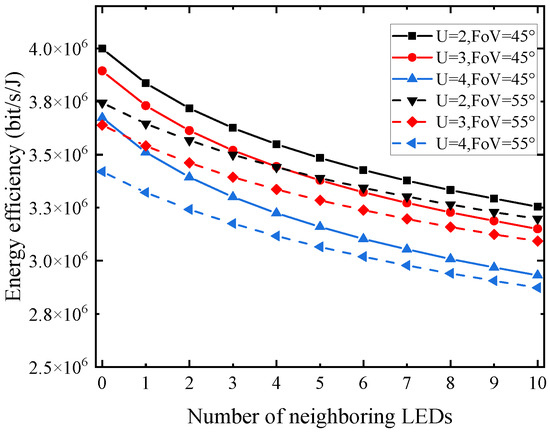
Figure 4.
EEversus number of neighboring LEDs for different number of users and FoV.
Figure 5 illustrates the maximum EE and the optimal PS coefficient for different minimum harvested energy requirements with the PS protocol. The optimal allocated power for each user is obtained through the first step of the PSO algorithm with a different number of users. Subsequently, the optimal PS coefficient is solved by Equations (21)–(23). The minimum harvested energy is set to 0.05–0.42 mJ. It shows that EE and the optimal power allocation ratio decline when the required harvested energy increases. In order to satisfy the minimum harvesting energy requirement, a larger power is required for energy harvesting, i.e., a smaller PS coefficient. A corresponding decrease in data rate leads to a decrease in EE. A power allocation coefficient of 0 indicates that the system is unable to satisfy the minimum harvested energy requirement while satisfying the minimum rate; hence, EE is 0.
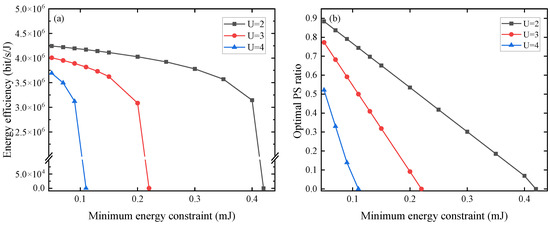
Figure 5.
Performance of the proposed algorithm with different minimum harvested energy constraints on: (a) energy efficiency; (b) optimal PS ratio.
Figure 6 discusses the effect of the user’s minimum data rate on EE and optimal PS coefficient. In this simulation, we change the minimum data rate from 0.5 to 1.3 Mbit/s while the harvested energy is limited to 0.6 mJ. As the minimum data rate requirement increases, EE remains constant until a certain minimum rate requirement is achieved. When the minimum required rate increases to a certain level, EE drops. In order to achieve higher data rate requirements, the optimal PS coefficient is required to be increased. However, in this circumstance, the remote user is unable to satisfy the minimum harvested energy but has to increase the transmit power to ensure the harvested energy. It causes the system rate and EE to decrease. In the end, it is unable to satisfy the requirements no matter how to adjust the power. At this point EE is 0, so that we order the PS coefficient to be 1.
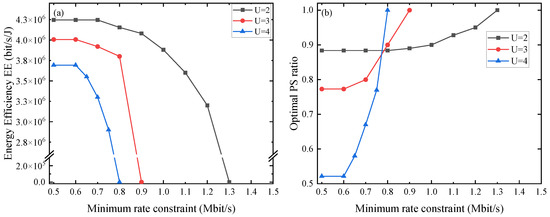
Figure 6.
Performance of the proposed algorithm with different minimum rate constraints on: (a) energy efficiency; (b) optimal PS ratio.
In the last simulation, we select two user systems as examples to provide a comprehensive understanding of the system’s performance. A comparative analysis was undertaken to assess the energy efficiency of the NOMA system with SLIPT and the OMA system with SLIPT in Figure 7. This assessment includes four distinct scenarios, namely before optimization and after optimization for both systems, showing the enhancement of optimization on energy efficiency. For the reason that the increment of the system sum rate is in excess of the increment of power consumption as the user’s transmit power changes in the range of 1–20 W, the energy efficiency appears as an increment with increasing total transmit power. In addition, it is clear that the EE in the SLIPT-enabled NOMA system of this paper is superior to the SLIPT-OFDMA system. The reason is that users in the NOMA system utilize the total bandwidth of the system and can achieve a higher data rate while each user in OFDMA only shares half of the bandwidth. This demonstrates that the SLIPT-enabled NOMA system can achieve a higher EE, which shows the strengths of applying SLIPT to NOMA systems. It can be inferred that the optimized system exhibits a superior energy efficiency due to the implementation of the proposed two-step PSO algorithm, thereby indicating the advantage of the approach described in this paper.
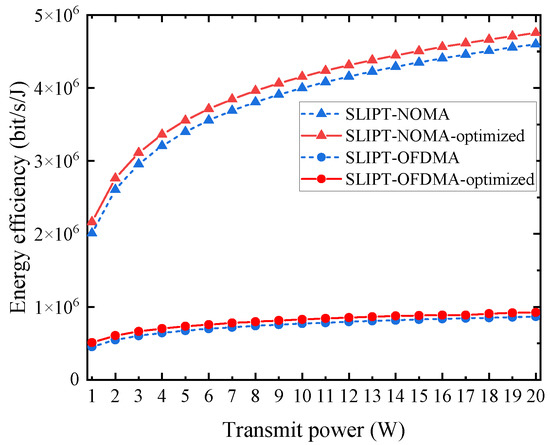
Figure 7.
Comparison of the impact of maximum transmit power on EE performance of SLIPT-enabled NOMA and SLIPT-enabled OFDMA system before and after optimization.
5. Conclusions
In this paper, a SLIPT-enabled NOMA system with PS protocol is proposed to improve the EE of a traditional VLC system. In addition, the power allocation and PS coefficient optimization is studied in this system by the PSO algorithm. Simulation results show that an appreciable EE performance can be achieved whilst satisfying constraints in terms of maximum transmitted power, minimum data rate and minimum harvested energy. In addition, the optimized SLIPT-enabled NOMA system achieves an EE that is bit/s/J higher than the SLIPT-OFDMA system when the transmit power is 20 W, demonstrating the advantage of applying SLIPT to NOMA systems. Some potential valuable future research directions may include designing grouping algorithms based on the users’ CSI, power requirements, data transmission requirements and other factors when considering SLIPT-enabled NOMA systems applied to scenarios of more users.
Author Contributions
Methodology, D.C. and Q.W.; validation, D.C., Q.W. and Z.L.; formal analysis, D.C. and Q.W.; investigation, Q.W., S.W. and R.H.; data curation, Q.W. and K.F.; writing—original draft preparation, D.C. and Q.W.; writing—review and editing, D.C., J.W. and H.L.; visualization, Z.L.; supervision, D.C. and J.W.; project administration, D.C.; funding acquisition, D.C., H.L. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by GuangDong Basic and Applied Basic Research Foundation (2021B1515120086, 2022A1515110770, 2022A1515110154); Fundamental Research Funds for the Central Universities (FRF-TP-22-044A1, FRF-IDRY-22-001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Relevant data are available from the authors upon reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Truitt, A.; Mahmoodi, S.N. A review on active wind energy harvesting designs. Int. J. Precis. Eng. Manuf. 2013, 14, 1667–1675. [Google Scholar] [CrossRef]
- Hao, D.; Qi, L.; Tairab, A.M.; Ahmed, A.; Azam, A.; Luo, D.; Pan, Y.; Zhang, Z.; Yan, J. Solar energy harvesting technologies for PV self-powered applications: A comprehensive review. Renew. Energy 2022, 188, 678–697. [Google Scholar] [CrossRef]
- Qian, H. Design of Forest IoT Monitoring Nodes Based on Energy Harvesting Technology. Master’s Thesis, Nanjing University of Information Engineering, Nanjing, China, 2022. [Google Scholar]
- Zhang, R.; Ho, C.K. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Abuella, H.; Elamassie, M.; Uysal, M.; Xu, Z.; Serpedin, E.; Qaraqe, K.A.; Ekin, S. Hybrid RF/VLC systems: A comprehensive survey on network topologies, performance analyses, applications, and future directions. IEEE Access 2021, 9, 160402–160436. [Google Scholar] [CrossRef]
- Chi, N.; Zhou, Y.; Wei, Y.; Hu, F. Visible light communication in 6G: Advances, challenges, and prospects. IEEE Veh. Technol. Mag. 2020, 15, 93–102. [Google Scholar] [CrossRef]
- Diamantoulakis, P.D.; Karagiannidis, G.K. Simultaneous lightwave information and power transfer (SLIPT) for indoor IoT applications. In Proceedings of the GLOBECOM 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Abdelhady, A.M.; Amin, O.; Chaaban, A.; Alouini, M.S. Resource allocation for outdoor visible light communications with energy harvesting capabilities. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Ye, K.; Wang, T.; Yang, F. Rate optimization for relaying VLC system with simultaneous lightwave information and power transfer. Opt. Express 2021, 29, 2184–2192. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tsonev, D.; Videv, S.; Haas, H. On the design of a solar-panel receiver for optical wireless communications with simultaneous energy harvesting. IEEE J. Sel. Areas Commun. 2015, 33, 1612–1623. [Google Scholar] [CrossRef]
- Pan, G.; Diamantoulakis, P.D.; Ma, Z.; Ding, Z.; Karagiannidis, G.K. Simultaneous lightwave information and power transfer: Policies, techniques, and future directions. IEEE Access 2019, 7, 28250–28257. [Google Scholar] [CrossRef]
- Wang, H.; Wang, F.; Li, R. Enhancing power allocation efficiency of NOMA aided-MIMO downlink VLC networks. Opt. Commun. 2020, 454, 124497. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Z.; Dai, X.; Zhang, R. An optimization perspective of the superiority of NOMA compared to conventional OMA. IEEE Trans. Signal Process. 2017, 65, 5191–5202. [Google Scholar] [CrossRef]
- Sung, J.Y.; Yeh, C.H.; Chow, C.W.; Lin, W.F.; Liu, Y. Orthogonal frequency-division multiplexing access (OFDMA) based wireless visible light communication (VLC) system. Opt. Commun. 2015, 355, 261–268. [Google Scholar] [CrossRef]
- Anzagira, A.; Edmonson, W. Non-orthogonal multiple access (NOMA) for LED-based visible light inter-satellite communications. In Proceedings of the 2018 6th IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Huntsville, AL, USA, 11–13 December 2018; IEEE: New York, NY, USA, 2018; pp. 24–29. [Google Scholar]
- Marshoud, H.; Kapinas, V.M.; Karagiannidis, G.K.; Muhaidat, S. Non-orthogonal multiple access for visible light communications. IEEE Photonics Technol. Lett. 2015, 28, 51–54. [Google Scholar] [CrossRef]
- Tennakoon, P.; Jayakody, D.N.K.; Affes, S. Simultaneous Lightwave Information and Power Transfer with Non-orthogonal Multiple Access. In Proceedings of the 2021 10th International Conference on Information and Automation for Sustainability (ICIAfS), Negambo, Sri Lanka, 11–13 August 2021; IEEE: New York, NY, USA, 2021; pp. 214–219. [Google Scholar]
- de Oliveira Filho, J.I.; Trichili, A.; Ooi, B.S.; Alouini, M.S.; Salama, K.N. Toward self-powered internet of underwater things devices. IEEE Commun. Mag. 2020, 58, 68–73. [Google Scholar] [CrossRef]
- Obeed, M.; Dahrouj, H.; Salhab, A.M.; Zummo, S.A.; Alouini, M.S. DC-bias and power allocation in cooperative VLC networks for joint information and energy transfer. IEEE Trans. Wirel. Commun. 2019, 18, 5486–5499. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Kizilirmak, R.C.; Rowell, C.R.; Uysal, M. Non-orthogonal multiple access (NOMA) for indoor visible light communications. In Proceedings of the 2015 4th International Workshop on Optical Wireless Communications (IWOW), Istanbul, Turkey, 7–8 September 2015; IEEE: New York, NY, USA, 2015; pp. 98–101. [Google Scholar]
- Li, C.; Jia, W.; Tao, Q.; Sun, M. Solar cell phone charger performance in indoor environment. In Proceedings of the 2011 IEEE 37th Annual Northeast Bioengineering Conference (NEBEC), Troy, NY, USA, 1–3 April 2011; IEEE: New York, NY, USA, 2011; pp. 1–2. [Google Scholar]
- Rakia, T.; Yang, H.C.; Gebali, F.; Alouini, M.S. Dual-hop VLC/RF transmission system with energy harvesting relay under delay constraint. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; IEEE: New York, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Masaracchia, A.; Da Costa, D.B.; Duong, T.Q.; Nguyen, M.N.; Nguyen, M.T. A PSO-based approach for user-pairing schemes in NOMA systems: Theory and applications. IEEE Access 2019, 7, 90550–90564. [Google Scholar] [CrossRef]
- Hasan, I.; Shamshiri, M.; Gan, C.K.; Ghani, M.; Yusoff, M. Using Particle Swarm Optimization Algorithm in the Distribution System Planning. Aust. J. Basic Appl. Sci. 2013, 7, 85–92. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).