Phase Imaging through Scattering Media Using Incoherent Light Source

Abstract

Phase imaging normally employs coherent a light source while an incoherent light source is not preferred due to its random wavefront. Another challenge for practical phase imaging is imaging through scattering media, which scatter the photons in a random manner and lead to seriously distorted images of speckles. Based on the convolutional neural network (CNN), this paper presents an approach for phase imaging through scattering media using an incoherent light source. A CNN was trained and utilized to reconstruct the target images from the captured images of speckles. Similarities of over 90% between the reconstructed images and their target images have been achieved. It was concluded that an incoherent light source can be used as an illumination source for scattering phase imaging with the assistance of deep learning technology. This phase imaging approach with an incoherent light source through scattering media can be used to record the refractive indices of transparent samples, which might lead to its application in biomedical imaging.

1. Introduction

The amplitude and phase in a light beam are excellent information transfer features in optical imaging. Optical imaging that records amplitude is referred to as bright field imaging, and that which records a phase is called phase imaging [1,2]. In biological imaging and astronomical observations, phase imaging is preferable to bright field imaging. In label-free biomedical tomography, for example, phase imaging can be used to obtain refractive index distributions by recording the phase of image light wave, and then realizing the fast, non-destructive, high-resolution imaging of transparent samples [3,4]. Both coherent and incoherent light can be used as illumination sources for bright field imaging, as their amplitudes can be readily modulated. The modulation of a light source in a phase is essential for phase imaging. However, it is a great challenge to modulate the phase of an incoherent beam due to its random wavefront, which leads to the absence of an incoherent light source in phase imaging. Coherent light sources have currently been adopted for phase imaging, but they are not considered ideal because of the speckle effect which results from the coherence [5]. Therefore, in successfully conducting phase imaging while avoiding the speckle effect induced by coherent light sources, the exploration of phase imaging with an incoherent light source is a worthwhile endeavor.

Imaging through scattering media is another inevitable obstacle for biological imaging or astronomical observations. Biological tissues or fogs that obscure the target might scramble its spatial information into random diffusion [6,7,8]. This topic has drawn significant research interests, as its solutions would benefit a multitude of applications such as deep tissue imaging [9,10], underwater imaging [11,12], imaging through fog [13,14], etc. However, the complexity of random transmission caused by the perturbations in scattering media makes it still challenging. A number of approaches, such as point spread functions [15,16], speckle correlation [17], transmission matrices [18], wave front shaping [19] and deep learning neural network-based methods [20,21], have been proposed in recent years for removing the effects of scattering media and achieving high-quality images. In these methods, with the advantages of higher accuracy, better robustness, faster processing speed and less requirements in hardware, deep-learning based methods have shown great potential in retrieving the original information from the images seriously distorted by scattering media. A variety of deep-learning networks have been proposed for the reconstruction of images degraded by scattering media. Li et al. reconstructed images through unseen diffusers by combining the CNN and speckle correlation, and their work was then extended to restore the targets hidden behind scattering media in unknown locations [22,23]. Similar work was reported by Rahmani and his collaborators, in which the CNN was utilized to reconstruct amplitude and phase images from the speckles through a multimode fiber [24]. Lai et al. proposed the reconstruction of images of two adjacent objects through a scattering medium via deep learning [25]. Based on a deep learning neural network, Qiao and his collaborators realized real-time X-ray phase-contrast imaging through random media [26]. In addition to the reconstruction of 2D images, the deep learning approach was demonstrated to produce a 3D phase image from a single shot [27]. By using a neural network, Zheng et al. realized incoherent bright field imaging through highly nonstatic and optically thick turbid media [28]. In general, deep learning has provided a powerful tool for the reconstruction of images through unseen diffusers. Realizing phase imaging with incoherent light sources while eliminating the influence of scattering media could be a worthwhile endeavor for the applications of biological imaging and astronomical observations. Therefore, we looked into this issue and proposed a phase imaging approach with an incoherent light source through scattering media with the aid of deep learning technology in this paper.

2. Experimental Setup

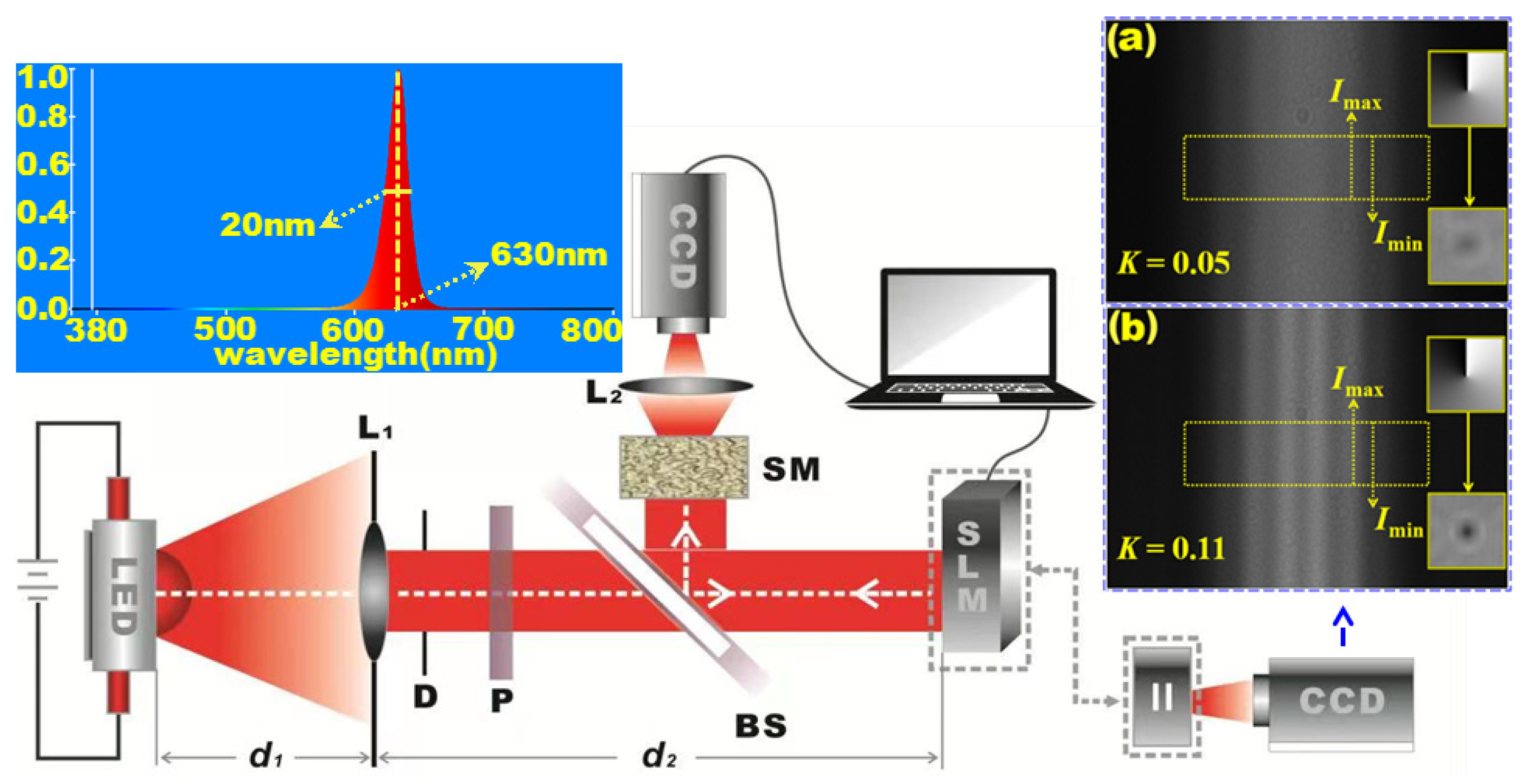
As shown in Figure 1, an experimental optical imaging platform was set up for the study of phase imaging with an incoherent light source through scattering media. A quasi-monochromatic red light emitting diode (LED: CREE 3W) was utilized as the incoherent illumination source, whose central wavelength and line width were 630 nm and 20 nm, respectively. The divergent incoherent beam emitted by the LED passed through a biconvex lens (L₁: focal length, f = 150 mm, clear aperture, Φ = 40 mm) and a diaphragm (D: clear aperture, Φ, = 10 mm), turning into an approximate paraxial beam. In order to improve the modulation effectiveness of the phase-only spatial light modulator (SLM: UPO-labs), a horizontal polarizer (P) that converted the paraxial beam into a horizontally polarized beam was placed behind the diaphragm. A beam splitter (BS) was inserted between the horizontal polarizer and the SLM, splitting the horizontally polarized beam into two portions. One portion was transmitted through the beam splitter and arrived at the SLM. As indicated in Figure 1, the distance of the illumination light propagating from the LED to SLM was z = d₁ + d₂. According to the van Cittert–Zernike principle, the spatial coherence of quasi-monochromatic light radiating from an incoherent light source can be expressed in a paraxial approximation as follows [29]:

$$\mu \left({\mathit{r}}_1-{\mathit{r}}_2,z\right)=\exp \left(i2\pi \frac{r_1{}^2-r_2{}^2}{2\lambda z}\right)\times \frac{{\displaystyle \underset{s}{\iint }I\left(x,y\right)\exp \left[-i2\pi \left(\frac{x_2-x_1}{\lambda z}x+\frac{y_2-y_1}{\lambda z}y\right)\right]dxdy}}{{\displaystyle \underset{s}{\iint }I\left(x,y\right)dxdy}}$$

(1)

In Equation (1), λ is the central wavelength of the quasi-monochromatic light, $I\left(x,y\right)$ is the intensity distribution in the source plane, and z is the propagation distance from the light source to the observation plane. ${\mathit{r}}_1=x_1{\mathit{e}}_x+y_1{\mathit{e}}_y$ and ${\mathit{r}}_2=x_2{\mathit{e}}_x+y_2{\mathit{e}}_y$ represent the spatial coordinates of two independent observations in the observation plane. Equation (1) indicates that the spatial coherence distribution of the beam is a function of the propagation distance and intensity distribution of the light source. Once the propagation distance is not zero, the beam changes from incoherent light to partially coherent light. For the beam incident to and modulated by the SLM, the observation plane locates it at the position of the SLM and the propagation distance is the distance from the LED to the SLM; that is, z = d₁ + d_2. It can be deduced that the beam at the position of the SLM is actually a partially coherent beam, although the original beam radiating from the LED illumination source is incoherent. That is, the beam changes from incoherent light to partially coherent light in transmission.

Figure 1. Optical experimental setup of incoherent phase imaging through scattering media, and the spectral characteristics of the red LED. P: polarizer, BS: beam splitter, SLM: spatial light modulator, L₁ and L₂: biconvex lens, SM: scattering media, and D: diaphragm. Inset (a): distribution of two-slit interference fringe when the propagation distance is 110 cm, and inset (b): distribution of two-slit interference fringe when the propagation distance is 120 cm.

Figure 1. Optical experimental setup of incoherent phase imaging through scattering media, and the spectral characteristics of the red LED. P: polarizer, BS: beam splitter, SLM: spatial light modulator, L₁ and L₂: biconvex lens, SM: scattering media, and D: diaphragm. Inset (a): distribution of two-slit interference fringe when the propagation distance is 110 cm, and inset (b): distribution of two-slit interference fringe when the propagation distance is 120 cm.

To verify the conclusion of the previous theoretical analysis, the coherence of the beam located at the position of the SLM without being modulated by the SLM was measured experimentally. The fringe contrast achieved from two-slit interference experiment reflected the coherence of a beam. For coherence measurement, two slits measuring 0.11 mm in slit width and 0.3 mm in slit spacing took the place of the SLM and a CCD camera behind the two slits captured the patterns of the interference fringes, as illustrated in the bottom right corner of Figure 1. As d₁ and d₂ were set to 10 cm and 100 cm, i.e., the propagation distance was 110 cm, the resultant two-slit interference fringe is shown in inset (a) of Figure 1. With d₁ = 20 cm and d₂ = 100 cm, the fringe is shown in the inset (b) of Figure 1. In both insets, I_max refers to the brightness of the maximum grey of the interference fringe, and I_min refers to the minimum. Substituting I_max and I_min into Equation (2) below, the contrasts of interference fringes (i.e., the value of K) can be obtained.

$$K=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}$$

(2)

According to Equation (2), the contrasts of interference fringes were calculated as 0.05 and 0.11, respectively, for different d₁ values of 10 cm and 20 cm, as labeled in the bottom left corners of inset (a) and (b) in Figure 1. It is well-known that K = 1 represents that the incident beam is completely coherent, whereas K = 0 corresponds to an incoherent beam. The measured fringe contrasts are between 0 and 1 and thus the beams incident on the two slits are partially coherent beams. Therefore in subsequent phase imaging experiments, the partially coherent beams incident on the SLM were phase-modulated by it and reflected back to the beam splitter.

Theoretical analysis and practical measurements showed that, the beams incident on the SLM were partially coherent and the values of the measured coherent contrasts of 0.05 and 0.11 were close to zero. It was essential to test whether or not such partially coherent beams can be effectively modulated by the SLM and used for phase imaging. The vortex phase illustrated in the top right corners of inset (a) and (b) in Figure 1 was loaded into the SLM to modulate the partially coherent beams and the beams were reflected back to the beam splitter. The beam splitter reflected the beams perpendicularly into a CCD camera (AVT PIKE F-421B, 2048 × 2048 pixels, pixel pitch = 7.5 μm) through another biconvex lens (L₂: focal length, f = 100 mm; clear aperture, Φ = 40 mm). The images captured by the CCD camera for different d₁ spacings are shown in the bottom right corners of inset (a) and (b) in Figure 1, which indicate the intensity distributions of the partially coherent beams phase-modulated by the SLM. The dark-grey circular patterns in the center of these images indicate that both partially coherent beams were successfully modulated by the SLM. The circular pattern in inset (b) is darker than that in inset (a), which suggests that the latter beam was modulated more effectively.

After the preparatory work described above, the experiments on phase imaging using incoherent light source through a scattering medium were carried out by inserting a scattering medium (SM: ground glass, THORLABS: DG100X100-120-100 mm × 100 mm N-BK7 Ground Glass Diffuser, 120 Grit) between BS and L₂, as shown in the experimental setup in Figure 1. Once a beam is modulated by the SLM, it carries the specific phase information that the SLM adds to it. The modulated beams reflected by BS entered the scattering medium, scattered into random speckles, and the phase information that they carried was scrambled in random diffusion. The random speckles produced by the SM were focused by lens L₂ and imaged by the CCD. Figure 2 shows a phase image loaded into the SLM to modulate the partially coherent beam and the corresponding speckle pattern captured by the CCD. There is no clue to the phase image at all from the speckle pattern due to the decorrelation caused by perturbations in the scattering medium.

3. Data Acquisition and Processing

As mentioned in the Introduction, deep learning neural network-based methods have been proposed to reconstruct the images affected by scatterers or diffusers. Taking the advantages of higher accuracy, better robustness, faster processing speed, more flexibility and better generalization ability, the method based on the convolutional neural network (CNN) was selected from a number of candidates for the goal of this paper. The CNN, which can be separated into unsupervised learning and supervised learning, is composed of a convolutional layer, pooling layer and up-sampling layer. Unsupervised learning involves learning sample data without a label or category to discover the structural knowledge of the sample data, while supervised learning involves learning a function or model from a given training data set, which can be employed to predict the result from new data [30]. Obviously, supervised learning is more desirable for reconstructing the phase information from speckle images. A supervised learning CNN of a U-net architecture was adopted in this study, the frame diagram of which is shown in Figure 3. There is an encoder and a decoder in the U-net, which can be divided into a contraction path and an expansion path. The decoder is connected with the corresponding feature layer of the encoder, and the information on different spatial scales is transmitted through this connection to retain the high-frequency information. The supervised learning U-net requires a data set that consists of the sample data with labels for network training. The images of handwritten digits in the MNIST dataset and the images of hand-drawn drawings in the Google Quick Draw dataset were displayed on the SLM as the phase images to modulate the incident partially coherent beams [31]. They were resized to 512 × 512 pixels and then loaded onto the SLM. The grayscale speckle images captured by the CCD were also of the size of 512 × 512 pixels.

The transmission distance, z, was firstly set to 110 cm and the coherent contrast, K, of the partially coherent beam incident on the SLM was 0.05. Briefly, 7000 images from the datasets were loaded onto the SLM as the phase images and 7000 speckle images were captured by the CCD. The phase images and their corresponding speckle images were paired to form an input–output dataset of 7000 data pairs. They were randomly grouped into two sets, a training set for the training network and a test set for evaluating network performance, in a ratio of 6 to 1. In order to improve training efficiency and reduce the training time, all the images in the training set were resized from 512 × 512 pixels to 256 × 256 pixels. The U-net was then trained by feeding the input–output data pairs in the training set into the network and optimized by an Adam (adaptive moment estimation) optimizer. The Adam optimizer utilizing the strategy of adaptive moment estimation was employed to minimize the loss function and optimize the training process [32]. The training program was implemented in the Keras/TensorFlow framework and sped up using a GPU (NVIDIA, RTX 2080 SUPER). Structural similarity (SSIM) was used to quantify the similarity of the reconstructed image to its corresponding phase image [33].

The handwritten digits reconstructed by the U-net as K = 0.05 are shown in Figure 4a and the reconstruction results of the hand-drawn drawings are shown in Figure 4b. The values at the top of the reconstructed images are the SSIM indexes that indicate the similarity of the reconstructed image to its corresponding phase image. Comparisons between phase images and reconstructed images demonstrate that the U-Net restored the phase images from the speckle images effectively. The features of the handwritten digits and the hand drawings, particularly their edges, have been retrieved from the speckle images and rendered on the reconstructed images accurately. The values of SSIM index of the reconstructed images indicate that structural similarities of about 0.9 for handwritten digits and over 0.7 for hand-drawn drawings were achieved in the reconstructions with the U-net.

An epoch in the network training process refers to a single pass through the entire training set, which is used to determine when to stop training. After each epoch, the structural similarity for the U-net trained with handwritten digits and that for the U-net trained with hand-drawn drawings are calculated and plotted in Figure 5. It could be found that the training converged and the structural similarities were almost at their maximums at the epoch of twelve. When the epoch number was less than eight, the red line was above the black line, while the situation was reversed as it became greater than eight. That is, the U-net performed better at reconstructing the hand-drawn drawings when it was undertrained. However, when it was sufficiently trained, it showed better performance in the reconstruction of the handwritten digits. This is because the relatively richer graphical information of hand drawings makes their features more recognizable to the network in the early epochs, which also makes them more difficult to be completely reconstructed in the final epochs. The results in Figure 4 and Figure 5 demonstrate that a partially coherent beam with a very low coherence (K = 0.05) emitted from an incoherent LED source can be used for phase imaging through scattering media.

As indicated by the coherence measurements described previously, the coherence of the partially coherent beam emitted by the LED could be increased by increasing the propagation distance, d₁. The coherence contrast, K, rises from 0.05 to 0.11 when d₁ is set to 20 cm. Figure 6 shows the reconstruction of the phase images through scattering media by the U-net when K is 0.11. By comparing the SSIM indexes in Figure 5 with the corresponding ones in Figure 6, it can be seen that the structural similarities of the reconstruction for the handwritten digits did not increase with the increase in the coherence of the modulated beam. However, for hand drawings, they were significantly improved and an average structural similarity of 0.84 was achieved.

The SSIM indexes for the reconstruction of handwritten digits and for the reconstruction of hand drawings as functions of the epoch number are plotted and shown in Figure 7 for when the coherence contrast of the incident partially coherent beam is 0.11. A similar trend indicated by the curves in Figure 5 is shown in this graph displaying that the SSIM rose gradually with the increase in the epoch number until it reached its maximum when the training of the network converged, and the reconstruction performance of the U-net for handwritten digits was slightly better than that for hand drawings. An obvious difference from Figure 5 is that the red line becomes very close to the black line. In conjunction with the discussion in the previous paragraph, it can be concluded that the improvement in the coherence of the partially coherent beam helps the U-net to reconstruct complex phase images more accurately. However, the U-net can reconstruct simple phase images through scattering media accurately even if the coherence of the modulated beam is very low, for example, when K = 0.05. To further clarify the relationship between reconstruction accuracy and the K value, the maximum SSIM as a function of the K value is plotted in Figure 8. A similar conclusion to the above can be drawn from the curves in the figure; that is, the U-net is capable of reconstructing simple phase images through scattering media accurately even with the modulated beam of very low coherence. However, for complex phase images, the increase in beam coherence helps to increase reconstruction accuracy.

In order to further verify the feasibility of phase imaging using an incoherent light source through scattering media, a hybrid training method was utilized, in which the training set consisting of both images of handwritten digits and hand drawings was employed to train the U-net. Then, the performance of the network was evaluated though the reconstruction of the images in the test set and the results are illustrated in Figure 9. In the case of K = 0.05, the U-net could accurately reconstruct the hand-drawn images but made errors in the reconstruction of handwritten digits. As K = 0.11, both images of handwritten digits and hand-drawn drawings were accurately reconstructed from speckle images and a final SSIM of over 0.8 was obtained.

Figure 10 illustrates the structural similarity indexes of the U-net during the hybrid training process. A significant improvement of over 30% in network performance was achieved when the partially coherent beam incident on the SLM had higher coherence. In the case of K = 0.11, although the coherence was still low, the accurate reconstruction of both images of handwritten digits and hand drawings with a final structural similarity of 0.8 was realized with the U-net trained through hybrid training. The results demonstrate that phase imaging through a scattering medium can be achieved using an incoherent light source by simply controlling the transmission distance between the incoherent light source and the target.

4. Conclusions

In summary, we have experimentally demonstrated that phase imaging through scattering media using an incoherent light source can be realized with the aid of a CNN. Quantitative analyses of the structural similarities between the original and reconstructed phase images were performed to indicate the fidelity of phase image reconstruction and to evaluate the performance of the network. The results of our study suggest that incoherent light sources can be used as illumination sources for phase imaging through scattering media. As the incoherent beam radiated from an incoherent light source propagates to the position of phase modulation, the beam converts from an incoherent one into a partially coherent automatically. The random wavefront phase of the dominant incoherent part of the beam does not fail in phase modulation and the CNN reconstructs the phase images from the speckle images caused by the scattering media. This phase imaging approach with an incoherent light source through scattering media can be used to record the refractive indices of transparent samples, which might lead to its application in biomedical imaging.