Trapping of Rayleigh Spheroidal Particles Using Tightly Focused Higher-Order Vector Vortex Beams
Abstract
1. Introduction
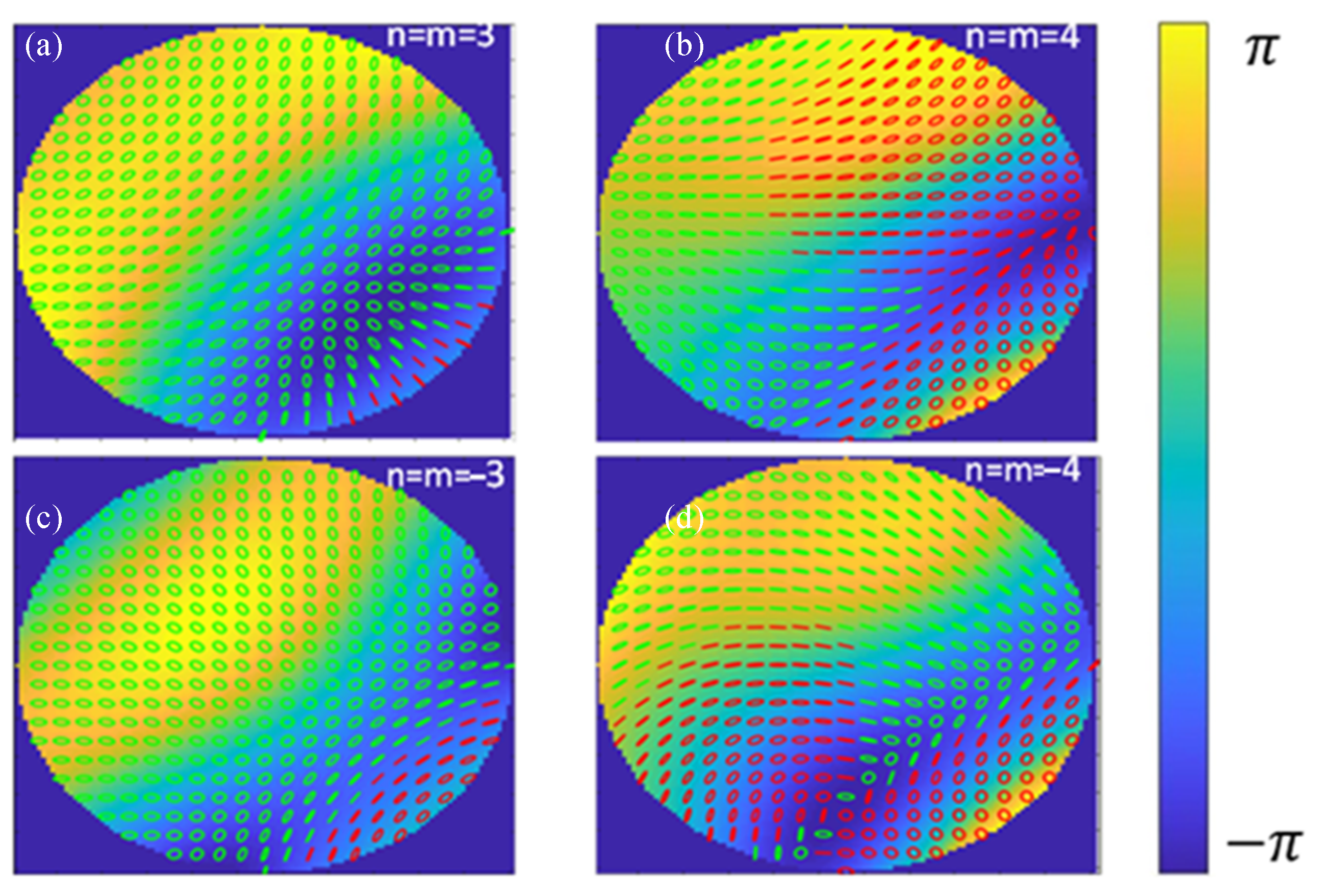
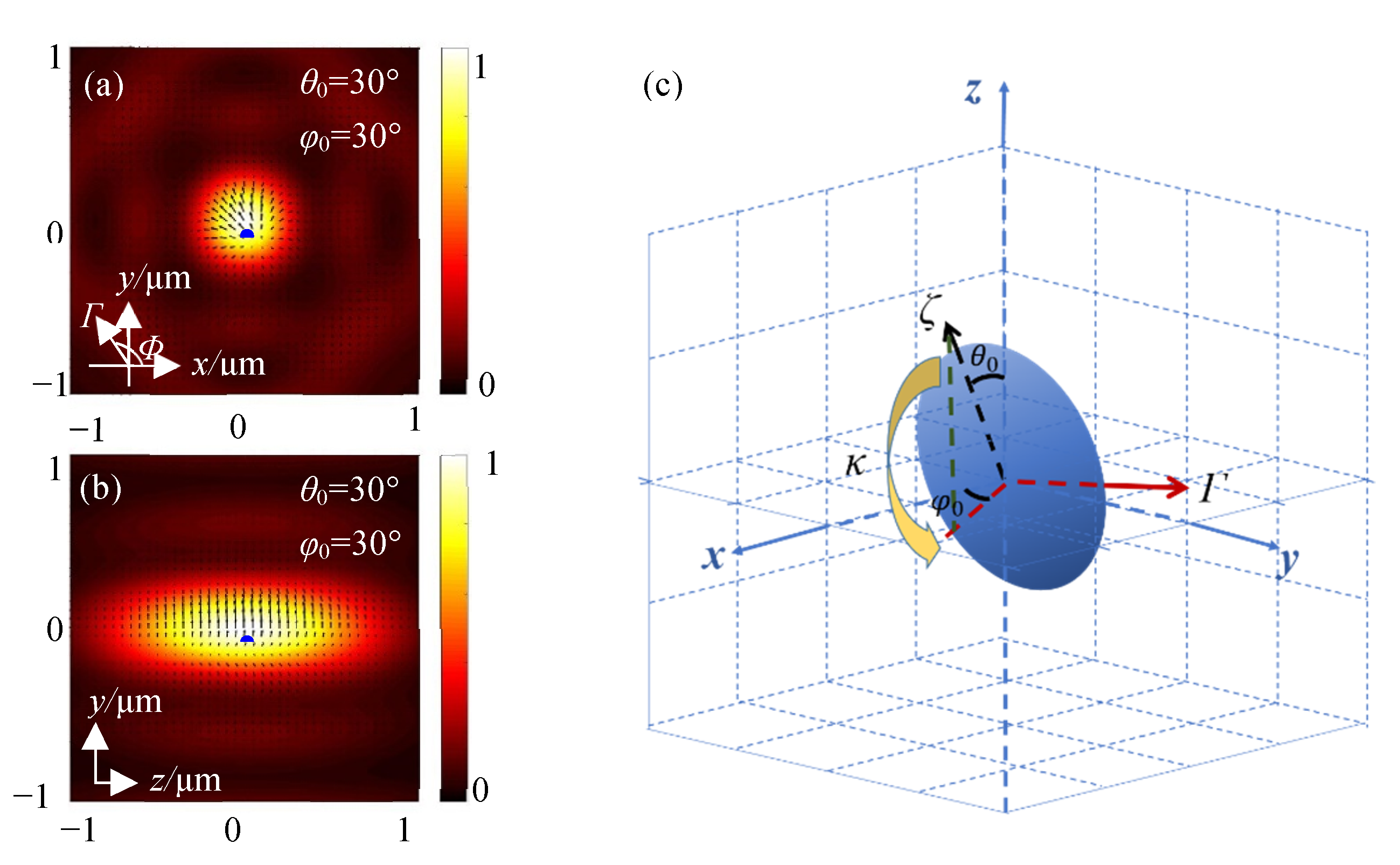
2. Properties of Tightly Focused HOVVBs
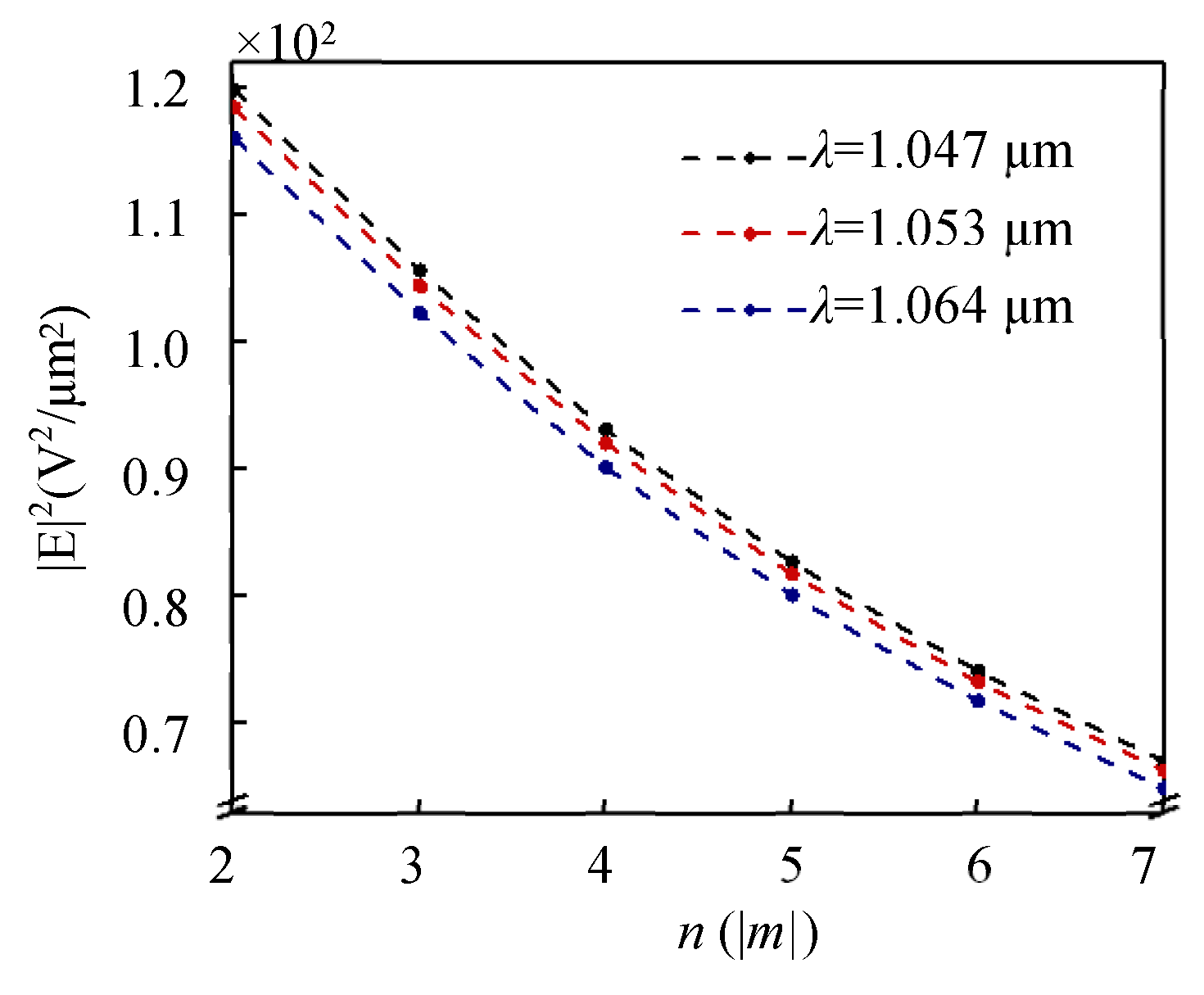
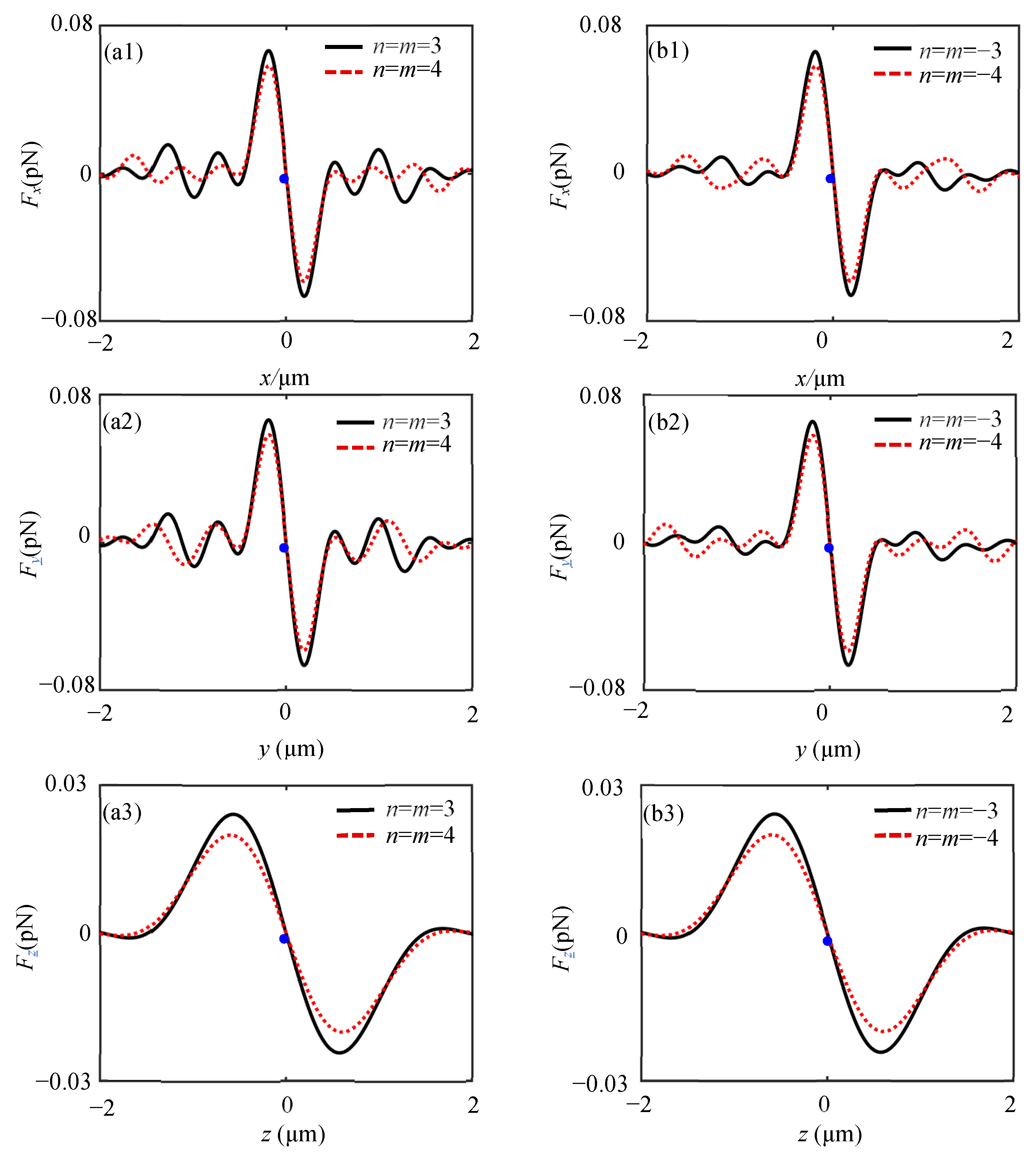
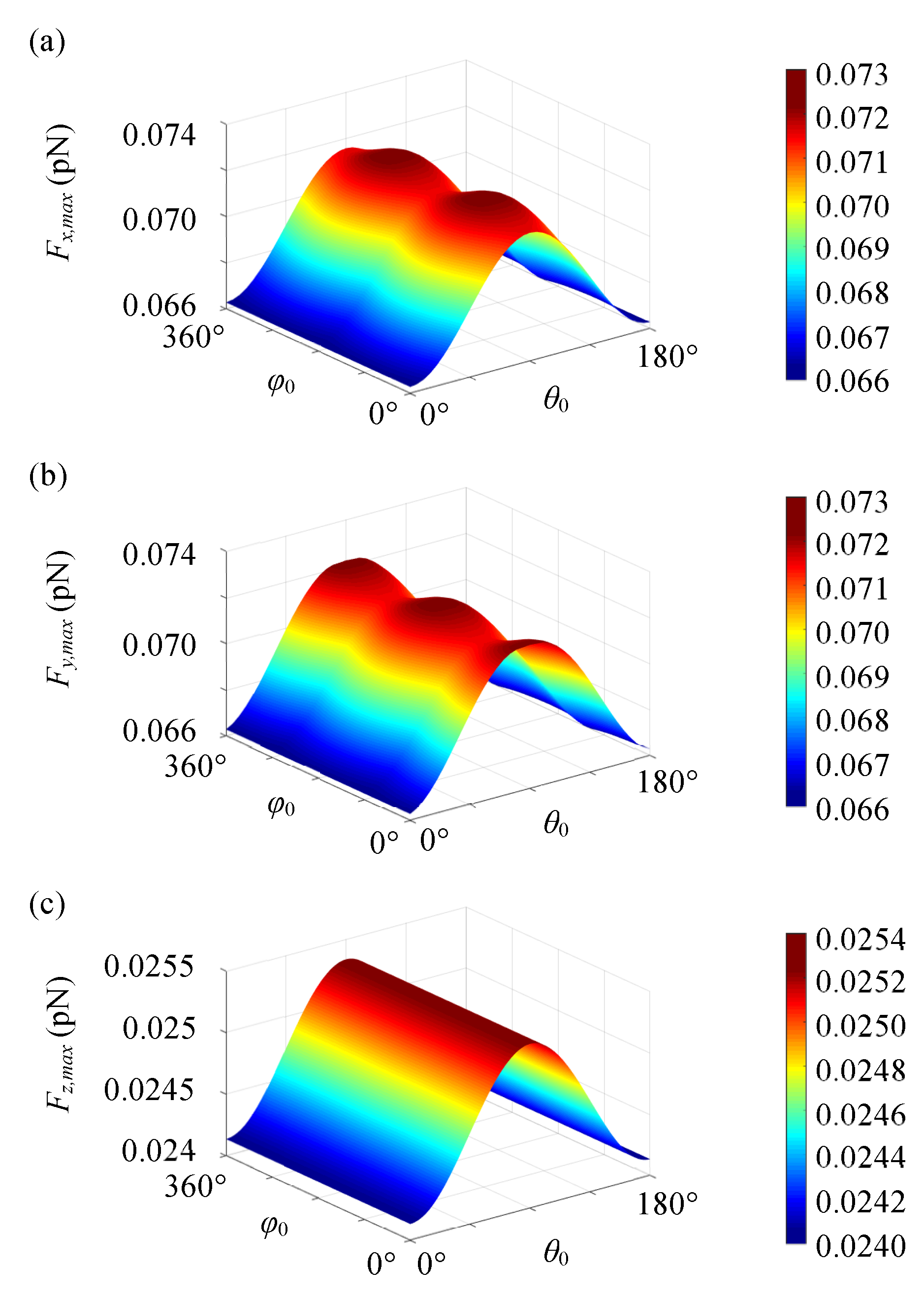
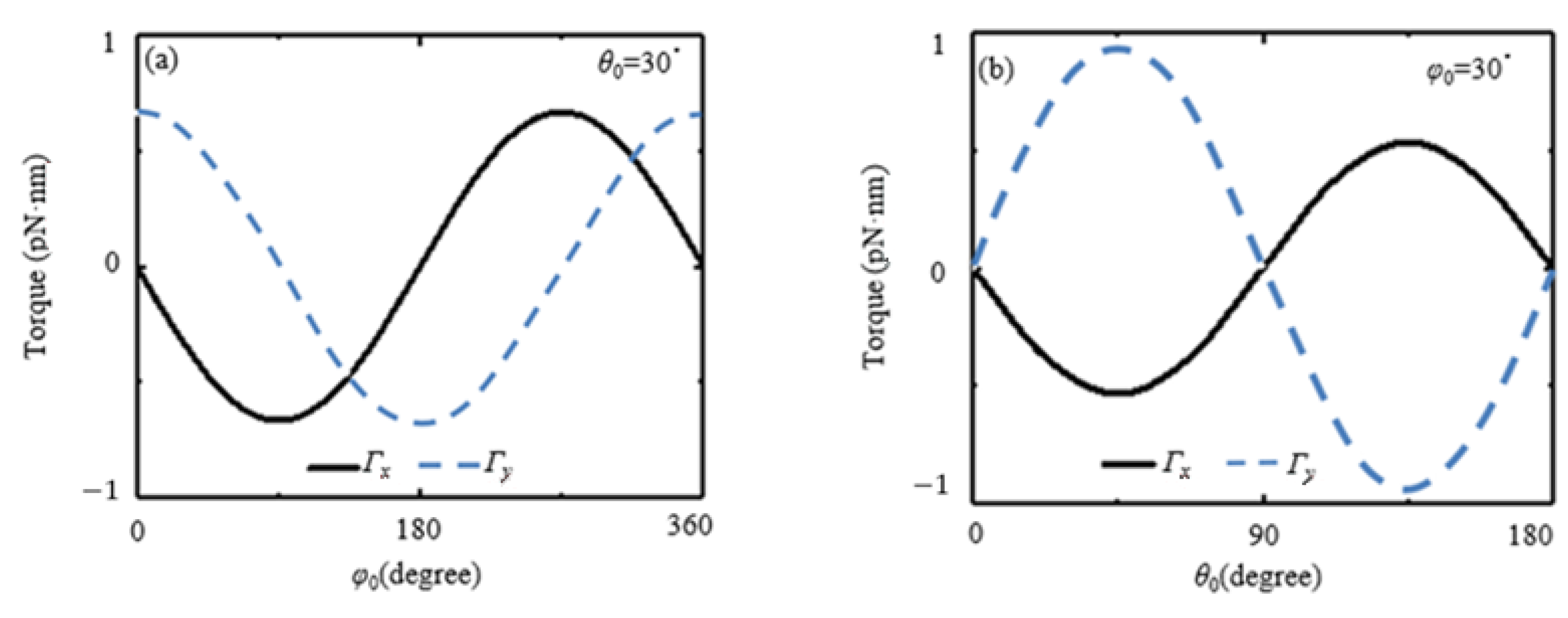
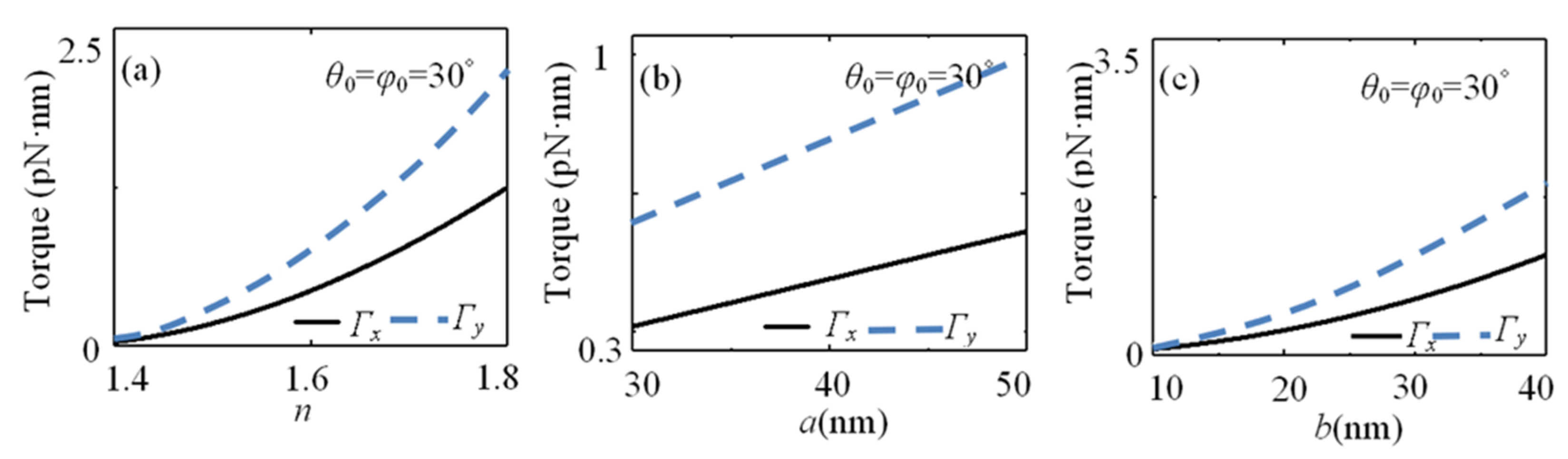
3. Optical Force and Torque of HOVVBs on Rayleigh Spheroidal Particles
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Chuang, C.-H.; Ho, C.-Y.; Hsiao, Y.-C.; Chiu, C.-P.; Wei, M.-D. Selection rule for cavity configurations to generate cylindrical vector beams with low beam quality factor. Opt. Express 2021, 29, 5043–5054. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Luo, D.; Pan, C.; Qin, Y.; Zhang, Y.; Wei, D.; Chen, H.; Gao, H.; Li, F. Collapse of hybrid vector beam in Rb atomic vapor. Opt. Lett. 2021, 46, 2614–2617. [Google Scholar] [CrossRef]
- Naidoo, D.; Fromager, M.; Ait-Ameur, K.; Forbes, A. Radially polarized cylindrical vector beams from a monolithic microchip laser. Opt. Eng. 2015, 54, 111304. [Google Scholar] [CrossRef]
- Wang, B.; Che, Y.; Zhong, X.; Yan, W.; Zhang, T.; Chen, K.; Li, X. Cylindrical vector beam revealing multipolar nonlinear scattering for superlocalization of silicon nanostructures. Photonics Res. 2021, 9, 950–957. [Google Scholar] [CrossRef]
- Niv, A.; Biener, G.; Kleiner, V.; Hasman, E. Manipulation of the Pancharatnam phase in vectorial vortices. Opt. Express 2006, 14, 4208–4220. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Chen, J.; Wang, X.-L.; Wang, H.-T. Twisted vector field from an inhomogeneous and anisotropic metamaterial. J. Opt. Soc. Am. B 2012, 29, 572–576. [Google Scholar] [CrossRef]
- Mathieu, L.J.; Maurizio, R.; Romain, Q. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349–356. [Google Scholar]
- Wu, M. Optoelectronic tweezers. Nat. Photonics 2011, 5, 322–324. [Google Scholar] [CrossRef]
- Li, J.; Zheng, Y. Optothermally Assembled Nanostructures. Acc. Mater. Res. 2021, 2, 352–363. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Z.; Liu, Y.; Kollipara, P.S.; Feng, Y.; Zhang, Z.; Zheng, Y. Opto-refrigerative tweezers. Sci. Adv. 2021, 7, eabh1101. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Trapping metallic Rayleigh particles with radial polarization. Opt. Express 2004, 12, 3377–3382. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, K.; Lu, X. Radiation force of highly focused Lorentz-Gauss beams on a Rayleigh particle. Opt. Express 2011, 19, 9708–9713. [Google Scholar] [CrossRef] [PubMed]
- Bi, L.; Yang, P.; Kattawar, G.W.; Kahn, R. Single-scattering properties of triaxial ellipsoidal particles for a size parameter range from the Rayleigh to geometric-optics regimes. Appl. Opt. 2008, 48, 114–126. [Google Scholar] [CrossRef]
- Bekshaev, A.; Bliokh, K.; Soskin, M. Internal flows and energy circulation in light beams. J. Opt. 2011, 13, 053001. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Lu, D.; Liu, Z.; Cheng, Z.; He, L. Measurement of the membrane elasticity of red blood cell with osmotic pressure by optical tweezers. Cryo Lett. 2009, 30, 89–95. [Google Scholar]
- Bayoudh, S.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Orientation of biological cells using plane-polarized Gaussian beam optical tweezers. J. Mod. Opt. 2003, 50, 1581–1590. [Google Scholar] [CrossRef]
- Cherney, D.P.; Bridges, T.E.; Harris, J.M. Optical Trapping of Unilamellar Phospholipid Vesicles: Investigation of the Effect of Optical Forces on the Lipid Membrane Shape by Confocal-Raman Microscopy. Anal. Chem. 2004, 76, 4920–4928. [Google Scholar] [CrossRef]
- Hinojosa-Alvarado, A.; Gutiérrez-Vega, J. Geometrical optics calculation of forces and torques produced by a ringed beam on a prolate spheroid. J. Opt. Soc. Am. B. 2010, 27, 1651–1658. [Google Scholar] [CrossRef]
- Cao, Y.; Song, W.; Ding, W.; Sun, F.; Zhu, T.; Zhu, T. Equilibrium orientations of oblate spheroidal particles in single tightly focused Gaussian beams. Opt. Express 2014, 22, 18113–18118. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Ren, K.; Gouesbet, G.; Cai, X.; Gréhan, G. Theoretical prediction of radiation pressure force exerted on a spheroid by an arbitrarily shaped beam. Phys. Rev. E 2007, 75, 026613. [Google Scholar] [CrossRef] [PubMed]
- Rui, G.; Li, Y.; Zhou, S.; Wang, Y.; Gu, B.; Cui, Y.; Zhan, Q. Optically induced rotation of Rayleigh particles by arbitrary photonic spin. Photon. Res. 2018, 7, 69–79. [Google Scholar] [CrossRef]
- Xu, F.; Lock, J.A.; Gouesbet, G.; Tropea, C. Radiation torque exerted on a spheroid: Analytical solution. Phys. Rev. A 2008, 78, 013843. [Google Scholar] [CrossRef]
- Huang, K.; Shi, P.; Cao, G.W.; Li, K.; Zhang, X.B.; Li, Y.P. Vector-vortex Bessel–Gauss beams and their tightly focusing properties. Opt. Lett. 2011, 36, 888–890. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, J.; Litchinitser, N.M.; Han, Y. Dynamical characteristics of tightly focused vortex beams with different states of polarization. J. Opt. 2018, 21, 015401. [Google Scholar] [CrossRef]
- Otte, E.; Tekce, K.; Denz, C. Tailored intensity landscapes by tight focusing of singular vector beams. Opt. Express 2017, 25, 20194–20201. [Google Scholar] [CrossRef]
- Zou, X.; Zheng, Q.; Wu, D.; Lei, H. Controllable cellular micromotors based on optical tweezers. Adv. Funct. Mater. 2020, 30, 2002081. [Google Scholar] [CrossRef]
- Vasse, G.F.; Buzón, P.; Melgert, B.N.; Roos, W.H.; van Rijn, P. Single Cell Reactomics: Real-Time Single-Cell Activation Kinetics of Optically Trapped Macrophages. Small Methods 2021, 5, 2000849. [Google Scholar] [CrossRef]
- Hu, S.; Ye, J.-Y.; Zhao, Y.; Zhu, C.-L. Advanced optical tweezers on cell manipulation and analysis. Eur. Phys. J. Plus 2022, 137, 1024. [Google Scholar] [CrossRef]
- Shen, Y.; Weitz, D.A.; Forde, N.R.; Shayegan, M. Line optical tweezers as controllable micromachines: Techniques and emerging trends. Soft Matter 2022, 18, 5359. [Google Scholar] [CrossRef]
- Chen, H.; Lin, H.; Jones, P.H.; Chen, Z.; Luo, S.; Pu, J. Influence of slow light effect on trapping force in optical tweezers. Opt. Lett. 2022, 47, 710–713. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Zhong, M.C.; Wang, Z.; Ke, Z.; Zhong, Z.; Zhou, J. Non-Invasive Dynamic Reperfusion of Microvessels In Vivo Controlled by Optical Tweezers. Front. Bioeng. Biotechnol. 2022, 10, 952537. [Google Scholar] [CrossRef] [PubMed]
- Hwang, H.; Byun, A.; Park, J.; de Léséleuc, S.; Ahn, J. Optical tweezers throw and catch single atoms. Optica 2023, 10, 401–406. [Google Scholar] [CrossRef]
- Quy, H.Q.; Tuan, D.Q.; Thanh, T.D.; Thang, N.M. Enhance of optical trapping efficiency by nonlinear optical tweezers. Opt. Commun. 2018, 427, 341–347. [Google Scholar] [CrossRef]
- Wei, W.; Zhu, L.; Tai, Y.; Li, X. Cycloid-structured optical tweezers. Opt. Lett. 2023, 48, 972–975. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Royal Society 1959, 253, 358–379. [Google Scholar]
- Youngworth, K.; Brown, T. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Liang, Y.; Zhang, P.; Yao, B. Transverse spinning of particles in highly focused vector vortex beams. Phys. Rev. A 2017, 95, 053802. [Google Scholar] [CrossRef]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.M.; McGloin, D.; Chiu, D.T. Spin-to-Orbital Angular Momentum Conversion in a Strongly Focused Optical Beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef]
- Kotlyar, V.; Stafeev, S.; Zaitsev, V.; Kozlova, E. Spin-Orbital Conversion with the Tight Focus of an Axial Superposition of a High-Order Cylindrical Vector Beam and a Beam with Linear Polarization. Micromachines 2022, 13, 1112. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Sykes, J.B.; Bell, J.S.; Dill, E.H. Electrodynamics of Continuous Media. Phys. Today 1961, 14, 48–50. [Google Scholar] [CrossRef]
- Simonot, L.; Hébert, M.; Hersch, R.D.; Garay, H. Ray scattering model for spherical transparent particles. JOSA A 2008, 25, 1521–1534. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Yurkin, M.A. On the concept of random orientation in far-field electromagnetic scattering by nonspherical particles. Opt. Lett. 2017, 42, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Draine, B.T. The discrete-dipole approximation and its application to interstellar graphite grains. Astrophys. J. 1988, 333, 848–872. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Yao, B.; Lei, M.; Yang, Y.; Min, J.; Dan, D. Trapping of Rayleigh spheroidal particles by highly focused radially polarized beams. J. Opt. Soc. Am. B 2015, 32, 468–472. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Yao, B.; Liang, Y.; Han, G.; Zhang, P. Optical trapping force and torque on spheroidal Rayleigh particles with arbitrary spatial orientations. JOSA A 2016, 33, 1341–1347. [Google Scholar] [CrossRef]
- Mitri, F.G. Optical Bessel beam illumination of a subwavelength prolate gold (Au) spheroid coated by a layer of plasmonic material: Radiation force, spin and orbital torques. J. Phys. Commun. 2017, 1, 015001. [Google Scholar] [CrossRef]
- Chaumet, P.; Nieto-Vesperinas, M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt. Lett. 2000, 25, 1065–1067. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhang, H.; Wei, C.; Zhang, Y.; Gao, X.; Wen, D.; Li, P.; Zhao, J. Trapping of Rayleigh Spheroidal Particles Using Tightly Focused Higher-Order Vector Vortex Beams. Photonics 2023, 10, 785. https://doi.org/10.3390/photonics10070785
Li D, Zhang H, Wei C, Zhang Y, Gao X, Wen D, Li P, Zhao J. Trapping of Rayleigh Spheroidal Particles Using Tightly Focused Higher-Order Vector Vortex Beams. Photonics. 2023; 10(7):785. https://doi.org/10.3390/photonics10070785
Chicago/Turabian StyleLi, Dong, Hongxu Zhang, Chengquan Wei, Yundi Zhang, Xize Gao, Dandan Wen, Peng Li, and Jianlin Zhao. 2023. "Trapping of Rayleigh Spheroidal Particles Using Tightly Focused Higher-Order Vector Vortex Beams" Photonics 10, no. 7: 785. https://doi.org/10.3390/photonics10070785
APA StyleLi, D., Zhang, H., Wei, C., Zhang, Y., Gao, X., Wen, D., Li, P., & Zhao, J. (2023). Trapping of Rayleigh Spheroidal Particles Using Tightly Focused Higher-Order Vector Vortex Beams. Photonics, 10(7), 785. https://doi.org/10.3390/photonics10070785





