Abstract
A new class of stationary electromagnetic sources radiating outward from the surface of an infinitely long cylinder is introduced via vectorial coherent mode representation. First, two particular types of such sources are discussed: with either an electric or magnetic field aligned with the cylinder’s axis. The former case represents a scalar scenario, while the latter leads to the two-component electric field. The combination of these two types of sources is then considered by forming the three-component electric field vector. An extension to the stationary case is then made in which the electric field correlations are shown to be described by the intrinsically cross-spectral density matrix. Several known theories of electromagnetic coherence and polarization are then invoked for the analysis of radiation, on and off the source surface. The results for the spectral density, degree of coherence, and degree of polarization are then discussed in detail. The effects of mutual correlation of modes are also outlined. The new family of sources is of importance for any application involving cylindrical sources with controllable radiation.
1. Introduction
With a very few exceptions, partially coherent and partially polarized fields treated in the optical literature are assumed to be emitted by planar sources and propagate into a half-space [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Several papers, however, have appeared in need of studying radiation emitted by the Sun, which have considered spherical sources and propagation into the entire three-dimensional space, e.g., [20,21,22]. Another fundamental type of non-planar sources that have been recently studied are cylindrical sources. Just like planar and spherical geometries, cylindrical geometry enjoys the analytical solution of the Helmholtz equation. Recently, the spectral density and coherence state of the radiation on the surface of the cylinder and on its propagation outward were analyzed in the scalar domain [23]. The spectral density and polarization characteristics have also been analyzed for the case of cylindrical electromagnetic sources [24]. In both cases, very interesting results were obtained. It has been found that the scattering of stationary electromagnetic fields by a cylinder leads to a highly oscillatory cross-spectral density whose characteristics cannot be modified at will [25]. Other authors have also analyzed the propagation of cylindrical electromagnetic waves in non-linear and inhomogeneous media [26,27].
In this work, we study in detail the polarization and especially the coherence characteristics of the radiation emitted by cylindrical sources in the electromagnetic case. From the new examples included, the full potential of this type of non-planar source is elucidated.
The article is structured as follows. This section constitutes the Introduction. In Section 2, the formalism and the different parameters that we are going to use in this work are briefly reviewed. The basis functions of the axial, tangential, and radial components and their propagation are studied in Section 3 and Section 4, respectively. The particular case of a partially coherent beam with uncorrelated expansion coefficients is analyzed in Section 5, with special emphasis on polarization. In Section 6, some examples are presented where the coherence and polarization properties of the radiation, both across the source and in propagation, are studied for different choices of the correlations among the expansion coefficients. Section 7 briefly summarizes the most important results of this work.
2. Preliminaries
Assuming cylindrical symmetry, a typical electric field can always be thought of as arising from the superposition of two orthogonally polarized contributions: one, , parallel to the axis of the cylinder (in the so-called E-polarization), and the other, , lying on the transverse plane, i.e., the plane perpendicular to the cylinder axis. In the latter case, it is the magnetic field that is supposed to be parallel to the cylinder axis (H-polarization). Such a decomposition makes it easier to obtain the solution to problems involving the scattering and/or the radiation from cylindrical sources [28,29].
Let us start by considering E-polarization (see Figure 1a). We denote by a the radius of the cylinder and use cylindrical coordinates z, r, and , and assume the cylinder to be of infinite extent along z. Since, due to the cylindrical symmetry, the emitted field is assumed to be independent of z, the electric field in the space outside can be expressed as a function of r and only. Denoting with k the wavenumber, according to [28,29] the outgoing irradiated field can be expanded into the series
with a suitable set of coefficients. Here, denotes an outgoing Hankel function [29], generally written as to distinguish it from the inward going function , which we will not use [28].
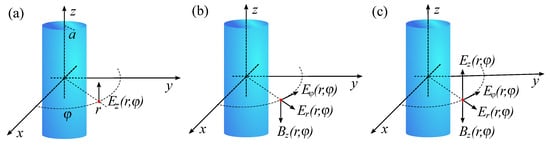
Figure 1.
Section of an infinitely long cylinder of radius a showing the generated electric field components in an arbitrary point for (a) E-polarization, (b) H-polarization, and (c) general polarization.
It is convenient to write the field component appearing in Equation (1) as
with
because in such a way, since , the coefficients correspond to the usual Fourier coefficients of along a circle .
Analogous expansions hold in the H-polarization for the components of the electric field across the transverse plane (see Figure 1b). In this case, the electric field in Equation (2) is replaced by (magnetic induction) and we have
where a different set of coefficients, , is used.
Assuming that the field propagates in vacuo, the corresponding electric field can be evaluated from Equation [29,30]
with c being the speed of light, which provides, for the two transverse components,
the prime denoting derivative with respect to the argument.
As for the case of E-polarization, we can set
and
Considering the contribution of the two polarizations [see Figure 1c], the following expressions for the three components (namely, radial, tangential, and axial) of the electric field all over the space can be written:
Note that, differently from the coefficients, does not represent the Fourier coefficients of any of the two transverse field components along the circle because neither nor equal one. We will refer to the functions , , and as radial, tangential, and axial basis functions of the field, respectively.
Let us now pass to the partially coherent case, where the coefficients and become random variables. We make use of the cross-spectral density matrix , which gives account of the two-point second-order correlations between the pairs of all the field components, and whose elements are defined as [1,31,32]
with the angle brackets denoting ensemble average.
The following are the explicit expressions of the nine elements of the CSD matrix in Equation (10), for the most general case:
The local properties of the field at the point are taken into account by the matrix
referred to as the polarization matrix. In particular, the spectral density of the field is
with Tr denoting the trace.
Several definitions of a degree of polarization (DOP) have been given for 3D fields. One of these, proposed in [33] reads
It is always limited to the interval , the two limiting cases corresponding to completely unpolarized or perfectly polarized fields, respectively. It is also interesting to note that the following relation holds:
where () are the eigenvalues of , so that takes the form
A significant aspect of this definition is that the DOP of a completely unpolarized 2D field turns out to be 1/2 (in such a case one of the eigenvalues is zero and the two remaining are equal to each other), denoting that a certain "polarization” exists, due to the fact that one of the three field components is missing.
Alternative definitions for a 3D DOP have been given. For example, Ellis et al. [34] introduced the following parameter, which reduces to the usual one for 2D field:
with the eigenvalues ordered in such a way that . In fact, if the field is 2D, then , and gives 0 for completely unpolarized fields () and 1 for completely polarized fields (). Comparisons and relationships between the above definitions can be found in [35,36,37].
On the other hand, several scalar quantities have been proposed to account for the coherence properties of the field [31,38,39,40,41,42,43], but most of them refer to paraxial fields, where the longitudinal field component can be neglected and the CSD matrix reduces to a matrix. In the most general case, an electromagnetic degree of coherence can be introduced as [31]
Since the following relation holds:
gives account of all correlations among the field components equally. According to such definition, the relation does not hold in general, as it does for the scalar case, because a non-perfect correlation may exist among the various field components at a single point. This happens when the field is non-perfectly polarized. In fact, it can be shown that
denoting that only attains to perfectly polarized fields.
Another definition for three-dimensional fields’ degree of coherence was introduced in Ref. [39]:
being consistent in form with that of the classic coherence theory, as it involves the linear CSD matrix norm. Since it is based on the trace of the CSD matrix alone, it carries information about correlations as are, in the absence of any devices of polarization optics. It also preserves the phase information, which has proven to be crucial in the remote directional control and singular optics.
3. The Basis Functions
All coherence and polarization properties of any field endowed with cylindrical symmetry are determined by the quantities in angular brackets in Equation (11), which give the correlations among the modes involved in the field expansions. However, some general features concerning the propagation of the fields expressed by those CSD elements can be deduced.
First of all, the asymptotic behaviors of the basis functions can be obtained from the corresponding expressions of the Hankel functions. In fact, applying the relation [44]
and the asymptotic formula for large arguments (),
yields
In particular, if , turns out to be proportional to , and the two corresponding components decrease with r at the same rate.
In Figure 2, the behaviors of , , and are shown for and different orders, as functions of the propagation distance normalized to the cylinder radius ().
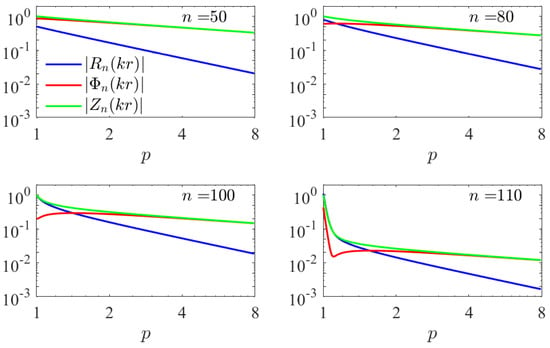
Figure 2.
Absolute value of the basis functions as a function of radial distance () for and some values of the order n.
Since for any value of the index n, the expansion coefficients of the radial and the tangential components coincide (see Equation (9)), the comparison of the corresponding curves (blue and red, respectively) also gives information about the relative weight of such components.
The asymptotic behaviors predicted by Equations (24)–(26) can be recognized: as for both the tangential and axial components (red and green curves, almost coinciding) and as for the radial component (blue curve). This implies that the latter component becomes decreasingly significant on moving away from the cylinder surface, in such a way that the electric field always turns out to be almost perpendicular to the radial direction at points far enough from the surface. On the other hand, it is interesting to note that the normalized distance where the asymptotic expression holds depends on the index n, being of the order of .
At shorter distances different behaviors are observed, depending on the ratio . For small n (compared to ), the tangential component is slightly lower than the axial one on the cylinder surface, but they reach very similar values at distances in the asymptotic limit, when . The radial component is significantly lower than the other ones already on the cylinder surface and decreases faster.
When the mode order increases (n comparable to ), near the cylinder surface, the radial component becomes comparable to the axial one, while the tangential component is quite lower. During propagation, when the asymptotic behavior is reached, the axial and tangential components become comparable while, as expected, the radial one becomes negligible.
For orders n above , a very fast decrease of all components can be noted in a small region in the vicinity of the cylinder surface, where their absolute values drop to a few percent of their initial ones for (for ). The decreasing rate becomes faster and faster on increasing n.
The above behaviors fully determine the evolution of the electric field components upon propagation and, consequently, the coherence and polarization properties of the radiated field.
4. Evolution of the Expansion Coefficients
The effect of propagation, from the cylinder surface outward, can be interpreted as a filtering process on the coefficients of the expansions appearing in Equation (9). The latter, in fact, can be written as
with
Such quantities, which, of course, equal 1 when , represent the weights by which the coefficients are multiplied during propagation. Their absolute values are shown in Figure 3 as functions of , for different choices of the cylinder radius a and the propagation distance . Although n takes integer values, continuous curves are presented for better visualization.
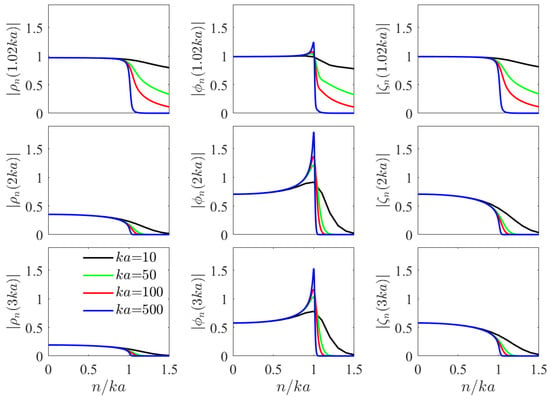
Figure 3.
Absolute value of the weighting functions for different values of the radial distance () and the cylinder radius (), as functions of order n normalized to .
It can be noticed that the radial component of the field becomes negligible with respect to the other ones for any n when the propagation distance exceeds some multiple of the cylinder radius. This is a consequence of the behavior of the basis function shown in the previous section. Furthermore, all components vanish for values of n sufficiently greater than , except very close to the surface. Since the parameter expresses the ratio between the circumference of the cylinder base and the wavelength, and the expanding basis functions are accompanied by the angular Fourier component , when n exceeds the involved phase details become smaller than the wavelength. The cutoff around means that such contributions do not propagate, exactly as happens for the evanescent waves produced by planar sources.
Analogous behavior has been observed in the past for spherical and cylindrical scalar sources [23,24,45].
5. The Basis Functions as Coherent Vector Modes
One of the simplest cases of a partially coherent field is obtained when all the involved expansion coefficients are mutually uncorrelated, that is, when in Equation (11) we take
where and are positive quantities and is the Kronecker delta. The elements of then become
which depend on , , and the angle difference. We would say that the above CSD matrix is angularly homogeneous [24].
This choice corresponds to considering the partially coherent field as the incoherent superposition of perfectly coherent and perfectly polarized vector modes [46,47]. In fact, it turns out that the following Mercer expansion holds:
with the modes given by
and the eigenvalues by
In fact, the above vector functions turn out to be orthogonal, i.e.,
but they are not normalized, as required by the modes of a source. However, to simplify the equations to come, we prefer not to add normalization factors and consider them as the modes of the source. This will not affect the presented results.
A simpler form is taken by the polarization matrix, too:
whose explicit expression is
with
They are apparently independent of , as are the spectral density
and all polarization properties of the radiated field. This is, of course, a consequence of the angular homogeneity of the corresponding CSD matrix. Some examples pertinent to the effects of different choices of the eigenvalues on the field across the source and on the propagated one will be shown in the next section.
6. Discussion
In this section, the main coherence and polarization characteristics of cylindrical sources are studied by means of some examples. In the first example, the results for each component (E- or H-polarization) are presented separately. The superposition of the two components is then considered, both when all modes are mutually uncorrelated [see Equation (29)] and when a certain correlation between them exists.
6.1. E-Polarization
When vanishes for all n, the field consists only of modes polarized along z, as can be observed in Figure 1a, and its polarization is complete for any choice of coefficients . Conversely, interesting results are obtained as far as its coherence properties are concerned, which is taken into account by the element of the CSD matrix (see Equation (30)). In this case, the formalism used for scalar sources and fields can be used profitably [23].
In this case, . Let us consider the following example:
Figure 4a shows the degree of coherence given in Equation (18) between a point located along a given radial line perpendicular to the cylinder axis and another point located at the intersection of this radial line with the source surface. Note that in this case, the degree of coherence given in Equation (20) coincides with the absolute value of the conventional degree of coherence for scalar sources [1]. Figure 4b shows the degree of coherence between two points on the same radial line, one of them at a distance from the cylinder axis and the other at . It is observed that when these two points coincide, the coherence is complete.
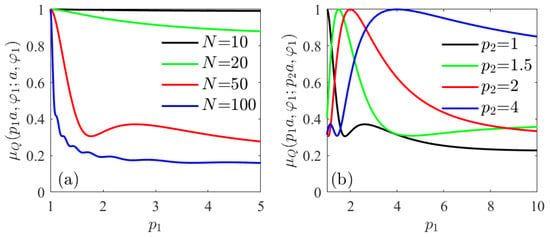
Figure 4.
Degree of coherence between two points along the same radial line, one of them at a distance and the second one (a) on the cylinder surface for several values of N (b) at several distances from the surface for . E-polarization source with correlation coefficients is given by Equation (39). The cylinder radius corresponds to .
The behavior of the degree of coherence between two points located on the cylinder surface but with different angular coordinates is shown in Figure 5a for various values of N. Figure 5b shows the behavior when the two points are at the same distance from the cylinder axis. This angular behavior is similar to a sync function [23].
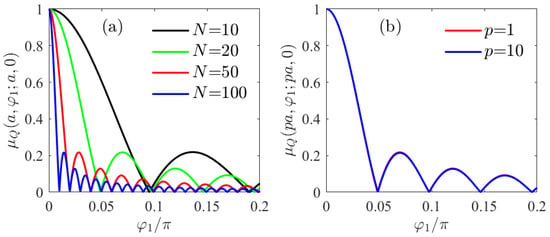
Figure 5.
Degree of coherence between two points located at angles and for several values of N (a) on the cylinder surface; (b) on a cylindrical surface at a given distance for . E-polarization source with correlation coefficients given by Equation (39). The radius of the cylinder corresponds to .
This field is completely polarized on the surface of cylinder and in the whole space outside of it.
6.2. H-Polarization
If we choose for all n, the E-polarization is zero and the z component vanishes. The resulting field is a two-dimensional field with nonzero radial and azimuthal components as it can be seen in Figure 1b. In general, the field will be partially polarized on the cylinder surface. Consider the following example:
Figure 6 shows a comparison of the degree of polarization outside the cylinder for several values of N when calculated following the definition of Setalä et al. [31] or that of Ellis et al. [34]. It can be observed that in the first case, the degree of polarization is always greater than 0.5, which is characteristic of a 2D field with that definition [31].
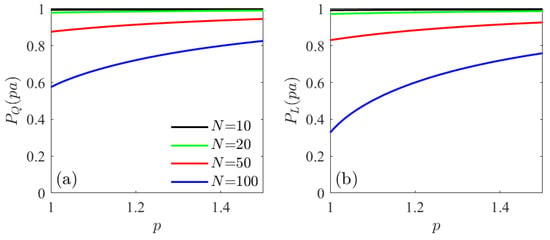
Figure 7a,b show the behavior of the degree of coherence between two points located on a given radial line. Although they are similar to the E-polarization case studied earlier, several differences are observed. The main one is that, in general, full coherence is not achieved. This is particularly evident on the cylinder surface when more and more modes are considered. This fact is also observed in Figure 8a where the degree of coherence between two points located at different angles on the cylinder surface is shown. It should be noted that this angular behavior deviates from a sinc, especially with respect to successive relative minima that no longer reach zero.
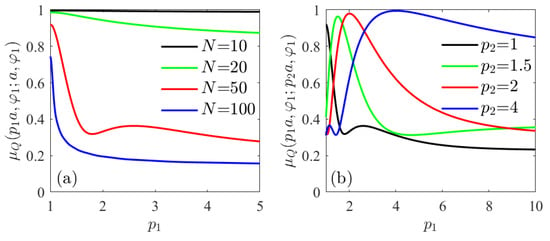
Figure 7.
Degree of coherence between two points along the same radial line, one of them at a distance and the second one (a) on the cylinder surface for several values of N (b) at several distances from the surface for . H-polarization source with correlation coefficients given by Equation (40). The radius of the cylinder corresponds to .
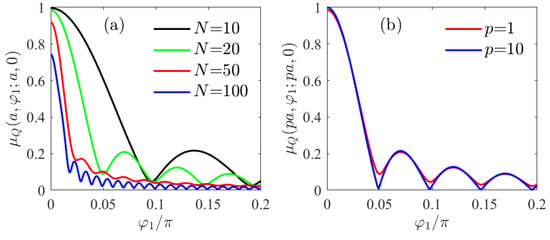
Figure 8.
Degree of coherence between two points located at angles and for several values of N (a) on the cylinder surface; (b) on a cylindrical surface at a given distance for . H-polarization source with correlation coefficients given by Equation (40). The radius of the cylinder corresponds to .
In Figure 8b it can be seen that when the field has propagated some distance from the cylinder surface, the angular behavior changes slightly with respect to the E-polarization case, and the field becomes slightly less coherent with the propagation distances.
Let us now consider another example where the E-polarization is not present , and the H-polarization modes are mutually uncorrelated, but their weights increase with the order of the modes following the relation:
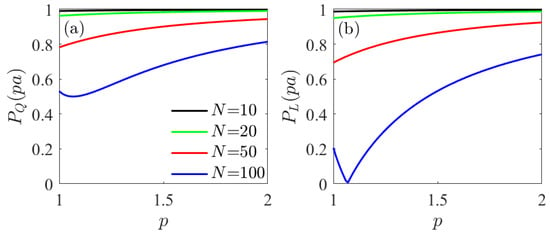
It is interesting to note that the degree of polarization following the definition of Equation (16) is, for this case, as can be seen in Figure 9a where this degree of polarization outside the cylinder is plotted for various values of N. However, using the definition of Equation (17), Figure 9b shows that at a given distance and sufficiently high values of N, the field is practically unpolarized (). This can be explained if the radial component is equal to the azimuthal component for a given distance and they are incoherent (sufficiently large number of modes).
As for the degree of coherence between two points, its behavior when the two points are located on the same radial line is similar to the previous cases but with lower values. In fact, Figure 10a shows that its value drops to almost zero when 100 modes are taken and the degree of coherence between a point more than from the cylinder axis and a point on the source surface is calculated.
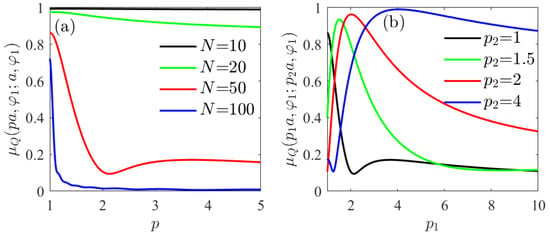
Figure 10.
Degree of coherence between two points along the same radial line, one of them at a distance and the second one (a) on the cylinder surface for several values of N (b) at several distances from the surface for . H-polarization source with correlation coefficients given by Equation (41). The radius of the cylinder corresponds to .
Now, the degree of coherence between two points located at different angles on the source surface presents minima well over zero and secondary lobes with relative maxima that are close to the absolute maximum (at least the first two or three secondary lobes), as can be observed in Figure 11a. For a given selection of the number of modes involved in the generation of the source, the minima observed in Figure 11a decrease with the propagation distance (see Figure 11b).
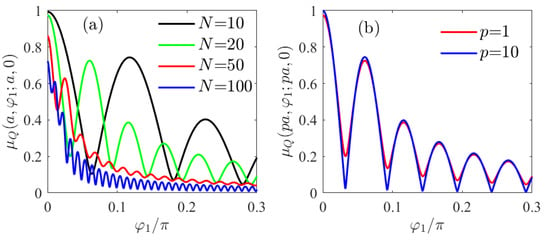
Figure 11.
Degree of coherence between two points located at angles and for several values of N (a) on the cylinder surface; (b) on a cylindrical surface at a given distance for . H-polarization source with correlation coefficients given by Equation (41). The radius of the cylinder corresponds to .
6.3. E- and H-Polarization
Consider a simple case where both E- and H-polarization are present, for example, if we take the values of the coefficients as
In this case, there are three non-zero orthogonal components of the electric field as it can be observed in Figure 1c. Figure 12a shows that the 3D degree of polarization defined in Equation (16) takes values less than 0.5 denoting the presence of all three components of the field. However, when the field propagates, the radial component decreases faster than the other two components, as can be seen in Figure 2. Therefore, the degree of polarization approaches 0.5 as the field propagates out of the cylinder. On the contrary, the degree of polarization calculated with Equation (17), evolves from a given value to almost zero as the field propagates, as can be seen in Figure 12b, denoting that the two remaining components reach a similar value and are uncorrelated.
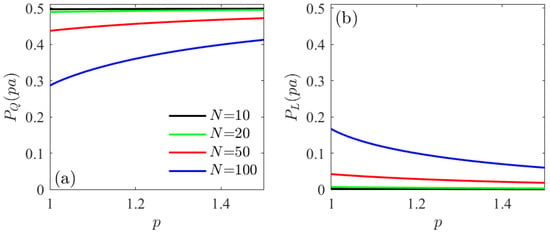
Figure 13 shows the degree of coherence defined by Equation (18) (Figure 13a,b) and by Equation (21) (Figure 13c,d) along a radial line, for several choices of parameters. From Figure 13a,b it can be noted that the degree of coherence between two points along a radial line is quite lower than in previous cases, but it follows a similar behavior. On the other hand (see Figure 13c,d) the degree of coherence given by Equation (21) shows the same qualitative behavior, although its absolute value is higher than that shown in Figure 13a,b. In fact, a nearly complete correlation is found for using Equation (21), while the degree of correlation drops to nearly 0.7 using Equation (18).
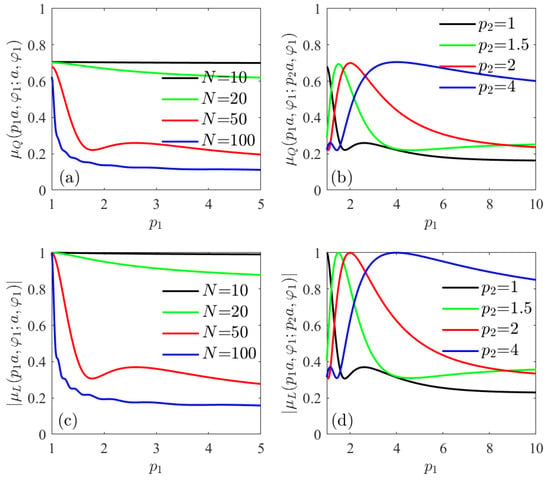
Figure 13.
Degree of coherence between two points along the same radial line. One of them is at the radial coordinate , while the second is: on the cylinder surface, for several values of N (a,c); at several distances from the surface, for fixed (b,d). The degree of coherence is defined according to Equation (18) (a,b) or to Equation (21) (c,d). The correlation coefficients are given by Equation (42) and the radius of the cylinder corresponds to .
The angular behavior of the degree of coherence for this case is also calculated using the two definitions presented in Section 2. It can be seen from Figure 14a,b that the degree of coherence calculated according to Equation (18) reaches lower values than in the cases where only E- or H-polarization was present. It can also be observed that the relative minima do not reach zero and that there are even some oscillations that disappear if the number of terms considered is sufficiently large. On the contrary, the absolute value of the degree of coherence given by Equation (21) is one for coincident points and goes to zero at several angles, as can be seen in Figure 14c,d. It is interesting that the angular behavior remains almost invariant in propagation (see Figure 14d).
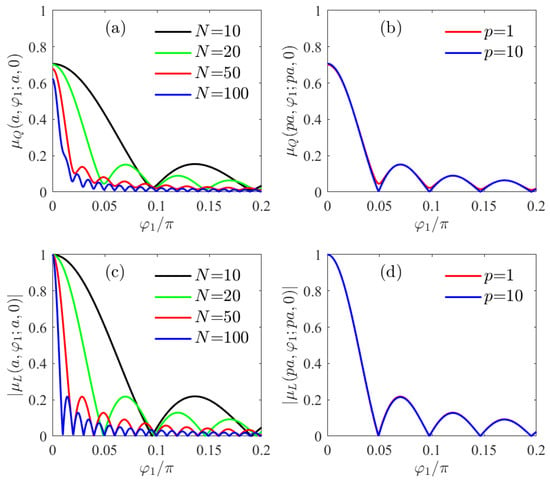
Figure 14.
Degree of coherence between two points located at the angles and , for several values of N: on the cylinder surface (a,c); on a cylindrical surface of radius , for (b,d). The degree of coherence is defined according to Equation (18) (a,b) or to Equation (21) (c,d). The correlation coefficients are given by Equation (42) and the radius of the cylinder corresponds to .
6.4. Mutually Correlated Modes
We now turn to the most general case considered so far, in which different s and s are correlated, restricting ourselves only to the spectral density and the degree of polarization analysis. For example, we set all the coefficients in Equation (29) to vanish except for the following ones:
Here D plays a role of an asymmetry parameter: for the modes symmetric with respect to mode are drawn, while for such a symmetry shifts to mode . On examining the spectral density and the degree of polarization radiated outwards from such a cylinder (see Figure 15), we notice that for both quantities form azimuthally dependent distributions radiating at right angles to the cylinder’s surface. In particular, the spectral density has a multi-petal structure (with the number of petals being ), various petals carrying different amounts of energy. The degree of polarization has a more complex azimuthal distribution, with a global minimum of 0.5 and is a combination of very thin petals in which it varies between 0.5 and 1. In the case of an additional tilt effect is observed, i.e., the spectral density and the degree of polarization form petals that are not orthogonal to the cylinder’s surface. It is observed that such a tilt becomes more and more pronounced as the absolute value of the parameter D increases, and that it changes direction as the sign of this parameter changes. Such an effect is comparable to a tilt produced by linearly correlated phases of fields radiated from planar surfaces (see Ref. [48] for the scalar case and [49] for the electromagnetic case).
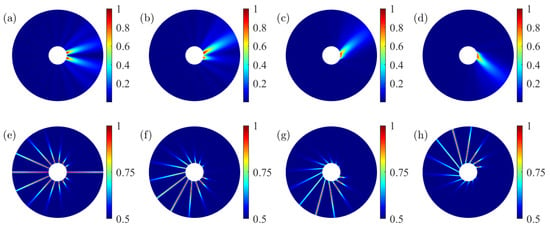
Figure 15.
(a–c) Spectral density and (e–h) degree of polarization outside the cylinder for coefficients in Equation (43) with and (a), (e) ; (b), (f) ; (c), (g) ; and (d), (h) . The radius of the cylinder is and the representation is for .
7. Conclusions
Light sources bearing cylindrical geometry constitute a very special case for statistical optics. First, they are more advanced than planar and spherical sources in the sense that their surface curvature depends on orientation (while planar and spherical surfaces have trivial and constant curvatures, respectively). This immediately implies that the properties of various single-point and, moreover, pair-point electric fields are expected to depend on the chosen points’ orientations, both on and off the cylinder’s surface. Second, the alignment of either the electric or magnetic field with the cylinder’s axis results in entirely different structures for the source and the radiated field, even in the purely deterministic radiation case. The combination of the two cases leads to the intrinsically 3D electric field in which all three components exhibit distinct behavior, being dependent on different basis functions. Third, on extending from deterministic (single-mode) to stationary (multi-mode or infinite-mode) electric vector field distributions, one obtains a tensor in which six out of nine components are governed by structurally different functions, whose strength is determined by three different sequences of mode coupling coefficients ( and self-correlations and their cross-correlations). Such complexity results in the unprecedentedly rich variety of possible spectral density distributions as well as those in coherence and polarization states, on and off the cylinder’s surface. More importantly, the access to individual electric-field components’ coupling coefficients delivers fine control over all the radiation’s statistics. In order to numerically illustrate possible outcomes for the spectral density, the degree of coherence, and the degree of polarization, we have separately discussed the E-polarization, H-polarization and mixed polarization cases and revealed qualitatively different behaviors of light in these scenarios. We have also illustrated through a number of examples that the specific choice of the mode coupling coefficients efficiently enhances/suppresses/redirects the light statistics in the planes orthogonal to the cylinder axis. We envision the use of such fine 360-degree control of radiation in directional illumination and sensing applications.
Author Contributions
Conceptualization, M.S., O.K., R.M.-H. and F.G.; methodology, M.S., J.C.G.d.S., G.P., and O.K.; software, M.S., J.C.G.d.S., G.P., and O.K.; formal analysis, M.S., J.C.G.d.S., G.P., O.K., R.M.-H. and F.G.;investigation, M.S., J.C.G.d.S., G.P., O.K., R.M.-H. and F.G.; writing—original draft preparation, M.S., J.C.G.d.S., G.P., and O.K.; writing—review and editing, M.S., J.C.G.d.S., G.P., and O.K.; visualization, M.S., J.C.G.d.S., G.P., and O.K.; supervision, R.M.-H. and F.G.; project administration, R.M.-H.; funding acquisition, R.M.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Spanish Ministerio de Economía y Competitividad, project PID2019-104268 GB-C21. OK acknowledges the Copper Fellowship program at the University of Miami.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSD | Cross-spectral density |
| DOP | Degree of polarization |
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- James, D.F.V. Change of polarization of light beams on propagation in free space. J. Opt. Soc. Am. A 1994, 11, 1641–1643. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Vicalvi, S.; Borghi, R.; Guattari, G. Beam coherence-polarization matrix. Pure Appl. Opt. J. Eur. Opt. Soc. Part A 1998, 7, 941. [Google Scholar] [CrossRef]
- Tervo, J. Azimuthal polarization and partial coherence. J. Opt. Soc. Am. A 2003, 20, 1974–1980. [Google Scholar] [CrossRef]
- Ramírez-Sánchez, V.; Piquero, G.; Santarsiero, M. Synthesis and characterization of partially coherent beams with propagation-invariant transverse polarization pattern. Opt. Commun. 2010, 283, 4484–4489. [Google Scholar] [CrossRef]
- Santarsiero, M.; Ramírez-Sánchez, V.; Borghi, R. Partially correlated thin annular sources: The vectorial case. J. Opt. Soc. Am. A 2010, 27, 1450–1456. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Tang, Z.; Liang, C.; Tan, Z. Intensity and spatial correlation properties of tightly focused partially coherent radially polarized vortex beams. Opt. Laser Technol. 2011, 43, 895–898. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Santarsiero, M.; Piquero, G.; Gori, F. Longitudinal polarization periodicity of unpolarized light passing through a double wedge depolarizer. Opt. Express 2012, 20, 27348–27360. [Google Scholar] [CrossRef]
- Santarsiero, M.; de Sande, J.C.G.; Piquero, G.; Gori, F. Coherence-polarization properties of fields radiated from transversely periodic electromagnetic sources. J. Opt. 2013, 15, 055701. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, F.; Liu, L.; Zhao, C.; Cai, Y.; Korotkova, O. Generation and propagation of a partially coherent vector beam with special correlation functions. Phys. Rev. A 2014, 89, 013801. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Electromagnetic Schell-model sources generating far fields with stable and flexible concentric rings profiles. Opt. Express 2016, 24, 5572–5583. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhou, Y.; Wu, H.W.; Chen, H.J.; Sheng, Z.Q.; Qu, J. Focus shaping of the radially polarized Laguerre–Gaussian-correlated Schell-model vortex beams. Opt. Express 2018, 26, 20076–20088. [Google Scholar] [CrossRef] [PubMed]
- Senthilkumar, M.; Rajesh, K.; Udhayakumar, M.; Jaroszewicz, Z.; Mahadevan, G. Focusing properties of spirally polarized sinh Gaussian beam. Opt. Laser Technol. 2019, 111, 623–628. [Google Scholar] [CrossRef]
- Hyde, M.W.; Xiao, X.; Voelz, D.G. Generating electromagnetic nonuniformly correlated beams. Opt. Lett. 2019, 44, 5719–5722. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zhu, X.; Lin, S.; Wang, F.; Gbur, G.; Cai, Y. Vector partially coherent beams with prescribed non-uniform correlation structure. Opt. Lett. 2020, 45, 3824–3827. [Google Scholar] [CrossRef] [PubMed]
- Hyde IV, M.W. Synthesizing General Electromagnetic Partially Coherent Sources from Random, Correlated Complex Screens. Optics 2020, 1, 8. [Google Scholar] [CrossRef]
- Tong, R.; Dong, Z.; Chen, Y.; Wang, F.; Cai, Y.; Setälä, T. Fast calculation of tightly focused random electromagnetic beams: Controlling the focal field by spatial coherence. Opt. Express 2020, 28, 9713–9727. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, J.; Wang, F.; Chen, Y.; Cai, Y.; Korotkova, O. Synthesis of vector nonuniformly correlated light beams by a single digital mirror device. Opt. Lett. 2021, 46, 2996–2999. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Piquero, G.; Santarsiero, M.; Gori, F.; González de Sande, J.C. A class of vectorial pseudo-Schell model sources with structured coherence and polarization. Opt. Laser Technol. 2022, 152, 108079. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Gbur, G.; Wolf, E. Coherence properties of sunlight. Opt. Lett. 2004, 29, 459–461. [Google Scholar] [CrossRef]
- Gori, F.; Korotkova, O. Modal expansion for spherical homogeneous sources. Opt. Commun. 2009, 282, 3859–3861. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Korotkova, O.; Martínez-Herrero, R.; Santarsiero, M.; Piquero, G.; Failla, A.V.; Gori, F. Partially coherent spherical sources with spherical harmonic modes. J. Opt. Soc. Am. A 2022, 39, C21–C28. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Korotkova, O.; Santarsiero, M.; Piquero, G.; de Sande, J.C.G.; Failla, A.V.; Gori, F. Cylindrical partially coherent scalar sources. Opt. Lett. 2022, 47, 5224–5227. [Google Scholar] [CrossRef] [PubMed]
- Santarsiero, M.; Sande, J.C.G.D.; Korotkova, O.; Martínez-Herrero, R.; Piquero, G.; Gori, F. Three-dimensional polarization of fields radiated by partially coherent electromagnetic cylindrical sources. Opt. Lett. 2023, 48, 2476–2479. [Google Scholar] [CrossRef] [PubMed]
- Hyde, M.W.; Bogle, A.E.; Havrilla, M.J. Scattering of a partially-coherent wave from a material circular cylinder. Opt. Express 2013, 21, 32327–32339. [Google Scholar] [CrossRef]
- Petrov, E.Y.; Kudrin, A.V. Exact Axisymmetric Solutions of the Maxwell Equations in a Nonlinear Nondispersive Medium. Phys. Rev. Lett. 2010, 104, 190404. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.G.; Huang, P.; Yang, X. Analytic description of cylindrical electromagnetic wave propagation in an inhomogeneous nonlinear and nondispersive medium. Phys. Rev. E 2010, 82, 057602. [Google Scholar] [CrossRef] [PubMed]
- Panofsky, W.K.H.; Philips, M. Classical Electricity and Magnetism; Addison-Wesley: Mineola, NY, USA, 1962. [Google Scholar]
- Gbur, G.J. Mathematical Methods for Optical Physics and Engineering; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Arfken, G.B.; Weberr, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier Academic Press: New York, NY, USA, 2005. [Google Scholar]
- Setälä, T.; Tervo, J.; Friberg, A.T. Complete electromagnetic coherence in the space–frequency domain. Opt. Lett. 2004, 29, 328–330. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007; p. 222. [Google Scholar]
- Setälä, T.; Shevchenko, A.; Kaivola, M.; Friberg, A.T. Degree of polarization for optical near fields. Phys. Rev. E 2002, 66, 016615. [Google Scholar] [CrossRef]
- Ellis, J.; Dogariu, A.; Ponomarenko, S.; Wolf, E. Degree of polarization of statistically stationary electromagnetic fields. Opt. Commun. 2005, 248, 333–337. [Google Scholar] [CrossRef]
- Auñón, J.M.; Nieto-Vesperinas, M. On two definitions of the three-dimensional degree of polarization in the near field of statistically homogeneous partially coherent sources. Opt. Lett. 2013, 38, 58–60. [Google Scholar] [CrossRef]
- Luis, A. Degree of polarization for three-dimensional fields as a distance between correlation matrices. Opt. Commun. 2005, 253, 10–14. [Google Scholar] [CrossRef]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Tervo, J.; Setälä, T.; Friberg, A.T. Degree of coherence for electromagnetic fields. Opt. Express 2003, 11, 1137–1143. [Google Scholar] [CrossRef]
- Korotkova, O.; Wolf, E. Spectral degree of coherence of a random three-dimensional electromagnetic field. J. Opt. Soc. Am. A 2004, 21, 2382–2385. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Borghi, R. Maximizing Young’s fringe visibility through reversible optical transformations. Opt. Lett. 2007, 32, 588–590. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Mejías, P.M. Maximum visibility under unitary transformations in two-pinhole interference for electromagnetic fields. Opt. Lett. 2007, 32, 1471–1473. [Google Scholar] [CrossRef] [PubMed]
- Luis, A. Degree of coherence for vectorial electromagnetic fields as the distance between correlation matrices. J. Opt. Soc. Am. A 2007, 24, 1063–1068. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Mejías, P.M.; Piquero, G. Characterization of Partially Polarized Light Fields; Springer Series in Optical Science; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Erdelyi, A. Higher Trascendental Functions; McGraw-Hill: New York, NY, USA, 1953; Vollume II. [Google Scholar]
- Borghi, R.; Gori, F.; Korotkova, O.; Santarsiero, M. Propagation of cross-spectral densities from spherical sources. Opt. Lett. 2012, 37, 3183–3185. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Simon, R.; Piquero, G.; Borghi, R.; Guattari, G. Coherent-mode decomposition of partially polarized, partially coherent sources. J. Opt. Soc. Am. A 2003, 20, 78–84. [Google Scholar] [CrossRef]
- Tervo, J.; Setälä, T.; Friberg, A.T. Theory of partially coherent electromagnetic fields in the space–frequency domain. J. Opt. Soc. Am. A 2004, 21, 2205–2215. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Chen, X. Phase structuring of the complex degree of coherence. Opt. Lett. 2018, 43, 4727–4730. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Chen, X.; Setälä, T. Electromagnetic Schell-model beams with arbitrary complex correlation states. Opt. Lett. 2019, 44, 4945–4948. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).