Abstract
Atmospheric effects including absorption and scattering, and turbulence could introduce signal power loss and severe mode crosstalk for the orbital angular momentum (OAM)-based free-space optical communication (FSOC). Therefore, it is of great significance to simultaneously increase signal power and mitigate mode crosstalk. In this paper, for the OAM beam from a coherent laser array with a discrete vortex (CLA-DV) based on coherent beam combining, we investigate its propagation characteristics by employing theoretical derivation and the random phase screens simulation in atmospheric propagation, respectively. The probability density and OAM spectrum are given and compared for CLA-DV and Gaussian vortex beam. The results demonstrate that the Gaussian vortex beam exhibits smaller mode crosstalk under weak atmospheric turbulence conditions, while CLA-DV shows a good performance on crosstalk mitigation for strong atmospheric turbulence conditions in long-distance links. Furthermore, with a specially designed radial phase-locked Gaussian laser array composed of two orthogonal polarized coherent laser arrays carrying different OAM states, a scheme of optical communication system possessing simultaneously polarization-division multiplexing and OAM multiplexing is proposed. The normalized energy weight matrices of all 16 non-zeroth-order OAM modes are numerically calculated. To verify the feasibility of the proposed scheme, the performance of an eight-bit grayscale Lena image facing various atmosphere turbulences is evaluated. The quality of transmitted images becomes worse with the turbulence strength and transmission distance increase, which is confirmed by the trend of average optical signal error rates. This work will provide theoretical insight for improving the performance of OAM-based FSOC under scattering conditions.
1. Introduction
Owing to instinct features of inherent orthogonality and unbounded states in principle [1,2], vortex beams carrying multiple orbital angular momentum (OAM) can be used as data carriers for mode-division multiplexing and potentially improve the communication system capacity without specific wavelength or polarization [3,4], which are more suitable for optical communication [5,6,7], especially for free-space wireless optical communication (FSOC) [8,9,10]. Therefore, OAM-based FSOC has attracted increasing interest in recent years, giving rise to many developments in deep-space and near-Earth optical communications [11] secure quantum communication [12], and so on. However, the performance of OAM-based FSOC seriously suffers from atmospheric absorption and scattering and atmospheric turbulence [13]. On the one hand, propagating laser power will be attenuated because of the existence of atmospheric absorption and scattering. In addition, the divergence of OAM beams may cause power loss [14]. These factors will lead to insufficient signal power and a poorer signal-to-noise ratio at the terminals. More seriously, due to the inhomogeneities of the atmospheric temperature and pressure, the random variations of the refractive index along the transmission path result in the phase distortion of the OAM mode, which in turn induces the portion of transmitted OAM mode to be coupled to adjacent OAM modes, generating the so-called mode crosstalk [15,16,17,18]. The quality of OAM-based FSOC will be seriously affected. Thus, it is of great significance to improve transmitted laser power and reduce mode crosstalk for OAM-based FSOC.
Up to now, many efforts have been devoted to addressing on these issues. To achieve sufficient signal power for data recovery, one approach is to enlarge the transmitted beam size and receiver aperture of the system, but the cost is less tolerant to the receiver angular error [19]. Another approach is to place a focusing lens in front of the transmitter to focus OAM modes [20] or use a special type of OAM beam, such as a nonzero ring Airy vortex beam [21], radial index Laguerre–Gaussian beam [22], and the multi-vortex geometric beam [23], under a limited-size receiving aperture, to obtain a smaller spot at the receiving end, thereby increasing the signal power. This method requires redesigning the transmitter, which will increase the complexity of the system and degrade its flexibility. At the same time, various approaches for mitigating mode crosstalk have been reported [18]. One possible approach is adaptive optics [24,25,26], whose working principle is to measure the distorted phase of OAM mode induced by atmospheric turbulence first, and then an error correction phase is introduced to eliminate the influence of atmospheric turbulence. However, the additional measuring devices make the system very complicated. It is found that the mode crosstalk can be suppressed by reducing the effective interaction area of OAM beams and atmospheric turbulence. Therefore, the reduction of mode crosstalk can be realized by using a focusing mirror [27]. However, in this scheme, once the transmission distance changes, the lens and other device parameters should be adjusted accordingly. Similarly, the mode crosstalk can be effectively alleviated by adopting the diffraction-free or autofocusing type of beams such as Bessel beams [28], Hypergeometric-Gaussian beams [29], autofocusing Airy beams [30], Airy Gaussian vortex beam array [31], pin-like optical vortex beams [32], and so on. However, these specially designed beams are generally generated by spatial light modulator (SLM), resulting in complexity and high cost of the system. Furthermore, the laser power is also limited by the damage threshold of the SLM.
Coherent beam combining (CBC) is an alternate approach for greatly scaling up the output power with ideal output beam quality [33]. By harnessing the active intensity, phase, or polarization control of each beamlet in a laser array, various structured beams, such as vector beams [34,35], airy beams [36] vortex beams [37,38,39], Bessel-Gaussian beams [40], and perfect vectorial vortex beams [41], have been proposed theoretically or experimentally. Furthermore, rapid switching between OAM states (with a frequency higher than GHz) can be realized with the method of CBC [42,43], which may provide potential solutions for high-speed optical communications. Based on the previous analysis, the OAM beams generated by CBC may be a candidate for OAM-based FSOC. However, its propagation characteristics have not been studied so far.
In this work, based on the theoretical derivation and the random phase screens simulation, we investigate the propagation characteristics of OAM beams generated by a coherent laser array with discrete vortex (CLA-DV) by using CBC in atmospheric propagation. The compared results of the probability density and the normalized energy weight of each OAM mode between Gaussian vortex beams and CLA-DV under the same conditions are numerically calculated, which are also verified by numerical simulation. Furthermore, a scheme of the optical communication link based on a specially designed radial phase-locked Gaussian laser array is proposed. The normalized energy weight matrices of 16 non-zeroth-order OAM modes are numerically calculated. Finally, an 8-bit grayscale Lena image transmitted through turbulent OAM channels is used to verify the feasibility of the proposed scheme. Our results provide a theoretical basis for improving the performance of OAM-based FSOC.
2. Simulation Analysis Method
2.1. Theoretical Derivation
By assuming a coherent laser array composed of N linearly polarized fundamental Gaussian beamlets with the same amplitude and waist width, the complex amplitude of nth beamlet located at central position (R0, ϕn) can be expressed as [40,41,44]
where R0 is the radius of the array, w0 is the waist width of the laser beam, ϕn = 2π(n − 1)/N is the angle between nth beamlet and x axis, and n is the number of beamlets (n = 1, 2…N), l0 is the topological charge. The superposition of coherent laser array at the source plane can be written as
The phase difference of adjacent beamlet Δϕ = 2πl0/N. Obviously, if the number of beamlets increases to enough large, the phase difference Δϕ will tend to be infinitesimal. In addition, the summation formula of Equation (2) about n can be approximately regarded as the integral formula about ϕ
Utilizing the integral formula [45]
where Il is the lth order modified Bessel function of the first kind. Equation (3) can be represented as [40]
Equation (5) shows that the CLA-DV is a Bessel-Gaussian vortex beam. In addition, Pinnell pointed out that a Bessel–Gaussian vortex beam can be recognized as a perfect vortex beam [46]. Therefore, the perfect vortex beams with desired topological charge can be flexibly generated with a CLA-DV by adjusting the phase difference of the adjacent beamlet.
With the Huygens–Fresnel integral, after propagation in free space, the electric field distribution of beam generated from a CLA-DV in the receiver plane can be described as
Substituting Equation (5) into Equation (6), we can get
According to integral formula [45]
where Jn is the nth order Bessel function of the first kind. Equation (7) can be simplified as
where , , , and . Prescribing a limit to weak atmospheric turbulence, the cumulative effect of atmospheric turbulence on the propagation path can be considered as adding a phase disturbance to the propagating beam. Using Rytov approximation, under the condition of weak atmospheric turbulence, the beam can be represented as [47]
where Ψ(ρ, φ, z) denotes the random phase disturbance generated by the atmospheric turbulence along the propagation path. Due to the orthogonality of the vortex beams, the vortex mode can be used as an orthogonal basis function to describe the beams distribution, namely, the beams can be considered as the superposition of vortex modes with different topological charges and different weight factors [48], that is
where al is the weight factor of lth order vortex mode. Based on the orthogonality of vortex mode, the expression of weight factor can be expressed as [49]
Substituting Equations (10) and (11) into (12), we can obtain the probability density ⟨|al (ρ, φ, z)|2⟩ for lth order vortex mode
where the symbol of ⟨ ⟩, * denote an ensemble average over the medium statistics and the conjugation operator, respectively. ⟨exp[Ψ *(ρ, φ1, z) + Ψ (ρ, φ2, z)]⟩ represents the ensemble average atmospheric turbulence, which can be expressed as
where is the coherence length of plane wave in the atmospheric turbulence, κ is the spatial frequency, Φn(κ) accounts for the spatial power spectrum of refractive index fluctuations of the random medium. Assuming that the atmospheric turbulence match with Kolmogorov statistical properties, Φn(κ) can be described by modified von Karman power spectrum as [50,51]
with
where αt is power index, km = c(αt)/lm, k0 = 2π/L0, L0 and lm are the outer and inner scales of turbulence, respectively. Cn2 is the refraction structure constant with units m−2/3.
By substituting Equations (9) and (14) into Equation (13), and employing the separation of variables integral method and unitizing the integral forums Equation (8), after complex integral calculation, the probability density of beam generated from a CLA-DV can be obtained as follows
To quantitatively characterize the crosstalk of vortex beam induced by atmospheric turbulence, we adopt the concept of orbital angular momentum (OAM) spectra, which is formed by the normalized energy weight of OAM mode Pl. The normalized energy weight Pl can be represented as [52]
where R is the radius of the receiving aperture. For comparison, the probability density of Gaussian vortex beam is given as [27]
Similarly, by substituting Equation (19) into Equation (18), we can obtain the normalized energy weight Pl of the Gaussian vortex beam. Consequently, the crosstalk characteristics of OAM beams based on coherent beam combining and Gaussian vortex beams can be calculated and compared under the same atmospheric turbulence conditions.
It can be found from Equations (17) and (19), when coherence length ρ0 tends to infinity and l ≠ l0, the probability density will be zero. This means that no matter for Gaussian vortex beam or the beam generated by the CLA-DV when they propagate in the free space, there will be no mode crosstalk between vortex modes, while for the case of atmospheric turbulence, mode crosstalk will inevitably occur, but the degree of mode crosstalk is different.
2.2. Random Phase Screens Method
In fact, each beamlet generally output laser after passing through an aperture, thus Equation (1) will be rewritten as
where circ (r0) denotes the transmittance function of the aperture. If r0 > 1, circ(r0) = 0; if r0 = 1, circ(r0) = 0.5; if r0 < 1, circ(r0) = 1 [41]. In addition, considering the limited number of beamlets, it is hard to achieve the analytical solution of probability density directly. Therefore, we take the random phase screens method to demonstrate our theoretical analysis.
As depicted in Figure 1, the process of the simulating beam propagating in atmospheric turbulence with the random phase screens method can be expressed as the whole propagation distance can be divided into N segments, and each segment is marked with Δz. In each segment, the beam first propagates Δz/2 in free space, then passes through a random phase screen used to represent phase distortion generated by the atmospheric turbulence, and finally, the beam again propagates Δz/2 in free space. By repeating this process until the beam passes through all segments, the beam distribution on the receiving screen can be obtained. This process can be expressed in the following mathematical form [53].
where FFT and FFT−1 stand for fast Fourier transform and inverse fast Fourier transform, respectively. k = 2π/λ is the wave number and λ is the wavelength, κx and κy are space wave number along x and y axis, respectively. Ω is the random phase distribution induced by atmospheric turbulence, which is given as [54]
where R(κx,κy) stands for complex Gaussian random matrix, the random phase power spectrumΦϕ(κx,κy) can be obtained with the relation: Φϕ(κx,κy) = 2πk2ΔzΦn(κ).
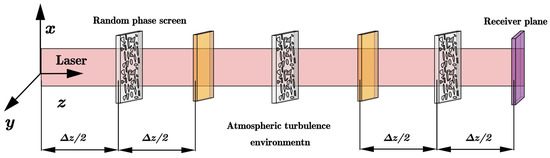
Figure 1.
Schematic illustration of beam propagating in atmospheric turbulence with random phase screens method.
3. Numerical Results and Discussion
Unless otherwise specified, other parameters in the following numerical calculation are set as: λ = 1064 nm, R= 0.2 m, L0 = 10 m, lm = 0.001 m, at = 11/3, Cn2 = 10−15 m−2/3, and l0 = 3.
3.1. Numerical Results Based on Theoretical Derivation
As reported in [49], there is an “optimum waist width” when a specific beam propagates in atmospheric turbulence. Here, the relationship between the received OAM spectrum Pl of and waist width w0 for the Gaussian vortex beam is numerically investigated, as illustrated in Figure 2. The calculated results show that the OAM spectrum increases with the waist width and decreases when the waist width exceeds the optimal beam waist.
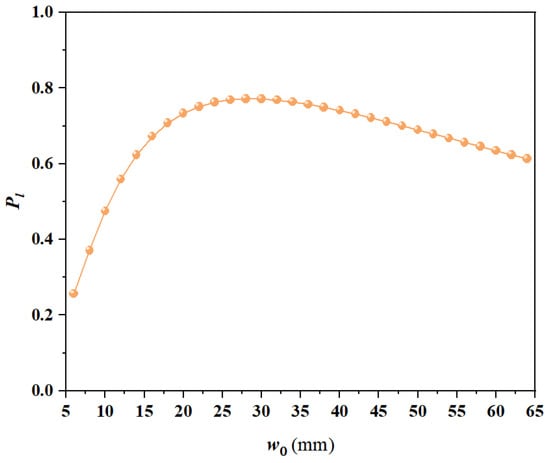
Figure 2.
The received OAM spectrum Pl for Gaussian vortex beam for different waist width w0.
Here, in order to give a more representative comparison candidate (target), the waist width of the Gaussian vortex beam is set as 35 mm in the following research. Meanwhile, to match the size of the Gaussian beam, the radius of the coherent laser array is also set as 35 mm, and the waist width of each beamlet is taken as 4 mm.
Figure 3 shows the received OAM spectra for the Gaussian vortex beam (first row) and beam generated by the CLA-DV (second row) propagating in the atmospheric turbulence varying with different propagation distances. One can find that received OAM spectra become wider and the normalized energy weight of central OAM mode becomes smaller with the increase of propagation distance. This indicates that growing propagation distance results in stronger phase distortion, which in turn leads to more severe mode crosstalk. By comparison, it can be found that the declining rate of the central OAM mode’ normalized energy weight of the CLA-DV was bigger than that of the Gaussian vortex beam. That is, the crosstalk of the Gaussian vortex beam is smaller for a short distance, while the crosstalk of CLA-DV is smaller for a longer distance.
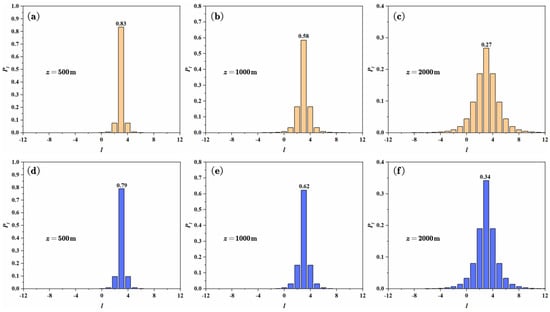
Figure 3.
The received OAM spectra Pl for (a–c) Gaussian vortex beam (d–f) and CLA-DV with propagation distance of 500 m, 1000 m, and 2000 m in the atmospheric turbulence.
To directly see the influence of atmospheric turbulence strength on the OAM mode crosstalk, we numerically study the normalized energy weight of central OAM mode for Gaussian vortex beam and beam CLA-DV propagating in the atmospheric turbulence with various refraction structure constant Cn2, as depicted in Figure 4. For weak atmospheric turbulence (Cn2 = 10−16 m−2/3), the central OAM mode’s normalized energy weight of Gaussian vortex beam is always greater than that of CLA-DV. While for the cases of Cn2 = 10−15 m−2/3 and Cn2 = 10−14 m−2/3, the central OAM mode’s normalized energy weight of Gaussian vortex beam is greater than that of CLA-DV at a short transmission distance, but the results are just the opposite for long transmission distance. Therefore, we can draw the following conclusions: (1) As for the weak atmospheric turbulence, the crosstalk of the Gaussian vortex beam is smaller regardless of the link length. (2) The CLA-DV possesses stronger immunity against strong atmospheric turbulence and is more suitable for strong atmospheric turbulence conditions in long distance links.
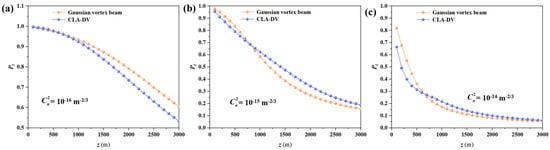
Figure 4.
The normalized energy weight of central OAM mode for Gaussian vortex beam and CLA-DV propagating in the atmospheric turbulence with different values of refraction structure constant Cn2. (a) Cn2 = 10−16 m−2/3, (b) Cn2 = 10−15 m−2/3, (c) Cn2 = 10−14 m−2/3.
3.2. Numerical Simulation Results Based on Random Phase Screens Method
In theoretical derivation, the number of beamlets is set as infinite, and the influence of output aperture is not considered. Thus, there is a deviation between the theoretical derivation and the practical application. In order to correct the deviation, we adopt the method of random phase screen to verify the propagation characteristics of CLA-DV and Gaussian vortex beam in atmospheric turbulence. The size of the simulation phase screen is 0.3 m with 512 × 512 pixels and 30 phase screens are placed among the 3000 m transmission links. In order to obtain sufficient statistics for the average normalized energy weight of OAM mode, 200 realizations for each propagation process have been independently simulated. Other parameters used in those simulations are consistent with the numerical analysis. Figure 5 illustrates the OAM spectra Pl of Gaussian vortex beam and CLA-DV in the receiving plane (z = 500 m, 1000 m, 2000 m, respectively). It can be found that, except for the higher normalized energy weight value, the trend of OAM spectra evolution is basically consistent to the theoretical derivation, which proves the correctness of theoretical derivation. The phenomenon of higher normalized energy weight value has been reported [32].
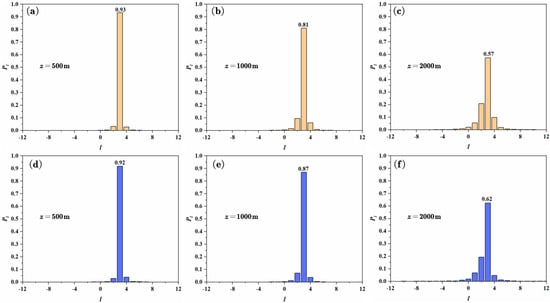
Figure 5.
The received OAM spectra Pl for (a–c) Gaussian vortex beam (d–f) and CLA-DV with propagation distances of 500 m, 1000 m and 2000 m in the atmospheric turbulence.
Figure 6 plots the central OAM mode’s normalized energy weight of the Gaussian vortex beam and CLA-DV with various turbulence strengths. It is found that, for both the Gaussian vortex beam and CLA-DV, the normalized energy weight of central OAM mode drops rapidly when the turbulence becomes stronger. At the same time, one can note that the trend of the central OAM mode’s normalized energy weight evolution agrees with that shown in Figure 4, which further proves the effectiveness of theoretical prediction.
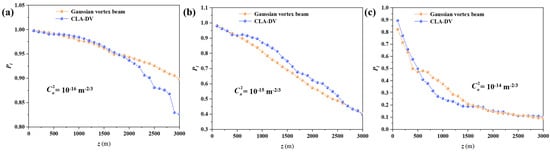
Figure 6.
The normalized energy weight of central OAM mode for Gaussian vortex beam and CLA-DV propagating in the atmospheric turbulence with different values of refraction structure constant Cn2. (a) Cn2 = 10−16 m−2/3, (b) Cn2 = 10−15 m−2/3, (c) Cn2 = 10−14 m−2/3.
4. Image Transmission Scheme by Employing Coherent Beam Combining
Here, based on the previous discussion, and taking advantage of the independent modulation of the phase and polarization of each beamlet, we propose a concept and principle of optical communication link with CLA-DV, as schematically depicted in Figure 7.
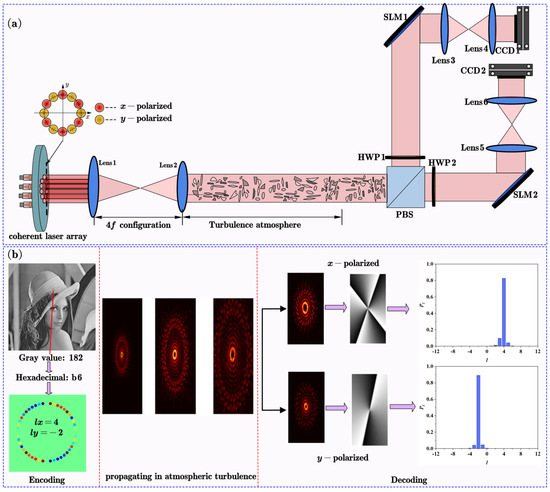
Figure 7.
Schematic illustration for optical communication link (a), and the principle of data encoding, transmission, and decoding (b) by employing the CLA-DV. HWP, quarter wave plate; PBS, polarization beam splitter; SLM, spatial light modulator; CCD, and charge coupled device.
The device for OAM mode generation and multiplexing is composed of two groups of coherent laser arrays arranged crosswise along a circular array arrangement with orthogonal polarization. For each coherent laser array, the vortex phase distribution with variable OAM can be constructed by flexibly adjusting the phase of each beamlet. Hence, the beams generated from the coherent laser array are the coaxial superposition propagating OAM beams with different l0 states, which provides data carriers. Here, an 8-bit grayscale Lena image composed of 256 × 256 pixels is used as a data packet. To encode information of the image with 256 gray levels, we use 16 non-zeroth-order OAM modes (e.g., topological charges from l0 = −8 to l0 = 8 at an interval of 1), as hexadecimal states. The gray valve (0–255) of each pixel in the grayscale image can be converted into two hexadecimal numbers. For example, as depicted in Figure 7b, the gray value of a pixel in the Lena grayscale image is 182, which can be expressed by two hexadecimal numbers b6, namely, 18210→b616. According to the definition, these two hexadecimal numbers of b and 6 correspond to the OAM mode with topological charge lx = 4 (along x polarization direction) and ly = −2 (along y polarization direction), respectively. More importantly, because atmospheric turbulence is insensitive to polarization, the distortion between two polarization components is far less than the distortion of complex-field profile of each polarization component, that is, the polarization crosstalk can be ignored. Therefore, the polarization mode coupling will not occur when the orthogonally polarized OAM modes with different topological charges coaxially propagate in atmospheric turbulence. Meanwhile, they can also be separated by a polarization beam splitter (PBS) easily. After passing through a quarter wave plate, the separated OAM mode with appropriate polarization is incident to the SLM loaded with spiral phase hologram with different topological charges. The intensity profile is captured by CCD after passing through a 4f optical system. By calculating the intensity value of the captured image in the central region corresponding to the spiral phase of different topological charges, the OAM spectra Pl can be obtained. Accordingly, the OAM mode can be demultiplexed, thus the data decoding can be realized. Notably, the scheme proposed in the manuscript combines polarization-division multiplexing and OAM multiplexing, which can greatly improve the data transmission capacity.
For each transmitted OAM mode at a given turbulence strength, we calculate the detected signals of each decoding channel. Figure 8 shows the normalized energy weight matrices of all OAM modes with various turbulence levels at different transmission distances. For weak turbulence (e.g., Cn2 = 10−16 m−2/3), the normalized energy weight of all OAM modes approach 1. Meanwhile, when the transmission distance increases, averaged normalized energy weight of all OAM modes will decrease slightly, in the case of OAM modes with larger topological charges happen more rapidly. As the turbulence strengthens (namely, Cn2 = 10−15 m−2/3), when the transmission distance is 500 m, the normalized energy weight of all OAM modes is greater than 0.8, while for a transmission distance of 1000 m, the normalized energy weight of larger OAM mode order drops to below 0.5, and the normalized energy weight of smaller OAM mode order remains around 0.8. Under the strongest turbulence strength in the simulation, the average normalized energy weight of all OAM modes is less than 0.5, and even some OAM modes are indistinguishable with the increase of transmission distance.
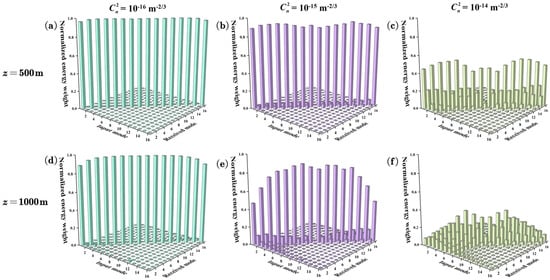
Figure 8.
The normalized energy weight matrices between OAM modes with their topological charges from l0 = −8 to l0 = 8 at an interval of 1 after transmission of 500 m and 1000 m at different turbulence strengths. (a,d), (b,e) and (c,f) correspond to Cn2 = 10−16 m−2/3, 10−15 m−2/3, and 10−14 m−2/3, respectively.
Lastly, to verify the feasibility proposed scheme, we numerically investigate the evolution of transmitted Lena grayscale images with the transmission distances and turbulence strengths corresponding to Figure 8, as presented in Figure 9. In the data decoding process, we choose the averaged normalized energy weight 0.5 as the threshold value. When the average normalized energy weight of a certain OAM mode is lower than 0.5, it is determined that it cannot be recognized, and a random value is assigned. Obviously, it can be seen from Figure 9a,d the image can be correctly decoded under weak turbulence strength. The stronger turbulence strength results in the performance degradation of transmitted image. As the transmission distance increases to 1000 m, the noise increases significantly, and the transmitted image is further degraded, as illustrated in Figure 9e. For the strongest turbulence strength, the quality of the transmitted image is the worst, and the image is almost indistinguishable.

Figure 9.
The numerical transmitted image data after transmission of 500 m and 1000 m with various turbulence strengths. (a,d), (b,e) and (c,f) correspond to Cn2 = 10−16 m−2/3, 10−15 m−2/3, 10−14 m−2/3, respectively.
To quantify the quality of the transmitted image, we choose average optical signal error rate (ER) as evaluation merit, and the formula of ER can be expressed as [55]
where N denotes the total number of OAM modes used, Pα is the probability of date α in the encoding, and Pα equals 1/N when data α is independently detected. Pβ|α accounts for conditional probability referring to the probability of detecting data α under condition of data β. Based on the normalized energy weight matrices, we calculate the ERs corresponding to Figure 9a–f, which are 1.28%, 3.56%, 8.28%, 23.60%, 51.58%, and 75.58%. The results show that the trend of ERs is consistent with the performance of transmitted image, and the larger ER corresponds to the poorer transmitted image quality.
Compared with the traditional scheme of using a spatial light modulator to generate and multiplex OAM beams, the scheme of generating and multiplexing OAM beams based on a coherent array laser contains more optical modules, including a laser module, emitting laser array configuration and dynamic control module, which inevitably results in making the system expensive and complicated. However, this approach also has its advantages. A coherent laser array can overcome the power limitation of single laser, significantly increasing the output power. Additionally, due to the high rate of electro-optic phase modulators and phase controllers (approximately gigahertz), fast switchable OAM beams based on coherent laser arrays can be achieved [42]. Therefore, a coherent laser array with high average power, fast switchable of the OAM beam generation and modulation capabilities has the potential to enable high-speed OAM multiplexing in FSOC.
5. Conclusions
In summary, the propagation characteristics of a CLA-DV in atmospheric turbulence are investigated by the theoretical derivation and numerical simulation method of random phase screen. The probability density and the normalized energy weight of each OAM mode (namely, the OAM spectrum) for CLA-DV and the Gaussian vortex beam are numerically calculated. The results show that the mode crosstalk of Gaussian vortex beam is smaller for the short distance and weak turbulence strength, while CLA-DV shows good performance in reducing the crosstalk of the OAM mode for long distances and strong atmospheric turbulence. These conclusions are also confirmed by the numerical simulation. Based on these, combined with coherent beam combining, a concept and principle of optical communication link with CLA-DV is proposed. The core device is a specially designed radial phase-locked Gaussian laser array composed of orthogonal polarized coherent laser array carrying different topological charges, which realize OAM mode coaxial generation and multiplexing. Using 16 non-zeroth-order OAM modes (e.g., topological charges from l0 = −8 to l0 = 8 at an interval of 1), the normalized energy weight matrices of all OAM modes are numerically calculated. In general, stronger turbulence strengths, longer transmission distance, and larger OAM mode order will lead to the rapid reduction of average normalized energy weight. An 8-bit grayscale Lena image transmitted through turbulent OAM channel is used to verify the feasibility of the proposed scheme. With the increase of turbulence strength and transmission distance, the quality of transmitted images becomes worse, which is verified by the trend of ERs. This work will have potential in the fields of FSOC under scattering conditions.
Author Contributions
P.J.: conceptualization, investigation, methodology, software, formal analysis, writing—original draft; W.F.: supervision, writing—review & editing. W.G.: investigation, numerical analysis; Z.L.: date processing; Q.G.: visualization. X.J.: data curation; T.Z.: supervision, writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Youth Innovation Promotion Association XIOPM-CAS (No. XIOPMQCH2021003), National Natural Science Foundation of China (Nos. 62171443, 62005310) and Key R & D Program of Shaanxi Province (Nos. 2021GY-298, 2023-ZDLGY-37, 2021ZDLGY10-03, 2022GY-225).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon. 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photonics Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Trichili, A.; Park, K.H.; Zghal, M.; Ooi, B.S.; Alouini, M.S. Communicating Using Spatial Mode Multiplexing: Potentials, Challenges, and Perspectives. IEEE Commun. Surv. Tutor. 2019, 21, 3175–3203. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2022, 11, 645–680. [Google Scholar] [CrossRef]
- Djordjevic, I.B. Deep-space and near-Earth optical communications by coded orbital angular momentum (OAM) modulation. Opt. Express 2011, 19, 14277–14289. [Google Scholar] [CrossRef] [PubMed]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B.; et al. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar] [CrossRef]
- Trichili, A.; Cox, M.A.; Ooi, B.S.; Alouini, M.-S. Roadmap to free space optics. J. Opt. Soc. Am. B 2020, 37, A184–A201. [Google Scholar] [CrossRef]
- Padgett, M.J.; Miatto, F.M.; Lavery, M.P.J.; Zeilinger, A.; Boyd, R.W. Divergence of an orbital-angular-momentum-carrying beam upon propagation. New J. Phys. 2015, 17, 023011. [Google Scholar] [CrossRef]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.J.; Padgett, M.J.; Boyd, R.W. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl. Opt. 2008, 47, 2414–2429. [Google Scholar] [CrossRef]
- Tyler, G.A.; Boyd, R.W. Influence of atmospheric turbulence on the propagation of quantum states of light carrying orbital angular momentum. Opt. Lett. 2009, 34, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Li, L.; Wang, J.; Gao, C.; Fu, S. Distortion Compensation for Orbital Angular Momentum Beams: From Probing to Deep Learning. J. Light. Technol. 2023, 41, 2041–2050. [Google Scholar] [CrossRef]
- Xie, G.; Li, L.; Ren, Y.; Huang, H.; Yan, Y.; Ahmed, N.; Zhao, Z.; Lavery, M.P.J.; Ashrafi, N.; Ashrafi, S.; et al. Performance metrics and design considerations for a free-space optical orbital-angular-momentum-multiplexed communication link. Optica 2015, 2, 357–365. [Google Scholar] [CrossRef]
- Li, L.; Xie, G.; Ren, Y.; Ahmed, N.; Huang, H.; Zhao, Z.; Liao, P.; Lavery, M.P.J.; Yan, Y.; Bao, C.; et al. Orbital-angular-momentum-multiplexed free-space optical communication link using transmitter lenses. Appl. Opt. 2016, 55, 2098–2103. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, A.; Deng, M.; Lu, B.; Guo, X. Free-space optical communication with quasi-ring Airy vortex beam under limited-size receiving aperture and atmospheric turbulence. Opt. Express 2021, 29, 32580–32590. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Xie, G.; Yan, Y.; Ren, Y.; Liao, P.; Zhao, Z.; Ahmed, N.; Wang, Z.; Bao, C.; Willner, A.J.; et al. Power loss mitigation of orbital-angular-momentum-multiplexed free-space optical links using nonzero radial index Laguerre–Gaussian beams. J. Opt. Soc. Am. B 2017, 34, 1–6. [Google Scholar] [CrossRef]
- Wan, Z.; Shen, Y.; Wang, Z.; Shi, Z.; Liu, Q.; Fu, X. Divergence-degenerate spatial multiplexing towards future ultrahigh capacity, low error-rate optical communications. Light Sci. Appl. 2022, 11, 144. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Xie, G.; Huang, H.; Ahmed, N.; Yan, Y.; Li, L.; Bao, C.; Lavery, M.P.J.; Tur, M.; Neifeld, M.A.; et al. Adaptive-optics-based simultaneous pre- and post-turbulence compensation of multiple orbital-angular-momentum beams in a bidirectional free-space optical link. Optica 2014, 1, 376–382. [Google Scholar] [CrossRef]
- Li, M.; Cvijetic, M.; Takashima, Y.; Yu, Z. Evaluation of channel capacities of OAM-based FSO link with real-time wavefront correction by adaptive optics. Opt. Express 2014, 22, 31337–31346. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Pre-turbulence compensation of orbital angular momentum beams based on a probe and the Gerchberg–Saxton algorithm. Opt. Lett. 2016, 41, 3185–3188. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, Y.; Wu, G.; Cai, Y. Reducing the cross-talk among different orbital angular momentum modes in turbulent atmosphere by using a focusing mirror. Opt. Express 2019, 27, 10280–10287. [Google Scholar] [CrossRef]
- Yuan, Y.; Lei, T.; Li, Z.; Li, Y.; Gao, S.; Xie, Z.; Yuan, X. Beam wander relieved orbital angular momentum communication in turbulent atmosphere using Bessel beams. Sci. Rep. 2017, 7, 42276. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Yang, G. Evolution of orbital angular momentum mode of the autofocusing Hypergeometric-Gaussian beams through moderate-to-strong anisotropic non-Kolmogorov turbulence. Opt. Commun. 2017, 405, 66–72. [Google Scholar] [CrossRef]
- Yan, X.; Guo, L.; Cheng, M.; Li, J.; Huang, Q.; Sun, R. Probability density of orbital angular momentum mode of autofocusing Airy beam carrying power-exponent-phase vortex through weak anisotropic atmosphere turbulence. Opt. Express 2017, 25, 15286–15298. [Google Scholar] [CrossRef]
- Yue, P.; Hu, J.; Yi, X.; Xu, D.; Liu, Y. Effect of Airy Gaussian vortex beam array on reducing intermode crosstalk induced by atmospheric turbulence. Opt. Express 2019, 27, 37986–37998. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Han, L.; Liang, H.; Wu, G.; Pang, X. Orbital angular momentum spectrum of pin-like optical vortex beams in turbulent atmosphere. J. Opt. Soc. Am. A 2022, 39, 1414–1419. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.Y. Laser beam combining for high-power, high-radiance sources. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 567–577. [Google Scholar] [CrossRef]
- Steven Kurti, R.; Halterman, K.; Shori, R.K.; Wardlaw, M.J. Discrete Cylindrical Vector Beam Generation from an Array of Optical Fibers. Opt. Express 2009, 17, 13982–13988. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.; Zhou, P.; Ma, Y.; Wang, X.; Su, R.; Liu, Z. Generation of azimuthally and radially polarized beams by coherent polarization beam combination. Opt. Lett. 2012, 37, 2658–2660. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Liu, Z.; Zhou, P. Generation of a high-power Airy beam by coherent combining technology. Laser Phys. Lett. 2013, 10, 125102. [Google Scholar] [CrossRef]
- Veinhard, M.; Bellanger, S.; Daniault, L.; Fsaifes, I.; Bourderionnet, J.; Larat, C.; Lallier, E.; Brignon, A.; Chanteloup, J.-C. Orbital angular momentum beams generation from 61 channels coherent beam combining femtosecond digital laser. Opt. Lett. 2021, 46, 25–28. [Google Scholar] [CrossRef]
- Hou, T.; Zhang, Y.; Chang, Q.; Ma, P.; Su, R.; Wu, J.; Ma, Y.; Zhou, P. High-power vortex beam generation enabled by a phased beam array fed at the nonfocal-plane. Opt. Express 2019, 27, 4046–4059. [Google Scholar] [CrossRef]
- Long, J.; Hou, T.; Chang, Q.; Yu, T.; Su, R.; Ma, P.; Ma, Y.; Zhou, P.; Si, L. Generation of optical vortex lattices by a coherent beam combining system. Opt. Lett. 2021, 46, 3665–3668. [Google Scholar] [CrossRef]
- Yu, T.; Xia, H.; Xie, W.; Xiao, G.; Li, H. The generation and verification of Bessel-Gaussian beam based on coherent beam combining. Results Phys. 2020, 16, 102872. [Google Scholar] [CrossRef]
- Ju, P.; Fan, W.; Gao, W.; Li, Z.; Gao, Q.; Li, G.; Jiang, X.; Zhang, T. Generation of perfect vectorial vortex beams by employing coherent beam combining. Opt. Express 2023, 31, 11885–11898. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Chang, Q.; Yu, T.; Long, J.; Chang, H.; Ma, P.; Su, R.; Ma, Y.; Zhou, P. Switching the orbital angular momentum state of light with mode sorting assisted coherent laser array system. Opt. Express 2021, 29, 13428–13440. [Google Scholar] [CrossRef] [PubMed]
- Aksenov, V.P.; Dudorov, V.V.; Kolosov, V.V.; Levitsky, M.E. Synthesized Vortex Beams in the Turbulent Atmosphere. Front. Phys. 2020, 8, 143. [Google Scholar] [CrossRef]
- Zhu, K.; Zhou, G.; Li, X.; Zheng, X.; Tang, H. Propagation of Bessel-Gaussian beams with optical vortices in turbulent atmosphere. Opt. Express 2008, 16, 21315–21320. [Google Scholar] [CrossRef] [PubMed]
- Abeamonwitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 5th ed.; Dover Publications: New York, NY, USA, 1966. [Google Scholar]
- Pinnell, J.; Rodríguez-Fajardo, V.; Forbes, A. How perfect are perfect vortex beams? Opt. Lett. 2019, 44, 5614–5617. [Google Scholar] [CrossRef]
- Paterson, C. Atmospheric Turbulence and Orbital Angular Momentum of Single Photons for Optical Communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef] [PubMed]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Management of the Angular Momentum of Light: Preparation of Photons in Multidimensional Vector States of Angular Momentum. Phys. Rev. Lett. 2001, 88, 013601. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Chen, M.; Zhang, Y.; Li, Y. Propagation of the OAM mode carried by partially coherent modified Bessel–Gaussian beams in an anisotropic non-Kolmogorov marine atmosphere. J. Opt. Soc. Am. A 2016, 33, 2277–2283. [Google Scholar] [CrossRef]
- von Kármán, T. Progress in the Statistical Theory of Turbulence. Proc. National Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef]
- Ostashev, V.E.; Brähler, B.; Mellert, V.; Goedecke, G.H. Coherence functions of plane and spherical waves in a turbulent medium with the von Karman spectrum of medium inhomogeneities. J. Acoust. Soc. Am. 1998, 104, 727–737. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C. Influences of atmospheric turbulence effects on the orbital angular momentum spectra of vortex beams. Photon. Res. 2016, 4, B1–B4. [Google Scholar] [CrossRef]
- Yong, K.; Tang, S.; Yang, X.; Zhang, R. Propagation characteristics of a ring Airy vortex beam in slant atmospheric turbulence. J. Opt. Soc. Am. B 2021, 38, 1510–1517. [Google Scholar] [CrossRef]
- Fleck, J.A.; Morris, J.R.; Feit, M.D. Time-dependent propagation of high energy laser beams through the atmosphere. Appl. Phys. 1976, 10, 129–160. [Google Scholar] [CrossRef]
- Zhu, Z.; Janasik, M.; Fyffe, A.; Hay, D.; Zhou, Y.; Kantor, B.; Winder, T.; Boyd, R.W.; Leuchs, G.; Shi, Z. Compensation-free high-dimensional free-space optical communication using turbulence-resilient vector beams. Nat. Commun. 2021, 12, 1666. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).