A Review of Variable-Beam Divergence Angle FSO Communication Systems

Abstract

Free-space optical (FSO) communication is widely used in satellites, ships, aircraft, and ground stations due to its advantages of high speed, large capacity, good confidentiality, and strong anti-interference ability. Variable-beam divergence angle (VBDA) technology makes FSO systems more flexible; this has the benefits of higher acquisition probability, stronger tracking ability, wider communication link range, and lower energy consumption. In other words, the study of VBDA has both theoretical significance and practical relevance. This paper conducts a comprehensive search of relevant scientific databases, journals, conference proceedings, patents, and books to identify publications related to VBDA technology. We analyze these publications, classify and organize various VBDA techniques based on their respective methods. To the best of our knowledge, this is the first review of VBDA technology. In this paper, we first explain the basic principle of changing the beam divergence angle by employing the ABCD matrix, and further furnish a detailed overview of the methods used for VBDA along with their corresponding advantages and disadvantages. In addition, we provide a comprehensive summary of the research conducted using VBDA technology across different link types. Lastly, we identify the challenges and potential future research directions for VBDA technology.

1. Introduction

Compared to 5G, 6G will use more advanced communication technology to support faster and wider communication scenarios [1,2], as shown in Figure 1. As the demand for data transmission and communication increases during the development of 6G, a large number of base stations will be required to support the expanding networks. Traditional base stations may not meet the requirements of high speed and large capacity communication that 6G demands. Therefore, new technologies and methods need to be explored to fulfill these requirements. In this case, free-space optical (FSO) communication technology is a viable solution, as it can significantly improve the performance and reliability of communication networks [3,4]. In particular, when building 6G networks in remote areas, deploying traditional base stations may not be practical or may be too costly. Therefore, FSO can be used to relay communication signals through satellites, high-altitude platforms (HAP), unmanned aerial vehicles (UAV), and other means to achieve seamless connections across long distances, thereby improving the coverage and availability of 6G networks for users in rural and remote areas.

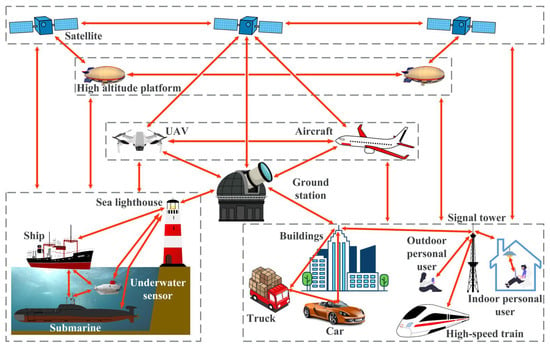
Figure 1. The extensive communication scenario contained in 6G.

Thus, FSO technology will occupy a significant proportion of 6G communication technology and become one of the driving forces in the development of 6G technology. Its application will help address the bandwidth and rate bottlenecks faced by current 5G networks, and lay the foundation for faster, smarter, and more reliable communication services in the future.

Taking the intensity modulation/direct detection (IM/DD) with on-off keying (OOK) FSO communication system as an example, Figure 2 illustrates its typical optical path. A laser diode (LD) is commonly used as the light source, although some manufacturers may use high-power LEDs [5]. At the transmitting end, the data is encoded and modulated [6]. The modulated light beam is then amplified and shaped by an optical amplifier, collimator, and optical antenna before entering free space. At the receiving end, the optical antenna focuses the received beam onto an optoelectronics diode (PD), which converts the received optical signal into electrical current. Finally, the demodulation process is performed to obtain the original transmission data.

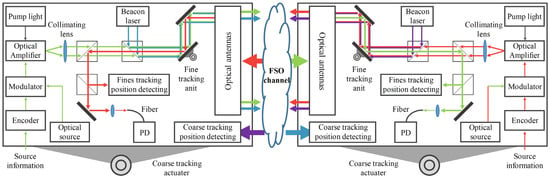
Figure 2. Optical path diagram of FSO communication terminal.

At present, FSO communications mostly use fixed-beam divergent angle scheme. It has several benefits, such as a wide selection of commercial components, compact structure, and ease of installation. However, there is still room for improvement in areas such as link reliability, communication link range, and power consumption [7]. Compared to fixed-beam divergent angle scheme, the variable-beam divergent angle (VBDA) scheme offers four significant advantages, which are illustrated in Figure 3. Each of these advantages will be discussed in detail below:

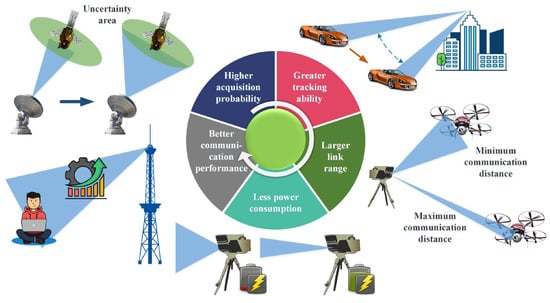
Figure 3. Advantages of FSO communication systems with VBDA scheme.

Higher acquisition probability. When targeting objects with a large uncertain area (such as targets moving at high speeds or drifting due to Global Positioning System (GPS) unavailability), traditional solutions involve using a large divergence angle beam to cover the uncertain area or scanning with a small divergence angle beam. However, these methods have drawbacks, such as reduced detection range or increased acquisition time. To address this problem, a solution using VBDA can be employed. As in [8], the beam divergence angle θ is set to 1/(2𝜙 + 1) times the size of the uncertain area, whose angle value is θ₀, as shown in Figure 4. Here, 𝜙 = 0, 1, 2, … represents the scanning phase, and scanning starts from the 𝜙 = 0 phase. If the beam is not detected, the system enters the next phase and continues to scan. At this time, 𝜙 = 1, and the value of θ becomes θ₀/(2 × 1 + 1). This process is repeated until the receiver detects the beam and starts tracking. Simulation results demonstrate that this new scanning strategy reduces acquisition time by approximately 80%, leading to a significant improvement in the probability of acquisition.

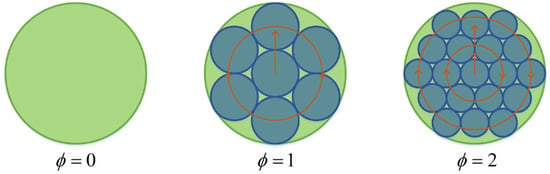
Figure 4. The acquisition strategy of using VBDA scheme [8]. Reprinted/adapted with permission from Ref. [8]. 2017, SPIE.

Greater tracking ability. Upon entering the tracking phase, the beam divergence angle can be further compressed by utilizing information from the coarse and fine tracking residuals. This results in improved optical power received by the coarse and fine tracking units, typically cameras and four quadrant detectors, respectively. The increase in optical power enhances the tracking ability. When coarse and fine tracking residuals increase due to turbulence or jitter in platform itself, appropriately increasing the beam divergence angle can improve the robustness of the coarse and fine tracking units to these disturbances, leading to more reliable communication due to an enlarged allowable pointing error.

Larger communication link range. In certain 6G use cases, the distance between FSO nodes would dynamically change [9], such as for communication between ground stations and UAVs. When the communication distance decreases, the beam radius has not yet significantly expanded, resulting in a smaller allowable pointing error. Consequently, the pointing error occurring during the beam steering interval easily exceeds the allowable limit. This indicates that the FSO link is more likely to be disconnected as the moving node approaches its paired node. To address this, appropriately increasing the beam divergence angle can effectively cover the uncertain area, thereby potentially reducing the minimum communication distance.

When the communication distance increases, the optical power loss increases by 6 dB every time the communication distance doubles [10]. Although it could be compensated for by a larger receiving aperture or higher transmission power, these compensation methods are very limited because a larger aperture or higher power light source will increase the SWaP (size, weight, and power) requirements of the optical system [11]. At this time, appropriately reducing the beam divergence angle can increase the received optical power, thereby further increasing the maximum communication distance. In summary, the use of a VBDA scheme could effectively increase the FSO communication link range.

Less power consumption. Fixed-beam divergence angle systems are often designed based on the worst-case scenario. In addition, the beam divergence angle will be slightly larger than the optimal beam divergence angle (OBDA) during communication, which results in a certain amount of energy waste. In applications where energy consumption is a critical factor, such as in satellites, UAVs, and personal handheld terminals, it is desirable to reduce unnecessary energy waste to extend the equipment’s endurance time. By selecting the appropriate beam divergence angle and optical power based on real-time link conditions, it is possible to reduce energy consumption while maintaining communication rates.

Better communication performance. During FSO communication, the performance of the link can be influenced by various factors. These include system parameters such as beam divergence angle, transmitted optical power, receiver’s field of view (FOV) angle, attenuation loss, atmospheric turbulence, pointing error, and angle-of-arrival (AOA) fluctuations. By adjusting the beam divergence angle and transmitted optical power, improved communication performance can be attained, resulting in lower outage probability (OP) and bit error rate (BER). In the existing studies, considering the aforementioned influencing factors, closed-form expressions of communication performance metrics such as OP and BER have been derived and simulated. This was achieved by deriving the expressions of probability density function (PDF) and cumulative distribution function (CDF) under different channel fading models, such as K distribution [12,13], Log-Normal distribution [14,15], $\mathrm{\Gamma }-\mathrm{\Gamma }$ distribution [16,17,18,19], and generalized Málaga distribution [20,21], etc. The results demonstrate a strong dependence of performance indices on adjustable system parameters, such as beam divergence angle, transmitted optical power, and receiver’s FOV angle [14,21,22,23]. Additionally, the OBDA varies with different factors, such as transmitted optical power [14,21,24,25,26,27]. Therefore, VBDA technology can facilitate achieving better communication performance.

In this paper, leveraging over 10 years of extensive experience in FSO communication [28,29,30,31,32,33,34], we present a comprehensive review of VBDA technology. To the best of our knowledge, this is the first review of VBDA technology. Distinguishing itself from previous studies, which focused on specific VBDA methods, this review classifies and organizes various VBDA techniques according to their respective methods, while summarizing the advantages and disadvantages of each method. By providing this comprehensive analysis, we aim to enhance the overall understanding of VBDA methods. The structure of this paper is as follows: Section 1 introduces the demand for FSO communication in the development of 6G, the basic structure of FSO communication systems, and the advantages of VBDA scheme; Section 2 introduces the transmission theory of the Gaussian beam and the basic optical principles of the VBDA method; and Section 3 provides a comprehensive overview of the currently employed VBDA methods, highlighting their respective advantages and disadvantages in detail. Additionally, the paper summarizes research on the utilization of VBDA technologies for different types of links. Finally, the challenges and possible future research directions of VBDA technology are summarized.

2. Optical Principle of VBDA Method

Single-mode fiber (SMF) has been widely used in FSO communication due to its advantages of low attenuation, low dispersion, and high-bandwidth capacity. Since the beam emitted in SMF can be approximated as a fundamental mode Gaussian beam, the transmission theory of Gaussian beams is used to analyze the principle of VBDA. Assume that the SMF emits a Gaussian beam with a waist radius of $w_0$, which is located on the end face of SMF, as shown in Figure 5. The ideal single lens is placed at a distance of $l$ from the source, has a focal length of $F$, and transforms the Gaussian beam into an outgoing beam with a waist radius of $w_0^{\prime }$. The distance from the rear surface of the lens to the outgoing beam waist is denoted as $l^{\prime }$. The $q$ parameters of the incident Gaussian beam at the waist and at the rear surface of the lens are denoted as $q_0$ and $q_F$, respectively. In the following analysis, we will use the ABCD law of Gaussian beam propagation [35] to determine the divergence angle of the outgoing beam.

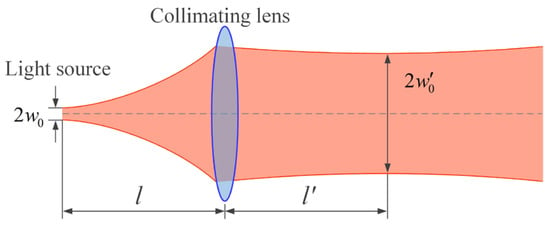
Figure 5. Characteristic schematic diagram of the basic Gaussian beam after lens transformation.

The $q$ parameter of incident Gaussian beam is:

$$q_0=i\frac{\pi w_0^2}{\lambda },$$

(1)

The ABCD matrix transmitted from the waist of the incident Gaussian beam to the front surface of the lens is given by $\left. [1, l; 0, 1\right]$. The ABCD matrix transmitted from the front surface of the lens to the rear surface of the lens is $\left. [1, 0; -1/F, 1\right]$. By the ABCD law, the ABCD transmission matrix from the beam waist position of the incident Gaussian beam to the rear surface of the lens is given by:

$$\left. [\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left. [\begin{array}{cc}1& 0\\ -1/F& 1\end{array}\right]\left. [\begin{array}{cc}1& l\\ 0& 1\end{array}\right]=\left. [\begin{array}{cc}1& l\\ -1/F& 1-l/F\end{array}\right],$$

(2)

The $q$ parameter of Gaussian beam at the rear surface of the lens can be obtained as follows:

$$q_F=\frac{A{q}_0+B}{C{q}_0+D}=\frac{i\frac{\pi w_0^2}{\lambda }+l}{-\frac{1}{F}\cdot i\frac{\pi w_0^2}{\lambda }+1--\frac{l}{F}},$$

(3)

And the $q$ parameter of Gaussian beam at the rear surface of the lens is:

$$q_F=q_0^{\prime }-l^{\prime }=i\frac{\pi {w_0^{\prime }}^2}{\lambda }-l^{\prime },$$

(4)

So:

$$q_F=\frac{i\frac{\pi w_0^2}{\lambda }+l}{-\frac{1}{F}i\frac{\pi w_0^2}{\lambda }+1--\frac{l}{F}}=i\frac{\pi {w_0^{\prime }}^2}{\lambda }-l^{\prime },$$

(5)

The solution is:

$${w_0^{\prime }}^2=\frac{F^2{w}_0^2}{{\left(F-l\right)}^2+{\left(\frac{\pi w_0^2}{\lambda }\right)}^2},$$

(6)

According to the calculation formula $\theta =2\lambda /\left(\pi w_0\right)$, the far-field divergence angle of a Gaussian beam can be obtained as follows:

$${\theta }_0^{\prime }=\frac{2\lambda }{\pi w_0^{\prime }}=\frac{2\lambda }{\pi F{w}_0}\sqrt{{\left(F-l\right)}^2+{\left(\frac{\pi w_0^2}{\lambda }\right)}^2},$$

(7)

The outgoing beam divergence angle ${\theta }_0^{\prime }$ is minimized when $F=l$, i.e., when the beam waist is positioned at the front focal plane of the collimating lens. This corresponds to the state of optimal collimation. As a result, the outgoing beam exhibits a minimized divergence angle of $2w_0/F$. According to Equation (7), any changes in the values of $F$, $l$, or $w_0$ will result in changes to the divergence angle ${\theta }_0^{\prime }$ of the outgoing beam. Since the mode field radius $w_0$ of SMF at a specific wavelength cannot be easily modified, the divergence angle of the exit beam can be altered by adjusting the focal length $F$ of the collimating lens or by varying the distance $l$ between the SMF end face and the collimating lens. The influence of $F$ and $l$ on the divergence angle ${\theta }_0^{\prime }$ of the outgoing beam is shown in Figure 6.

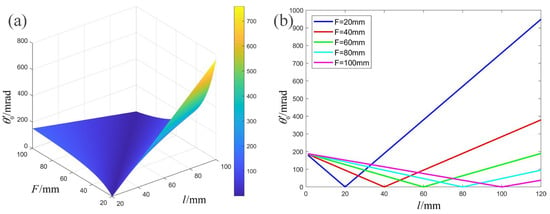
Figure 6. (a) The divergence angle ${\theta }_0^{\prime }$ versus $F$ and $l$. (b) The divergence angle ${\theta }_0^{\prime }$ versus $l$ with different values of $F$.

Furthermore, one way to change $l$ is by altering the optical path length between the SMF end face and collimating lens. For example, one can insert a parallel flat glass as shown in Figure 7, which alters the ABCD matrix. The ABCD matrix transmitted from the waist of the incident Gaussian beam to the front surface of the plate is $\left. [1, b; 0, 1\right]$. The ABCD matrix transmitted from the front surface of the plate to the back surface of the plate is $\left. [1, d/n; 0, 1\right]$. The ABCD matrix transmitted from the back surface of the plate to the front surface of the lens is $\left. [1, l-b-d; 0, 1\right]$.

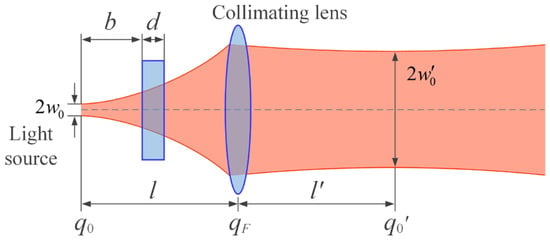
Figure 7. Schematic diagram of the method for changing the optical path length between the light source and the collimating lens.

Therefore, the ABCD transmission matrix from the beam waist position of the incident Gaussian beam to the rear surface of the lens is changed to:

$$\begin{array}{ll}\left. [\begin{array}{cc}A& B\\ C& D\end{array}\right]& =\left. [\begin{array}{cc}1& 0\\ -1/F& 1\end{array}\right]\left. [\begin{array}{cc}1& l-b-d\\ 0& 1\end{array}\right]\left. [\begin{array}{cc}1& d/n\\ 0& 1\end{array}\right]\left. [\begin{array}{cc}1& b\\ 0& 1\end{array}\right]\hfill \\ & =\left. [\begin{array}{cc}1& l-\left(1-\frac{1}{n}\right)d\\ -1/F& \left(-1/F\right)\left. [l-\left(1-\frac{1}{n}\right)d\right]+1\end{array}\right]\hfill \end{array}$$

(8)

Substituting this into Equation (3), we obtain:

$$q_F=\frac{i\frac{\pi w_0^2}{\lambda }+l-\left(1-\frac{1}{n}\right)d}{-\frac{1}{F}i\frac{\pi w_0^2}{\lambda }+\left(-\frac{1}{F}\right)\left. [l-\left(1-\frac{1}{n}\right)d\right]+1}=i\frac{\pi {w_0^{\prime }}^2}{\lambda }-l^{\prime },$$

(9)

The solution is:

$${w_0^{\prime }}^2=\frac{F^2{w}_0^2}{{\left(F-a\right)}^2+{\left(\frac{\pi w_0^2}{\lambda }\right)}^2},\left. [a=l-\left(1-\frac{1}{n}\right)d\right],$$

(10)

Substituting this into $\theta =2\lambda /\left(\pi w_0\right)$, we obtain:

$${\theta }_0^{\prime }=\frac{2\lambda }{\pi w_0^{\prime }}=\frac{2\lambda }{\pi F{w}_0}\sqrt{{\left. [F-l+\left(1-\frac{1}{n}\right)d\right]}^2+{\left(\frac{\pi w_0^2}{\lambda }\right)}^2},$$

(11)

According to Equation (11), altering the refractive index $n$ or thickness $d$ of the parallel flat glass can change the divergence angle ${\theta }_0^{\prime }$ of the outgoing beam, as shown in Figure 8.

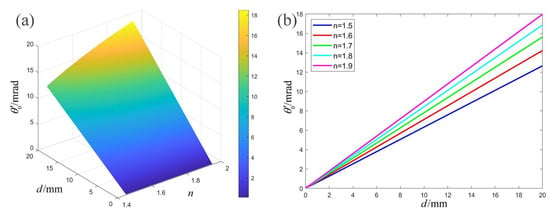
Figure 8. (a) The divergence angle ${\theta }_0^{\prime }$ versus $n$ and $d$. (b) The divergence angle ${\theta }_0^{\prime }$ versus $d$ with different values of $n$.

As mentioned above, the divergence angle of the outgoing beam can be modified by adjusting the focal length $F$ of the collimating lens or the optical path length between the beam waist and the collimating lens. Based on these two categories, the existing techniques for achieving VBDA are classified and depicted in Figure 9. The following sections provide a detailed description of these methods.

Figure 9. Existing methods of varying divergence angle.

3. Existing Methods for VBDA

In this section, we will delve into the two main VBDA methods. We will highlight how each method works, how it is implemented, and its pros and cons. With a thorough examination of these methods, readers will be able to better understand the two main VBDA methods and choose the technique that best suits their application scenarios.

3.1. Vary Beam Divergence by Adjusting the Focal Length F of the Collimating Lens

3.1.1. Using Zoom Group

Figure 10 illustrates the operating principle, which involves adjusting the distance between two or more zoom lenses to alter the focal length of the lens group, subsequently changing the beam divergence angle. The technique offers several advantages, including a wide range of continuous divergence angle changes and the relatively mature technology of the zoom lens group. However, designing a zoom lens group with a large zoom ratio is costly, and high-quality guide rails or actuators are necessary, which can be a potential disadvantage.

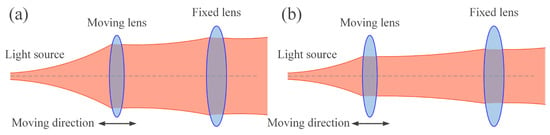
Figure 10. The principal diagram of VBDA by using zoom group. (a) Collimation state, (b) Large divergence angle state.

The research on this method is as follows: K.K. Han [36] and J.J. Ma et al. [37] used two positive lenses combined as a VBDA mechanism. Y.L. Yang et al. [38] varied the beam divergence angle from 0.7 mrad to 1.2 mrad by moving the rod lens connected with optical fiber along the axial direction. X.L. Xie et al. [39] designed a VBDA mechanism by altering the distance between the primary mirror and the secondary mirror of a Cassegrin transmitting antenna. The VBDA mechanism designed and fabricated by A. Carrasco-Casado et al. [40] is shown in Figure 11. Its beam divergence angle can be continuously adjusted between 90 and 6250 μrad (full width at half maximum, FWHM), with optical axis stability of less than 5% during the transformation process. The system’s optical aberrations were evaluated using a shear interferometer, and the outgoing beam exhibited good wavefront quality.

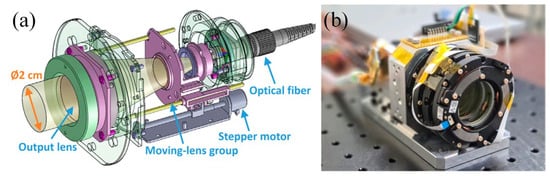
Figure 11. (a) 3D model of the beam divergence angle control system, (b) first prototype of the beam divergence angle control system [40]. Reprinted/adapted with permission from Ref. [40]. 2022, Carrasco-Casado, A.

3.1.2. Using Zoom Lens

This method involves using the adjustable focal length of a liquid lens to introduce defocus and change the beam divergence angle. At present, there are three types of liquid lenses commonly used:

Electro-wetting liquid lens. Figure 12a shows the cavity of this liquid lens, which contains two liquids of similar density and mutually insoluble. The liquid–liquid contact surface forms a refractive surface [41,42], and the radius of curvature of the surface can be changed by voltage, thereby changing the focal length. The advantage of using it to change the beam divergence angle is that the principle is simple, the zoom range is large, and no mechanical displacement element is needed. Additionally, it can spontaneously form lenses with very high-surface quality. However, it also faces the challenge of difficulty in making the aperture larger. When the lens aperture is greater than 5 mm, the wavefront aberration caused by gravity becomes non-negligible [43].

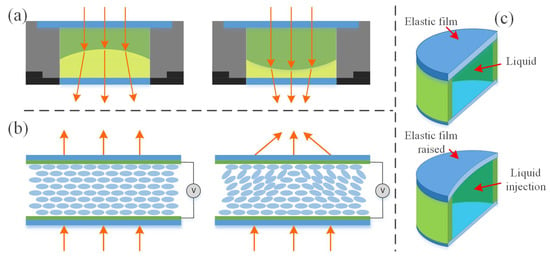
Figure 12. Working principal diagram of liquid lens. (a) Electro-wetting liquid lens. (b) Liquid crystal material liquid lens. (c) Mechanical hydraulic-driven liquid lens.

Liquid crystal material liquid lens. By applying a voltage to a specially shaped electrode, the liquid lens generates a gradient-varying electric field which changes the refractive index and focal length of the lens [44,45], as shown in Figure 12b. One advantage of it is that the liquid crystal layer can be made very thin, down to tens of μm. And the required driving voltage is small. However, the lens is usually used with a polarizer, which results in low light transmittance and makes it unsuitable for high-power laser applications.

Mechanical hydraulic-driven liquid lens. Typically, this technique involves confining the liquid within a closed cavity using a stretchable elastic film [46,47], as shown in Figure 12c. By applying external pressure to change the curvature radius of the elastic film, the focal length of the liquid lens can be changed. One advantage of it is its short response time. However, its disadvantage is that the rough surface of the elastic film would affect light transmittance, the uneven deformation of the film layer would reduce image quality, and the outer surface of the elastic film is prone to absorbing dust and other small particles.

Overall, using a liquid lens to change the beam divergence angle has several advantages, including a short response time, a large variation range for the divergence angle, a simple structure, and the ability to reduce the mechanical actuator and terminal volume. However, it also faces the challenge of the difficulty of making the aperture larger. Therefore, liquid lenses with larger apertures are best used in vertical and downward positions and are not suitable for rotation with a turntable.

A. J. Williams et al. [48] and V. V. Mai et al. [49] used liquid lenses to change beam divergence angles. M. ZOHRABI et al. [50] used three mechanical hydraulic liquid lenses in combination with wide-angle fisheye lenses to achieve 2D beam scanning of ±75°, as shown in Figure 13. Tunable liquid lens 1 was used to maintain the beam divergence angle while tunable liquid lens 2 and tunable liquid lens 3 were decentered in the Y and X directions, respectively, acting as prisms to control the beam deflection angle. V. V. Mai et al. [51] also used three liquid lenses to achieve adaptive control of beam steering and divergence angle, as shown in the inset of Figure 14, called VFL system. The authors found that deterioration of the beam quality can be clearly observed when the liquid lens is aligned horizontally. Therefore, a vertical arrangement of the liquid lens was suggested. Later V. V. Mai et al. [52,53,54] used the above system to perform an experimental demonstration of wavelength-division-multiplexing (WDM) transmission, as shown in Figure 14. The channel spacing of WDM is 0.8 nm, and the four communication wavelengths are 1549.2 nm, 1550 nm, 1550.8 nm, and 1551.6 nm, respectively. It was the first study on a WDM FSO system capable of non-mechanical optical beam steering and divergence control realized by liquid lenses.

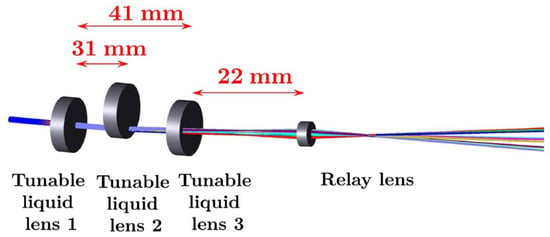
Figure 13. The schematic of the full 2D scan setup [50]. Reprinted/adapted with permission from Ref. [50]. 2016, The Optical Society.

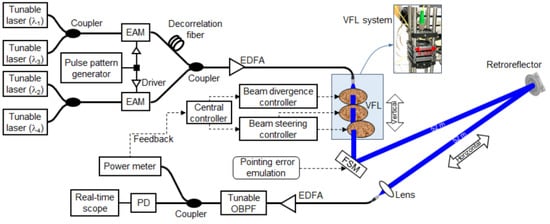
Figure 14. Experimental light path diagram of WDM based on liquid lens beam steering and divergence angle control system [53]. Reprinted/adapted with permission from Ref. [53]. 2022, Kim, H.

3.1.3. Using Lens with Different F

This method of VBDA can switch between small and large angles. There are two main ways to do this: switching collimators with different focal lengths or inserting different defocus lenses, as shown in Figure 15. Figure 15a demonstrates the use of an optical switch to select a collimator with a different focal length for transmitting the beam. K. H. Heng et al. [55] used this method to change the beam divergence angle.

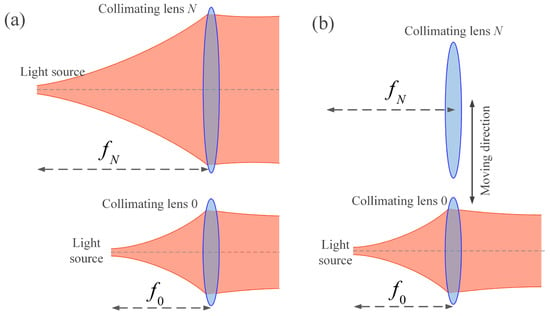
Figure 15. Schematic diagram of VBDA method by: (a) switching collimators with different focal lengths. (b) inserting different defocus lenses.

Figure 15b shows lenses with different focal lengths that are moved to the optical axis using an electric drive. Y. Hu et al. [56] used this method. N. Yang et al. [57] fixed multiple collimating lenses with different focal lengths on a disk and switched between them by driving the rotation of the disk, achieving a graded and adjustable beam divergence angle.

This VBDA method has the advantage of a simple principle and easy operation. However, its disadvantage lies in the high requirements for repeated positioning accuracy of the electric displacement mechanism. Failure to meet these requirements may result in significant beam drift. This method can only be used in grades and cannot continuously change the divergence angle. Furthermore, the communication link will experience an outage when the divergence angle is switched.

3.2. Vary Beam Divergence by Adjusting the Optical Path Length between the Beam Waist and the Collimating Lens

3.2.1. Axial Translation of Light Source or Collimating Lens

Figure 16 is the schematic diagram of this method. (Note that the mode field diameter of a normal 1550 nm SMF is only about 10.4 μm and is exaggerated for convenience in this and the following figures). The lens or light source is fixed on a linear electric stage, which adjusts the beam divergence angle by changing the distance between the light source and the collimating lens. This method has the advantages of a simple principle and device and could achieve a large range of divergence angle changes. The risk of introducing additional wavefront distortion is reduced because no extra zoom elements are inserted into the optical path. Despite its benefits, this method has a notable disadvantage; it demands an exceptionally high level of parallelism in the linear electric stage. In [58], it was suggested that the lateral motion (eccentricity) of the lens or light source should not exceed 3 μm.

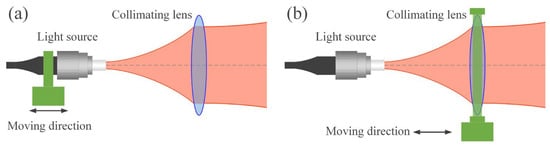
Figure 16. Schematic diagram of VBDA by axial translation light source or collimating lens (a) Moving light source. (b) Moving collimating lens.

Previous studies [57,59,60,61,62,63,64] adjusted the beam divergence angle by moving the light source, while only [65] moved the lens. The light source, often a fiber head of a SMF, is smaller and easier to manipulate than collimating lenses, making it a more popular choice in experiments.

By using this VBDA method, N. Yang et al. [57] and L. Zhu et al. [60] achieved the beaconless acquisition function of an FSO system. C.M. Kelway [59] and V. Gianfranco et al. [61] mitigated the influence of different atmospheric attenuation on the received optical power. J. Ma et al. [62] designed a satellite FSO communication terminal test device with VBDA. Refs. [63,64,65] improved optical tracking characteristics. The VBDA mechanism and its FSO terminal, as presented in [63], are shown in Figure 17.

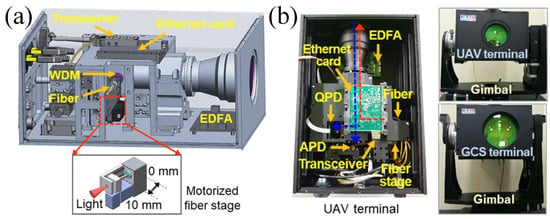
Figure 17. (a) FSO terminal and its VBDA mechanism. (b) Prototype of FSO communication terminal principle [63]. Reprinted/adapted with permission from Ref. [63]. 2021, Elsevier.

3.2.2. Inserting Parallel Plate

The schematic diagram in Figure 18 illustrates the method. A motor drives a parallel plate glass to insert into the optical path, thereby altering the optical path length between the light source and the collimating lens. This enables the switch between small and large divergence angles. The advantages of this method are its simplicity in principle and ability to greatly relax the requirement for lateral positioning accuracy. Additionally, it does not require precise location determination, so the mechanical properties of the motor driver can be simple and economical. However, the method cannot continuously change the divergence angle, and switching between large and small divergence angles introduces scintillation, which causes the link to experience an outage during insertion time.

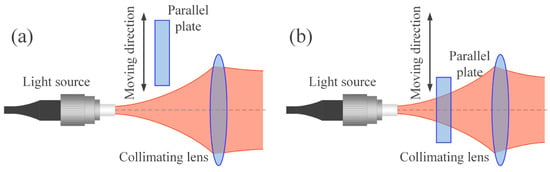
Figure 18. Schematic diagram of VBDA achieved by inserting a parallel plate. (a) Collimation state. (b) Large divergence angle state.

G.A. Mitchell [66] applied this method to pickup and camera systems, enabling quick and easy focusing between different film surfaces by moving in and out of parallel plate glass. In the context of laser communication systems, this method can be implemented using a group of parallel plates of varying thickness. The plates can be selected and moved into the optical path by electric actuators, allowing for different beam divergence angles to be achieved by using plates of different thickness or by simultaneously selecting multiple plates.

3.2.3. Using Optical Wedge Pair

The schematic diagram in Figure 19 shows the optical wedge pair used in the optical path, where the thickness of the pair is adjusted by adjusting the moving optical wedge to change the beam divergence angle. This method offers several advantages, including a wide range of divergence angle changes, low impact on the optical axis deflection during adjustment, and a large tolerance for lateral positioning errors. This method requires a tradeoff between the range of VBDA and wavefront aberrations. If the wedge angle is reduced, the range of VBDA will be narrowed. Conversely, if the wedge angle is increased, astigmatism will be introduced, causing the outgoing beam to become oval.

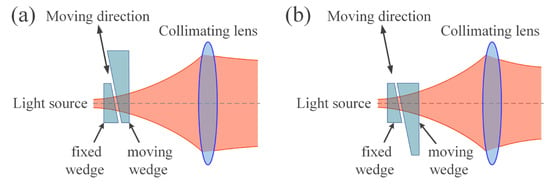
Figure 19. Schematic diagram of the VBDA method using wedge-pair. (a) Collimation state. (b) Large divergence angle state.

R.F. Schuma et al. [67] used a set of optical wedge pair of the same size between two lens groups in the beam expander to achieve the function of VBDA. M.H. Keith et al. [58] placed the wedge pair in front of the collimating lens and achieved continuous adjustment of the beam divergence angle between 38 μrad and 300 μrad (full width at half maximum (FWHM)), as shown in the green dotted box in Figure 20. Building upon this mechanism, J.M. Roth et al. [68] designed and manufactured a FSO communication system with continuously adjustable beam divergence angle and optical power, also shown in Figure 20. To minimize the terminal SWaP, the beacon and signal beams (at different wavelengths) were amplified by the same HPOA, and the relative power level of each beam was dynamically controlled using an electronically controlled variable optical attenuator (VOA).

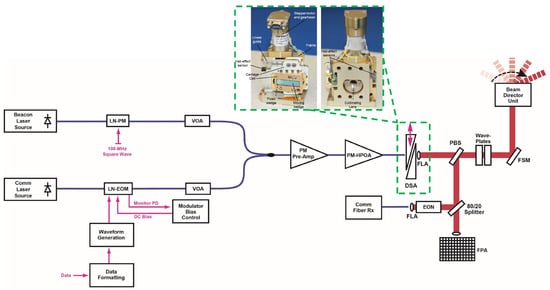
Figure 20. Optical path diagram of FSO communication system with continuously adjustable beam divergence angle and optical power [58,68]. Reprinted/adapted with permission from Ref. [58]. 2015, SPIE. Reprinted/adapted with permission from Ref. [68]. 2019, Roth, J.M.

In summary, we have thoroughly investigated various VBDA methods in FSO communication systems. The key parameters of all current VBDA mechanisms in Table 1, including the wavelength, range of beam divergence angles, power range, communication distance, data rate, and bit error rate (BER). Moreover, we have assessed the advantages and disadvantages of different VBDA methods and compiled them in Table 2. This comprehensive overview can help designers and researchers compare and evaluate the performance of different VBDA techniques for various FSO applications. By highlighting the benefits and limitations of each method, we aim to provide readers with a clear understanding of the trade-offs involved in selecting a particular VBDA technique.

Table 1. Summary of variable-beam diverging angle methods.

Method	Year	Author	Wavelength/nm	Experiment/Simulation	Beam Divergence Angle Range	Power Range	Communication Distance	Date Rate	BER
Using zoom group	2014	K.K. Han et al. [36]	532	Experiment	1–200 mrad	Constant
	2016	J.J. Ma et al. [37]		Patent
	2018	Y.L. Yang [38]	1550	Experiment	0.7–1.2 mrad	Constant	3 km	1.25 Gbps
	2022	X.L. Xie et al. [39]		Patent
	2022	A, C.C. et al. [40]	1550	Experiment	90–6250 µrad (FWHM)	Maximum 2 W	600 km: 10 Gb/s; 1200 km: 2.5 Gb/s
Using zoom lens	2016	M. Zohrabi [50]	visible and near–infrared	Experiment	few mm to few cm beam diameter
	2017	J.W. Andrew et al. [8]	486/520	Experiment	collimated to 13°
	2021	V.V Mai et al. [49]	1530	Experiment	377.1–1131.4 μrad		104 m	10 Gbps	1 × 10−3
	2021	V.V Mai et al. [51]	1530	Experiment	0.84–2.2 mrad				1 × 10−3
	2022	V.V Mai et al. [52,53,54]	1549.2/ 1550.0/ 1550.8/1551.6	Experiment	0.84–2.2 mrad			4 × 10 Gbps (WDM)	3.5 × 10−6
Using lens with different F	2008	K.H. Heng et al. [10,55]		Simulation		Constant	Maximum 4 km
	2009				6–96 mrad (Discrete)	800 mW	300 m–10 km
	2015	Y. Hu et al. [56]	1550	Simulation	15/500 μrad	Constant	5/10/20 km
	2022	Y. Ning et al. [57]		Patent
Axial translation of light source or collimating lens	2003	L. Zhu et al. [60]		Patent	1.5–30 mrad
	2003	C.M. Kelway [59]		Patent
	2004	V. Gianfranco [61]		Patent
	2008	J. Ma et al. [62]		Patent	0.1–1 mrad
	2006	P. LoPresti [65]	632.8	Experiment		1–100 mW	2/1.75/1.5/1.25/1/0.5 km
	2021	S. Park et al. [63,64]	1530/ 1590	Experiment	Maximum 8.84 mrad	Maximum 200 mW	13.6 km	1.25 Gbit/s	1 × 10−12
	2022					200 mW	50 m
	2022	R. Harada et al. [9]	1550	Simulation	0.4–6 mrad	10 dBm	5–200 m	100 Gbit/s
Inserting parallel plate	1951	G.A. Mitchell [66]		Patent
Using optical wedge-pair	1989	R.F. Schuma et al. [67]		Patent
	2015	K.M. Hinrichs et al. [58]	1530– 1570	Experiment	58.8–509 μrad	Constant
	2019	J.M. Roth et al. [68]		Experiment	64.5–679 μrad (Discrete)	0–1 mW

Table 2. Summary of the characteristics of several methods of VBDA.

Method	VBDA Range *	If Varies Continuously	Response Time	Others
Using zoom group	90 μrad (FWHM)–200 mrad	Yes	Seconds	The technology behind zoom lens groups has reached a relatively mature stage and it requires high-quality guide rails and actuators.
Using zoom lens	377.1 μrad–13°	Yes	Milliseconds to seconds	It is not necessary to use a mechanical mechanism, which could reduce the terminal volume. However, the system may be affected by gravity and enlarging the aperture may be difficult.
Using lens with different F	15 μrad– 96 mrad	No	Milliseconds/seconds	The principle is simple, but the communication link will experience an outage when switching angles.
Axial translation of fiber or lens	100 μrad–30 mrad	Yes	Seconds	The parallelism of linear displacement table is very high.
Inserting parallel plate		No	Milliseconds to seconds	The principle is simple and can greatly relax the requirement for lateral positioning accuracy. The communication link will experience an outage when switching angles.
Using optical wedge-pair	58.8 μrad– 0.679 mrad	Yes	Seconds	The influence on the optical axis deflection is small. As the wedge angle increases, lager astigmatism is introduced.

* The data here comes from Table 1.

Furthermore, we have presented Table 3, which summarizes the current studies that have applied VBDA technology to different link types, such as ground terminal platforms, air platforms, high-speed train (HST) platforms, underwater platforms, and satellite platforms. It is worth noting that each VBDA method described in this paper has its unique characteristics, and designers should choose the appropriate technique for the given FSO link situation and communication terminal conditions. Factors such as power consumption, beam quality, cost, and environmental robustness must be carefully considered when selecting a VBDA method. We hope that the comprehensive analysis and discussion in this paper will contribute to the advancement of VBDA technology and its successful integration into practical FSO systems.

Table 3. The platform/link types have applied VBDA technology.

Link Types	Year	Major Contribution	Ref
Ground terminal platform - Ground terminal platform	2003	Proposed a function which incorporates building sway statistics, system parameters, and the required BER to minimize transmitter power. The function achieved this optimization by optimizing the transmitter gain.	[69]
	2008	Provided closed-form expressions for BER and outage probability (OP) of IM/DD with OOK FSO system. The OBDA was determined by searching and calculating.	[70]
	2013	Analyzed the impact of beam radius and divergence angle on the power design of FSO communication, and the OBDA was determined.	[71,72]
	2016	Derived the OBDA which corresponds to different pointing errors. Found that the system availability can be significantly improved by using the OBDA.	[27]
Ground terminal platform - Air platform	2020	Developed closed-form statistical channel models under log-normal (LN) and gamma–gamma (GG) atmospheric turbulence models. The OBDA, which maximizes the average SNR, was given by searching and analyzing.	[73]
	2021	Through indoor 90 m and outdoor >100 m full-duplex 1.25 Gbps communication experiments, it was found that increasing the beam divergence angle can effectively improve the stability of the communication link.	[63]
	2022	Proposed a PAT system based on quadrant photodiode (QPD) and VBDA mechanism by moving the light source. This PAT system can achieve beacon-free acquisition and shorten the tracking time to 1/4.5 of the original.	[64]
Ground terminal platform - HST platform	2017	This is the first work that compared the narrow and wide beam used in FSO communications for HSTs. A wide beam divergence angle range of [0.07$°$, 2.002$°$] was suggested to relax the steering speed of the FSM, as well as to overcome the negative effects of train vibration.	[74]
	2021	Evaluated the complexity of ground and aerial PAT systems using angular velocity and maximum acceptable delay as two indexes. The results showed that the UAV relay performed better than the ground relay.	[75]
	2022	Obtained the OBDA to maximize the received optical power and thereby reduced the minimum communication distance between a mobile node with a speed of 100 km/h and a fixed terminal from the original 20 m to 5 m.	[9]
	2022	Proposed a strategy of VBDA according to the communication distance for ultra-high-speed trains in evacuated tubes. This strategy reduced the number of base stations and power consumption.	[76]
Surface terminal platform - Underwater platform	2017	Developed a new scanning strategy using VBDA, which decreased the acquisition time by 80% in simulation. The robust acquisition and tracking with only navar-received optical power have been successfully demonstrated.	[8]
Air platform - Air platform	2008	Found that the OBDA was 1.4 times the angular size of the combination of the certainty area and jitter. In this case, the attenuation caused by geometrical and pointing loss was the smallest.	[55]
	2009	Compared the transmission distances for the systems equipped with VBDA mechanism (A and B) and a system with fixed-beam divergence angle (C). The A and B showed a significant improvement in the maximum transmission distance compared to system C, which was increased from 2 km to 10 km.	[10]
	2013	Derived the expression of OP, differentiated it with respect to the divergence angle, and gave the expression of the OBDA which minimized the OP.	[77]
	2018	Used a generalized two-dimensional Gaussian distribution to represent the pointing error, and a closed-form expression of OBDA was derived under two strategies (maximizing link availability and minimizing transmitter power).	[26]
	2019	Provided a closed-form expression for the OBDA which minimized the OP. A zoom lens was used to adjust the beam size, thereby alleviating the performance degradation caused by angle of arrival (AoA) fluctuations and pointing errors.	[78,79]
	2020	Derived closed-form expressions of link availability and OBDA. Additionally, the system’s tolerance to AoA fluctuations was increased by 2 times by using VBDA control technology on a 104 m 10 Gb/s FSO link.	[80]
Air platform - Satellite platform	2009	Derived a closed-form solution for the transmit gain which minimized the link OP.	[81]
Satellite platform - Satellite platform	2016	Created a square approximation of the circular detector region to derive a simple algebraic solution for the OBDA and concluded that the communication quality with a dynamic divergence control scheme was much better than that with a fixed divergence control scheme.	[25]
	2017	The effect of pointing error on the average ABEP of intersatellite optical communication link was studied and gave a closed-form expression for calculating the instantaneous channel gain using the Marcum Q-function.	[82]
	2018	Provided a closed-form expression for calculating the instantaneous channel state by using the Marcum Q-function, without any approximations. Additionally, a simple algebraic expression for the optimal beam waist radius was derived, under the condition that the instantaneous aiming error angle was known.	[83]
	2020	Gave the best waist width expression to minimize the average BER for LEO satellites in the 100 kg class; the expression was approximated by using the asymptotic form of the improved Bessel function.	[84]
	2020	Proposed numerical and analytical methods of the channel gain which based on the Marcum Q-function and obtained an accurate approximation of the optimal waist width to achieve the best LEO-to-GEO communication performance.	[85]
	2022	Determined the OBDA by the attitude error, load pointing error, positioning error, and real-time link distance between satellites and gave the corresponding beam divergence angle control scheme.	[39]
Others	2008	Compared the impact of the VBDA scheme and fixed divergence angle scheme on BER and link availability. In the VBDA scheme, a small number of discrete beam divergence angles were set to balance the performance and complexity of the system well.	[86]
	2010	Derived a closed-form expression for the average channel capacity, and the OBDA to maximize the average channel capacity under different pointing errors and different wavelengths was given by search and calculation analysis.	[87]
	2011	Gave the average BER and the corresponding OBDA for the uncoded and coded systems, respectively. The authors found that the OBDA of coded FSO communication system was smaller than that of uncoded system.	[88]
	2012	Studied the relationship between the OBDA and the transmitted optical power and the communication distance and found that the OBDA was much more affected by the communication distance than the transmitted optical power.	[89]
	2012	Used the simulation package OptSim to study the Q-factor, BER, and Eye Map at different divergence angles from 0.1–3 mrad. The results showed that the link could withstand greater attenuation by reducing the beam divergence angle.	[90]
	2013	Simulated and analyzed the influence of different beam divergence angles on the received optical power and the mitigation effect on transmitter tilt in short-range FSO communication. The authors proposed the need for a trade-off between the received optical power and the mitigation effect on transmitter tilt.	[91]
	2014	Derived the calculation formula of the OBDA, and it was found that the maximum allowable pointing error could be increased by 121% when the beam was adjusted to the OBDA.	[92]
	2015	Gave the formula of the required transmitted optical power corresponding to the beam radius of the receiver and obtained the OBDA which minimized the transmitted optical power.	[93]
	2015	Gave the formula of the maximum allowable pointing error varying with beam divergence angle under different transmitting optical power and obtained the OBDA.	[94]
	2017	Derived the closed-form expressions for the channel capacity of the direct detection system and the coherent detection system, and the OBDA which maximized the channel capacity under different turbulence conditions was given by searching and calculating methods.	[95]
	2021	Expressed the OBDA as a closed-form function of the random displacement statistics of the target, in order to maintain sufficient average power and reduce the outage probability; this provided an idea for the system design.	[23]

4. Challenges and Future Work

This paper provides a comprehensive overview of various VBDA methods used in FSO communication, focusing on the advantages and disadvantages of different methods. It also sorts out the research on the use of VBDA methods for different link types. Despite significant advances in VBDA technology, several challenges still remain. To address these challenges, we propose several promising research directions and provide potential measures for overcoming these challenges, which will be discussed below.

4.1. Reduce the Computational Cost of OBDA

Computing the OBDA involves complex mathematical calculations and requires a large amount of computing resources, which would consume considerable power. This presents a significant challenge for FSO communication remote nodes with limited SWaP budgets. To promote the widespread adoption of FSO communication on various platforms, the computational cost of OBDA must be reduced to some extent. Potential measures for overcoming this challenge are shown below:

• Algorithm Optimization: Use different algorithms of varying complexity to compute the OBDA for different types of terminals. Large communication terminals, such as ground stations, can use relatively complex and advanced OBDA algorithms due to their high tolerance for high computing costs. For remote small units, relatively simple OBDA algorithms can be used, and the computational accuracy can be appropriately reduced to alleviate the computational pressure;
• Distributed Computing: Assign the task of computing the OBDA for each communication party to a node with powerful computing capabilities. And the computing results are then transmitted to the remote communication node via FSO communication or RF link. This measure could reduce the computational burden and power consumption of small communication nodes. However, it introduces additional delay. Therefore, it is essential to comprehensively consider the capabilities of terminal and relay equipment, communication environment, and application requirements to achieve optimal performance and efficiency;
• Machine Learning Techniques: Utilize machine learning to improve the accuracy and efficiency of the OBDA algorithm. By leveraging the complex relationship between the link factors and OBDA, machine learning can improve accuracy and efficiency, resulting in reduced computational costs. In addition, neural network hardware accelerators combined with field-programmable gate array (FPGA) can be reconfigured for different target applications while maintaining low power consumption. This measure leverages the ability of FPGA parallel computing to achieve low-delay processing.

By implementing these measures, the computational cost of OBDA can be reduced, leading to lower power consumption. This can enable FSO communication on platforms with limited power supplies and facilitate its proliferation in various scenarios, such as military operations, disaster relief, and remote sensing applications.

4.2. Achieve Better Reliability and Environmental Adaptability

FSO communication terminals must operate in a wide range of environments, including varying temperatures, humidity levels, and vibrations. As a result, there are high expectations for the reliability and adaptability of the VBDA system. Temperature, in particular, is a crucial factor that affects the system’s performance. For instance, reference [40] reported that the beam’s divergence angle was 7.5 times wider than expected at −30 °C and 4.7 times wider than expected at 60 °C. Therefore, designing and manufacturing a VBDA mechanism with strong environmental adaptability and temperature insensitivity is of great significance. Various measures can be used to achieve this goal, such as:

• Reducing the impact of temperature: There are two ways to approach this issue. ① Selecting materials with low thermal expansion coefficients. This helps to maintain the stability and performance of the VBDA mechanism across a wide range of temperatures. ② Adding a temperature compensation mechanism. This compensates for any thermal-induced changes, ensuring the VBDA mechanism remains within the appropriate temperature range;
• Real-time measurement of transmitted beam divergence angle: By continuously measuring the beam divergence angle in real time, feedback can be provided to the VBDA mechanism. This feedback can be adjusted immediately to compensate for changes caused by temperature fluctuations, ensuring accurate beam alignment and reliable communication;
• Performing temperature tests and creating a lookup table: Conducting temperature tests on the VBDA mechanism helps to understand its performance characteristics under different temperature conditions. Based on the results, a lookup table can be created that maps temperature variations to the corresponding correction values for the beam divergence angle. This lookup table can then be used to apply real-time corrections during operation, compensating for the effects of temperature changes.

These examples demonstrate various approaches to enhance the reliability and environmental adaptability of the VBDA mechanism in FSO communication terminals. By implementing such measures, the performance of the system can be improved, resulting in more effective and dependable communication capabilities.

4.3. Reduce Hardware Costs

While VBDA technology has been successfully verified in experiments [8,38,40,49,50,51,52,53,54,56,58,63,64,65,68], it has not yet been commercialized on a large scale. Therefore, it is necessary to consider the challenges and opportunities associated with scaling up the technology. One critical factor in making this technology more accessible and appealing to potential users is to reduce its cost. Several measures can be employed to achieve this goal.

• Modular design: Implement a modular design for the VBDA system, where different components are divided into modules that can be easily replaced when a failure occurs. This can significantly reduce the cost of maintenance and repair, improving the system’s overall maintainability. Additionally, by adding new modules, the system’s functionality can be easily extended without significantly affecting its overall design. This makes the system more adaptable and able to meet various application scenarios and requirements;
• Design for Manufacturing (DFM): The design should apply principles that prioritize ease of manufacturing and assembly. It should be simplified to reduce the number of complex parts and manufacturing steps. The use of materials should be optimized to minimize waste and lower production costs. It is important to ensure that the design is compatible with existing manufacturing processes and technologies, thereby avoiding the need for expensive production modifications;
• Utilize commercially manufactured components: Consider using commercially available components to minimize the number of unique parts needed. This can significantly reduce the costs and time associated with producing custom components. Commercial components are often mass produced and have established quality standards, which ensure the reliability and consistency of the final product.

It is important to note that reducing the cost of this technology should not come at the expense of its quality and performance. Maintaining a high standard of performance and reliability is essential to ensure that VBDA technology meets the needs and expectations of users. By addressing this challenge, researchers and industry professionals can unlock the potential of this innovative technology and create new opportunities for growth and innovation.

4.4. Other Future Trends

In addition to the above trends, VBDA technology can be combined with other technologies in FSO communication to achieve better performance. For example:

4.4.1. To Realize UAV Swarm Communication and Positioning under Electromagnetic Suppression Conditions

During UAV swarm flight on the battlefield, the communication and navigation systems may be disrupted by electromagnetic suppression, which may result in failure. To maintain the safety and stability of the swarm, the VBDA system can be used for communication and navigation at different distances. For instance, when swarm members are closer together, the beam divergence angle can be increased to cover uncertain areas. However, when the leader directs the swarm members to depart from the swarm to perform independent tasks, the beam divergence angle can be reduced to maintain communication under the increasing communication distance. This flexibility enhances the ability of UAV swarm to perform a wide range of operations.

4.4.2. Applied to Quantum Key Distribution (QKD)

VBDA technology can be applied to QKD to improve its performance. QKD is a novel cryptographic technique used to establish private encryption keys. One of the challenges of QKD is the loss of photons during transmission, which would reduce the signal-to-noise ratio (SNR) and transmission distance [96,97]. The use of VBDA can help reduce this loss by adjusting the beam divergence angle based on the communication distance and the link quality, thereby improving the received optical power. This can enable secure distribution of quantum keys over longer communication distances.

4.4.3. Applied to MIMO

Multiple-input multiple-output (MIMO) technology achieves diversity through the use of multiple-transmit and receive antennas, which improves the SNR at the receiver and minimizes the outage probability [98]. Because the impact of spot quality variations on the receiving end can vary significantly [99,100,101], VBDA technology can be applied to MIMO to adjust the beam divergence angle and optical power of multiple transmitting inputs, achieving a good compromise between link availability and communication rate. For example, the dartboard scheme proposed in reference [102] uses two concentric laser beams with different divergence angles for superposition, significantly improving the average data rate of the link. Simulations showed that, at 10 dBm transmit power, the dartboard scheme provides 53% higher data rate than 4-level pulse-amplitude modulation (4-PAM) and 79% higher than OOK. Therefore, VBDA technology can be applied to MIMO in FSO communication in the future to further improve the performance and reliability of the communication link.

5. Conclusions

This paper organizes a comprehensive overview of various VBDA techniques used in FSO communication. It mainly contains the following content:

• Explanation of the application significance of VBDA technology in FSO communication, emphasizing its ability to enhance system performance in terms of higher acquisition probability, greater tracking ability, larger communication link range, and lower power consumption;
• Introduction to the transmission theory of Gaussian beams and the basic principle of the VBDA method, laying the foundation for the following discussion;
• In-depth research on different types of VBDA methods, including:

  a.

  Using zoom groups or axial translation of fiber or lens: This method has the advantage of mature zoom lens groups technology and simple principles. However, it requires high-quality guide rails and actuators;

  b.

  Using zoom lenses: This method has the advantages of having no mechanical mechanism and being small in size, but the system may be affected by gravity, and enlarging the aperture may be difficult;

  c.

  Using lenses with different F or inserting parallel plates: These methods, respectively, have the advantage of simplicity and can greatly relax the requirement for lateral positioning accuracy. However, the communication link will experience an outage when switching angles;

  d.

  Using an optical wedge-pair: The advantage is that the influence on the optical axis deflection is small. However, a trade-off must be made between the VBDA range and larger astigmatism;

  e.

  The research on using VBDA technologies for different types of links and how they can enhance performance.

These characteristics require the appropriate choose of VBDA method for the given FSO link situation and communication terminal conditions. Factors such as power consumption, beam quality, cost, and environmental robustness must be carefully considered;

4.

Emphasis on the challenges faced by VBDA technology and potential future research directions.

The comprehensive analysis and discussion provided in the paper aim to contribute to the advancement of VBDA technology and its successful integration into practical FSO systems.