Study on the Difference of Wavefront Distortion on Beams Caused by Wavelength Differences in Weak Turbulence Region
Abstract
1. Introduction
2. Theory
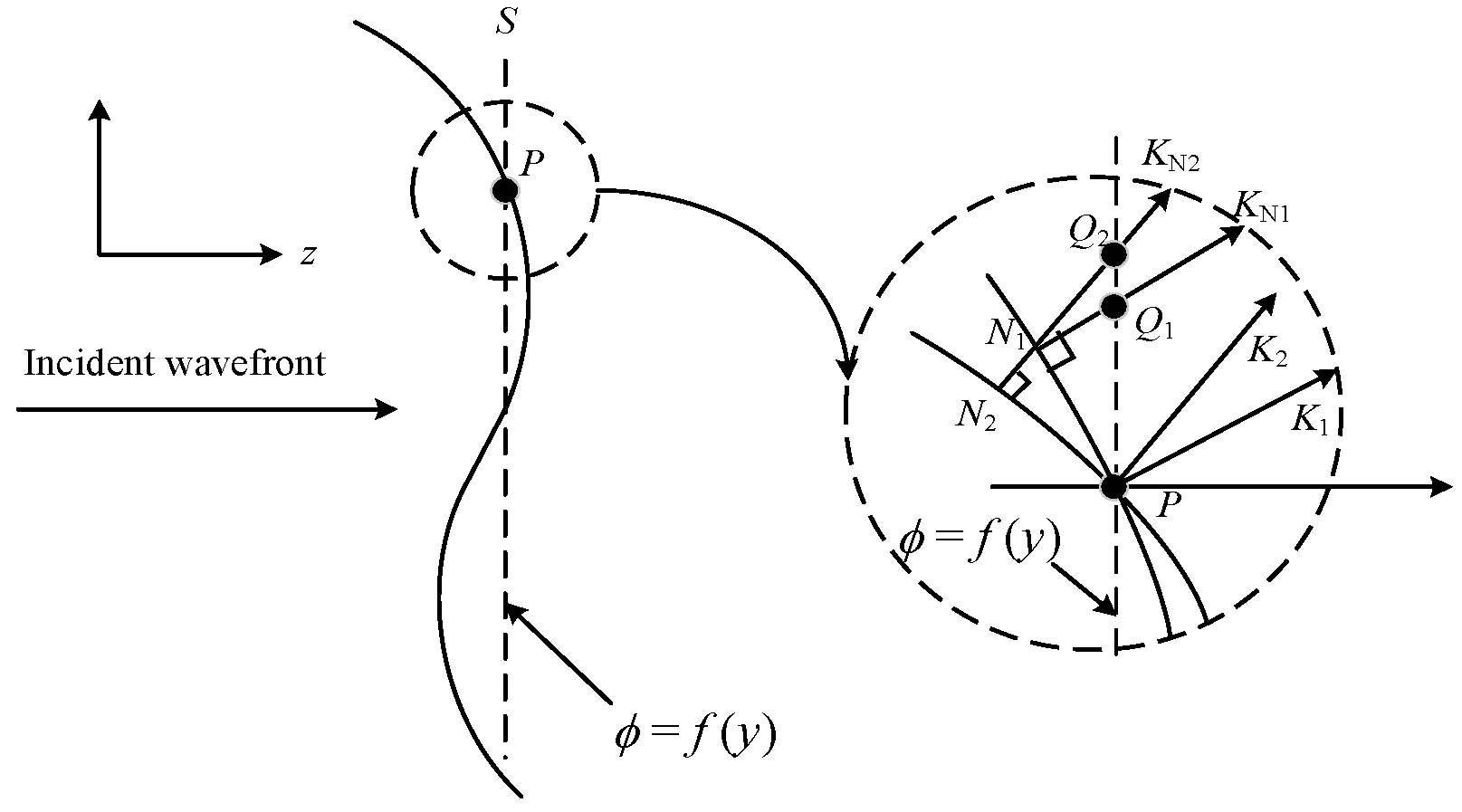
2.1. Correlation Function of the AOA Fluctuation at Different Wavelengths
2.2. Phase Relationship between Gaussian Beams of Different Wavelengths
3. Simulation
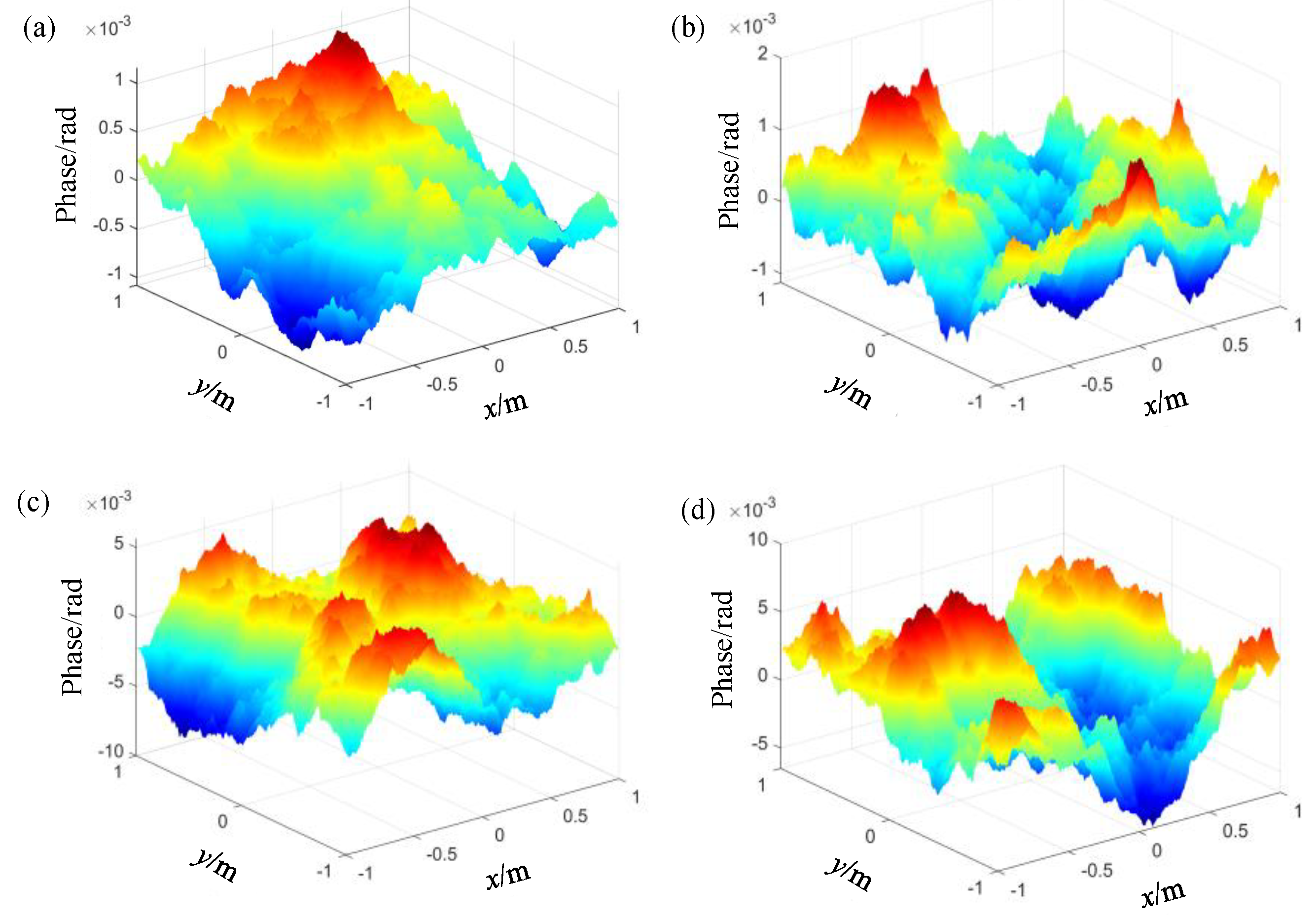
3.1. Propagation Characteristics of Gaussian Beams with Different Wavelengths in the Same Atmospheric Channel
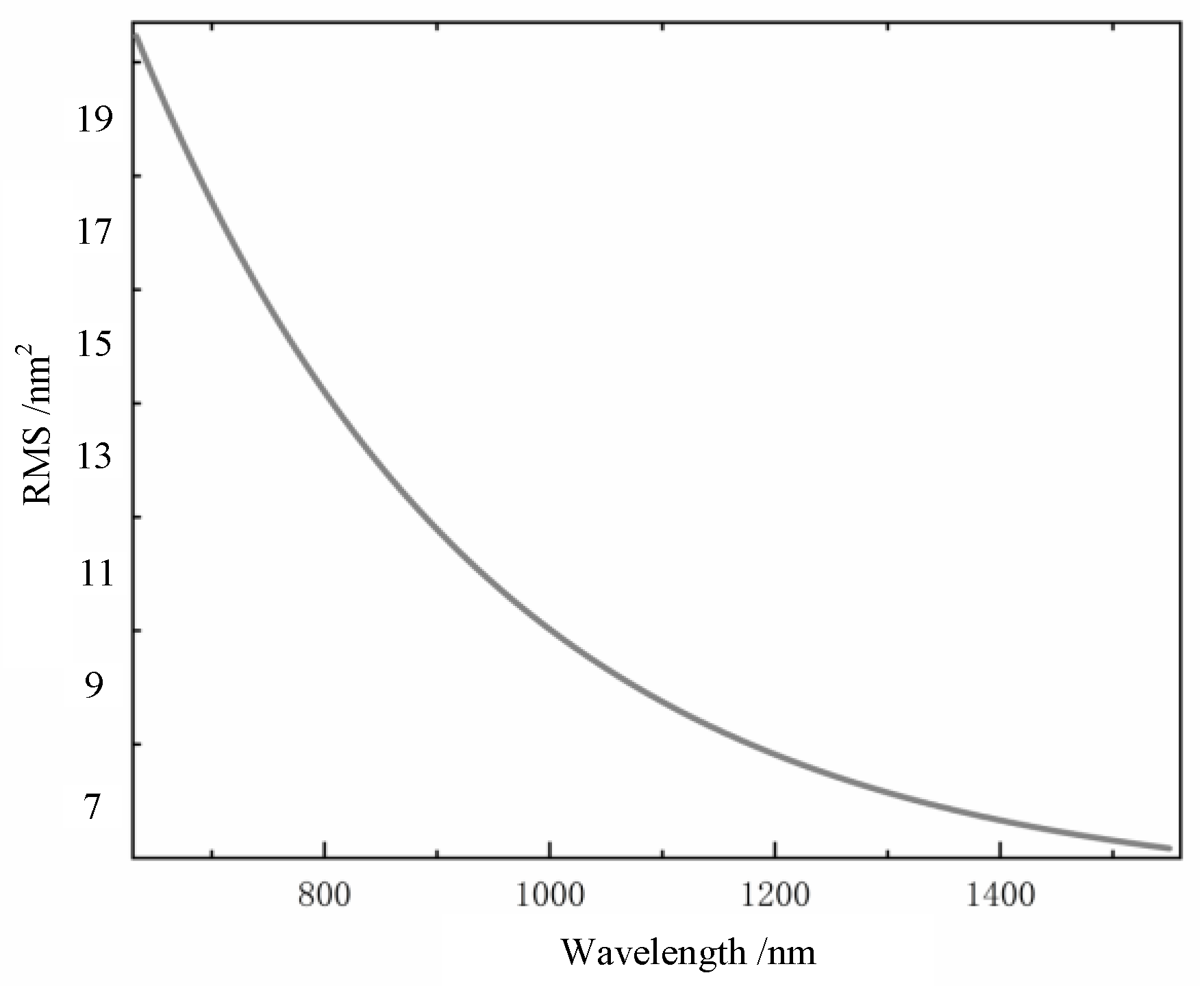
3.2. Correlation of Variance of the Arrival Angle Fluctuation of Gaussian Beams with Different Wavelengths
4. Experiment
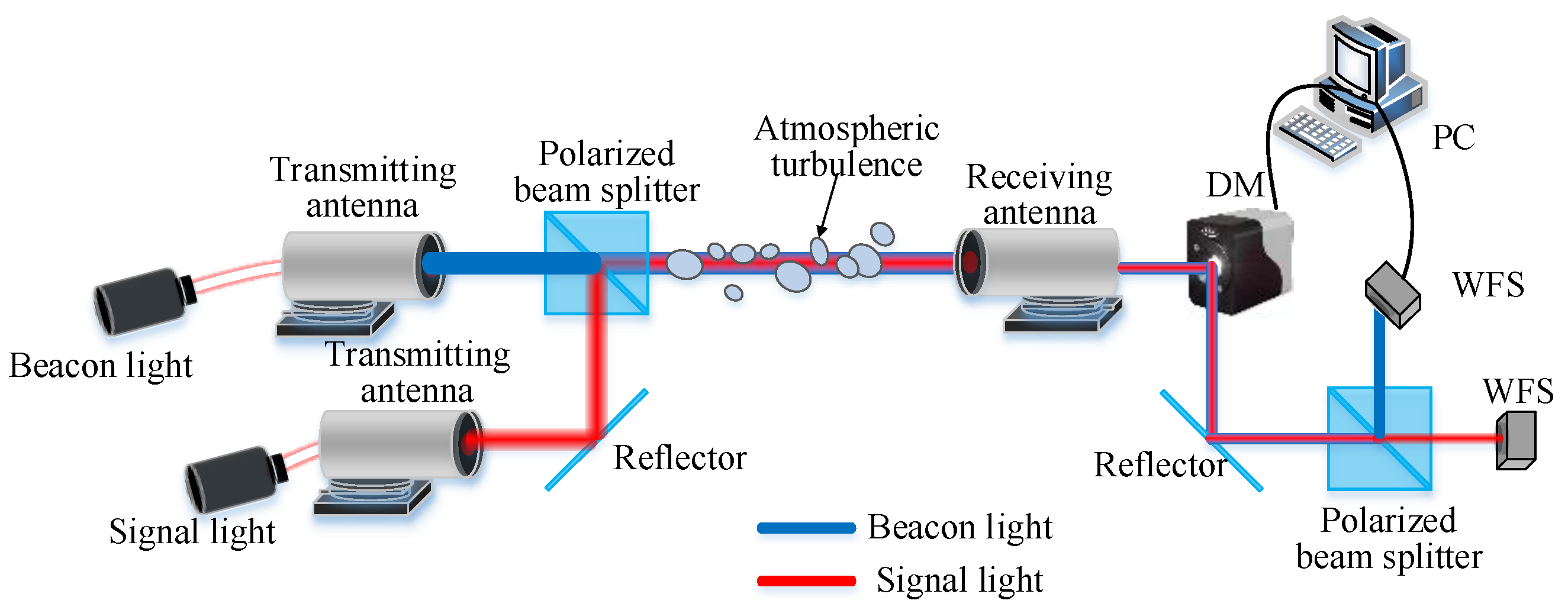
4.1. Wavefront Distortion Correction Compensation for a Dual-Wavelength FSO Communication System
4.2. Experimental Device
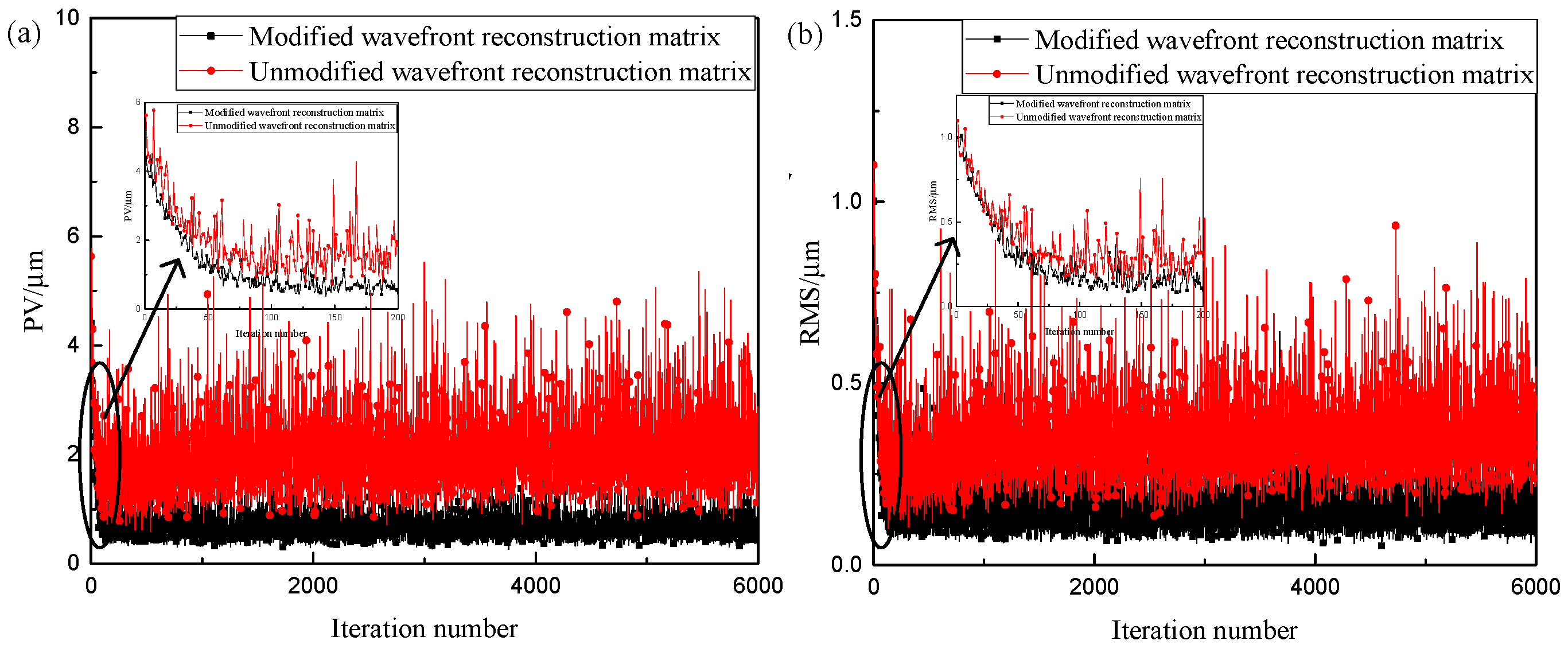
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Wei, D.; Wroblowski, O.; Chen, Q.; Mantel, K.; Olschewski, F.; Kaufmann, M.; Riese, M. Analysis and correction of distortions in a spatial heterodyne spectrometer system. Appl. Opt. 2019, 58, 2190–2197. [Google Scholar] [CrossRef]
- Wu, J.; Ke, X. Development of adaptive optical correction and polarization control modules for 10-km free-space coherent optical communications. J. Mod. Opt. 2019, 67, 1–7. [Google Scholar]
- Zhang, J.; Masouros, C. Beam drift in millimeter wave links: Beamwidth tradeoffs and learning based optimization. IEEE Trans. Commun. 2021, 69, 6661–6674. [Google Scholar] [CrossRef]
- Baykal, Y. Adaptive optics corrections of scintillations of Hermite–Gaussian modes in an oceanic medium. Appl. Opt. 2020, 59, 4826–4832. [Google Scholar] [CrossRef]
- Li, M.; Cvijetic, M. Coherent free space optics communications over the maritime atmosphere with use of adaptive optics for beam wavefront correction. Appl. Opt. 2015, 54, 1453–1462. [Google Scholar] [CrossRef]
- Li, M.; Gao, W.; Cvijetic, M. Slant-path coherent free space optical communications over the maritime and terrestrial atmospheres with the use of adaptive optics for beam wavefront correction. Appl. Opt. 2017, 56, 284–297. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, S.E.; Kong, Y.J. Performance prediction of a laser-guide star adaptive optics system for a 1.6 m telescope. Curr. Opt. Photonics 2018, 2, 269–279. [Google Scholar]
- Yang, S.; Ke, X.; Wu, J.; Ding, D. Dual-mirror adaptive-optics fiber coupling for free-space coherent optical communication. Opt. Eng. 2021, 60, 076109. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, S.; Tan, L.; Ma, J. Approach for recognizing and tracking beacon in inter-satellite optical communication based on optical flow method. Opt. Express 2018, 26, 28080–28090. [Google Scholar] [CrossRef]
- Jian, H.; Kai, W.; Kai, J.; Gongchang, W.; Min, L.; Yudong, Z. Study on spot size and photo return of a sodium laser guide star. Infrared Laser Eng. 2019, 48, 0106004. [Google Scholar] [CrossRef]
- Shen, F.; Jiang, W.H. Modal decomposition of anisoplanatic error of atmospheric turbulence for a laser guide star. Acta Opt. Sin. 2003, 23, 348–355. [Google Scholar]
- Luo, X.; Li, X.Y. Investigation of anisoplanatic effect in atmospheric turbulence probing with beaconⅠ: Numerical modeling. Chin. J. Lasers 2014, 41, 232–241. [Google Scholar]
- Han, Y.; Yang, C.P. Study on geometric method for angle-of-arrival distribution according to phase fluctuation. Laser Technol. 2008, 32, 534–535. [Google Scholar]
- Gao, C.; Tan, L.Y.; Ma, J. Experimental research of angle-of-arrival fluctuations in free-space optical communications. High Power Laser Part. Beams 2007, 19, 177–181. [Google Scholar]
- Toselli, I.; Andrews, L.C.; Phillips, R.L.; Ferrero, V. Angle of arrival fluctuations for free space laser beam propagation through non kolmogorov turbulence. In Proceedings of the SPIE 6551, Atmospheric Propagation IV, Orlando, FL, USA, 11–12 July 2007; pp. 149–160. [Google Scholar]
- Voelz, D.; Wijerathna, E.; Muschinski, A.; Xiao, X. Computer simulations of optical turbulence in the weak- and strong-scattering regime: Angle-of-arrival fluctuations obtained from ray optics and wave optics. Opt. Eng. 2018, 57, 102–104. [Google Scholar] [CrossRef]
- Conan, R.; Borgnino, J.; Ziad, A.; Martin, F. Analytical solution for the covariance and for the decorrelation time of the angle of arrival of a wave front corrugated by atmospheric turbulence. JOSA A 2000, 17, 1807–1818. [Google Scholar] [CrossRef]
- Ben-Yosef, N.N.; Goldner, E.; Weitz, A. Two-color correlation of scintillations. Appl. Opt. 1986, 25, 3486–3489. [Google Scholar] [CrossRef]
- Gorelaya, A.V.; Shubenkova, E.V.; Dmitriev, D.I.; Dmitrieva, A.D.; Kudryashov, A.V.; Lovchiy, I.L.; Shalymov, E.V.; Sheldakova, Y.V.; Tsvetkov, A.D.; Venediktov, D.V.; et al. Investigation of dual-wavelength laser beam propagation along the in-door atmospheric path. In Proceedings of the SPIE 9641, Optics in Atmospheric Propagation and Adaptive Systems XVIII, Amsterdam, The Netherlands, 22 September 2014; p. 96410C. [Google Scholar]
- Li, F.; Rong, J.; Zhong, X.-C.; Ding, X.-K. Study on correcting angle-of-arrival fluctuations of space optical communication with AO. In Proceedings of the Second International Conference on Space Information Technology, Wuhan, China, 10 November 2007; pp. 141–146. [Google Scholar]
- Kibblewhite, E.J.; Chun, M.R. Design of tip-tilt and adaptive optics servos using measured angle-of-arrival and phase power spectra. Adapt. Opt. Syst. Technol. SPIE 1998, 33, 522–530. [Google Scholar]
- Lukin, V.P. Efficiency of some correction systems. Opt. Lett. 1979, 4, 15–17. [Google Scholar] [CrossRef]
- Jolissaint, L.; Kendrew, S. Modeling the Chromatic Correction Error in Adaptive Optics: Application to the Case of Mid-Infrared Observations in Dry to Wet Atmospheric Conditions. In Proceedings of the 1st AO4ELT Conference—Adaptive Optics for Extremely Large Telescopes, Paris, France, 22–26 June 2009; p. 05021. [Google Scholar]
- Ke, X.Z.; Chen, X.Z. Correcting wavefront distortion of dual-wavelength beams due to atmospheric turbulence with a correction coefficient. Opt. Photonics J. 2020, 10, 64–77. [Google Scholar] [CrossRef]
- Zhang, Y.X. Arrival Angle of Beam Wave Propagation in Turbulent Atmosphere. Chin. J. Quantum Electron. 1987, 12, 70–75. [Google Scholar]
- Goodman, J.W.; Qin, K.C. Statistical Optics, 1st ed.; Science Press: Beijing, China, 1992; pp. 132–134. [Google Scholar]
- Liu, Z.-W.; Li, Z.-D.; Zhou, Z.-Q.; Yuan, X.-W. Adaptive optics correction technique based onfuzzy control. Acta Phys. Sin. 2016, 65, 014206. [Google Scholar]






| Device | Type | Parameters |
|---|---|---|
| Wavefront Sensor | THORLABS-HASO4-NIR | Wavelength range: 1500–1600 nm Number of micro-lenses: 32 × 40 |
| Wavefront Sensor | THORLABS-HASO4-FIRST | Wavelength range: 400–1100 nm Number of micro-lenses: 32 × 40 |
| Beacon Laser | MW-GX-650 | Wavelength: 650 nm, linewidth: 0–3 nm, output power: 35 mW |
| Signal Laser | KOHERA-BASIK Module | Wavelength: 1550 nm, linewidth: 0.1 kHz, output power: 0–200 mW |
| Deformable Mirror | ALPAO-DM | Actuator number: 69, effective aperture: 10.5 mm, frequency: 800 Hz |
| Antenna | Maksutov–Cassegrain | Diameter: 25 mm, focal length: 300 mm |
| Laser Collimator | F810APC | Wavelength: 1550 nm/650 nm, focal length: 37.13 mm |
| Open-Loop Value | Closed-Loop Value | Mean Value | Variance Value | |
|---|---|---|---|---|
| Unmodified wavefront PV | 5.63 μm | 1.78 μm | 2.05 μm | 0.46 μm2 |
| Unmodified wavefront RMS | 1.10 μm2 | 0.24 μm2 | 0.35 μm2 | 0.01 μm2 |
| Modified wavefront PV | 4.41 μm | 0.51 μm | 0.69 μm | 0.08 μm2 |
| Modified wavefront RMS | 1.01 μm2 | 0.11 μm2 | 0.16 μm2 | 0.005 μm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Ke, X.; Kang, W.; Liang, J.; Ke, C. Study on the Difference of Wavefront Distortion on Beams Caused by Wavelength Differences in Weak Turbulence Region. Photonics 2023, 10, 725. https://doi.org/10.3390/photonics10070725
Wu J, Ke X, Kang W, Liang J, Ke C. Study on the Difference of Wavefront Distortion on Beams Caused by Wavelength Differences in Weak Turbulence Region. Photonics. 2023; 10(7):725. https://doi.org/10.3390/photonics10070725
Chicago/Turabian StyleWu, Jiali, Xizheng Ke, Weilong Kang, Jingyuan Liang, and Chenghu Ke. 2023. "Study on the Difference of Wavefront Distortion on Beams Caused by Wavelength Differences in Weak Turbulence Region" Photonics 10, no. 7: 725. https://doi.org/10.3390/photonics10070725
APA StyleWu, J., Ke, X., Kang, W., Liang, J., & Ke, C. (2023). Study on the Difference of Wavefront Distortion on Beams Caused by Wavelength Differences in Weak Turbulence Region. Photonics, 10(7), 725. https://doi.org/10.3390/photonics10070725





