TSDSR: Temporal–Spatial Domain Denoise Super-Resolution Photon-Efficient 3D Reconstruction by Deep Learning
Abstract
1. Introduction
2. Related Work
2.1. Reconstruction Photon-Efficient Imaging
2.2. Single-Image Super-Resolution
3. Method
3.1. Forward Model
3.2. Network Architecture
3.2.1. Generator
3.2.2. Discriminator
3.2.3. Loss Function
4. Experiments
4.1. Dataset and Training Detail
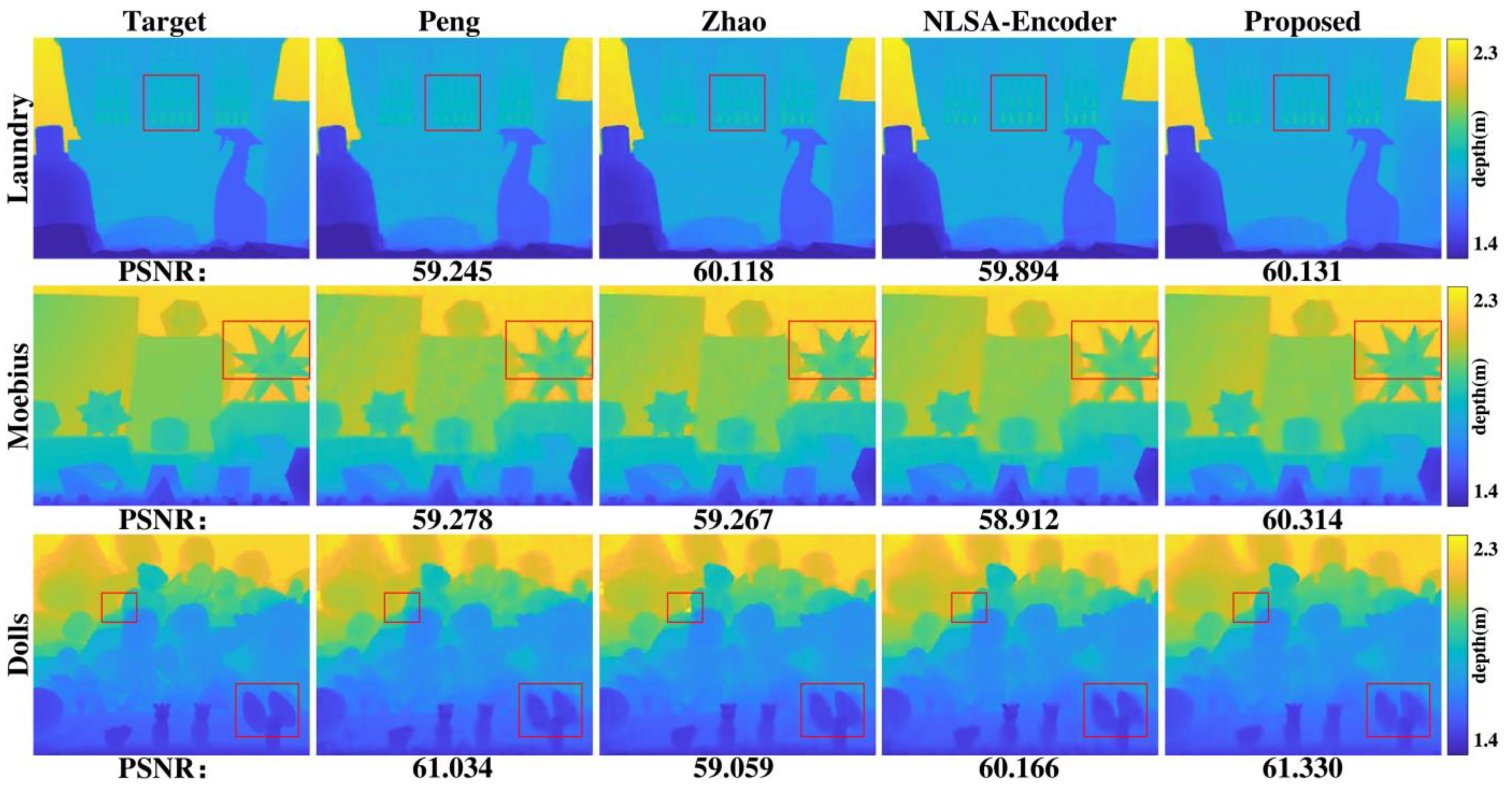
4.2. Numerical Simulation
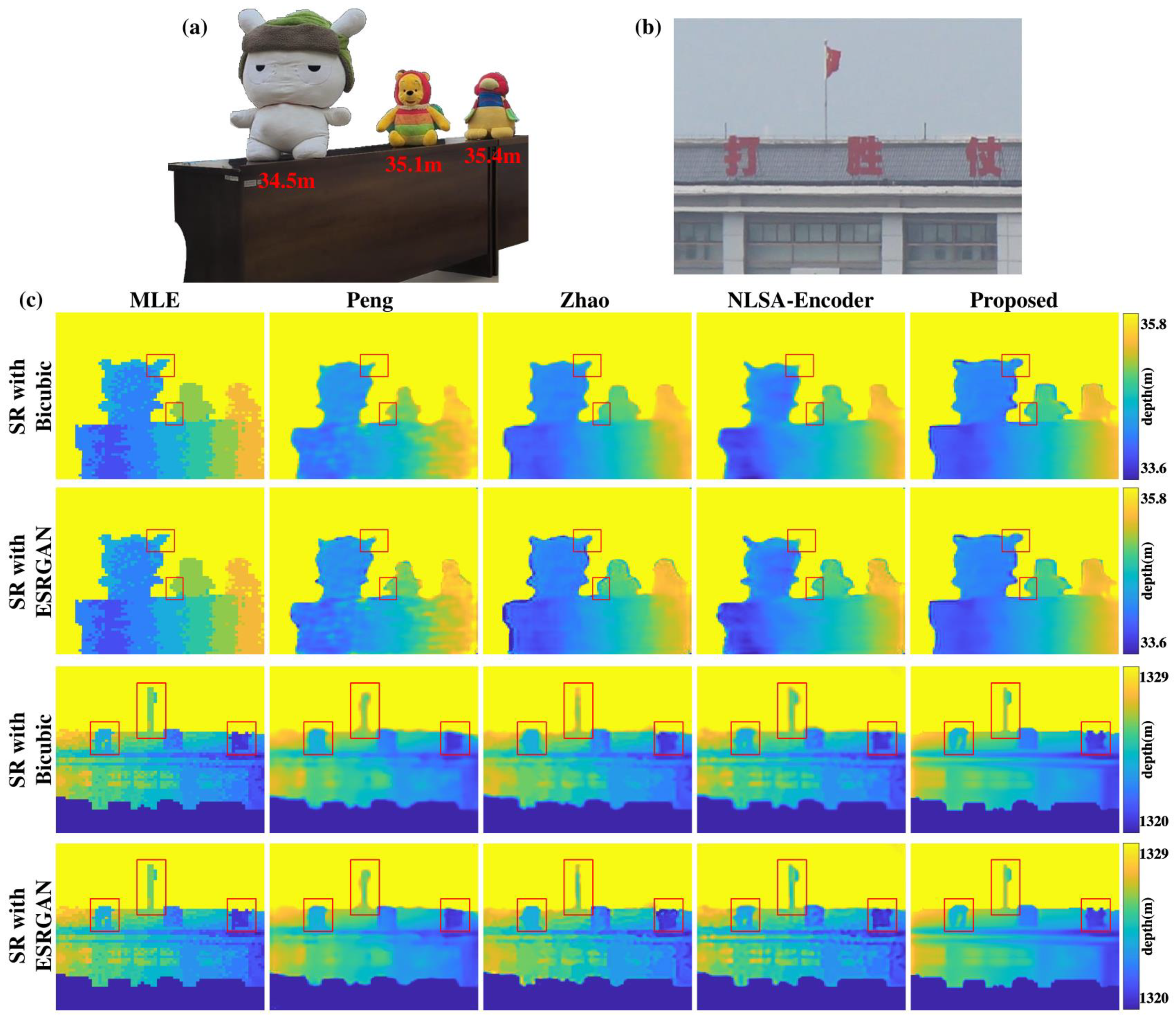
4.3. Real-World Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.-P.; Ye, J.-T.; Huang, X.; Jiang, P.-Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-Photon Imaging over 200 km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Yang, J.; Li, J.; He, S.; Wang, L.V. Angular-Spectrum Modeling of Focusing Light inside Scattering Media by Optical Phase Conjugation. Optica 2019, 6, 250–256. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; McCarthy, A.; Ren, X.; Warburton, R.E.; Wallace, A.M.; Moffat, J.; Petillot, Y.; Buller, G.S. Underwater Depth Imaging Using Time-Correlated Single-Photon Counting. Opt. Express 2015, 23, 33911–33926. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.A.; Grant, L.A.; Henderson, R.K. Low Dark Count Single-Photon Avalanche Diode Structure Compatible With Standard Nanometer Scale CMOS Technology. IEEE Photonics Technol. Lett. 2009, 21, 1020–1022. [Google Scholar] [CrossRef]
- Shin, D.; Kirmani, A.; Goyal, V.K.; Shapiro, J.H. Photon-Efficient Computational 3-D and Reflectivity Imaging With Single-Photon Detectors. IEEE Trans. Comput. Imaging 2015, 1, 112–125. [Google Scholar] [CrossRef]
- Shin, D.; Xu, F.; Venkatraman, D.; Lussana, R.; Villa, F.; Zappa, F.; Goyal, V.K.; Wong, F.N.C.; Shapiro, J.H. Photon-Efficient Imaging with a Single-Photon Camera. Nat. Commun. 2016, 7, 12046. [Google Scholar] [CrossRef] [PubMed]
- Rapp, J.; Goyal, V.K. A Few Photons Among Many: Unmixing Signal and Noise for Photon-Efficient Active Imaging. IEEE Trans. Comput. Imaging 2017, 3, 445–459. [Google Scholar] [CrossRef]
- Halimi, A.; Maccarone, A.; Lamb, R.A.; Buller, G.S.; McLaughlin, S. Robust and Guided Bayesian Reconstruction of Single-Photon 3D Lidar Data: Application to Multispectral and Underwater Imaging. IEEE Trans. Comput. Imaging 2021, 7, 961–974. [Google Scholar] [CrossRef]
- Chen, S.; Halimi, A.; Ren, X.; McCarthy, A.; Su, X.; McLaughlin, S.; Buller, G.S. Learning Non-Local Spatial Correlations To Restore Sparse 3D Single-Photon Data. IEEE Trans. Image Process. 2020, 29, 3119–3131. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yao, G.; Liu, Y.; Su, H.; Hu, X.; Pan, Y. Deep Domain Adversarial Adaptation for Photon-Efficient Imaging. Phys. Rev. Appl. 2022, 18, 54048. [Google Scholar] [CrossRef]
- Lindell, D.B.; O’Toole, M.; Wetzstein, G. Single-Photon 3D Imaging with Deep Sensor Fusion. ACM Trans. Graph. 2018, 37, 111–113. [Google Scholar] [CrossRef]
- Peng, J.; Xiong, Z.; Huang, X.; Li, Z.-P.; Liu, D.; Xu, F. Photon-Efficient 3d Imaging with a Non-Local Neural Network. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Volume 16, pp. 225–241. [Google Scholar]
- Zang, Z.; Xiao, D.; Li, D.D.-U. Non-Fusion Time-Resolved Depth Image Reconstruction Using a Highly Efficient Neural Network Architecture. Opt. Express 2021, 29, 19278–19291. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Jiang, X.; Han, A.; Mao, T.; He, W.; Chen, Q. Photon-Efficient 3D Reconstruction Employing a Edge Enhancement Method. Opt. Express 2022, 30, 1555–1569. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Tong, Z.; Jiang, P.; Xu, L.; Wu, L.; Hu, J.; Yang, C.; Zhang, W.; Zhang, Y.; Zhang, J. Deep-Learning Based Photon-Efficient 3D and Reflectivity Imaging with a 64 64 Single-Photon Avalanche Detector Array. Opt. Express 2022, 30, 32948–32964. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Volume 13, pp. 184–199. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Hussein, S.A.; Tirer, T.; Giryes, R. Correction Filter for Single Image Super-Resolution: Robustifying off-the-Shelf Deep Super-Resolvers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1428–1437. [Google Scholar]
- Wang, L.; Dong, X.; Wang, Y.; Ying, X.; Lin, Z.; An, W.; Guo, Y. Exploring Sparsity in Image Super-Resolution for Efficient Inference. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4917–4926. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European conference on computer vision (ECCV) workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; Zhou, J. Structure-Preserving Super Resolution with Gradient Guidance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7769–7778. [Google Scholar]
- Li, W.; Zhou, K.; Qi, L.; Lu, L.; Lu, J. Best-Buddy Gans for Highly Detailed Image Super-Resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 1412–1420. [Google Scholar]
- Liang, J.; Zeng, H.; Zhang, L. Details or Artifacts: A Locally Discriminative Learning Approach to Realistic Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5657–5666. [Google Scholar]
- Mei, Y.; Fan, Y.; Zhou, Y. Image Super-Resolution with Non-Local Sparse Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3517–3526. [Google Scholar]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Informatics 2019, 16, 4681–4690. [Google Scholar] [CrossRef]
- Schonfeld, E.; Schiele, B.; Khoreva, A. A U-Net Based Discriminator for Generative Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8207–8216. [Google Scholar]
- Houwink, Q.; Kalisvaart, D.; Hung, S.-T.; Cnossen, J.; Fan, D.; Mos, P.; Ülkü, A.C.; Bruschini, C.; Charbon, E.; Smith, C.S. Theoretical Minimum Uncertainty of Single-Molecule Localizations Using a Single-Photon Avalanche Diode Array. Opt. Express 2021, 29, 39920–39929. [Google Scholar] [CrossRef] [PubMed]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor Segmentation and Support Inference from Rgbd Images. ECCV 2012, 7576, 746–760. [Google Scholar]
- Scharstein, D.; Pal, C. Learning Conditional Random Fields for Stereo. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Wang, Z.; Bovik, A.C. A Universal Image Quality Index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]





| SBR | RMSE | Accuracy (δ = 1.03) | ||||||
| Peng | Zhao | NSE | Proposed | Peng | Zhao | NSE | Proposed | |
| 10:2 | 0.0205 | 0.0174 | 0.0211 | 0.0189 | 0.9763 | 0.9786 | 0.9798 | 0.9788 |
| 10:10 | 0.0204 | 0.0177 | 0.0211 | 0.0191 | 0.9759 | 0.9785 | 0.9796 | 0.9789 |
| 10:50 | 0.0207 | 0.0198 | 0.0213 | 0.0194 | 0.9759 | 0.9779 | 0.9791 | 0.9784 |
| 5:2 | 0.0218 | 0.0189 | 0.0214 | 0.0201 | 0.9743 | 0.9770 | 0.9781 | 0.9783 |
| 5:10 | 0.0220 | 0.0212 | 0.0217 | 0.0205 | 0.9740 | 0.9765 | 0.9770 | 0.9783 |
| 5:50 | 0.0233 | 0.0278 | 0.0229 | 0.0217 | 0.9723 | 0.9698 | 0.9747 | 0.9771 |
| 2:2 | 0.0245 | 0.0232 | 0.0234 | 0.0224 | 0.9694 | 0.9720 | 0.9739 | 0.9756 |
| 2:10 | 0.0262 | 0.0355 | 0.0248 | 0.0241 | 0.9660 | 0.9672 | 0.9700 | 0.9728 |
| 2:50 | 0.0318 | 0.0364 | 0.0308 | 0.0304 | 0.9534 | 0.9624 | 0.9538 | 0.9592 |
| AVG | 0.0235 | 0.0242 | 0.0232 | 0.0218 | 0.9708 | 0.9733 | 0.9740 | 0.9753 |
| SBR | PSNR | UIQI | ||||||
| Peng | Zhao | NSE | Proposed | Peng | Zhao | NSE | Proposed | |
| 10:2 | 60.729 | 62.188 | 61.009 | 61.192 | 0.9791 | 0.9825 | 0.9811 | 0.9823 |
| 10:10 | 60.691 | 62.119 | 60.837 | 61.194 | 0.9788 | 0.9835 | 0.9813 | 0.9831 |
| 10:50 | 60.316 | 58.082 | 60.644 | 60.757 | 0.9740 | 0.9803 | 0.9804 | 0.9809 |
| 5:2 | 59.874 | 60.159 | 60.265 | 60.903 | 0.9758 | 0.9799 | 0.9792 | 0.9813 |
| 5:10 | 59.780 | 57.824 | 59.973 | 60.661 | 0.9752 | 0.9781 | 0.9790 | 0.9805 |
| 5:50 | 59.004 | 57.576 | 59.336 | 59.926 | 0.9717 | 0.9705 | 0.9760 | 0.9786 |
| 2:2 | 58.219 | 58.753 | 58.933 | 59.616 | 0.9692 | 0.9727 | 0.9752 | 0.9761 |
| 2:10 | 57.465 | 55.249 | 58.062 | 58.388 | 0.9649 | 0.9563 | 0.9696 | 0.9717 |
| 2:50 | 55.093 | 54.574 | 55.415 | 55.264 | 0.9492 | 0.9508 | 0.9523 | 0.9524 |
| AVG | 59.019 | 58.503 | 59.386 | 59.767 | 0.9709 | 0.9727 | 0.9749 | 0.9763 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Z.; Jiang, X.; Hu, J.; Xu, L.; Wu, L.; Yang, X.; Zou, B. TSDSR: Temporal–Spatial Domain Denoise Super-Resolution Photon-Efficient 3D Reconstruction by Deep Learning. Photonics 2023, 10, 744. https://doi.org/10.3390/photonics10070744
Tong Z, Jiang X, Hu J, Xu L, Wu L, Yang X, Zou B. TSDSR: Temporal–Spatial Domain Denoise Super-Resolution Photon-Efficient 3D Reconstruction by Deep Learning. Photonics. 2023; 10(7):744. https://doi.org/10.3390/photonics10070744
Chicago/Turabian StyleTong, Ziyi, Xinding Jiang, Jiemin Hu, Lu Xu, Long Wu, Xu Yang, and Bo Zou. 2023. "TSDSR: Temporal–Spatial Domain Denoise Super-Resolution Photon-Efficient 3D Reconstruction by Deep Learning" Photonics 10, no. 7: 744. https://doi.org/10.3390/photonics10070744
APA StyleTong, Z., Jiang, X., Hu, J., Xu, L., Wu, L., Yang, X., & Zou, B. (2023). TSDSR: Temporal–Spatial Domain Denoise Super-Resolution Photon-Efficient 3D Reconstruction by Deep Learning. Photonics, 10(7), 744. https://doi.org/10.3390/photonics10070744






