Abstract
In this work, we report the use of different waist diameters of tapered fiber to generate a four-wave mixing (FWM) effect. The FWM conversion efficiencies obtained from the tapered fiber with 10 µm, 20 µm, and 30 µm waist diameters were −37.81 dB, −38.50 dB, and −39.01 dB, respectively, at 1.584 W pump power. The FWM-based outputs were stable over a 60 min measurement at a 1.5 µm wavelength operation, with a small fluctuation range of 0.21 to 0.45 dB. Furthermore, the setup could generate the FWM effect with a maximum tuning range of 9.5 nm (10 µm and 20 µm) and 9.0 nm (30 µm). The numerical simulation results showed a high nonlinearity at the air-cladding region when the tapered waist diameter was reduced. These characteristics of the tapered fiber can be used as an excellent medium for studying nonlinear phenomena, which could result in the development of new photonic devices for high-power optical communication.
1. Introduction
All-optical signal processing has been a popular approach to replace electronic signal processing systems due to its speed and operation bandwidth advantages. An example is four-wave mixing (FWM), generated by third-order nonlinear susceptibility (ꭓ3) based on optical Kerr effects. FWM usually occurs when new wavelengths are generated from two or more optical signals launched at different wavelengths in nonlinear materials. FWM has a wide range of applications, such as wavelength conversion [1], phase-sensitive amplification [2], quantum entanglement [3], signal demultiplexing [4], and many others. The performance of four-wave mixing has been investigated using highly nonlinear fiber (HNLF) [5], microfiber [6,7], side-polished fiber [8,9], and photonic crystal fiber [10].
Recently tapered fibers and microfibers have been widely used to investigate nonlinear optical applications and in sensing, such as temperature sensors [11], humidity sensors [12], and many more. Tapered fibers have been used to induce supercontinuum generation [13], as a mode locker in fiber lasers [14], and also in four-wave mixing [15] due to their advantages of lower transmission loss, strong evanescent-field, and near-field interactions. Furthermore, the significant refractive index difference between the silica core and the surrounding air-clad provides tight optical confinement, leading to a strong nonlinear interaction [16]. The main concerns in tapered optical fiber are the shape of the tapered profile [17,18] and the instabilities caused during the pulling process [19]. The fabrication process must be well-controlled to ensure the adiabaticity of the tapered shape [20]. Light propagating along the fiber will incur a relatively low loss if the transitions of the tapered profile are gradual. In addition, the tapered waist must also be uniform for optimal performance, especially in nonlinear applications such as for broad supercontinuum generation [21]. However, research on FWM performance using different waist diameters of tapered fiber is still unavailable, which can be an important study.
In this work, the tapered fiber was fabricated with different waist diameters of 10 µm, 20 µm, and 30 µm. The fiber nonlinearity was also numerically simulated at the different waist diameters of the tapered fiber. The FWM performance at different waist diameters will then be evaluated to determine which will give the highest efficiency. The content is structured as follows: the theory and simulation method will be described in Section 2. In Section 3, the fabrication process of the tapered fiber will be discussed. The simulation results will be shown in Section 4, and the experimental setup will be described in Section 5. Lastly, the complete analysis of FWM performance at different tapered waist diameters will be addressed.
2. Theory and Simulation Method
The modes propagated inside an optical fiber can be obtained by solving the Helmholtz equation [22]:
and considering the appropriate boundary conditions. In Equation (1), n is the refractive index, k0 is the free space wave vector, and E is the electric field, given by
where β is the propagation constant along the fiber axis. The influences of tapered fiber waist diameter on the fundamental mode inside the tapered fiber can be explored by extending the mode fields to cover the tapered region. By tapering the optical fiber, the mode fields of the guiding lights will be exposed, and then it modifies the structure of the waveguide tapered devices. Thus, the propagation constant, β of the fundamental mode that is given by
will be changed, as well as the effective index, neff of the tapered fiber. The dispersion parameter, D, can be acquired from the propagation constant as
where c is the speed of light and λ is the operating wavelength. The material dispersion is taken into account using the Sellmeier equation [22]:
where ai and bi are the coefficients of the Sellmeier series. The nonlinear coefficient of fiber can be expressed as [22]
where n2 is the nonlinear refractive index of a material, and Aeff is the effective mode area, which can be calculated using [23]
In this case, n2 = 2.6 × 10−20 m2/W, the nonlinear refractive index of silica [23]. The optical properties of tapered fiber will be computed using the finite difference analysis method (FDM) [24]. The FDM is a popular method for numerically simulating electromagnetic wave equations in an optical medium [25,26].
3. Fabrication and Characterization of Tapered Fiber
The fabrication of tapered fiber consists of a two-step process that simultaneously heats and stretches the single-mode fiber (SMF). This is known as the flame brushing technique [27], and the setup is shown in Figure 1. A short section of SMF’s coating was removed before placing it onto the linear stage. Both sides of the SMF are held at fiber holders and connected to a tunable laser source (TLS) and optical power meter (OPM) at the ends of the fibers. The OPM was used to monitor the tapered fiber’s power loss during fabrication.
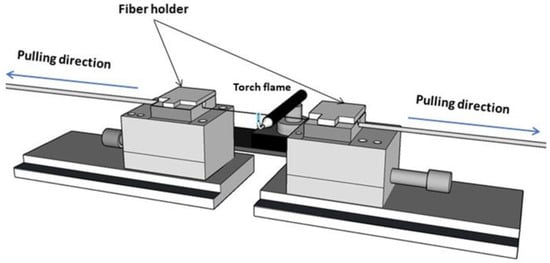
Figure 1.
Schematic diagram of flame brushing technique.
The flame was generated using oxy-LPG gases emitting from a 1 mm torch nozzle. There are two translation stages for pulling the fiber and a torch stage for horizontally moving the flame left and right repeatedly. The flame tip brushes the uncoated section, softening the SMF with uniform heat, while the fiber holders simultaneously pulled the SMF from both sides of the translation stage. This method produces a tapered fiber with a narrow waist diameter.
Three tapered fibers with varied waist diameters were fabricated using flame brushing. The characteristics of all tapered fibers are summarized in Table 1. Based on Table 1, the insertion loss value for all three tapered fibers was approximately 4 dB. A tapered fiber with a 10 µm waist diameter has the longest interaction length of 80 mm compared to the others. This is because the translation stage is pulled further to produce a smaller waist diameter, resulting in a long interaction length.

Table 1.
Characteristics of tapered fiber.
Furthermore, Figure 2a–c show the microscopic image of a tapered fiber with waist diameters of 10 µm, 20 µm, and 30 µm, respectively. It was achieved using an Olympus BX53M microscope with a 10x objective lens. The next section will analyze the performance of three tapered fibers with different diameters in generating the FWM effect.
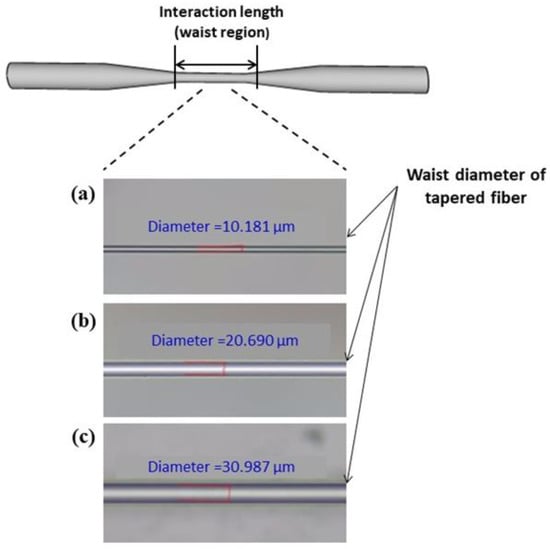
Figure 2.
Waist diameters of tapered fiber for (a) 10 µm, (b) 20 µm, and (c) 30 µm.
4. Simulation Results
The propagation characteristics of the tapered fiber have been calculated using FDM in the simulation to analyze the effect of the taper waist diameter. The following fiber parameters were used in this simulation, as stated in Table 2.

Table 2.
Fiber parameters used in the simulation method.
Figure 3a–c show the calculated effective refractive index, neff, effective mode area, Aeff, and nonlinear coefficient, γ, for the tapered fiber at different waist diameters. From the results, neff, Aeff, and γ were influenced and changed when the waist diameter of the tapered fiber changed. The major factor that can impact the FWM conversion efficiency is the nonlinear coefficient, γ, of the fiber. Thus, based on the simulation results, a smaller waist diameter will have a high nonlinear coefficient due to its low effective mode area, Aeff, as stated in Equation (6). This information can be used to experimentally evaluate the FWM performance of tapered fiber at different waist diameters.
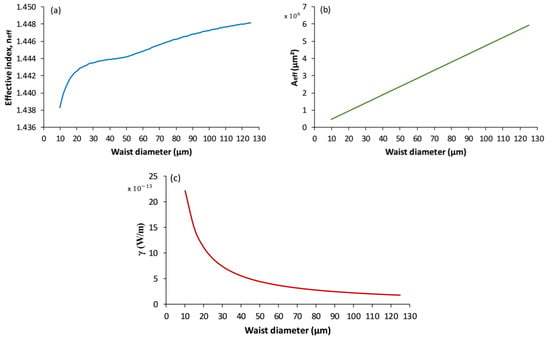
Figure 3.
Calculated propagation characteristics of the tapered fiber at different waist diameters: (a) effective refractive index, (b) effective mode area, and (c) nonlinear coefficient.
5. Experimental Setup
The experimental setup for inducing the FWM effect utilizing three different tapered fibers is shown in Figure 4. This configuration used two TLS units, designated TLS 1 and TLS 2 as the pump and signal sources. The two laser sources were connected to a polarization controller (PC), which was used to change the input signals’ polarization state to achieve maximum FWM efficiency. Then, using a 3-dB coupler, both laser sources were combined and directed to an Erbium-doped fiber amplifier (EDFA). The input signal was amplified using EDFA to enhance the nonlinear effect, which is generally observable at high optical power.
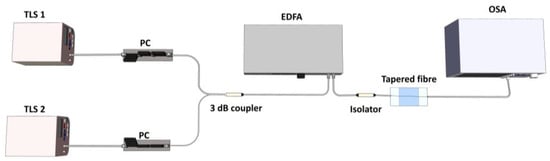
Figure 4.
The schematic diagram for generating the FWM effect using tapered fiber (TLS: tunable laser source; PC: polarization controller; EDFA: erbium-doped fiber amplifier; OSA: optical spectrum analyzer).
Next, the amplified signal was sent through an isolator before interacting with tapered fiber to induce the FWM effect. Finally, the FWM spectrum was measured using a Yokogawa optical spectrum analyzer (OSA) with a 0.02 nm resolution. Before connecting to OSA, the output power was attenuated using a fixed attenuator to less than 10 dBm. It is a precautionary measure to protect the OSA from excessive optical power input damage.
6. Experimental Results and Discussion
The pump and signal wavelengths were set at 1550.55 nm and 1551 nm, respectively. Figure 4 displays the FWM optical spectra for 10 µm, 20 µm, and 30 µm waist diameter tapered fibers, consisting of pump and signal wavelengths with two newly generated wavelengths known as idlers. Furthermore, two new wavelengths, λ3 and λ4, were generated at 1550.05 nm and 1551.5 nm, respectively. Based on the spectra in Figure 5, the FWM conversion efficiency for different waist diameters of tapered fiber was marginally different.
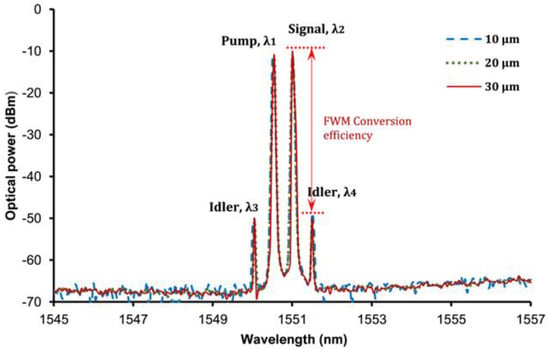
Figure 5.
FWM output spectrum for 10, 20, and 30 µm waist diameter tapered fibers.
The FWM conversion efficiency can be physically measured from the FWM spectrum by comparing the optical power of the input signal to the optical power of the newly generated idlers [8,28]. The calculated conversion efficiencies are −37.81 dB, −38.50 dB, and −39.01 dB for the 10 µm, 20 µm, and 30 µm tapered waist diameter, respectively. The results show that smaller waist diameters lead to enhanced FWM conversion efficiency. This agrees with Equation (6) and the simulation results, which show that at a smaller waist diameter of the tapered fiber, the effective mode area, Aeff value, is lower, resulting in high nonlinearity at the waist region. From this experiment, it can also be noted that the interaction length contributes to the higher nonlinear effect, which improves the conversion efficiency [29].
The FWM-based output was measured for 60 min to analyze the laser’s stability for long-term operation. Figure 6 shows the FWM optical spectrum with a 10 min step size using a 10 µm tapered fiber waist diameter. As can be seen in the contour graph, the output power was stable over time. The stability of the FWM employing 20 µm and 30 µm tapered fibers exhibited a similar trend. Furthermore, the relationship between conversion efficiency and time is plotted and presented in Figure 7 for all three tapered fibers. The graph shows that the output FWM conversion efficiencies were constant throughout the test period, with only minor fluctuations and no wavelength shifting. The fluctuations of FWM conversion efficiency were determined to be 0.21 dB, 0.24 dB, and 0.45 dB for tapered fiber with waist diameters of 10 µm, 20 µm, and 30 µm, respectively.
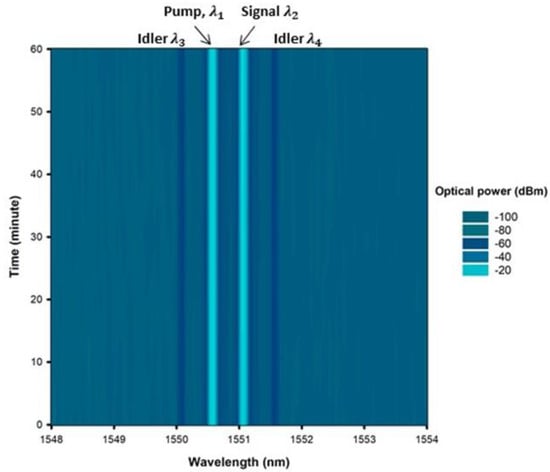
Figure 6.
Top-view FWM optical spectrum for 60 min stability measurement using 10 µm tapered fiber waist diameter.
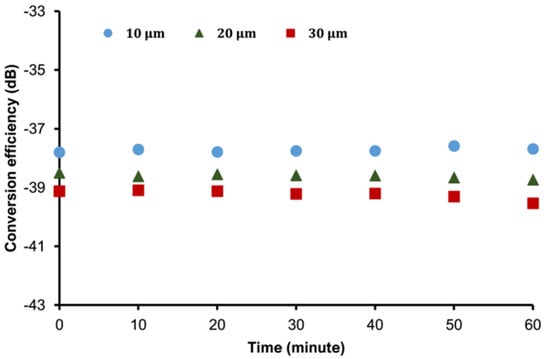
Figure 7.
Graph of FWM conversion efficiency versus time for 10, 20, and 30 µm waist diameters.
Furthermore, another crucial measurement was to examine the wavelength tunability of FWM-based output employing three different tapered fibers. Figure 8 shows the output spectrum of FWM generated by varying the signal wavelength at a constant launched pump power of 1.584 W. Figure 8a,b show the variation in signal wavelength that produced observable idlers from 1551.0 nm to 1560.5 nm at a fixed pump wavelength of 1550.5 nm. The graph shows that as the distance between the pump and signal inputs increases, the optical power of the newly generated wavelength decreases. For example, for the 10 µm and 20 µm tapered fibers, the wavelength spacing between the pump and signal could be tuned up to 9.5 nm. In contrast, for 30 µm tapered fiber, the wavelength could only be tuned until 9.0 nm, as shown in Figure 8c. No idlers were identified above the wavelength tuning range. Hence, no FWM effect occurred.
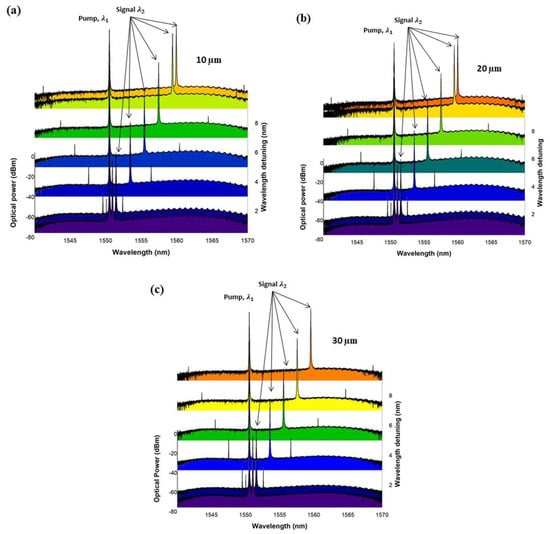
Figure 8.
FWM output spectra at different wavelength tuning for tapered fiber with waist diameters of (a) 10 µm, (b) 20 µm, and (c) 30 µm. Note: the different colors are for the simply to differentiate between the various spectra.
Figure 9 shows the relationship between FWM conversion efficiency and the wavelength tuning for tapered fiber with waist diameters of 10 µm, 20 µm, and 30 µm. Based on the figure, FWM conversion efficiency decreases as the wavelength spacing between the pump and signal lasers increases, and vice versa. The highest conversion efficiency was obtained at 0.5 nm wavelength spacing with −37.81 dB using 10 µm waist diameter tapered fiber. In addition, the tunability for 10 µm and 20 µm waist diameter tapered fiber was up to 9.5 nm, giving a conversion efficiency of approximately −59 dB. However, the tunability for 30 µm tapered fiber was only 9 nm with a conversion efficiency of −58 dB. Above the range of 9 nm (for 30 µm) and 9.5 nm (for 10 µm and 20 µm), the idlers were not generated due to a more significant phase mismatch occurring at higher wavelength spacing [30].
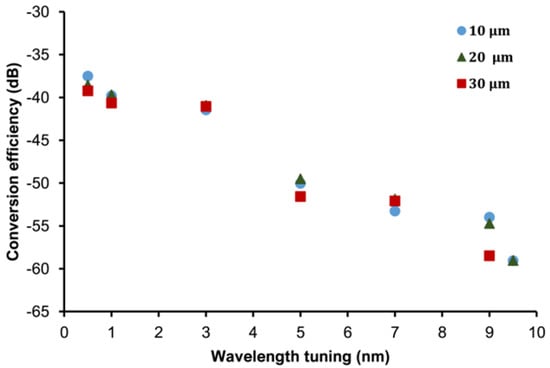
Figure 9.
Conversion efficiency versus wavelength tuning for each tapered fiber.
Moreover, the relationship between FWM conversion efficiency and launched pump power is shown in Figure 10. The graph demonstrates that the conversion efficiency improves when the pump power increases from 0.316 W to 1.584 W. The conversion efficiency increased in direct proportion to the launched pump power. The conversion efficiency of 10 µm, 20 µm, and 30 µm tapered fibers have initial values of −50.12 dB, −49.97 dB, and −51.32 dB, respectively, which increased to −37.81 dB, −38.50 dB, and −39.01 dB at 1.584 W launched pump power and 0.5 nm wavelength spacing.
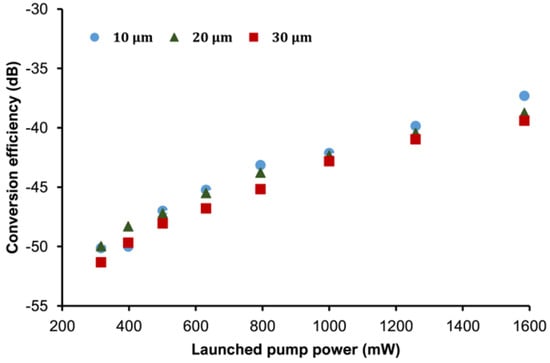
Figure 10.
The relationship between conversion efficiency and pump power.
Furthermore, Table 3 summarizes the FWM performance of three tapered fibers undertaken in this work. Based on the table, the highest conversion efficiency of −37.81 dB was achieved in a tapered fiber with a 10 µm waist diameter. In addition, 10 µm and 20 µm waist diameter tapered fibers achieved a maximum tuning range of 9.5 nm. However, for the thicker 30 µm waist diameter, the FWM conversion efficiency and wavelength tuning range are marginally low, with −39.01 dB and 9.0 nm, respectively. Based on the findings, the FWM performance can be improved by using tapered fiber with a reduced waist diameter and integrating it with nonlinear materials to enhance the nonlinear effects. Thus, tapered fiber is a potential device for facilitating evanescent-field interaction, which will benefit various applications in high-power optical communication and nonlinear optics.

Table 3.
FWM performance comparison with different waist diameters of tapered fiber.
7. Conclusions
This work successfully demonstrated the utilization of various waist diameters of tapered fiber in generating the FWM effect. The FWM conversion efficiencies obtained from the tapered fiber with 10 µm, 20 µm, and 30 µm waist diameter were −37.81 dB, −38.50 dB, and −39.01 dB, respectively, at 1.584 W pump power. Numerical simulations show that for a smaller waist diameter of the tapered fiber, high nonlinearity can be attained at the waist region due to the smaller effective mode area of fiber. Thus, it enhanced the FWM conversion efficiency of the fiber device. Furthermore, the generated FWM-based output was stable over a 60 min test period at 1.5 µm wavelength operation, with the conversion efficiency fluctuation ranging from 0.21 to 0.45 dB. Furthermore, the FWM-based setup has a wavelength tuning capability, with a maximum tuning range of 9.5 nm (10 µm and 20 µm) and 9.0 nm (30 µm). Thus, tapered fibers are an excellent medium for studying the nonlinear phenomena inside the optical fiber due to their strong evanescent field, which could develop novel photonic devices in FWM applications.
Author Contributions
Conceptualization, supervision, writing—reviewing and editing: H.A.; methodology, investigation, writing—original draft preparation: M.F.S. and M.K.A.Z.; formal analysis; resources: M.Z.S.; resources: M.F.I.; and editing: S.A.R. All authors have read and agreed to the published version of the manuscript.
Funding
The Ministry of Higher Education, Malaysia, funded this research through the HiCoE Grant (PRC-2022) and Universiti Malaya, grant numbers RU005-2021 and MG023-2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tyagi, L.K.; Jaiswal, A.K.; Kumar, M.; Joshi, T. Performance analysis of four wave mixing based wavelength conversion in commercial optical fibers. Int. J. Sci. Res. Publ. 2012, 2, 1–5. [Google Scholar]
- Tong, Z.; Lundström, C.; Andrekson, P.; McKinstrie, C.; Karlsson, M.; Blessing, D.; Tipsuwannakul, E.; Puttnam, B.; Toda, H.; Grüner-Nielsen, L. Towards ultrasensitive optical links enabled by low-noise phase-sensitive amplifiers. Nat. Photonics 2011, 5, 430–436. [Google Scholar] [CrossRef]
- Zhang, Z.; Voss, P.L. A quantum-dynamical theory for nonlinear optical interactions in graphene. arXiv 2011, arXiv:1106.4838. [Google Scholar] [CrossRef]
- Fagotto, E.; Abbade, M. All-optical demultiplexing of 4-ASK optical signals with four-wave mixing optical gates. Opt. Commun. 2010, 283, 1102–1109. [Google Scholar] [CrossRef]
- Kibria, R.; Austin, M.W. All optical signal-processing techniques utilizing four wave mixing. Photonics 2015, 2, 200–213. [Google Scholar] [CrossRef]
- Abedin, K.S.; Gopinath, J.T.; Ippen, E.P.; Kerbage, C.E.; Windeler, R.S.; Eggleton, B.J. Highly nondegenerate femtosecond four-wave mixing in tapered microstructure fiber. Appl. Phys. Lett. 2002, 81, 1384–1386. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, B.; Cheng, Y.; Rao, Y.; Gong, Y.; Zhou, X.; Wu, B.; Chiang, K.S. Four-wave mixing in a microfiber attached onto a graphene film. IEEE Photonics Technol. Lett. 2013, 26, 249–252. [Google Scholar] [CrossRef]
- Ahmad, H.; Zaini, M.K.A.; Kamely, A.A.; Samion, M.Z.; Ismail, M.F.; Lim, K.S.; Zamzuri, A.K.; Thambiratnam, K. Generation of four-wave mixing in molybdenum ditelluride (MoTe2)-deposited side-polished fibre. J. Mod. Opt. 2021, 68, 425–432. [Google Scholar] [CrossRef]
- Ahmad, H.; Kamely, A.; Zaini, M.; Samion, M.; Chong, W.; Zamzuri, A.; Lim, K. Generation of four-wave mixing with nonlinear Vanadium-carbide (V2C)-deposited side-polished fiber (SPF) in 1.5-and 2.0-µm wavelength operation. Opt. Laser Technol. 2022, 145, 107458. [Google Scholar] [CrossRef]
- Zhang, A.; Demokan, M.S. Broadband wavelength converter based on four-wave mixing in a highly nonlinear photonic crystal fiber. Opt. Lett. 2005, 30, 2375–2377. [Google Scholar] [CrossRef]
- Yadav, T.; Mustapa, M.; Bakar, M.A.; Mahdi, M. Study of single mode tapered fiber-optic interferometer of different waist diameters and its application as a temperature sensor. J. Eur. Opt. Soc. -Rapid Publ. 2014, 9, 14024. [Google Scholar] [CrossRef]
- Liu, H.; Miao, Y.; Liu, B.; Lin, W.; Zhang, H.; Song, B.; Huang, M.; Lin, L. Relative humidity sensor based on S-taper fiber coated with SiO 2 nanoparticles. IEEE Sens. J. 2015, 15, 3424–3428. [Google Scholar] [CrossRef]
- Wang, F.; Wang, K.; Yao, C.; Jia, Z.; Wang, S.; Wu, C.; Qin, G.; Ohishi, Y.; Qin, W. Tapered fluorotellurite microstructured fibers for broadband supercontinuum generation. Opt. Lett. 2016, 41, 634–637. [Google Scholar] [CrossRef]
- Ahmad, H.; Ramli, R.; Yusoff, N.; Reduan, S.; Zamzuri, A.; Thambiratnam, K. Performance of Nb2C MXene coated on tapered fiber as saturable absorber for the generation of mode-locked erbium-doped fiber laser. Infrared Phys. Technol. 2021, 114, 103647. [Google Scholar] [CrossRef]
- Jin, Q.; Lu, J.; Li, X.; Yan, Q.; Gao, Q.; Gao, S. Performance evaluation of four-wave mixing in a graphene-covered tapered fiber. J. Opt. 2016, 18, 075502. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Wang, L. Demonstration of almost octave-spanning cascaded four-wave mixing in optical microfibers. Opt. Lett. 2012, 37, 3441–3443. [Google Scholar] [CrossRef]
- Kenny, R.; Birks, T.; Oakley, K. Control of optical fibre taper shape. Electron. Lett. 1991, 18, 1654–1656. [Google Scholar] [CrossRef]
- Birks, T.A.; Li, Y.W. The shape of fiber tapers. J. Light. Technol. 1992, 10, 432–438. [Google Scholar] [CrossRef]
- Dewynne, J.; Ockendon, J.; Wilmott, P. On a mathematical model for fiber tapering. SIAM J. Appl. Math. 1989, 49, 983–990. [Google Scholar] [CrossRef]
- Love, J.; Henry, W.; Stewart, W.; Black, R.; Lacroix, S.; Gonthier, F. Tapered single-mode fibres and devices. Part 1: Adiabaticity criteria. IEE Proc. J. Optoelectron. 1991, 138, 343–354. [Google Scholar] [CrossRef]
- Leon-Saval, S.; Birks, T.; Wadsworth, W.; Russell, P.S.J.; Mason, M. Supercontinuum generation in submicron fibre waveguides. Opt. Express 2004, 12, 2864–2869. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, M.F. Nonlinear Effects in Optical Fibers; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Agrawal, G. Nonlinear Fiber Optics; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Vassallo, C. Improvement of finite difference methods for step-index optical waveguides. IEEE Proc. J. Optoelectron. 1992, 139, 137–142. [Google Scholar] [CrossRef]
- Zhu, Z.; Brown, T.G. Full-vectorial finite-difference analysis of microstructured optical fibers. Opt. Express 2002, 10, 853–864. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Wiktor, M.; Mrozowski, M. Efficient finite difference analysis of microstructured optical fibers. Opt. Express 2005, 13, 10349–10359. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.S.; Harun, S.W.; Arof, H.; Ahmad, H. Fabrication and Applications of Microfiber. In Selected Topics on Optical Fiber Technology; Books on Demand: Norderstedt, Germany, 2012. [Google Scholar]
- Xu, K. Silicon electro-optic micro-modulator fabricated in standard CMOS technology as components for all silicon monolithic integrated optoelectronic systems. J. Micromech. Microeng. 2021, 31, 054001. [Google Scholar] [CrossRef]
- Wu, D.; Shen, L.; Ren, H.; Huang, M.; Lacava, C.; Campling, J.; Sun, S.; Hawkins, T.W.; Gibson, U.J.; Petropoulos, P.; et al. Four-Wave Mixing-Based Wavelength Conversion and Parametric Amplification in Submicron Silicon Core Fibers. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4300111. [Google Scholar] [CrossRef]
- Qu, Y.; Wu, J.; Yang, Y.; Zhang, Y.; Liang, Y. Enhanced nonlinear four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films. Adv. Opt. Mater. 2020, 8, 2001048. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).