Abstract
In this paper, we focus on the study of the negative energy flow in the tight focusing of a radially polarized vortex beam. We know that, because of the coupling of the polarization state and the vortex charge, the on-axis energy flow in the focal region can be well modulated by changing the polarization order and the vortex charge of the incident vector beam. This shows that when the polarization order and the vortex charge satisfy the specific relation, the on-axis negative energy flow can be obtained in the focal region. Moreover, the initial phases of two polarization unit vectors also affect the evolution of the on-axis negative energy flow in the tight focusing of the radially polarized beam. The phase difference modulation of the two polarization unit vectors indicates two different modulations of the polarization state. Our work provides a more flexible modulation method for focal shaping and optical modulation.
1. Introduction
A radially polarized beam is a type of structured beam with a non-uniform polarization state, which is a particular solution of the Helmholtz equation [1,2,3,4,5,6,7]. In recent years, the radially polarized beam has become a research focus in optics and photonics, because of its extensive potential applications in optical trapping, imaging, optical communication, etc. [1,7,8,9,10,11,12,13,14,15].
There are some interesting phenomena in the tight focusing of radially polarized beams, such as the spin to orbital angular momentum conversion, the on-axis negative energy, the spin Hall effect, and the spin–orbit Hall effect, etc. [16,17,18,19,20,21,22]. Kotlyar et al. showed that there is an on-axis negative energy flow in the tight focusing of a second-order radially polarized beam [23]. Moreover, the on-axis negative energy flow also can be obtained in the tight focusing of a radially polarized vortex beam, which can be modulated by changing the vortex charge and the polarization order of the incident beam. It is known that the initial phase of the polarization state describes a type of rotation operation on two polarization unit vectors; for example, the radial polarization state will evolve into an azimuthal polarization state when its initial phase changes from 0 to . Meanwhile, if the phase difference of two polarization unit vectors is not equal to zero, it means that both the polarization state and the amplitude of two field components are modulated with the change in the initial phase of the two polarization unit vectors. All of these indicate that the initial phase modulation of the polarization state also plays an important role in the tight focusing of radially polarized beams.
In this paper, we focus on the study of the negative energy flow in the tight focusing of the radially polarized vortex beam. When the polarization order and the vortex charge satisfy a specific relation, the on-axis negative energy flow in the focal region can be well controlled by the joint modulation of the polarization order and the vortex charge of the incident vector beam. Furthermore, by modulating the initial phases of two polarization unit vectors, the on-axis negative energy flow also can be obtained when the polarization order and the vortex charge satisfy the specific relation. If the initial phases of the two polarization unit vectors are modulated simultaneously, the polarization state distribution is rotated in its entirety for the high-order radially polarized beams. Interestingly, if the modulation of the initial phases of the two polarization unit vectors is not synchronous, it means that both the polarization state and the amplitude of the incident radially polarized beam are modulated. We find that the initial phases of the two polarization unit vectors also affect the evolution of the on-axis negative energy flow in the tight focusing of the radially polarized beam. Our work provides a more flexible modulation method for focal shaping and optical modulation.
2. Theoretical Model
The electric and magnetic field components of the focal field in the tight focusing of vector vortex beams can be obtained through the Richards–Wolf formula in Debye approximation as follows [7,23]:
where
where is the complex amplitude of the incident field; for the sake of simplicity, we take . is the vortex charge, is the focal length, , and we take and in our numerical simulation, respectively. and are the unit vectors of the polarization state; for the radial polarization state, its forms can be described by and . is the polarization order, and and are the initial phases of the polarization unit vectors. The phase difference of the polarization unit vectors can be modulated by changing the initial phases and . Generally, the polarization unit vectors and should satisfy the relationship ; this means that the two polarization unit vectors are modulated synchronously, and the phase difference of the polarization unit vectors is equal to zero (). It is known that the initial phase of the polarization state indicates the rotation operation on the polarization unit vector. If the initial phases of two polarization unit vectors are modulated simultaneously, the polarization state distribution is rotated in its entirety for the high-order radially polarized beam. However, if the phase difference of two polarization unit vectors is not equal to zero, , both the polarization state and the amplitude of two transverse field components are modulated with the change in the initial phases of the two polarization unit vectors.
According to Equation (1), we can obtain the electric field components of the focal field as follows:
where
in which , and is an n-th order Bessel function. It shows that the focal field is determined by the polarization order and the vortex charge of the incident vector beam. According to the expression of the electric field components, Figure 1 and Figure 2 show the intensity patterns of the focal field in the focal plane when the vortex charge . It is shown that the focal pattern is closely related to the polarization order of the incident vector beam, and the focal spots will be split or concentrated with the increase in initial phase (or ). In fact, for a second-order polarized beam, the focal field pattern does not change with the simultaneous modulation of the initial phase of the polarization state. If only one initial phase of the polarization state is modulated, both the polarization state and the amplitude of the incident beam are changed. Thus, the initial phase modulation of the polarization state can affect the focal field property, as shown in Figure 1 and Figure 2.
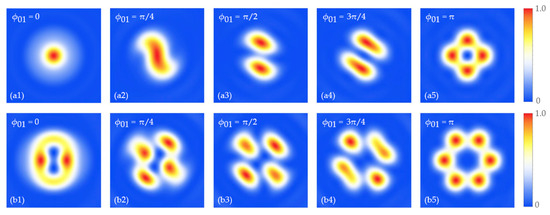
Figure 1.
Evolution of intensity patterns of focal field in the focal plane () with the change in initial phase , when vortex charge and initial phase of polarization state . The polarization order is (a) ; (b) .
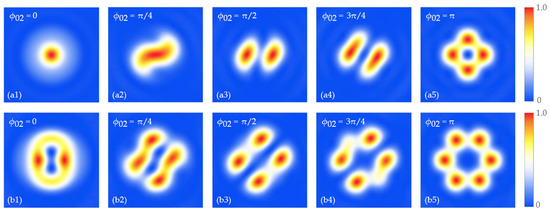
Figure 2.
Evolution of intensity patterns of focal field in the focal plane () with the change in initial phase , when vortex charge and initial phase of polarization state . The polarization order is (a) ; (b) .
Figure 3 displays the intensity pattern of the focal field when the incident vector beam possesses a vortex charge and the initial phase of the polarization state . Compared with the results shown in Figure 1 and Figure 2, it shows that the vortex charge plays a key role in the tight focusing of vector beams. We find that the focal pattern shows different distribution properties with the change in the initial phase . More importantly, when the polarization order is equal to the vortex charge, , the focal field pattern evolves into a spot, and the initial phase does not affect the property of the focal spot. Because of the rotation symmetry of Equation (2) on the polarization order and vortex charge, the intensity distribution at a negative vortex charge is the same as that at a positive charge, as seen in Figure 4. It is known that although the radially polarized beams do not possess spin angular momentum, the initial phase of the polarization state can affect the distribution property of the spin angular momentum [19]. All these results indicate that the initial phase of the polarization state can directly affect the spin–orbit coupling in the tight focusing of a radially polarized vortex beam. In the next section, we will focus on the evolution of the negative energy flow in the focal region.
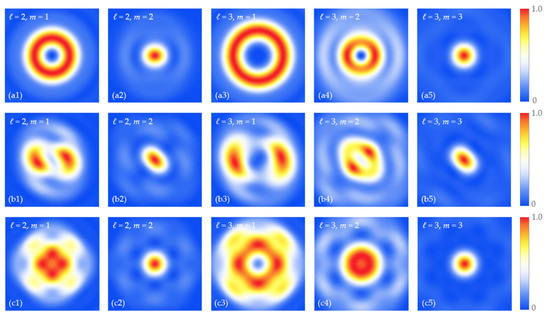
Figure 3.
Evolution of intensity patterns of focal field in the focal plane () with different vortex charges and , (a) ; (b) ; (c) . Columns (1) and (2) are , (1) ; (2) . Columns (3)~(5) are , (3) ; (4) ; (5) .
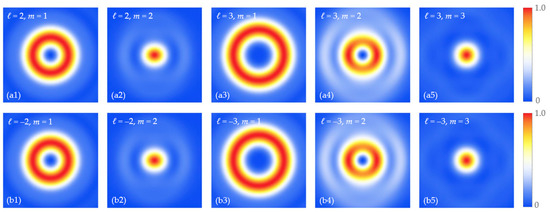
Figure 4.
Evolution of intensity patterns of focal field in the focal plane () with different vortex charges and , . Row (a) is and (b) is . The intensity distribution at is the same as that at .
3. Negative Energy Flow in Focal Region
In this section, we will investigate the evolution property of the energy flow in the focal region. The energy flow can be described by the Poynting vector, which has the following form [23,24,25,26]:
and the longitudinal component of the energy flow density in the focal plane can be expressed as
The expression of the magnetic field components can be derived from Equation (2) directly,
where
Then, the evolution properties of the longitudinal energy flow can be easily obtained according to Equation (4). Figure 5 shows the evolution properties of the longitudinal energy flow in the focal plane () when the incident vector beam is without a vortex charge and the initial phase . We can see that when the incident vector beam does not possess a vortex charge and the polarization order equals 2, a negative on-axis energy flow can be obtained, and it can be changed by modulating the initial phase . When the polarization order of the incident radially polarized beam is greater than 2, the on-axis energy flow always is zero. Interestingly, we find that when the initial phase , the energy flow is negative in these two cases. In fact, when the initial phase , the incident beam possesses a linear polarization state, and its amplitude is modulated by the sinusoidal function.
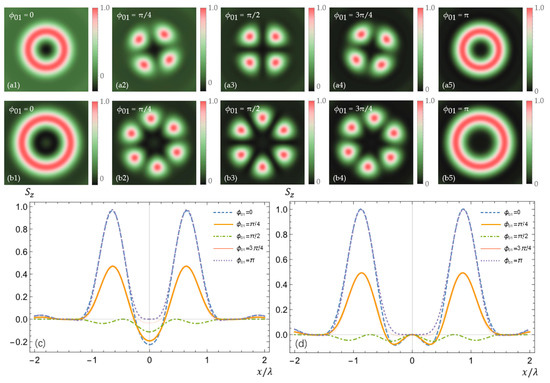
Figure 5.
Evolution properties of longitudinal energy flow in the focal plane when and . Rows (a) () and (b) () show the longitudinal energy flow’s evolution with initial phase changing from 0 to . (c) () and (d) () plot the longitudinal energy flow in the focal plane.
Figure 6 and Figure 7 show the evolution properties of the longitudinal energy flow in the focal plane () when the incident vector beam has a vortex charge and the initial phase . The vortex charge plays a key role in the appearance of the on-axis negative energy flow. By comparison with the results shown in Figure 5, we can see that the on-axis negative energy flow can be obtained when the vortex charge and the polarization order satisfy a specific relation . It indicates that the sign of the vortex charge does not affect the evolution property of the on-axis negative energy flow in the focal region. Obviously, if the vortex charge takes a value of zero, the evolution of the on-axis negative energy flow is consistent with the result shown in [18,19]. Meanwhile, the on-axis negative flow can be modulated by changing the initial phase of the polarization state. This is because the initial phase of the polarization state can change the distribution property of the spin angular momentum and affect the spin–orbit coupling in the tight focusing of vector beams.
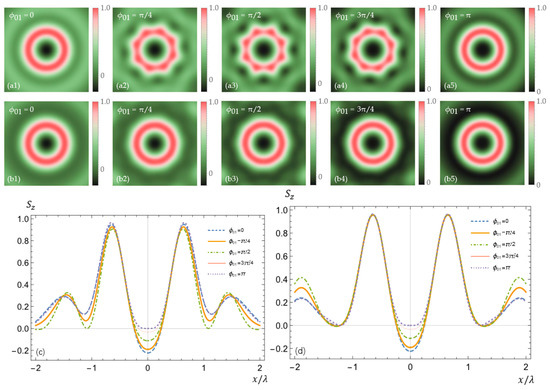
Figure 6.
Evolution properties of longitudinal energy flow in the focal plane when and . Rows (a) () and (b) () show the longitudinal energy flow’s evolution with initial phase changing from 0 to . (c) () and (d) () plot the longitudinal energy flow in the focal plane.
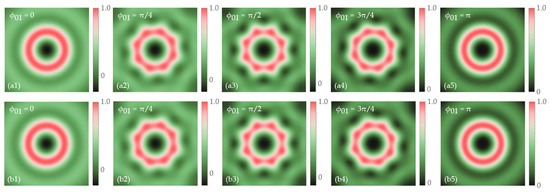
Figure 7.
Evolution properties of longitudinal energy flow in the focal plane when . Rows (a) () and (b) () show the longitudinal energy flow’s evolution with initial phase changing from 0 to . The longitudinal energy flow at is the same as that at .
4. Conclusions
In this paper, we focused on the evolution of the on-axis negative flow in the tight focusing of radially polarized vortex beams. It was shown that, as with the polarization order of the incident radially polarized beam, the vortex charge also plays a key role in the appearance of the on-axis negative energy flow in the tight focusing of vector beams. It was demonstrated that the on-axis negative energy flow can be obtained in the tight focusing of a second-order radially polarized beam. Then, if the incident radially polarized beams possess a vortex charge, when the vortex charge and the polarization order satisfy a specific relation, the on-axis negative energy flow can be obtained in the focal region. Furthermore, by modulating the initial phases of two polarization unit vectors, the on-axis negative energy flow can be well controlled. In fact, if the initial phases of the two polarization unit vectors are modulated simultaneously, the polarization state distribution is rotated in its entirety for high-order radially polarized beams. If the modulation of the initial phases of the two polarization unit vectors is not synchronous, it means that both the polarization state and the amplitude of the incident radially polarized beam are modulated. Our work provides a more flexible modulation method for focal shaping, including the focal field intensity and optical angular momentum, and gives a potential technique to generate a customized focal field for optical manipulation and optical micro-fabrication.
Author Contributions
Conceptualization, H.L.; Software, R.C.; Formal analysis, T.S.; Investigation, Y.L.; Writing—original draft, R.C.; Writing—review & editing, H.L.; Supervision, H.L. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC), grant numbers 11974101, 11974102.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rosales-Guzmán, C.; Ndagano, B.; Forbes, A. A Review of Complex Vector Light Fields and Their Applications. J. Opt. 2018, 20, 123001. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical Vector Beams: From Mathematical Concepts to Applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V. Grating-Based Optical Scheme for the Universal Generation of Inhomogeneously Polarized Laser Beams. Appl. Opt. 2010, 49, 1734–1738. [Google Scholar] [CrossRef]
- Chen, J.; Wan, C.; Zhan, Q. Vectorial Optical Fields: Recent Advances and Future Prospects. Sci. Bull. 2018, 63, 54–74. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V.; Jeffrey, M.R. Chapter 2 Conical Diffraction: Hamilton’s Diabolical Point at the Heart of Crystal Optics. Prog. Opt. 2007, 50, 13–50. [Google Scholar]
- He, C.; Shen, Y.; Forbes, A. Towards Higher-Dimensional Structured Light. Light. Sci. Appl. 2022, 11, 205. [Google Scholar] [CrossRef]
- Youngworth, K.; Brown, T. Focusing of High Numerical Aperture Cylindrical-Vector Beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Bhebhe, N.; Rosales-Guzman, C.; Forbes, A. Classical and Quantum Analysis of Propagation Invariant Vector Flat-Top Beams. Appl. Opt. 2018, 57, 5451–5458. [Google Scholar] [CrossRef]
- Michihata, M.; Hayashi, T.; Takaya, Y. Measurement of axial And Transverse Trapping Stiffness of Optical Tweezers In Air Using a Radially Polarized Beam. Appl. Opt. 2009, 48, 6143–6151. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Optical Trapping of Micrometer-Sized Dielectric Particles by Cylindrical Vector Beams. Opt. Express 2010, 18, 10828–10833. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Zhang, G.-L.; Wang, Q.; Wang, M.; Tu, C.; Li, Y.; Wang, H.-T. Spin-to-Orbital Angular Momentum Conversion via Light Intensity Gradient. Optica 2021, 8, 1231–1236. [Google Scholar] [CrossRef]
- Segawa, S.; Kozawa, Y.; Sato, S. Resolution Enhancement of Confocal Microscopy by Subtraction Method with Vector Beams. Opt. Lett. 2014, 39, 3118–3121. [Google Scholar] [CrossRef]
- Steger, M.; Gautham, C.; Snoke, D.W.; Pfeiffer, L.; West, K. Slow Reflection and Two-Photon Generation of Microcavity Exciton–Polaritons. Optica 2015, 2, 1–5. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J. High-Base Vector Beam Encoding/Decoding for Visible-Light Communications. Opt. Lett. 2015, 40, 4843–4846. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xue, Y.; Zhu, Z.; Rui, G.; Cui, Y.; Gu, B. Theoretical Investigation on Asymmetrical Spinning and Orbiting Motions of Particles in a Tightly Focused Power-Exponent Azimuthal-Variant Vector Field. Opt. Express 2018, 26, 4318–4329. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhao, C.; Dong, Y.; Dong, Y.; Cai, Y. Generation and Tight-Focusing Properties of Cylindrical Vector Circular Airy Beams. Appl. Phys. B 2014, 117, 905–913. [Google Scholar] [CrossRef]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.M.; McGloin, D.; Chiu, D.T. Spin-to-Orbital Angular Momentum Conversion in a Strongly Focused Optical Beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G. Energy Density and Energy Flux in the Focus of an Optical Vortex: Reverse Flux of Light Energy. Opt. Lett. 2018, 43, 2921–2924. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, C.; Tang, M.; Li, X. Controlled Negative Energy Flow in the Focus of a Radial Polarized Optical Beam. Opt. Express 2020, 28, 18607–18615. [Google Scholar] [CrossRef]
- Li, H.; Ma, C.; Wang, J.; Tang, M.; Li, X. Spin-Orbit Hall Effect in the Tight Focusing of a Radially Polarized Vortex Beam. Opt. Express 2021, 29, 39419. [Google Scholar] [CrossRef]
- Novitsky, A.; Novitsky, D. Negative Propagation of Vector Bessel Beams. J. Opt. Soc. Am. A 2007, 24, 2844–2849. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, P.B.; Neto, P.A.M.; Nussenzveig, H.M. Angular Momentum of Focused Beams: Beyond the Paraxial Approximation. Phys. Rev. A 2009, 79, 033830. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Energy Backflow in the Focus of a Light Beam with Phase or Polarization Singularity. Phys. Rev. A 2019, 99, 033840. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Degtyarev, S.A. Inverse Energy Flux of Focused Radially Polarized Optical Beams. Phys. Rev. A 2018, 98, 043823. [Google Scholar] [CrossRef]
- Helseth, L. Optical Vortices in Focal Regions. Opt. Commun. 2004, 229, 85–91. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Nori, F. Dual Electromagnetism: Helicity, Spin, Momentum and Angular Momentum. New J. Phys. 2013, 15, 033026. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).