Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence
Abstract
1. Introduction
2. Analytical Formulas of the Laguerre Non-Uniformly Correlated Beams in Turbulence
3. Statistical Properties of LNUC Beams
3.1. In the Source Plane
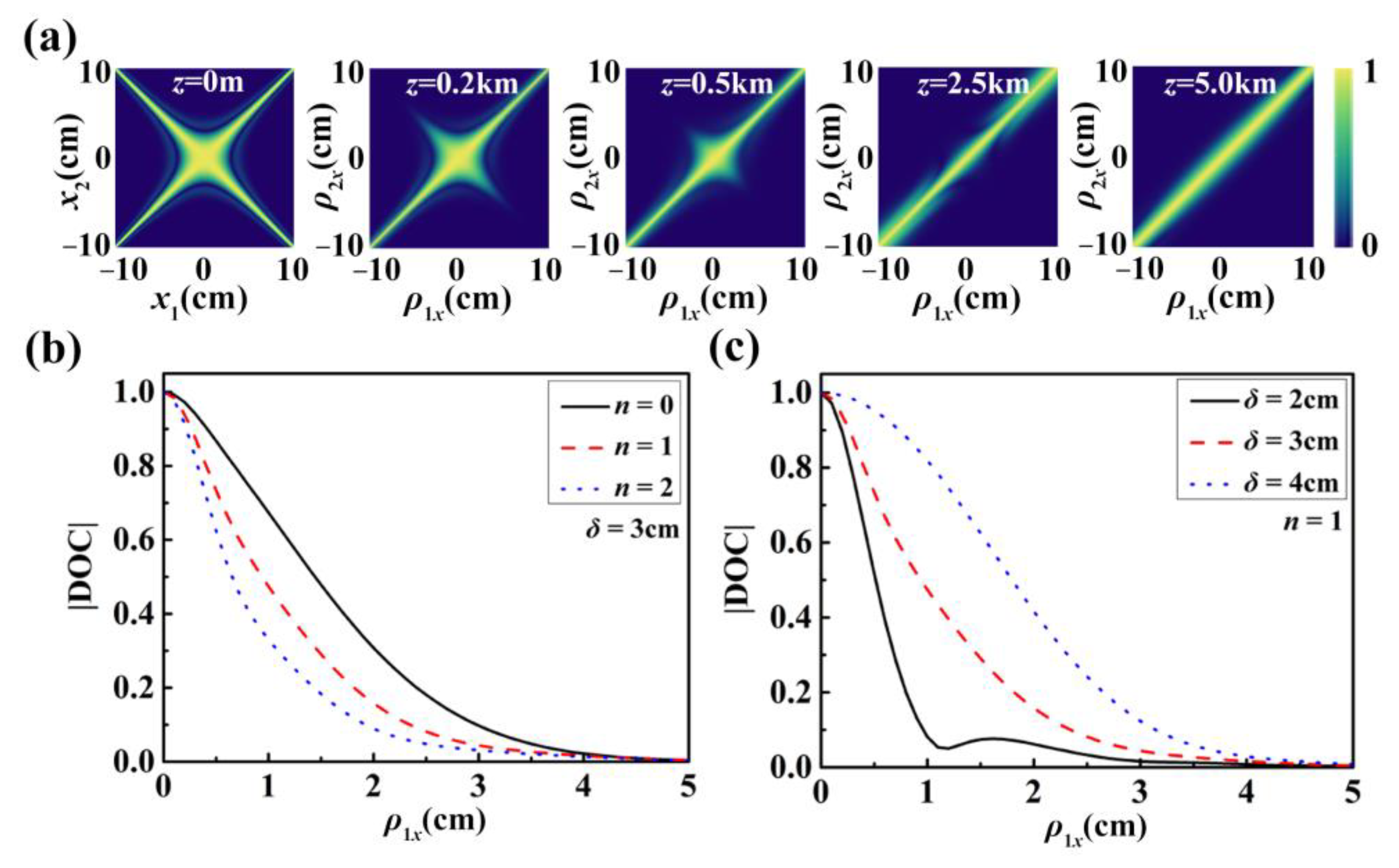
3.2. Propagation in Free Space
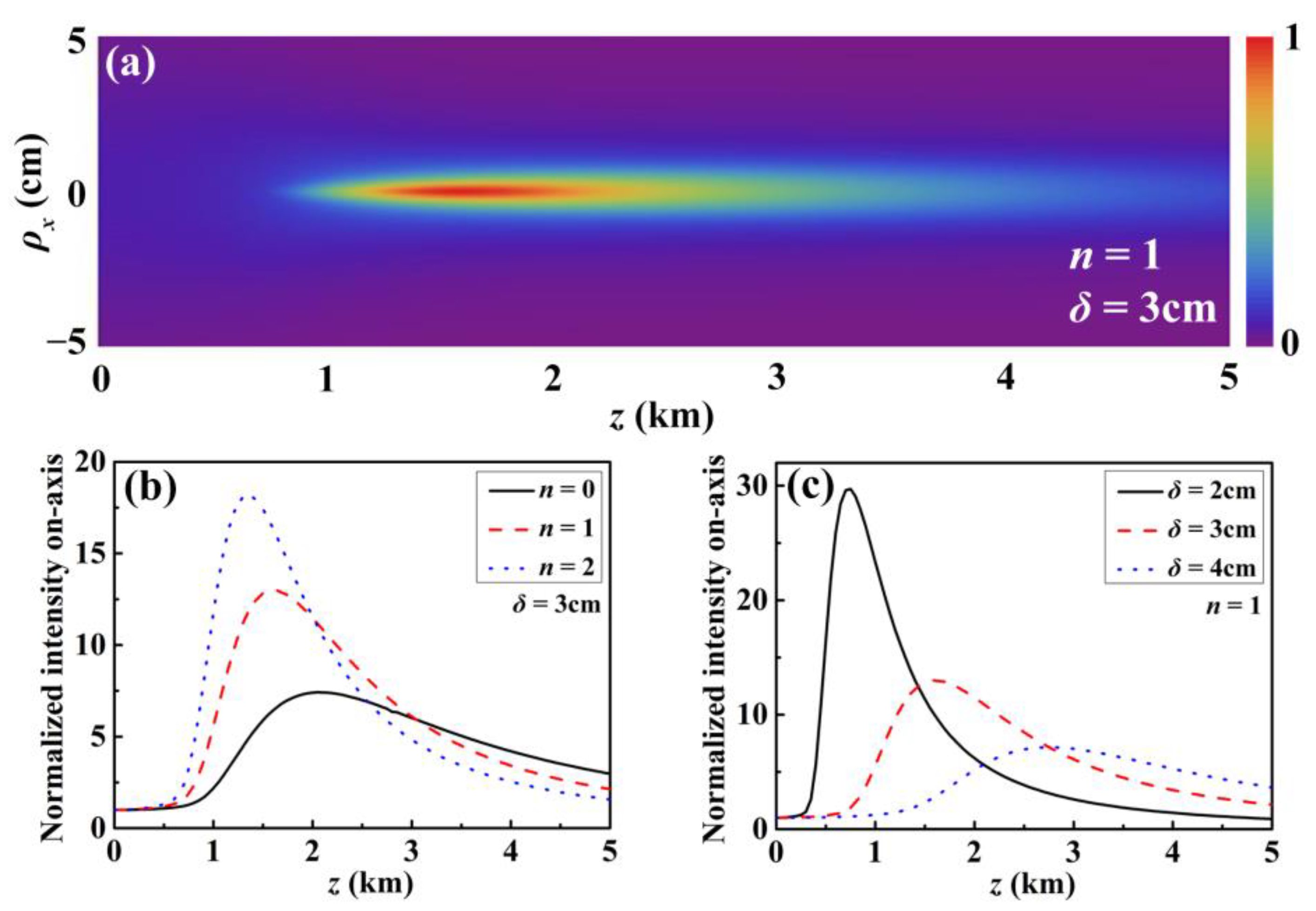
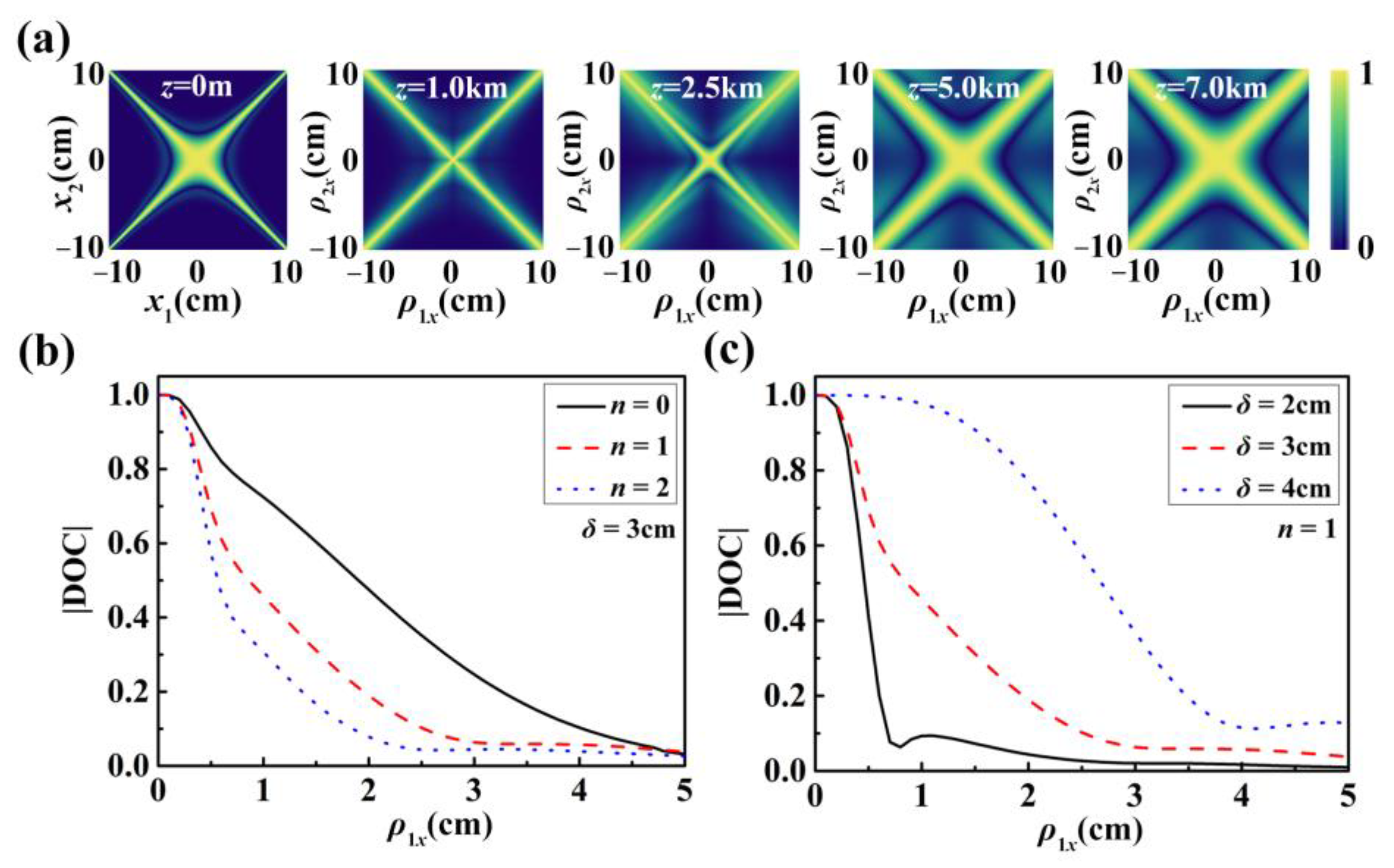
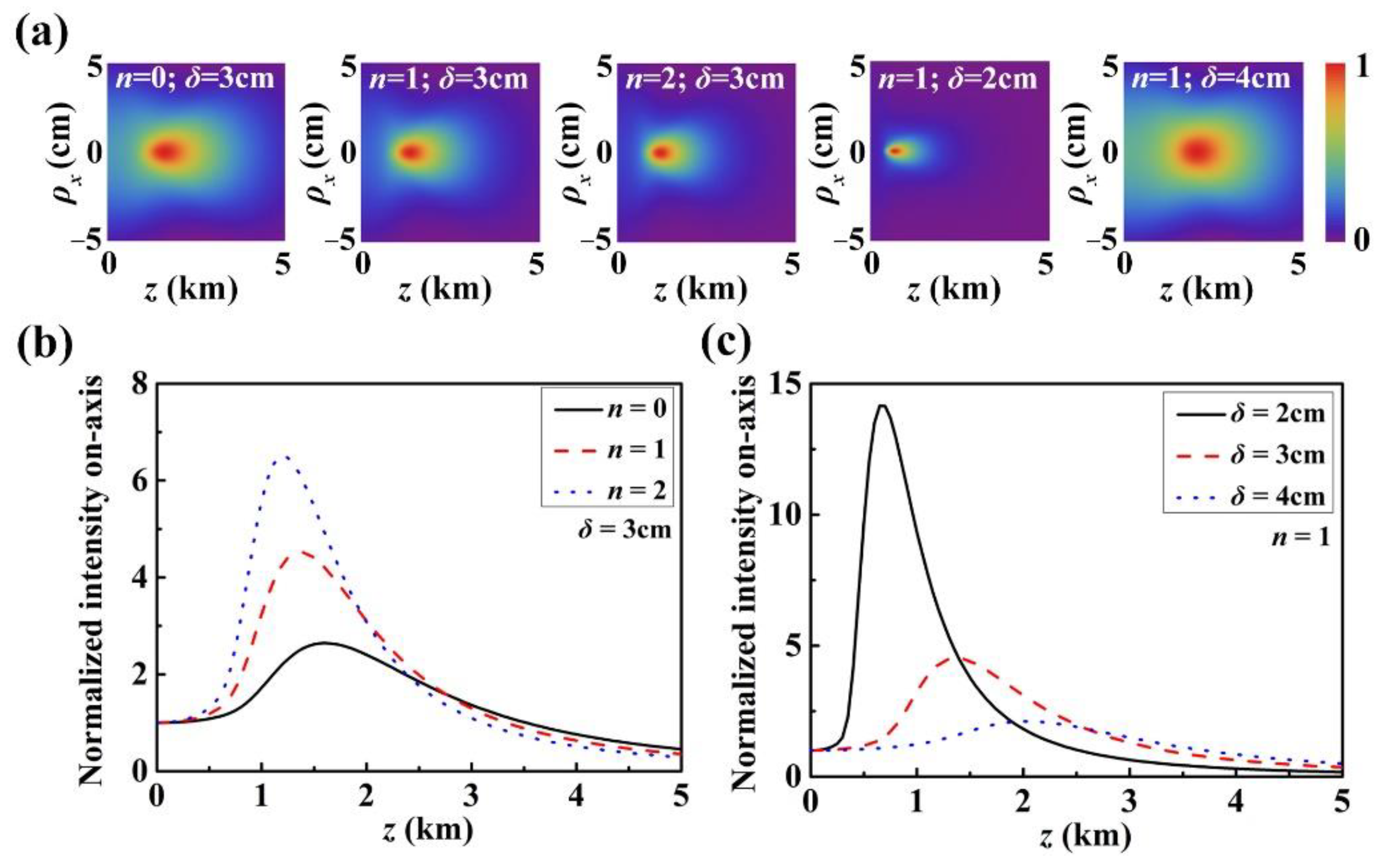
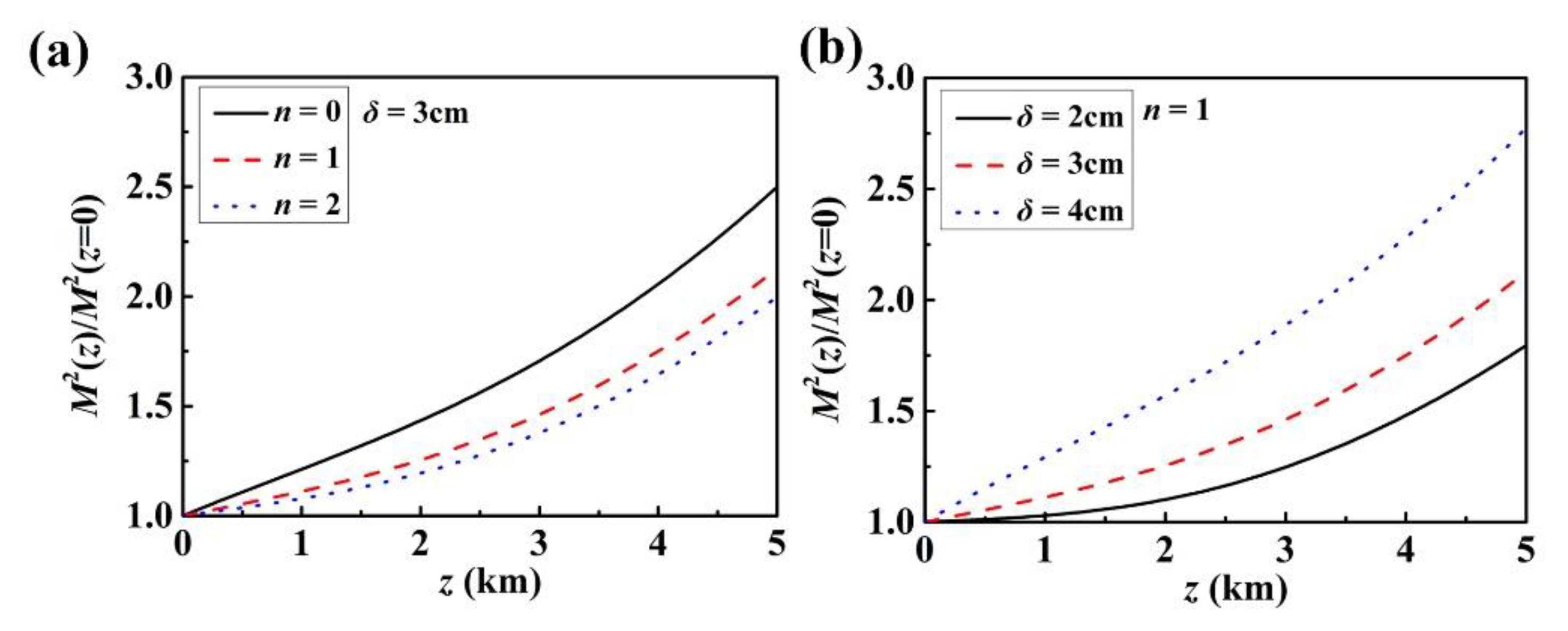
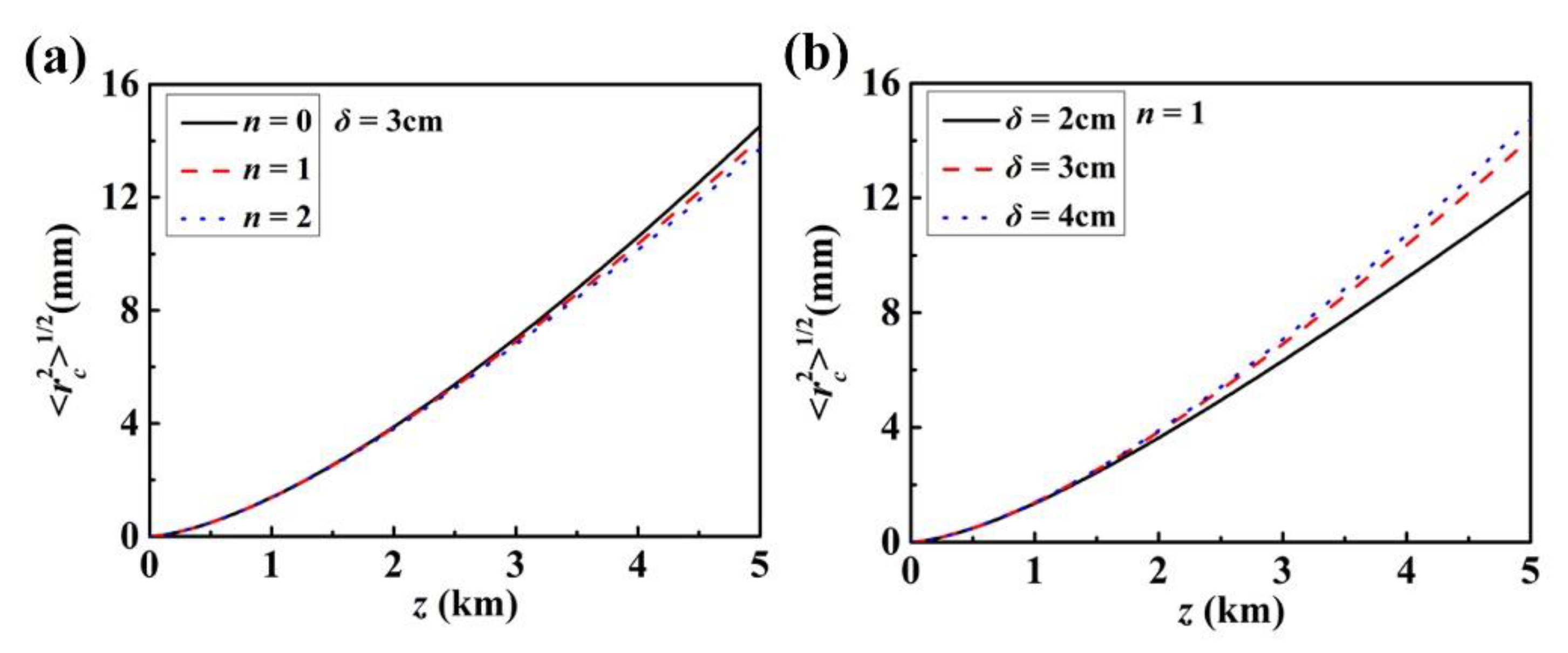
3.3. Propagation in Turbulence
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forbes, A.; Oliveira, M.D.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, MA, USA, 1995. [Google Scholar]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of partially coherent beams. Prog. Opt. 2017, 62, 157–223. [Google Scholar]
- Korotkova, O.; Gbur, G. Applications of optical coherence theory. Prog. Opt. 2020, 65, 43–104. [Google Scholar]
- Chen, Y.; Wang, F.; Cai, Y. Partially coherent light beam shaping via complex spatial coherence structure engineering. Adv. Phys. X 2022, 7, 2009742. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Variant-coherence Gaussian sources. Photonics 2021, 8, 403. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Santarsiero, M.; Piquero, G.; González de Sande, J.C. A new type of shape-invariant beams with structured coherence: Laguerre-Christoffel-Darboux beams. Photonics 2021, 8, 134. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Horoshko, D.; Zhao, Z.; Pan, L. Evolution of Spatiotemporal Intensity of Partially Coherent Pulsed Beams with Spatial Cosine-Gaussian and Temporal Laguerre–Gaussian Correlations in Still, Pure Water. Photonics 2021, 8, 102. [Google Scholar] [CrossRef]
- Sun, B.; Lü, H.; Wu, D.; Wang, F.; Cai, Y. Propagation of a modified complex Lorentz–Gaussian-correlated beam in a marine atmosphere. Photonics 2021, 8, 82. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, DC, USA, 2005; pp. 35–56. [Google Scholar]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6–15. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. A 2014, 31, 2038–2045. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: A review (Invited review). Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. J. Opt. Soc. Am. A 2001, 18, 150–156. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef]
- Yu, J.; Wang, F.; Liu, L.; Cai, Y.; Gbur, G. Propagation properties of Hermite non-uniformly correlated beams in turbulence. Opt. Express 2018, 26, 16333–16343. [Google Scholar] [CrossRef]
- Yu, J.; Cai, Y.; Gbur, G. Rectangular Hermite nonuniformly correlated beams and its propagation properties. Opt. Express 2018, 26, 27894–27906. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, X.; Lin, S.; Wang, F.; Gbur, G.; Cai, Y. Vector partially coherent beams with prescribed non-uniform correlation structure. Opt. Lett. 2020, 45, 3824–3827. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of nonuniformly correlated beams in atmospheric turbulence. Opt. Lett. 2013, 38, 1395–1397. [Google Scholar] [CrossRef]
- Lin, S.; Wang, C.; Zhu, X.; Lin, R.; Wang, F.; Gbur, G.; Cai, Y.; Yu, J. Propagation of radially polarized Hermite non-uniformly correlated beams in a turbulent atmosphere. Opt. Express 2020, 28, 27238–27249. [Google Scholar] [CrossRef]
- Yu, J.; Xu, Y.; Lin, S.; Zhu, X. Longitudinal optical trapping and manipulating Rayleigh particles by spatial nonuniform coherence engineering. Phys. Rev. A 2022, 106, 033511. [Google Scholar] [CrossRef]
- Dan, Y.; Zhang, B. Second moments of partially coherent beams in atmospheric turbulence. Opt. Lett. 2009, 34, 563–565. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Herrero, R.; Mejías, P.M.; Piquero, G. Quality improvement of partially coherent symmetric-intensity beams caused by quartic phase distortions. Opt. Lett. 1992, 17, 1650–1651. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M.; Sona, A. The change of width for a partially coherent beam on paraxial propagation. Opt. Commun. 1991, 82, 197. [Google Scholar] [CrossRef]
- Xiao, X.; Voelz, D. Beam wander analysis for focused partially coherent beams propagating in turbulence. Opt. Eng. 2012, 51, 026001. [Google Scholar] [CrossRef]
- Toselli, I.; Andrews, L.C.; Phillips, R.L.; Ferrero, V. Free-space optical system performance for laser beam propagation through non-Kolmogorov turbulence. Opt. Eng. 2008, 47, 026003. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yan, Z.; Wang, Y.; Liu, L.; Zhu, X.; Guo, B.; Yu, J. Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence. Photonics 2023, 10, 837. https://doi.org/10.3390/photonics10070837
Zhao Y, Yan Z, Wang Y, Liu L, Zhu X, Guo B, Yu J. Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence. Photonics. 2023; 10(7):837. https://doi.org/10.3390/photonics10070837
Chicago/Turabian StyleZhao, Yang, Zhiwen Yan, Yibo Wang, Liming Liu, Xinlei Zhu, Bohan Guo, and Jiayi Yu. 2023. "Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence" Photonics 10, no. 7: 837. https://doi.org/10.3390/photonics10070837
APA StyleZhao, Y., Yan, Z., Wang, Y., Liu, L., Zhu, X., Guo, B., & Yu, J. (2023). Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence. Photonics, 10(7), 837. https://doi.org/10.3390/photonics10070837





