Phase Regeneration of QPSK Signals Based on Kerr Soliton Combs
Abstract
1. Introduction
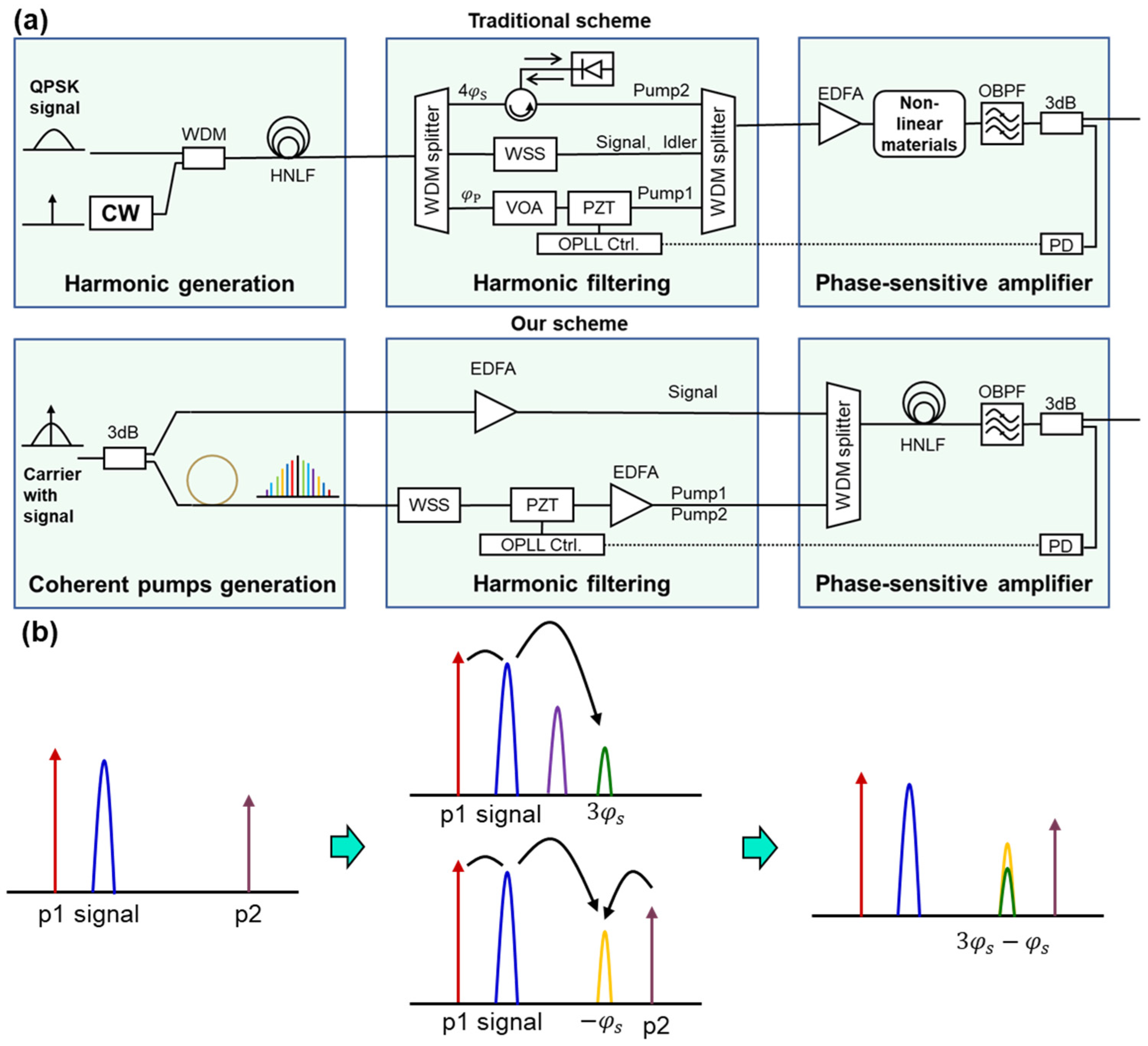
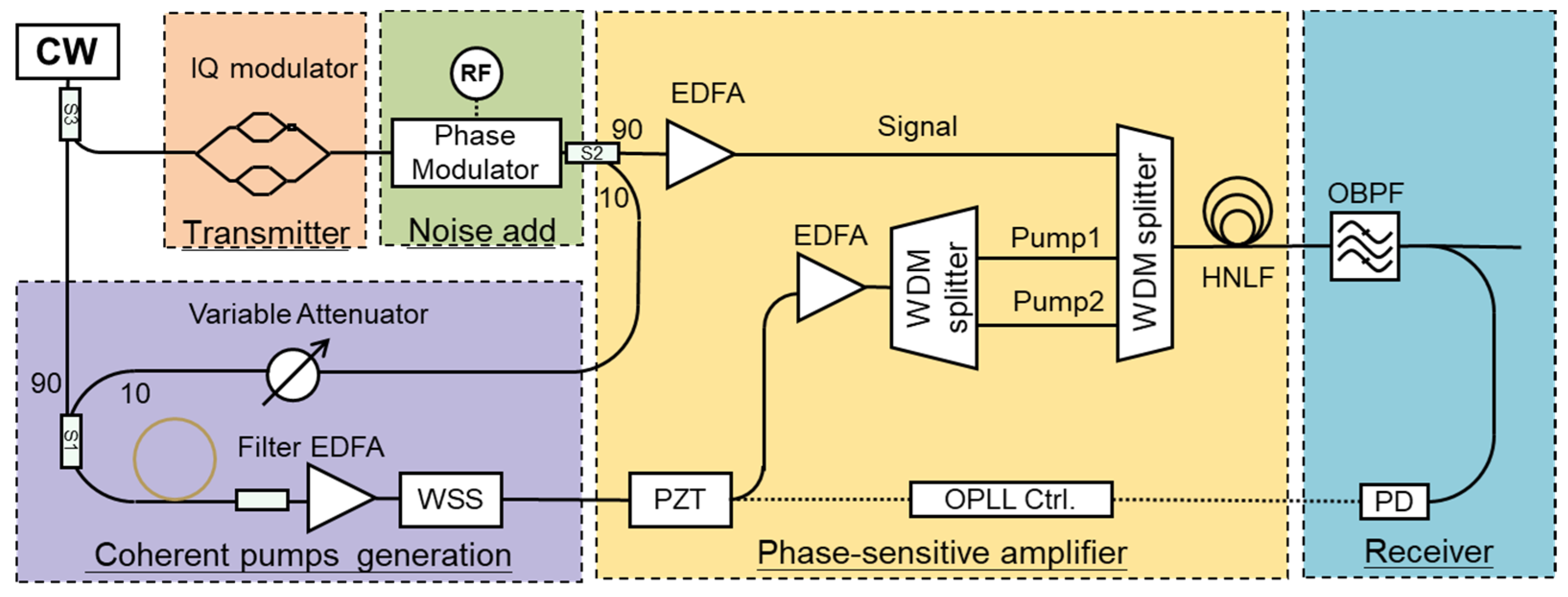
2. Materials and Methods
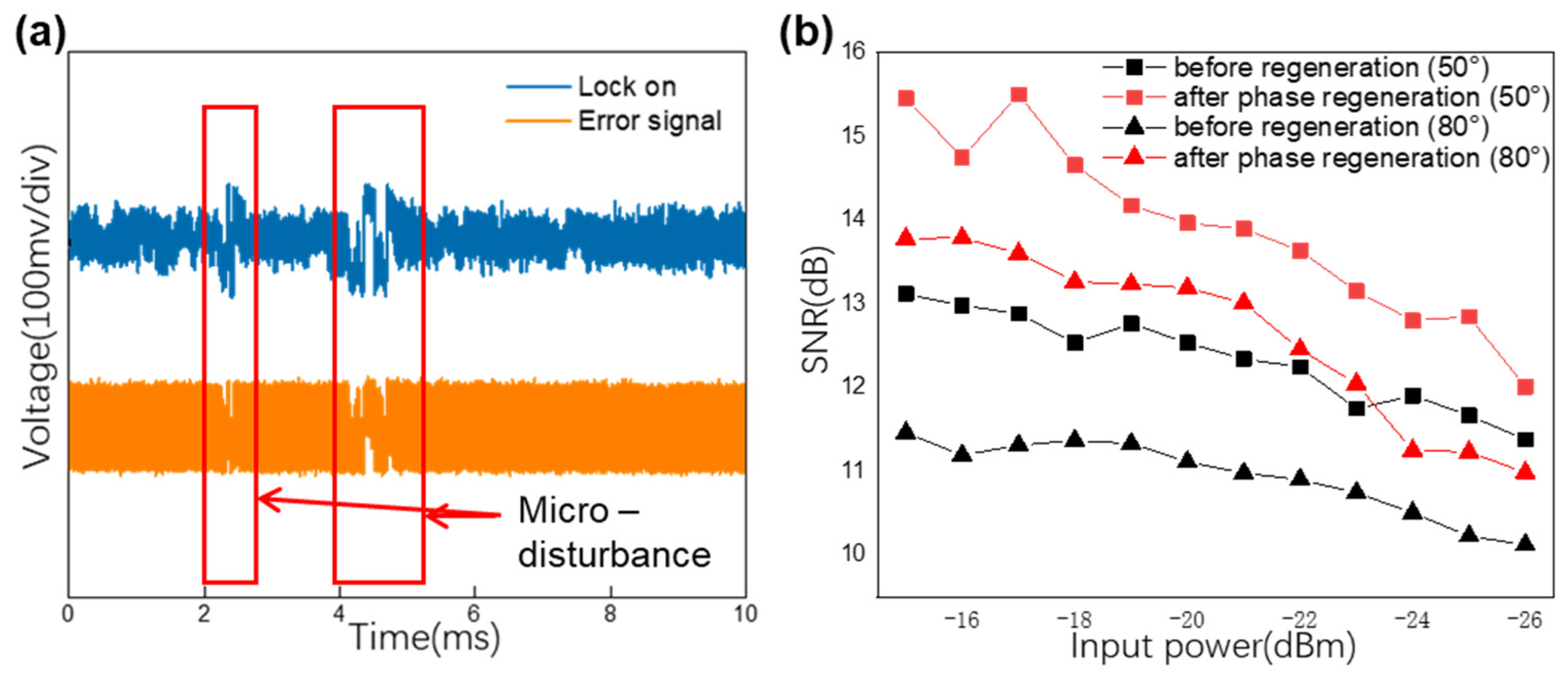
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wabnitz, S.; Eggleton, B.J. All-Optical Signal Processing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Willner, E.; Khaleghi, S.; Chitgarha, M.R.; Yilmaz, O.F. All-optical signal processing. J. Light. Technol. 2014, 32, 660. [Google Scholar] [CrossRef]
- Tong, Z.; Lundström, C.; Andrekson, P.A.; McKinstrie, C.J.; Karlsson, M.; Blessing, D.J.; Tipsuwannakul, E.; Puttnam, B.J.; Toda, H.; Grüner-Nielsen, L. Towards ultrasensitive optical links enabled by low-noise phase-sensitive amplifiers. Nat. Photonics 2011, 5, 430–436. [Google Scholar] [CrossRef]
- Slavík, R.; Parmigiani, F.; Kakande, J.; Lundström, C.; Sjödin, M.; Andrekson, P.A.; Weerasuriya, R.; Sygletos, S.; Ellis, A.D.; Grüner-Nielsen, L.; et al. All-optical phase and amplitude regenerator for next-generation telecommunications systems. Nat. Photonics 2010, 4, 690–695. [Google Scholar] [CrossRef]
- Umeki, T.; Asobe, M.; Takenouchi, H. In-line phase sensitive amplifier based on PPLN waveguides. Opt. Express 2013, 21, 12077–12084. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; Parmigiani, F.; Liu, S.; Kakande, J.; Petropoulos, P.; Gallo, K.; Richardson, D. Phase sensitive amplification based on quadratic cascading in a periodically poled lithium niobate waveguide. Opt. Express 2009, 17, 20393–20400. [Google Scholar] [CrossRef] [PubMed]
- Kakande, J.; Slavík, R.; Parmigiani, F.; Bogris, A.; Syvridis, D.; Grüner-Nielsen, L.; Phelan, R.; Petropoulos, P.; Richardson, D.J. Multilevel quantization of optical phase in a novel coherent parametric mixer architecture. Nat. Photonics 2011, 5, 748–752. [Google Scholar] [CrossRef]
- Andrekson, P.A. Progress in phase-sensitive fiber-optic parametric amplifiers and their applications. In CLEO: Science and Innovations; Optica Publishing Group: Washington, DC, USA, 2011; p. CWD1. [Google Scholar]
- Liebig, E.; Sackey, I.; Richter, T.; Gajda, A.; Peczek, A.; Zimmermann, L.; Petermann, K.; Schubert, C. Performance evaluation of a silicon waveguide for phase regeneration of a QPSK signal. J. Light. Technol. 2017, 35, 1149–1156. [Google Scholar] [CrossRef]
- Hammani, K.; Ettabib, M.A.; Bogris, A.; Kapsalis, A.; Syvridis, D.; Brun, M.; Labeye, P.; Nicoletti, S.; Richardson, D.; Petropoulos, P. Optical properties of silicon germanium waveguides at telecommunication wavelengths. Opt. Express 2013, 21, 16690–16701. [Google Scholar] [CrossRef] [PubMed]
- Lacava, M.; Ettabib, A.; Petropoulos, P. Nonlinear silicon photonic signal processing devices for future optical networks. Appl. Sci. 2017, 7, 103. [Google Scholar] [CrossRef]
- Leuthold, J.; Koos, C.; Freude, W. Nonlinear silicon photonics. Nat. Photonics 2010, 4, 535–544. [Google Scholar] [CrossRef]
- Bottrill, K.R.; Hesketh, G.; Jones, L.; Parmigiani, F.; Richardson, D.J.; Petropoulos, P. Full quadrature regeneration of QPSK signals using sequential phase sensitive amplification and parametric saturation. Opt. Express 2017, 25, 696–705. [Google Scholar] [CrossRef] [PubMed]
- Grüner-Nielsen, L.; Herstrøm, S.; Dasgupta, S.; Richardson, D.; Jakobsen, D.; Lundström, C.; Andrekson, P.A.; Pedersen, M.E.V.; Pálsdóttir, B. Silica-based highly nonlinear fibers with a high SBS threshold. In Proceedings of the IEEE Photonics Society Winter Topical Meeting, Keystone, CO, USA, 10–12 January 2011. [Google Scholar]
- Stern, L.; Stone, J.R.; Kang, S.; Cole, D.C.; Suh, M.-G.; Fredrick, C.; Newman, Z.; Vahala, K.; Kitching, J.; Diddams, S.A.; et al. Direct Kerr frequency comb atomic spectroscopy and stabilization. Sci. Adv. 2020, 6, eaax6230. [Google Scholar] [CrossRef]
- Kakande, J.; Bogris, A.; Slavík, R.; Parmigiani, F.; Syvridis, D.; Sköld, M.; Westlund, M.; Petropoulos, P.; Richardson, D.J. QPSK phase and amplitude regeneration at 56 Gbaud in a novel idler-free non-degenerate phase sensitive amplifier. In Proceedings of the Conference on Optical Fiber Communication, Technical Digest (Optical Society of America, 2011), Los Angeles, CA, USA, 6–10 March 2011; p. OMT4. [Google Scholar]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Herr, T.; Hartinger, K.; Riemensberger, J.; Wang, C.Y.; Gavartin, E.; Holzwarth, R.; Gorodetsky, M.L.; Kippenberg, T.J. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photonics 2012, 6, 480–487. [Google Scholar] [CrossRef]
- Bottrill, K.R.H.; Kakarla, R.; Parmigiani, F.; Venkitesh, D.; Petropoulos, P. Phase Regeneration of QPSK Signal in SOA using Single-stage, Wavelength Converting PSA. IEEE Photonics Technol. Lett. 2016, 28, 205–208. [Google Scholar] [CrossRef]
- Zhou, H.; Geng, Y.; Cui, W.; Huang, S.-W.; Zhou, Q.; Qiu, K.; Wong, C.W. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities. Light Sci. Appl. 2019, 8, 50. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Geng, Y.; Ke, H.; Qiu, K. Phase Regeneration of QPSK Signals Based on Kerr Soliton Combs. Photonics 2023, 10, 701. https://doi.org/10.3390/photonics10060701
Han X, Geng Y, Ke H, Qiu K. Phase Regeneration of QPSK Signals Based on Kerr Soliton Combs. Photonics. 2023; 10(6):701. https://doi.org/10.3390/photonics10060701
Chicago/Turabian StyleHan, Xinjie, Yong Geng, Haocheng Ke, and Kun Qiu. 2023. "Phase Regeneration of QPSK Signals Based on Kerr Soliton Combs" Photonics 10, no. 6: 701. https://doi.org/10.3390/photonics10060701
APA StyleHan, X., Geng, Y., Ke, H., & Qiu, K. (2023). Phase Regeneration of QPSK Signals Based on Kerr Soliton Combs. Photonics, 10(6), 701. https://doi.org/10.3390/photonics10060701



