Abstract
In recent years, dynamically tunable structural color has attracted great interest. Here, we introduce the guided-mode resonance (GMR) filter and the phase-change material Sb2S3 to design a reflective optical metasurface to produce tunable structural color, in which the combination of the GMR filter, with narrow resonant wavelength, and the Sb2S3, with a much larger bandgap and higher refractive index, helps to produce high-quality tunable structural color. The simulation results indicate that through the phase transition between the amorphous and crystalline states of Sb2S3, the proposed metasurface can generate tunable structural color that can be perceived by the naked eye. Furthermore, the metasurface can sensitively sense environmental changes through changes in structural color. This work provides a new method for realizing dynamically tunable structural color, and paves the way for the application of controllable structural color in dynamic displays, optical stealth, colorimetric sensing, and other fields.
1. Introduction
Light, which carryies a large amount of information, enters the eyes through the pupils, helping people to understand the colorful world. One of the most intuitive manifestations of this information is color. Human beings have studied and applied color for thousands of years. Currently, dyes and pigments still play a leading role in our lives as coloring materials. The common colors in nature are mainly divided into pigment colors and structural colors, according to their production mechanism. The oldest scientific description of structural color is found in ‘Micrographia’, written by Hooke, in 1665 [1]. In the past 30 years, structural color has attracted great attention as a promising alternative to dye- and pigment-based color [2]. Structural color is obtained by the scattering, diffraction, and interference of light from periodic micro-nanostructures [3]. Therefore, it has the advantages of large gamut, high saturation, high-resolution, and environmental friendliness, among others [4]. Halas et al. designed a tunable visible color-changing metasurface, which can be used as both a strain sensor and a localized surface-plasmon-resonance refractive-index sensor, with remarkable color tenability [5]. Lin et al. experimentally demonstrated the refractive-index-sensing property of a metamaterial grating device integrated with a polydimethylsiloxane microfluidic chip. The color changes of the metamaterial grating device induced by the refractive index in an ambient light environment were clear to the naked eye [6]. Based on previous research, we can conclude that structural colors mainly include metal-metasurface structural colors and all-dielectric metasurface structural colors from the perspective of material composition [4,5,6,7,8,9]. Metal-metasurface structural color has subwavelength resolution but suffers from low intensity and small gamut because of the inherent ohmic loss of metal. All-dielectric metasurface structural color has a high level of brightness, but its resolution is not as high as that of metal metasurfaces. In addition to the optimization of parameters, dynamic adjustment is also one of the key factors in determining the practicality of structural color [10]. With the further development of micro-nano-processing technology, dynamically tunable structural color will become increasingly possible.
One way to achieve tunable structural color is to turn individual elements on or off with predetermined colors. For example, Chen et al. proposed a polarization-sensitive color filter based on a titanium-oxide metasurface and realized hue- and saturation-tuned color [11], but it was difficult to realize the miniaturization of the device with the design strategy proposed. Another way to realize tunable structural color is to directly change the refractive index of the surrounding environment of the metasurface by controlling the state or component of the material. This is an ideal method with which to obtain dynamic structural colors. Duan et al. designed a magnesium-based pixelated Fabry–Pérot cavity to generate tunable color displays [12]. The hydrogenation/dehydrogenation kinetics of magnesium cause dynamic changes in FP resonance, resulting in significant color alterations. However, the color-change process requires a long response time, which affects its practical application. Shang et al. designed a microfluidic reconfigurable metasurface and realized real-time adjustable structural color [13]. However, the manufacturing process is complicated. In the past decade, an increasing number of studies have been performed on the use of phase-change materials (PCMs) in dynamically tunable structural color [14,15]. Due to their narrow bandwidths, GMR filters have great potential for realizing the high saturation of structural color and improving the sensitivity of devices to refractive-index changes. In this study, we attempted to integrate a GMR filter and a phase-change material, Sb2S3, into the metasurface to realize dynamically tunable structural color. We present the design of an optical metasurface and the investigation of the optical characteristics of the GMR filter in Section 2. We obtained three primary colors by setting the appropriate structural parameters, and took the red color as an example to investigate dynamically tunable structural color, as reported in Section 3. We found that when Sb2S3 is in the amorphous state, the chromaticity coordinates are (0.5920, 0.3238) and, when Sb2S3 is in the crystalline state, the chromaticity coordinates are (0.5692, 0.3809). The linear distance between the two chromaticity coordinates is approximately 0.06. It can be concluded that changing the phase state of the material Sb2S3 can obtain tunable structural color with noticeable changes that can be perceived by the naked eye, as shown in the CIE 1931 chromaticity diagram. Finally, we defined the sensing sensitivity s of the metasurface and calculated the maximum and minimum values of the sensing sensitivity s when the refractive index of the surrounding environment changed by 0.1, according to whether the Sb2S3 is amorphous or crystalline. The results show that the designed metasurface can sensitively display changes in environmental media, similar to a colorimeter.
2. Design of Metasurface
2.1. Main Structure
The transition of PCMs between different states can change their refractive indices, thereby altering the optical response characteristics. Hence, we can use this feature of PCMs to realize dynamic tuning of structural color. Based on previous research results, we attempted to use Sb2S3 in a GMR structure to achieve dynamically tunable structural color. The schematic diagram of tunable0structural-color metasurface with the GMR grating is shown in Figure 1. In our designed structure, both the grating layer and waveguide layer are composed of Si3N4, and have the same refractive index, n2 = n3. Furthermore, p is the period of grating, h denotes the height of grating layer, and h3, h4, and h5 represent the thickness of waveguide layer, substrate, and phase-change material, respectively.
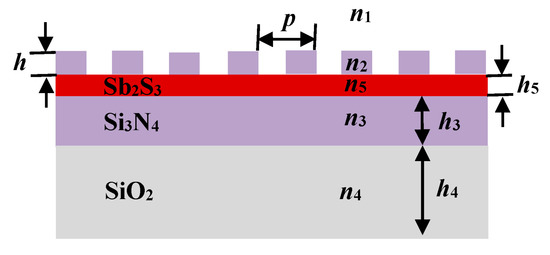
Figure 1.
The schematic diagram of reflective tunable-structural-color metasurface.
2.2. Optical Property of GMR Filter
The GMR represents a kind of phenomenon observed in waveguide-grating structures, where the intensity of diffractive field undergoes a rapid variation within small parameter ranges when an incident wave is coupled into a leaky waveguide mode [16,17]. The GMR filter is a unique kind of filter, and the full width half maximum (FWHM) of reflection/transmission spectrum can reach below 5 nm [18,19,20]. The reflectance of resonance peak is higher than 95%, and the sideband reflectance can be made lower than 5% [18]. Therefore, it is theoretically possible to obtain high-purity filtered light by using a GMR filter. In our work, we attempted to use the metasurface structure containing GMR filter with different parameters to generate the three primary colors. The schematic diagram of the side view (a) and the top view (b) of the optical metasurface obtaining GMR filter is shown in Figure 2. The region L2 is the grating layer with refractive index n2, the region L3 is the waveguide layer with refractive index n3, the cover layer L1 is the environmental medium with refractive index n1, and the lower layer L4 is the substrate with refractive index n4.
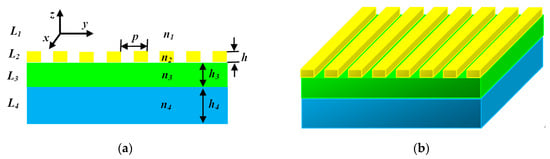
Figure 2.
The schematic diagram of the side view (a) and the top view (b) of GMR filter.
When a beam of light is incident on the grating surface, there are two polarization states of the light, which transmits through the one-dimensional (1D) grating. According to [21], the light is transmitted only when the magnetic field, H, is parallel to the slits. As a consequence, only the incident wave with TM-polarized mode can excite the GMR for 1D grating. When the TM-polarized light in y–z plane is incident on the grating surface at any angle, the diffraction wave with certain order through the grating resonates with the guided mode of the waveguide layer, provided the refractive indices of the filter material meet the following condition:
where is the effective refractive index of the grating, and f is the duty cycle. The coupled wave propagates along the y direction in the waveguide layer, and it meets the relation as follows [22]:
where is the component of the incident wave vector ki parallel to the x–y plane, is the wave vector regulated by the periodic grating structure, is the wave vector of n-order diffraction wave, λi is the wavelength in free-space, θi is the incident angle, p is the period of the grating, and is a positive integer representing the diffraction order. When the wave vector of the diffraction wave matches the counterpart of the guided-mode, the resonance occurs and the light field in the waveguide layer is redistributed. As we know, the first-order diffraction wave can excite the strongest resonance. Therefore, we consider the coupling between the first-order diffraction wave and the guided mode, and the resonance wavelength is denoted as . Using the equation:
we can obtain the resonant wavelength , which is the wavelength of the guided mode propagating in the waveguide layer. From Equation (3), we also know that the wavelength of GMR can be adjusted by changing the grating period p.
In order to obtain high-quality color with GMR filter, we investigated a large number of previous research results. The investigation found that the materials most frequently used in the grating layer of the GMR structure are SiO2 and Si3N4, and the materials most frequently used in the waveguide layer are Si3N4 and HfO2. In our work, in order to facilitate the device preparation, we used the same material, Si3N4, in the grating layer and the waveguide layer, as in [23]. Furthermore, we used finite-difference time-domain (FDTD) solutions to analyze the optical property of the GMR filter. A series of reflection spectra were obtained by changing the period p of the grating in the simulation, as shown in Figure 3. The maximum value of all reflection spectra was above 98%. The FWHM of the reflection spectrum was about 6.5 nm to 8.5 nm, and increased slighly with the red shift of the wave peak. That is to say, when the period p was 251 nm, the FWHM was 6.5 nm, and when the period p was 395 nm, the FWHM was 8.5 nm. We also found that when the period p increased by about 35 nm, the resonance peak shifted red by about 50 nm. Therefore, it can be concluded that the GMR filter has very high reflectivity throughout the visible light band from 400 nm to 700 nm.
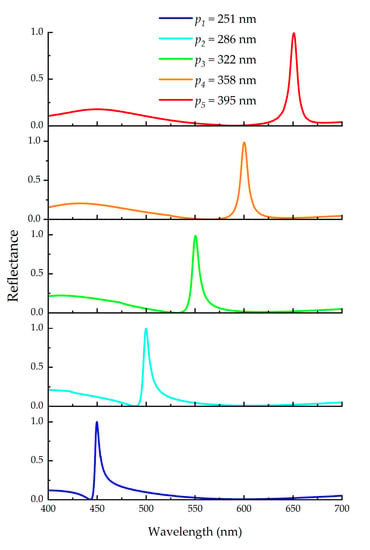
Figure 3.
The reflection spectra corresponding to different grating period, p.
From the electric field distributions, we found that the strong electric energy was confined in the waveguide layer. Through further simulation, we found that the incident light was mainly coupled into the metasurface through the ridges of the grating and formed resonance in the waveguide layer. The electric and magnetic field distributions at the resonance wavelength in the GMR filter are shown in Figure 4. The waveguide layer and the ridge of the grating are marked with white dashed lines in the figures, which verify that the GMR occurred and the coupled wave propagated along the y direction in the waveguide layer. The changes in parameters, such as the grating period p and the thickness of waveguide layer h3, had a significant impact on GMR.
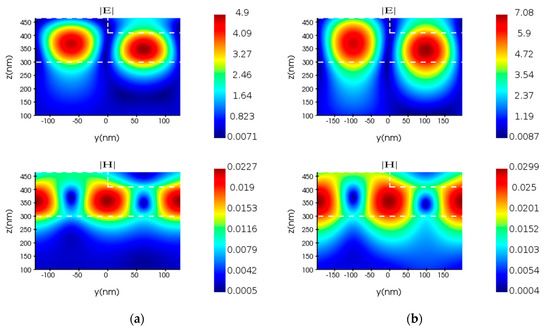
Figure 4.
The electric and magnetic field distribution maps in GMR filter correspond to the grating periods (a) p = 251 nm and (b) p = 395 nm, respectively.
2.3. Optical Properties of Sb2S3
The use of PCMs has attracted significant interest from scholars researching structural color because of its unique optical properties [24]. Optical or electrical pulses and mechanical stress can be utilized to switch materials between amorphous and crystalline states, so as to make the refractive index of PCMs change sharply and obtain a different ability to confine the light field. Common PCMs include GeTe, Ge2Sb2Te5 (GST), Ge2Sb2Se4Te1 (GSST), VO2, and TiO2, etc. [25,26,27,28]. The phase-state switching of GST is non-volatile in nature, while the phase transition of VO2 is volatile [29]. Compared with materials that require a constant energy supply to maintain their phase and optical properties, non-volatile PCMs are more attractive for practical applications [30].
Furthermore, Sb2S3 is an unconventional phase-change material, which has a much larger bandgap and, concomitantly, lower absorption. Its higher refractive index and low phonon frequency make it attractive for applications that require high transmission from the visible to the mid-infrared [30,31]. According to [31], we know the refractive indices of Sb2S3 in the visible-light band, as shown in Figure 5. Here, aSb2S3 represents Sb2S3 in the amorphous state and cSb2S3 represents Sb2S3 in the crystalline state.
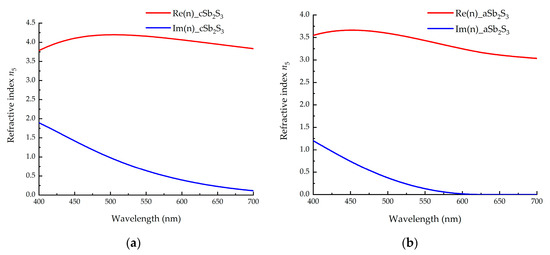
Figure 5.
The refractive-index distribution of Sb2S3 in (a) crystalline and (b) amorphous states in visible-light band. The red line represents the real part of the refractive index n5, and the blue line represents the imaginary part of the refractive index n5.
We can see that the real part of the refractive index of Sb2S3 is relatively large in the visible light band, and it has a strong ability to confine light. At the same time, the imaginary part of its refractive index is small, indicating that the absorption of light is very weak. In fact, in the visible-light band, the extinction coefficient of Sb2S3 is much smaller than that of the GST, and the real part of the refractive index of the Sb2S3 is larger than that of the GST in the crystalline state [30]. Compared with the GST and VO2, the refractive index of Sb2S3 varies greatly during the structural-phase transition in the visible range [32]. Therefore, Sb2S3 is well suited to tunable active photonics.
3. Simulations of Dynamically Tunable Structural Color
3.1. Structural Color Characteristics of the Designed Metasurface
Herein, we mainly study the characteristics of the wave reflected from the metasurface in Figure 1. The thickness of the substrate silica is relatively large. In our simulation, the thickness h4 of the substrate was always greater than 200 nm. After many simulations, the optimal thickness h5 of Sb2S3 was 10 nm, and the optimum value of the grating-duty cycle was 0.5. On the basis of these results, we further studies the optical properties of the designed metasurface by changing one of the parameters h, p, and h3. We used FDTD solutions to sweep one of the three parameters while keeping the other two unchanged. When p = 360 nm, h = 70 nm, and h3 = 80 nm, the best red color was obtained. The reflection spectrum and the CIE 1931 chromaticity diagram are shown in Figure 6, which contains the results of three different grating heights. When h was adjusted, the reflectivity at the resonance wavelength changed little, but the sidebands on both sides changed significantly. During the simulation, we found that the influence of the thickness of the phase-change material Sb2S3 on the position of the resonant peak was greater than that of the waveguide layer. Next, we obtained the best green color when p = 290 nm, h = 70 nm, and h3 = 80 nm. The corresponding reflection spectrum and the chromaticity diagram are shown in Figure 7, which contains the results of three different grating periods. As the period p increased, the resonance peak shifts red and the reflectivity also increased. Finally, we obtained the best blue color when p = 260 nm, h = 100 nm, and h3 = 60 nm. The corresponding reflection spectrum and the chromaticity diagram are shown in Figure 8, which contains the results of three different thicknesses of the waveguide layer.
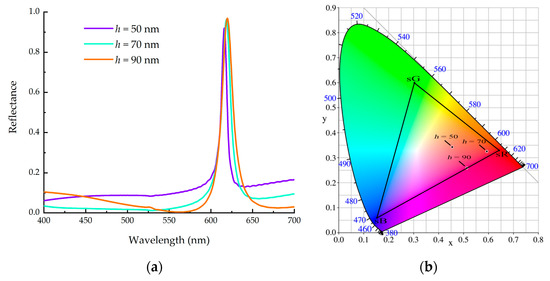
Figure 6.
(a) the reflection spectrum and (b) the CIE 1931 chromaticity diagram corresponding to red color.
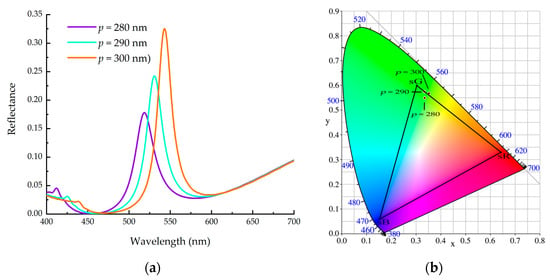
Figure 7.
(a) the reflection spectrum and (b) the CIE 1931 chromaticity diagram corresponding to green color.
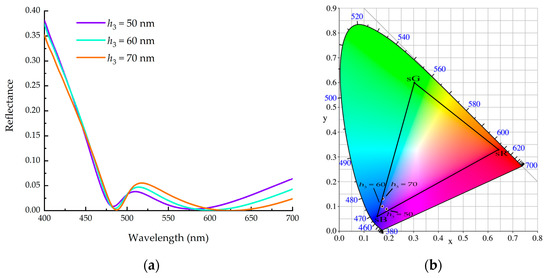
Figure 8.
(a) the reflection spectrum and (b) the CIE 1931 chromaticity diagram corresponding to blue color.
From the simulation results, we found that the efficiency of the generation of green and blue colors by using the proposed metasurface structure was relatively low. This was mainly caused by the optical properties of the phase-change material itself, as the Sb2S3 had relatively large extinction coefficients in the green and blue bands. The results in Figure 3 indicate that the GMR filter can efficiently generate three primary colors. However, from the results in Figure 7 and Figure 8, it can be seen that the combination of the GMR filter and PCMs was not yet perfect. This is a further problem that we need to strive to solve by, for example, searching for materials with lower extinction coefficients in the green and blue bands to replace Sb2S3. After preliminary investigation, In2Se3 was found to be a possible candidate material, which is expected to generate both green and blue colors more efficiently.
3.2. Dynamic Tuning Characteristics
As shown in Section 2.3, we found that the refractive index of the phase-change material, Sb2S3, underwent a significant change as it transitioned from the amorphous to the crystalline state. In this section, we take the red band as an example to study the color-dynamic-tuning ability of the designed optical metasurface. Firstly, we simulated a case in which the Sb2S3 was in the amorphous state. The heights h of the grating were set to 60 nm, 70 nm, and 80 nm, respectively. The period p was set to 350 nm, 360 nm, and 370 nm, respectively. Secondly, we simulated a case in which the Sb2S3 was in the crystalline state. The values of the parameters h and p were the same as those in the amorphous state. The simulated results are shown in Figure 9. Compared with the simulation results, it was found that when the Sb2S3 was amorphous, the metasurface had a higher reflectivity, as shown in Figure 9a,c,e, and the obtained structural-color brightness is better. This was related to the low extinction coefficient of the amorphous Sb2S3. Additionally, it can be seen from the chromaticity diagram that when the Sb2S3 was amorphous, changing the height h or period p of the grating resulted in a more obvious change in the obtained structural color, as shown in Figure 9b,d,f. In these three figures, the ap and cp represent the parameters of period p when the Sb2S3 was in the amorphous and crystalline states, respectively. The figures show that the designed metasurface structure was more sensitive when the Sb2S3 was amorphous. From the reflection spectrum, we also found that the resonance wavelength shifted red with the increase in the grating period p. This was consistent with the theoretical prediction given by Equation (3). From the color palettes in Figure 9g, we found that when changing the phase state of the Sb2S3, significant color changes were observed in the metasurface structure, even with different parameters. In Figure 9g, the horizontal axis represents the height h of the grating and the phase state of the Sb2S3, and the vertical axis represents the period p of the grating. For example, the three color blocks in the first column, from the bottom to the top, correspond to the colors where Sb2S3 is in an amorphous state, the grating height h is 60 nm, and the grating periods p are 350 nm, 360 nm, and 370 nm, respectively.
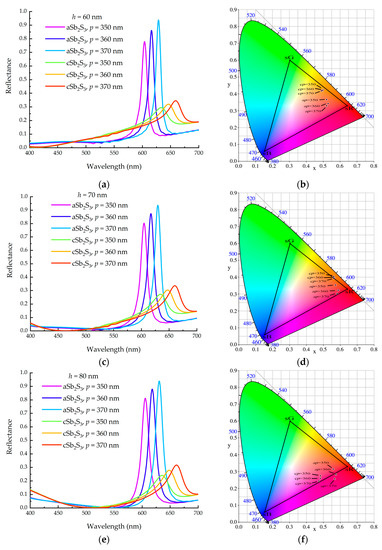
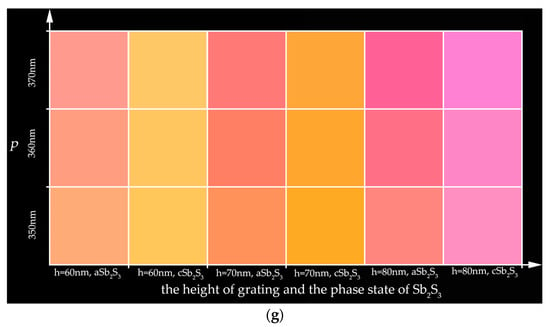
Figure 9.
The tunable structural color obtained from the designed metasurface with Sb2S3 in amorphous and crystalline states: (a,c,e) are the reflection spectra corresponding to h = 60 nm, 70 nm, 80 nm, respectively; (b,d,f) are the chromaticity diagrams corresponding to h = 60 nm, 70 nm, 80 nm, respectively; (g) is the color palettes corresponding to these reflection spectra.
We can transform Sb2S3 from the amorphous to the crystalline state by heating the material. Using electrical or optical pulses with tunable pulse length and power can reversibly crystallize and amorphize Sb2S3. Compared to optical switching excitation, electrical switching excitation has more advantages because it does not require complex alignment processes. Fang et al. found that the material Sb2S3 started to crystallize at ≈523 K, and the grain growth reached completion at 573 K [33]. Muskens et al. found that the transition temperature of Sb2S3 is 543 K [31].By heating the material above its melting temperature and then quenching the sample faster than the crystallization speed, we can also change Sb2S3 from the crystalline to the amorphous state [31,33]. The material Sb2S3 can be switched between amorphous and crystalline states on a nanosecond time scale, and the switching time is about 78 ns [30]. Mei et al. confirmed through experiments that the cycling durability that Sb2S3 can achieve is 7000 cycles [34].
Compared to materials such as GST, GSST, and VO2, Sb2S3 has a larger band gap [33,35,36,37], resulting in lower light absorption and, thus, greater structural color brightness. The phase-change temperature of Sb2S3 is higher than those of GST and VO2 [14,31] and lower than that of GSST [31], indicating that Sb2S3 is not be the best choice if energy consumption is the primary consideration. The crystallization switching time of Sb2S3 is 78 ns, which is equivalent to that of GST and better than that of GSST [26,38]. The switching time of VO2 between the metal and the semiconductor is about 2~3 ns in an electrically driven manner [39]. In short, the switching time of Sb2S3 is sufficient in terms of practicality. The cycling endurance of GST and GSST is about 105 cycles [25,40], which is far better than that of Sb2S3. Of course, with the progress of technology and the improvement of heating methods, the cycling durability of Sb2S3 will be further improved. The main parameters of the four PCMs mentioned above are shown in Table 1.

Table 1.
Comparison between main parameters of Sb2S3 and those of other common PCMs.
In general, the higher the refractive index of a material, the stronger its ability to localize light. The greater the change in refractive index of PCMs during the phase-change process, the stronger their ability to tune structural color. The smaller the extinction coefficient of a material, the less light it absorbs, and the resulting structural color brightness is higher. Based on these principles, we analyzed the ability of these four PCMs to tune structural color by comparing their refractive index, extinction coefficient, and refractive-index-variation values. In contrast, Sb2S3 has a higher ability to tune structural color.
3.3. Environment-Sensing Properties of Tunable Structural Color Metasurface
In this section, we report the simulation of an application scenario in which the designed metasurface was used to characterize the change of the refractive index n1 of the cover layer. When the Sb2S3 remained in the amorphous or crystalline state, we swept the refractive index n1 from 1 to 1.5 in steps of 0.1. The obtained chromaticity diagrams and color palettes are shown in Figure 10. When Sb2S3 was in the amorphous state and the refractive index n1 changed from 1 to 1.5, the chromaticity coordinates were (0.5920, 0.3238), (0.6088, 0.3232), (0.5759, 0.2899), (0.4687, 0.2150), (0.4131, 0.1992), and (0.3842, 0.2198), respectively. Additionally, when the refractive index n1 changed by 0.1, the minimum linear distance between the chromaticity coordinates before and after the refractive index change was about 0.017, and the maximum linear distance was about 0.131. When the Sb2S3 was in the crystalline state and the refractive index n1 changed from 1 to 1.5, the chromaticity coordinates were (0.5692, 0.3809), (0.5727, 0.3949), (0.5047, 0.3516), (0.3759, 0.2433), (0.3286, 0.2265), and (0.3107, 0.2544), respectively. Furthermore, when the refractive index n1 changed by 0.1, the minimum linear distance between the chromaticity coordinates before and after the refractive index change was about 0.014, and the maximum linear distance was about 0.168. We define the sensing sensitivity s of the metasurface, and the equation for s is as follows:
where Δn is the change in the refractive index of the environmental medium, and Δd is the linear distance between the chromaticity coordinates caused by Δn. According to Equation (4), when Sb2S3 is in the amorphous state and the refractive index n1 changes by 0.1, the maximum sensing sensitivity s of the designed metasurface is 1.31, and the minimum value of the sensing sensitivity s is 0.17. When Sb2S3 is in the crystalline state and the refractive index n1 changes by 0.1, the maximum sensing sensitivity s of the designed metasurface is 1.68, and the minimum value of sensing sensitivity s is 0.14.
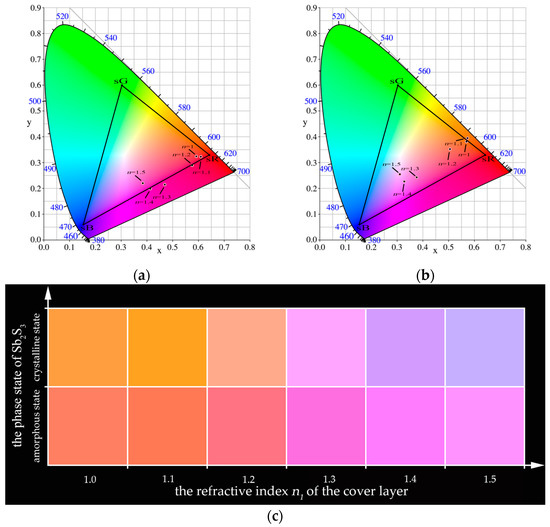
Figure 10.
The chromaticity diagrams and color palettes with different refractive indices and phase states: (a) chromaticity diagram when Sb2S3 is in amorphous state; (b) chromaticity diagram when Sb2S3 is in crystalline state; (c) color palettes corresponding to different refractive indices of the cover layer and different phase states of Sb2S3.
On the other hand, when the refractive index n1 remains constant between 1~1.5, the minimum linear distance between the chromaticity coordinates before and after the phase transition of Sb2S3 is 0.061, and the maximum linear distance is 0.097. These results show that the designed metasurface is sensitive to small changes in the refractive index of the cover layer. We can conclude that the metasurface with the phase-change material Sb2S3 can sensitively display changes in ambient temperature, humidity, or material composition through color. This is very useful in instruments such as colorimeters.
4. Conclusions
In summary, we investigated the optical properties of a GMR filter and the phase-change characteristic of the material Sb2S3, and introduced a GMR filter and Sb2S3 into the optical metasurface to produce tunable structural color. The simulation results show that dynamically tunable structural color can be obtained through the phase transition of Sb2S3 between the amorphous and crystalline states. Taking the red color as an example, when Sb2S3 changes from the amorphous to the crystalline state, the chromaticity coordinate changes from (0.5920, 0.3238) to (0.5692, 0.3809). The linear distance between two chromaticity coordinates is about 0.06. Finally, we applied the designed optical metasurface to check the refractive-index changes caused by changes in ambient temperature, humidity, or material composition. It can be concluded that the metasurface we proposed can sensitively sense changes in the environment. This work provides a new idea for realizing dynamically tunable structural color, and paves the way for the application of controllable structural color in dynamic displays, optical stealth, colorimetric sensing, and other fields. We believe that dynamically controllable structural color will increasingly enter individuals’ lives with the further development of nano-processing technology.
Author Contributions
Conceptualization, S.L.; methodology, X.H.; software, Z.Z. (Zhaojian Zhang); data curation, S.L. and X.L.; writing—original draft preparation, S.L.; writing—review and editing, Z.Z. (Zhaojian Zhang) and J.Y.; visualization, S.L.; supervision, M.F. and J.Y.; project administration, Z.Z. (Zhenfu Zhang) and J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (60907003, 61805278, 12272407, 62275269, 62275271); National Key R&D Program of China (2022YFF0706005); China Postdoctoral Science Foundation (2018M633704); Foundation of NUDT (JC13-02-13, ZK17-03-01); Hunan Provincial Natural Science Foundation of China (13JJ3001); and Program for New Century Excellent Talents in University (NCET-12-0142).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kinoshita, S.; Yoshioka, S.; Miyazaki, J. Physics of structural colors. Rep. Prog. Phys. 2008, 71, 076401. [Google Scholar] [CrossRef]
- Baek, K.; Kim, Y.; Mohd-Noor, S.; Hyun, J.K. Mie Resonant Structural Colors. ACS Appl. Mater. Interfaces 2020, 12, 5300–5318. [Google Scholar] [CrossRef] [PubMed]
- Nagasaki, Y.; Suzuki, M.; Takahara, J. All-Dielectric Dual-Color Pixel with Subwavelength Resolution. Nano Lett. 2017, 17, 7500–7506. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, S.; Song, Q.; Liu, Y.; Wu, Y.; Wang, S.; Yu, J.; Han, J.; Tsai, D.-P. All-dielectric metasurface for high-performance structural color. Nat. Commun. 2020, 11, 1864 . [Google Scholar] [CrossRef]
- Cerjan, B.; Gerislioglu, B.; Link, S.; Nordlander, P.; Halas, N.J.; Griep, M. Towards scalable plasmonic Fano-resonant metasurfaces for colorimetric sensing. Nanotechnology 2022, 33, 405201. [Google Scholar] [CrossRef]
- Zheng, D.Y.; Wen, Y.; Xu, X.C.; Lin, Y.S. Metamaterial grating for colorimetric chemical sensing applications. Mater. Today Phys. 2023, 33, 101056. [Google Scholar] [CrossRef]
- Tan, S.J.; Zhang, L.; Zhu, D.; Goh, X.M.; Wang, Y.M.; Kumar, K.; Qiu, C.W.; Yang, J.K.W. Plasmonic Color Palettes for Photorealistic Printing with Aluminum Nanostructures. Nano Lett. 2014, 14, 4023–4029. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.L.; Vannahme, C.; Hojlund-Nielsen, E.; Mortensen, N.A.; Kristensen, A. Plasmonic colour laser printing. Nat. Nanotechnol. 2016, 11, 325–329. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, Z.X.; Zhang, C.; Gao, Y.S.; Duan, Z.H.; Xiao, S.M.; Song, Q.H. All-Dielectric Full-Color Printing with TiO2 Metasurfaces. ACS Nano 2017, 11, 4445–4452. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.; Zhuo, X.L.; Wang, J.F. Advanced Plasmonic Materials for Dynamic Color Display. Adv. Mater. 2018, 30, 1704338. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Liu, W.W.; Li, Z.C.; Cheng, H.; Chen, S.Q.; Tian, J.G. Polarization-Sensitive Structural Colors with Hue-and-Saturation Tuning Based on All-Dielectric Nanopixels. Adv. Opt. Mater. 2018, 6, 1701009. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Duan, X.Y.; Matuschek, M.; Zhou, Y.M.; Neubrech, F.; Duan, H.G.; Liu, N. Dynamic Color Displays Using Stepwise Cavity Resonators. Nano Lett. 2017, 17, 5555–5560. [Google Scholar] [CrossRef]
- Sun, S.; Yang, W.H.; Zhang, C.; Jing, J.X.; Gao, Y.S.; Yu, X.Y.; Song, Q.H.; Xiao, S.M. Real-Time Tunable Colors from Microfluidic Reconfigurable All-Dielectric Metasurfaces. ACS Nano 2018, 12, 2151–2159. [Google Scholar] [CrossRef] [PubMed]
- Raeis-Hosseini, N.; Rho, J. Metasurfaces Based on Phase-Change Material as a Reconfigurable Platform for Multifunctional Devices. Materials 2017, 10, 1046. [Google Scholar] [CrossRef] [PubMed]
- Schlich, F.F.; Zalden, P.; Lindenberg, A.M.; Spolenak, R. Color Switching with Enhanced Optical Contrast in Ultrathin Phase-Change Materials and Semiconductors Induced by Femtosecond Laser Pulses. Acs Photonics 2015, 2, 178–182. [Google Scholar] [CrossRef]
- Liu, W.; Lai, Z.; Guo, H.; Liu, Y. Guided-mode resonance filters with shallow grating. Opt. Lett. 2010, 35, 865–867. [Google Scholar] [CrossRef]
- Priambodo, P.S.; Maldonado, T.A.; Magnusson, R. Fabrication and characterization of high-quality waveguide-mode resonant optical filters. Appl. Phys. Lett. 2003, 83, 3248–3250. [Google Scholar] [CrossRef]
- Tibuleac, S.; Magnusson, R. Reflection and transmission guided-mode resonance filters. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1997, 14, 1617–1626. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Wang, S.; Zheng, W. Wavelength-tunable perfect absorber based on guided-mode resonances. Appl. Opt. 2016, 55, 3176–3181. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, D.; Xu, B.; Huang, Y.; Tao, C.; Wang, C.; Li, B.; Ni, Z.; Zhuang, S. Colored image produced with guided-mode resonance filter array. Opt. Lett. 2011, 36, 4698–4700. [Google Scholar] [CrossRef]
- Sakat, E.; Vincent, G.; Ghenuche, P.; Bardou, N.; Dupuis, C.; Collin, S.; Pardo, F.; Haidar, R.; Pelouard, J.L. Free-standing guided-mode resonance band-pass filters: From 1D to 2D structures. Opt. Express 2012, 20, 13082–13090. [Google Scholar] [CrossRef] [PubMed]
- Collin, S.; Pardo, F.; Teissier, R.; Pelouard, J.L. Strong discontinuities in the complex photonic band structure of transmission metallic gratings. Phys. Rev. B 2001, 63, 033107. [Google Scholar] [CrossRef]
- Uddin, M.J.; Magnusson, R. Highly efficient color filter array using resonant Si3N4 gratings. Opt. Express 2013, 21, 12495–12506. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Bhaskaran, H.; Taubner, T. Phase-change materials for non-volatile photonic applications. Nat. Photonics 2017, 11, 465–476. [Google Scholar] [CrossRef]
- Carrillo, S.G.C.; Trimby, L.; Au, Y.Y.; Nagareddy, V.K.; Rodriguez-Hernandez, G.; Hosseini, P.; Ros, C.; Bhaskaran, H.; Wright, C.D. A Nonvolatile Phase-Change Metamaterial Color Display. Adv. Opt. Mater. 2019, 7, 1801782. [Google Scholar] [CrossRef]
- Simpson, R.E.; Krbal, M.; Fons, P.; Kolobov, A.V.; Tominaga, J.; Uruga, T.; Tanida, H. Toward the Ultimate Limit of Phase Change in Ge2Sb2Te5. Nano Lett. 2010, 10, 414–419. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Bakan, G.; Ahuja, R.; Adam, J.; Mishra, Y.K.; Ahmadivand, A. The role of Ge2Sb2Te5 in enhancing the performance of functional plasmonic devices. Mater. Today Phys. 2020, 12, 100178. [Google Scholar] [CrossRef]
- Kepič, P.; Ligmajer, F.; Hrtoň, M.; Ren, H.; Menezes, L.d.S.; Maier, S.A.; Šikola, T. Optically Tunable Mie Resonance VO2 Nanoantennas for Metasurfaces in the Visible. ACS Photonics 2021, 8, 1048–1057. [Google Scholar] [CrossRef]
- de Galarreta, C.R.; Sinev, I.; Alexeev, A.M.; Trofimov, P.; Ladutenko, K.; Carrillo, S.G.C.; Gemo, E.; Baldycheva, A.; Bertolotti, J.; Wright, C.D. Reconfigurable multilevel control of hybrid all-dielectric phase-change metasurfaces. Optica 2020, 7, 476–484. [Google Scholar] [CrossRef]
- Dong, W.; Liu, H.; Behera, J.K.; Lu, L.; Ng, R.J.H.; Sreekanth, K.V.; Zhou, X.; Yang, J.K.W.; Simpson, R.E. Wide Bandgap Phase Change Material Tuned Visible Photonics. Adv. Funct. Mater. 2019, 29, 1806181. [Google Scholar] [CrossRef]
- Delaney, M.; Zeimpekis, I.; Lawson, D.; Hewak, D.W.; Muskens, O.L. A New Family of Ultralow Loss Reversible Phase-Change Materials for Photonic Integrated Circuits: Sb2S3 and Sb2Se3. Adv. Funct. Mater. 2020, 30, 2002447. [Google Scholar] [CrossRef]
- Li, H.X.; Zhang, X.; Zhou, F.; Xiao, X.S.; Xu, Y.L.; Zhang, Z.P. Tunable color gamut based a symmetric microcavity governed by Sb2S3. Opt. Commun. 2022, 508, 127683. [Google Scholar] [CrossRef]
- Fang, Z.R.; Zheng, J.J.; Saxena, A.; Whitehead, J.; Chen, Y.Y.; Majumdar, A. Non-Volatile Reconfigurable Integrated Photonics Enabled by Broadband Low-Loss Phase Change Material. Adv. Opt. Mater. 2021, 9, 2002049. [Google Scholar] [CrossRef]
- Gao, K.; Du, K.; Tian, S.M.; Wang, H.; Zhang, L.; Guo, Y.X.; Luo, B.C.; Zhang, W.D.; Mei, T. Intermediate Phase-Change States with Improved Cycling Durability of Sb2S3 by Femtosecond Multi-Pulse Laser Irradiation. Adv. Funct. Mater. 2021, 31, 2103327. [Google Scholar] [CrossRef]
- Lee, B.S.; Abelson, J.R.; Bishop, S.G.; Kang, D.H.; Cheong, B.K.; Kim, K.B. Investigation of the optical and electronic properties of Ge2Sb2Te5 phase change material in its amorphous, cubic, and hexagonal phases. J. Appl. Phys. 2005, 97, 093509. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Zhang, W. First-principles investigation of amorphous Ge-Sb-Se-Te optical phase-change materials. Opt. Mater. Express 2022, 12, 2497–2506. [Google Scholar] [CrossRef]
- Rana, R.S.; Nolte, D.D.; Chudnovski, F.A. Optical bistability from a thermodynamic phase transition in vanadium dioxide. Opt. Lett. 1992, 17, 1385–1387. [Google Scholar] [CrossRef]
- Wang, H.; Guo, T.; Xue, Y.; Lv, S.; Yao, D.; Zhou, Z.; Song, S.; Song, Z. The phase change memory features high-temperature characteristic based on Ge-Sb-Se-Te alloys. Mater. Lett. 2019, 254, 182–185. [Google Scholar] [CrossRef]
- Markov, P.; Marvel, R.E.; Conley, H.J.; Miller, K.J.; Haglund, R.F.; Weiss, S.M. Optically Monitored Electrical Switching in VO2. ACS Photonics 2015, 2, 1175–1182. [Google Scholar] [CrossRef]
- Sahoo, D.; Naik, R. GSST phase change materials and its utilization in optoelectronic devices: A review. Mater. Res. Bull. 2022, 148, 111679. [Google Scholar] [CrossRef]
- Lee, H.C.; Jeong, J.H.; Choi, D.J. Characterization of phase-change behavior of a Ge2Sb2Te5 thin film using finely controlled electrical pulses for switching. Semicond. Sci. Technol. 2016, 31, 095006. [Google Scholar] [CrossRef]
- De Leonardis, F.; Soref, R.; Passaro, V.M.N.; Zhang, Y.F.; Hu, J.J. Broadband Electro-Optical Crossbar Switches Using Low-Loss Ge2Sb2Se4Te1 Phase Change Material. J. Light. Technol. 2019, 37, 3183–3191. [Google Scholar] [CrossRef]
- Sun, X.N.; Qu, Z.M.; Yuan, J.H.; Cheng, E.W.; Wang, P.P.; Wang, Q.G. Voltage-induced phase transition of VO2@SiO2 nanoparticles. Ceram. Int. 2021, 47, 29011–29022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).