Abstract
The characteristics of high-power vortex Bessel beams in the terahertz range ( μm) obtained with the use of diffractive axicons (DAs) illuminated by a Gaussian beam of the Novosibirsk free-electron laser were studied. Two of the three possible types of DA recently described in our previous paper, namely, binary spiral silicon axicons (BAs), forming beams with a topological charge l equal to 0–4 and 9, and a diamond “holographic” axicon (HA), forming a beam with , were used in the experiments. These axicons formed beams whose cross sections in the region of inner Bessel rings were close to those of ideal Bessel beams, but their intensities varied in azimuth with a frequency of l and for the BAs and HA, respectively. However, in the case of the BAs, the beams had a pronounced helical structure at the periphery, whereas for the HA, the beam was axisymmetric. By focusing these beams with a lens, we studied the structure of the so-called “perfect” beams (PBs). While an ideal Bessel beam exhibits a PB as a thin ring, in the case of the BAs, we observed a broadened ring structure consisting of short spirals, and for the HA, we observed a narrow ring with maxima in azimuth. A comparison of the numerical calculations and experiments showed that the observed azimuthal intensity variations can be attributed to inaccuracies in the preparation of the axicon relief and/or discrepancies between the calculated and actual wavelengths, within a few percent. The results of this work enable the establishment of quality requirements for axicon manufacture and the appropriate selection of the axicon type in accordance with the requirements for the beam.
1. Introduction
Photon beams with orbital angular momentum [1,2,3], or vortex beams, play an increasingly important role in modern optics and various applications. Most of these applications relate to the visible and infrared spectra [4,5]. For example, optical tweezers allow the manipulation of not only the spatial position of particles but also the various degrees of freedom associated with them. The trapping and manipulation of liquid crystal droplets, as well as dielectric and metal particles, have been demonstrated in [6,7]. Optical tweezers enable the manipulation of proteins, DNA, and enantiomers [8,9] and can be used for single-cell microsurgery [10].
Vortex beams have expanded the scope of imaging optics. Several papers have demonstrated the use of vortex beams to achieve resolution beyond the diffraction limit [11], enable phase contrast imaging in microscopy [12], determine the topography of a target [13], study turbulence in the atmosphere [14] and the ocean [15], and measure the rotation speed of objects [16]. The orbital angular momentum of vortex beams has opened up new possibilities in materials processing technology [17,18,19,20].
One of the promising applications of vortex beams is in communication systems. The possibility of using one frequency to transmit information through several beams with different topological charges enables the creation of multiplex transmission lines in free space [21,22], including those in the long-wave band [23,24,25].
The methods used to generate vortex beams vary significantly (see, e.g., [26,27,28]). Currently, the most widely used devices for generating vortex beams are spatial light modulators (SLMs). In the visible range, the most convenient technique for the formation of vortex beams is the application of liquid crystal SLMs. They are computer-controlled, have a high spatial resolution, and their amplitude-phase function can be changed with a high frequency. In [29], for example, the generation of liquid crystal helical axicons for the optical range is described. Digital holograms formed with SLMs are also widely employed for the modal decomposition of arbitrary wave fields. In [30,31,32,33,34,35,36], methods that enable the determination of both the radial and azimuthal wave numbers of vortex beams are discussed.
In the terahertz range, the development of SLMs is just beginning. The progress in this field is described in [37,38,39,40], but these modulators have not yet reached the level required in practical applications in terms of resolution, speed of operation, and the number of resolved elements. Additionally, when working with high-power terahertz radiation sources, such as gyrotrons [41,42] and free-electron lasers [43,44,45,46], liquid crystal devices can be damaged by radiation. For this reason, classical diffractive optical elements [47,48] currently remain the most suitable devices for controlling terahertz radiation beams, including the formation of beams of a given mode composition.
In our previous works, we have designed and manufactured a wide range of diffractive optical elements (DOEs), including binary and continuous-relief elements, for the control of high-power terahertz radiation. These elements include focusing elements [49,50,51], elements for generating beams with different mode compositions [52], elements for concentrating terahertz radiation into specific two- or three-dimensional domains [53,54], sub-wavelength metastructures that produce vector beams with different polarization states [55,56], and others. When DOEs are used to transform the mode content of a beam, they can be considered computer-synthesized holograms [57,58]. These DOEs have been studied by applying high-power continuous-wave terahertz radiation from the Novosibirsk free-electron laser (NovoFEL [44]).
In this paper, we focus on Bessel beams, which are used in many applications due to their unique properties. It is well known that it is impossible to create an ideal Bessel beam in real life since it would need to be infinitely wide and, consequently, have infinite energy. Real beams whose properties closely resemble those of Bessel beams are produced by applying phase radial diffraction gratings and axicons. A zero-order quasi-Bessel beam can be obtained with axisymmetric axicons, whereas for the production of beams of higher orders, the phase function of the axicon must ensure the azimuthal rotation of the beam. Vortex Bessel beams in the terahertz range were first experimentally obtained via the transformation of the Gaussian beam of the NovoFEL with binary spiral axicons [59,60]. Later, terahertz vortex beams were obtained through other methods (see [61]).
The generation of terahertz Bessel beams paves the way for the development of new applications. In [62,63], it was shown that the diffraction of a Bessel beam by a periodic two-dimensional grating in the Talbot planes results in the formation of periodic gratings of annular microbeams, which can be regarded as analogs of perfect beams. A very interesting application was demonstrated in [64], where beams with orbital angular momentum were first used to excite vortex surface plasmon polaritons propagating along a cylindrical conductor for a distance of up to 150 mm. The Bessel beam was first transformed by means of a lens into the so-called “perfect beam” of an annular configuration [65,66,67,68] (see detailed description in Section 3.3), which when diffracting at the front edge of the cylinder [69,70,71], excited vortex plasmons around the perimeter. Using this method to excite a superposition of vortex plasmons by beams with different topological charges, each encoding a separate portion of information, opens up the possibility of creating a multiplex plasmonic transmission line. The properties of the generated plasmons and the efficiency of their generation are significantly dependent on the properties of the excitation of vortex beams. Clearly, in all other applications, the characteristics of beams are also of significant, or even decisive, importance.
In [72], the wave fields of quasi-Bessel beams formed by three types of axicons (binary, kinoform, and holographic) were calculated numerically (and analytically for a binary axicon). In the experiments described below, we investigate beams formed by five binary silicon axicons and one diamond holographic axicon, listed in Table 1. We analyze the Bessel beams produced by these two types of diffractive axicons and their correlation with the ideal Bessel beam, described by Equation (1), as well as with each other, and compare the results with numerical simulations.
2. Materials and Methods
2.1. Diffractive Axicons
Ideal Bessel beams are known to be described analytically by the Bessel function [73]
which occupies all free space and has an infinite width and, therefore, infinite energy. Here, is the radial wave number, is the azimuthal angle, is the axial component of the wavevector , and l is the azimuthal quantum number, known as the “topological charge” (TC). The function can be expanded to a superposition of conically converging plane waves
under an angle
The Fourier amplitudes in Equation (2) are

Table 1.
Design parameters used in the manufacture of binary axicons (BA) and holographic axicons (HA) (see Figure 1). is the period of the binary axicons, l is the topological charge modulus of the beam produced by the axicon, R is the radius of the axicon, and is the distance at which the Bessel beam decays (see Figure 2). The HA9 is not periodic in radius; the width of its zones corresponds to the Bessel beam with a wave number of (see Equation (8) below). The axicons are designed for a radiation wavelength of 141 μm.
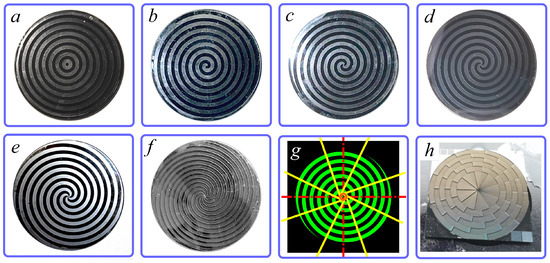
Figure 1.
Photographs of axicons used in this work. (a–f) Silicon helical binary axicons with diameters of 50 mm. (a–e) Axicons with and period mm. (f) Axicon with and mm. (h) Diamond holographic axicon with a diameter of 20 mm and . (g) Yellow lines: local normals to Archimedean spiral of axicon shown in (c); red circle: evolute of spirals. (c). Axicons form beams with positive topological charges when the initial Gaussian beam is incident normally onto the axicon surface. To generate beams with a negative topological charge, the axicons should be rotated by about the vertical axis. The aperture of the axicons was limited by frames, and their radii are indicated in Table 1.
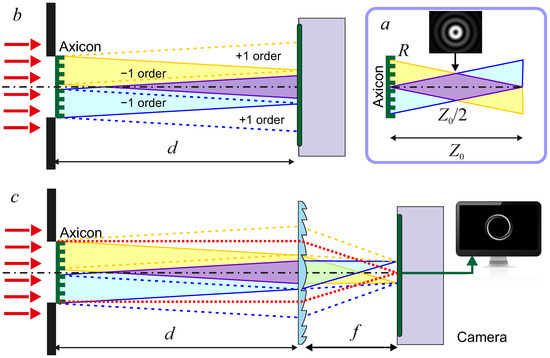
Figure 2.
Experimental schematics. (a) Conically converging plane waves (minus first-order diffraction on helical binary or annular holographic phase grating) forming a Bessel beam. For clarity, the converging and divergent waves from different sides of the axicon are shown in different colors. The optimal region for the formation of the Bessel beam lies in the vicinity of , and the beam collapses at a distance of . (b) Beams behind the axicon. Dashed lines indicate beams of plus first-order diffraction. (c) Formation of the perfect beam with a kinoform polypropylene lens ( mm, mm). Dotted red lines indicate the plain wave that passed through the axicon in the experiments (for details, see text).
Table 1.
Design parameters used in the manufacture of binary axicons (BA) and holographic axicons (HA) (see Figure 1). is the period of the binary axicons, l is the topological charge modulus of the beam produced by the axicon, R is the radius of the axicon, and is the distance at which the Bessel beam decays (see Figure 2). The HA9 is not periodic in radius; the width of its zones corresponds to the Bessel beam with a wave number of (see Equation (8) below). The axicons are designed for a radiation wavelength of 141 μm.
| Axicon | BA0 | BA1 | BA2 | BA3 | BA4 | BA3-2 | BA9 | HA9 |
|---|---|---|---|---|---|---|---|---|
| l | 0 | 1 | 2 | 3 | 4 | 3 | 9 | 9 |
| p, mm | 3.1 | 3.1 | 3.1 | 3.1 | 3.1 | 2.03 | 2.03 | N/A |
| R, mm | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 10 |
| Z, mm | 550 | 550 | 550 | 550 | 550 | 360 | 360 | 144 |
The ideal Bessel beam cannot exist in reality, but a quasi-Bessel beam of limited diameter with features similar to those of the ideal Bessel beam can exist within a limited distance along the optical axis if an optical element forming conically converging plane waves is used (Figure 2a). A volumetric optical element (see Figure 1a in [72]), which forms conically converging twisted beams, is a combination of a refractive conical lens (axicon) and a spiral plate with a phase that linearly increases in azimuth. Its phase function is
where n is the refractive index of the substrate material of the optical element. In [72], three types of diffractive optical elements, which can replace such elements, were described: (1) a binary spiral axicon, (2) a holographic axicon, and (3) a continuous relief spiral kinoform axicon (KA). The latter is a diffractive analog of a refractive spiral axicon (RSA) with the phase function
The function fix converts a real number into an integer, discarding the fractional part. This axicon can be considered as a blazed-helical-phase diffraction grating. The characteristics of the Bessel beams formed by these three elements and their Fourier transforms, obtained through analytical and numerical calculations, are described in the aforementioned paper.
In this paper, we study beams formed by two types of axicons, binary and holographic, and compare the beam characteristics with the results of numerical simulations performed within the framework of the scalar theory of diffraction. The phase functions of these axicons are
where
and
where
is the Heaviside step function.
A spiral phase plate is an optical element with a transmission function proportional to . It was first fabricated and investigated in [74]. A spiral phase plate can be realized as a diffractive optical element by means of the reduction of the phase of the transmission function to the range of []. The results of an investigation of optical-range spiral phase plates realized through lithography, the molding technique, and the use of a liquid crystal modulator are presented in [75,76,77], where it was experimentally shown that the spiral phase plate enables the generation of a beam with an orbital angular momentum (OAM) of order l. Digital holography methods [78] could also be applied to the design of optical elements that generate beams with orbital angular momentum (OAM). One of the first such elements with phase function was described in [78]. A silicon binary axicon with spiral zones and the transmission function (7) was used in [57] for generating terahertz beams with orbital angular momentum.
2.2. Experimental Setup
Experiments using axicons were carried out at the Novosibirsk free-electron laser facility. The laser beam at the input to the workstation had an almost flat wavefront and its intensity was well approximated by the Gaussian function , where the beam radius was mm. The irradiation consisted of an infinite sequence of pulses with a duration of about 100 ps, followed by a repetition rate of 5.6 MHz. The average radiation power in the experiments was several tens of watts. The laser generation wavelength could vary over a very wide range. Most of the experiments were carried out at a wavelength of μm, for which the axicons were designed, with a generation spectrum width of about 1 μm. However, we also carried out experiments at other wavelengths that differed from the calculated values. In particular, a helical binary axicon was shown to efficiently form a Bessel beam at a wavelength of μm, as well as at the third harmonic wavelength of μm. In the latter case, the Bessel beam was formed at a distance of .
Figure 2b,c show the optical systems used for the study of the beams. The laser beam was incident on an axicon installed in the input aperture of the optical system. The beam images were recorded with one of two terahertz cameras: a microbolometer array or a pyroelectric camera called Pyrocam IV. The receiving matrix of the first camera had a size of mm2 ( pixels), whereas the size of the second camera was mm2 ( pixels). Scheme (b) was used for the study of the beam cross-section as a function of distance. A quasi-Bessel beam was formed in the zone of intersection of the minus-first order of diffraction beams (solid lines in the figure) from the incident Gaussian beam. By analogy with the Ronchi linear binary phase grating, it can be assumed that the fraction of energy carried by these beams was approximately 40.5% of the energy of the incident wave that had passed through the phase element (without taking into account the Fresnel reflection losses). Beams of the plus-first order of diffraction diverging from the axis (dashed lines) also carried the same fraction of energy. The intensity of beams of higher diffraction orders was negligible.
As shown in Figure 2a, the distance at which the waves of negative diffraction order intersect depended on the diffracting beam radius, which was limited either by the diameter of the illuminating beam or by the diameter of the axicon frame. The radii of the axicon apertures in the experiments are presented in Table 1. The Bessel beams were formed within the diamond-shaped area, which is highlighted in the figure in purple, and collapsed at a distance of . Divergent beams of the first positive order of diffraction did not participate in the formation of a Bessel beam, but in the case of a large-diameter lens installed in the optical system, as shown in Figure 2c, they contributed to the formation of the Fourier transform of the beam.
So far, we have not taken into account the Fresnel reflections. However, the material of our diffractive elements had high refractive indices: for silicon and for diamond. Therefore, additional beams may have appeared behind the axicons in the experiments, which distorted the mode structure of the Bessel beam. In particular, in the case of a binary axicon (see Section 3.3), the double internal reflection produced a plane wave of lower power at the output [57]. With the holographic axicon, the reflections were more complex, though less intense, but they could also distort the output wave.
2.3. Axicons: Fabrication and Profile Measurements
Helical axicons were fabricated at Samara University using the lithography technique. As demonstrated below, the manufacturing accuracy of axicons can affect the quality of the beams produced, resulting in a deviation of their mode composition from the theoretically calculated beam. The microrelief of the fabricated binary silicon axicons was measured at Samara University using a WLI DMR white-light interferometer (Fraunhofer Institute, Jena, Germany).
The deviations of the surfaces of the axicons from parallelism were measured with an accuracy of several nanometers using a Fizeau Intellium Z100 interferometer at the Institute of Automation and Electrometry of the Siberian Branch of the Russian Academy of Sciences (IA&E SB RAS). The method is based on the interference of the reference wave reflected from the reference surface and the object wave reflected from the surface of the axicon. Based on the resulting interference pattern, the deviation of the surface from the front of the reference wave was determined. The study of the axicons was carried out from both the front and back sides. The inaccuracy of the period of the fabricated binary axicons was measured using photographs taken at the IA&E SB RAS.
A 20 mm diameter continuous-relief holographic axicon made of synthetic diamond was fabricated at the General Physics Institute of the Russian Academy of Sciences. The fabrication method and optical characteristics of the holographic axicon are described elsewhere. This diffractive element is an intermediate type of axicon, with a piecewise continuous phase relief in the azimuthal direction, and can be referred to as a kinoform element, whereas in the radial direction, it has a stepwise profile.
2.4. Analytical Calculations and Numerical Simulations
Experiments carried out on large-scale facilities, such as the Novosibirsk free-electron laser, are very expensive, and researchers often have limited time to conduct them. In such cases, analytical and numerical calculations make it possible to model the processes under study in a wider range of parameters and help interpret the experimental results. In this work, in both the planning of the experiments and the data processing, we used analytical and numerical calculations of beams propagating in our optical systems. We compared these beams with ideal Bessel beams (see Figure 3) in which the intensity distribution was calculated according to Equation (1). Here and after all the calculated images have dimensions of mm2.
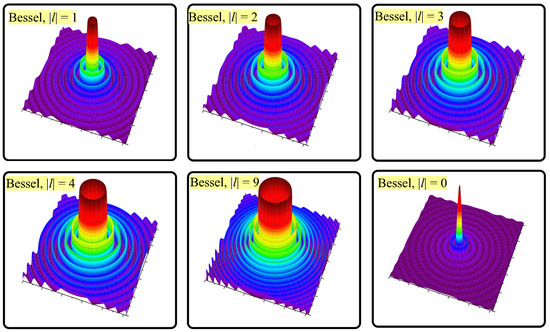
Figure 3.
Intensity distribution for ideal Bessel beams with different topological charges calculated according to Equation (1).
The numerical calculations of the complex amplitude of the electric field in the optical systems shown in Figure 2 were performed using the approximation of the scalar theory of diffraction [79]. The phase functions of the axicons were calculated according to Equations (7) and (8). Since the axicons and the kinoform lens employed in the experiments can be considered flat masks, it is more convenient to use the Rayleigh–Sommerfeld integral [80] for the calculations. To calculate the optical fields in our optical systems, we used the program described in [81] with minor modifications. For the geometric parameters corresponding to our experiments and the dimensions of the recording arrays in the case of terahertz radiation, the impulse response function approximation had to be used in the calculations when the distance from a transparency along the z-axis exceeded 30 mm. It is important to note that the Fresnel reflections were not taken into account in the numerical calculations.
We have previously derived analytical expressions describing the electromagnetic field of a quasi-Bessel beam behind a binary helical axicon [57], as well as the Fourier transform of this beam in the focal plane of a lens (“perfect” beam) [72]. We compared these experiments with each other for various configurations of optical systems. The results obtained from the analytical expressions coincided with the results of the numerical simulations with high accuracy, indicating the reliability of the latter. In this paper, for the sake of brevity, we do not present the results of the analytical calculations.
3. Results and Discussion
3.1. Bessel Beams Obtained Experimentally
In Figure 4, we present 3D surface plots depicting the intensity distributions in the cross-sections of beams formed by the axicons listed in Table 1. The measurements were conducted at a wavelength of 141 μm in the optical system configuration shown in Figure 2b. In this and other figures, we utilize 3D representation of graphs to enhance the visibility of subtle details in the distributions when compared to 2D images. Here and after all images have dimensions of mm2 unless otherwise noted.
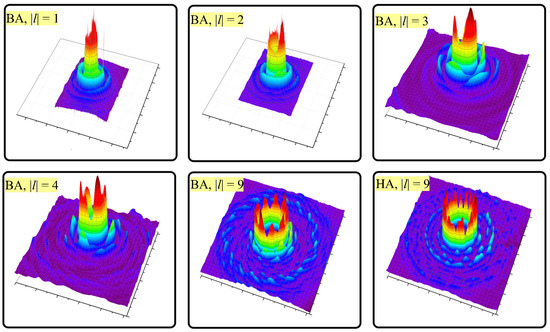
Figure 4.
Intensity distributions in cross-sections of quasi-Bessel beams formed by axicons listed in Table 1. Axicons were illuminated with a Gaussian laser beam with a wavelength of 141 μm and a beam radius of 12.1 mm. The corresponding optical setup is presented in Figure 2b. The first two images were recorded with a microbolometer array camera, which is described in [82,83], and the other images were recorded with a pyroelectric camera, the Pyrocam IV.
First, we compared the experimentally obtained distributions with the ideal Bessel beams shown in Figure 3. We can see that the diameters of the rings of the experimentally obtained beams, particularly their first rings, are nearly identical to those of the rings of ideal beams, but there are also significant differences. In the experiment, the intensities of the Bessel rings clearly varied in azimuth. In the case of the binary helical axicons, the number of peaks corresponded to the topological charge of the beam . At , the beam was almost symmetrical (the beveling of the beam can be explained by the inhomogeneity of the axicon illumination), and at higher topological charges, this dependence was also evident. We explain this effect below.
The binary axicon with formed a beam on the periphery that differed from the beams generated by the other binary axicons. The outer ring observed in it consisted of segments of spirals, with the number of segments being twice the value of the topological charge. This ring can be explained as a pattern formed by diffracted beams of the plus-first order originating from the axial zone of the axicon. The diameter of this ring, approximately 20 mm, closely corresponded to the diffraction angle of the grating. In the other axicons, the outer rings were less pronounced. The outer annular structure, composed of spirals, can be qualitatively explained as the result of the rotation of the center of curvature of local normals over the evolute (see an example in Figure 1g).
Next, we compared (see the right column in Figure 4) the Bessel beams with the same topological charge but created by different types of axicons. It can be seen that near the optical axis, the Bessel beams with formed by the binary helical and holographic axicons were very similar; however, the beam formed by the HA had 18 azimuthal lobes instead of 9, as seen in the case of the binary helical axicon. However, at the periphery, the structures of the beams exhibited significant differences. Instead of the spiral structures discussed in the case of the BA, the beam formed by the HA was axisymmetric, and in terms of intensity distribution, it was closer to the ideal Bessel beam. Although weaker, the symmetrical outer ring observed for the HA case can also be attributed to the diffraction of the plus-first order. The reason for these differences is clear when we compare the geometries of these axicons in their corresponding photographs shown in Figure 1f,h. The expectation of distinct symmetries in the beams formed by the BAs and HAs can be verified mathematically. In the analytical expression (8), which describes the phase function of a holographic axicon, the variables are separated. However, this is not the case for a spiral axicon, as shown in Equation (7). When the diffraction problem is solved in the spiral axicon case, the diffraction pattern will inevitably be non-axisymmetric.
To conclude this section, in Figure 5, we present the cross-sections of beams from binary and holographic axicons, which were recorded using a pyroelectric camera at a distance of 50–150 mm from the axicon (reprinted with permission from Computer Optics Editorial [84]). To ensure an accurate comparison, we limited the size of the illuminating beam for both types of axicons by using a diaphragm with a diameter of 20 mm. It can be seen that the beam cross-section closely resembled that of the Bessel beam at a distance of approximately 80 mm, as expected with such a diaphragm. The holographic axicon beam in the region of diffraction order intersection at a distance of up to 150 mm was mainly axially symmetric, whereas the binary axicon beam had a pronounced helical structure at the periphery.
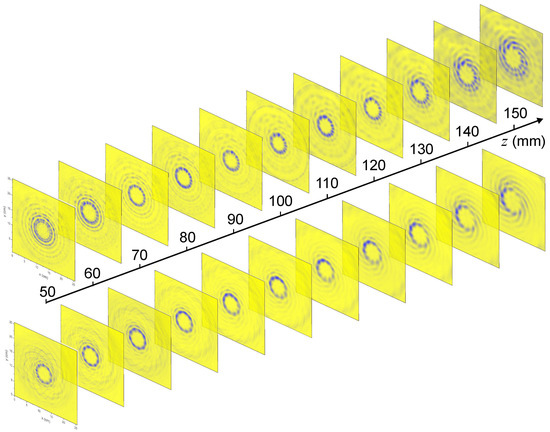
Figure 5.
Comparison of cross-sections of beams formed with spiral axicons (bottom row) and holographic axicons (top row) using the experimental configuration shown in Figure 2b. The aperture radius for both cases was 10 mm. Reprinted with permission from Computer Optics Editorial [84].
3.2. Numerical Simulations: Effect of Wavelength Change and Phase Profile Inaccuracy
In this section, we present the results of numerical simulations of Bessel beams and compare them with data for ideal beams and experimental data. The calculation algorithm is described in Section 2.4. For the sake of brevity, we consider only beams generated by three axicons (BA3, BA9, and HA9), which allows us to find patterns common to all axicons. In columns (a) and (d) of Figure 6, we include the necessary graphs from Figure 3 and Figure 4. We have rearranged the latter in a format that is more convenient for comparison with calculations. The intensity distributions obtained from the numerical simulation with a wavelength of 141 μm are shown in column (b). The simulation results agree well with the analytical expressions, and for the BAs, the agreement is better compared to the HA. However, the simulation for the HA shows better agreement with the experimental data.
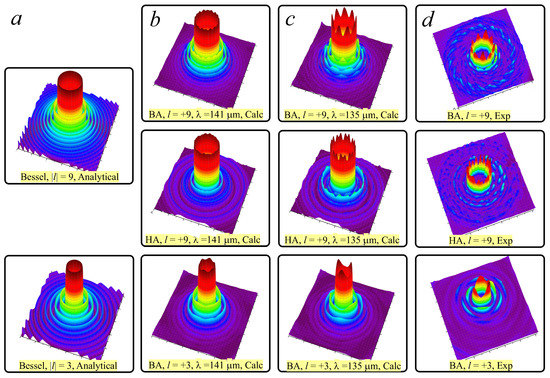
Figure 6.
(a) Ideal Bessel beams (Equation (1)). (b,c) Numerically simulated Bessel beams formed with diffractive axicons BA9, HA9, and BA3 illuminated by a Gaussian beam with a radius of 12.1 mm at wavelengths of 141 and 135 μm. Axicons are designed for wavelengths of 141 μm. (d) Experimentally recorded Bessel beams.
The small variations in the intensity along the azimuth of the rings in the calculated cross-sections of the beams can be attributed to calculation errors. However, we did not observe pronounced azimuthal variations, as seen in the experimental beams. We assumed that they could be caused either by a shift in the wavelength of the illuminating laser beam from the calculated value of 141 μm (taking into account the laser generation bandwidth of approximately 1 μm) or by profile errors in the manufacture of an axicon. The latter can be one of two types: variations in the thickness of the silicon or diamond plate, or errors in the etching depth or width of the grooves (profile inaccuracy in the case of a holographic axicon).
We have explored all possible causes for binary axicons (see Section 2.3). For a binary silicon axicon, the groove depth should be , which is 29.1 μm for the given wavelength. The depth of the grooves was measured along two mutually perpendicular diameters. The measurement results for axicons BA3 and BA9 are shown in Figure 7a. The depth spread for them was and μm, respectively, that is, about 3–10% of the average value. Inaccuracies in the length of the period and the width of the grooves may have also contributed to the error. The inaccuracy in the period of the axicons, as seen in Figure 7b, was approximately 1–3%. The non-parallelism of the outer surfaces of the axicons throughout the area was approximately 5 μm but was not localized and did not introduce any noticeable error.
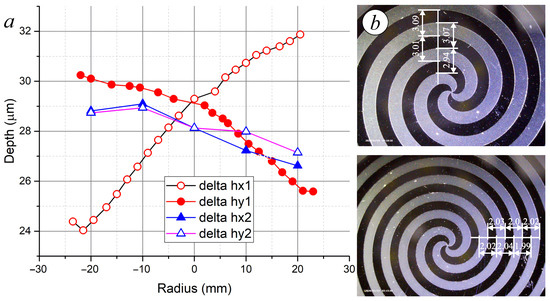
Figure 7.
(a) Depth of grooves of binary axicons along two perpendicular diameters: circles—BA9; triangles—BA3. (b) Examples of measuring periods of binary axicons BA3 and BA3-2 (not used in other experiments) with different periods (see Table 1), which formed beams with a topological charge of .
To understand whether these deviations could cause the appearance of “teeth” on the beam rings produced by the axicons, we calculated the cross-sections of the beams at a wavelength of 135 μm, i.e., at a wavelength shift of 4%. The results are shown in column (c) in Figure 6. It can be seen that the calculation results, including the number of peaks, are now in good agreement with the experimental results. We did not measure the profile of the diamond axicon, but it can be assumed that in this case, the peaks were caused by a mismatch in the wavelength and local errors in the manufacture of the profile.
3.3. Perfect Beams Formed with Binary and Holographic Axicons
In recent years, in the field of vortex beams, much attention has been paid to the perfect beams [65,85,86,87], that is, beams that are formed by quasi-Bessel beams in the focal plane of a lens. Their name reflects the fact that, in the case of ideal Bessel beams, an ideal ring corresponding to Expression (4) is expected to form in this plane. However, in experiments, these rings are far from perfect.
The beam images obtained in the focal plane of a lens with a focal length of 75 mm are shown in Figure 8. In the case of the binary axicons, the cross-sections of the beams exhibited the form of rings divided into segments of nested spirals. The number of spirals corresponded to twice the topological charge l. These spirals were twisted inward if the beam had a positive topological charge, and outward otherwise. The beams obtained from the numerical simulations had the same helical ring structure with very high accuracy. However, because they agreed so well with the experimental data, we chose not to present them here. The only difference was that they did not have a central peak, which was observed in the experimental results.
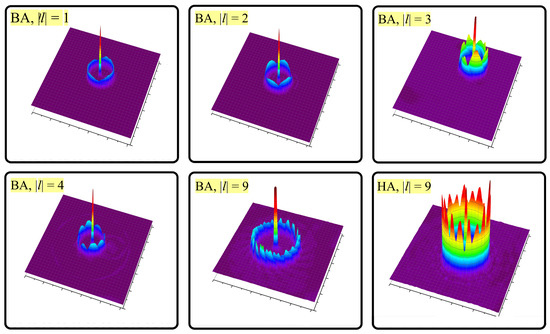
Figure 8.
Perfect vortex beams: cross-section of Fourier transform of Bessel beams formed by binary axicons () and holographic axicon (), recorded using the configuration in Figure 2c.
The origin of the central peak can be easily explained [57] in the case of the binary axicon as being due to internal Fresnel reflection. The plane wave reflected twice from different levels on the front and back faces of the binary axicon had a phase difference of . In the case of the silicon axicon, this value was , indicating that the secondary waves interfered constructively at the output, whereas the primary wave, with a phase difference of , interfered destructively. Thus, the plane wave passed through the axicon with an intensity approximately equal to 10% of the intensity of the diffracting waves. Interestingly, this conclusion holds for silicon binary elements of any type, designed for any wavelength.
In the case of the holographic axicon, we also observed a central peak, although with lower intensity. In this case, the secondary plane wave in the axicon did not appear due to internal reflections since its faces were inclined. The appearance of a zero order of diffraction can be explained, in particular, by the imperfection of the profile manufacturing. It should be emphasized that the perfect beam formed by the holographic axicon was much closer to an ideal one compared to that formed by the binary axicon. It had the shape of a narrow ring. The only difference from the perfect beam was the intensity variation in azimuth. The number of peaks was also equal to .
It is important to note that information about the intensity distribution in the cross-section of perfect beams is crucial for planning and conducting experiments on the excitation of vortex plasmons on cylindrical samples [64] (see Section 1). Plasmons were excited on a brass cylinder coated with a ZnS dielectric layer using the end-fire coupling technique. Consequently, the excitation efficiency could be estimated by calculating the overlap integral between the field of the perfect beam and the expected field distribution of the surface plasmon polariton. The results of this section show that the holographic axicon facilitates the formation of vortex surface plasmons with higher efficiency and uniformity along the front edge of a cylindrical conductor.
4. Conclusions
Zero-order and higher-order Bessel beams carrying orbital angular momentum are widely used in a variety of practical applications in the visible and infrared ranges. Undoubtedly, the use of such beams in the region of long wavelengths also has broad prospects. Many optical schemes and technologies that have successfully been implemented in the shortwave bands are yet to be extended to longer wavelengths. This is especially true for applications in which the characteristic resonant frequencies of a substance lie within these ranges. For example, the use of terahertz and microwave vortex beams for plasma diagnostics was discussed in [88,89,90]. Another promising application is communication systems [91,92]. Radiation sources in the terahertz (free-electron lasers) and millimeter (gyrotrons and backward wave lamps [70]) ranges have been shown to generate beams with a wavefront that closely resembles the Gaussian profile. A Gaussian beam can be transformed into a Bessel beam with an optical element that is a combination of a spiral phase plate and an axicon lens. Such an element in the long-wavelength range, especially in the case of high-order beams, would be impractical due to excessive thickness and absorption. Another approach for forming Bessel beams is through the use of phase diffractive optical elements. At high radiation powers, the best DOE substrate materials are high-resistant silicon and synthetic diamond. At low powers, the DOE can be made of plastic.
In real life, when Bessel beams are formed by any type of axicons, they can exist only in a limited interval along the optical axis. If they are created by diffractive axicons, then the degree of agreement between their cross-section and the cross-section of an ideal Bessel beam essentially depends on the type of axicon used. There are three types of basic profiles of diffractive axicons, two of which were studied experimentally and via numerical calculations in this work. We aimed to solve two problems that were not previously studied or studied insufficiently. First, we aimed to find out how much quasi-Bessel beams obtained using real phase axicons differed from ideal Bessel beams, as well as the level of agreement between the observed beam cross-sections and the cross-sections calculated within the framework of the scalar diffraction theory. Within the framework of this task, we aimed to study the influence of axicon fabrication imperfections and the radiation spectrum illuminating the axicons on the shape of the beams. Second, we compared the beams produced by a binary helical axicon and a holographic axicon.
Bessel beams produced using a binary silicon axicon with a profile consisting of nested Archimedean spirals tended to helicity at the beam periphery. In the case of a holographic axicon whose phase profile closely approximated the axisymmetric phase profile of a Bessel function of a given order, the resulting Bessel beams had a ring structure even at the periphery. Additionally, the perfect beams that formed in the focal plane when Bessel beams were focused by a lens and theoretically represented a homogeneous narrow ring also had characteristic differences. For binary axicons, the broadened ring was a set of nested segments of spirals, with the number of segments equal to twice the topological charge of the beam, whereas, in the case of a holographic axicon, indeed, a narrow ring was observed.
An important result of the experiments was the discovery of regular intensity variations in the azimuthal direction in the rings of Bessel and perfect beams. The number of maxima in Bessel beams created by binary axicons was equal to the topological charge of the beam. In the case of a holographic axicon, the number of maxima was twice the topological charge, as observed for all perfect beams. A comparison between the observed beam cross-sections and the results of the numerical calculations, where the radiation wavelength was varied close to that used for the axicon calculations, helped explain the appearance of these variations. Three factors were found to contribute to these variations, although to varying degrees. The first factor was the shift in the wavelength from the calculated value and the width of the laser emission spectrum. The second factor was related to manufacturing inaccuracies in the axicons, i.e., variations in the depth of the grooves for binary axicons and the height of the steps for the holographic axicon. The third factor involved variations in the period of Archimedes’ spirals or errors in the width of the zones of the holographic axicon. The measured scatter in the geometric characteristics of the axicons provided a satisfactory explanation for the observed variations.
Overall, it has been shown that the fabricated axicons facilitated the creation of quasi-Bessel and perfect beams of sufficiently good quality. The choice of axicon type for the formation of such beams can be made based on the experiments performed in this paper, the numerical calculations described in [72], and the specific application requirements for the beam in question.
Author Contributions
Conceptualization, B.K.; methodology, B.K., N.O., M.K. and V.P.; software, O.K., N.O. and B.K.; investigation, N.O., V.G., Y.C., and B.K.; materials, K.T., M.K. and V.P.; writing—original draft preparation, B.K. and N.O.; writing—review and editing, B.K., N.O. and V.P.; visualization, N.O. and Y.C.; supervision, B.K.; project administration, B.K.; funding acquisition, B.K., M.K. and V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Russian Foundation for Basic Research, grant no. 18-32-20226.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
The authors are grateful to V.I. Konov, G.N. Kulipanov, V.A. Soifer, and N.A. Vinokourov for their support of the research underlying this paper. The authors also thank the NovoFEL team, Ya. V. Getmanov, Ya. I. Gorbachev, M. A. Scheglov, D. A. Skorokhod, and O. A. Shevchenko, for their technical support, as well as I.G. Sokolova for help with the preparation of the manuscript. V.S. Pavelyev is grateful to IPSI RAS—Branch of the FSRC “Crystallography and Photonics” RAS—for support in the design and production of silicon diffractive axicons. The experiments were carried out at the Novosibirsk Free-Electron Laser Facility, which is part of the “Siberian Synchrotron and Terahertz Radiation Center” of the Budker Institute of Nuclear Physics of SB RAS. The authors thank the Shared Equipment Center “Spectroscopy and Optics” at the Institute of Automation and Electrometry SB RAS and express their gratitude to Alexey Matochkin and Nazar Nikolaev for the axicon surface profile investigation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. A review of multiple optical vortices generation: Methods and applications. Front. Optoelectron. 2019, 12, 52–68. [Google Scholar] [CrossRef]
- Pavlov, D.; Porfirev, A.; Khonina, S.; Pan, L.; Kudryashov, S.; Kuchmizhak, A. Coaxial hole array fabricated by ultrafast femtosecond-laser processing with spatially multiplexed vortex beams for surface enhanced infrared absorption. Appl. Surf. Sci. 2021, 541, 148602. [Google Scholar] [CrossRef]
- Brasselet, E.; Murazawa, N.; Misawa, H.; Juodkazis, S. Optical vortices from liquid crystal droplets. Phys. Rev. Lett. 2009, 103, 103903. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Hu, Z.; Yuan, G.; Min, C.; Fang, H.; Yuan, X.C. Visualizing orbital angular momentum of plasmonic vortices. Opt. Lett. 2012, 37, 4627–4629. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, X. Unraveling DNA condensation with optical tweezers. Science 2004, 305, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Brullot, W.; Vanbel, M.K.; Swusten, T.; Verbiest, T. Resolving enantiomers using the optical angular momentum of twisted light. Sci. Adv. 2016, 2, e1501349. [Google Scholar] [CrossRef]
- Jeffries, G.D.; Edgar, J.S.; Zhao, Y.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Xie, G.; Song, H.; Zhao, Z.; Milione, G.; Ren, Y.; Liu, C.; Zhang, R.; Bao, C.; Li, L.; Wang, Z.; et al. Using a Complex Optical Orbital-Angular-Momentum Spectrum to Measure Object Parameters: A Spatial Domain Approach. arXiv 2017, arXiv:1705.09051. [Google Scholar]
- Fu, S.; Gao, C. Influences of atmospheric turbulence effects on the orbital angular momentum spectra of vortex beams. Photonics Res. 2016, 4, B1–B4. [Google Scholar] [CrossRef]
- Li, Y.; Yu, L.; Zhang, Y. Influence of anisotropic turbulence on the orbital angular momentum modes of Hermite-Gaussian vortex beam in the ocean. Opt. Express 2017, 25, 12203–12215. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.; Barnett, S.M.; Speirits, F.C.; Padgett, M.J. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body. Optica 2014, 1, 1–4. [Google Scholar] [CrossRef]
- Cheng, W.; Polynkin, P. Micromachining of borosilicate glass surfaces using femtosecond higher-order Bessel beams. JOSA B 2014, 31, C48–C52. [Google Scholar] [CrossRef]
- Oosterbeek, R.N.; Ashforth, S.; Bodley, O.; Simpson, M.C. Measuring the ablation threshold fluence in femtosecond laser micromachining with vortex and Bessel pulses. Opt. Express 2018, 26, 34558–34568. [Google Scholar] [CrossRef]
- Baltrukonis, J.; Ulčinas, O.; Orlov, S.; Jukna, V. High-order vector bessel-gauss beams for laser micromachining of transparent materials. Phys. Rev. Appl. 2021, 16, 034001. [Google Scholar] [CrossRef]
- Lutz, C.; Schwarz, S.; Marx, J.; Esen, C.; Hellmann, R. Multi-Bessel Beams Generated by an Axicon and a Spatial Light Modulator for Drilling Applications. Photonics 2023, 10, 413. [Google Scholar] [CrossRef]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Communication with spatially modulated light through turbulent air across Vienna. New J. Phys. 2014, 16, 113028. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef]
- Wei, X.; Liu, C.; Zhang, Z.; Zhu, L.; Wang, J.; Wang, K.; Yang, Z.; Liu, J. Orbit angular momentum encoding at 0.3 THz via 3D printed spiral phase plates. In Infrared, Millimeter-Wave, and Terahertz Technologies III; SPIE: Manhattan, NY, USA, 2014; Volume 9275, pp. 260–265. [Google Scholar]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Yang, Y.; Qiu, C.W. Generation of Optical Vortex Beams. In Electromagnetic Vortices: Wave Phenomena and Engineering Applications; Wiley-IEEE Press: Manhattan, NY, USA, 2021; pp. 223–244. [Google Scholar]
- Yang, Y.; Li, Y.; Wang, C. Generation and expansion of Laguerre–Gaussian beams. J. Opt. 2022, 51, 910–926. [Google Scholar] [CrossRef]
- Pereiro-García, J.; García-de Blas, M.; Geday, M.A.; Quintana, X.; Caño-García, M. Flat variable liquid crystal diffractive spiral axicon enabling perfect vortex beams generation. Sci. Rep. 2023, 13, 2385. [Google Scholar] [CrossRef]
- Litvin, I.A.; Dudley, A.; Roux, F.S.; Forbes, A. Azimuthal decomposition with digital holograms. Opt. Express 2012, 20, 10996–11004. [Google Scholar] [CrossRef]
- Flamm, D.; Naidoo, D.; Schulze, C.; Forbes, A.; Duparré, M. Mode analysis with a spatial light modulator as a correlation filter. Opt. Lett. 2012, 37, 2478–2480. [Google Scholar] [CrossRef]
- Mazilu, M.; Mourka, A.; Vettenburg, T.; Wright, E.M.; Dholakia, K. Simultaneous determination of the constituent azimuthal and radial mode indices for light fields possessing orbital angular momentum. Appl. Phys. Lett. 2012, 100, 231115. [Google Scholar] [CrossRef]
- Mourka, A.; Mazilu, M.; Wright, E.M.; Dholakia, K. Modal characterization using principal component analysis: Application to Bessel, higher-order Gaussian beams and their superposition. Sci. Rep. 2013, 3, 1422. [Google Scholar] [CrossRef] [PubMed]
- Dudley, A.; Mhlanga, T.; Lavery, M.; McDonald, A.; Roux, F.S.; Padgett, M.; Forbes, A. Efficient sorting of Bessel beams. Opt. Express 2013, 21, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Trichili, A.; Mhlanga, T.; Ismail, Y.; Roux, F.S.; McLaren, M.; Zghal, M.; Forbes, A. Detection of Bessel beams with digital axicons. Opt. Express 2014, 22, 17553–17560. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Guan, S.; Cheng, J.; Chang, S. Recent Progress of Terahertz Spatial Light Modulators: Materials, Principles and Applications. Micromachines 2022, 13, 1637. [Google Scholar] [CrossRef]
- Petrov, N.V.; Sokolenko, B.; Kulya, M.S.; Gorodetsky, A.; Chernykh, A.V. Design of broadband terahertz vector and vortex beams: I. Review of materials and components. Light. Adv. Manuf. 2022, 3, 54. [Google Scholar] [CrossRef]
- Shen, Y.; Shen, Z.; Zhao, G.; Hu, W. Photopatterned liquid crystal mediated terahertz Bessel vortex beam generator. Chin. Opt. Lett. 2020, 18, 080003. [Google Scholar] [CrossRef]
- Shen, Z.X.; Tang, M.J.; Chen, P.; Zhou, S.H.; Ge, S.J.; Duan, W.; Wei, T.; Liang, X.; Hu, W.; Lu, Y.Q. Planar terahertz photonics mediated by liquid crystal polymers. Adv. Opt. Mater. 2020, 8, 1902124. [Google Scholar] [CrossRef]
- Glyavin, M.Y.; Luchinin, A.G.; Golubiatnikov, G.Y. Generation of 1.5-kW, 1-THz Coherent Radiation from a Gyrotron with a Pulsed Magnetic Field. Phys. Rev. Lett. 2008, 100, 015101. [Google Scholar] [CrossRef]
- Glyavin, M. Development and applications of THz gyrotrons. EPJ Web Conf. 2017, 149, 01008. [Google Scholar] [CrossRef]
- Tan, P.; Huang, J.; Liu, K.; Xiong, Y.; Fan, M. Terahertz radiation sources based on free electron lasers and their applications. Sci. China Inf. Sci. 2012, 55, 1–15. [Google Scholar] [CrossRef]
- Kulipanov, G.N.; Bagryanskaya, E.G.; Chesnokov, E.N.; Choporova, Y.Y.; Gerasimov, V.V.; Getmanov, Y.V.; Kiselev, S.L.; Knyazev, B.A.; Kubarev, V.V.; Peltek, S.E.; et al. Novosibirsk free electron laser—facility description and recent experiments. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 798–809. [Google Scholar] [CrossRef]
- Petrillo, V.; Andreone, A.; Bacci, A.; Bosotti, A.; Broggi, F.; Drebot, I.; Galzerano, G.; Giannotti, D.; Giove, D.; Koral, C.; et al. High brilliance Free-Electron Laser Oscillator operating at multi-MegaHertz repetition rate in the short-TeraHertz emission range. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1040, 167289. [Google Scholar] [CrossRef]
- Helm, M.; Winnerl, S.; Pashkin, A.; Klopf, J.; Deinert, J.C.; Kovalev, S.; Evtushenko, P.; Lehnert, U.; Xiang, R.; Arnold, A.; et al. The ELBE infrared and THz facility at Helmholtz-Zentrum Dresden-Rossendorf. Eur. Phys. J. Plus 2023, 138, 158. [Google Scholar] [CrossRef]
- Soifer, V.A. Methods for Computer Design of Diffractive Optical Elements; John Wiley & Sons, Inc.: New York, NY, USA, 2001; p. 784. [Google Scholar]
- Tudor, R.; Bulzan, G.A.; Kusko, M.; Kusko, C.; Avramescu, V.; Vasilache, D.; Gavrila, R. Multilevel Spiral Axicon for High-Order Bessel–Gauss Beams Generation. Nanomaterials 2023, 13, 579. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, T.V.; Knyazev, B.A.; Sovyk, D.N.; Pavelyev, V.S.; Komlenok, M.S.; Komandin, G.A.; Konov, V.I. Silicon kinoform cylindrical lens with low surface roughness for high-power terahertz radiation. Opt. Laser Technol. 2020, 123, 105953. [Google Scholar] [CrossRef]
- Komlenok, M.S.; Kononenko, T.V.; Konov, V.I.; Choporova, Y.Y.; Osintseva, N.D.; Knyazev, B.A.; Pavelyev, V.S.; Tukmakov, K.N.; Soifer, V.A. Silicon diffractive optical element with piecewise continuous profile to focus high-power terahertz radiation into a square area. J. Opt. Soc. Am. B 2021, 38, B9. [Google Scholar] [CrossRef]
- Komlenok, M.; Kononenko, T.; Sovyk, D.; Pavelyev, V.; Knyazev, B.; Ashkinazi, E.; Reshetnikov, A.; Komandin, G.; Pashinin, V.; Ralchenko, V.; et al. Diamond diffractive lens with a continuous profile for powerful terahertz radiation. Opt. Lett. 2021, 46, 340. [Google Scholar] [CrossRef]
- Pavelyev, V.; Choporova, Y.; Osintseva, N.; Tukmakov, K.; Knyazev, B. Control of transverse mode content and polarization structure of terahertz coherent beams. Comput. Opt. 2019, 43, 1103–1108. [Google Scholar] [CrossRef]
- Agafonov, A.N.; Volodkin, B.O.; Volotovsky, S.G.; Kaveev, A.K.; Knyazev, B.A.; Kropotov, G.I.; Tykmakov, K.N.; Pavelyev, V.S.; Tsygankova, E.V.; Tsypishka, D.I.; et al. Optical elements for focusing of terahertz laser radiation in a given two-dimensional domain. Opt. Mem. Neural Netw. 2014, 23, 185–190. [Google Scholar] [CrossRef]
- Agafonov, A.N.; Volodkin, B.O.; Kachalov, D.G.; Knyazev, B.A.; Kropotov, G.I.; Tukmakov, K.N.; Pavelyev, V.S.; Tsypishka, D.I.; Choporova, Y.Y.; Kaveev, A.K. Focusing of Novosibirsk Free Electron Laser (NovoFEL) radiation into paraxial segment. J. Mod. Opt. 2016, 63, 1051–1054. [Google Scholar] [CrossRef]
- Pavelyev, V.S.; Degtyarev, S.A.; Tukmakov, K.N.; Reshetnikov, A.S.; Knyazev, B.A.; Choporova, Y.Y. Silicon subwavelength axicons for terahertz beam polarization transformation. J. Phys. Conf. Ser. 2021, 1745, 012022. [Google Scholar] [CrossRef]
- Pavelyev, V.; Khonina, S.; Degtyarev, S.; Tukmakov, K.; Reshetnikov, A.; Gerasimov, V.; Osintseva, N.; Knyazev, B. Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State. Sensors 2023, 23, 1579. [Google Scholar] [CrossRef]
- Choporova, Y.Y.; Knyazev, B.A.; Kulipanov, G.N.; Pavelyev, V.S.; Scheglov, M.A.; Vinokurov, N.A.; Volodkin, B.O.; Zhabin, V.N. High-power Bessel beams with orbital angular momentum in the terahertz range. Phys. Rev. A 2017, 96, 023846. [Google Scholar] [CrossRef]
- Choporova, Y.; Knyazev, B.; Pavelyev, V. Holography with high-power CW coherent terahertz source: Optical components, imaging, and applications. Light. Adv. Manuf. 2022, 3, 525–541. [Google Scholar] [CrossRef]
- Knyazev, B.; Choporova, Y.Y.; Mitkov, M.; Pavelyev, V.; Volodkin, B. Generation of terahertz surface plasmon polaritons using nondiffractive Bessel beams with orbital angular momentum. Phys. Rev. Lett. 2015, 115, 163901. [Google Scholar] [CrossRef] [PubMed]
- Choporova, Y.Y.; Knyazev, B.A.; Mitkov, M.S. Holography as imaging technique for the THz range. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Knyazev, B.A.; Serbo, V. Beams of photons with nonzero projections of orbital angular momenta: New results. Physics-Uspekhi 2018, 61, 449. [Google Scholar] [CrossRef]
- Knyazev, B.; Kameshkov, O.; Vinokurov, N.; Cherkassky, V.; Choporova, Y.; Pavelyev, V. Quasi-Talbot effect with vortex beams and formation of vortex beamlet arrays. Opt. Express 2018, 26, 14174. [Google Scholar] [CrossRef]
- Kotelnikov, I.A.; Kameshkov, O.E.; Knyazev, B.A. Diffraction of bessel beams on 2D amplitude gratings—A new branch in the talbot effect study. J. Opt. 2020, 22, 065603. [Google Scholar] [CrossRef]
- Gerasimov, V.; Kameshkov, O.; Knyazev, B.; Osintseva, N.; Pavelyev, V. Vortex surface plasmon polaritons on a cylindrical waveguide: Generation, propagation, and diffraction. J. Opt. 2021, 23, 10LT01. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; Rickenstorff-Parrao, C.; Arrizón, V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator. Opt. Lett. 2013, 38, 534–536. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fang, Z.X.; Ren, Y.X.; Gong, L.; Lu, R.D. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device. Appl. Opt. 2015, 54, 8030–8035. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Yang, Q.; Xu, Q.; Jiang, X.; Wu, T.; Gu, J.; Han, J.; Zhang, W. Multichannel terahertz quasi-perfect vortex beams generation enabled by multifunctional metasurfaces. Nanophotonics 2022, 11, 3631–3640. [Google Scholar] [CrossRef]
- Ahmed, H.; Intaravanne, Y.; Ming, Y.; Ansari, M.A.; Buller, G.S.; Zentgraf, T.; Chen, X. Multichannel superposition of grafted perfect vortex beams. Adv. Mater. 2022, 34, 2203044. [Google Scholar] [CrossRef]
- Stegeman, G.; Wallis, R.; Maradudin, A. Excitation of surface polaritons by end-fire coupling. Opt. Lett. 1983, 8, 386–388. [Google Scholar] [CrossRef]
- Edelmann, A.; Moeller, L.; Jahns, J. Coupling of terahertz radiation to metallic wire using end-fire technique. Electron. Lett. 2013, 49, 884–886. [Google Scholar] [CrossRef]
- Fisher, C.; Botten, L.C.; Poulton, C.G.; McPhedran, R.C.; de Sterke, C.M. Efficient end-fire coupling of surface plasmons in a metal waveguide. JOSA B 2015, 32, 412–425. [Google Scholar] [CrossRef]
- Knyazev, B.; Cherkassky, V.; Kameshkov, O. “Perfect” Terahertz Vortex Beams Formed Using Diffractive Axicons and Prospects for Excitation of Vortex Surface Plasmon Polaritons. Appl. Sci. 2021, 11, 717. [Google Scholar] [CrossRef]
- Simon, D.S. Bessel beams, self-healing, and diffraction-free propagation. In A Guided Tour of Light Beams (Second Edition); 2053–2563; IOP Publishing: Bristol, UK, 2020; pp. 5-1–5-22. [Google Scholar] [CrossRef]
- Khonina, S.; Kotlyar, V.; Shinkaryev, M.; Soifer, V.; Uspleniev, G. The phase rotor filter. J. Mod. Opt. 1992, 39, 1147–1154. [Google Scholar] [CrossRef]
- Cheong, W.; Lee, W.; Yuan, X.C.; Zhang, L.S.; Dholakia, K.; Wang, H. Direct electron-beam writing of continuous spiral phase plates in negative resist with high power efficiency for optical manipulation. Appl. Phys. Lett. 2004, 85, 5784–5786. [Google Scholar] [CrossRef]
- Oemrawsingh, S.; Van Houwelingen, J.; Eliel, E.; Woerdman, J.; Verstegen, E.; Kloosterboer, J.; ’t Hooft, G.W. Production and characterization of spiral phase plates for optical wavelengths. Appl. Opt. 2004, 43, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Sundbeck, S.; Gruzberg, I.; Grier, D.G. Structure and scaling of helical modes of light. Opt. Lett. 2005, 30, 477–479. [Google Scholar] [CrossRef]
- Heckenberg, N.; McDuff, R.; Smith, C.; White, A. Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 1992, 17, 221–223. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Voelz, D.G. Computational Fourier Optics: A MATLAB Tutorial; SPIE Press: Bellingham, WA, USA, 2011; Volume 534. [Google Scholar]
- Kameshkov, O.; Knyazev, B. Simulating diffraction on a series of amplitude-phase masks for experiments at the Novosibirsk free electron laser. Bull. Russ. Acad. Sci. Phys. 2019, 83, 184–189. [Google Scholar] [CrossRef]
- Dem’yanenko, M.A.; Esaev, D.G.; Knyazev, B.A.; Kulipanov, G.N.; Vinokurov, N.A. Imaging with a 90 frames/s microbolometer focal plane array and high-power terahertz free electron laser. Appl. Phys. Lett. 2008, 92, 131116. [Google Scholar] [CrossRef]
- Dem’yanenko, M.A.; Esaev, D.G.; Ovsyuk, V.N.; Fomin, B.I.; Aseev, A.L.; Knyazev, B.A.; Kulipanov, G.N.; Vinokurov, N.A. Microbolometer detector arrays for the infrared and terahertz ranges. J. Opt. Technol. 2009, 76, 739. [Google Scholar] [CrossRef]
- Osintseva, N.; Gerasimov, V.; Knyazev, B.; Komlenok, M.; Pavelyev, V.; Yablokov, D. Terahertz Bessel and “perfect” vortex beams generated with a binary axicon and axicon with continuous relief. Comput. Opt. 2022, 46, 375–380. [Google Scholar] [CrossRef]
- Chen, M.; Mazilu, M.; Arita, Y.; Wright, E.M.; Dholakia, K. Dynamics of microparticles trapped in a perfect vortex beam. Opt. Lett. 2013, 38, 4919–4922. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Pinnell, J.; Rodríguez-Fajardo, V.; Forbes, A. How perfect are perfect vortex beams? Opt. Lett. 2019, 44, 5614–5617. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Ding, W.; Bai, L.; Wu, Z. Propagation of arbitrarily polarized terahertz Bessel vortex beam in inhomogeneous unmagnetized plasma slab. Phys. Plasmas 2018, 25, 123505. [Google Scholar] [CrossRef]
- Durrani, I. Photon orbital angular momentum in a plasma vortex. Bull. Pure Appl. Sci.-Phys. 2012, 31, 103–111. [Google Scholar]
- Li, H.; Honary, F.; Wu, Z.; Shang, Q.; Bai, L. Reflection, transmission, and absorption of vortex beams propagation in an inhomogeneous magnetized plasma slab. IEEE Trans. Antennas Propag. 2018, 66, 4194–4201. [Google Scholar] [CrossRef]
- Li, J.S.; Cheng, J.; Zhang, D.P. Terahertz Bessel beam generator. Appl. Opt. 2023, 62, 4197–4202. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, Y.; Zhang, D.; Ding, X.; Ratni, B.; Burokur, S.N.; Lu, M.; Tang, K.; Wu, Q. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 2018, 26, 1351–1360. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).