Quantum Light Source Based on Semiconductor Quantum Dots: A Review
Abstract
1. Introduction
2. Ideal Single Photon Source
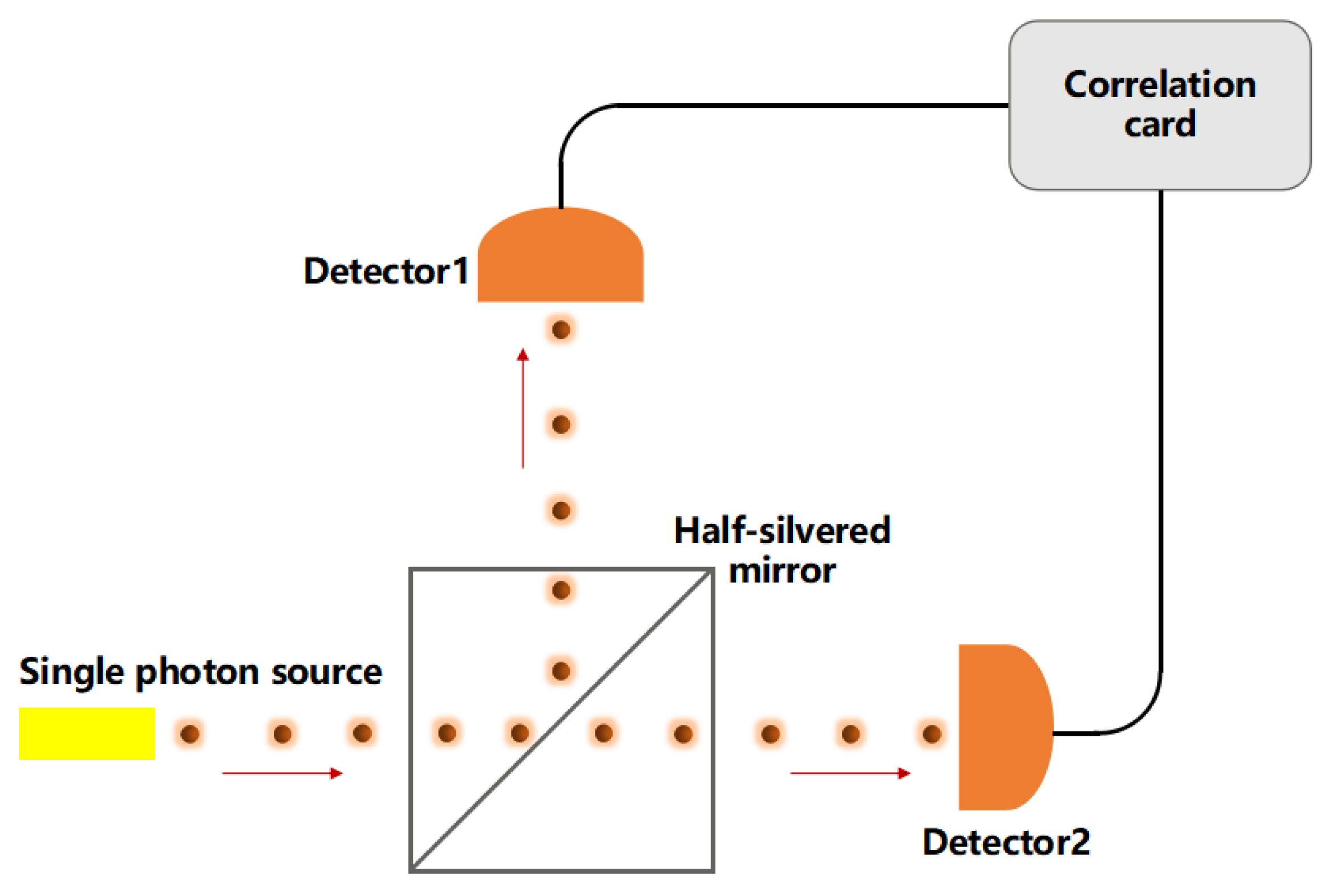
2.1. Single-Photon Purity
2.2. Photon Indistinguishability
2.3. Single-Photon Efficiency
3. Self-Assembled Semiconductor Quantum Dots
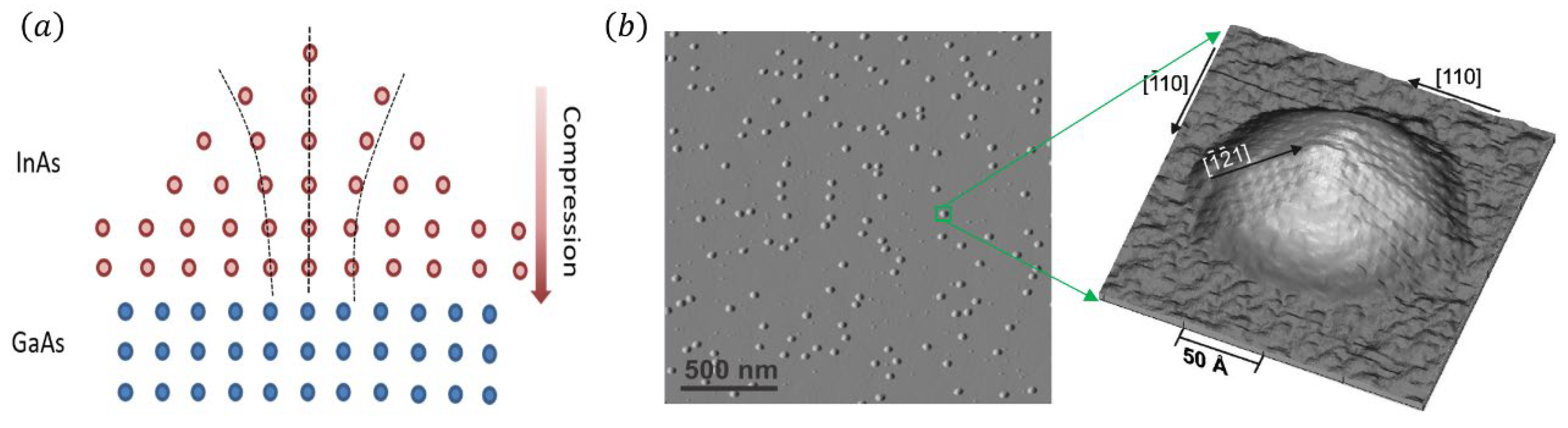
3.1. Growth of Self-Assembled Semiconductor Quantum Dots
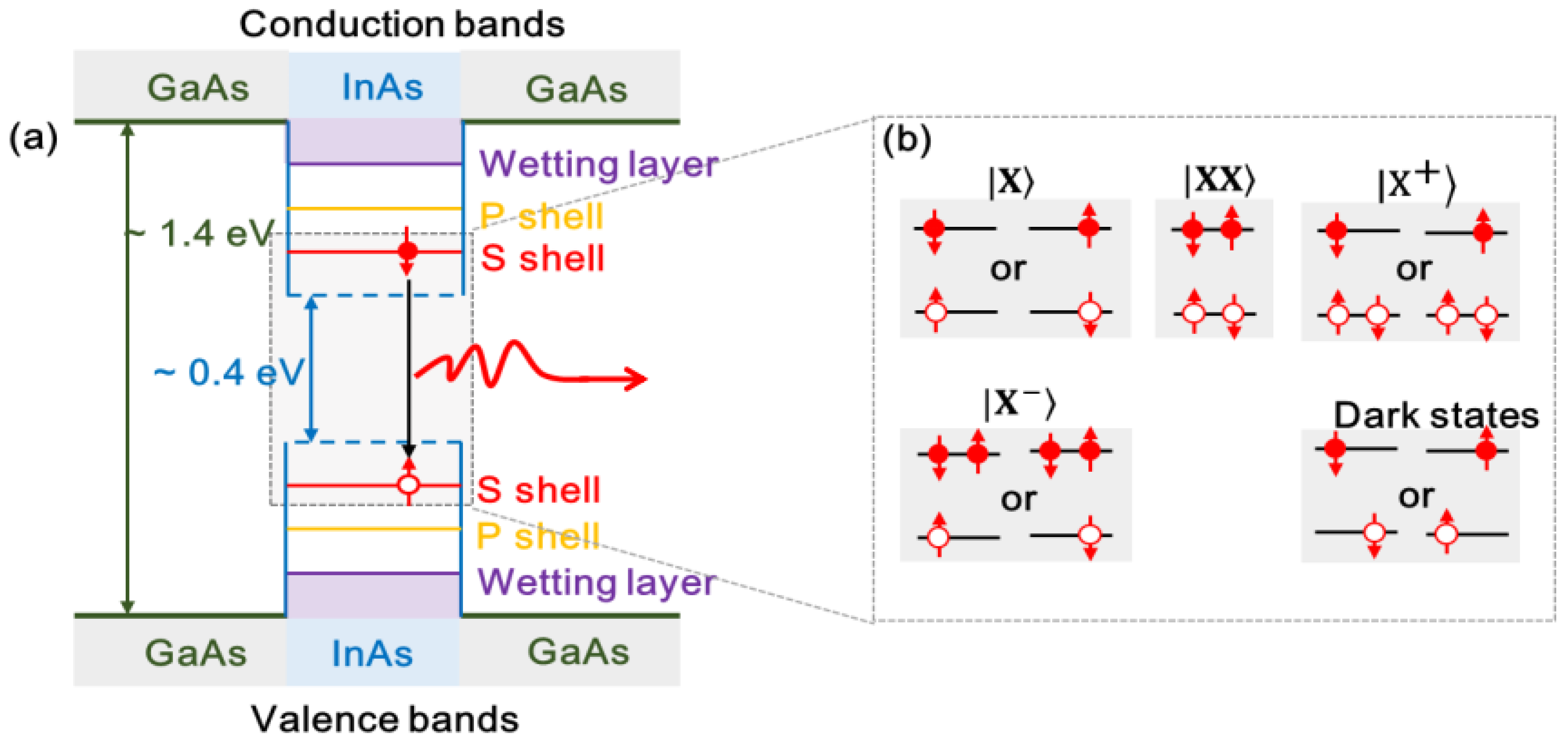
3.2. Band Structure of Self-Assembled Semiconductor Quantum Dots
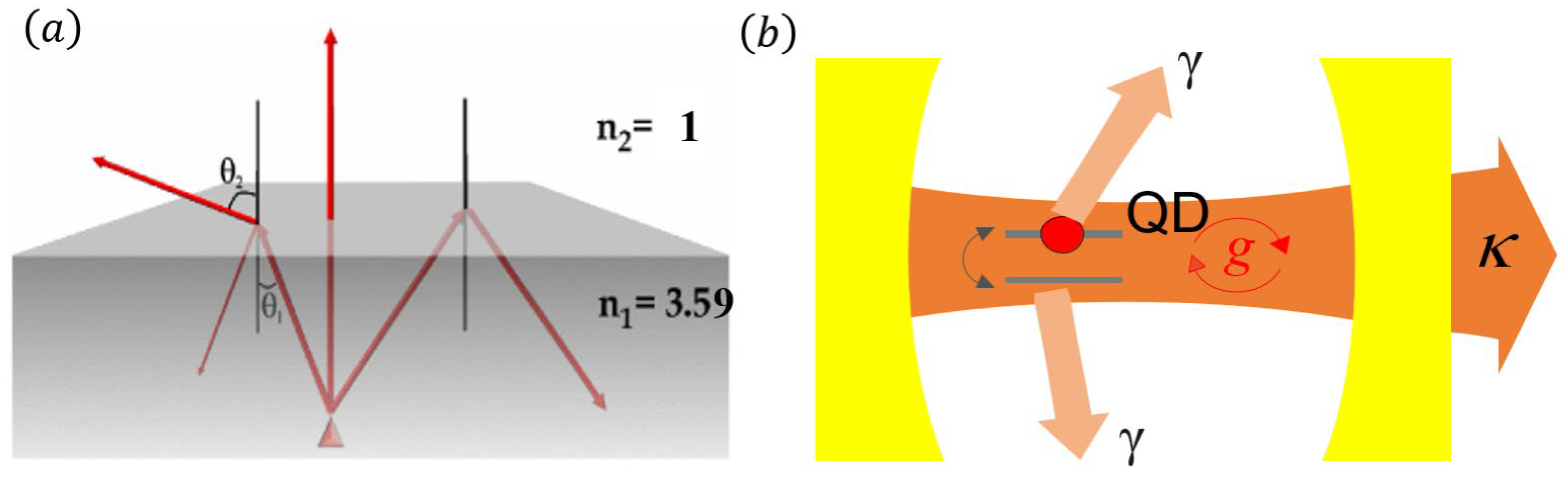
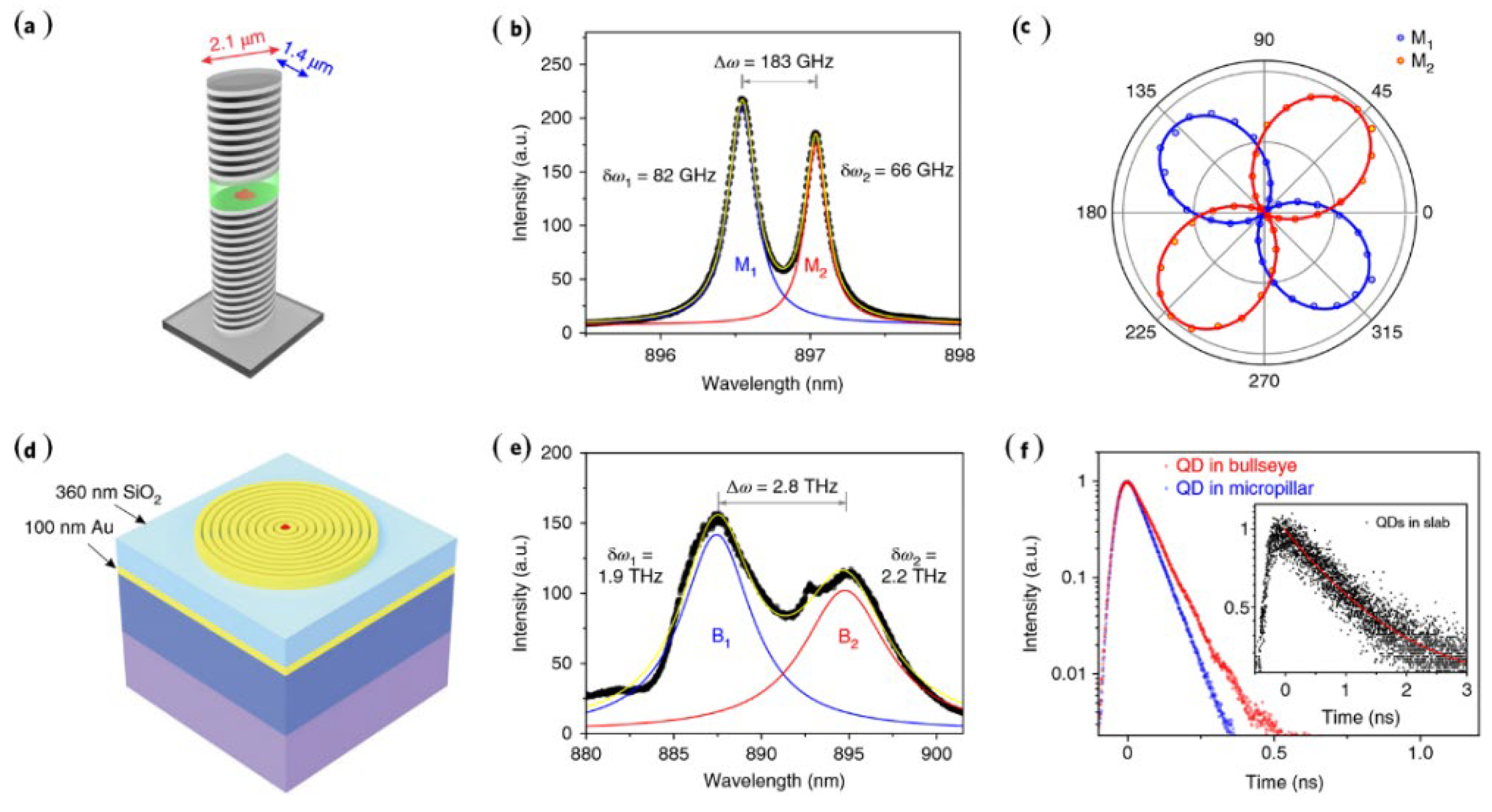
4. Artificial-Microstructure Enhanced Single Photon Emission from Single Semiconductor Quantum Dot

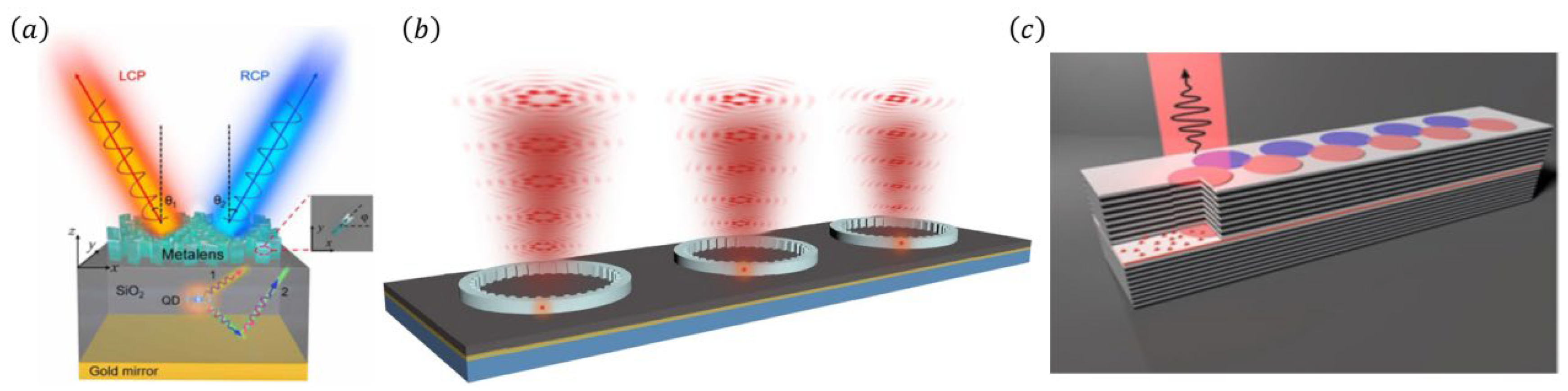
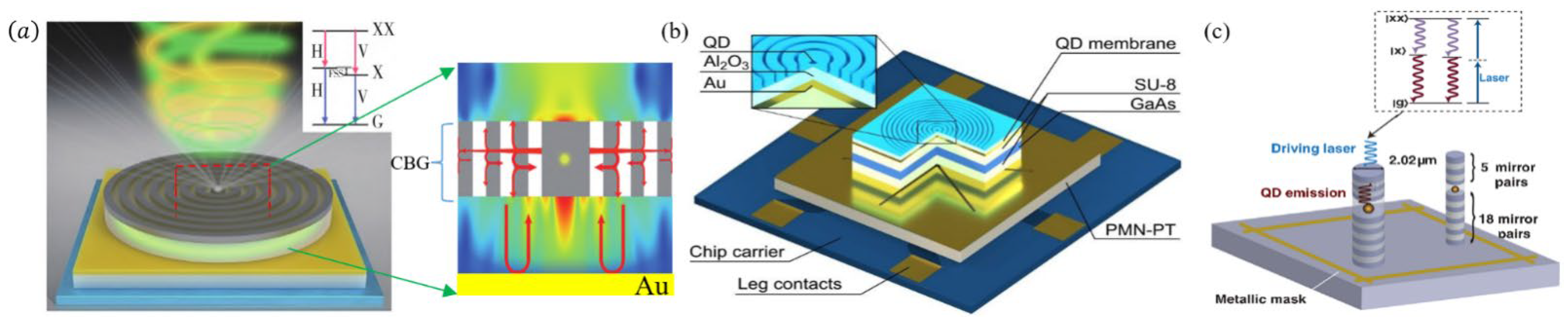
5. Artificial Microstructures Enhanced Entangled Photon Emission from Semiconductor Quantum Dots
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. Simulating physics with computers. In Feynman and Computation; CRC Press: Boca Raton, FL, USA, 2018; pp. 133–153. [Google Scholar]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.-K.; Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1992, 439, 553–558. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum computers can search arbitrarily large databases by a single query. Phys. Rev. Lett. 1997, 79, 4709. [Google Scholar] [CrossRef]
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. Quantum computation. Science 1995, 270, 255–261. [Google Scholar] [CrossRef]
- Bao, X.-H.; Reingruber, A.; Dietrich, P.; Rui, J.; Dück, A.; Strassel, T.; Li, L.; Liu, N.-L.; Zhao, B.; Pan, J.-W. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nat. Phys. 2012, 8, 517–521. [Google Scholar] [CrossRef]
- Maccone, L.; Ren, C. Quantum radar. Phys. Rev. Lett. 2020, 124, 200503. [Google Scholar] [CrossRef]
- O’brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef]
- Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 2008, 453, 1016–1022. [Google Scholar] [CrossRef]
- Häffner, H.; Roos, C.F.; Blatt, R. Quantum computing with trapped ions. Phys. Rep. 2008, 469, 155–203. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
- Scappucci, G.; Kloeffel, C.; Zwanenburg, F.A.; Loss, D.; Myronov, M.; Zhang, J.-J.; De Franceschi, S.; Katsaros, G.; Veldhorst, M. The germanium quantum information route. Nat. Rev. Mater. 2021, 6, 926–943. [Google Scholar] [CrossRef]
- Zhou, L.; Lin, J.; Jing, Y.; Yuan, Z. Twin-field quantum key distribution without optical frequency dissemination. Nat. Commun. 2023, 14, 928. [Google Scholar] [CrossRef]
- Politi, A.; Cryan, M.J.; Rarity, J.G.; Yu, S.; O’Brien, J.L. Silica-on-silicon waveguide quantum circuits. Science 2008, 320, 646–649. [Google Scholar] [CrossRef]
- Darquié, B.; Jones, M.P.A.; Dingjan, J.; Beugnon, J.; Bergamini, S.; Sortais, Y.; Messin, G.; Browaeys, A.; Grangier, P. Controlled single-photon emission from a single trapped two-level atom. Science 2005, 309, 454–456. [Google Scholar] [CrossRef]
- Lounis, B.; Moerner, W.E. Single photons on demand from a single molecule at room temperature. Nature 2000, 407, 491–493. [Google Scholar] [CrossRef]
- Sipahigil, A.; Jahnke, K.D.; Rogers, L.J.; Teraji, T.; Isoya, J.; Zibrov, A.S.; Jelezko, F.; Lukin, M.D. Indistinguishable photons from separated silicon-vacancy centers in diamond. Phys. Rev. Lett. 2014, 113, 113602. [Google Scholar] [CrossRef]
- He, Y.M.; Clark, G.; Schaibley, J.R.; Chen, M.-C.; Wei, Y.-J.; Ding, X.; Zhang, Q.; Yao, W.; Xu, X.; Lu, C.-Y.; et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 2015, 10, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Bray, K.; Ford, M.J.; Toth, M.; Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 2016, 11, 37–41. [Google Scholar] [CrossRef] [PubMed]
- Senellart, P.; Solomon, G.; White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039. [Google Scholar] [CrossRef] [PubMed]
- Michler, P. Nonclassical light from single semiconductor quantum dots. In Single Quantum Dots: Fundamentals, Applications, and New Concepts; Springer: Berlin/Heidelberg, Germany, 2003; pp. 315–347. [Google Scholar]
- Fischer, K.A.; Müller, K.; Lagoudakis, K.G.; Vučković, J. Dynamical modeling of pulsed two-photon interference. New J. Phys. 2016, 18, 113053. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Twiss, R.Q. A test of a new type of stellar interferometer on Sirius. Nature 1956, 178, 1046–1048. [Google Scholar] [CrossRef]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef]
- Khitrova, G.; Gibbs, H.M.; Kira, M.; Koch, S.W.; Scherer, A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2006, 2, 81–90. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef]
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamoğlu, A. Quantum nature of a strongly coupled single quantum dot–cavity system. Nature 2007, 445, 896–899. [Google Scholar] [CrossRef]
- Reithmaier, J.P.; Sęk, G.; Löffler, A.; Hofmann, C.; Kuhn, S.; Reitzenstein, S.; Keldysh, L.V.; Kulakovskii, V.D.; Reinecke, T.L.; Forchel, A. Strong coupling in a single quantum dot–semiconductor microcavity system. Nature 2004, 432, 197–200. [Google Scholar] [CrossRef]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.M.; Rupper, G.; Ell, C.; Shchekin, O.B.; Deppe, D.G. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Benson, O. Assembly of hybrid photonic architectures from nanophotonic constituents. Nature 2011, 480, 193–199. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Stranski, I.N.; Krastanow, L. Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander. Mon. Chem. Verwandte Teile And. Wiss. 1937, 71, 351–364. [Google Scholar] [CrossRef]
- Marquez, J.; Geelhaar, L.; Jacobi, K. Atomically resolved structure of InAs quantum dots. Appl. Phys. Lett. 2001, 78, 2309–2311. [Google Scholar] [CrossRef]
- Gschrey, M.; Gericke, F.; Schüßler, A.; Schmidt, R.; Schulze, J.-H.; Heindel, T.; Rodt, S.; Strittmatter, A.; Reitzenstein, S. In situ electron-beam lithography of deterministic single-quantum-dot mesa-structures using low-temperature cathodoluminescence spectroscopy. Appl. Phys. Lett. 2013, 102, 251113. [Google Scholar] [CrossRef]
- Nowak, A.K.; Portalupi, S.L.; Giesz, V.; Gazzano, O.; Savio, C.D.; Braun, P.-F.; Karrai, K.; Arnold, C.; Lanco, L.; Sagnes, I.; et al. Deterministic and electrically tunable bright single-photon source. Nat. Commun. 2014, 5, 3240. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Kim, J.; Benson, O.; Kan, H.; Yamamoto, Y. A single-photon turnstile device. Nature 1999, 397, 500–503. [Google Scholar] [CrossRef]
- Michler, P.; Kiraz, A.; Becher, C.; Schoenfeld, W.V.; Petroff, P.M.; Zhang, L.; Hu, E.; Imamoglu, A. A quantum dot single-photon turnstile device. Science 2000, 290, 2282–2285. [Google Scholar] [CrossRef]
- Yuan, Z.; Kardynal, B.E.; Stevenson, R.M.; Shields, A.J.; Lobo, C.J.; Cooper, K.; Beattie, N.S.; Ritchie, D.A.; Pepper, M. Electrically driven single-photon source. Science 2002, 295, 102–105. [Google Scholar] [CrossRef] [PubMed]
- Santori, C.; Fattal, D.; Vučković, J.; Solomon, G.S.; Yamamoto, Y. Indistinguishable photons from a single-photon device. Nature 2002, 419, 594–597. [Google Scholar] [CrossRef] [PubMed]
- Badolato, A.; Hennessy, K.; Atature, M.; Dreiser, J.; Hu, E.; Petroff, P.M.; Imamoglu, A. Deterministic coupling of single quantum dots to single nanocavity modes. Science 2005, 308, 1158–1161. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.H.; Chen, W.Y.; Chang, H.S.; Hsieh, T.P.; Chyi, J.I.; Hsu, T.M. Efficient single-photon sources based on low-density quantum dots in photonic-crystal nanocavities. Phys. Rev. Lett. 2006, 96, 117401. [Google Scholar] [CrossRef] [PubMed]
- Strauf, S.; Stoltz, N.G.; Rakher, M.T.; Coldren, L.A.; Petroff, P.M.; Bouwmeester, D. High-frequency single-photon source with polarization control. Nat. Photonics 2007, 1, 704–708. [Google Scholar] [CrossRef]
- Press, D.; Götzinger, S.; Reitzenstein, S.; Hofmann, C.; Löffler, A.; Kamp, M.; Forchel, A.; Yamamoto, Y. Photon antibunching from a single quantum-dot-microcavity system in the strong coupling regime. Phys. Rev. Lett. 2007, 98, 117402. [Google Scholar] [CrossRef]
- Toishi, M.; Englund, D.; Faraon, A.; Vucković, J. High-brightness single photon source from a quantum dot in a directional-emission nanocavity. Opt. Express 2009, 17, 14618–14626. [Google Scholar] [CrossRef]
- Claudon, J.; Bleuse, J.; Malik, N.S.; Bazin, M.; Jaffrennou, P.; Gregersen, N.; Sauvan, C.; Lalanne, P.; Gérard, J.-M. A highly efficient single-photon source based on a quantum dot in a photonic nanowire. Nat. Photonics 2010, 4, 174–177. [Google Scholar] [CrossRef]
- Rivoire, K.; Buckley, S.; Majumdar, A.; Kim, H.; Petroff, P.; Vučković, J. Fast quantum dot single photon source triggered at telecommunications wavelength. Appl. Phys. Lett. 2011, 98, 083105. [Google Scholar] [CrossRef]
- Reimer, M.E.; Bulgarini, G.; Akopian, N.; Hocevar, M.; Bavinck, M.B.; Verheijen, M.A.; Bakkers, E.P.; Kouwenhoven, L.P.; Zwiller, V. Bright single-photon sources in bottom-up tailored nanowires. Nat. Commun. 2012, 3, 737. [Google Scholar] [CrossRef]
- Birowosuto, M.D.; Sumikura, H.; Matsuo, S.; Taniyama, H.; van Veldhoven, P.J.; Nötzel, R.; Notomi, M. Fast Purcell-enhanced single photon source in 1550-nm telecom band from a resonant quantum dot-cavity coupling. Sci. Rep. 2012, 2, 321. [Google Scholar] [CrossRef] [PubMed]
- Laucht, A.; Pütz, S.; Günthner, T.; Hauke, N.; Saive, R.; Frédérick, S.; Bichler, M.; Amann, M.-C.; Holleitner, A.W.; Kaniber, M.; et al. A waveguide-coupled on-chip single-photon source. Phys. Rev. X 2012, 2, 011014. [Google Scholar] [CrossRef]
- Munsch, M.; Malik, N.S.; Dupuy, E.; Delga, A.; Bleuse, J.; Gerard, J.-M.; Claudon, J.; Gregersen, N.; Moerk, J. Dielectric GaAs antenna ensuring an efficient broadband coupling between an InAs quantum dot and a Gaussian optical beam. Phys. Rev. Lett. 2013, 110, 177402. [Google Scholar] [CrossRef] [PubMed]
- Gazzano, O.; de Vasconcellos, S.M.; Arnold, C.; Nowak, A.; Galopin, E.; Sagnes, I.; Lanco, L.; Lemaître, A.; Senellart, P. Bright solid-state sources of indistinguishable single photons. Nat. Commun. 2013, 4, 1425. [Google Scholar] [CrossRef]
- He, Y.M.; He, Y.; Wei, Y.J.; Wu, D.; Atature, M.; Schneider, C.; Hofling, S.; Kamp, M.; Lu, C.-Y.; Pan, J.-W. On-demand semiconductor single-photon source with near-unity indistinguishability. Nat. Nanotechnol. 2013, 8, 213–217. [Google Scholar] [CrossRef]
- Madsen, K.H.; Ates, S.; Liu, J.; Javadi, A.; Albrecht, S.M.; Yeo, I.; Stobbe, S.; Lodahl, P. Efficient out-coupling of high-purity single photons from a coherent quantum dot in a photonic-crystal cavity. Phys. Rev. B 2014, 90, 155303. [Google Scholar] [CrossRef]
- Giesz, V.; Portalupi, S.L.; Grange, T.; Antón, C.; De Santis, L.; Demory, J.; Somaschi, N.; Sagnes, I.; Lemaître, A.; Lanco, L.; et al. Cavity-enhanced two-photon interference using remote quantum dot sources. Phys. Rev. B 2015, 92, 161302. [Google Scholar] [CrossRef]
- Gschrey, M.; Thoma, A.; Schnauber, P.; Seifried, M.; Schmidt, R.; Wohlfeil, B.; Krüger, L.; Schulze, J.-H.; Heindel, T.; Burger, S.; et al. Highly indistinguishable photons from deterministic quantum-dot microlenses utilizing three-dimensional in situ electron-beam lithography. Nat. Commun. 2015, 6, 7662. [Google Scholar] [CrossRef]
- Sapienza, L.; Davanço, M.; Badolato, A.; Srinivasan, K. Nanoscale optical positioning of single quantum dots for bright and pure single-photon emission. Nat. Commun. 2015, 6, 7833. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Duan, Z.-C.; Gregersen, N.; Chen, M.-C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Höfling, S.; et al. On-demand single photons with high extraction efficiency and near-unity indistinguishability from a resonantly driven quantum dot in a micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Heindel, T.; Thoma, A.; von Helversen, M.; Schmidt, M.; Schlehahn, A.; Gschrey, M.; Schnauber, P.; Schulze, J.-H.; Strittmatter, A.; Beyer, J.; et al. A bright triggered twin-photon source in the solid state. Nat. Commun. 2017, 8, 14870. [Google Scholar] [CrossRef] [PubMed]
- Su, R.; Liu, S.; Wei, Y.; Yu, Y.; Liu, J.; Yu, S.; Wang, X. Bright and pure single-photons from quantum dots in micropillar cavities under up-converted excitation. Sci. Bull. 2018, 63, 739–742. [Google Scholar] [CrossRef] [PubMed]
- Rutckaia, V.; Heyroth, F.; Novikov, A.; Shaleev, M.; Petrov, M.; Schilling, J. Quantum dot emission driven by Mie resonances in silicon nanostructures. Nano Lett. 2017, 17, 6886–6892. [Google Scholar] [CrossRef]
- Kroychuk, M.K.; Shorokhov, A.S.; Yagudin, D.F.; Rakhlin, M.V.; Klimko, G.V.; Toropov, A.A.; Shubina, T.V.; Fedyanin, A.A. Quantum Dot Photoluminescence Enhancement in GaAs Nanopillar Oligomers Driven by Collective Magnetic Modes. Nanomaterials 2023, 13, 507. [Google Scholar] [CrossRef]
- Moczała-Dusanowska, M.; Dusanowski, Ł.; Iff, O.; Huber, T.; Kuhn, S.; Czyszanowski, T.; Schneider, C.; Höfling, S. Strain-tunable single-photon source based on a circular Bragg grating cavity with embedded quantum dots. ACS Photonics 2020, 7, 3474–3480. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Wei, Y.; Ma, J.; Song, C.; Yu, Y.; Su, R.; Geng, W.; Ni, H.; Liu, H.; et al. Bright semiconductor single-photon sources pumped by heterogeneously integrated micropillar lasers with electrical injections. Light Sci. Appl. 2023, 12, 65. [Google Scholar] [CrossRef]
- Chen, Z.S.; Ma, B.; Shang, X.J.; Ni, H.Q.; Wang, J.L.; Niu, Z.C. Bright single-photon source at 1.3 μm based on InAs bilayer quantum dot in micropillar. Nanoscale Res. Lett. 2017, 12, 378. [Google Scholar] [CrossRef]
- Liu, F.; Brash, A.J.; O’Hara, J.; Martins, L.M.P.P.; Phillips, C.; Coles, R.J.; Royall, B.; Clarke, E.; Bentham, C.; Prtljaga, N.; et al. High Purcell factor generation of indistinguishable on-chip single photons. Nat. Nanotechnol. 2018, 13, 835–840. [Google Scholar] [CrossRef]
- Kolatschek, S.; Nawrath, C.; Bauer, S.; Huang, J.; Fischer, J.; Sittig, R.; Jetter, M.; Portalupi, S.L.; Michler, P. Bright Purcell enhanced single-photon source in the telecom O-band based on a quantum dot in a circular Bragg grating. Nano Lett. 2021, 21, 7740–7745. [Google Scholar] [CrossRef]
- Xu, S.-W.; Wei, Y.-M.; Su, R.-B.; Li, X.-S.; Huang, P.-N.; Liu, S.-F.; Huang, X.-Y.; Yu, Y.; Liu, J.; Wang, X.-H. Bright single-photon sources in the telecom band by deterministically coupling single quantum dots to a hybrid circular Bragg resonator. Photonics Res. 2022, 10, B1–B6. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.M.; Chung, T.H.; Hu, H.; Yu, Y.; Chen, S.; Ding, X.; Chen, M.-C.; Qin, J.; Yang, X.; et al. Towards optimal single-photon sources from polarized microcavities. Nat. Photonics 2019, 13, 770–775. [Google Scholar] [CrossRef]
- Wang, X.-L.; Cai, X.-D.; Su, Z.-E.; Chen, M.-C.; Wu, D.; Li, L.; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Stav, T.; Faerman, A.; Maguid, E.; Oren, D.; Kleiner, V.; Hasman, E.; Segev, M. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 2018, 361, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Lin, Q.; Su, R.; Zhou, Z.-K.; Song, J.; Li, J.; Wang, X.-H. On-demand spin-state manipulation of single-photon emission from quantum dot integrated with metasurface. Sci. Adv. 2020, 6, eaba8761. [Google Scholar] [CrossRef]
- Chen, B.; Wei, Y.; Zhao, T.; Liu, S.; Su, R.; Yao, B.; Yu, Y.; Liu, J.; Wang, X. Bright solid-state sources for single photons with orbital angular momentum. Nat. Nanotechnol. 2021, 16, 302–307. [Google Scholar] [CrossRef]
- Cai, X.; Wang, J.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.; Sorel, M.; O’brien, J.L.; Thompson, M.G.; Yu, S. Integrated compact optical vortex beam emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Yan, Q.; Hu, X.; Fu, Y.; Lu, C. Quantum topological photonics. Adv. Opt. Mater. 2021, 9, 2001739. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Bell, B.; Oren, D.; Eggleton, B.J.; Segev, M. Topological protection of biphoton states. Science 2018, 362, 568–571. [Google Scholar] [CrossRef] [PubMed]
- Mittal, S.; Goldschmidt, E.A.; Hafezi, M. A topological source of quantum light. Nature 2018, 561, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Mittal, S.; Orre, V.V.; Goldschmidt, E.A.; Hafezi, M. Tunable quantum interference using a topological source of indistinguishable photon pairs. Nat. Photonics 2021, 15, 542–548. [Google Scholar] [CrossRef]
- Dai, T.; Ao, Y.; Bao, J.; Mao, J.; Chi, Y.; Fu, Z.; You, Y.; Chen, X.; Zhai, C.; Tang, B.; et al. Topologically protected quantum entanglement emitters. Nat. Photonics 2022, 16, 248–257. [Google Scholar] [CrossRef]
- Jurkat, J.; Klembt, S.; De Gregorio, M.; Meinecke, M.; Buchinger, Q.; Harder, T.H.; Beierlein, J.; Egorov, O.A.; Emmerling, M.; Krause, C.; et al. Single-Photon Source in a Topological Cavity. Nano Lett. 2023, 23, 820–826. [Google Scholar] [CrossRef]
- Stevenson, R.M.; Young, R.J.; Atkinson, P.; Cooper, K.; Ritchie, D.A.; Shields, A.J. A semiconductor source of triggered entangled photon pairs. Nature 2006, 439, 179–182. [Google Scholar] [CrossRef]
- Schimpf, C.; Reindl, M.; Huber, D.; Lehner, B.; Da Silva, S.F.C.; Manna, S.; Vyvlecka, M.; Walther, P.; Rastelli, A. Quantum cryptography with highly entangled photons from semiconductor quantum dots. Sci. Adv. 2021, 7, eabe8905. [Google Scholar] [CrossRef]
- Orieux, A.; Versteegh, M.A.M.; Jöns, K.D.; Ducci, S. Semiconductor devices for entangled photon pair generation: A review. Rep. Prog. Phys. 2017, 80, 076001. [Google Scholar] [CrossRef]
- Jöns, K.D.; Schweickert, L.; Versteegh, M.A.M.; Dalacu, D.; Poole, P.J.; Gulinatti, A.; Giudice, A.; Zwiller, V.; Reimer, M.E. Bright nanoscale source of deterministic entangled photon pairs violating Bell’s inequality. Sci. Rep. 2017, 7, 1700. [Google Scholar] [CrossRef]
- Aumann, P.; Prilmüller, M.; Kappe, F.; Ostermann, L.; Dalacu, D.; Poole, P.J.; Ritsch, H.; Lechner, W.; Weihs, G. Demonstration and modeling of time-bin entangled photons from a quantum dot in a nanowire. AIP Adv. 2022, 12, 055115. [Google Scholar] [CrossRef]
- Chen, Y.; Zopf, M.; Keil, R.; Ding, F.; Schmidt, O.G. Highly-efficient extraction of entangled photons from quantum dots using a broadband optical antenna. Nat. Commun. 2018, 9, 2994. [Google Scholar] [CrossRef] [PubMed]
- Hopfmann, C.; Nie, W.; Sharma, N.L.; Weigelt, C.; Ding, F.; Schmidt, O.G. Maximally entangled and gigahertz-clocked on-demand photon pair source. Phys. Rev. B 2021, 103, 075413. [Google Scholar] [CrossRef]
- Liu, J.; Su, R.; Wei, Y.; Yao, B.; da Silva, S.F.C.; Yu, Y.; Iles-Smith, J.; Srinivasan, K.; Rastelli, A.; Li, J.; et al. A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability. Nat. Nanotechnol. 2019, 14, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hu, H.; Chung, T.H.; Qin, J.; Yang, X.; Li, J.-P.; Liu, R.-Z.; Zhong, H.-S.; He, Y.-M.; Ding, X.; et al. On-demand semiconductor source of entangled photons which simultaneously has high fidelity, efficiency, and indistinguishability. Phys. Rev. Lett. 2019, 122, 113602. [Google Scholar] [CrossRef]
- Rota, M.B.; Krieger, T.M.; Buchinger, Q.; Beccaceci, M.; Neuwirth, J.; Huet, H.; Horová, N.; Lovicu, G.; Ronco, G.; da Silva, S.F.C.; et al. A source of entangled photons based on a cavity-enhanced and strain-tuned GaAs quantum dot. arXiv 2022, arXiv:2212.12506. [Google Scholar]
- Ginés, L.; Moczała-Dusanowska, M.; Dlaka, D.; Hošák, R.; Gonzales-Ureta, J.R.; Lee, J.; Ježek, M.; Harbord, E.; Oulton, R.; Höfling, S.; et al. High extraction efficiency source of photon pairs based on a quantum dot embedded in a broadband micropillar cavity. Phys. Rev. Lett. 2022, 129, 033601. [Google Scholar] [CrossRef]
- Zeuner, K.D.; Jons, K.D.; Schweickert, L.; Hedlund, C.R.; Lobato, C.N.; Lettner, T.; Wang, K.; Gyger, S.; Schöll, E.; Steinhauer, S.; et al. On-demand generation of entangled photon pairs in the telecom C-band with InAs quantum dots. ACS Photonics 2021, 8, 2337–2344. [Google Scholar] [CrossRef]
- Lettner, T.; Gyger, S.; Zeuner, K.D.; Schweickert, L.; Steinhauer, S.; Hedlund, C.R.; Stroj, S.; Rastelli, A.; Hammar, M.; Trotta, R.; et al. Strain-controlled quantum dot fine structure for entangled photon generation at 1550 nm. Nano Lett. 2021, 21, 10501–10506. [Google Scholar] [CrossRef]
- Liu, F.Q.; Li, L.; Wang, L.; Liu, J.; Zhang, W.; Zhang, Q.; Liu, W.; Lu, Q.; Wang, Z. Solid source MBE growth of quantum cascade lasers. Appl. Phys. A 2009, 97, 527–532. [Google Scholar] [CrossRef]
- Fei, T.; Zhai, S.; Zhang, J.; Lu, Q.; Zhuo, N.; Liu, J.; Wang, L.; Liu, S.; Jia, Z.; Li, K.; et al. 3 W Continuous-Wave Room Temperature Quantum Cascade Laser Grown by Metal-Organic Chemical Vapor Deposition. Photonics 2023, 10, 47. [Google Scholar] [CrossRef]

| Photonic Structure | Life Time (ns) | Wavelength (nm) | References | |
|---|---|---|---|---|
| Micropillar | 0.65 | ~917 | 0.05 | [47] |
| Micropillar | 0.015 | ~956 | 0.18 | [48] |
| Photonic crystal cavities | 0.045 | ~944 | 0.05 | [49] |
| Tapered nanowires | 2.4 | ~915 | <0.008 | [50] |
| Photonic crystal cavities | ~1 | ~1550 | 0.43 ± 0.04 | [51] |
| Tapered nanowires | 1.7 ± 0.1 | ~881 | 0.12 | [52] |
| Photonic crystal cavities | 0.2 | ~1550 | 0.10 ± 0.02 | [53] |
| Photonic crystal cavities | 0:87 ± 0:15 | ~910 | 0:27 ± 0:07 | [54] |
| Nano-trumpet | 0.82 | ~907 | 0.31 | [55] |
| Micropillar | 0.265–0.270 | ~932 | 0.05 | [56] |
| Micropillar | ~0.39 | ~941 | 0.012(2) | [57] |
| Photonic crystal cavities | 1.61 | ~905 | 0.04 ± 0.05 | [58] |
| Adiabatic pillar | 0.14 ± 0.04 | ~945 | 0.10 ± 0.03 | [59] |
| Microlens | ~1 | ~925 | <0.01 | [60] |
| Circular Bragg grating(CBG) cavities | 0.52 | ~907 | 0.009 ± 0.005 | [61] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Liu, F.; Lu, Q. Quantum Light Source Based on Semiconductor Quantum Dots: A Review. Photonics 2023, 10, 639. https://doi.org/10.3390/photonics10060639
Li R, Liu F, Lu Q. Quantum Light Source Based on Semiconductor Quantum Dots: A Review. Photonics. 2023; 10(6):639. https://doi.org/10.3390/photonics10060639
Chicago/Turabian StyleLi, Rusong, Fengqi Liu, and Quanyong Lu. 2023. "Quantum Light Source Based on Semiconductor Quantum Dots: A Review" Photonics 10, no. 6: 639. https://doi.org/10.3390/photonics10060639
APA StyleLi, R., Liu, F., & Lu, Q. (2023). Quantum Light Source Based on Semiconductor Quantum Dots: A Review. Photonics, 10(6), 639. https://doi.org/10.3390/photonics10060639




