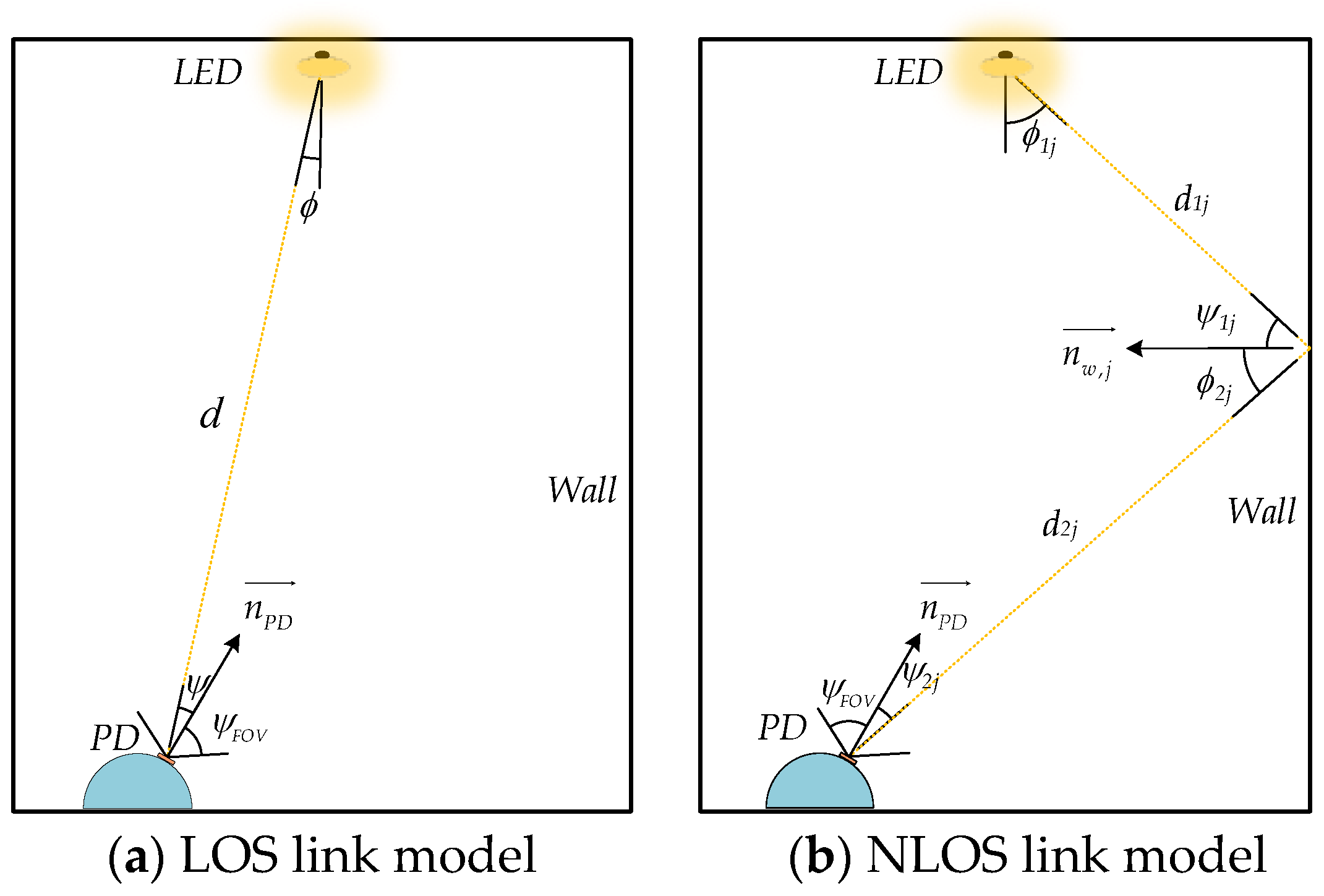
4.1. Construction of Fingerprint Database
The robot moves in an indoor space area, and the maximum height during its activities is uncertain. In this study, we took the average height of a person, 1.7 m, as the maximum height during robot activity. Therefore, a volume of 4 m × 4 m × 1.7 m in the room was used as the positioning space, divided into sections of 0.18 m × 0.18 m × 0.18 m. The four vertices of each small square area after division were used as reference points, the robot head receiver model was placed at each reference point, and the top center point coincided with the reference point. We used three PDs to acquire optical signals and then filtered them. Thus, we obtained two signals of different frequencies and calculated their optical power values. Finally, we recorded the optical power value and position coordinates obtained at the reference point in the fingerprint database. The fingerprint data at the
-th reference point can be expressed as:
where
is the optical power value of the
-th LED light source received by the
-th PD at the
-th reference point, and
are the position coordinates at the
-th reference point. Therefore, the VLP fingerprint database
could be constructed as
where
N is the number of reference points.
After dividing the positioning space into 0.18 m × 0.18 m × 0.18 m sections, the data obtained at the reference point were used as the training set. In addition, the positioning space was divided into 0.24 m × 0.24 m × 0.24 m sections, and the data obtained at this reference point were used as the test set. The training set was used to train the network model and provide it with a predictive ability, and the test set was used to evaluate the performance of the trained network model.
4.3. Selection of Performance Indicators
We used the mean squared error (MSE) and root mean squared error (RMSE) to evaluate the performance of the GRU network and VLP models.
The loss and evaluation functions of the GRU network model used MSE, which could effectively represent the error between the predicted and actual output of the network. In the process of neural network training, the gradient obtained by the loss function was input into the optimizer for gradient descent, and then the network weight was updated by backpropagation. We repeatedly trained the network to continuously improve its predictive capabilities. Finally, the test set was substituted into the trained network model for evaluation, and the network performance was evaluated by MSE. The MSE was calculated as follows:
where
is the number of sample sets,
are the true values of the
-th sample point of the sample set, and
are the predicted values of the
-th sample point of the sample set.
In the positioning process, the RMSE could better reflect the relationship between the predicted and true positions, so the RMSE was used to calculate the VLP error. The RMSE between the true and predicted coordinates of the
-th reference point could be expressed as
where
are the true coordinates of the
-th reference point in the test set, and
are the predicted coordinates of the
-th reference point in the test set. Therefore, the average positioning error was
4.4. Building the GRU Network Model
We used the Python 3.9 compiler for the experiments and Tensorflow 2.6 and the Keras 2.6 deep learning framework to build the GRU network models. When building a network model, its initial weights are random, and so the predictions of the trained model differ each time. Therefore, in order to achieve reproducible experimental results, we had to fix the random seed before building the network model. In addition, in the process of network model construction, one must manually configure the number of GRU network layers and the number of neurons in the network layer. Furthermore, before training the network, one must also set the hyperparameters, such as the learning rate, number of iterations, and batch size. These parameters affect the complexity and performance of a model, so they need to be set appropriately. Below, we present the comparison and analysis of different hyperparameter values.
To explore the influence of the number of neurons on the accuracy of the model, we compared the values at intervals of eight.
As shown in
Figure 5, the average positioning error was lower when the number of neurons in the GRU network layer was 24. However, the complexity of the model also increased when the number of neurons exceeded 24, and the average positioning error did not change significantly with an increase in the number of neurons. Therefore, the number of neurons in the GRU layer of the network model was set to 24.
After settling on 24 network neurons, we analyzed the influence of the number of GRU network layers on the model performance.
From
Table 2, one can see that the mean squared error and average localization error of the GRU network were smaller when the number of layers was two, and the model performance was improved. Furthermore, as the number of network layers increased, the error increased. When the number of layers is greater than two, increasing the number of layers of the network requires assigning more weights and training time to the network, which will lead to increased complexity of the network model and overfitting of the model, reducing the accuracy of the model. Therefore, we set the number of layers in the GRU network to two.
The batch size is the number of samples selected for training at one time, and backpropagation is performed by calculating the gradient of these samples, so it affects the degree of optimization and speed of a model.
In this study, the compared batch sizes were 16, 32, 64, 128, and 256. From
Table 3, one can see that when the batch size was too small, the gradient of calculation was unstable due to the paucity of samples, and the network did not easily converge, causing the model accuracy to decrease. However, the network generalization ability was reduced when the batch size was too large, though the network model error did not change significantly.
Table 3 also shows that the training time decreased as the batch size increased. According to our comparative analysis, the model was more effective when the batch size was set to 128.
Table 4 shows the effect of the learning rate on the model performance. The model performance was more favorable when the learning rate was set to 0.01, and the decreasing curve of the network loss function is shown in
Figure 6.
Figure 6 shows that when the number of iterations was around 950, the downward curve of the loss function was relatively flat, and there was no downward trend in subsequent iterations. To prevent overfitting and reduce training time, the maximum number of iterations of the network set to 950.
During network training, the gradient descent was slow when the learning rate was too small; thus, the training time needed to be increased to bring the model closer to the local optimum. However, the gradient decreased quickly when the learning rate was too large. Oscillation is easy in the later stage of training, but stabilization to local optimality is not straightforward, and gradient explosion may occur. In order to ensure that the network converged quickly at the beginning of training and more effectively at the end of training, we proposed a strategy to adjust the learning rate dynamically. Thus, the learning rate decay curve could be expressed as:
where
is the iteration number of network training, and
,
, and
are set values, satisfying
> 0,
> 0, and
> 0. Here,
is the upper convergence boundary of the learning rate decay curve, and the value of
is
when
= 0. If
<< 1,
is closer to
. Therefore,
can be regarded as the initial learning rate. In this study,
= 0.01 was adopted. The value denoted as
is the inflection point of the curve;
is larger in the interval of
, so the gradient descent is faster and the network converges rapidly. Additionally,
decreases continuously after
, so the gradient descent slows down, which effectively suppresses the gradient oscillation it the late training period, and the network is more easily stabilized to the local optimum. The component
is related to the decrease in the curve at the inflection point; the higher the value of
, the faster the curve falls at the inflection point. Based on continuous testing, the average positioning error was small when
= 0.01,
= 700, and
= 0.02, and the corresponding learning rate decay curve is shown in
Figure 7.
As shown in
Table 5, the learning rate decay strategy proposed in this paper corresponded to a higher VLP system accuracy, indicating that the method was effective.
Therefore, the GRU network model was constructed according to the parameters established above, and its structure is shown in
Figure 8.
The model contained an input layer and three output layers, that is, the power data were input into the network, and the output comprised three coordinates. The hidden layer used three identical network structures, each containing two GRU network layers. In order to transform the data format of the GRU layer output into the final output data format, a dense layer was added before the output layer, and the network model parameters are shown in
Table 6.