The Analysis and Experiment of Pixel-Matching Method for Space-Dimensional Dual-Coded Spectropolarimeter
Abstract
1. Introduction
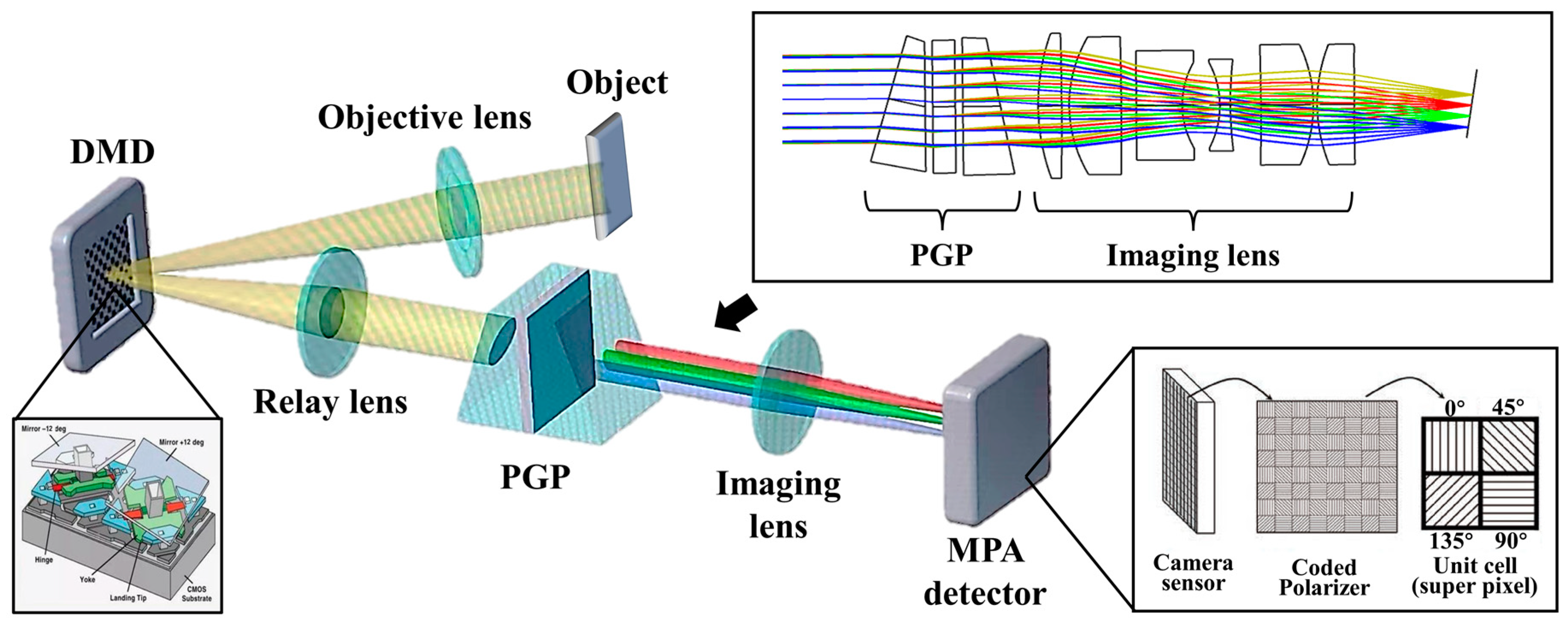
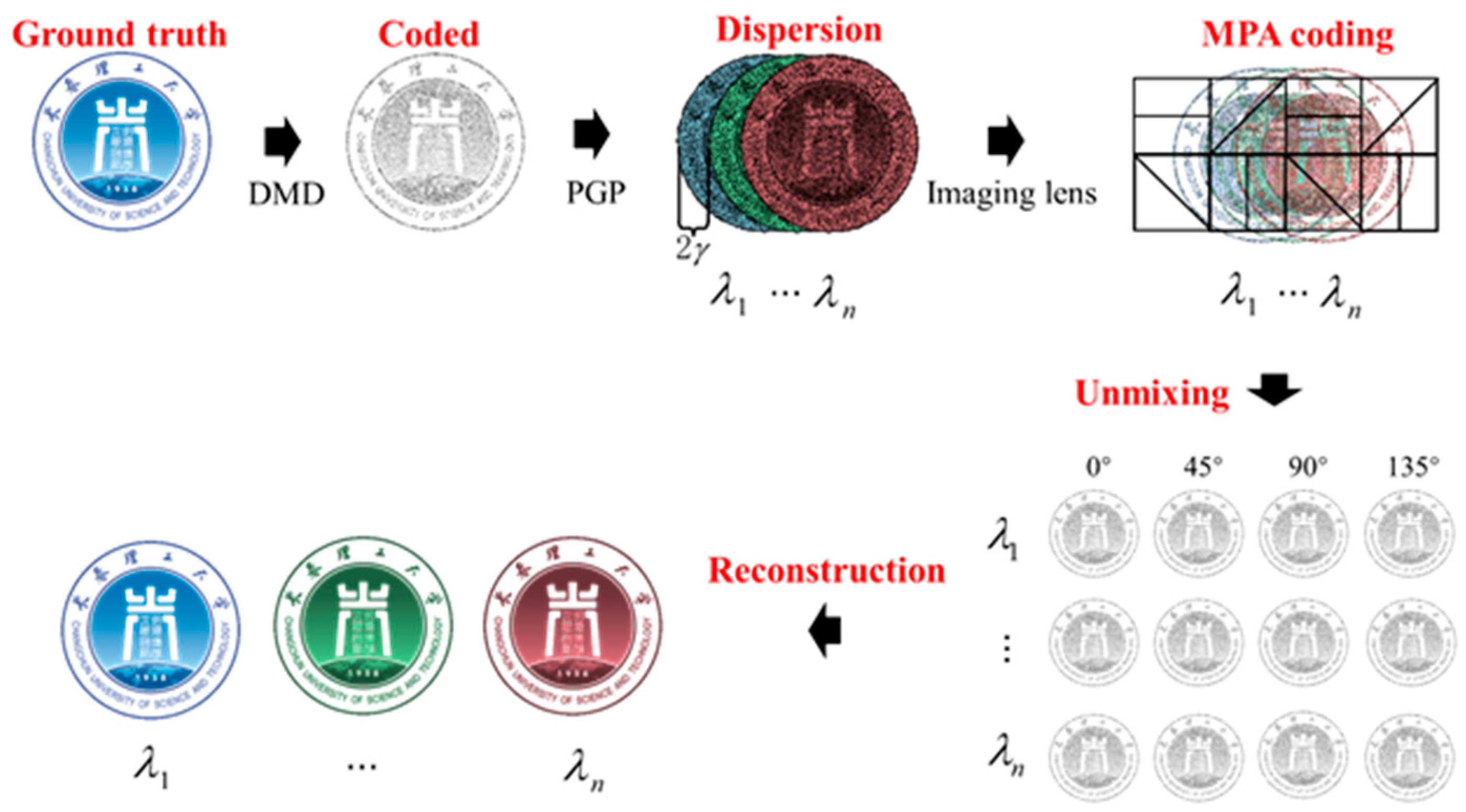
2. Principle
2.1. Imaging Configuration
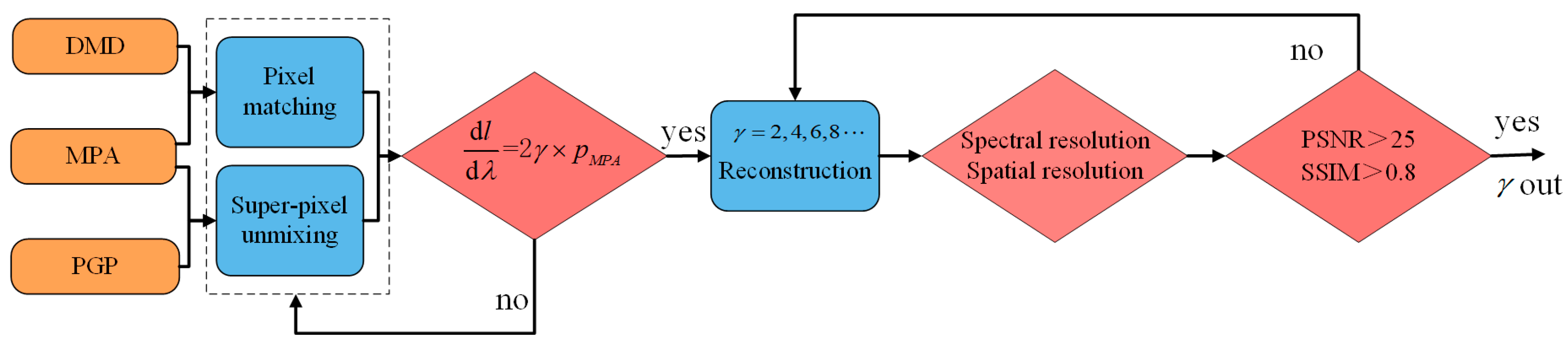
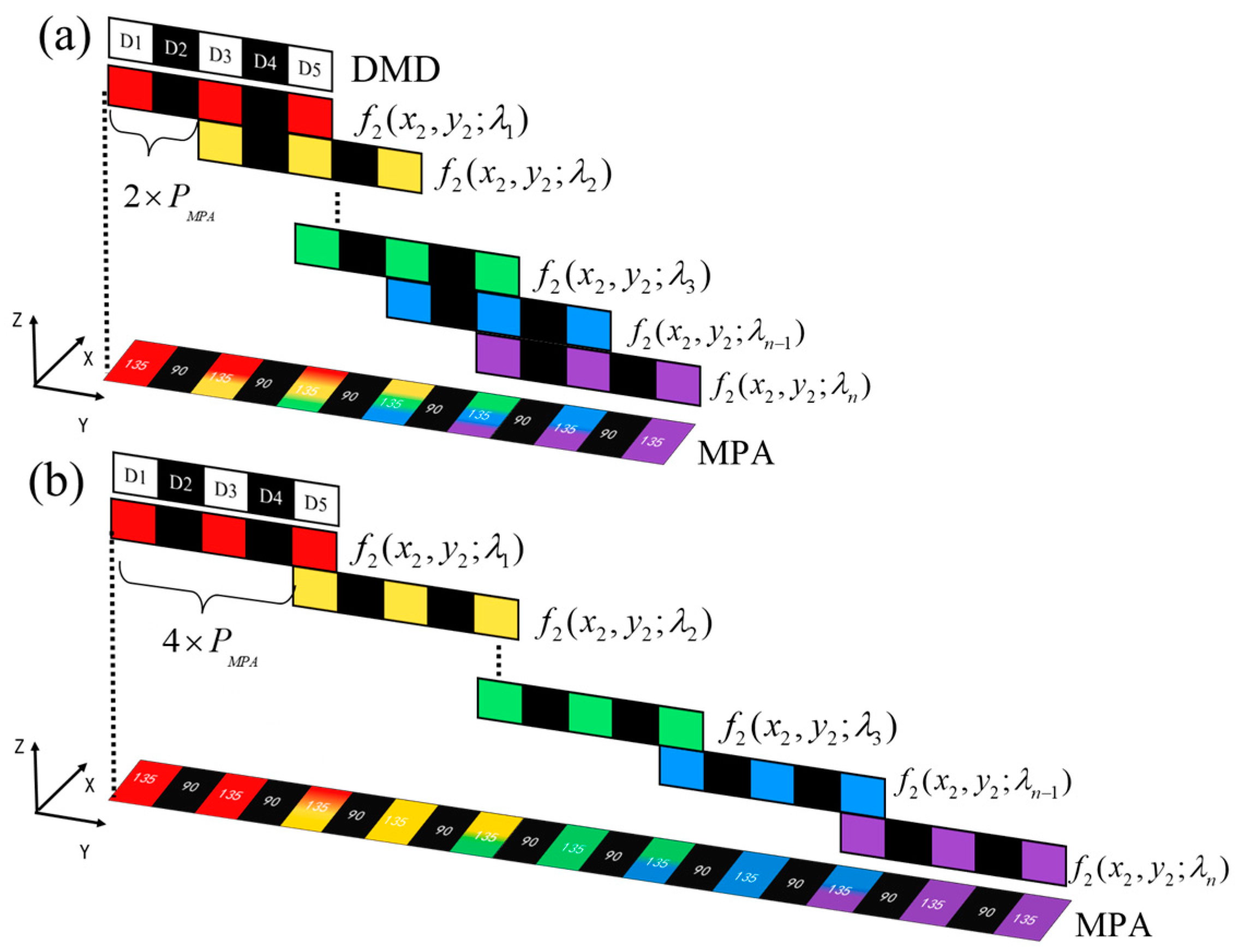
2.2. Matching Model
3. Experiment
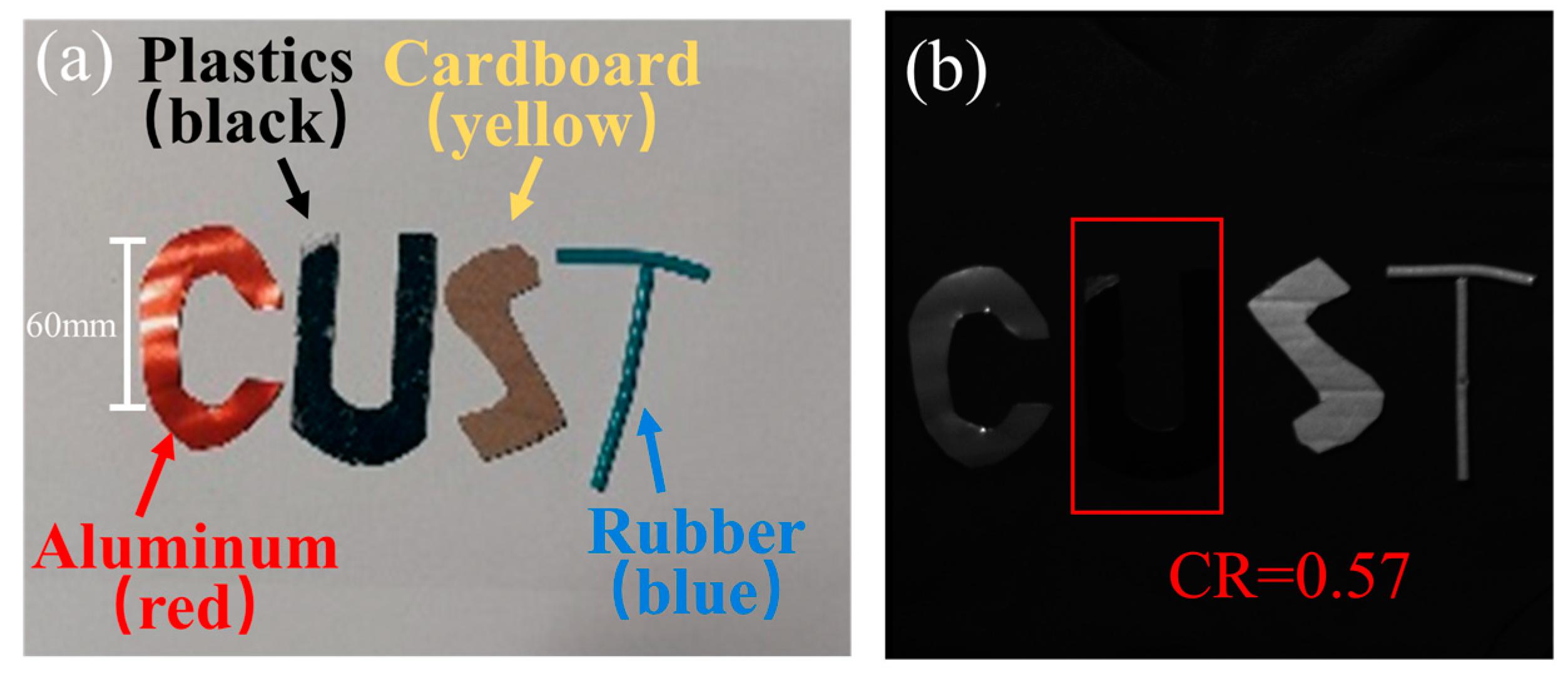
3.1. Experimental Platform
3.2. Contrast of Reconstruction Results
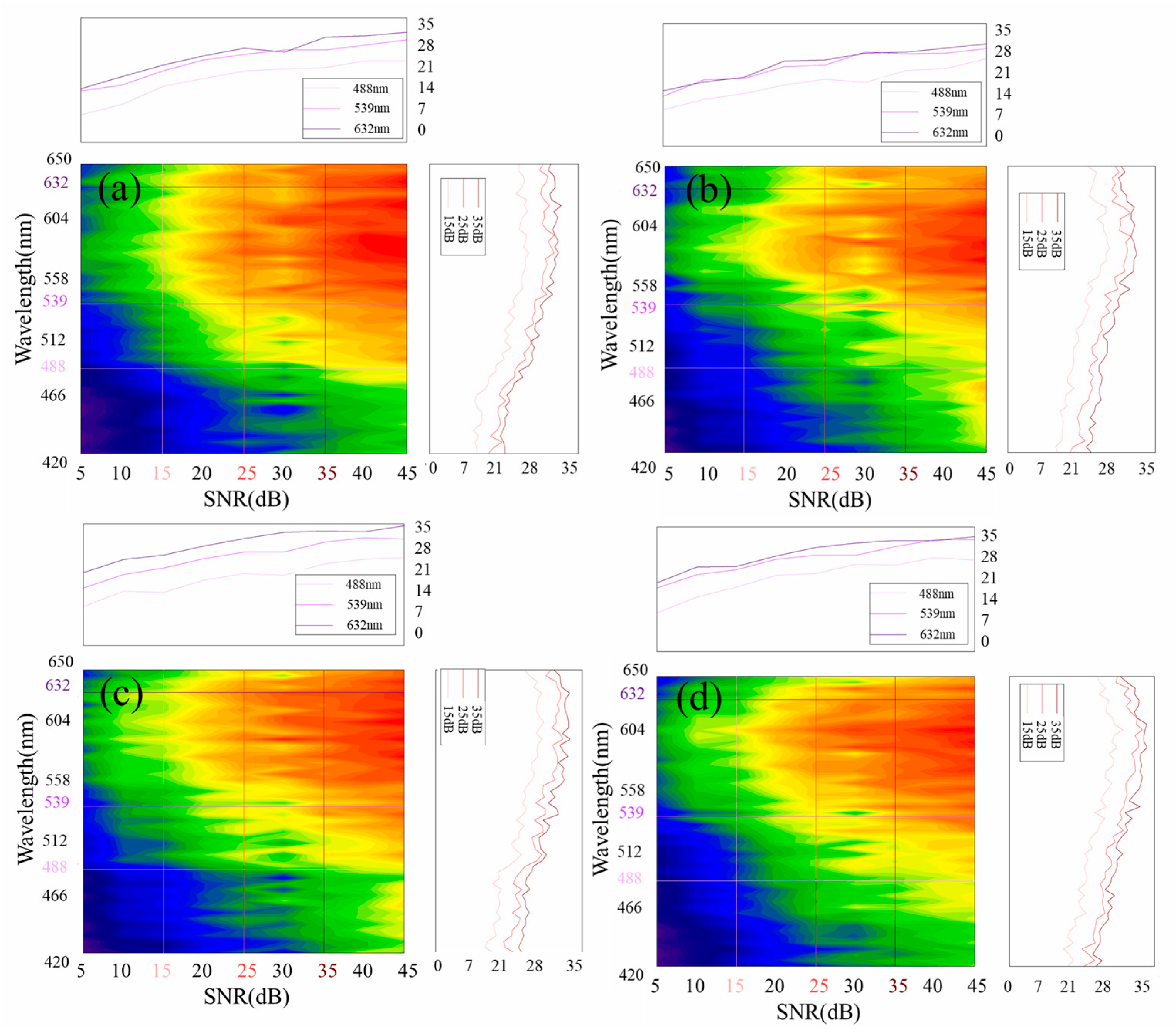
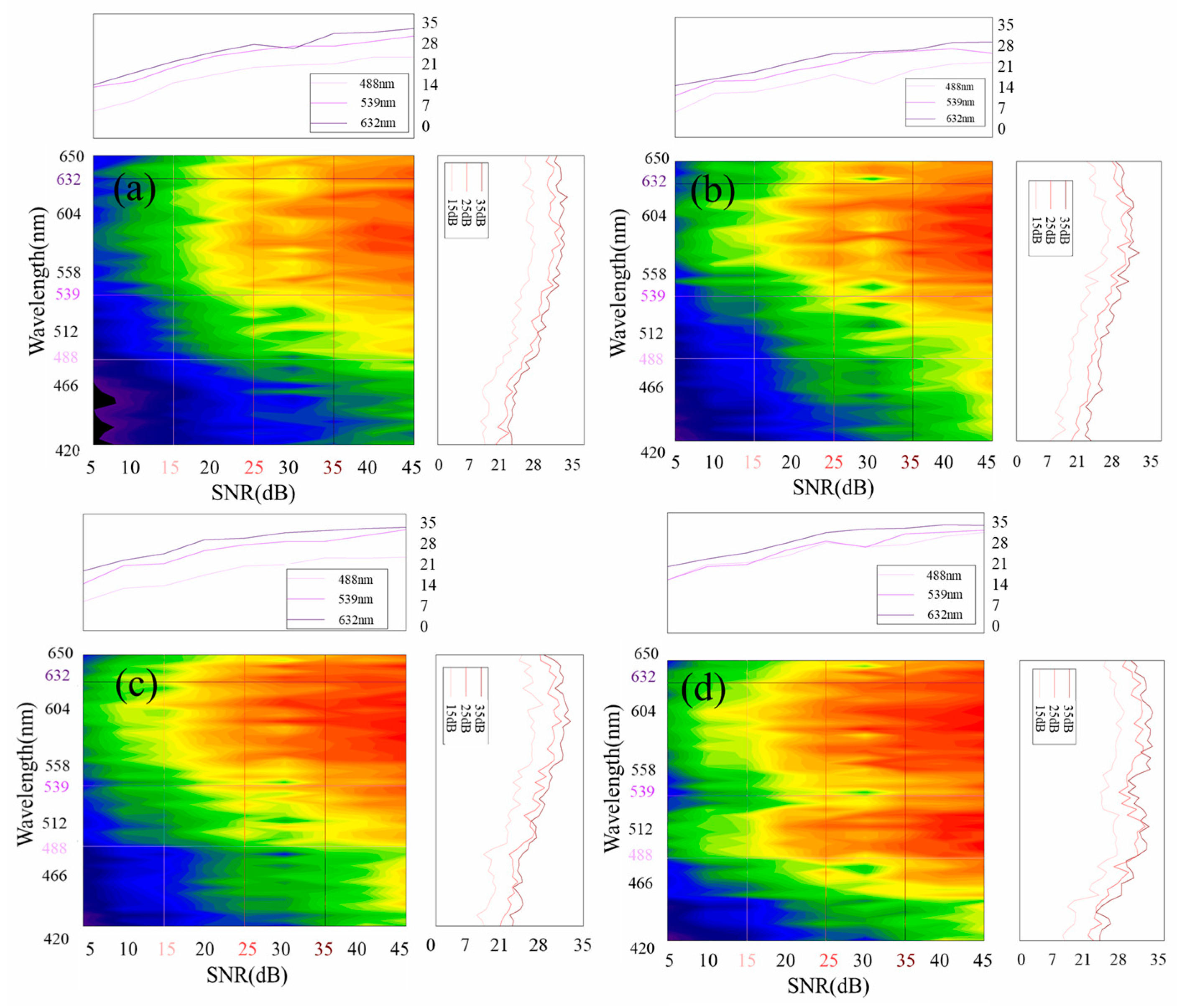
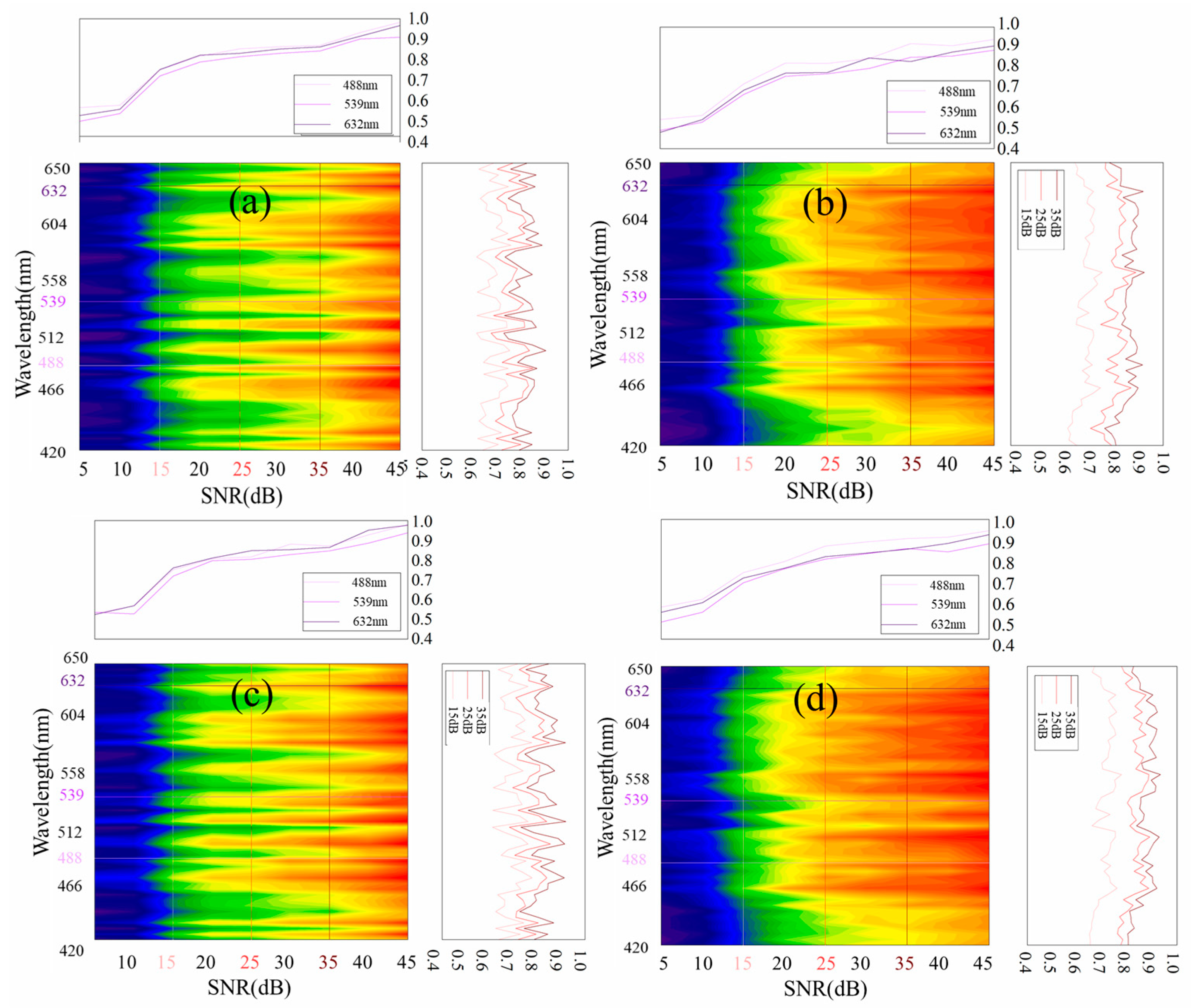
3.3. Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Habashi, A.; Bowles, J.; Foster, R.; Gray, D.; Chami, M. Polarized Observations for Advanced Atmosphere-Ocean Algorithms Using Airborne Multi-Spectral Hyper-Angular Polarimetric Imager. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107515. [Google Scholar] [CrossRef]
- Qi, J.; He, C.; Elson, D.S. Real Time Complete Stokes Polarimetric Imager Based on a Linear Polarizer Array Camera for Tissue Polarimetric Imaging. Biomed. Opt. Express 2017, 8, 4933. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Cherney, J.H.; Cherney, D.J.R.; Digman, M.F. Practical Considerations for Using the NeoSpectra-Scanner Handheld Near-Infrared Reflectance Spectrometer to Predict the Nutritive Value of Undried Ensiled Forage. Sensors 2023, 23, 1750. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yang, Z.-H.; Yu, Y.-J.; Wu, L.-A.; Song, M.-Y.; Zhao, Z.-H. Chromatic-Aberration-Corrected Hyperspectral Single-Pixel Imaging. Photonics 2023, 10, 7. [Google Scholar] [CrossRef]
- Zhu, M.; Qi, J.; Yi, W.; Du, J.; Fu, M.; Zhu, S.; Liu, J.; Li, X. Design and Dispersion Calibration of Direct-Vision Push-Broom Compressive Double-Amici-Prism Hyperspectral Imager. Photonics 2022, 9, 732. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, C.; Mu, T.; Wang, Y.; He, Y.; Yan, T.; Chen, Z. Coded Aperture Full-Stokes Imaging Spectropolarimeter. Opt. Laser Technol. 2022, 150, 107946. [Google Scholar] [CrossRef]
- Islam, M.N.; Tahtali, M.; Pickering, M. Specular Reflection Detection and Inpainting in Transparent Object through MSPLFI. Remote Sens. 2021, 13, 455. [Google Scholar] [CrossRef]
- Li, S.; Jiao, J.; Wang, C. Research on Polarized Multi-Spectral System and Fusion Algorithm for Remote Sensing of Vegetation Status at Night. Remote Sens. 2021, 13, 3510. [Google Scholar] [CrossRef]
- Ren, S.; Wu, H.; Chen, W.; Li, D. Polarization Domain Spectrum Sensing Algorithm Based on AlexNet. Sensors 2022, 22, 8946. [Google Scholar] [CrossRef]
- Alouini, M.; Goudail, F.; Grisard, A.; Bourderionnet, J.; Dolfi, D.; Bénière, A.; Baarstad, I.; Løke, T.; Kaspersen, P.; Normandin, X.; et al. Near-Infrared Active Polarimetric and Multispectral Laboratory Demonstrator for Target Detection. Appl. Opt. 2009, 48, 1610. [Google Scholar] [CrossRef]
- Gendre, L.; Foulonneau, A.; Lapray, P.-J.; Bigué, L. Database of Polarimetric and Multispectral Images in the Visible and NIR Regions. Unconv. Opt. Imaging 2018, 10677, 666–679. [Google Scholar] [CrossRef]
- Tu, X.; Spires, O.J.; Tian, X.; Brock, N.; Liang, R.; Pau, S. Division of Amplitude RGB Full-Stokes Camera Using Micro-Polarizer Arrays: Erratum. Opt. Express 2018, 26, 4192. [Google Scholar] [CrossRef] [PubMed]
- Rehbinder, J.; Vizet, J.; Park, J.; Ossikovski, R.; Vanel, J.-C.; Nazac, A.; Pierangelo, A. Depolarization Imaging for Fast and Non-Invasive Monitoring of Cervical Microstructure Remodeling in Vivo during Pregnancy. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef]
- Lv, X.; Li, Y.; Zhu, S.; Guo, X.; Zhang, J.; Lin, J.; Jin, P. Snapshot Spectral Polarimetric Light Field Imaging Using a Single Detector. Opt. Lett. 2020, 45, 6522. [Google Scholar] [CrossRef] [PubMed]
- Ono, S. Snapshot Multispectral Imaging Using a Pixel-Wise Polarization Color Image Sensor. Opt. Express 2020, 28, 34536. [Google Scholar] [CrossRef] [PubMed]
- Shinoda, K.; Ohtera, Y. Alignment-Free Filter Array: Snapshot Multispectral Polarization Imaging Based on a Voronoi-like Random Photonic Crystal Filter. Opt. Express 2020, 28, 38867. [Google Scholar] [CrossRef] [PubMed]
- Altaqui, A.; Sen, P.; Schrickx, H.; Rech, J.; Lee, J.-W.; Escuti, M.; You, W.; Kim, B.J.; Kolbas, R.; O’Connor, B.T.; et al. Mantis Shrimp–Inspired Organic Photodetector for Simultaneous Hyperspectral and Polarimetric Imaging. Sci. Adv. 2021, 7. [Google Scholar] [CrossRef]
- Bo, J.; Gu, Y.; Xing, W.; Ju, X.; Yan, C.; Wang, X. Spatially Modulated Snapshot Computed Tomographic Polarization Imaging Spectrometer. Appl. Opt. 2021, 60, 5860. [Google Scholar] [CrossRef]
- Tsai, T.-H.; Brady, D.J. Coded Aperture Snapshot Spectral Polarization Imaging. Appl. Opt. 2013, 52, 2153. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, C.; Mu, T.; Yan, T.; Bao, D.; Chen, Z.; He, Y. Coded Aperture Snapshot Linear-Stokes Imaging Spectropolarimeter. Opt. Commun. 2019, 450, 72–77. [Google Scholar] [CrossRef]
- Xu, B.; Jin, Z.; Dai, X.; Shui, C.; Zhao, Z.; Lan, Z. Pixelated polarizers array based coded aperture snapshot spectropolarimetric imaging with side information. Opt. Commun. 2022, 517, 128329. [Google Scholar] [CrossRef]
- Ning, J.; Xu, Z.; Wu, D.; Zhang, R.; Wang, Y.; Xie, Y.; Zhao, W.; Ren, W. Compressive Circular Polarization Snapshot Spectral Imaging. Opt. Commun. 2021, 491, 126946. [Google Scholar] [CrossRef]
- Wang, J.; Shi, H.; Liu, J.; Li, Y.; Fu, Q.; Wang, C.; Jiang, H. Compressive Space-Dimensional Dual-Coded Hyperspectral Polarimeter (CSDHP) and Interactive Design Method. Opt. Express 2023, 31, 9886. [Google Scholar] [CrossRef] [PubMed]
- Chipman, R.A.; Sze, W.; Young, G. Polarized Light and Optical Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; p. 64. ISBN 9781498700573. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
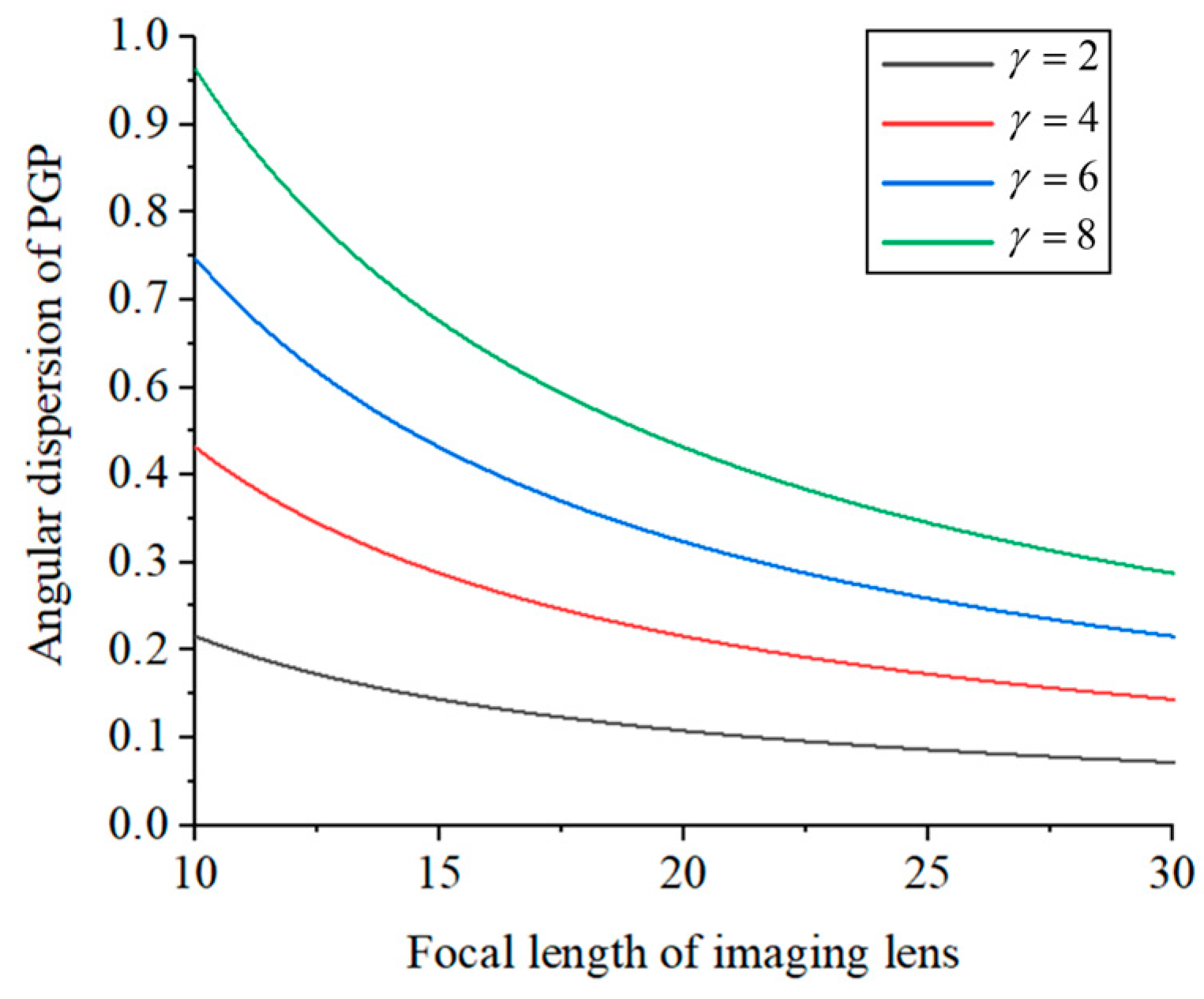




| Spatial Resolution | Spectral Channels Theoretically | PSNR (dB) | SSIM (dB) | |
|---|---|---|---|---|
| 2 | 1089 | 26.4326 | 0.8163 | |
| 4 | 545 | 28.9519 | 0.9256 | |
| 6 | 363 | 29.1449 | 0.9317 | |
| 8 | 273 | 29.2426 | 0.9343 | |
| 10 | 217 | 29.2930 | 0.9360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Shi, H.; Liu, J.; Li, Y.; Fu, Q.; Wang, C.; Wang, Q.; Liu, H.; Jiang, H. The Analysis and Experiment of Pixel-Matching Method for Space-Dimensional Dual-Coded Spectropolarimeter. Photonics 2023, 10, 632. https://doi.org/10.3390/photonics10060632
Wang J, Shi H, Liu J, Li Y, Fu Q, Wang C, Wang Q, Liu H, Jiang H. The Analysis and Experiment of Pixel-Matching Method for Space-Dimensional Dual-Coded Spectropolarimeter. Photonics. 2023; 10(6):632. https://doi.org/10.3390/photonics10060632
Chicago/Turabian StyleWang, Jiayu, Haodong Shi, Jianan Liu, Yingchao Li, Qiang Fu, Chao Wang, Qi Wang, Haiying Liu, and Huilin Jiang. 2023. "The Analysis and Experiment of Pixel-Matching Method for Space-Dimensional Dual-Coded Spectropolarimeter" Photonics 10, no. 6: 632. https://doi.org/10.3390/photonics10060632
APA StyleWang, J., Shi, H., Liu, J., Li, Y., Fu, Q., Wang, C., Wang, Q., Liu, H., & Jiang, H. (2023). The Analysis and Experiment of Pixel-Matching Method for Space-Dimensional Dual-Coded Spectropolarimeter. Photonics, 10(6), 632. https://doi.org/10.3390/photonics10060632






