Solar Cell Detection and Position, Attitude Determination by Differential Absorption Imaging in Optical Wireless Power Transmission

Abstract

In optical wireless power transmission, position, size, and attitude of photovoltaic device (PV) must be determined from light source. A method proposed in the previous report is based on selective absorption characteristics of PV, and it is detected by differentiating images of strongly absorbable wavelength and one not. In this study, using two infrared wavelengths, two kinds of targets were detected by differential absorption imaging. One was a GaAs substrate which simulates diffuse rear surface, and the other was a real GaAs PV. It was found that the substrate’s reflective characteristic was diffuse, and the solar cell’s was mainly non-diffuse and accompanied by small diffuse component supporting wide-angle reflection. Using this feature, the position of the GaAs solar cell could be determined within a wide range of angle. Its attitude could also be determined with an accuracy of ±10 degrees to its normal. The position of diffuse GaAs substrate could be determined within a wide range of angles, and its attitude determination was proposed by exploiting its varying apparent size with tilt angle. Broad reflection characteristics of the GaAs substrate enabled attitude determination for a wide-angle range, and determination around normal would be erroneous.

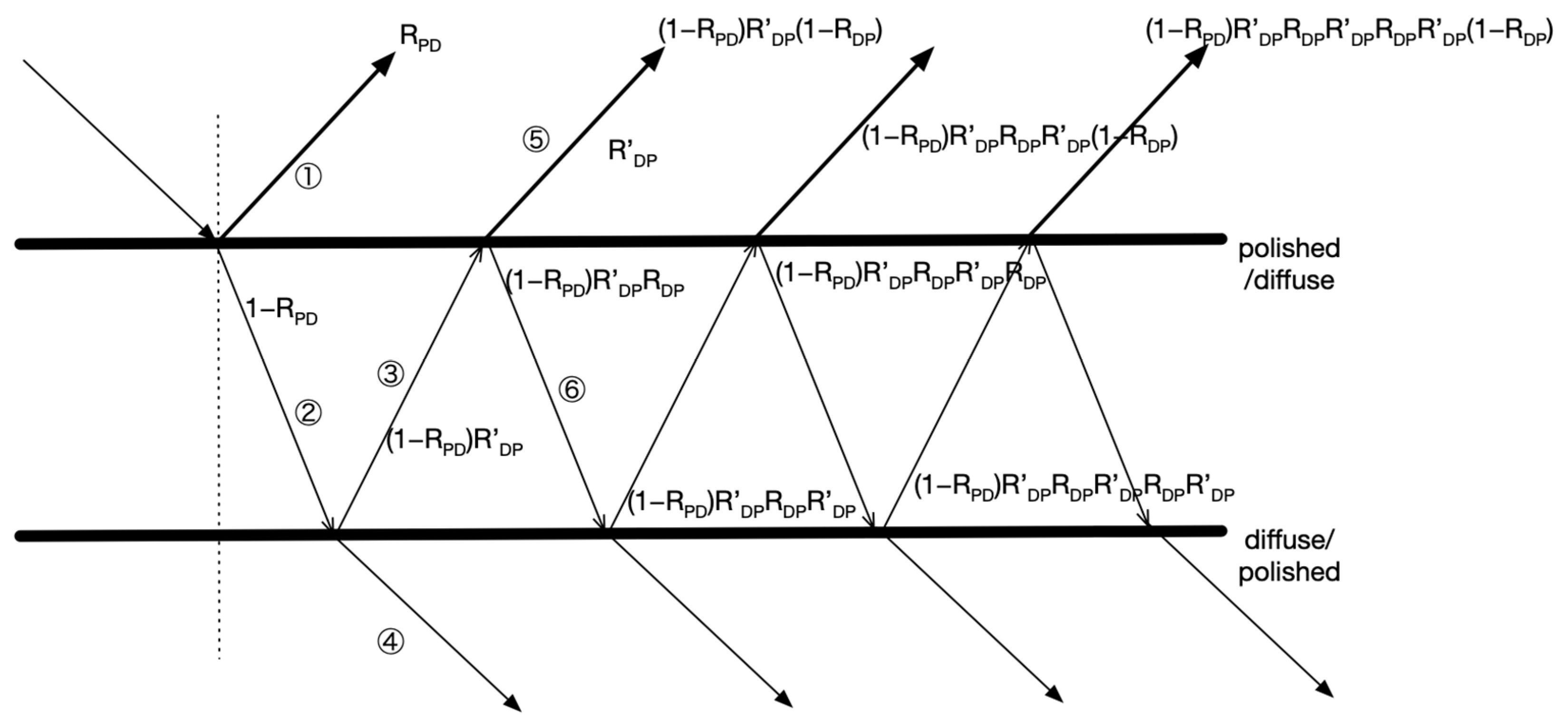
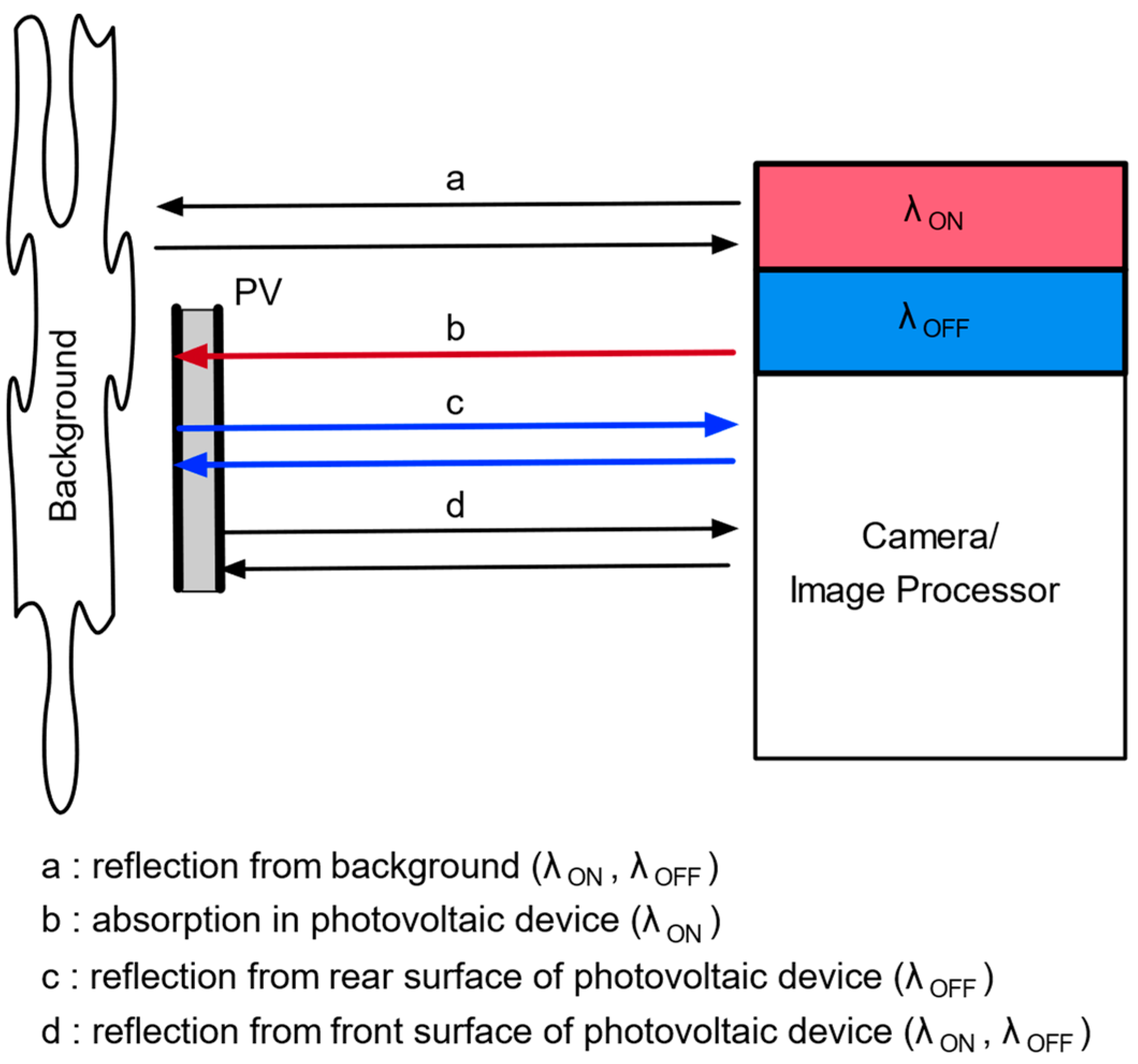
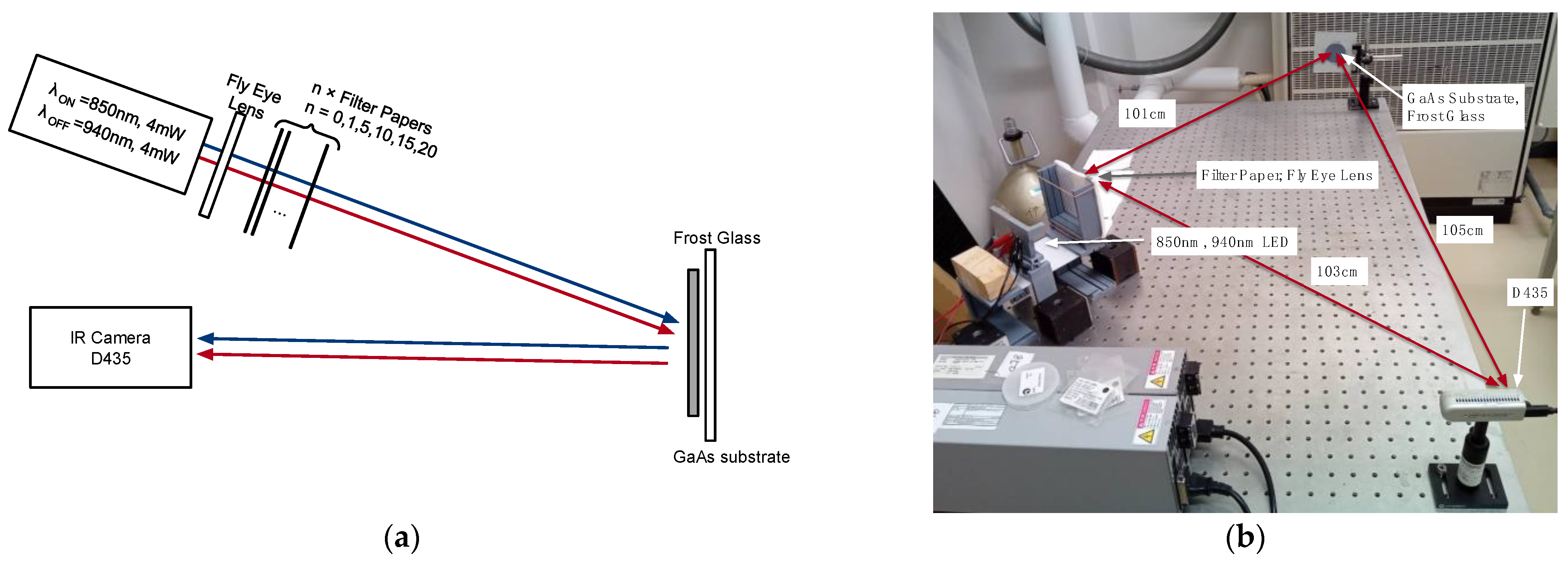
1. Introduction

In the coming wireless society [1], Optical Wireless Power Transmission (OWPT) is expected to play an important role [2,3,4]. Since it irradiates light beam to photovoltaic device (PV) from light source, it has advantage of transmitting power to a long-distance target [5,6,7,8]. To increase power generation efficiency to irradiated power, sophisticated beam alignment and shaping combined with some relaxation strategy [9,10] is necessary. Moreover, PV’s position, size, and attitude must be accurately determined from the light source. Therefore, detecting solar cells’ position and attitude are essential building blocks of the operational OWPT system. However, studies regarding them are not so many so far. In former researches, PV detection are studied by means of image processing of its outline or specific markers [11,12]. It is reported that detection became unstable in case of varying background illumination by weather or time [11].

Thus, robust detection of PV is one of critical technical challenges in OWPT. In the method proposed previously, robustness is achieved by utilizing intrinsically built-in feature of PV. PV is detected by differentiating images of wavelength which is strongly absorbed by it (hereafter ${\lambda }_{ON}$) and one which is not (hereafter ${\lambda }_{OFF}$). During this differentiation, the unnecessary background is subtracted. Differential technique is widely used in many technical areas both in signal and image processing [13,14,15]. This technique was applied to solar cell detection in OWPT [16]. A proof-of-concept study was conducted utilizing $\lambda$ = 532 nm and Si substrate as a target. In this study, following the previous one, detection and determination of position, area and attitude of GaAs substrate and real GaAs PV were investigated utilizing two infrared wavelengths 850 nm (${\lambda }_{ON}$), and 940 nm (${\lambda }_{OFF}$).

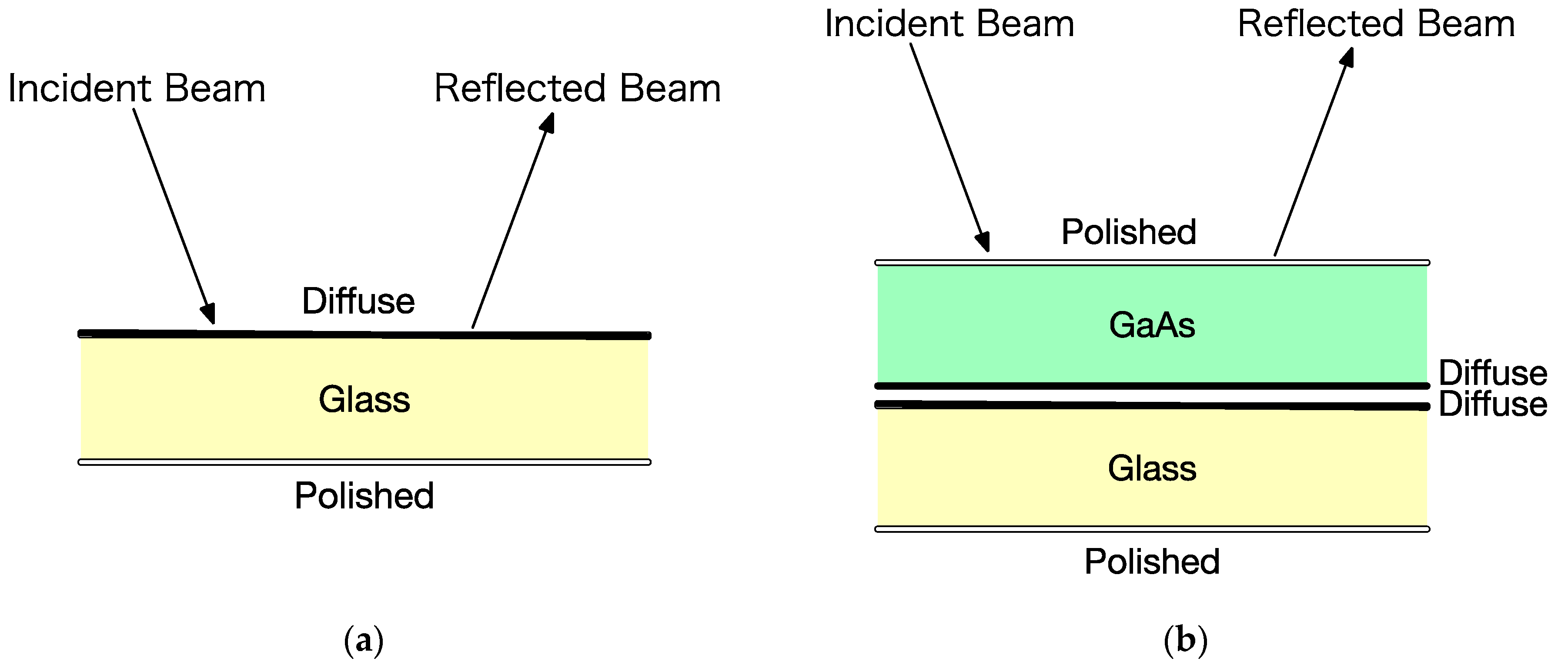
Two options would be expected for rear surface treatment of solar cells. One is diffuse, and the other is non-diffuse. Angle dependence of detection were analyzed for both options and attitude determination were proposed. GaAs substrate showed broad diffuse reflection characteristic. On the other hand, PV showed sharp angular dependence of reflection. The existence of solar cells could be detected within a wide angle range for both targets. Regarding attitude detection, normality of PV could be detected within ±10 degrees. For a diffuse GaAs substrate, attitude determination based on apparent width of the target was investigated and experimentally validated.

The structure of this paper is as follows. Detection experiments of GaAs substrate, including determining its center coordinates and area, are reported in Section 2. The ‘threshold equation’ is derived in Section 3, which connects signal electron number and minimum grayscale level of differential absorption image at the threshold. In Section 4, real thin-film GaAs solar cell detection experiments are reported. Angular characteristics of GaAs substrate and solar cell detection are reported and discussed in Section 4 and Section 5. Finally, in Section 6, the outcomes of this study are summarized.

2. GaAs Target Detection by Means of Infrared Differential Imaging

2.1. Configuration of Experimental Apparatus

PV detection by differential absorption imaging utilizes selective absorption characteristics of PV between two different wavelengths. The principle of solar cell detection by differential imaging is described in Figure 1 and [16] in detail.

In the previous study, experiments were conducted with $\lambda$ = 532 nm, and differential images were generated from Si substrate and frost glass images [16]. Then, determination of X and Y center coordinates, and area of the Si substrate were discussed, including their accuracies. In this study, similar experiments were conducted using more realistic targets. In many PV, semiconductors such as Si or GaAs are utilized, and differential absorption imaging takes advantage of the wavelength dependence of absorption of semiconductors. Absorbable wavelength ${\lambda }_{ON}$ should be set below and non-absorbable wavelength ${\lambda }_{OFF}$ should be above the bandgap wavelength of semiconductors. Two wavelengths should be close enough so that the two wavelengths experience almost the same background, and the image-capturing camera in Figure 1 should have sensitivity for both wavelengths. In the experiments in this study, the Si sensor camera was exploited like in the previous one, GaAs was chosen as the target material, and ${\lambda }_{ON}$, ${\lambda }_{OFF}$ were selected as 850 nm and 940 nm, respectively.

Figure 2 shows configuration and layout of this experiment. The transmitter assembly consists of series-connected two LEDs for both 850 nm and 940 nm. Emitting power of individual LED is calculated as 2 mW from the data sheets [17,18]. For the infrared camera, Intel D435^TM [19] depth camera was used, and one of its two infrared output streams (left channel) was inputted to the image processor (PC). As for software running on the image processor, D435 SDK [20], Python [21] and Open CV [22] were used to control the camera. Irradiated power onto the target is controlled by changing the number of filter papers, which has scattering and reflection characteristics, in front of the fly eye lens in Figure 2a. In this paper, such ‘power control status’ is denoted as P0, P1, etc. P0 means that fly eye lens with no filter paper, and P1 means that fly eye lens and 1 (one) filter paper, etc.

Regarding parameters setting of D435, gain was set to 240, and image size of raw data was set to 640 × 480 px throughout this study. Other internal parameters were not changed from their default values.

Images were captured by varying exposure times as 25, 50, 100, 250, 500, 1000, 2500, 5000, 10,000, 25,000, 50,000, 100,000, 200,000 μs, and power control status as P0, P1, P5, P10, P15. Captured 640 × 480 px images were trimmed down to 34 × 33, 51 × 49, 68 × 66, 102 × 99, 170 × 165, 238 × 231, 324 × 330, 324 × 480, 640 × 480 px (non-trimmed). Differential and binarized images were generated for all combinations of the parameter sets, and GaAs substrate images were extracted from the binarized images. For image processing of the captured images, Mathematica^TM [23] was used.

2.2. GaAs Substrate Detection by Means of Infrared Imaging

Infrared GaAs images captured by the measurement system are shown in Figure 3 (Exposure time 200,000 μs, P0).

Comparing ${\lambda }_{OFF}$ image (Figure 3a) with that of ${\lambda }_{ON}$ (Figure 3b), the latter is brighter than the former due to the wavelength dependence of the camera’s sensitivity. Instead of applying brightness correction, the grayscale level of each pixel in the differential image (${gs}_{diff}$) is calculated by Equation (1), which can be referred to as ‘over subtraction’. This formula does not affect the target region in which ${\lambda }_{OFF}$ image is expected to be brighter than ${\lambda }_{ON}$. On the other hand, it eliminates unnecessary background in which ${\lambda }_{ON}$ image is expected to be brighter than ${\lambda }_{OFF}$.

$${gs}_{diff}=\left\{\begin{array}{ccc}{gs}_{OFF}-{gs}_{ON},& & {gs}_{OFF}\ge {gs}_{ON}\\ 0,& & {gs}_{OFF}<{gs}_{ON}\end{array}\right.$$

(1)

The threshold of binarization is determined by Otsu algorithm [24] like in [16]. Specification of target GaAs substrate is that manufacturer AXT Inc. Fremont, CA, USA [25], n-type, carrier concentration $2~3\times {10}^{18} {\mathrm{c}\mathrm{m}}^{-3}$, diameter 2”, thickness $350 \mathsf{\mu }\mathrm{m},$ surface orientation (001). Detection of the target by differentiation and binarization is demonstrated in Appendix A. The center coordinates and the area, as shown in Figure 4, are estimated from each detected GaAs image.

Figure 5 is an excerpt from data reduction products, whose image size is 34 × 33 px. After estimating the center coordinates and the area from each image, their mean values with 1 (one) $\sigma$ error is plotted in the figure. System requirements for the center coordinates and the area can be calculated by the method described in [16]. Assume OWPT is a cooperative configuration in which the transmitter and receiver cooperate to align their attitude with each other. The irradiated beam size is 50 % of the receiver size at its entrance, as in the case of utilizing a fly-eye lens module [7,26,27]. The requirement for misalignment is determined by power generation ratio calculation [7].

Assuming the power generation ratio = 80% is the limiting case, the requirement for the center coordinate is given by $0.718\times \mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s} \mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}/\sqrt{2}$. The radius of the GaAs substrate was directly read from the captured images, and its mean value was 7.6 px. The requirement for the center coordinates is 3.86 px. The requirement for the area is ±0.4 S, where S is the area of the substrate. The mean value of the substrate area was 181.94 px. The requirement for the area becomes ±72.78 px. These requirements are included in Figure 5 as horizontal dashed lines. It can be seen from Figure 5 that requirements are accommodated, and the target is detectable.

3. Comparison of GaAs Substrate Detection by Infrared Imaging with Si Substrate Detection by Visible Light Detection

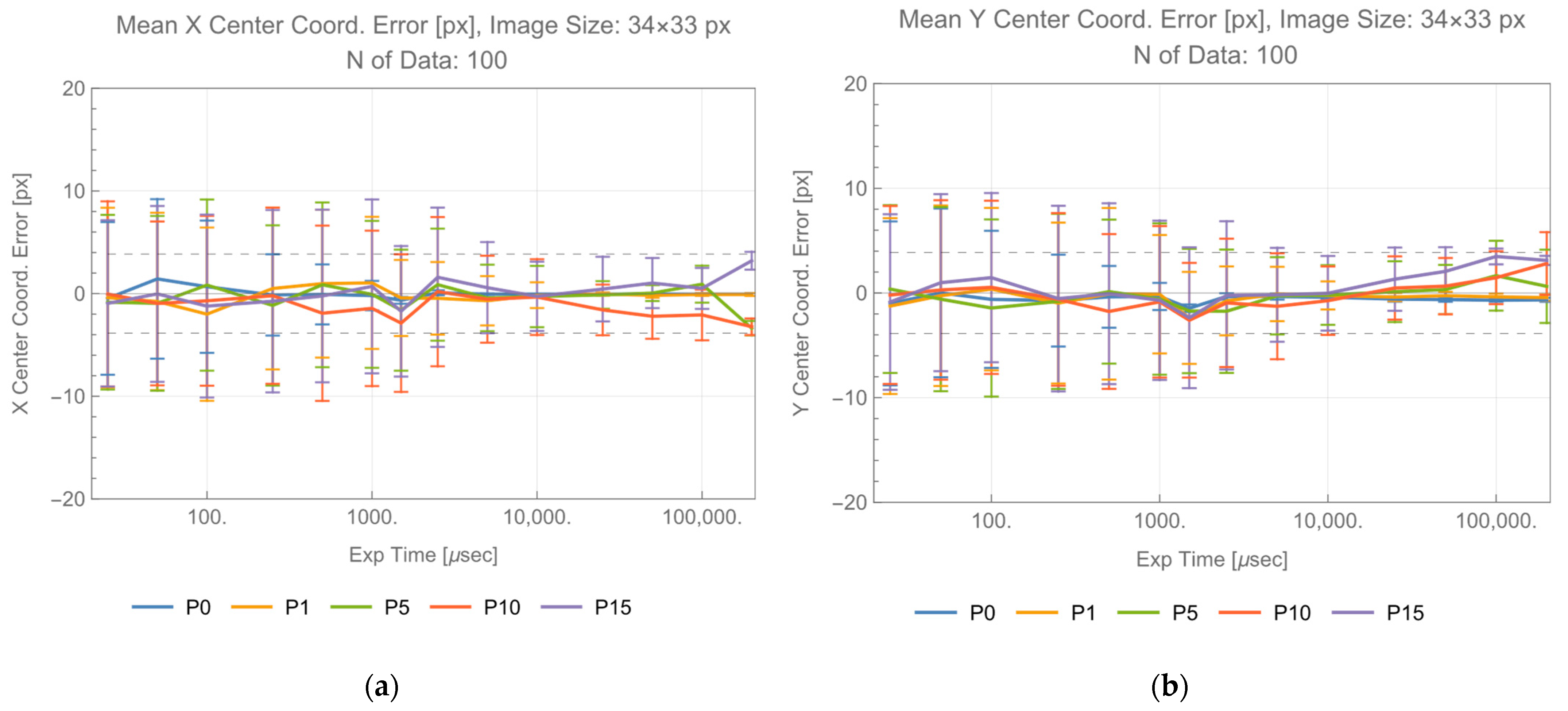
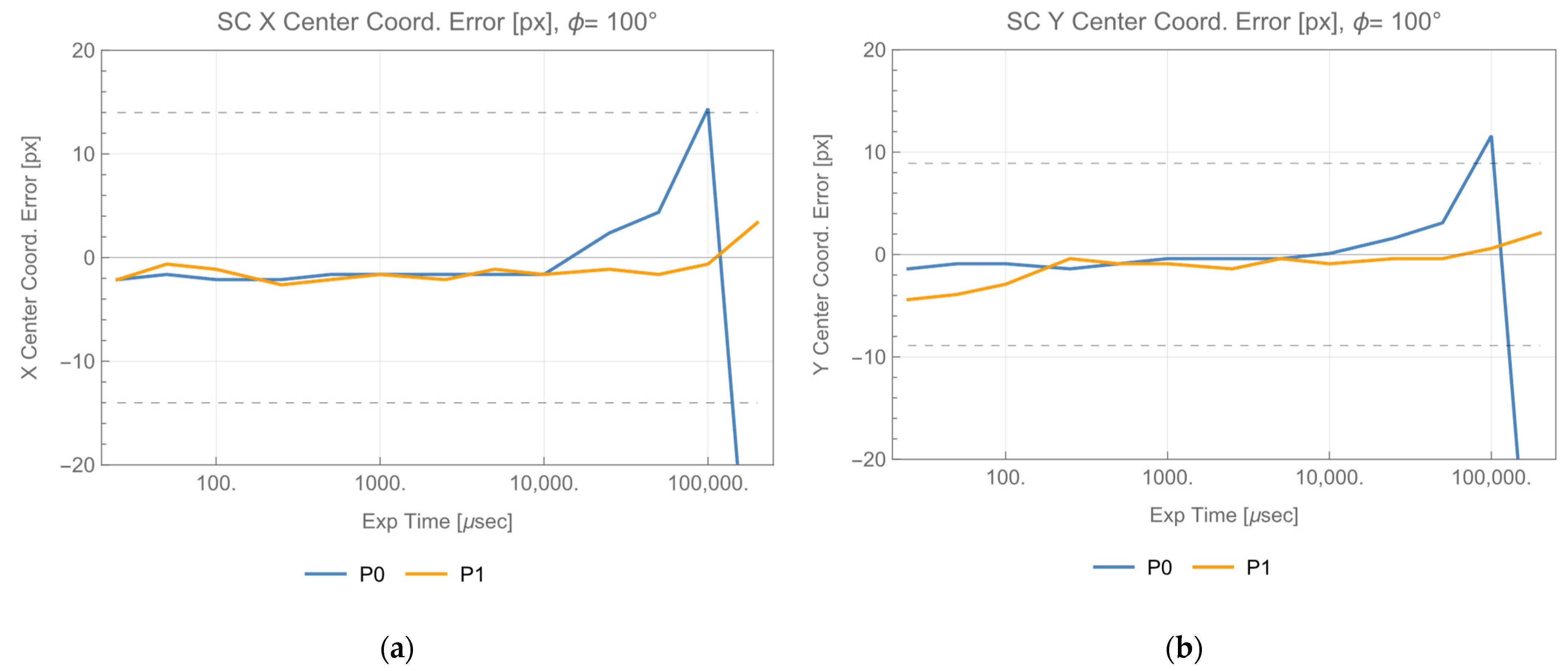
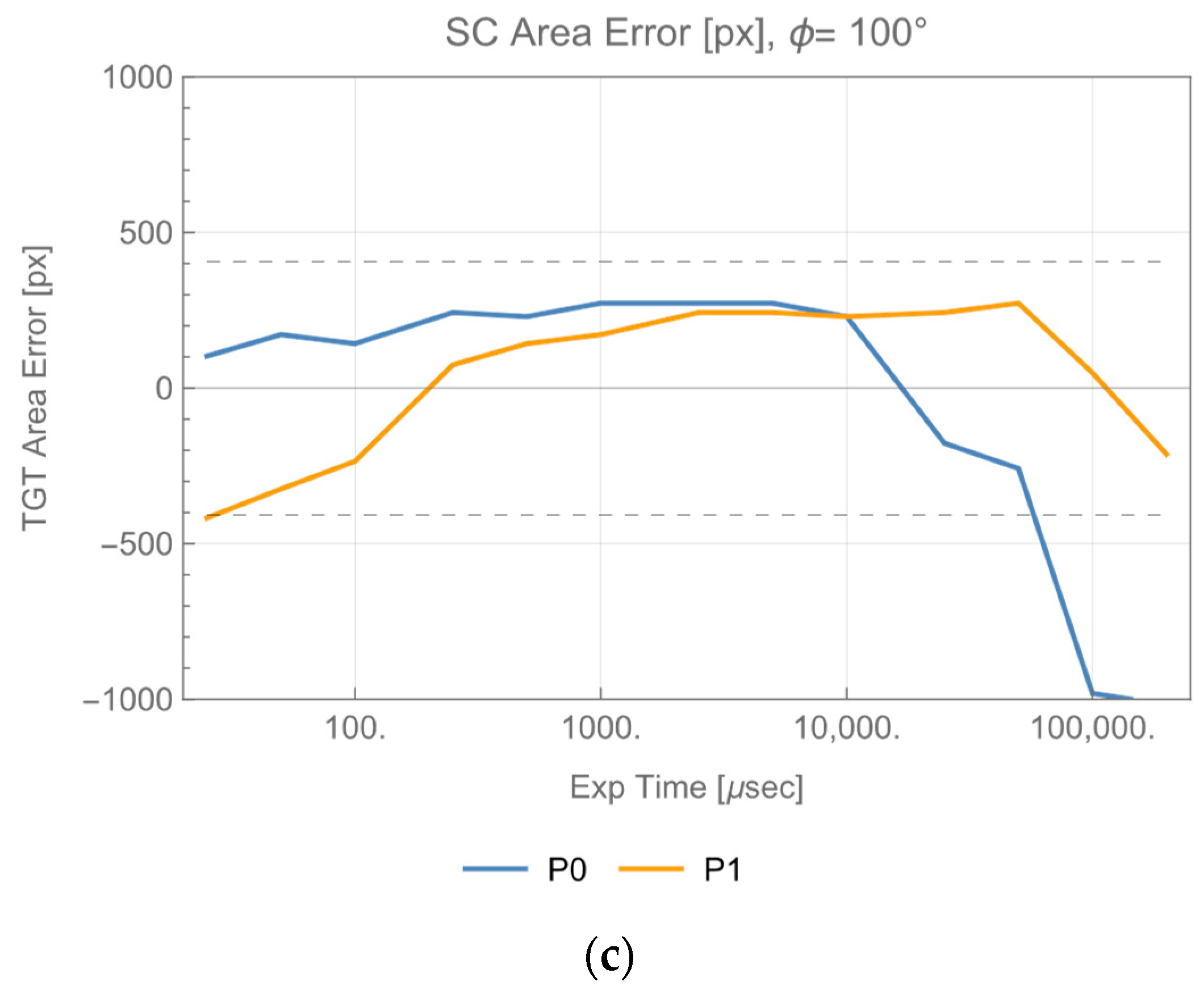
From the data in Figure 5, both X, and Y center coordinates are within the requirements limit for every exposure time of P0 and P1. The areas are within them for exposure time longer than 1000 μs for P0, and 15,000 μs for P1. Data using visible light are included in [16]. Comparing these threshold exposure time of detectability, ratio of infrared to visible is constant regardless of power control status, as shown in

Table 1. The threshold exposure time of visible and infrared experiments.

Power Control Status	Threshold Exposure Time in Visible Experiments	Threshold Exposure Time in Infrared Experiments	Ratio (Infrared/Visible)
P0	78 μs	1000 μs	12.8
P1	1250 μs	15,000 μs	12.0
P5	10,000 μs	─	─

.

The number of signal electrons generated in image capturing camera is calculated as Equation (2) proposed in [16],

$$N_s={{\left(\lambda /hc\right)\eta }_r{\eta }_t\eta }_Q{P}_{t}F\left(R\right)\rho A_{r}Exp/\pi R^2$$

(2)

where ${\eta }_Q$: quantum efficiency of the camera sensor, ${\eta }_r$: efficiency of camera optics, $\rho$: diffuse reflectivity of the target, $hc/\lambda$: photon energy of the incident beam, $Exp:\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}$, $P_t$: incident beam power, $A_{tr}$: area of irradiated beam at the target point, ${\eta }_t$: efficiency of transmitter optics (including intensity reduction due to fly eye lens and filter papers), $R$: distance to the target, $A_{SC}$: Area of the target, and $F\left(R\right)$ is defined in Equation (3).

$$F\left(R\right)\equiv \left\{\begin{array}{cc}1\hfill & for A_{SC}\ge A_{TR}\\ A_{SC}/A_{tr}\hfill & for A_{SC}<A_{tr}\end{array}\right.$$

(3)

The ratio of the threshold exposure time of visible to the one of infrared is evaluated using Equation (2). Regarding signal electron number of infrared, one for $\lambda$ = 940 nm is necessary for evaluation. The parameters, $F\left(R\right)$, ${\eta }_r$, ${\eta }_t$, $A_{tr}$, $A_r$, $R$ can be regarded as same between the two experiments. The other parameters are distinguished by adding subscripts ‘532’ for parameters included in $\lambda$ = 532 nm experiment and ‘940’ for $\lambda$ = 940 nm. Then,

$$\frac{N_{s532}}{N_{s940}}=\frac{{532\eta }_{Q532}{P_{t532}\rho }_{532}{Exp}_{532}}{{940\eta }_{Q940}{P}_{t940}{\rho }_{940}{Exp}_{940}}$$

(4)

Each parameter is evaluated as follows.

• Exposure time

From the data of the two experiments,

$$\frac{{Exp}_{532}}{{Exp}_{940}}=12~13$$

(5)

2.

Quantum efficiency

Since the quantum efficiency data of the Si sensor inside D435 is not disclosed, this parameter should be evaluated by other available CMOS sensor data. Several commercial CMOS sensor data are compiled in the datasheets [28]. The ratio of quantum efficiency of CMOS sensor at $\lambda$ = 532 nm to $\lambda$ = 940 nm looks roughly varying from 4:1 to 10:1, and

$$\frac{{\eta }_{Q532}}{{\eta }_{Q940}}=7$$

(6)

is adopted as the mean value.

3.

Power

Since $\lambda$ = 532 nm experiments, its power was 5 mW [16], power can be evaluated as

$$\frac{N_{s532}}{N_{s940}}=\frac{5 mW}{4 mW}=1.25$$

(7)

4.

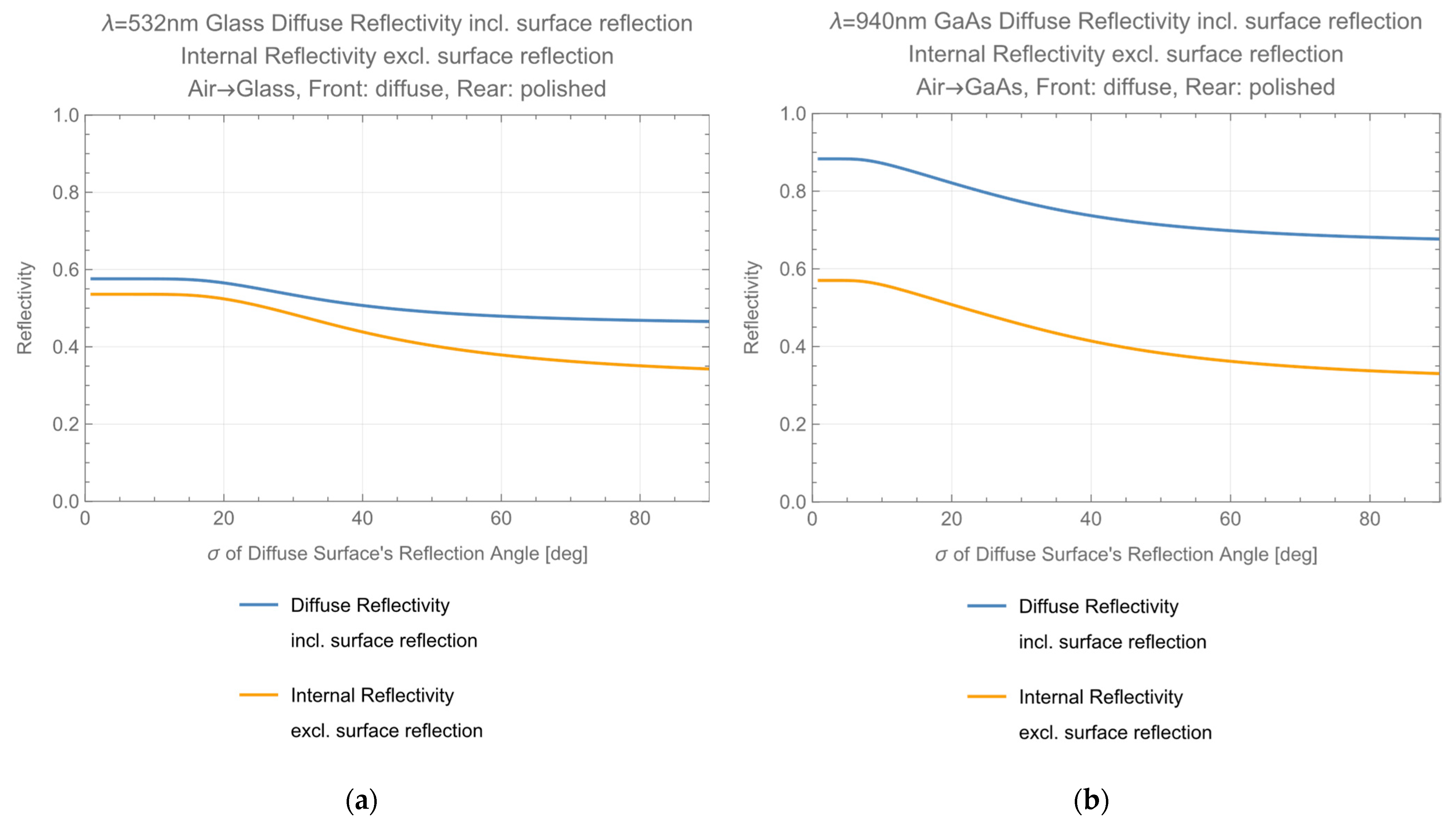
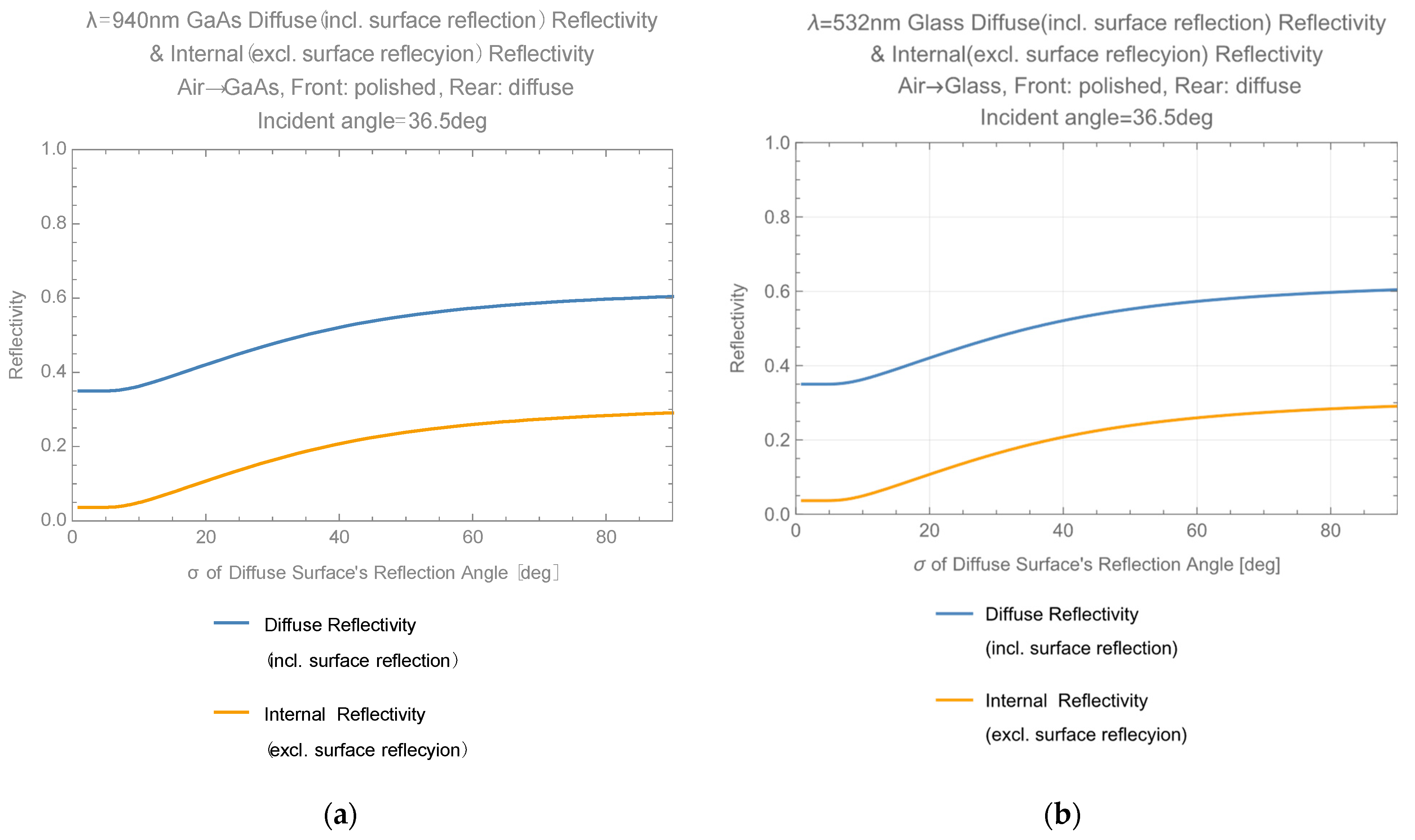
Diffuse reflectivity

It is evaluated as

$$\frac{{\rho }_{532}}{{\rho }_{940}}=1.7~2.75$$

(8)

Details are described in Appendix B.

From the series of evaluations above,

$$\frac{N_{s532}}{N_{s940}}=0.65~1.13$$

(9)

Since this ratio is close to 1 (one), the threshold number of electrons for GaAs and Si substrate detection would be conjectured as constant regardless of wavelength ${({\left.N_s\right|}_{threshold}\equiv N}_{\mathrm{s}532}=N_{\mathrm{s}940})$. On the other hand, ${\left.N_s\right|}_{threshold}$ would be proportional to the grayscale threshold level, identified as the binarization threshold.

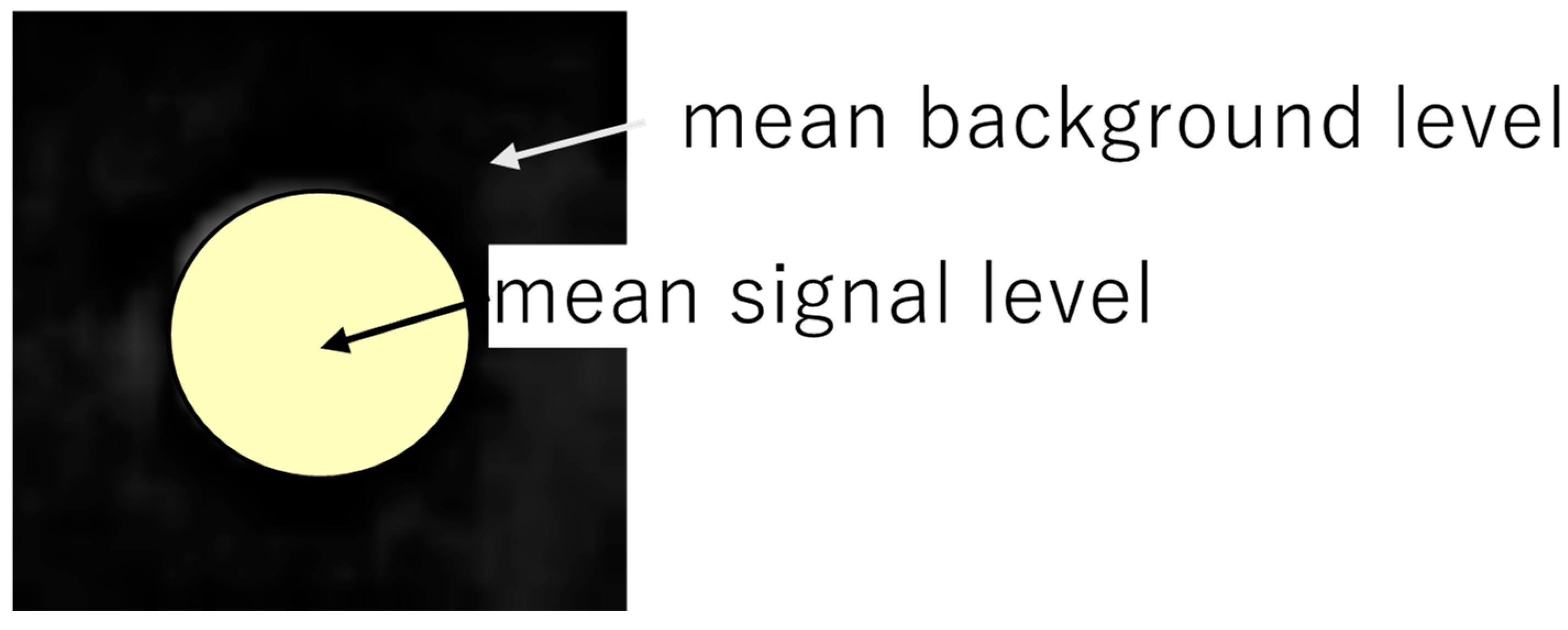
Differential intensity ($I_{diff}$) is defined as follows.

$$I_{diff}={\stackrel{-}{I}}_{TGT}-{\stackrel{-}{I}}_{BG}$$

(10)

where ${\stackrel{-}{I}}_{TGT}$ is mean level inside the target region in Figure 6, and ${\stackrel{-}{I}}_{BG}$ is mean background level. As a result, $I_{diff}$ is mean signal level inside the target region.

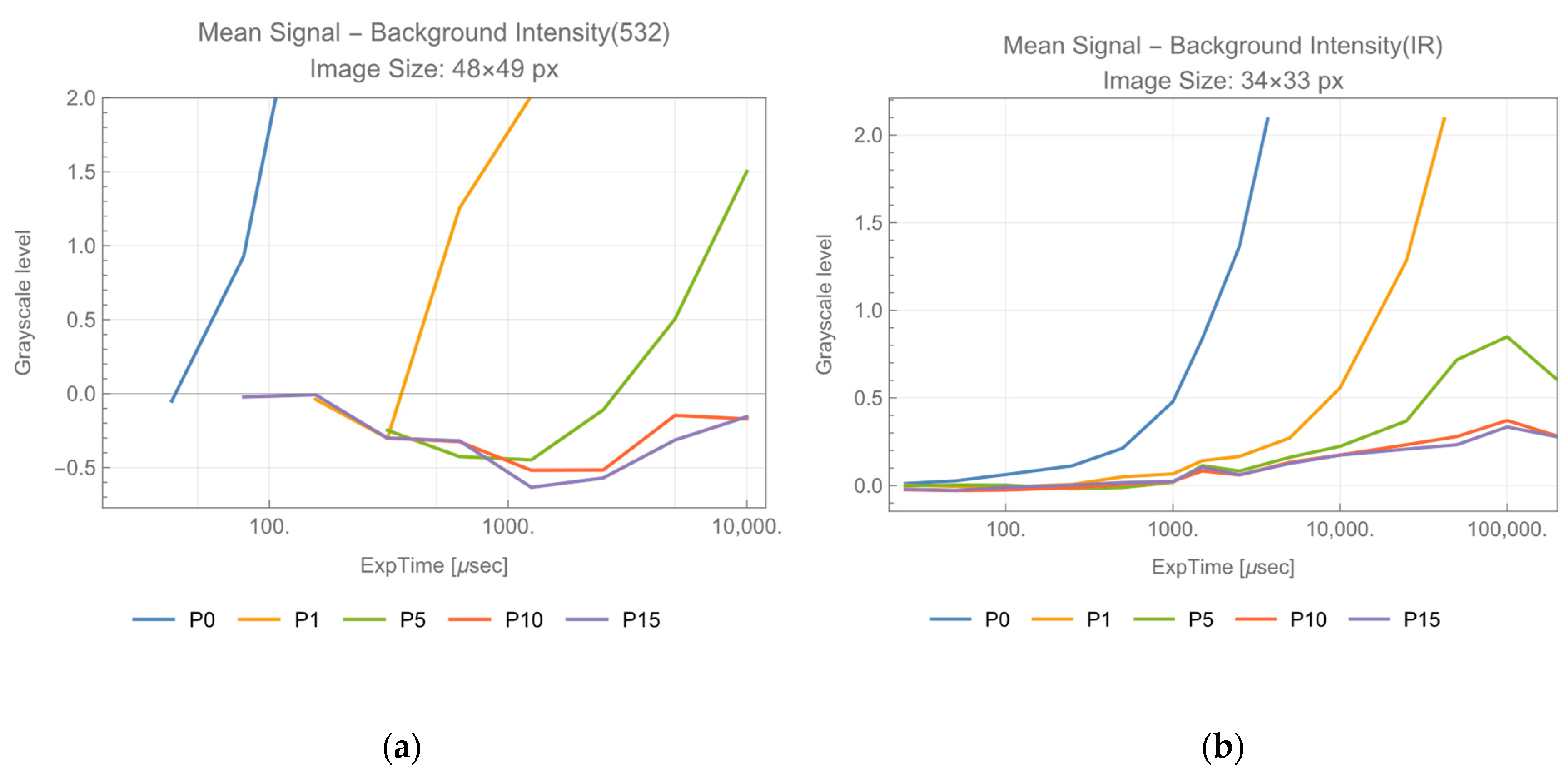
Considering sensor output is 8-bit grayscale, $I_{diff}$ is normalized by 1/255, which is the minimum resolution of 8-bit. Figure 7 shows the normalized $I_{diff}$ plot against exposure time.

These plots show that threshold exposure time of both visible and infrared experiments correspond to the unit value 1 (one) in the longitudinal axis. The above discussions show that threshold signal electron number and threshold differential intensity are constants between the two experiments. This suggests that the following ‘threshold equation’ holds at the threshold of target detection regardless of wavelength used in the two differential absorption imaging experiments.

$${\left[{{K\left(\lambda /hc\right)\eta }_r{\eta }_t\eta }_Q{P}_{t}F\left(R\right)\rho A_{r}Exp/\pi R^2\right]}_{threshold}={\mathsf{\Delta }I}_{diff}$$

(11)

Here, ${\mathsf{\Delta }I}_{diff}$ represents threshold differential intensity which is identified as binarization threshold and whose minimum value is 1 (one) bit of grayscale level (1/255 for 8 bit), and K represents coefficient to transform signal electron number to a grayscale level which also depends on configuration of measurement system. All parameters on the left-hand side of Equation (11) are for ${\lambda }_{OFF}$. The generalized form of the equation is obtained by including a term for ${\lambda }_{ON}$ which is negligible in these experiments.

$${\left[\left({\left.{{K\left(\lambda /hc\right)\eta }_r{\eta }_t\eta }_Q{P}_t\rho A_r\right|}_{{\lambda }_{OFF}}-{\left.{{K\left(\lambda /hc\right)\eta }_r{\eta }_t\eta }_Q{P}_t\rho A_r\right|}_{{\lambda }_{ON}}\right)F\left(R\right)Exp/\pi R^2\right]}_{threshold}={\mathsf{\Delta }I}_{diff}$$

(12)

The first term of Equation (12) in the left-hand side parenthesis represents the parameters for ${\lambda }_{OFF}$ and the second one represents ${\lambda }_{ON}$. A set of parameters on the left-hand side of Equation (11) or (12) determines the threshold differential intensity (maximally settable binarization threshold) on the right-hand side. The right-hand side of the threshold requires the necessary parameters in the left-hand side to support the binarization threshold to be set. It should be noted that Equations (11) and (12) are defined by mean noise value in a certain region and noise is generated randomly within such regions. Consider that noise covers uniformly over the entire image of ${\lambda }_{OFF}$ and ${\lambda }_{ON}$.This case would occur with a long exposure time. Differentiating ${\lambda }_{OFF}$ and ${\lambda }_{ON}$ images by Equation (1) would cause noise reduction in the resultant differential image. This is observed in Figure 8. It shows images of various exposure time with constant binarizing threshold of 1/255. It is seen that increments of exposure time cause noise reduction. In Figure 8a, whose exposure time is 500 μs, a tiny white dot of noise is spread over the entire image, and the GaAs image cannot be seen. As exposure time increases in Figure 8b,c, such noise decreases gradually, and the GaAs image appears at the center. Finally, in Figure 8d, only GaAs image can be seen. In this case, the second term of Equation (11) would be ignorable, and a globally clear noiseless image can be generated even for differential intensity ${\mathsf{\Delta }I}_{diff}$ = 1/255. Long exposure time causes noise reduction even for non-trimming images.

In case that noise would not cover the entire image, such noise would remain in some regions in the differential image after differentiation. This case would occur in a short exposure time. In such a case, there would be two strategies to avoid the noise effect. One is to increase ${\mathsf{\Delta }I}_{diff}$ from 1/255 to an appropriate value. This causes an impact on the system parameters on the left-hand side of Equation (12), such as an increment of irradiation power. The other option would be trimming images to an appropriate size in which the target size dominates the entire image. For example, in Figure 7, images were trimmed to 48 × 49 px for visible and 34 × 33 px for infrared. For short exposure time data in Figure 7, this trimming looks helpful to reduce noise and make ${\mathsf{\Delta }I}_{diff}$ minimum. However, the larger the size of the images, the noisier the resultant images become. This phenomenon was observed in the experiments in [16]. For longer exposure time data in Figure 7, both long exposure time and trimming effects would have cooperatively caused noise reduction in the resultant images.

Exposure time should be determined by system requirements, especially by its real-time requirement. It would be necessary to estimate the noise remaining in the differential images according to the determined exposure time and develop plans of ${\mathsf{\Delta }I}_{diff}$ setting. Equations (11) and (12) provide logic for such system design strategies.

4. GaAs Solar Cell Detection by Means of Infrared Differential Absorption Imaging and Its Attitude Determination

A real thin film GaAs solar cell detection experiments were conducted (Manufacturer Advanced Technology Institute, Tokyo, Japan [29], five cell series connected). The GaAs solar cell size is 6 cm × 4 cm. Its front surface is GaAs solar cell, and its rear surface is a copper electrode. The solar cell is fixed on a rotatable stage, and its rotation angle $\varphi$ is set to 90 degrees when it faces normal to the camera.

During trial phase, strong non-diffuse reflection was observed near the solar cell normal and weak diffuse reflection from large angles. From exposure time point of view, a short exposure time would be enough to detect vital components near the normal, and a long one would be necessary to detect weak components in large angles. Considering the noise reduction effect described in the last section, large angle components are expected to be detected by setting long exposure time and global binarization threshold of ${\mathsf{\Delta }I}_{diff}$ = 1/255. Regarding the detection of strong components near the normal, there are two options. One is to increase the binarization threshold, since such reflection is due to high reflectivity in the left-hand side of Equation (12), ${\mathsf{\Delta }I}_{diff}$ can be increased accordingly. Another option is that ${\mathsf{\Delta }I}_{diff}$ is kept globally at its minimum 1/255. Since the solar cell detection algorithm in these experiments is that the connected component with the maximum area in the binarized image is regarded as the solar cell, the area of the connected solar cell image generated by strong reflection would become dominant even in the noisy image of short exposure time. In such a case, the solar cell image would be detected even with short exposure time and minimum ${\mathsf{\Delta }I}_{diff}$. The second option looked simpler and was tried. ${\mathsf{\Delta }I}_{diff}$ was kept globally 1/255 for every exposure time, and the solar cell was successfully detected.

Experiments were conducted for various angles of the rotatable stage shown in Figure 9. They are 50, 60, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 130, and 140 degrees. An excerpt of ${\lambda }_{ON}$ image (a) and ${\lambda }_{OFF}$ (b) are shown in Figure 10 (Exposure time 25,000 μs, P0, $\varphi$ = 95 degrees).

The solar cell was detected in two image sizes. One is 82 × 83 px, the same size as the background frost glass. The other is non-trimmed 640 × 480 px. The solar cell was detected successfully in both image sizes. Appendix C includes a data set of 82 × 83 px. The center coordinates, and the area was determined. An excerpt from the data reduction products is shown in Figure 11. In this case, 82 × 83 px images were used for determination.

In Figure 11, the requirements shown as horizontal dashed lines were calculated like the GaAs substrate case. The values vary with the angle ϕ. In the case of $\varphi$ = 100 degrees, the requirements for the X, Y center coordinates are 41.5 and 43.5 px, respectively, and the requirements for the area are 803.5 px. These requirements are different from the requirements plotted in Figure 5. This is because the experiment layout of Figure 9 for this solar cell detection differs from Figure 2 for the GaAs substrate. All the requirements are stably accommodated from exposure time = 25 μs. In case of prolonged exposure time, accommodation fails. This reflects the situation that both ${\lambda }_{ON}$ and ${\lambda }_{OFF}$ images are saturated, and solar cell images cannot be detected by differentiating the two images. Appropriate exposure time should be set to avoid such saturation. Generally, the minimum exposure time which accommodates the requirements depends on the rotation angle $\varphi$. 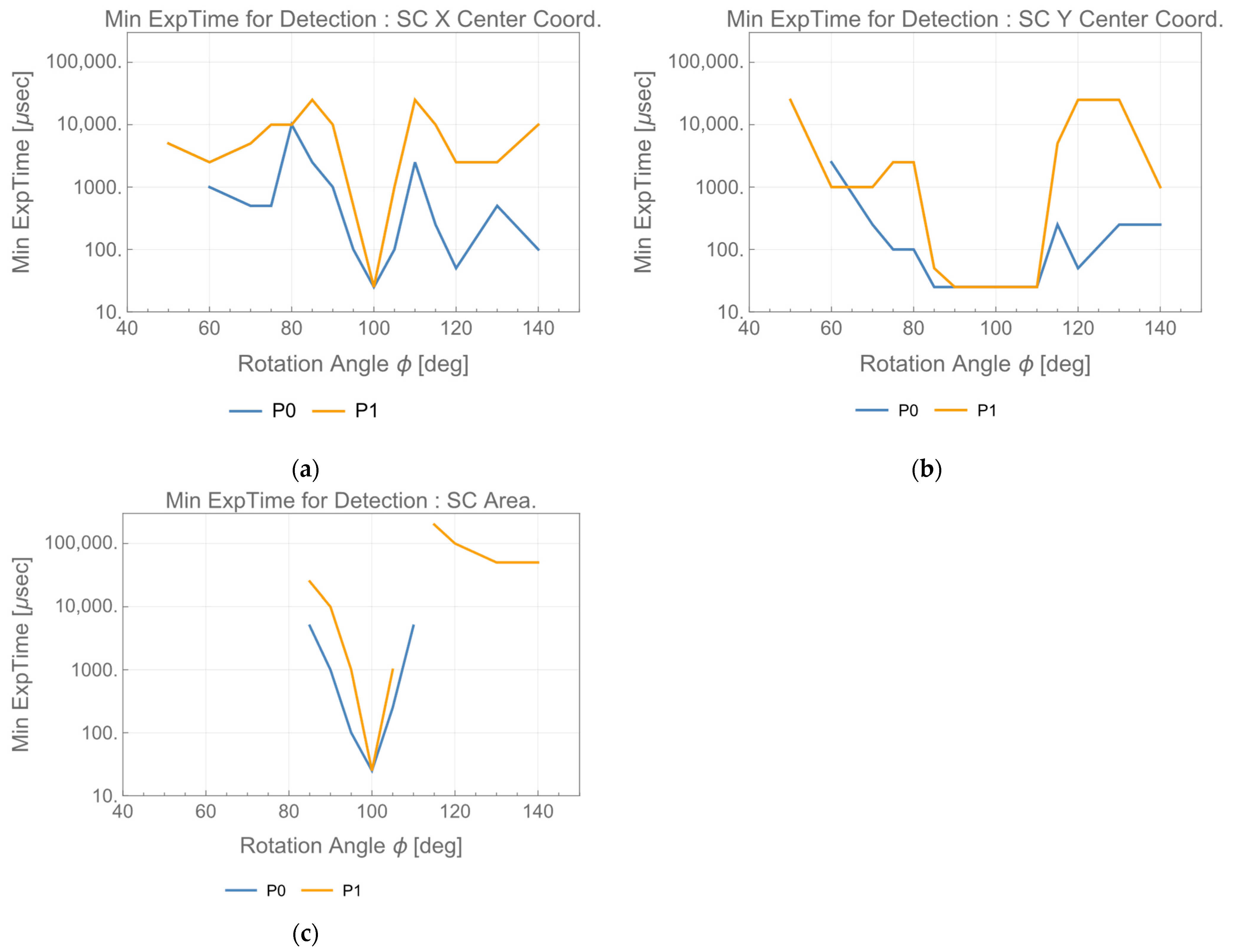Figure 12 shows the angular dependence of the minimum exposure time, accommodating the requirements.

In addition to non-diffuse, rear surface treatment of solar cells has diffuse options. To investigate the attitude determination of this case, similar experiments were conducted using GaAs substrate. GaAs substrate could be stably detected within the range of 50~140 degrees. Like Figure 12, the angular dependence of minimum exposure time, which accommodates the requirements, is plotted in Figure 13. In the case of $\varphi$ = 100 degrees, requirements are calculated as 43.1 and 46.4 px for X, and Y center coordinates, respectively and 1017.4 px for the area. Also, in this case, the binarization threshold was set to 1/255 regardless of image size.

5. Discussion

All the plots in Figure 12 have concave-shaped peaks around $\varphi$ = 100 degrees. This shows that the rear surface of the GaAs solar cell has non-diffuse reflection characteristic. The peak angle corresponds to the angle that the incident beam is reflected to the camera. This can be calculated by using the dimensions in Figure 9a. Figure 12 shows that the X, Y coordinates can be determined within the range of $\varphi$ = 50~140 degrees. On the other hand, the area determination is limited within the range of ±10 degrees around $\varphi$ = 100 degrees. The fact that the weak large-angle reflection is detected means that small diffuse reflection component accompanies the main non-diffuse one. Exploiting this feature, determination of the solar cell normal would be feasible. Detectability criteria proposed in [16] require that the X, Y center coordinate and the area should simultaneously accommodate the system requirements. For the GaAs solar cell, these criteria are satisfied in the area near the normal of the solar cell. For a cooperative OWPT, in which a transmitter and a receiver mutually align their attitude with each other, such alignment would be initiated and performed with solar cell X, Y coordinates information. The area criterion and, finally, the detectability criteria would come to be satisfied in the region near the normal. For a non-cooperative OWPT with a large transmitter-receiver tilt angle, detection of the solar cell is limited to X, Y center coordinates.

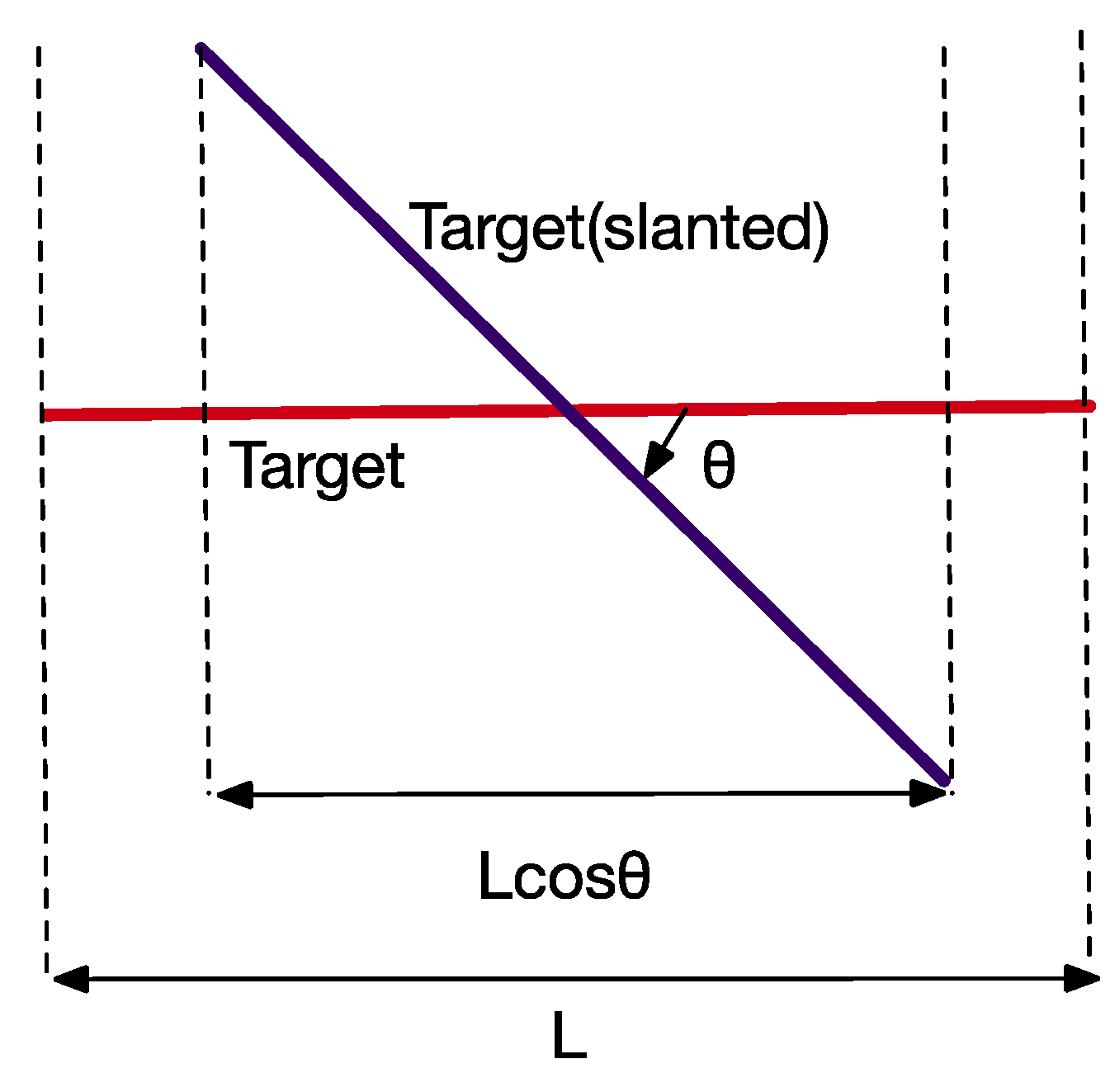
In the case of the GaAs substrate, requirements for the X, Y center coordinates and the area are accommodated within a wide angular range. Any sharp concave-shaped peaks are not noticeable in Figure 13. This suggests that there is no non-diffuse component in reflection from the GaAs substrate. Attitude determination exploiting such a wide angular detection range was investigated. The method utilizes the apparent width of a target of width L, which varies as $Lcos\theta$ with the tilt angle $\theta (=\varphi -90 deg)$ in Figure 14. Details are described in Appendix D.

.

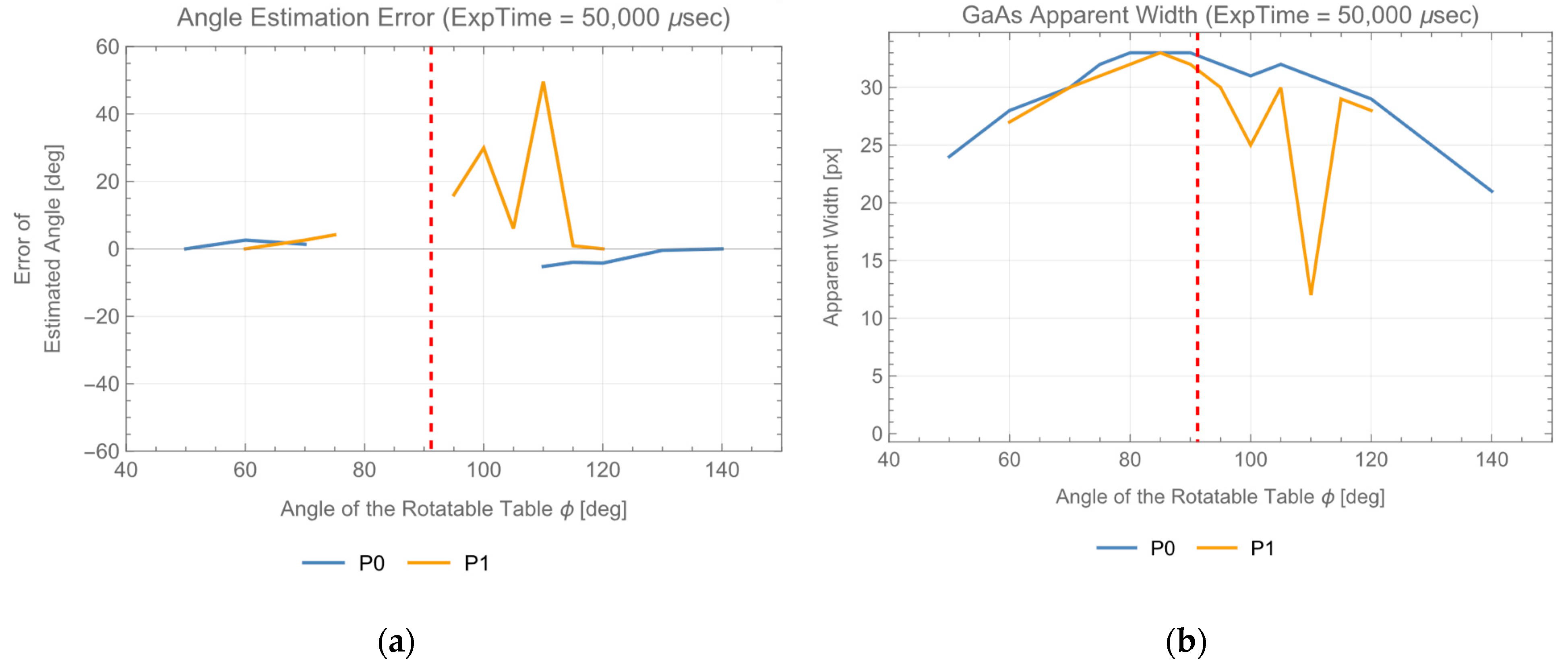
The attitude determination error is shown in Figure 15a, and the estimated apparent width of the GaAs substrate is shown in Figure 15b. The angular center of the rotatable stage is estimated as $\varphi =$ 91.2 degrees from P0 data and 91.8 degrees from P1 data. They are included in Figure 15 as a vertical red dashed line. Attitude determination fails or becomes erroneous within about ±20 degrees near the normal. Excluding this difficulty, the diffuse target’s detectability criteria would be satisfied within a wide angular range from the normal regardless of cooperative or non-cooperative OWPT. One of the reasons for this near-normal difficulty in the diffuse experiment is that variation of the apparent width becomes small near the angular center of the rotatable stage. The other would be that Fresnel reflection from the front surface becomes saturated or dominant, and this causes difficulty in observation of reflected ${\lambda }_{OFF}$ beam from the rear surface. In the region around the normal, its attitude determination may cause an error of about ±20 degrees. Compared with the requirement of ±645 mrad (37 degrees) within 100 m target-receiver distance based on the power generation ratio [7], this error is still within the requirement.

In Figure 15b, the width of the GaAs substrate is stably determined in the P0 image except for a little increment of error at 100 degrees. Therefore, failure of attitude determination in the range 75~105 degrees would be caused by the small variation of apparent width. Regarding P1 data, the error became large in the 100~110 degrees range due to failure of determination of the apparent width. By the way, Figure 12 shows the non-diffuse reflection characteristics of the rear surface of the real GaAs solar cell, and strong reflection from the rear surface is observed in the 90~110 degrees range. Since the layouts are the same for the two experiments, both angular ranges are quite similar. Even though non-diffuse solid reflection comes from the rear surface, which helps solar cell detection, a parallel reflection comes from the front surface in the GaAs substrate experiment. Such strong reflection caused difficulty in observing reflection from the rear surface. As a result, determination of the apparent width would have failed. Irradiation by the transmitter assembly used in the experiments causes strong non-diffuse reflection from the front surface. Its effect does not appear uniformly over the entire GaAs substrate, but causes a mottled pattern of saturation. These degrades observation of rear surface reflection in some partial areas. For example, in P0 data, apparent width was successfully estimated by incomplete information from the area where reflection from the rear surface was observed. However, in P1, due to lower irradiation (reflection) level than in the P0, the estimation failed. This would be the reason that causes the significant difference in apparent width determination in P0 and P1 at $\varphi =$ 110 degrees. The front surface of the GaAs substrate used in the experiments is not anti-reflection treated. The issue coming from the strong non-diffuse reflection of the front surface would be improved by anti-reflection treatment. On the other hand, failure of attitude determination below 90 degrees would come from the small apparent width variation like in P0.

6. Conclusions

In this study, a GaAs substrate simulating a solar cell and a real thin-film GaAs solar cell were detected using two infrared wavelengths 850 nm and 940 nm. The ‘threshold equation ‘, which holds at threshold regardless of wavelength, was derived and verified by experimental data.

In OWPT, there would be non-diffuse and diffuse options for the rear surface treatment of solar cell that affects the reflection of ${\lambda }_{OFF}$. The real GaAs solar cell used in the experiments mainly has a non-diffuse reflection characteristic accompanied by diffuse one. In this case, since the center coordinates can be determined within a wide angular range, the existence of the solar cell can be determined. The area of the solar cell can be determined within ±10 degrees around its normal. Its normality can be detected by exploiting this feature. For diffuse targets, the GaAs substrate used in these experiments, both the center coordinates and the area can be determined within a wide angular range. Therefore, attitude can be determined accurately for a large angle from its normal.

One of the issues in solar cell detection using differential absorption imaging is the difficulty of observing ${\lambda }_{OFF}$ reflection from its rear surface in the presence of strong ${\lambda }_{ON}$ and ${\lambda }_{OFF}$ reflection from its front surface. It should be recommended for solar cells for OWPT use that front surface reflection should be reduced for both ${\lambda }_{ON}$ and ${\lambda }_{OFF}$. For both non-diffuse and diffuse targets, surface anti-reflection treatment improves this issue.

There would be an OWPT system which utilizes other solar cell materials. Wavelengths used in differential imaging and detail of reflection characteristics of solar cells in this report would be different in other state-of-the-art solar cell materials. However, even though each parameter takes a different value in other OWPT systems, experiments and analyses conducted in this report are still applicable. This study would be a step towards operational OWPT social infrastructure.