Nonlinear Optical Materials: Predicting the First-Order Molecular Hyperpolarizability of Organic Molecular Structures
Abstract
1. Introduction
2. Materials and Methods
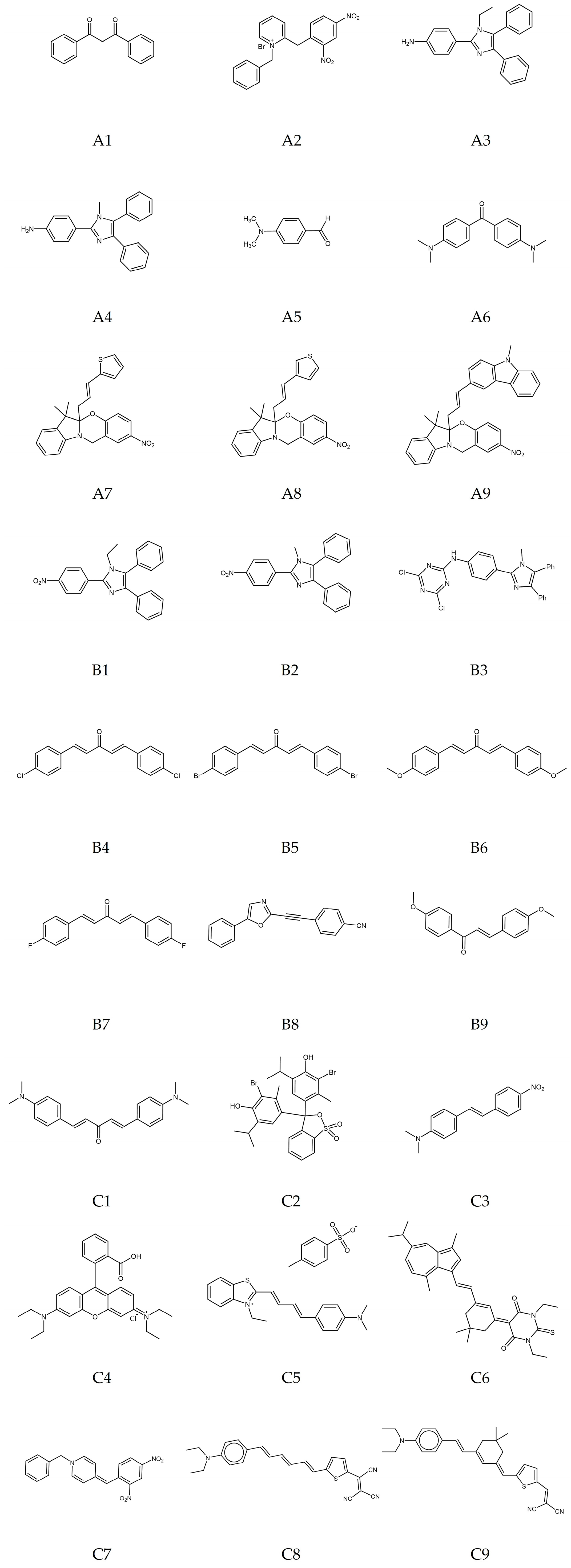
2.1. Investigated Compounds
2.2. First-Order Hyperpolarizability and Quantum Chemical Calculations
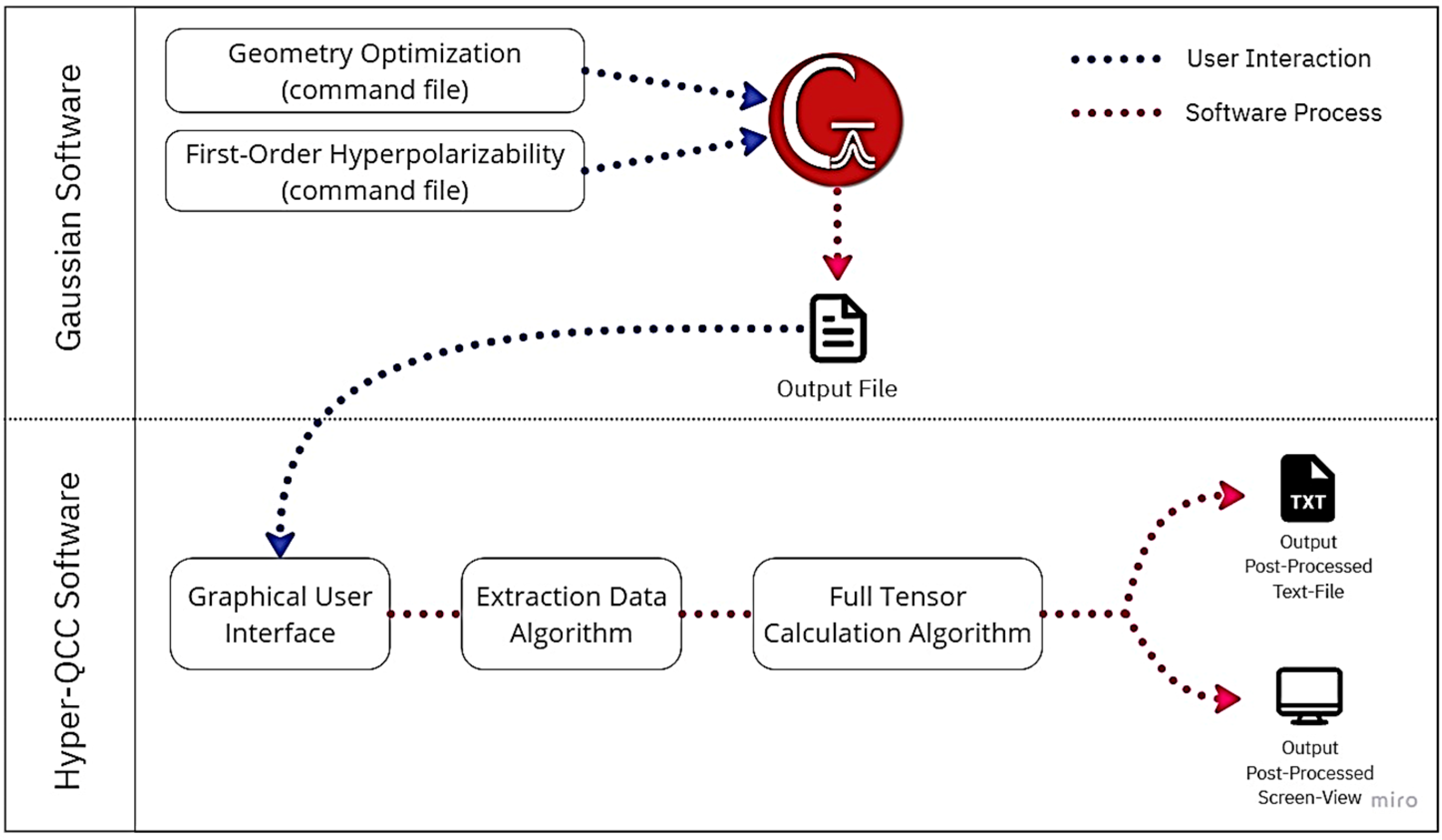
2.3. Hyper-QCC: Post-Processing Software
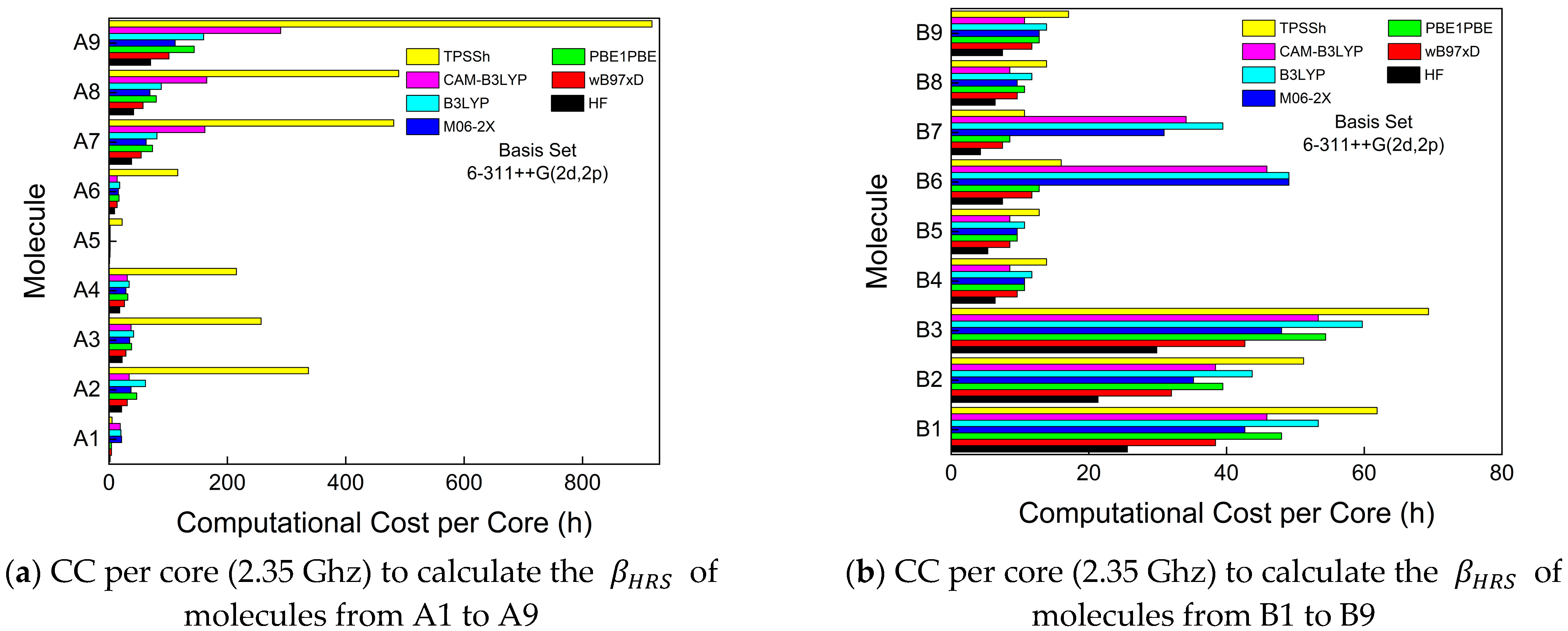
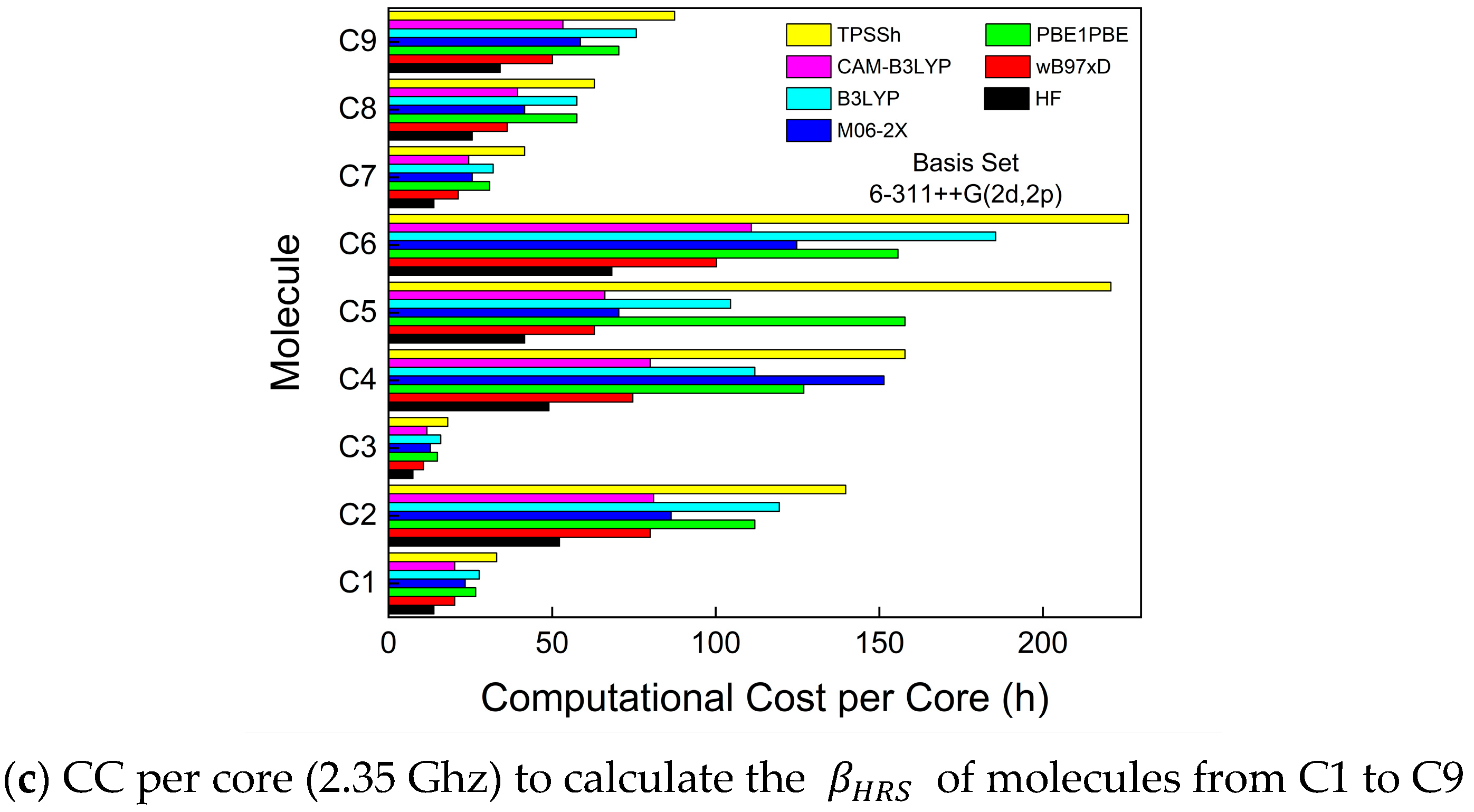
3. Results and Discussion
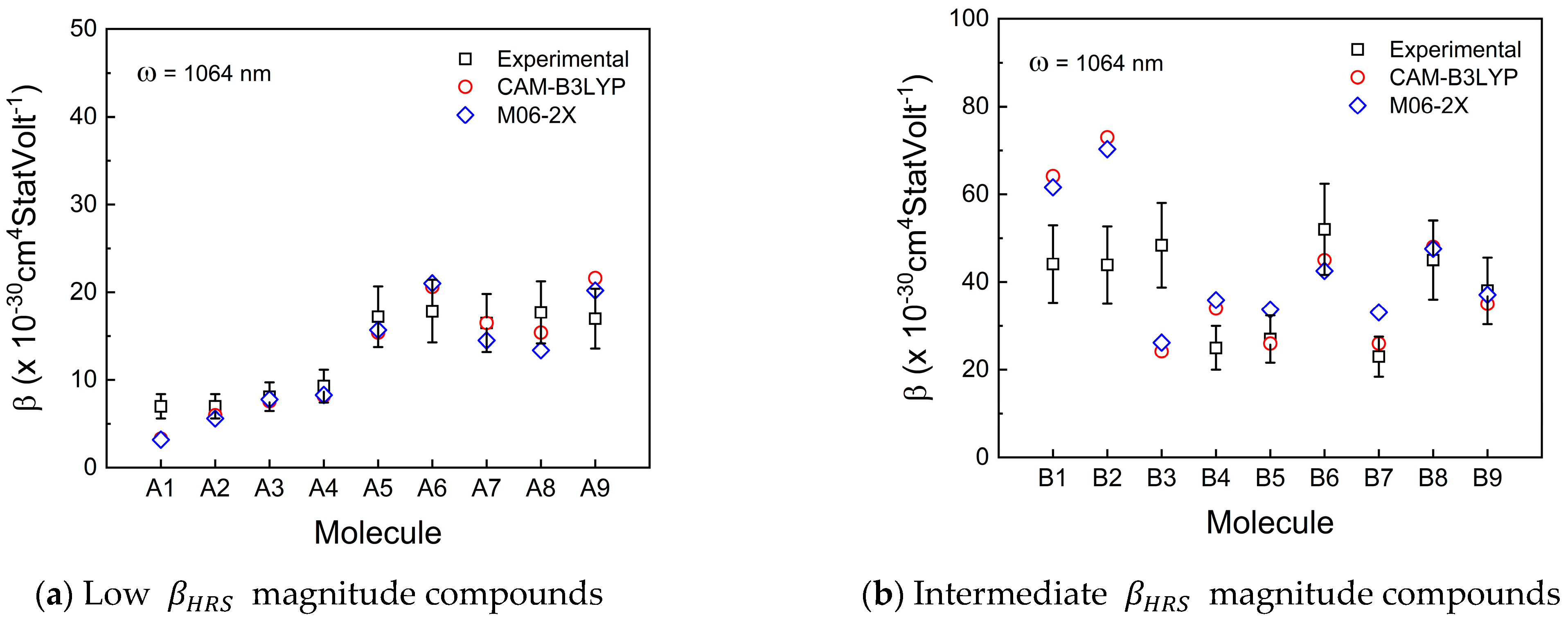
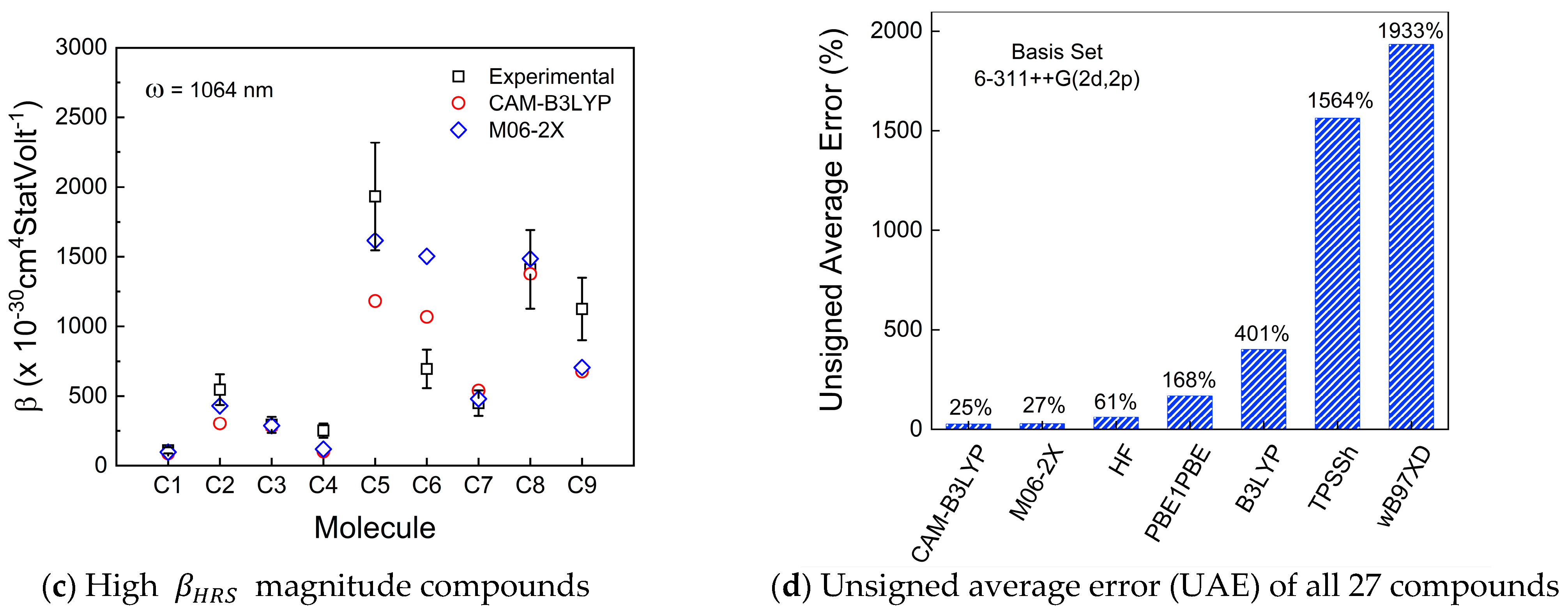
3.1. First-Order Molecular Hyperpolarizability
3.2. Applications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franken, P.A.; Hill, A.E.; Peters, C.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118. [Google Scholar] [CrossRef]
- Clays, K.; Persoons, A. Hyper-Rayleigh scattering in solution. Phys. Rev. Lett. 1991, 66, 2980. [Google Scholar] [CrossRef] [PubMed]
- Maser, A.; Gmeiner, B.; Utikal, T.; Götzinger, S.; Sandoghdar, V. Few-photon coherent nonlinear optics with a single molecule. Nat. Photonics 2016, 10, 450–453. [Google Scholar] [CrossRef]
- Lacroix, P.G.; Malfant, I.; Lepetit, C. Second-order nonlinear optics in coordination chemistry: An open door towards multi-functional materials and molecular switches. Coord. Chem. Rev. 2016, 308, 381–394. [Google Scholar] [CrossRef]
- Lou, A.J.-T.; Marks, T.J. A twist on nonlinear optics: Understanding the unique response of π-twisted chromophores. Acc. Chem. Res. 2019, 52, 1428–1438. [Google Scholar] [CrossRef]
- Parthasarathy, V.; Pandey, R.; Das, P.K.; Castet, F.; Blanchard-Desce, M. Linear and Nonlinear Optical Properties of Tricyanopropylidene-Based Merocyanine Dyes: Synergistic Experimental and Theoretical Investigations. ChemPhysChem 2018, 19, 187–197. [Google Scholar] [CrossRef]
- de Araújo, R.S.; de Alcântara, A.M.; Abegao, L.M.; de Souza, Y.P.; Silva, A.C.B.; Machado, R.; Rodrigues, J.J., Jr.; Júnior, J.R.P.; d’Errico, F.; Valle, M.S. Second harmonic generation in pyrazoline derivatives of dibenzylideneacetones and chalcone: A combined experimental and theoretical approach. J. Photochem. Photobiol. A Chem. 2020, 388, 112147. [Google Scholar] [CrossRef]
- Gu, B.; Zhao, C.; Baev, A.; Yong, K.-T.; Wen, S.; Prasad, P.N. Molecular nonlinear optics: Recent advances and applications. Adv. Opt. Photonics 2016, 8, 328–369. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, L.; Sun, L.; Zhen, Y.; Dong, H.; Wei, Z.; Hu, W. Uncovering the intramolecular emission and tuning the nonlinear optical properties of organic materials by cocrystallization. Angew. Chem. Int. Ed. 2016, 55, 14023–14027. [Google Scholar] [CrossRef]
- Semin, S.; Li, X.; Duan, Y.; Rasing, T. Nonlinear optical properties and applications of fluorenone molecular materials. Adv. Opt. Mater. 2021, 9, 2100327. [Google Scholar] [CrossRef]
- Colombo, A.; Dragonetti, C.; Guerchais, V.; Roberto, D. An excursion in the second-order nonlinear optical properties of platinum complexes. Coord. Chem. Rev. 2021, 446, 214113. [Google Scholar] [CrossRef]
- Ullah, F.; Ayub, K.; Mahmood, T. Remarkable second and third order nonlinear optical properties of organometallic C6Li6–M3O electrides. New J. Chem. 2020, 44, 9822–9829. [Google Scholar] [CrossRef]
- Schaller, R.R. Moore’s law: Past, present and future. IEEE Spectr. 1997, 34, 52–59. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Castet, F.; Bogdan, E.; Plaquet, A.; Ducasse, L.; Champagne, B.; Rodriguez, V. Reference molecules for nonlinear optics: A joint experimental and theoretical investigation. J. Chem. Phys. 2012, 136, 024506. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Lu, J. Remarkably enhanced first hyperpolarizability and nonlinear refractive index of novel graphdiyne-based materials for promising optoelectronic applications: A first-principles study. Appl. Surf. Sci. 2020, 512, 145544. [Google Scholar] [CrossRef]
- Pielak, K.; Bondu, F.; Sanguinet, L.; Rodriguez, V.; Champagne, B.; Castet, F. Second-order nonlinear optical properties of multiaddressable indolinooxazolidine derivatives: Joint computational and hyper-Rayleigh scattering investigations. J. Phys. Chem. C 2017, 121, 1851–1860. [Google Scholar] [CrossRef]
- Abegão, L.M.; Fonseca, R.D.; Santos, F.A.; Souza, G.B.; Barreiros, A.L.B.; Barreiros, M.L.; Alencar, M.; Mendonca, C.R.; Silva, D.L.; De Boni, L. Second-and third-order nonlinear optical properties of unsubstituted and mono-substituted chalcones. Chem. Phys. Lett. 2016, 648, 91–96. [Google Scholar] [CrossRef]
- Silva, D.L.; Fonseca, R.D.; Vivas, M.G.; Ishow, E.; Canuto, S.; Mendonca, C.R.; De Boni, L. Experimental and theoretical investigation of the first-order hyperpolarizability of a class of triarylamine derivatives. J. Chem. Phys. 2015, 142, 064312. [Google Scholar] [CrossRef]
- Yang, X.; Lin, X.; Zhao, Y.S.; Yan, D. Recent advances in micro-/nanostructured metal–organic frameworks towards photonic and electronic applications. Chem.–A Eur. J. 2018, 24, 6484–6493. [Google Scholar] [CrossRef]
- Reshef, O.; De Leon, I.; Alam, M.Z.; Boyd, R.W. Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 2019, 4, 535–551. [Google Scholar] [CrossRef]
- Kariduraganavar, M.Y.; Doddamani, R.V.; Waddar, B.; Parne, S.R. Nonlinear Optical Responsive Molecular Switches. In Nonlinear Optics: From Solitons to Similaritons; Books on Demand: Paris, France, 2021; Volume 187. [Google Scholar]
- Wang, Y.; Yang, H.; Dong, W.; Lei, L.; Xu, J.; Zhang, X.; Xu, P. Highly Nonlinear Organic-Silicon Slot Waveguide for Ultrafast Multimode All-Optical Logic Operations. IEEE Photonics J. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, L.; Liu, S.; Zhang, Y.; He, Z.; Li, W.; Zhang, F.; Shi, Y.; Lü, W.; Li, Y. Ultrathin metal–organic framework: An emerging broadband nonlinear optical material for ultrafast photonics. Adv. Opt. Mater. 2018, 6, 1800561. [Google Scholar] [CrossRef]
- Mingalone, C.K.H.; Liu, Z.; Hollander, J.M.; Garvey, K.D.; Gibson, A.L.; Banks, R.E.; Zhang, M.; McAlindon, T.E.; Nielsen, H.C.; Georgakoudi, I. Bioluminescence and second harmonic generation imaging reveal dynamic changes in the inflammatory and collagen landscape in early osteoarthritis. Lab. Investig. 2018, 98, 656–669. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.-B.; Li, Y.; Tang, B.Z.; Yoon, J. Assembly strategies of organic-based imaging agents for fluorescence and photoacoustic bioimaging applications. Chem. Soc. Rev. 2020, 49, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Parodi, V.; Jacchetti, E.; Osellame, R.; Cerullo, G.; Polli, D.; Raimondi, M.T. Nonlinear optical microscopy: From fundamentals to applications in live bioimaging. Front. Bioeng. Biotechnol. 2020, 8, 1174. [Google Scholar] [CrossRef]
- Khadria, A.; de Coene, Y.; Gawel, P.; Roche, C.; Clays, K.; Anderson, H.L. Push–pull pyropheophorbides for nonlinear optical imaging. Org. Biomol. Chem. 2017, 15, 947–956. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hartree, D.R.; Hartree, W. Self-consistent field, with exchange, for beryllium. Proc. R. Soc. London Ser. A—Math. Phys. Sci. 1935, 150, 9–33. [Google Scholar]
- Dwivedi, Y.; Tamashiro, G.; De Boni, L.; Zilio, S.C. Nonlinear optical characterizations of dibenzoylmethane in solution. Opt. Commun. 2013, 293, 119–124. [Google Scholar] [CrossRef]
- Houbrechts, S.; Clays, K.; Persoons, A.; Pikramenou, Z.; Lehn, J.-M. Hyper-Rayleigh scattering investigation of nitrobenzyl pyridine model compounds for optical modulation of the hyperpolarisability. Chem. Phys. Lett. 1996, 258, 485–489. [Google Scholar] [CrossRef]
- Srinivas, K.; Prabhakar, C.; Sitha, S.; Bhanuprakash, K.; Rao, V.J. Enhanced molecular first hyperpolarizability in s-triazine derivatives: Combined experimental and computational studies. J. Mol. Struct. 2014, 1075, 118–123. [Google Scholar] [CrossRef]
- Kaatz, P.; Shelton, D.P. Polarized hyper-Rayleigh light scattering measurements of nonlinear optical chromophores. J. Chem. Phys. 1996, 105, 3918–3929. [Google Scholar] [CrossRef]
- Beaujean, P.; Bondu, F.; Plaquet, A.; Garcia-Amoros, J.; Cusido, J.; Raymo, F.M.; Castet, F.; Rodriguez, V.; Champagne, B. Oxazines: A new class of second-order nonlinear optical switches. J. Am. Chem. Soc. 2016, 138, 5052–5062. [Google Scholar] [CrossRef]
- Santos, F.A.; Abegão, L.M.; Fonseca, R.D.; Alcântara, A.M.; Mendonça, C.R.; Alencar, M.A.; Valle, M.S.; Kamada, K.; De Boni, L.; Rodrigues, J.J., Jr. Nonlinear optical study in a set of dibenzylideneacetone derivatives with potential for optical frequency conversion. Photonics 2020, 7, 8. [Google Scholar] [CrossRef]
- Santos, F.A.; Abegao, L.M.; Fonseca, R.D.; Alcantara, A.M.; Mendonca, C.R.; Valle, M.S.; Alencar, M.; Kamada, K.; De Boni, L.; Rodrigues, J., Jr. Bromo-and chloro-derivatives of dibenzylideneacetone: Experimental and theoretical study of the first molecular hyperpolarizability and two-photon absorption. J. Photochem. Photobiol. A Chem. 2019, 369, 70–76. [Google Scholar] [CrossRef]
- Abegao, L.M.; Fonseca, R.D.; Santos, F.A.; Rodrigues, J.J.; Kamada, K.; Mendonça, C.R.; Piguel, S.; De Boni, L. First molecular electronic hyperpolarizability of series of π-conjugated oxazole dyes in solution: An experimental and theoretical study. RSC Adv. 2019, 9, 26476–26482. [Google Scholar] [CrossRef]
- Abegao, L.M.; Santos, F.A.; Fonseca, R.D.; Barreiros, A.L.; Barreiros, M.L.; Alves, P.B.; Costa, E.V.; Souza, G.B.; Alencar, M.A.; Mendonca, C.R. Chalcone-based molecules: Experimental and theoretical studies on the two-photon absorption and molecular first hyperpolarizability. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 227, 117772. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Liu, S.; Wang, C.C.; Wang, C. Dispersion of the first hyperpolarizability of a strongly charge-transfer chromophore investigated by tunable wavelength hyper-Rayleigh scattering. J. Chem. Phys. 2001, 114, 7103–7108. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Shu, C.-F.; Huang, T.-H.; Wang, C.; Lin, J.-L.; Wang, Y.-K.; Zang, Y.-L. Hyper-Rayleigh scattering of thiophene-incorporated polyene chromophores with π-configuration locking. Chem. Phys. Lett. 1997, 274, 466–472. [Google Scholar] [CrossRef]
- Brasselet, S.; Zyss, J. Multipolar molecules and multipolar fields: Probing and controlling the tensorial nature of nonlinear molecular media. JOSA B 1998, 15, 257–288. [Google Scholar] [CrossRef]
- Bogdan, E.; Plaquet, A.; Antonov, L.; Rodriguez, V.; Ducasse, L.; Champagne, B.; Castet, F. Solvent effects on the second-order nonlinear optical responses in the keto− enol equilibrium of a 2-Hydroxy-1-naphthaldehyde derivative. J. Phys. Chem. C 2010, 114, 12760–12768. [Google Scholar] [CrossRef]
- de Wergifosse, M.; Grimme, S. Nonlinear-response properties in a simplified time-dependent density functional theory (sTD-DFT) framework: Evaluation of the first hyperpolarizability. J. Chem. Phys. 2018, 149, 024108. [Google Scholar] [CrossRef]
- Verbiest, T.; Clays, K.; Rodriguez, V. Second-Order Nonlinear Optical Characterization Techniques: An Introduction; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Li, J.; Huang, J.; Qin, T.; Liu, Y.-M.; Zhong, F.; Zhang, W.; Li, Z.-R. Long-Range Charge Transfer Driven by External Electric Field in Alkalides M–LCaL–M (M= Li or Na, L= All-cis 1, 2, 3, 4, 5, 6-Hexafluorocyclohexane): Facially Polarized Janus-Type Second Order Nonlinear Molecular Optical Switches. J. Phys. Chem. C 2019, 123, 23610–23619. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Kita, H.; Yamakado, R.; Fukuuchi, R.; Konishi, T.; Kamada, K.; Haketa, Y.; Maeda, H. Switching of Two-Photon Optical Properties by Anion Binding of Pyrrole-Based Boron Diketonates through Conformation Change. Chem.–A Eur. J. 2020, 26, 3404–3410. [Google Scholar] [CrossRef]
- Klausen, M.; Dubois, V.; Clermont, G.; Tonnelé, C.; Castet, F.; Blanchard-Desce, M. Dual-wavelength efficient two-photon photorelease of glycine by π-extended dipolar coumarins. Chem. Sci. 2019, 10, 4209–4219. [Google Scholar] [CrossRef]
- Samanta, P.K.; Alam, M.M.; Misra, R.; Pati, S.K. Tuning of hyperpolarizability, and one-and two-photon absorption of donor–acceptor and donor–acceptor–acceptor-type intramolecular charge transfer-based sensors. Phys. Chem. Chem. Phys. 2019, 21, 17343–17355. [Google Scholar] [CrossRef]
- Shalin, N.I.; Fominykh, O.D.; Balakina, M.Y. Effect of acceptor moieties on static and dynamic first hyperpolarizability of azobenzene chromophores. Chem. Phys. Lett. 2019, 717, 21–28. [Google Scholar] [CrossRef]
- Besalú-Sala, P.; Sitkiewicz, S.P.; Salvador, P.; Matito, E.; Luis, J.M. A new tuned range-separated density functional for the accurate calculation of second hyperpolarizabilities. Phys. Chem. Chem. Phys. 2020, 22, 11871–11880. [Google Scholar] [CrossRef]
- Champagne, B.; Beaujean, P.; De Wergifosse, M.; Cardenuto, M.H.; Liégeois, V.; Castet, F. Quantum Chemical Methods for Predicting and Interpreting Second-Order Nonlinear Optical Properties: From Small to Extended π-Conjugated Molecules. In Frontiers of Quantum Chemistry; Springer: Singapore, 2018; pp. 117–138. [Google Scholar]
- Pielak, K.; Bondu, F.; Sanguinet, L.; Rodriguez, V.; Castet, F.; Champagne, B. Acido-triggered switching of the second-order nonlinear optical properties of a ferrocenyl-containing indolino-oxazolidine derivative. Dye. Pigment. 2019, 160, 641–646. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward chemical accuracy in the computation of NMR shieldings: The PBE0 model. Chem. Phys. Lett. 1998, 298, 113–119. [Google Scholar] [CrossRef]
- Suponitsky, K.Y.; Liao, Y.; Masunov, A.E. Electronic hyperpolarizabilities for donor−acceptor molecules with long conjugated bridges: Calculations versus experiment. J. Phys. Chem. A 2009, 113, 10994–11001. [Google Scholar] [CrossRef] [PubMed]
- Suponitsky, K.Y.; Tafur, S.; Masunov, A.E. Applicability of hybrid density functional theory methods to calculation of molecular hyperpolarizability. J. Chem. Phys. 2008, 129, 044109. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, Y.; Tian, X.; Yuan, J.; Sun, J. High first-hyperpolarizabilities of thiobarbituric acid derivative-based donor-π-acceptor nonlinear optical-phores: Multiple theoretical investigations of substituents and conjugated bridges effect. Int. J. Quantum Chem. 2020, 120, e26176. [Google Scholar] [CrossRef]
- Johnson, L.E.; Dalton, L.R.; Robinson, B.H. Optimizing calculations of electronic excitations and relative hyperpolarizabilities of electrooptic chromophores. Acc. Chem. Res. 2014, 47, 3258–3265. [Google Scholar] [CrossRef]
- Adamo, C.; Cossi, M.; Scalmani, G.; Barone, V. Accurate static polarizabilities by density functional theory: Assessment of the PBE0 model. Chem. Phys. Lett. 1999, 307, 265–271. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Şirikci, G.; Ancın, N.A.; Öztaş, S.G. Theoretical studies of organotin (IV) complexes derived from ONO-donor type schiff base ligands. J. Mol. Model. 2015, 21, 221. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Sutradhar, D.; Chandra, A.K.; Zeegers-Huyskens, T. Theoretical study of the interaction of fluorinated dimethyl ethers and the ClF and HF molecules. Comparison between halogen and hydrogen bonds. Int. J. Quantum Chem. 2016, 116, 670–680. [Google Scholar] [CrossRef]
- Safdari, F.; Raissi, H.; Shahabi, M.; Zaboli, M. DFT calculations and molecular dynamics simulation study on the adsorption of 5-fluorouracil anticancer drug on graphene oxide nanosheet as a drug delivery vehicle. J. Inorg. Organomet. Polym. Mater. 2017, 27, 805–817. [Google Scholar] [CrossRef]
- Lohith, T.; Hema, M.; Karthik, C.; Sandeep, S.; Mallesha, L.; Alsaiari, N.S.; Sridhar, M.; Katubi, K.M.; Abualnaja, K.M.; Lokanath, N. Persistent prevalence of non-covalent interaction in pyrimidine containing sulfonamide derivative: A quantum computational analysis. J. Mol. Struct. 2022, 1266, 133378. [Google Scholar] [CrossRef]
- Hadji, D.; Rahmouni, A. Molecular structure, linear and nonlinear optical properties of some cyclic phosphazenes: A theoretical investigation. J. Mol. Struct. 2016, 1106, 343–351. [Google Scholar] [CrossRef]
- Ejuh, G.; Tchangnwa Nya, F.; Ottou Abe, M.; Jean-Baptiste, F.; Ndjaka, J. Electronic structure, physico-chemical, linear and non linear optical properties analysis of coronene, 6B-, 6N-, 3B3N-substituted C24H12 using RHF, B3LYP and wB97XD methods. Opt. Quantum Electron. 2017, 49, 382. [Google Scholar] [CrossRef]
- Al-Hamdani, U.J.; Hassan, Q.M.; Zaidan, A.M.; Sultan, H.; Hussain, K.A.; Emshary, C.; Alabdullah, Z.T. Optical nonlinear properties and all optical switching in a synthesized liquid crystal. J. Mol. Liq. 2022, 361, 119676. [Google Scholar] [CrossRef]
- Prakasam, M.; Anbarasan, P. Second order hyperpolarizability of triphenylamine based organic sensitizers: A first principle theoretical study. RSC Adv. 2016, 6, 75242–75250. [Google Scholar] [CrossRef]
- Karakas, A.; Karakaya, M.; Ceylan, Y.; El Kouari, Y.; Taboukhat, S.; Boughaleb, Y.; Sofiani, Z. Ab-initio and DFT methodologies for computing hyperpolarizabilities and susceptibilities of highly conjugated organic compounds for nonlinear optical applications. Opt. Mater. 2016, 56, 8–17. [Google Scholar] [CrossRef]
- Maidur, S.R.; Patil, P.S.; Rao, S.V.; Shkir, M.; Dharmaprakash, S. Experimental and computational studies on second-and third-order nonlinear optical properties of a novel D-π-A type chalcone derivative: 3-(4-methoxyphenyl)-1-(4-nitrophenyl) prop-2-en-1-one. Opt. Laser Technol. 2017, 97, 219–228. [Google Scholar] [CrossRef]
- Castet, F.; Rodriguez, V.; Pozzo, J.-L.; Ducasse, L.; Plaquet, A.; Champagne, B. Design and characterization of molecular nonlinear optical switches. Acc. Chem. Res. 2013, 46, 2656–2665. [Google Scholar] [CrossRef] [PubMed]
- Tolbin, A.Y.; Dzuban, A.V.; Shestov, V.I.; Gudkova, Y.I.; Brel, V.K.; Tomilova, L.G.; Zefirov, N.S. Peripheral functionalisation of a stable phthalocyanine J-type dimer to control the aggregation behaviour and NLO properties: UV-Vis, fluorescence, DFT, TDHF and thermal study. RSC Adv. 2015, 5, 8239–8247. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Tamer, Ö.; Şimşek, M.; Avcı, D.; Atalay, Y. First and second order hyperpolarizabilities of flavonol derivatives: A density functional theory study. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 283, 121728. [Google Scholar] [CrossRef]
- Sciuti, L.F.; Abegão, L.M.; Dos Santos, C.H.; Zucolotto Cocca, L.H.; da Costa, R.G.; Limberger, J.; Misoguti, L.; Mendonça, C.R.; De Boni, L. Modeling the First-Order Molecular Hyperpolarizability Dispersion from Experimentally Obtained One-and Two-Photon Absorption. J. Phys. Chem. A 2022, 126, 2152–2159. [Google Scholar] [CrossRef]
- Lescos, L.; Sitkiewicz, S.P.; Beaujean, P.; Blanchard-Desce, M.; Champagne, B.; Matito, E.; Castet, F. Performance of DFT functionals for calculating the second-order nonlinear optical properties of dipolar merocyanines. Phys. Chem. Chem. Phys. 2020, 22, 16579–16594. [Google Scholar] [CrossRef]
- Devi, C.L.; Yesudas, K.; Makarov, N.S.; Rao, V.J.; Bhanuprakash, K.; Perry, J.W. Combined experimental and theoretical study of one-and two-photon absorption properties of D–π–A–π–D type bis (carbazolylfluorenylethynyl) arene derivatives: Influence of aromatic acceptor bridge. Dye. Pigment. 2015, 113, 682–691. [Google Scholar] [CrossRef]
- Matczyszyn, K.; Olesiak-Banska, J.; Nakatani, K.; Yu, P.; Murugan, N.A.; Zalesny, R.; Roztoczynska, A.; Bednarska, J.; Bartkowiak, W.; Kongsted, J. One-and Two-Photon Absorption of a Spiropyran–Merocyanine System: Experimental and Theoretical Studies. J. Phys. Chem. B 2015, 119, 1515–1522. [Google Scholar] [CrossRef]
- Kang, G.; Nasiri Avanaki, K.; Mosquera, M.A.; Burdick, R.K.; Villabona-Monsalve, J.P.; Goodson, T., III; Schatz, G.C. Efficient modeling of organic chromophores for entangled two-photon absorption. J. Am. Chem. Soc. 2020, 142, 10446–10458. [Google Scholar] [CrossRef] [PubMed]
- Abegão, L.M.; Fonseca, R.D.; Ramos, T.N.; Mahuteau-Betzer, F.; Piguel, S.; Joatan, R.J., Jr.; Mendonca, C.R.; Canuto, S.; Silva, D.L.; De Boni, L. Oxazole dyes with potential for photoluminescence bioprobes: A two-photon absorption study. J. Phys. Chem. C 2018, 122, 10526–10534. [Google Scholar] [CrossRef]
- Marder, S.R.; Beratan, D.N.; Cheng, L.-T. Approaches for optimizing the first electronic hyperpolarizability of conjugated organic molecules. Science 1991, 252, 103–106. [Google Scholar] [CrossRef] [PubMed]
- Orr, B.; Ward, J. Perturbation theory of the non-linear optical polarization of an isolated system. Mol. Phys. 1971, 20, 513–526. [Google Scholar] [CrossRef]
- Nénon, S.; Champagne, B. SCC-DFTB calculation of the static first hyperpolarizability: From gas phase molecules to functionalized surfaces. J. Chem. Phys. 2013, 138, 204107. [Google Scholar] [CrossRef]
- Hu, Y.-Y.; Sun, S.-L.; Muhammad, S.; Xu, H.-L.; Su, Z.-M. How the number and location of lithium atoms affect the first hyperpolarizability of graphene. J. Phys. Chem. C 2010, 114, 19792–19798. [Google Scholar] [CrossRef]
- Srivastava, R.; Al-Omary, F.A.; El-Emam, A.A.; Pathak, S.K.; Karabacak, M.; Narayan, V.; Chand, S.; Prasad, O.; Sinha, L. A combined experimental and theoretical DFT (B3LYP, CAM-B3LYP and M06-2X) study on electronic structure, hydrogen bonding, solvent effects and spectral features of methyl 1H-indol-5-carboxylate. J. Mol. Struct. 2017, 1137, 725–741. [Google Scholar] [CrossRef]
- Rasool, F.; Hussain, A.; Yar, M.; Ayub, K.; Sajid, M.; Asif, H.M.; Imran, M.; Assiri, M.A. Nonlinear optical response of 9, 10-bis (phenylethynyl) anthracene mediated by electron donating and electron withdrawing substituents: A density functional theory approach. Mater. Sci. Semicond. Process. 2022, 148, 106751. [Google Scholar] [CrossRef]
- Kodikara, M.S.; Stranger, R.; Humphrey, M.G. Long-Range Corrected DFT Calculations of First Hyperpolarizabilities and Excitation Energies of Metal Alkynyl Complexes. ChemPhysChem 2018, 19, 1537–1546. [Google Scholar] [CrossRef]
- Capobianco, A.; Centore, R.; Noce, C.; Peluso, A. Molecular hyperpolarizabilities of push–pull chromophores: A comparison between theoretical and experimental results. Chem. Phys. 2013, 411, 11–16. [Google Scholar] [CrossRef]
- de Wergifosse, M.; Champagne, B. Electron correlation effects on the first hyperpolarizability of push–pull π-conjugated systems. J. Chem. Phys. 2011, 134, 074113. [Google Scholar] [CrossRef]
- Pielak, K.; Tonnelé, C.; Sanguinet, L.; Cariati, E.; Righetto, S.; Muccioli, L.; Castet, F.; Champagne, B. Dynamical behavior and second harmonic generation responses in acido-triggered molecular switches. J. Phys. Chem. C 2018, 122, 26160–26168. [Google Scholar] [CrossRef]
- Tonnelé, C.; Champagne, B.; Muccioli, L.; Castet, F. Second-order nonlinear optical properties of Stenhouse photoswitches: Insights from density functional theory. Phys. Chem. Chem. Phys. 2018, 20, 27658–27667. [Google Scholar] [CrossRef] [PubMed]
- Bondu, F.; Quertinmont, J.; Rodriguez, V.; Pozzo, J.L.; Plaquet, A.; Champagne, B.; Castet, F. Second-Order Nonlinear Optical Properties of a Dithienylethene–Indolinooxazolidine Hybrid: A Joint Experimental and Theoretical Investigation. Chem.–A Eur. J. 2015, 21, 18749–18757. [Google Scholar] [CrossRef] [PubMed]
- Singh, I.; El-Emam, A.A.; Pathak, S.K.; Srivastava, R.; Shukla, V.K.; Prasad, O.; Sinha, L. Experimental and theoretical DFT (B3LYP, X3LYP, CAM-B3LYP and M06-2X) study on electronic structure, spectral features, hydrogen bonding and solvent effects of 4-methylthiadiazole-5-carboxylic acid. Mol. Simul. 2019, 45, 1029–1043. [Google Scholar] [CrossRef]
- Custodio, J.M.; Gotardo, F.; Vaz, W.F.; D’Oliveira, G.D.; de Almeida, L.R.; Fonseca, R.D.; Cocca, L.H.; Perez, C.N.; Oliver, A.G.; De Boni, L. Benzenesulfonyl incorporated chalcones: Synthesis, structural and optical properties. J. Mol. Struct. 2020, 1208, 127845. [Google Scholar] [CrossRef]
- Fonseca, R.D.; Vivas, M.G.; Silva, D.L.; Eucat, G.; Bretonnière, Y.; Andraud, C.; De Boni, L.; Mendonca, C.R. First-order hyperpolarizability of triphenylamine derivatives containing cyanopyridine: Molecular branching effect. J. Phys. Chem. C 2018, 122, 1770–1778. [Google Scholar] [CrossRef]
- Vivas, M.G.; Barboza, C.A.; Germino, J.C.; Fonseca, R.D.; Silva, D.L.; Vazquez, P.A.; Atvars, T.D.; Mendonca, C.R.; De Boni, L. Molecular Structure–Optical Property Relationship of Salicylidene Derivatives: A Study on the First-Order Hyperpolarizability. J. Phys. Chem. A 2020, 125, 99–105. [Google Scholar] [CrossRef]
- Tonnelé, C.; Pielak, K.; Deviers, J.; Muccioli, L.; Champagne, B.; Castet, F. Nonlinear optical responses of self-assembled monolayers functionalized with indolino–oxazolidine photoswitches. Phys. Chem. Chem. Phys. 2018, 20, 21590–21597. [Google Scholar] [CrossRef] [PubMed]
- Chai, Z.; Hu, X.; Wang, F.; Niu, X.; Xie, J.; Gong, Q. Ultrafast all-optical switching. Adv. Opt. Mater. 2017, 5, 1600665. [Google Scholar] [CrossRef]
- Röcker, C.; Weinert, P.; Villeval, P.; Lupinski, D.; Delaigue, M.; Hönninger, C.; Weber, R.; Graf, T.; Ahmed, M.A. Nonlinear absorption in lithium triborate frequency converters for high-power ultrafast lasers. Opt. Express 2022, 30, 5423–5438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.-y.; Huang, J.Y.; Wang, H.; Wong, K.; Wong, G. Second-harmonic generation from regeneratively amplified femtosecond laser pulses in BBO and LBO crystals. JOSA B 1998, 15, 200–209. [Google Scholar] [CrossRef]
- Akbari, R.; Major, A. Optical, spectral and phase-matching properties of BIBO, BBO and LBO crystals for optical parametric oscillation in the visible and near-infrared wavelength ranges. Laser Phys. 2013, 23, 035401. [Google Scholar] [CrossRef]
- Karuppasamy, P.; Kamalesh, T.; Anitha, K.; Kalam, S.A.; Pandian, M.S.; Ramasamy, P.; Verma, S.; Rao, S.V. Synthesis, crystal growth, structure and characterization of a novel third order nonlinear optical organic single crystal: 2-amino 4, 6-dimethyl pyrimidine 4-nitrophenol. Opt. Mater. 2018, 84, 475–489. [Google Scholar] [CrossRef]
- Liu, J.; Ouyang, C.; Huo, F.; He, W.; Cao, A. Progress in the enhancement of electro-optic coefficients and orientation stability for organic second-order nonlinear optical materials. Dye. Pigment. 2020, 181, 108509. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Z.; Wang, D.; Cao, H. Molecular structures and second-order nonlinear optical properties of ionic organic crystal materials. Crystals 2016, 6, 158. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, F.A.; Cardoso, C.E.R.; Rodrigues, J.J., Jr.; De Boni, L.; Abegão, L.M.G. Nonlinear Optical Materials: Predicting the First-Order Molecular Hyperpolarizability of Organic Molecular Structures. Photonics 2023, 10, 545. https://doi.org/10.3390/photonics10050545
Santos FA, Cardoso CER, Rodrigues JJ Jr., De Boni L, Abegão LMG. Nonlinear Optical Materials: Predicting the First-Order Molecular Hyperpolarizability of Organic Molecular Structures. Photonics. 2023; 10(5):545. https://doi.org/10.3390/photonics10050545
Chicago/Turabian StyleSantos, Francisco A., Carlos E. R. Cardoso, José J. Rodrigues, Jr., Leonardo De Boni, and Luis M. G. Abegão. 2023. "Nonlinear Optical Materials: Predicting the First-Order Molecular Hyperpolarizability of Organic Molecular Structures" Photonics 10, no. 5: 545. https://doi.org/10.3390/photonics10050545
APA StyleSantos, F. A., Cardoso, C. E. R., Rodrigues, J. J., Jr., De Boni, L., & Abegão, L. M. G. (2023). Nonlinear Optical Materials: Predicting the First-Order Molecular Hyperpolarizability of Organic Molecular Structures. Photonics, 10(5), 545. https://doi.org/10.3390/photonics10050545




