First-Principle Prediction of Stress-Tunable Single-Photon Emitters at Telecommunication Band from Point Defects in GaN
Abstract
1. Introduction
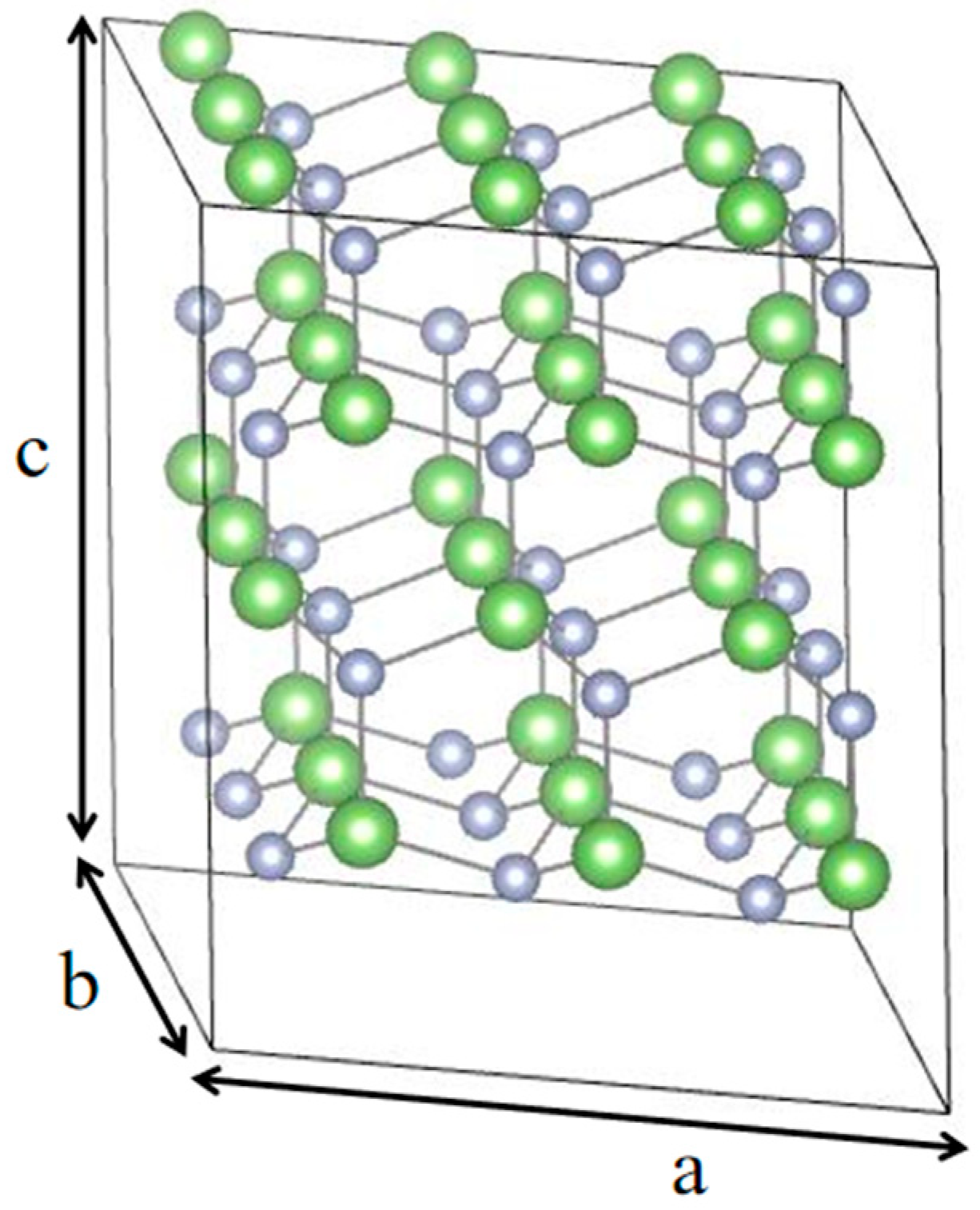
2. Calculation Methods
3. Results
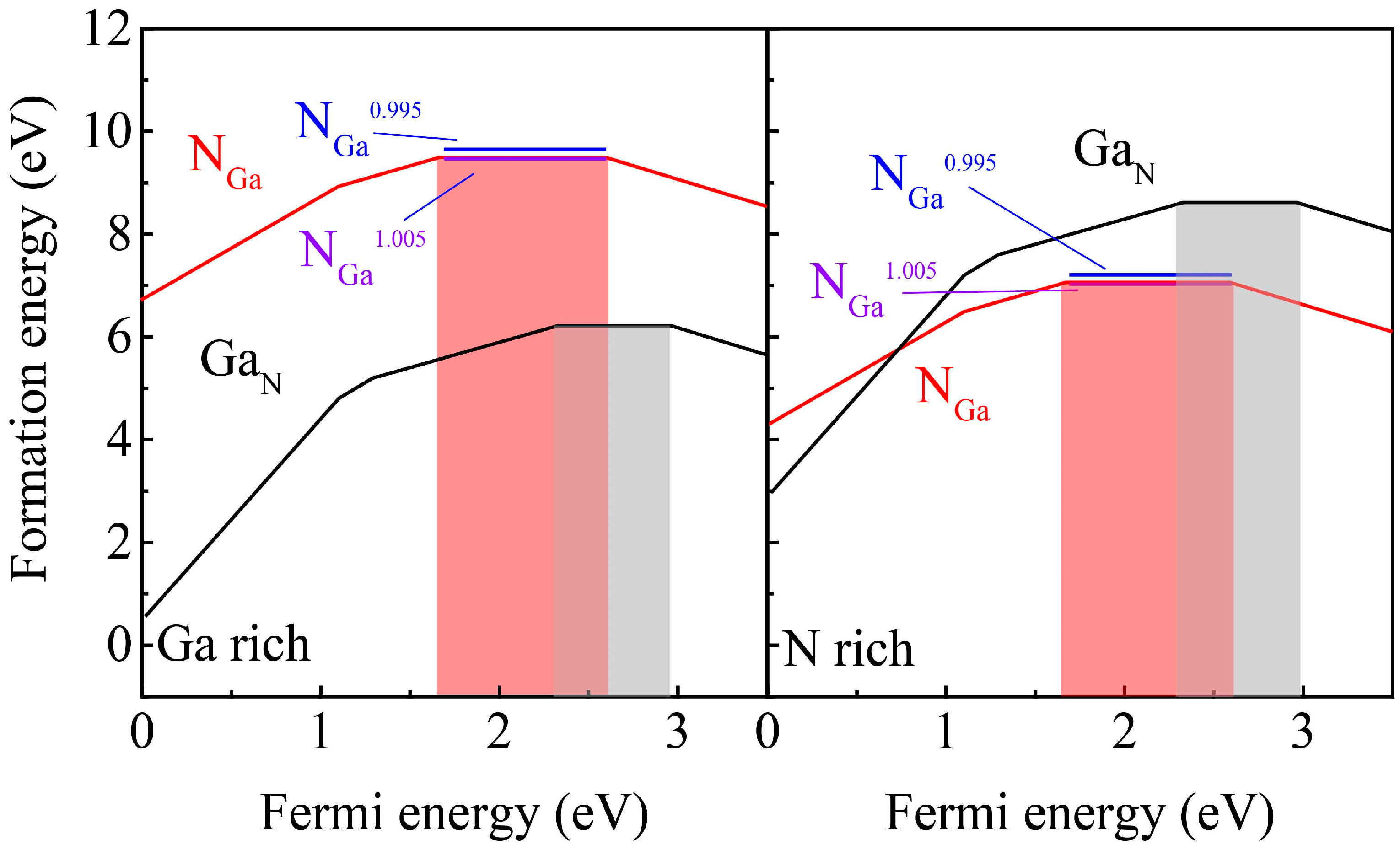
3.1. Formation Energy and Thermodynamic Stability of Single-Atom Defects
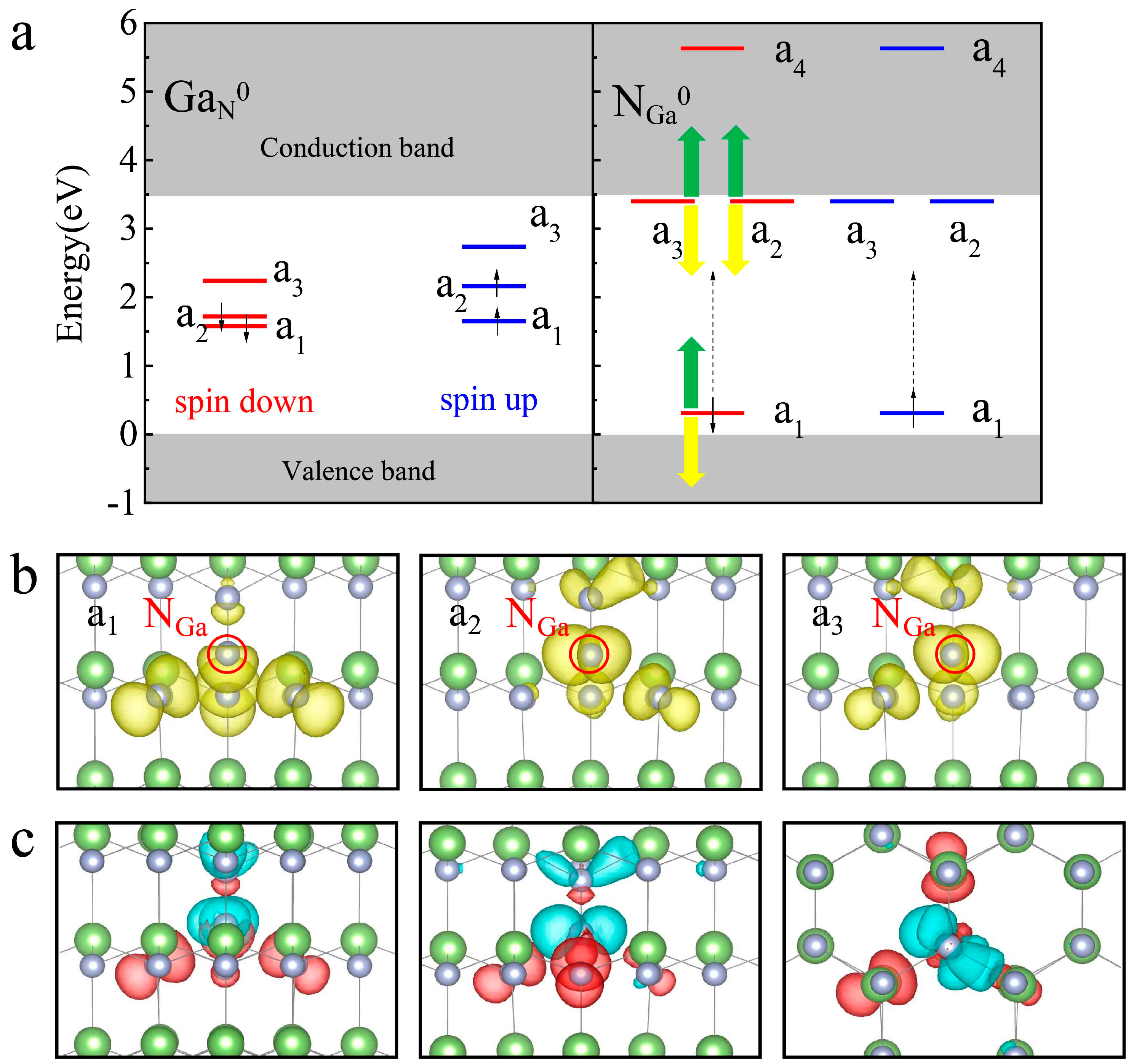
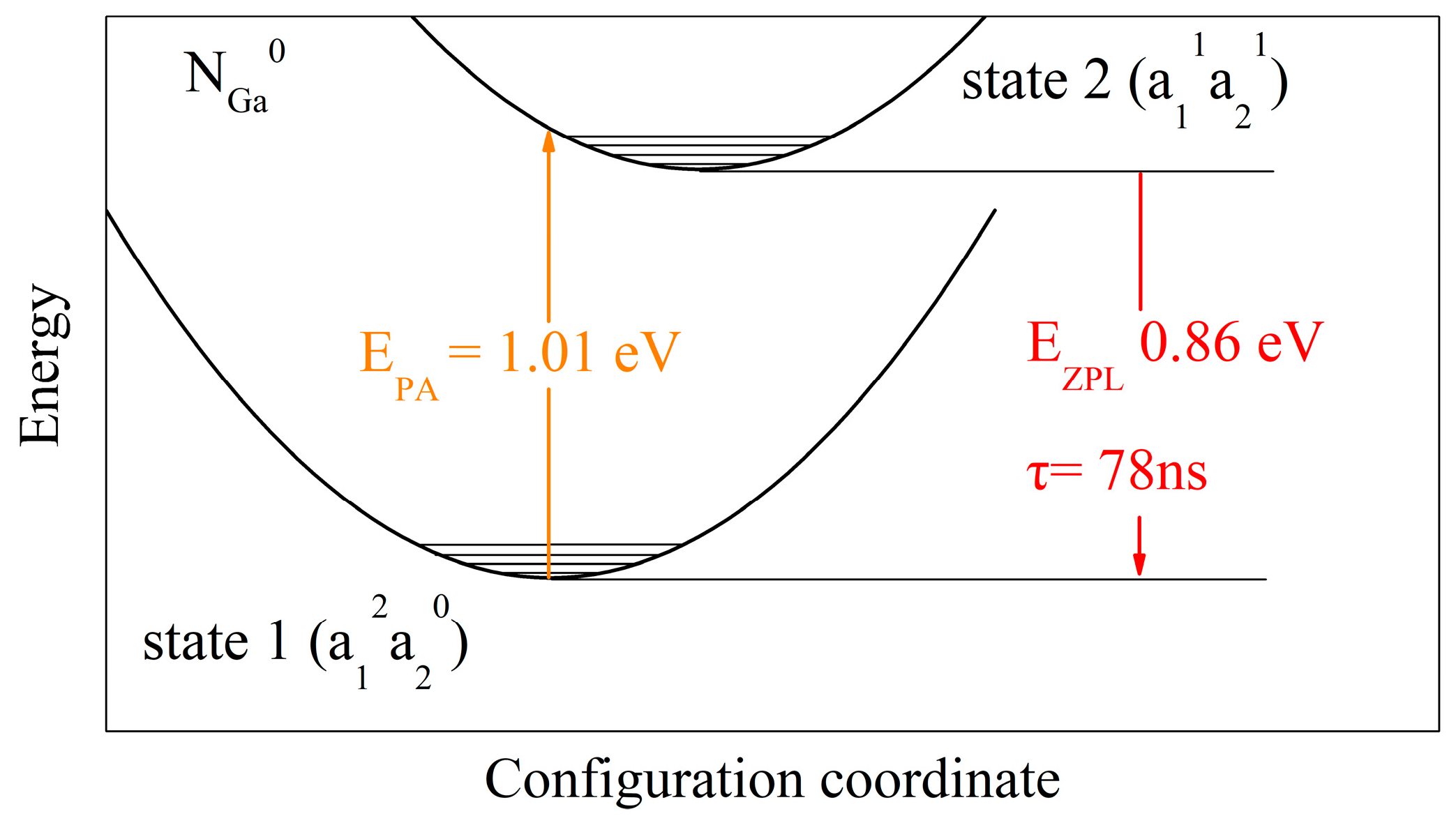
3.2. Transition Channel and SPE Quality of Single-Atom Defects in GaN
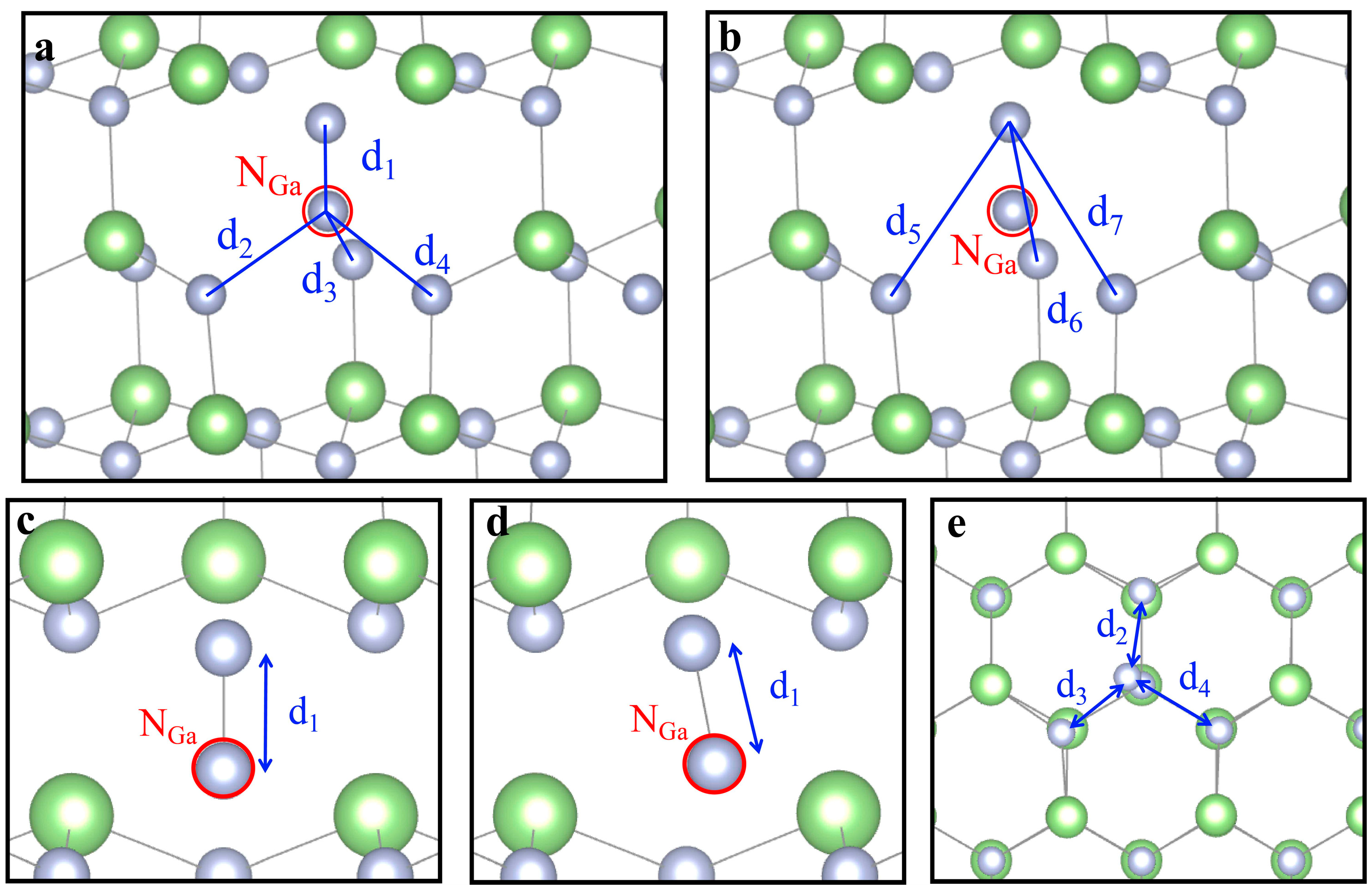
3.3. Defect Structure under Strain
3.4. The Single Photon Emission Property under Strain
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dietrich, A.; Doherty, M.W.; Aharonovich, I.; Kubanek, A. Solid-state single photon source with Fourier transform limited lines at room temperature. Phys. Rev. B 2020, 101, 081401. [Google Scholar] [CrossRef]
- Ortigoza, M.A.; Stolbov, S. Thermodynamic stability and optical properties of C-doping-induced defects in hexagonal boron nitride as potential single-photon emitters. Phys. Rev. B 2022, 105, 165306. [Google Scholar] [CrossRef]
- Aharonovich, I.; Englund, D.; Toth, M. Solid-state single-photon emitters. Nat. Photonics 2016, 10, 631–641. [Google Scholar] [CrossRef]
- Weber, J.R.; Koehl, W.F.; Varley, J.B. Quantum computing with defects. Proc. Natl. Acad. Sci. USA 2010, 107, 8513–8518. [Google Scholar] [CrossRef]
- De Martini, F.; Di Giuseppe, G.; Marrocco, M. Single-Mode Generation of Quantum Photon States by Excited Single Molecules in a Microcavity Trap. Phys. Rev. Lett. 1996, 76, 900. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Wang, P.; Wang, T.; Chen, L.; Chen, Z.; Gao, K.; Wang, X. Single-photon emission from isolated monolayer islands of InGaN. Light. Sci. Appl. 2020, 9, 159. [Google Scholar] [CrossRef]
- Norman, V.A.; Majety, S.; Wang, Z.; Casey, W.H.; Curro, N.; Radulaski, M. Novel color center platforms enabling fundamental scientific discovery. InfoMat 2021, 3, 869. [Google Scholar] [CrossRef]
- Aharonovich, I.; Castelletto, S.; Simpson, D.A.; Su, C.H.; Greentree, A.D.; Prawer, S. Diamond-based single-photon emitters. Rep. Prog. Phys. 2011, 74, 076501. [Google Scholar] [CrossRef]
- Herranz, C.E.; Scholl, E.; Picard, R.; Laini, M.; Gyger, S.; Elshaari, A.W.; Branny, A.; Wennberg, U.; Barbat, S.; Renaud, T.; et al. Resonance Fluorescence from Waveguide-Coupled, StrainLocalized, Two-Dimensional Quantum Emitters. ACS Photonics 2021, 8, 1069–1076. [Google Scholar] [CrossRef]
- Rakhlin, M.; Sorokin, S.; Kazanov, D.; Sedova, I.; Shubina, T.; Ivanov, S.; Mikhailovskii, V.; Toropov, A. Bright Single-Photon Emitters with a CdSe Quantum Dot and Multimode Tapered Nanoantenna for the Visible Spectral Range. Nanomaterials 2021, 11, 916. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, H.; Xie, N.; Yang, Q.; Xu, F.; Shen, B.; Shi, J.-J.; Jiang, D.; Dou, X.; Yu, T.; et al. Single-Photon Emission from Point Defects in Aluminum Nitride Films. J. Phys. Chem. Lett. 2020, 11, 2689–2694. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Zopf, M.; Ding, F. Telecom wavelength single photon sources. J. Semicond. 2019, 40, 071901. [Google Scholar] [CrossRef]
- Nguyen, M.A.P.; Hite, J.; Mastro, M.A.; Kianinia, M.; Toth, M.; Aharonovich, I. Site control of quantum emitters in gallium nitride by polarity. Appl. Phys. Lett. 2021, 118, 021103. [Google Scholar] [CrossRef]
- Bishop, S.G.; Hadden, J.P.; Hekmati, R.; Cannon, J.K.; Langbein, W.W.; Bennett, A.J. Enhanced light collection from a gallium nitride color center using a near index-matched solid immersion lens. Appl. Phys. Lett. 2022, 120, 114001. [Google Scholar] [CrossRef]
- Li, D.; Jiang, K.; Sun, X.; Guo, C. AlGaN photonics: Recent advances in materials and ultraviolet devices. Adv. Opt. Photonics 2018, 10, 43–110. [Google Scholar] [CrossRef]
- Berhane, A.M.; Jeong, K.Y.; Bodrog, Z.; Fiedler, S.; Schröder, T.; Triviño, N.V.; Palacios, T.; Gali, A.; Toth, M.; Englund, D.; et al. Bright Room-Temperature Single Photon Emission from Defects in Gallium Nitride. Adv. Mater. 2017, 29, 1605092. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Z.; Rasmita, A.; Kim, S.; Berhane, A.; Bodrog, Z.; Adamo, G.; Gali, A.; Aharonovich, I.; Gao, W.-B. Room temperature solid-state quantum emitters in the telecom range. Sci. Adv. 2018, 4, eaar3580. [Google Scholar] [CrossRef]
- Zang, H.; Sun, X.; Jiang, K. Cation Vacancy in Wide Bandgap III-Nitrides as Single-Photon Emitter: A First-Principles Investigation. Adv. Sci. 2021, 8, 2100100. [Google Scholar] [CrossRef]
- Grosso, G.; Moon, H.; Lienhard, B.; Ali, S.; Efetov, D.K.; Furchi, M.M.; Jarillo-Herrero, P.; Ford, M.J.; Aharonovich, I.; Englund, D. Tunable and high-purity room temperature single-photon emission from atomic defects in hexagonal boron nitride. Nat. Commun. 2017, 8, 705. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Jia, W.; Fu, J.; Cao, Z.; Wang, L.; Chi, X.; Gao, W.; Wang, L.-W. Fast plane wave density functional theory molecular dynamics calculations on multi-GPU machines. J. Comput. Phys. 2013, 251, 102–115. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Demchenko, D.O.; Diallo, I.C.; Reshchikov, M.A. Hydrogen-carbon complexes and the blue luminescence band in GaN. J. Appl. Phys. 2016, 119, 035702. [Google Scholar] [CrossRef]
- Yuan, J.; Hou, Y.; Yang, Z.; Chen, F.; Li, Q. GaN as a material platform for single-photon emitters: Insights from ab initio study. Adv. Opt. Mater. 2023, 11, 2202158. [Google Scholar] [CrossRef]
- Diallo, C.; Demchenko, O. Native Point Defects in GaN: A Hybrid-Functional Study. Phys. Rev. Appl. 2016, 6, 064002. [Google Scholar] [CrossRef]
- Xie, Z.; Sui, Y.; Buckeridge, J.; Catlow, C.R.A.; Keal, T.W.; Sherwood, P.; Walsh, A.; Farrow, M.R.; Scanlon, D.O.; Woodley, S.M.; et al. Donor and acceptor characteristics of native point defects in GaN. J. Phys. D Appl. Phys. 2019, 52, 335104. [Google Scholar] [CrossRef]
- Kyrtsos, A.; Matsubara, M.; Bellotti, E. Migration mechanisms and diffusion barriers of carbon and native point defects in GaN. Phys. Rev. B 2016, 93, 245201. [Google Scholar] [CrossRef]
- Suo, Z.J.; Luo, J.W.; Li, S.S.; Wang, L.W. Image charge interaction correction in charged-defect calculation. Phys. Rev. B 2020, 102, 174110. [Google Scholar] [CrossRef]
| strain σ | 99.5% | 100% | 100.5% |
| a1 (eV) | 0.459 | 0.334 | 0.224 |
| a2 (eV) | 3.537 | 3.400 | 3.280 |
| a2-a1 (eV) | 3.078 | 3.066 | 3.056 |
| State | Ground State | Excited State | ||||
|---|---|---|---|---|---|---|
| strain σ | 99.5% | 100% | 100.5% | 99.5% | 100% | 100.5% |
| d1 (Å) | 1.30316 | 1.28135 | 1.26637 | 1.31961 | 1.29306 | 1.27982 |
| d2 (Å) | 2.97155 | 3.01326 | 3.05002 | 2.94662 | 3.02600 | 3.07573 |
| d3 (Å) | 2.97246 | 3.01415 | 3.04992 | 3.03867 | 3.06722 | 3.10357 |
| d4 (Å) | 2.97159 | 3.01335 | 3.05011 | 2.94824 | 3.02790 | 3.07888 |
| d5 (Å) | 2.13592 | 2.18277 | 2.22577 | 2.02450 | 2.10169 | 2.15069 |
| d6 (Å) | 2.13668 | 2.18351 | 2.22578 | 2.38010 | 2.45753 | 2.52477 |
| d7 (Å) | 2.13595 | 2.18284 | 2.22584 | 2.02631 | 2.10348 | 2.15338 |
| Strain | 99.5% | 100% | 100.5% |
| Lifetime τ (ns) | 86.002 | 78.928 | 18.028 |
| ZPL (eV) | 0.84921 | 0.86482 | 0.98468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Wang, K.; Hou, Y.; Chen, F.; Li, Q. First-Principle Prediction of Stress-Tunable Single-Photon Emitters at Telecommunication Band from Point Defects in GaN. Photonics 2023, 10, 544. https://doi.org/10.3390/photonics10050544
Yuan J, Wang K, Hou Y, Chen F, Li Q. First-Principle Prediction of Stress-Tunable Single-Photon Emitters at Telecommunication Band from Point Defects in GaN. Photonics. 2023; 10(5):544. https://doi.org/10.3390/photonics10050544
Chicago/Turabian StyleYuan, Junxiao, Ke Wang, Yidong Hou, Feiliang Chen, and Qian Li. 2023. "First-Principle Prediction of Stress-Tunable Single-Photon Emitters at Telecommunication Band from Point Defects in GaN" Photonics 10, no. 5: 544. https://doi.org/10.3390/photonics10050544
APA StyleYuan, J., Wang, K., Hou, Y., Chen, F., & Li, Q. (2023). First-Principle Prediction of Stress-Tunable Single-Photon Emitters at Telecommunication Band from Point Defects in GaN. Photonics, 10(5), 544. https://doi.org/10.3390/photonics10050544





