Intensity Modulation of Two Weakly Coupled Stimulated Oscillating Mechanical Modes in an Optomechanical Microbubble Resonator
Abstract
1. Introduction
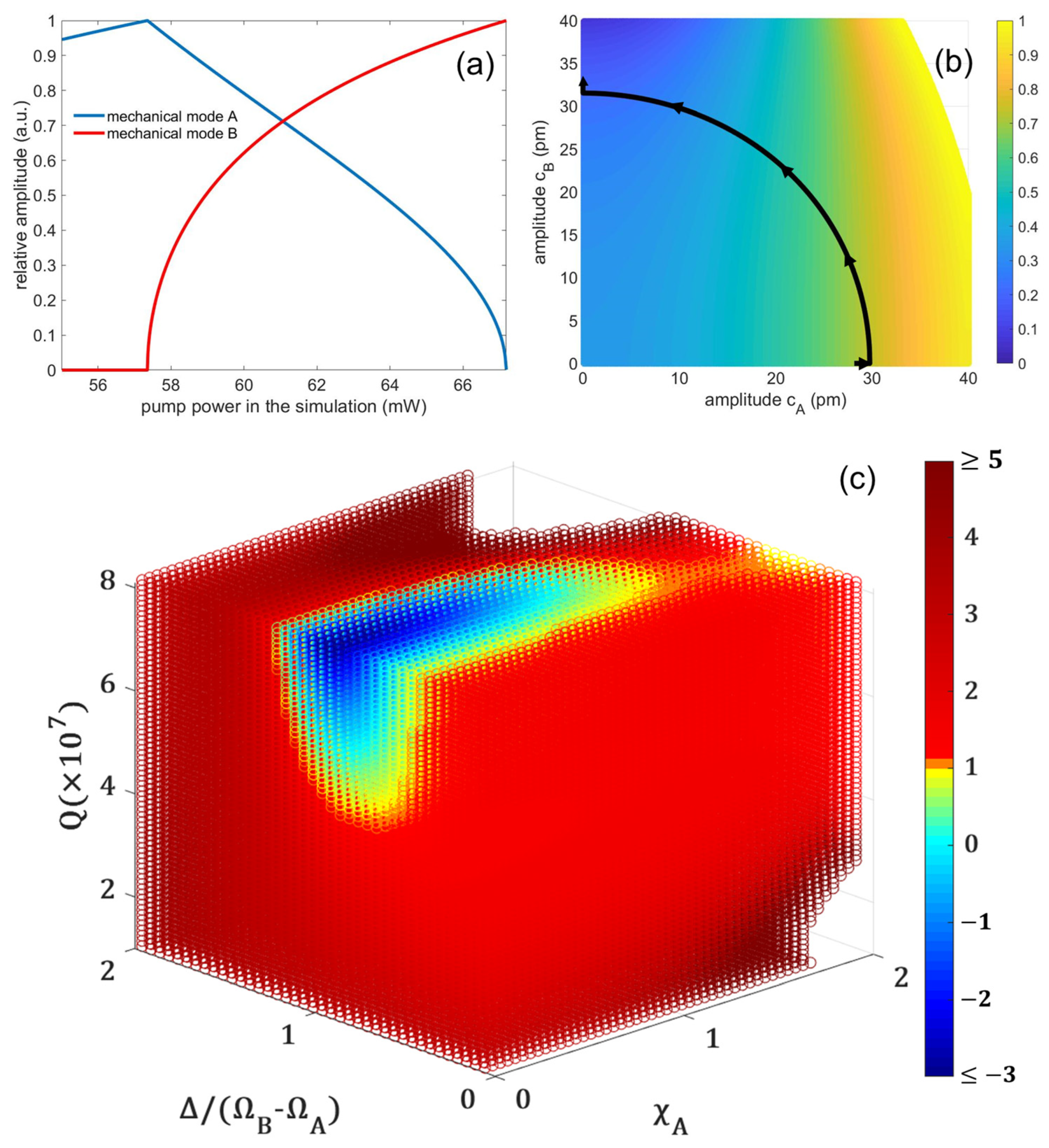
2. Two Mechanical Modes Coupling Theory in Optomechanical System
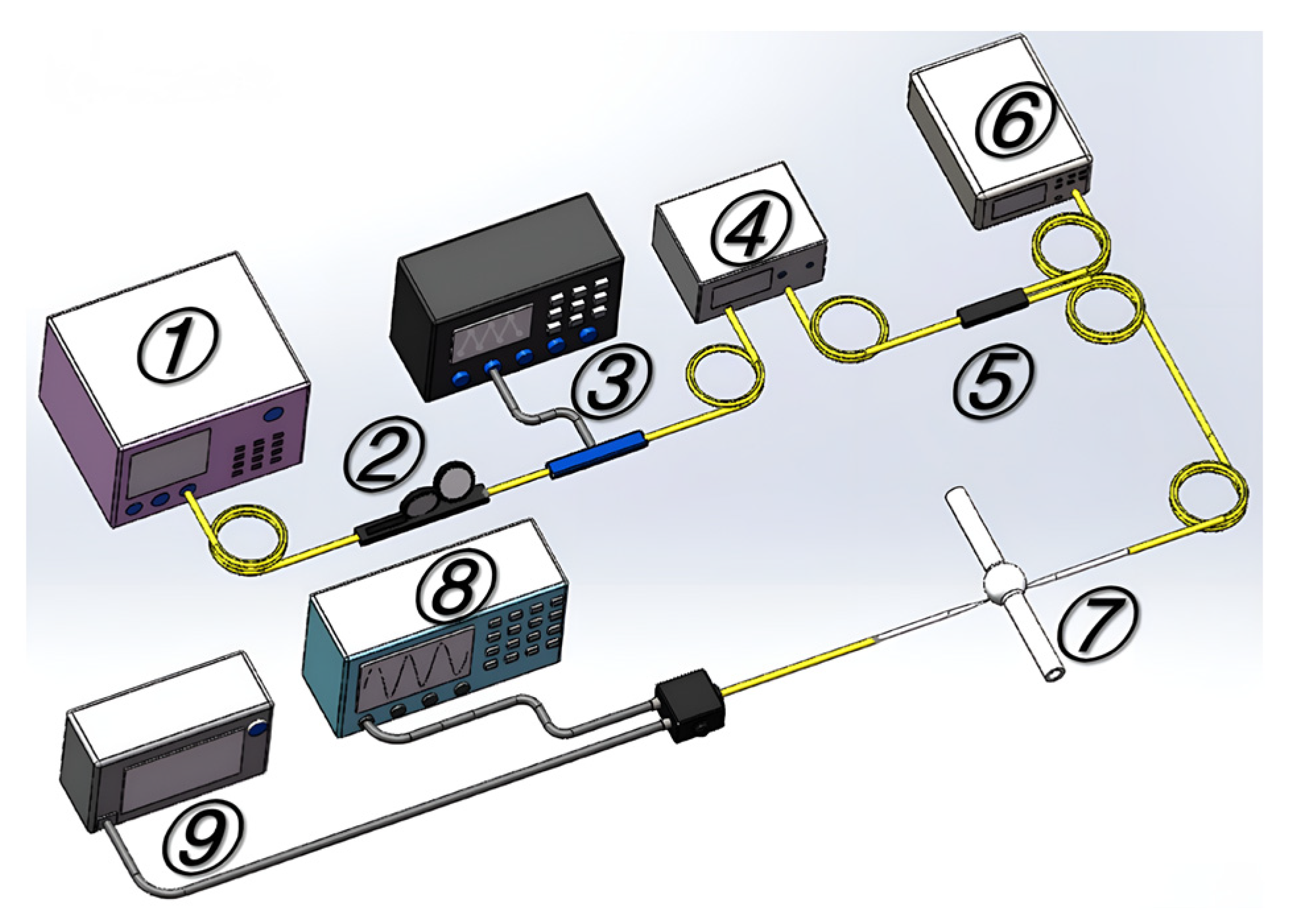
3. Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
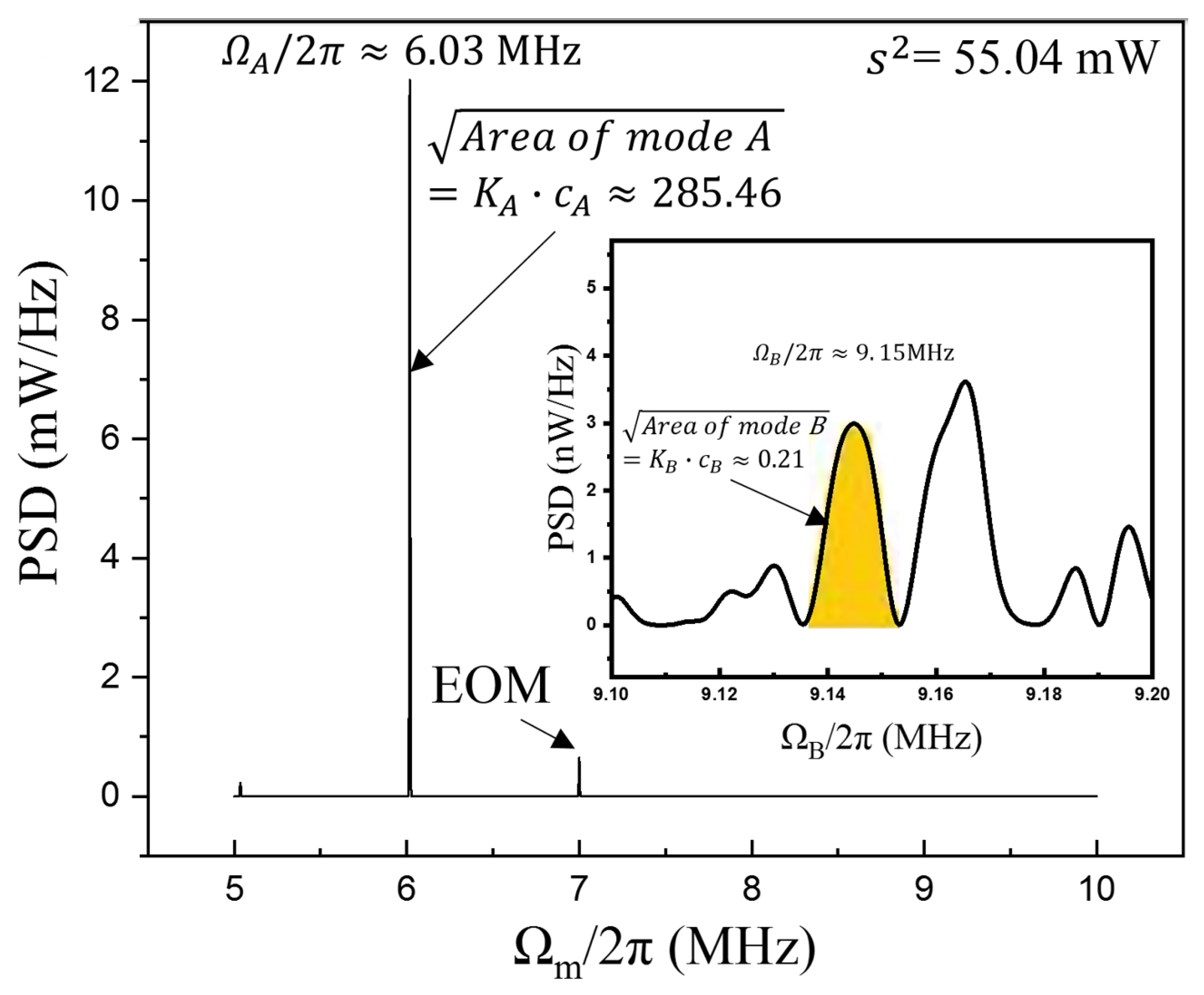
| Pump Power | 53.02 mW | 55.04 mW | 57.03 mW |
| Mechanical mode A | 255.09 | 285.46 | 284.15 |
| Mechanical mode B | 0.15 | 0.21 | 66.26 |
References
- Kippenberg, T.J.; Vahala, K.J. Cavity Opto-Mechanics. Opt. Express 2007, 15, 17172–17205. [Google Scholar] [CrossRef] [PubMed]
- Braginsky, V.B.; Manukin, A.; Tikhonov, M.Y. Investigation of Dissipative Ponderomotive Effects of Electromagnetic Radiation. Sov. Phys. JETP-USSR 1970, 31, 829–834. [Google Scholar]
- Braginsky, V.B.; Strigin, S.; Vyatchanin, S.P. Parametric oscillatory instability in Fabry-Perot interferometer. Phys. Lett. A 2001, 287, 331–338. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 4, 1391–1452. [Google Scholar] [CrossRef]
- Rokhsari, H.; Yang, L.; Kippenberg, T.J.; Vahala, K.; Carmon, T. Temporal Behavior of Radiation-Pressure-Induced Vibrations of an Optical Microcavity Phonon Mode. Phys. Rev. Lett. 2005, 94, 223902. [Google Scholar] [CrossRef]
- Rokhsari, H.; Kippenberg, T.J.; Carmon, T.; Vahala, K.J. Radiation-pressure-driven micro-mechanical oscillator. Opt. Express 2005, 13, 5293–5301. [Google Scholar] [CrossRef]
- Cross, M.C.; Vahala, K.; Carmon, T. Chaotic Quivering of Micron-Scaled On-Chip Resonators Excited by Centrifugal Optical Pressure. Phys. Rev. Lett. 2007, 98, 167203. [Google Scholar] [CrossRef]
- Grudinin, I.S.; Lee, H.; Painter, O.; Vahala, K.J. Phonon Laser Action in a Tunable Two-Level System. Phys. Rev. Lett. 2010, 104, 0839018. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Pruessner, M.W.; Stievater, T.; Rabinovich, W.S. Laser-Rate-Equation Description of Optomechanical Oscillators. Phys. Rev. Lett. 2012, 108, 22390422. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Pruessner, M.W.; Stievater, T.H.; Rabinovich, W.S. Optically pumped coherent mechanical oscillators: The laser rate equation theory and experimental verification. New J. Phys. 2010, 14, 105022. [Google Scholar] [CrossRef]
- Yang, L.; Xiao, M.; He, B. Dynamical phonon laser in coupled active-passive microresonators. Phys. Rev. A 2016, 94, 31802. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, B.; Özdemir, Ş.K.; Pichler, K.; Krimer, D.O.; Zhao, G.; Nori, F.; Liu, Y.X.; Rotter, S.; Yang, L. A phonon laser operating at an exceptional point. Nat. Photonics 2018, 12, 479–484. [Google Scholar] [CrossRef]
- Schliesser, A.; Kippenberg, T.J. Cavity optomechanics with whispering-gallery-mode optical micro-resonators. Adv. At. Mol. Opt. Phys. 2010, 58, 207–323. [Google Scholar]
- Massel, F.; Cho, S.; Pirkkalainen, J.; Hakonen, P.; Heikkila, T.; Sillanpaa, M.A. Multimode circuit optomechanics near the quantum limit. Nat. Commun. 2012, 3, 987. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Yang, C.; Wu, H.; Sheng, J. Self-Organized Synchronization of Phonon Lasers. Phys. Rev. Lett. 2020, 124, 053604. [Google Scholar] [CrossRef]
- Grutter, K.E.; Davanco, M.; Srinivasan, K. Slot-mode optomechanical crystals: A versatile platform for multimode optomechanics. Optica 2015, 2, 994–1001. [Google Scholar] [CrossRef] [PubMed]
- Colombano, M.F.; Arregui, G.; Capuj, N.E.; Pitanti, A.; Maire, J.; Griol, A.; Garrido, B.; Martínez, A.; Sotomayor-Torres, C.M.; Navarro-Urrios, D. Synchronization of Optomechanical Nanobeams by Mechanical Interaction. Phys. Rev. Lett. 2019, 123, 017402. [Google Scholar] [CrossRef]
- Mercade, L.; Pelka, K.; Burgwal, R.; Xuereb, A.; Martinez, A.; Verhagen, E. Floquet Phonon Lasing in Multimode Optomechanical Systems. Phys. Rev. Lett. 2021, 127, 073601. [Google Scholar] [CrossRef]
- Kemiktarak, U.; Durand, M.; Metcalfe, M.; Lawall, J. Mode Competition and Anomalous Cooling in a Multimode Phonon Laser. Phys. Rev. Lett. 2014, 113, 030802. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, T.; Tian, F.; Du, H.; Zou, Y.; Chau, F.S.; Zhou, G. Mode competition and hopping in optomechanical nano-oscillators. Appl. Phys. Lett. 2018, 112, 15350215. [Google Scholar] [CrossRef]
- Dong, C.; Zhang, J.; Fiore, V.; Wang, H. Optomechanically induced transparency and self-induced oscillations with Bogoliubov mechanical modes. OPTICA 2014, 1, 425–428. [Google Scholar] [CrossRef]
- Lamb, W.E. Theory of an Optical Maser. Phys. Rev. 1964, 134, 1429. [Google Scholar] [CrossRef]
- Kasumie, S.; Lei, F.; Yang, L.; Ward, J.; Chormaic, S.N. Raman Laser Switching Induced by Cascaded Light Scattering. Laser Photonics Rev. 2019, 13, 1900138. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V. Switchable Cascade Raman Lasing in a Tellurite Glass Microresonator. ACS Photonics 2023, 10, 123–128. [Google Scholar] [CrossRef]
- Hyun Kim, K.; Bahl, G.; Lee, W.; Liu, J.; Tomes, M.; Fan, X.; Carmon, T. Cavity optomechanics on a microfluidic resonator with water and viscous liquids. Light Sci. Appl. 2013, 2, e110. [Google Scholar] [CrossRef]
- Zhu, K.; Han, K.; Carmon, T.; Fan, X.; Bahl, G. Opto-acoustic sensing of fluids and bioparticles with optomechanofluidic resonators. Eur. Phys. J. Spec. Top. 2014, 223, 1937–1947. [Google Scholar] [CrossRef]
- Schliesser, A.; Del, P.; Nooshi, N.; Vahala, K.; Kippenberg, T.J. Radiation Pressure Cooling of a Micromechanical Oscillator Using Dynamical Backaction. Phys. Rev. Lett. 2006, 97, 243905. [Google Scholar] [CrossRef]
- Rokhsari, H.; Kippenberg, T.; Carmon, T.; Vahala, K.J. Theoretical and experimental study of radiation pressure-induced mechanical oscillations (parametric instability) in optical microcavities. IEEE J. Sel. Top. Quant. 2006, 12, 96–107. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; Liu, L.; Xu, L. Kerr parametric oscillations and frequency comb generation from dispersion compensated silica micro-bubble resonators. Opt. Express 2013, 21, 16908–16913. [Google Scholar] [CrossRef]
- Fork, R.L.; Tomlinson, W.J. Properties of Gaseous Optical Masers in Weak Axial Magnetic Fields. Phys. Rev. 1967, 164, 466–483. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Xu, L.; Liu, L. Intensity Modulation of Two Weakly Coupled Stimulated Oscillating Mechanical Modes in an Optomechanical Microbubble Resonator. Photonics 2023, 10, 365. https://doi.org/10.3390/photonics10040365
Yu X, Xu L, Liu L. Intensity Modulation of Two Weakly Coupled Stimulated Oscillating Mechanical Modes in an Optomechanical Microbubble Resonator. Photonics. 2023; 10(4):365. https://doi.org/10.3390/photonics10040365
Chicago/Turabian StyleYu, Xiayuqi, Lei Xu, and Liying Liu. 2023. "Intensity Modulation of Two Weakly Coupled Stimulated Oscillating Mechanical Modes in an Optomechanical Microbubble Resonator" Photonics 10, no. 4: 365. https://doi.org/10.3390/photonics10040365
APA StyleYu, X., Xu, L., & Liu, L. (2023). Intensity Modulation of Two Weakly Coupled Stimulated Oscillating Mechanical Modes in an Optomechanical Microbubble Resonator. Photonics, 10(4), 365. https://doi.org/10.3390/photonics10040365





