Lines of Quasi-BICs and Butterworth Line Shape in Stacked Resonant Gratings: Analytical Description

Abstract

We propose analytical approximations of the reflection and transmission spectra of a stacked dielectric diffraction grating consisting of two identical resonant guided-mode gratings with a Lorentzian line shape. These approximations, derived using the scattering matrix formalism, are functions of both angular frequency $\omega$ and the tangential wave vector component $k_x$ of the incident wave. We analytically demonstrate and, using full-wave simulations with rigorous coupled-wave analysis technique, numerically confirm that by a proper choice of the thickness of the dielectric layer separating the gratings, one can tailor the resonant optical properties of the stacked structure. In particular, it is possible to obtain lines of quasi-bound states in the continuum in the $\omega –k_x$ parameter space with the quality factor decaying proportionally to $k_x^{-4}$ or $k_x^{-6}$. In addition, the stacked structure can be used as a spectral or spatial Butterworth filter operating in reflection. The presented results may find application in the design of optical filters and sensors based on stacked resonant gratings.

1. Introduction

Despite a long history, investigation of resonant effects in subwavelength resonant gratings remains a subject of intensive research [1]. Usually, resonant effects in diffraction gratings are manifested as sharp peaks and dips in the reflection and transmission spectra described by the Fano line shape. Resonant structures possessing a resonant peak on a near-zero background are described by a special case of the Fano line shape, namely, the Lorentzian line shape. Even more interesting for filtering application are the structures possessing a flat-top line shape [2,3,4,5], which can be obtained by stacking resonant structures. The optical properties of such stacked (cascaded) structures are governed by the coupling of the eigenmodes of each grating [2,5,6,7,8,9,10,11]. In the theory of analog electronic filters, such flat-top resonances can be implemented using Butterworth filters [12].

A fundamental parameter of a Fano (Lorentzian) resonance is the quality factor describing the decay rate of the corresponding eigenmode. In recent years, much attention was paid to the investigation of non-decaying eigenmodes of structures with open scattering channels. Such modes are referred to as bound states in the continuum (BICs) and are of great interest from both fundamental and practical points of view, since they enable obtaining resonances with extremely high quality factors, which is important for filtering, sensing, lasing, and nonlinear optics applications [13]. BICs can be obtained in resonant diffraction gratings and have been extensively studied [13,14]. Usually, the tuning of two independent physical parameters is required to obtain a BIC, e.g., the frequency and angle of incidence of light impinging on the structure.

In the present work, we investigate stacked structures constituted by two identical resonant gratings exhibiting resonances with a Lorentzian line shape separated by a homogeneous dielectric layer (Figure 1). We derive a theoretical model analytically describing the optical properties of such structures in the $\omega –k_x$ parameter space, where $\omega$ is the angular frequency and $k_x$ is the tangential wave vector component of the incident wave. The obtained theoretical $\omega –k_x$ model is based on the analytical approximations previously derived by the present authors for single resonant gratings [15,16,17] and generalizes the results presented in [2,5,6], where only the $\omega$ dependence for stacked structures was considered. By analyzing the developed model, we establish that a properly designed stacked structure may support lines of quasi-BICs in the $\omega –k_x$ space, i.e., may possess a very-high-Q resonance at each angle of incidence. Such structures are important for nonlinear applications, in which enhancing the light–matter interactions at several frequencies is important [18]. We also demonstrate that the proposed model describes the formation of second-order temporal Butterworth filters and spatial filters with the frequency response of a fourth-order Butterworth filter. We believe that the obtained results are promising for the design of optical filters and sensors.

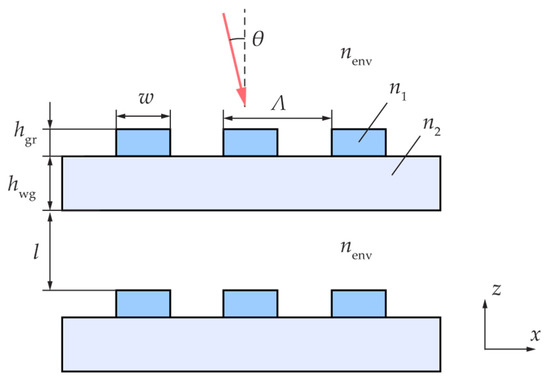
Figure 1. Geometry of a stacked structure containing two identical resonant gratings.

The paper is organized as follows. In Section 2, following the Introduction, we revisit the $\omega –k_x$ approximations for the reflection and transmission coefficients of a single resonant grating. In Section 3, we present the model for the considered stacked grating and derive the corresponding $\omega –k_x$ approximations. In the following two sections, we consider two important particular cases describing the formation of the Butterworth line shapes (Section 4) and lines of quasi-BICs in the $\omega –k_x$ parameter space (Section 5). Section 6 concludes the paper.

2. ω—k_x Lorentzian Line Shape in a Single Resonant Grating

2.1. Scattering Matrix

Let us start by considering a single lossless grating with period $\mathsf{\Lambda }$ along the x axis (Figure 2a). We assume that the grating is subwavelength, so that it supports only the zeroth propagating diffraction orders (reflected and transmitted). Let a plane wave with a certain linear polarization (transverse electric or transverse magnetic), angular frequency $\omega$, and in-plane wave vector component $k_x=(\omega /c)n_{\mathrm{env}}\sin \theta$ impinge on the structure at the angle $\theta$. Here, $n_{\mathrm{env}}$ is the refractive index of the surrounding medium. It is convenient to describe the optical properties of the structure using the scattering matrix formalism. In this formalism, it is assumed that two waves having the same $k_x$ value are incident on the structure from the superstrate and substrate regions. By denoting the complex amplitudes of these waves by $I_u$ and $I_d$, respectively, we introduce the scattering matrix $S\left(k_x,\omega \right)$ as

$$\left[\begin{array}{c}R\left(k_x,\omega \right)\\ T\left(k_x,\omega \right)\end{array}\right]=S\left(k_x,\omega \right)\left[\begin{array}{c}{I}_{\mathrm{u}}\\ I_{\mathrm{d}}\end{array}\right],$$

(1)

where $R\left(k_x,\omega \right)$ and $T\left(k_x,\omega \right)$ are the complex amplitudes of the scattered waves (see Figure 2a). The elements of the scattering matrix are the following:

$$S\left(k_x,\omega \right)=\left[\begin{array}{cc}{r}_{\mathrm{u}}\left(k_x,\omega \right)& t\left(k_x,\omega \right)\\ t\left(k_x,\omega \right)& r_{\mathrm{d}}\left(k_x,\omega \right)\end{array}\right],$$

(2)

where $r_{\mathrm{u}}$ and $r_{\mathrm{d}}$ are the complex reflection coefficients for the waves’ incident from the substrate and superstrate, respectively, and $t$ is the transmission coefficient. Note that the scattering matrix of Equation (2) is written for a structure possessing a vertical symmetry plane. In this case, due to reciprocity, the transmission coefficients are equal for the waves’ incident from above and from below [19]. We will assume that the complex amplitudes of the incident and scattered waves $I_{\mathrm{u}}$, $I_{\mathrm{d}}$, $R$, and $T$ are defined in such a way that their squared absolute values represent the corresponding intensities (energy density flux through the plane $z=\mathrm{const}$). In this case, the scattering matrix of Equation (2) is unitary ($S\cdot S^{†}=I$).

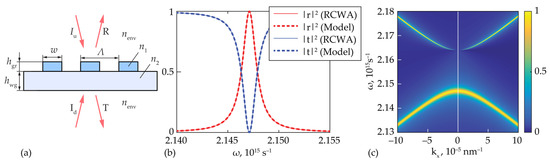
Figure 2. (a) Geometry of the considered guided-mode resonant grating: period $\mathsf{\Lambda }=700 \mathrm{nm}$, grating height $h_{\mathrm{gr}}=70 \mathrm{nm}$, waveguide layer thickness $h_{\mathrm{wg}}=290 \mathrm{nm}$, grating ridge width $w=40 \mathrm{nm}$, refractive indices $n_1=1.99$ (${\mathrm{Si}}_3{\mathrm{N}}_4$), $n_2=1.45$ (${\mathrm{SiO}}_2$), and $n_{\mathrm{env}}=1$. (b) Reflectance ${\left|r\left(\omega \right)\right|}^2={\left|r_{\mathrm{u},\mathrm{d}}\left(\omega \right)\right|}^2$ and transmittance ${\left|t\left(\omega \right)\right|}^2$ of the grating for the case of a TE-polarized normally incident wave. Dashed lines show the approximations calculated using Equation (8); solid lines show the rigorously calculated spectra. (c) Reflection coefficient $\left|r\left(k_x,\omega \right)\right|$ of the grating calculated using RCWA (left half, $k_x<0$) and using the resonant approximation (8) (right half, $k_x>0$). Approximation parameters: ${\omega }_{\mathrm{p}1}=\left(2147.11-0.80\mathrm{i}\right)\cdot {10}^{12} {\mathrm{s}}^{-1}$, ${\omega }_{\mathrm{p}2}=2.1640\hspace{0.17em}\cdot {10}^{15}\hspace{0.17em}{\mathrm{s}}^{-1}$, $v_{\mathrm{g}}=0.695\hspace{0.17em}\mathrm{c}$, $\phi =-2.72$, $\xi =-0.32$.

2.2. $\omega -k_x$ Lorentzian Line Shape in a Symmetric Structure

Let us now consider a grating possessing not only a vertical, but also a horizontal symmetry plane. In this case, $r_{\mathrm{u}}\left(k_x,\omega \right)=r_{\mathrm{d}}\left(k_x,\omega \right)=r\left(k_x,\omega \right)$ and the scattering matrix of Equation (2) takes the form

$$S_{\mathrm{sym}}\left(k_x,\omega \right)=\left[\begin{array}{cc}r\left(k_x,\omega \right)& t\left(k_x,\omega \right)\\ t\left(k_x,\omega \right)& r\left(k_x,\omega \right)\end{array}\right].$$

(3)

First, let us discuss the frequency dependence of the elements of the scattering matrix. For resonant gratings, each element of $S_{\mathrm{sym}}\left(\omega \right)$ is a fraction with the denominator $\omega -{\omega }_{\mathrm{p}}$, where ${\omega }_{\mathrm{p}}$ is the complex frequency of the eigenmode of the structure:

$$r\left(\omega \right)=r_0\frac{\omega -{\omega }_{\mathrm{zr}}}{\omega -{\omega }_{\mathrm{p}}},\hspace{1em}t\left(\omega \right)=t_0\frac{\omega -{\omega }_{\mathrm{zt}}}{\omega -{\omega }_{\mathrm{p}}}.$$

(4)

Applying the unitarity condition enables expressing the reflection and transmission zeros ${\omega }_{\mathrm{zr}}$ и ${\omega }_{\mathrm{zt}}$ through the eigenfrequency ${\omega }_p$ and the non-resonant reflection and transmission coefficients $r_0$ and $t_0$ [15]:

$${\omega }_{\mathrm{zr}}=\mathrm{Re}{\omega }_{\mathrm{p}}\pm \mathrm{i}\frac{t_0}{r_0}\mathrm{Im}{\omega }_{\mathrm{p}},\hspace{1em}{\omega }_{\mathrm{zt}}=\mathrm{Re}{\omega }_{\mathrm{p}}\pm \mathrm{i}\frac{r_0}{t_0}\mathrm{Im}{\omega }_{\mathrm{p}},$$

(5)

where the upper signs should be used to describe a z-symmetric (even) eigenmode and the lower signs correspond to a mode that is antisymmetric (odd) with respect to the horizontal symmetry plane.

For filtering applications, resonant structures exhibiting sharp reflectance peaks on a low background are widely used [1,20,21]. Low background reflection appears when $r_0$ tends to zero. In this case, the non-resonant (background) transmission coefficient $t_0$ becomes a unit-magnitude number ($t_0={\mathrm{e}}^{\mathrm{i}\varphi }$) and Equation (4) takes the following well-known form describing the Lorentzian line shape:

$$r\left(\omega \right)=\pm {\mathrm{e}}^{\mathrm{i}\phi }\frac{\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}}}{\omega -{\omega }_{\mathrm{p}}},\hspace{1em}t\left(\omega \right)={\mathrm{e}}^{\mathrm{i}\phi }\frac{\omega -\mathrm{Re}{\omega }_{\mathrm{p}}}{\omega -{\omega }_{\mathrm{p}}}={\mathrm{e}}^{\mathrm{i}\phi }+{\mathrm{e}}^{\mathrm{i}\phi }\frac{\mathrm{i}\hspace{0.17em}\mathrm{Im}{\omega }_{\mathrm{p}}}{\omega -{\omega }_{\mathrm{p}}},$$

(6)

where $\phi$ is the phase of the non-resonant transmission coefficient. Here, as in Equation (5), the sign of the reflection coefficient defines the symmetry of the considered eigenmode.

It is important to note that the form of the coefficients $r\left(\omega \right)$ and $t\left(\omega \right)$ provided by Equation (6) satisfies the energy conservation law ${\left|r\left(\omega \right)\right|}^2+{\left|t\left(\omega \right)\right|}^2=1$. According to Equation (6), the reflectance ${\left|r\left(\omega \right)\right|}^2$ reaches unity at $\omega =\mathrm{Re}{\omega }_p$. The width of the reflection peak is determined by the imaginary part of the complex pole ${\omega }_p$. Indeed, from Equation (6), it is easy to obtain that the full width at half maximum of the reflectance peak (and of the resonant dip of the transmittance ${\left|t\left(\omega \right)\right|}^2$) amounts to $\Delta =-2\mathrm{Im}{\omega }_{\mathrm{p}}$ (here, we use the time convention of ${\mathrm{e}}^{-\mathrm{i}\hspace{0.17em}\omega \hspace{0.17em}t}$, so that the imaginary part of the pole is negative).

In order to analyze the resonant properties of stacked gratings presented in the following sections, we will require to generalize the Lorentzian line shape defined by Equation (6) to the case, in which the reflection and transmission coefficients are considered as functions of two variables: angular frequency $\omega$ and in-plane wave vector component $k_x$. To obtain such a generalization, we will use the $\omega -k_x$ Fano line shape for resonant gratings [16], which follows from the spatiotemporal coupled-mode theory. For the structures possessing both horizontal and vertical symmetry planes, the following approximate relations for the transmission and reflection coefficients in the vicinity of normal incidence ($k_x=0$) take place:

$$r\left(k_x,\omega \right)=r_0\frac{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{zr}}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)}{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)},\hspace{1em}t\left(k_x,\omega \right)=t_0\frac{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{zt}}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)}{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)},$$

(7)

where $v_{\mathrm{g}}\in ℝ$ is the group velocity [16], and ${\omega }_{p1}\in ℂ$ and ${\omega }_{p2}\in ℝ$ are the frequencies of the eigenmodes of the structure (the poles of the reflection and transmission coefficients at $k_x=0$) corresponding to x-symmetric and x-antisymmetric modes, respectively. Note that the pole ${\omega }_{p2}$ is real, since the corresponding antisymmetric mode is a symmetry-protected bound state in the continuum (BIC), which cannot be excited by the normally incident radiation [17]. Let us also note that due to the presence of a vertical symmetry plane (the yz plane), resonant approximations of Equation (7) depend on $k_x^2$, i.e., are even functions with respect to $k_x$. Since at ${\omega }_{\mathrm{p}}={\omega }_{\mathrm{p}1}$, Equation (7) is a generalization of Equation (4), the reflection and transmission zeros ${\omega }_{\mathrm{zr}}$ and ${\omega }_{\mathrm{zt}}$ in Equation (7) are defined by Equation (5).

Let us now substitute Equation (5) with ${\omega }_p={\omega }_{p1}$ to Equation (7) and consider the limiting case $r_0\to 0$. This provides us with the following approximations for the reflection and transmission coefficients:

$$r\left(k_x,\omega \right)=\pm {\mathrm{e}}^{\mathrm{i}\phi }\frac{\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(\omega -{\omega }_{\mathrm{p}2}\right)}{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)},\hspace{1em}t\left(k_x,\omega \right)={\mathrm{e}}^{\mathrm{i}\phi }\left(1-\frac{\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(\omega -{\omega }_{\mathrm{p}2}\right)}{v_{\mathrm{g}}^2{k}_x^2-\left(\omega -{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)}\right).$$

(8)

Note that at $k_x=0$, this equation becomes Equation (6) describing a resonant grating with a Lorentzian line shape. Therefore, Equation (8) generalizes the Lorentzian line shape of Equation (6) to the case of non-zero $k_x$ and, in what follows, will be referred to as $\omega -k_x$ Lorentzian line shape. It is also worth noting that the scattering matrix (3) with $r$ and $t$ defined by Equation (8) satisfies the unitarity condition. The expressions for the reflection and transmission coefficients of Equation (8) depend on only four independent parameters: the phase $\phi$ defining the non-resonant transmission coefficient, the frequencies of the BIC ${\omega }_{\mathrm{p}2}$ and of the “bright” mode ${\omega }_{\mathrm{p}1}$ defining the resonant properties of the grating at normal incidence, and, finally, the group velocity $v_{\mathrm{g}}$ defining the dispersion law of the eigenmodes. According to Figure 2c, the dispersion law used in approximations (7) and (8) has a hyperbolic form with the slope of its asymptotes defined by $v_{\mathrm{g}}$ [16]. Hence, $v_{\mathrm{g}}$ is indeed the group velocity of the eigenmodes at large $k_x$ values.

2.3. $\omega -k_x$ Lorentzian Line Shape in a Structure without a Horizontal Symmetry Plane

The resonant approximations of Equation (8) were obtained for gratings possessing both horizontal and vertical symmetry planes. For gratings with only a vertical symmetry plane, the “upper” and “lower” reflection coefficients are different but, due to the energy conservation law, have the same magnitude ($\left|r_{\mathrm{u}}\left(k_x,\omega \right)\right|=\left|r_{\mathrm{d}}\left(k_x,\omega \right)\right|$) yet, in the general case, different phases. Let us show that this phase difference depends neither on $\omega$ nor on $k_x$. First, let us note that resonant approximations for $r_{\mathrm{u}}$, $r_{\mathrm{d}}$, and $t$ have exactly the same denominator, which is the determinant of the scattering matrix inverse. The term $\left(\omega -{\omega }_{\mathrm{p}2}\right)$ appearing in the numerator of both $r_{\mathrm{u}}$ and $r_{\mathrm{d}}$ is real since ${\omega }_{\mathrm{p}2}$ is the frequency of the symmetry-protected BIC supported by the gratings. Therefore, the most general form of $r_{\mathrm{u}}$ and $r_{\mathrm{d}}$ is the following:

$$r_u\left(k_x,\omega \right)={\mathrm{e}}^{–\mathrm{i}\xi }r\left(k_x,\omega \right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{r}_d\left(k_x,\omega \right)={\mathrm{e}}^{\mathrm{i}\xi }r\left(k_x,\omega \right),$$

(9)

where $\xi$ is half the phase difference between the two reflection coefficients. Therefore, the scattering matrix (2) for a grating without a horizontal symmetry plane takes the following form:

$$S\left(k_x,\omega \right)=\left[\begin{array}{cc}{\mathrm{e}}^{–\mathrm{i}\xi }r\left(k_x,\omega \right)& t\left(k_x,\omega \right)\\ t\left(k_x,\omega \right)& {\mathrm{e}}^{\mathrm{i}\xi }r\left(k_x,\omega \right)\end{array}\right],$$

(10)

where $r$ and $t$ are defined by Equation (8).

2.4. Numerical Example

Let us demonstrate the accuracy of the approximations of Equation (8) by considering a guided-mode resonant filter shown in Figure 2a. The parameters of the structure are presented in the figure caption. Figure 2b shows the reflectance and transmittance spectra exhibiting a resonance with a Lorentzian line shape. These spectra were calculated using the rigorous coupled-wave analysis (RCWA) [22,23] for the case of normal incidence of a TE-polarized plane wave (solid lines). Dashed lines in Figure 2b show the approximations of the spectra calculated using Equations (8) and (9) at the parameters presented in the figure caption. From Figure 2b, it is evident that at normal incidence, the rigorous simulation results and the resonant approximations are in good agreement. High accuracy of the derived $\omega -k_x$ Lorentzian approximation of Equations (8) and (9) is illustrated by the dependence of the reflection coefficient $\left|r\left(k_x,\omega \right)\right|$ presented in Figure 2c. In the left half of Figure 2c, the reflection coefficient calculated using RCWA is presented, whereas the right half of the plot was calculated using the derived resonant approximation. Let us note that for calculating the eigenfrequencies ${\omega }_{\mathrm{p}1}$, ${\omega }_{\mathrm{p}2}$, and the group velocity $v_{\mathrm{g}}$, the rigorous numerical method presented in [24] was utilized, whereas the phase $\phi$ was determined by fitting the rigorously calculated reflection coefficient at a single frequency. We refer the reader to the appendix of ref. [25], where a more detailed description of the algorithm for rigorous estimation of the parameters of Equations (7) and (8) is presented.

Finally, the phase $\xi$ was found by calculating the difference between the phases of the reflection coefficients $r_{\mathrm{u}}$ and $r_{\mathrm{d}}$. Figure 2c demonstrates an excellent agreement between the rigorous simulation results and the resonant approximation of the reflection coefficient. Indeed, in the $\omega -k_x$ range shown in Figure 2c, the left and right parts of the figure are visually indistinguishable.

3. ω—k_x Resonant Approximation for Stacked Resonant Gratings

In this section, we will obtain $\omega -k_x$ resonant approximations for a structure consisting of two identical resonant gratings separated by a homogeneous dielectric layer with thickness $l$ (Figure 1). In the general case, the gratings can be coupled by several propagating and/or evanescent diffraction orders (see, e.g., [20,21]); however, in the present work, we will focus on the case when the gratings are coupled only by the zeroth propagating diffraction order. This happens when $\left|k_x\pm 2\pi /\mathsf{\Lambda }\right|>k_0{n}_{\mathrm{env}}$ and the thickness $l$ is large enough so that the near-field interaction between the gratings is negligibly small. In addition, we assume that the gratings possess only a vertical symmetry plane, exhibit a resonance with a Lorentzian line shape (Equation (8)), and hence have a scattering matrix defined by Equation (10).

The scattering matrix of the stacked structure can be expressed through the scattering matrix of a single grating as

$$S_2\left(k_x,\omega \right)=S\left(k_x,\omega \right)★L\left(k_x,\omega \right)★S\left(k_x,\omega \right),$$

(11)

where the symbol ★ denotes the Redheffer star product [23] and $L\left(k_x,\omega \right)$ is the scattering matrix of the homogeneous separating layer. Upon the propagation through this layer, the plane waves corresponding to the zeroth diffraction orders acquire a phase shift

$$\psi \left(k_x,\omega \right)=l\sqrt{{\left(n_{\mathrm{env}}\omega /\mathrm{c}\right)}^2-k_x^2}.$$

(12)

Hence, the scattering matrix of the layer has the form

$$L\left(k_x,\omega \right)=\left[\begin{array}{cc}0& \exp \left\{\mathrm{i}\psi \left(k_x,\omega \right)\right\}\\ \exp \left\{\mathrm{i}\psi \left(k_x,\omega \right)\right\}& 0\end{array}\right].$$

(13)

By substituting Equations (12) and (13) into Equation (11), we obtain the scattering matrix $S_2$ of the stacked structure with the reflection and transmission coefficients $r_{2\mathrm{u}}=r_2{\mathrm{e}}^{-\mathrm{i}\xi }$, $r_{2\mathrm{d}}=r_2{\mathrm{e}}^{\mathrm{i}\xi }$, and $t_2$, where

$$\begin{array}{c}{r}_2\left(k_x,\omega \right)=\pm {\mathrm{e}}^{\mathrm{i}\left(2\phi +\psi \right)}2\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(\omega -{\omega }_{\mathrm{p}2}\right)\frac{\cos \left(\phi +\psi \right)\cdot \left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)\right]+\sin \left(\phi +\psi \right)\cdot \mathrm{Im}{\omega }_{\mathrm{p}1}\left(\omega -{\omega }_{\mathrm{p}2}\right)}{\left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -{\omega }_{\mathrm{mode},1}\right)\right]\cdot \left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -{\omega }_{\mathrm{mode},2}\right)\right]},\\ t_2\left(k_x,\omega \right)={\mathrm{e}}^{\mathrm{i}\left(2\phi +\psi \right)}\frac{{\left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)\right]}^2}{\left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -{\omega }_{\mathrm{mode},1}\right)\right]\cdot \left[k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -{\omega }_{\mathrm{mode},2}\right)\right]}.\end{array}$$

(14)

Here,

$$\begin{array}{l}{\omega }_{\mathrm{mode},1}=\mathrm{Re}{\omega }_{\mathrm{p}1}+\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(1-{\mathrm{e}}^{\mathrm{i}\left(\phi +\psi \right)}\right),\\ {\omega }_{\mathrm{mode},2}=\mathrm{Re}{\omega }_{\mathrm{p}1}+\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(1+{\mathrm{e}}^{\mathrm{i}\left(\phi +\psi \right)}\right).\end{array}$$

(15)

The corresponding eigenmodes appear due to the “in-phase” and “out-of-phase” coupling of the eigenmodes with complex frequency ${\omega }_{\mathrm{p}1}$ of the upper and lower gratings. The analytical expressions (14) provide a useful tool for investigating and controlling the shapes of the reflectance and transmittance spectra. For example, by choosing the thickness of the dielectric layer l, we can obtain the $\psi$ values making either the sine or the cosine in the numerator of $r_2\left(k_x,\omega \right)$ in Equation (14) vanish (at certain values of $\omega$ and $k_x$). These two important cases will be investigated in the following two sections.

4. Butterworth Filters Based on Stacked Resonant Gratings

In this section, we will be interested in the optical properties of the structure in the vicinity of the frequency $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ and at small angles of incidence (near $k_x=0$). In this case, the phase shift $\psi$ can be considered constant:

$$\psi =l{n}_{\mathrm{env}}\mathrm{Re}{\omega }_{\mathrm{p}1}/\mathrm{c}.$$

(16)

Let us consider a particular case, in which the cosine in Equation (14) vanishes. This happens when

$$\phi +\psi =\pi /2+\pi m, m\in \mathbb{Z}.$$

(17)

According to Equation (16), the corresponding thickness of the dielectric layer equals $l=\left(\pi /2-\phi +\pi m\right)c/\left(n_{\mathrm{env}}\mathrm{Re}{\omega }_{\mathrm{p}1}\right)$, where $m$ is chosen so that $l>0$. In this case, the quantities ${\omega }_{\mathrm{mode},1}$ and ${\omega }_{\mathrm{mode},2}$ used in Equation (14) become the eigenfrequencies of the stacked structure at $k_x=0$ and take the form

$$\begin{array}{l}{\omega }_{\mathrm{mode},1}=\mathrm{Re}{\omega }_{\mathrm{p}1}+\left(\mathrm{i}+1\right)\mathrm{Im}{\omega }_{\mathrm{p}1},\\ {\omega }_{\mathrm{mode},2}=\mathrm{Re}{\omega }_{\mathrm{p}1}+\left(\mathrm{i}-1\right)\mathrm{Im}{\omega }_{\mathrm{p}1}.\end{array}$$

(18)

Note that these eigenfrequencies have the same imaginary part and lie on a circle in the complex plane with the center at the point $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ and the radius ${\Delta }_{\omega }=-\sqrt{2}\mathrm{Im}{\omega }_{\mathrm{p}1}$.

4.1. Second-Order Butterworth Filter for Temporal Signals

Let us consider the case of normal incidence of light, i.e., assume the tangential wave vector component to be fixed at $k_x=0$. In this case, using Equations (16)–(18), we can rewrite the reflection coefficient of Equation (14) as

$$r_2\left(k_x=0,\omega \right)=\mp \frac{2{\mathrm{e}}^{\mathrm{i}\phi }{\left(\mathrm{Im}{\omega }_{\mathrm{p}1}\right)}^2}{\left[\omega -\left(\mathrm{Re}{\omega }_{\mathrm{p}1}+\left(\mathrm{i}+1\right)\mathrm{Im}{\omega }_{\mathrm{p}1}\right)\right]\cdot \left[\omega -\left(\mathrm{Re}{\omega }_{\mathrm{p}1}+\left(\mathrm{i}-1\right)\mathrm{Im}{\omega }_{\mathrm{p}1}\right)\right]},$$

(19)

which becomes a function depending solely on the angular frequency. Thus, the investigated stacked structure can be considered as a narrowband wavelength filter or a filter, which transforms the envelope of the incident optical pulse (signal) [26]. It is important to note that the filter described by Equation (19) is a second-order Butterworth filter. Indeed, according to Equations (18) and (19), its two poles are evenly spaced on the lower half of a circle in the complex plane. Moreover, the reflectance ${\left|r_2\left(k_x=0,\omega \right)\right|}^2$ of the structure has the form

$${\left|r_2\left(k_x=0,\omega \right)\right|}^2=\frac{1}{1+{\left[(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1})/{\Delta }_{\omega }\right]}^4},$$

(20)

which is equal to the squared absolute value of the transfer function of the second-order Butterworth filter with the cutoff frequency ${\Delta }_{\omega }$ [27].

In comparison with a structure with a conventional Lorentzian line shape, the “Butterworth line shape” of Equation (20) provides a significantly more rectangular shape of the reflectance peak as shown in Figure 3a. Note that the dashed red line in Figure 3a was calculated using Equation (20) with the parameters presented in the caption to Figure 2. The distance between the structures was equal $l=6740 \mathrm{nm}$.

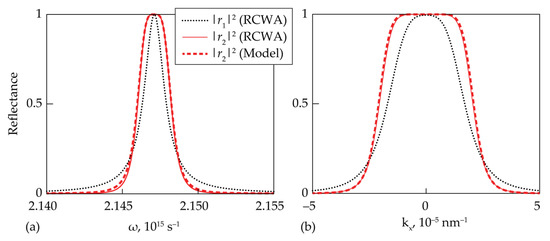
Figure 3. Rigorously calculated reflectance of the stacked structure satisfying the condition (17) vs. angular frequency at $k_x=0$ (a) and vs. tangential wavevector component at $\omega =\mathrm{Re}{\omega }_{p1}$ (b) (solid lines); squared absolute values of the “model” reflectance ${\left|r_2\left(k_x=0,\omega \right)\right|}^2$ of Equation (20) (a) and ${\left|r_2\left(k_x,\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}\right)\right|}^2$ of Equation (22) (b) of the corresponding Butterworth filters (dashed red lines). Dotted lines show the reflectance of the single resonant grating calculated using RCWA.

4.2. Fourth-Order Quasi-Butterworth Filter for Spatial Signals

Let us now consider the filtering properties of the stacked structure at a fixed frequency $\omega =\mathrm{Re}{\omega }_{p1}$ and varying tangential wave vector component $k_x$. In this case, the reflection coefficient takes the form

$$r_2\left(k_x,\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}\right)=\mp \frac{2e^{\mathrm{i}\phi }{\left(\mathrm{Re}{\omega }_{\mathrm{p}1}-{\omega }_{\mathrm{p}2}\right)}^2{\left(\mathrm{Im}{\omega }_{\mathrm{p}1}\right)}^2}{\left[k_x^2{v}_{\mathrm{g}}^2+\left(\mathrm{Re}{\omega }_{\mathrm{p}1}-{\omega }_{\mathrm{p}2}\right)\left(\mathrm{i}+1\right)\mathrm{Im}{\omega }_{\mathrm{p}1}\right]\cdot \left[k_x^2{v}_{\mathrm{g}}^2+\left(\mathrm{Re}{\omega }_{\mathrm{p}1}-{\omega }_{\mathrm{p}2}\right)\left(\mathrm{i}-1\right)\mathrm{Im}{\omega }_{\mathrm{p}1}\right]}.$$

(21)

In this case, the stacked structure can be regarded as a narrowband spatial filter or a filter, which transforms the profile of the incident optical beam [27]. The reflectance of the structure reads as

$${\left|r_2\left(k_x,\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}\right)\right|}^2=\frac{1}{1+{\left(k_x/{\Delta }_k\right)}^8},$$

(22)

where ${\Delta }_k=\sqrt[4]{2}\sqrt{-\mathrm{Im}{\omega }_{\mathrm{p}1}\left|\mathrm{Re}{\omega }_{\mathrm{p}1}-{\omega }_{\mathrm{p}2}\right|}{v}_{\mathrm{g}}^{-1}$. From Equation (22), it follows that this filter has the same frequency response as the fourth-order Butterworth filter; however, its phase response is different, since Equation (21) has the poles lying both in the upper and lower half-planes. Note that the order of the spatial filter is twice higher than the order of the frequency Butterworth filter described by Equation (20) due to the presence of a vertical symmetry plane of the stacked structure. The performance of the designed spatial filter is shown in Figure 3b.

5. BICs and Lines of Quasi-BICs in Stacked Resonant Gratings

Let us now consider a different particular case, in which the thickness of the intermediate layer is chosen so that the sine in Equation (14) vanishes. This happens when

$$\phi +\psi =\pi m, m\in \mathbb{Z}.$$

(23)

According to Equation (16), the corresponding thickness of the layer amounts to

$$l=\left(\pi m-\phi \right)\mathrm{c}/\left(n_{\mathrm{env}}\mathrm{Re}{\omega }_{\mathrm{p}1}\right).$$

(24)

In this case, the frequencies ${\omega }_{\mathrm{mode},1}$ and ${\omega }_{\mathrm{mode},2}$ in Equation (14) become

$${\omega }_{\mathrm{mode},1}=\mathrm{Re}{\omega }_{\mathrm{p}1}, {\omega }_{\mathrm{mode},2}=\mathrm{Re}{\omega }_{\mathrm{p}1}+2\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}$$

(25)

at even $m$ and vice versa at odd $m$.

Substituting Equation (25) into Equation (14), we derive the following expressions for the reflection and transmission coefficients:

$$\begin{array}{c}{r}_2\left(k_x,\omega \right)=\pm e^{\mathrm{i}\phi }\frac{2\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left(\omega -{\omega }_{\mathrm{p}2}\right)}{k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -\left(\mathrm{Re}{\omega }_{\mathrm{p}1}+2\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\right)\right)},\\ t_2\left(k_x,\omega \right)={\left(-1\right)}^m{e}^{\mathrm{i}\phi }\frac{k_x^2{v}_{\mathrm{g}}^2-\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}\right)\left(\omega -{\omega }_{\mathrm{p}2}\right)}{k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -\left(\mathrm{Re}{\omega }_{\mathrm{p}1}+2\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\right)\right)}.\end{array}$$

(26)

Comparing expressions (26) with the general case in Equation (14), one can see that the term $k_x^2{v}_{\mathrm{g}}^2-\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}\right)$ in the denominators of the reflection and transmission coefficients is canceled out with the corresponding terms in the numerators. This suggests that the considered stacked structure supports two lines of bound states in the continuum with the following dispersion law:

$$k_x^2{v}_{\mathrm{g}}^2=\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}\right).$$

(27)

Indeed, since all the parameters in Equation (27) are real numbers, at every real $k_x$ we can find two real BIC frequencies. At the same time, it is important to note that Equations (23)–(27) were obtained using Equation (16), which assumes the phase shift $\psi$ to be constant (i.e., independent of both $k_x$ and $\omega$). Strictly speaking, Equation (16) is exact only at $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ and $k_x=0$. Therefore, the dispersion law of Equation (27) describes a line of quasi-BICs (very-high-Q resonances) containing two “true” BICs at the frequencies $\omega ={\omega }_{\mathrm{p}2}$ and $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ at $k_x=0$. The BIC with the frequency ${\omega }_{\mathrm{p}2}$ is the symmetry-protected BIC supported by each resonant grating constituting the stacked structure, whereas the BIC with the frequency $\mathrm{Re}{\omega }_{\mathrm{p}1}$ is the Fabry–Perot BIC provided by the proper choice of the layer thickness l. This is illustrated in Figure 4 (the used thickness of the dielectric layer l is presented in the figure caption). The left half of this figure was calculated using RCWA, and the right half was obtained using the proposed model without assuming $\psi$ to be constant (i.e., using Equation (14)). The quasi-BIC lines are barely visible on this plot due to extremely high quality factors of these resonances. In order to demonstrate the presence of the quasi-BIC lines, we show several magnified fragments of the left part of the figure. The left and right parts of Figure 4 are in good agreement, which confirms high accuracy of the developed model.

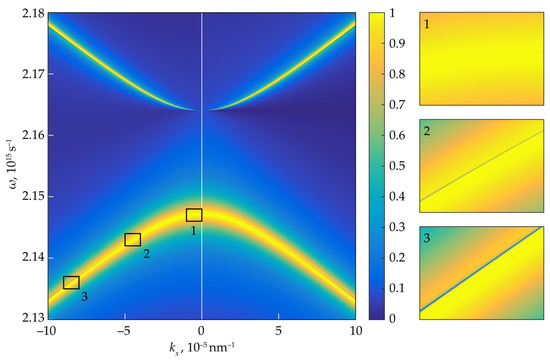
Figure 4. Magnitude of the reflection coefficient $\left|r_2\left(k_x,\omega \right)\right|$ of the stacked structure calculated using RCWA (left half, $k_x<0$) and using the resonant approximation (14) (right half, $k_x>0$) (TE polarization) with the intermediate layer thickness $l=6.522 \mathsf{\mu }\mathrm{m}$ The insets show the magnified fragments of the left part of the figure.

We numerically demonstrated that the resonances along the quasi-BIC lines have high quality factors. To explain why the quality factor remains high along the whole considered $k_x$ range, let us investigate the quality factor decay law as we move away from $k_x=0$. To do this, let us write the dispersion law taking into account the dependence of the phase shift $\psi$ on $k_x$ and $\omega$ as defined by Equation (12). Let us remind that in the considered case, the dielectric layer thickness $l$ is defined by Equation (24). At even $m$ values, the mode with the frequency ${\omega }_{\mathrm{mode},1}$ becomes a BIC at $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ and $k_x=0$ (see Equation (15)); at odd $m$, the mode with the frequency ${\omega }_{\mathrm{mode},2}$ becomes a BIC. By equating to zero the corresponding term in the denominator of Equation (14), we arrive at the following dispersion equation:

$$k_x^2{v}_{\mathrm{g}}^2=\left(\omega -{\omega }_{\mathrm{p}2}\right)\left(\omega -\mathrm{Re}{\omega }_{\mathrm{p}1}-\mathrm{i}\mathrm{Im}{\omega }_{\mathrm{p}1}\left[1-\exp \left\{\mathrm{i}\left(\phi -\pi m\right)+\mathrm{i}l\sqrt{{\left(n_{\mathrm{env}}\omega /\mathrm{c}\right)}^2-k_x^2}\right\}\right]\right),$$

(28)

which is a more accurate version of Equation (27). We are interested in solving Equation (28) with respect to the frequency $\omega$ considering $k_x$ as a parameter; however, this equation is too complex to be solved analytically. By applying the perturbation theory, we can find the solution for the eigenmode frequency $\omega \left(k_x\right)$ in the following Taylor series form: $\omega \left(k_x\right)=a_0+a_1{k}_x+a_2{k}_x^2+a_3{k}_x^3+a_4{k}_x^4+O\left(k_x^5\right)$. We will focus on the dispersion line containing the “true” BIC frequency $\mathrm{Re}{\omega }_{\mathrm{p}1}$; thus, we set $a_0=\mathrm{Re}{\omega }_{\mathrm{p}1}$. The odd-power terms $a_1$ and $a_3$ are zero due to symmetry, whereas the term $a_2$ is non-zero and equal to

$$a_2=\frac{1}{\mathrm{Re}{\omega }_{\mathrm{p}1}-\left(\pi m-\varphi \right)\mathrm{Im}{\omega }_{\mathrm{p}1}}\left(\frac{\mathrm{Re}{\omega }_{\mathrm{p}1}{v}_g^2}{\mathrm{Re}{\omega }_{\mathrm{p}1}-{\omega }_{\mathrm{p}2}}-\frac{{\mathrm{c}}^2\left(\pi m-\varphi \right)\mathrm{Im}{\omega }_{\mathrm{p}1}}{2n_{\mathrm{env}}^2\mathrm{Re}{\omega }_{\mathrm{p}1}}\right),$$

(29)

which is a real number. In contrast, the coefficient $a_4$ is a complex number, but its form is too cumbersome to present it here.

The fact that the $k_x^2$ term is real means that the quality factor $Q=\mathrm{Re}\omega /(-2\mathrm{Im}\omega )~\mathrm{Re}{a}_0/(-2\mathrm{Im}{a}_4{k}_x^4)$ has a quartic decay law:$Q~k_x^{-4}$. Let us note that “conventional” BICs have a quadratic decay law for the quality factor: $Q~k_x^{-2}$ [28]. In particular, this is the case for the symmetry-protected BIC appearing in a single grating and shown in Figure 2c. Therefore, the $k_x^{-4}$ decay rate of the quality factor explains why the line width remains very small along the whole dispersion curve.

To confirm the presented analysis of the quality-factor decay law, we rigorously calculated the quality factors of the resonances around the symmetry-protected BIC supported by the single grating (Figure 5a) and the Fabry–Perot BIC at $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$ in the stacked grating (Figure 5b). Figure 5 also presents the plots of the functions $k_x^{-2}$, $k_x^{-4}$, and $k_x^{-6}$ scaled to intersect the rigorously calculated quality factor plots at $k_x=\pm 2\cdot {10}^{-5} {\mathrm{nm}}^{-1}$. By comparing the plots, we can conclude that the quasi-BIC line does indeed exhibit the $Q~k_x^{-4}$ decay law.

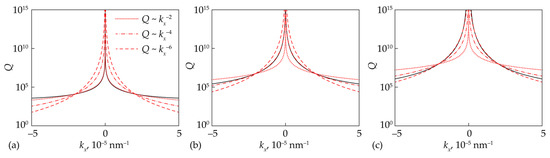
Figure 5. Rigorously calculated quality factors (solid black lines) of the eigenmodes as functions of $k_x$ (a) for the single grating near the BIC at $k_x=0$, $\omega ={\omega }_{\mathrm{p}2}$, (b) for the stacked structure with $l=6.522 \mathsf{\mu }\mathrm{m}$ near the BIC at $k_x=0$, $\omega =\mathrm{Re}{\omega }_{\mathrm{p}1}$, and (c) for the stacked structure with $l=6.469 \mathsf{\mu }\mathrm{m}$ near the BIC at $k_x=0$, $\omega ={\omega }_{\mathrm{p}2}$. Dotted, dash-dotted, and dashed red lines show the $k_x^{-2}$, $k_x^{-4}$, and $k_x^{-6}$ decay laws, respectively.

Let us note that by changing the thickness of the separating layer $l$, one can shift the position of the true BIC point on the quasi-BIC lines. In particular, if, instead of Equation (24), we assume $l=\left(\pi m-\phi \right)c/\left(n_{\mathrm{env}}{\omega }_{\mathrm{p}2}\right)$, the Fabry–Perot BIC can be placed exactly at the position of the symmetry-protected BIC ($\omega ={\omega }_{\mathrm{p}2}$, $k_x=0$). In this case, according to Figure 5c, the quality factor decays as $Q~k_x^{-6}$. This fact can also be confirmed by the proposed analytical model using the perturbation theory for Equation (28) with the corresponding value of $l$.

6. Conclusions

In this work, we proposed a simple $\omega –k_x$ analytical approximation of the reflection and transmission spectra of a resonant guided-mode grating supporting a resonance with a Lorentzian line shape. Using this approximation and the scattering matrix formalism, we derived approximate $\omega –k_x$ expressions for the reflection and transmission coefficients of a stacked structure consisting of two identical resonant gratings with Lorentzian line shape separated by a homogenous dielectric layer. We analytically demonstrated that by appropriately adjusting the thickness of this layer, it is possible to implement spectral and angular filters with a Butterworth line shape. Choosing a different thickness of the dielectric layer allows one to obtain lines of quasi-bound states in the continuum with a high-order decay law of the quality factor ($Q~k_x^{-4}$ or $Q~k_x^{-6}$). The full-wave numerical simulation results are in excellent agreement with the obtained analytical predictions. We believe that the presented results are promising for the design of stacked resonant structures for filtering, sensing, and optical information processing applications.