Abstract
As a promising platform for versatile electromagnetic (EM) manipulations, metasurfaces have drawn wide interest in recent years due to their unique EM properties and small footprints. However, although great efforts have been made to achieve multifunctionalities, the design of tunable metasurfaces with high compactness is still challenging. Here, a simple yet powerful design methodology for single-layered reconfigurable metasurfaces composed of nonvolatile phase-change material Ge2Sb2Se4Te1 (GSST) is proposed with average working amplitudes of 72.6% and 53% at different crystallization levels. The proposed metasurfaces could not only enable independent phase control at different crystallization levels but also introduced another polarization degree of freedom. As a proof of concept, we numerically demonstrate three kinds of metadevices in the infrared region achieving a multi-focus metalens with tunable foci, multistate vortex beam generator with adjustable topological charges and multi-channel meta-hologram with three independent information channels. It is believed that these multifunctional metasurfaces with both tunability and compactness are promising for various applications including information encryption, chiroptical spectroscopy, chiral imaging and wireless communication.
1. Introduction
As the planar version of metamaterials, metasurfaces composed of periodically arranged subwavelength meta atoms have attracted wide interest in recent years due to their enriched degree of freedoms to manipulate and control electromagnetic (EM) waves in terms of amplitude, phase and polarization [1,2,3,4]. By introducing strong localized interactions between incident EM waves and meta atoms, metasurfaces with planar geometries and small footprints can achieve similar or even better performances than traditional bulky and heavy optical devices, and exhibits great advantages in modern optics and photonics for integration and miniaturization [5,6,7]. To date, many exotic phenomena and applications based on metasurfaces have been realized such as beam deflection [8,9], perfect EM absorption [10,11], full-color nanopainting [12,13,14], gain enhancement [15,16], spatial filter [17], sub-diffraction imaging [18,19,20] and meta-holography [21,22,23]. Moreover, recent research has also demonstrated that properly designed metasurfaces can even achieve counterintuitive multi-functionalities by merging different manipulation mechanisms such as carpet cloaking [24,25], direction multiplexing [26,27,28], intelligent antennas [29] and spin decoupling [30,31].
Although great efforts have been made to improve the performances and enrich the functionalities of metasurfaces, a great challenge in this field is that most of the current designs lack the flexibility and their EM performances are fixed once fabricated, which further hindered their practical applications. As a result, reconfigurable metasurfaces with freely adjustable EM properties have been proposed. By introducing external stimuli, such as heat, electrostatic, stress or magnetic forces, their corresponding performances can be actively manipulated [32,33,34]. Among them, reconfigurable metasurfaces based on phase-change materials (PCMs) have been treated as promising candidates for next-generation tunable devices since their optical performance can be easily changed by heating or laser ablation. So far, various PCM-based platforms, including GeSbTe alloys [35,36,37,38], Sb2S3 [39,40], vanadium dioxide (VO2) [41,42] and many others [43,44], have been proposed and various promising applications such as switchable optical modulation [45,46], tunable wavefront control [47,48], active chirality [49] and dynamic color [50] display have been demonstrated. However, although the above mentioned works have further improved the tunability of phase-change metasurfaces, how to integrate more functionalities without the sacrifice of compactness is still challenging.
In this work, we proposed a design methodology for single-layered metasurfaces achieving both polarization- and crystallinity-dependent wavefront manipulations in infrared region. By taking advantage of the tunability of PCM Ge2Sb2Se4Te1 (hereinafter referred to as GSST) and combining multiple phase manipulation mechanisms, three independent information channels can be obtained with low cross talk. To further illustrate this issue, Figure 1 depicts the schematic of the proposed methodology. As shown in Figure 1a, when GSST is in the amorphous state (A-state), two different meta-holograms can be observed in the far field under right-handed circularly polarized (RCP) and left-handed circularly polarized (LCP) incidences. When varying the crystallinity of GSST to the crystalline state (C-state), as shown in Figure 1b, another meta-hologram can be observed and previous images in the A-state are perfectly hidden. Compared with previously reported works [37,38,39,40], the proposed metasurfaces could not only enable independent phase control at different crystallization levels but also introduce another polarization degree of freedom, which may pave a new way to realize active and multifunctional EM devices.
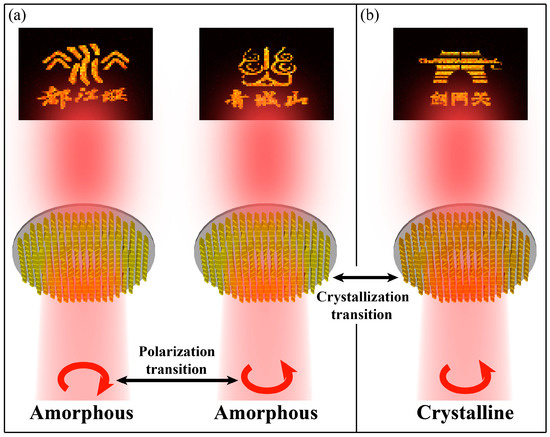
Figure 1.
Schematic diagram of the proposed metasurface at different crystallization levels. (a) When GSST is in A-state, two different meta-holograms can be observed under RCP and LCP incidence. (b) When GSST changes to C-state, another meta-hologram can be observed and previous images in A-state are perfectly hidden.
2. Design Principles and Simulation Results
The three-dimensional and top view of the proposed meta atom is shown in Figure 2a,b, respectively, which consists of a rectangular GSST nanofin on a barium fluoride (BaF2) substrate. The optimized period for the meta atom is p = 5 μm and the thickness for all meta atoms is fixed at H = 7 μm. The working wavelength for the proposed meta atoms is designed for λ = 10.6 μm, which is the operation wavelength of commercial CO2 lasers. By adjusting the length L and width W, six-levelled phase shift meta atoms are optimized to cover 0-2π both in the A- and C-states. As a result, a total number of 6 × 6 meta atoms are designed. The detailed geometric parameters and optical responses are shown in Figure S1 and Table S1. Figure 2c,d shows the simulated transmitted cross-polarized phase shift and amplitude, respectively, where i and j represent the number of the meta atom while the color of the pixel corresponds to the results in the A-state and the position of each pixel indicates the results in the C-state. It can be inferred from Figure 2c that for a given phase shift at A-state, six kinds of meta atoms can be chosen that can fully cover 0–2π at C-state. The average cross-polarized amplitude for the A- and C-states is 72.6% and 53%, respectively, which is sufficient for most wavefront manipulation applications. Finite element method in CST Microwave Studio is employed with unit cell boundaries in the xy directions and open boundary in the z direction. A fine tetrahedral mesh was applied with an adaptive mesh refinement to ensure the accuracy of the results. The optical constants data of the used materials are given in Figure S2 [51,52]. Here, the use of a BaF2 substrate is due to its low permittivity in the infrared region that could reduce the reflectance at the bottom surface. Meanwhile, the choice of GSST as the PCM in the proposed design can be attributed to two main reasons. Firstly, GSST possesses high optical transparency with ultralow loss in both the A- and C-states in the simulated working wavelength, which is essential for wavefront manipulations [53]. Secondly, GSST exhibits a large optical contrast (Δn > 1.5) between the A- and C-states, which makes the optimization of 6 × 6 meta atoms accessible [52].
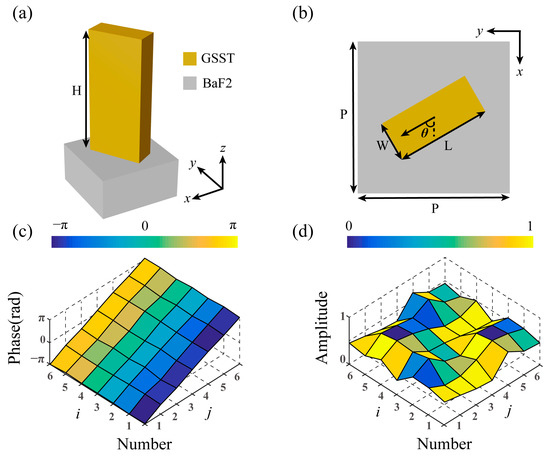
Figure 2.
Simulated results for the meta atom. (a) Three-dimensional and (b) top view of the meta atom. (c) The simulated transmitted cross-polarized phase shift at A- and C-state. (d) The simulated transmitted cross-polarized amplitude at A- and C-state. i and j represent the number of the meta atom while the color of the pixel corresponds to the results at A-state and the position of each pixel indicates the results at C-state.
To further illustrate the working mechanism of the proposed design, when considering the circularly polarized incidence of [1 − iσ]T normally illuminating the meta atoms, the resulting transmitted EM wave can be described as [28]
where φ is the polarization-independent propagation phase determined by the geometric parameters of the meta atom. −2σθ is the geometric phase (also known as the Pancharatnam–Berry phase) where σ = ±1 denotes the circular polarization direction of the transmitted wave and θ is the rotation angle for the meta atom as shown in Figure 2b. δ is the phase difference for two orthogonal linear polarizations along the major and minor axes and can be assumed as δ = π in our case since only the cross-polarized components are considered. Therefore, when GSST is in the A-state, the implemented phase for the cross-polarized components under RCP and LCP incidence can be described as φA ± 2θ, where φA is the propagation phase in A-state. In such case, if two independent phase distributions ψ1 and ψ2 are designed for opposite spin states, φA and θ can be expressed by [54]
where n1 and n2 are two arbitrary integers and are both chosen as zero in our case. Therefore, ψ1 and ψ2 can be calculated as
When GSST changes to the C-state, the geometric phase remains unchanged since it is only determined by the rotation angle for the meta atom, while the propagation phase φC can be designed accordingly. Therefore, the implemented phase for the cross-polarized components under RCP and LCP incidences can be described as φC ± 2θ. It should be mentioned that since θ is fixed according to Equation (3), desired phase distributions ψ3 can only be encoded to a certain circular polarization. For example, if ψ3 is encoded for the RCP incidence, it can be written as
In such case, the implemented phase ψ4 under the LCP incidence can be calculated as
Since the parameters on the right side of Equation (7) have been determined by Equations (2)–(4), ψ4 cannot be designed arbitrarily and often results to meaningless far field results. Therefore, by properly choosing the sizes and arrangements of the meta atoms, three independent information channels denoted by ψ1, ψ2 and ψ3 can be obtained. To further demonstrate the versatility of the proposed design methodology, three kinds of multifunctional metasurfaces are simulated and characterized in the following part.
The first functional device is multi-focus metalens whose focus can be adjusted by changing the crystallization levels of GSST and the incident circular polarization. To reduce the simulation complexity, the diameter of the metalens is set as 120 μm with 24 meta atoms in length. The implemented phase distributions for ψi (i = 1, 2, 3) can be described by
where (x, y) is the spatial location, (xi, yi) is the lateral displacement of the focal points and fi is the designed focal lengths. In our case, (x1, y1) = (0,0), (x2, y2) = (0, −30 μm), (x3, y3) = (30 μm, 0) and fi is fixed at 60 μm as shown in Figure S3. The time domain solver of CST Microwave Studio was employed for the simulations with open boundaries in all directions. Figure 3 depicts the corresponding simulated electric field distributions at different observation planes obtained by the built-in electric field monitors in CST Microwave Studio at λ = 10.6 μm. It can be inferred that the simulated results agreed well with the designs based on Equation (6). Moreover, the observed results in Figure 3e,i also indicate that the cross talk between different information channels can be ignored. The slight distortion of the focus can be attributed to the limited sample size and can be further improved with a larger diameter. Compared with previously reported works with fixed or symmetrical focal performance [55,56], the proposed metalens had the capability to adjust the focus, which may find many exciting applications for imaging and sensing.
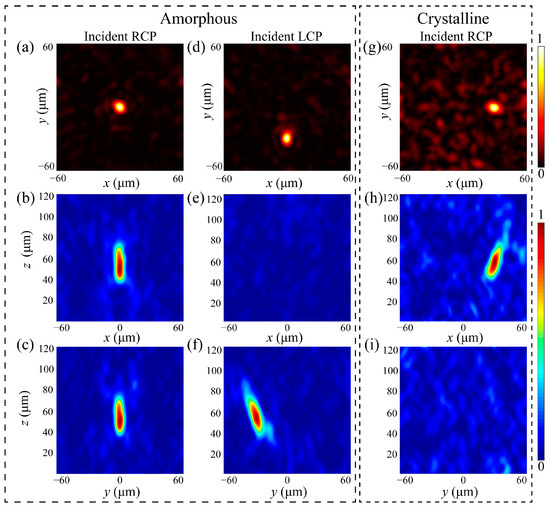
Figure 3.
Simulated performance of the designed multi-focus metalens at different observation planes. (a–c) Electric field distributions when GSST is in A-state under RCP incidence. (d–f) Electric field distributions when GSST is in A-state under LCP incidence. (g–i) Electric field distributions when GSST is in C-state under RCP incidence. The upper row shows the Exoy results at z = 60 μm. The middle row shows the Exoz results at y = 0. The bottom row shows the Eyoz results at x = 0.
The second functional device is a multistate vortex beam generator as shown in Figure S4 in which the topological charge of the generated vortex beam can be actively tuned. A vortex beam is a light beam carrying orbital angular momentum (OAM) that exhibits a spiral phase front of exp (ilϕ) [57], where ϕ = arctan (x/y) is the azimuthal angle and l is the topological charge. Since l can be any integer, vortex beams have been considered to be promising information carriers in optical and quantum communication systems. In the design process, the diameter of the designed vortex beam generator is the same as that for the above metalens. The phase distributions for focused vortex beam with different topological charges are encoded to ψi (i = 1, 2, 3) that can be described by
where f = 80 μm, li = −1, +2 and 0 for i = 1, 2 and 3. The simulated electric field distributions at z = f is shown in Figure 4a–c. As illustrated in Figure 4a,b, the donut-shaped patterns can be observed that demonstrate the generation of vortex beams. Moreover, the diameter of the donut-shaped pattern in Figure 4b was larger than those in Figure 4a,c indicating that the topological charge in this case was larger than the other cases, which is also a typical feature for vortex beams. The corresponding calculated results based on vectorial diffraction theory [58] are shown in Figure 4d–f. It can be inferred that the simulated results agreed quite well with their theoretical counterparts, which further demonstrates the validation of the proposed design method.
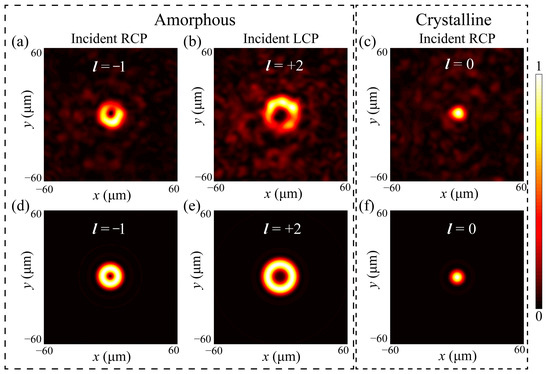
Figure 4.
Simulated and theoretical performance of the designed multistate vortex beam generator. (a,b) The simulated electric field distributions when GSST is in A-state under RCP (a) and LCP (b) incidences. (c) The simulated electric field distributions when GSST is in C-state under RCP incidence. (d–f) The calculated results correspond to those in (a–c).
Moreover, the simultaneous polarization- and crystallinity-dependent performance provided by the proposed metasurface can also find a wide variety of applications associated with information encryption. As a proof of concept, the third functional device is a multi-channel meta-hologram in which the observed images can be tuned under certain conditions. In the design process, the metasurface contained 1 × 106 meta atoms with dimensions of 5 mm × 5 mm. To calculate the phase distributions for the meta-hologram, the Gerchberg–Saxton (GS) algorithm was used. Since the image plane is designed in the Fraunhofer region, the ideal phase distribution can be calculated after several iterations of Fourier transforms. Then, the implemented phase distributions ψi (i = 1, 2, 3) can be obtained by discretizing the ideal phase distributions to six levels as shown in Figure 5d–f. Figure 5g–i shows the calculated far field intensity distributions under different polarized incidences and crystallization levels at λ = 10.6 μm, which was obtained by using the vectorial diffraction theory. The amplitude and phase at each location on the metasurface was retrieved from corresponding simulated results in Figure 2c,d. It can be inferred that when GSST is in the A-state, different information can be read out under opposite incident spin states. Then, when GSST changes to the C-state, the previous holographic images in the A-state can barely be observed and another new image can be observed, which confirms that the information coded in a certain crystallization level cannot be decoded in the other state.

Figure 5.
Multistate meta-hologram for information encryption. (a–c) Target images. (d–f) Calculated phase distributions based on GS algorithm. (g–h) Calculated far field results when GSST is in A-state under RCP (g) and LCP (h) incidences. (i) Calculated far field results when GSST is in C-state under RCP incidence.
3. Conclusions
It should be mentioned that although subsequent experiments were not carried out in this work, the fabrication of structured phase-change meta atoms with high aspect ratios and the corresponding optical measurements have been demonstrated by many previously reported works and is accessible by the state-of-the-art nanofabrication and measurement technologies [37,38]. To illustrate this issue, a feasible fabrication process and a measurement setup is schematically proposed in Figures S5 and S6, respectively. Moreover, although the reamorphization of GSST meta atoms with large thicknesses is still challenging and the fully reamorphization of the proposed devices may not be achievable at present, this problem may be solved in the near future since the theoretically reversible thickness of GSST films can approach several micrometers and the achieved reamorphization thickness has already increased from initial tens of nanometers to the current hundreds of nanometers. Moreover, by applying the proposed methodology at higher frequencies, the thickness of GSST can be further reduced to meet the requirement for reamorphization according to the scalability of Maxwell’s equations.
In summary, a generalized design methodology for multifunctional reconfigurable metasurfaces is proposed in this paper. By taking advantage of properly designed meta atoms and the large optical contrast of GSST, independent multi-channel wavefront manipulation can be achieved according to the incident circular polarization and GSST crystallization levels. To illustrate the priority of the presented principle, three kinds of functional metasurfaces were theoretically calculated and numerically simulated and all metasurfaces exhibited polarization- and crystallinity-dependent performance with low cross talk. The physical mechanism for the proposed devices can be attributed to the combined effect of geometric phase and propagation phase. Moreover, owing to the scalability of Maxwell’s equations, the design methodology can be further used for other frequencies, which may enable more fascinating applications in integrated optics and photonics.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics10030344/s1, Figure S1: Optimization graphs of the simulated unit cells with different geometries. Figure S2: Optical constants data of used materials. Figure S3: The schematic illustration for the multi-focus metalens. Figure S4: The schematic illustration for the multistate vortex beam generator. Figure S5: A feasible fabrication process for the designed sample. Figure S6: Schematic illustration of the measurement setup. Table S1: Geometric parameters and corresponding optical responses in A- and C- states.
Author Contributions
Conceptualization, Y.H. and J.H.; methodology, J.H. and Z.T.; software, J.H., Y.H. and L.L.; validation, J.H., Y.H. and Z.T.; formal analysis, investigation, resources, data curation, writing—original draft preparation, J.H., Y.C. and Y.H.; writing—review and editing, J.H., Y.C., X.L. and Q.D.; visualization, W.Z. and H.C.; supervision, project administration, funding acquisition, L.L. and Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (62105228), the Natural Science Foundation of Sichuan Province (2022NSFSC2000) and the Opening Foundation of State Key Laboratory of Optical Technologies on Nano-Fabrication and Micro-Engineering.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Luo, X. Metamaterials and Metasurfaces. Adv. Opt. Mater. 2019, 7, 1900885. [Google Scholar] [CrossRef]
- Yu, P.; Besteiro, L.V.; Huang, Y.; Wu, J.; Fu, L.; Tan, H.H.; Jagadish, C.; Wiederrecht, G.P.; Govorov, A.O.; Wang, Z. Broadband Metamaterial Absorbers. Adv. Opt. Mater. 2019, 7, 1800995. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent Advances in Planar Optics: From Plasmonic to Dielectric Metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Chen, M.K.; Wu, Y.; Feng, L.; Fan, Q.; Lu, M.; Xu, T.; Tsai, D.P. Principles, Functions, and Applications of Optical Meta-Lens. Adv. Opt. Mater. 2021, 9, 2001414. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Z.; Chen, S.; Tian, J. Emergent Functionality and Controllability in Few-Layer Metasurfaces. Adv. Mater. 2015, 27, 5410–5421. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 6054, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Wang, Y.; Deng, Z.-L.; Ye, X.; Dai, Z.; Cao, Y.; Guan, B.-O.; Xiao, S.; Li, X. All-Dielectric Kissing-Dimer Metagratings for Asymmetric High Diffraction. Adv. Opt. Mater. 2019, 7, 1901389. [Google Scholar] [CrossRef]
- Huang, Y.; Luo, J.; Pu, M.; Guo, Y.; Zhao, Z.; Ma, X.; Li, X.; Luo, X. Catenary Electromagnetics for Ultra-Broadband Lightweight Absorbers and Large-Scale Flat Antennas. Adv. Sci. 2019, 6, 1801691. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L.; Pu, M.; Li, X.; Ma, X.; Luo, X. A Refractory Metamaterial Absorber for Ultra-Broadband, Omnidirectional and Polarization-Independent Absorption in the UV-NIR Spectrum. Nanoscale 2018, 10, 8298–8303. [Google Scholar] [CrossRef]
- Song, M.; Feng, L.; Huo, P.; Liu, M.; Huang, C.; Yan, F.; Lu, Y.; Xu, T. Versatile Full-Colour Nanopainting Enabled by a Pixelated Plasmonic Metasurface. Nat. Nanotechnol. 2023, 18, 71–78. [Google Scholar] [CrossRef]
- Huo, P.; Song, M.; Zhu, W.; Zhang, C.; Chen, L.; Lezec, H.J.; Lu, Y.; Agrawal, A.; Xu, T. Photorealistic Full-Color Nanopainting Enabled by a Low-Loss Metasurface. Optica 2020, 7, 1171–1172. [Google Scholar] [CrossRef] [PubMed]
- Fu, R.; Chen, K.; Li, Z.; Yu, S.; Zheng, G. Metasurface-Based Nanoprinting: Principle, Design and Advances. Opto-Electron. Sci. 2022, 1, 220011. [Google Scholar] [CrossRef]
- Adibi, S.; Honarvar, M.A.; Lalbakhsh, A. Lalbakhsh Gain Enhancement of Wideband Circularly Polarized UWB Antenna Using FSS. Radio Sci. 2021, 56, e2020RS007098. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Hayat, T.; Esselle, K.P.; Mandal, K. All-Metal Wideband Metasurface for near-Field Transformation of Medium-to-High Gain Electromagnetic Sources. Sci. Rep. 2021, 11, 9421. [Google Scholar] [CrossRef]
- Paul, G.S.; Mandal, K.; Lalbakhsh, A. Single-Layer Ultra-Wide Stop-Band Frequency Selective Surface Using Interconnected Square Rings. AEU-Int. J. Electron. Commun. 2021, 132, 153630. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H.; et al. A Broadband Achromatic Metalens in the Visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Huo, P.; Zhang, C.; Zhu, W.; Liu, M.; Zhang, S.; Zhang, S.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett. 2020, 20, 2791–2798. [Google Scholar] [CrossRef]
- Zhang, Y.; Pu, M.; Jin, J.; Lu, X.; Guo, Y.; Cai, J.; Zhang, F.; Ha, Y.; He, Q.; Xu, M.; et al. Crosstalk-Free Achromatic Full Stokes Imaging Polarimetry Metasurface Enabled by Polarization-Dependent Phase Optimization. Opto-Electron. Adv. 2022, 5, 220058. [Google Scholar] [CrossRef]
- Zhang, X.; Pu, M.; Guo, Y.; Jin, J.; Li, X.; Ma, X.; Luo, J.; Wang, C.; Luo, X. Colorful Metahologram with Independently Controlled Images in Transmission and Reflection Spaces. Adv. Funct. Mater. 2019, 29, 1809145. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Z.; Huang, Y.; Ma, X.; Pu, M.; Guo, Y.; Li, X.; Luo, X. Asymmetric Transmission and Wavefront Manipulation toward Dual-Frequency Meta-Holograms. ACS Photonics 2019, 6, 1541–1546. [Google Scholar] [CrossRef]
- Wang, D.; Hwang, Y.; Dai, Y.; Si, G.; Wei, S.; Choi, D.-Y.; Gómez, D.E.; Mitchell, A.; Lin, J.; Yuan, X. Broadband High-Efficiency Chiral Splitters and Holograms from Dielectric Nanoarc Metasurfaces. Small 2019, 15, 1900483. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Jing, L.; Zheng, B.; Hao, R.; Yin, W.; Li, E.; Soukoulis, C.M.; Chen, H. Full-Polarization 3D Metasurface Cloak with Preserved Amplitude and Phase. Adv. Mater. 2016, 28, 6866–6871. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Pu, M.; Zhang, F.; Luo, J.; Li, X.; Ma, X.; Luo, X. Broadband Functional Metasurfaces: Achieving Nonlinear Phase Generation toward Achromatic Surface Cloaking and Lensing. Adv. Opt. Mater. 2019, 7, 1801480. [Google Scholar] [CrossRef]
- Chen, K.; Ding, G.; Hu, G.; Jin, Z.; Zhao, J.; Feng, Y.; Jiang, T.; Alù, A.; Qiu, C.-W. Directional Janus Metasurface. Adv. Mater. 2020, 32, 1906352. [Google Scholar] [CrossRef]
- Tang, Z.; Li, L.; Zhang, H.; Yang, J.; Hu, J.; Lu, X.; Hu, Y.; Qi, S.; Liu, K.; Tian, M.; et al. Multifunctional Janus Metasurfaces Achieving Arbitrary Wavefront Manipulation at Dual Frequency. Mater. Des. 2022, 223, 111264. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-Optical Controlled-NOT Logic Gate Achieving Directional Asymmetric Transmission Based on Metasurface Doublet. Opto-Electron. Adv. 2023, 6, 220073. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Simorangkir, R.B.V.B.; Bayat-Makou, N.; Kishk, A.A.; Esselle, K.P. Chapter 2—Advancements and Artificial Intelligence Approaches in Antennas for Environmental Sensing. In Artificial Intelligence and Data Science in Environmental Sensing; Asadnia, M., Razmjou, A., Beheshti, A., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 19–38. ISBN 978-0-323-90508-4. [Google Scholar]
- Naveed, M.A.; Kim, J.; Javed, I.; Ansari, M.A.; Seong, J.; Massoud, Y.; Badloe, T.; Kim, I.; Riaz, K.; Zubair, M.; et al. Novel Spin-Decoupling Strategy in Liquid Crystal-Integrated Metasurfaces for Interactive Metadisplays. Adv. Opt. Mater. 2022, 10, 2200196. [Google Scholar] [CrossRef]
- Naveed, M.A.; Ansari, M.A.; Kim, I.; Badloe, T.; Kim, J.; Oh, D.K.; Riaz, K.; Tauqeer, T.; Younis, U.; Saleem, M.; et al. Optical Spin-Symmetry Breaking for High-Efficiency Directional Helicity-Multiplexed Metaholograms. Microsyst. Nanoeng. 2021, 7, 5. [Google Scholar] [CrossRef]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and Reconfigurable Metasurfaces and Metadevices. Opto-Electron. Adv. 2018, 1, 180009. [Google Scholar] [CrossRef]
- Esfandiyari, M.; Lalbakhsh, A.; Jarchi, S.; Ghaffari-Miab, M.; Mahtaj, H.N.; Simorangkir, R.B.V.B. Tunable Terahertz Filter/Antenna-Sensor Using Graphene-Based Metamaterials. Mater. Des. 2022, 220, 110855. [Google Scholar] [CrossRef]
- Esfandiari, M.; Lalbakhsh, A.; Nasiri Shehni, P.; Jarchi, S.; Ghaffari-Miab, M.; Noori Mahtaj, H.; Reisenfeld, S.; Alibakhshikenari, M.; Koziel, S.; Szczepanski, S. Recent and Emerging Applications of Graphene-Based Metamaterials in Electromagnetics. Mater. Des. 2022, 221, 110920. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Xie, Z.; Zheng, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; Zhu, J.; Müller-Buschbaum, P.; et al. Multistate Nonvolatile Metamirrors with Tunable Optical Chirality. ACS Appl. Mater. Interfaces 2021, 13, 45890–45897. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Xie, Z.; Zheng, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; Zhu, J.; Li, L. Reconfigurable Phase-Change Metasurfaces from Efficient Wavefront Manipulation to Perfect Absorption. J. Mater. Sci. 2022, 57, 5426–5437. [Google Scholar] [CrossRef]
- Zhang, F.; Xie, X.; Pu, M.; Guo, Y.; Ma, X.; Li, X.; Luo, J.; He, Q.; Yu, H.; Luo, X. Multistate Switching of Photonic Angular Momentum Coupling in Phase-Change Metadevices. Adv. Mater. 2020, 32, 1908194. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.; Lee, S.-Y.; Mun, S.-E.; Lee, G.-Y.; Sung, J.; Yun, H.; Yang, J.-H.; Kim, H.-O.; Hwang, C.-Y.; Lee, B. Metasurface with Nanostructured Ge2Sb2Te5 as a Platform for Broadband-Operating Wavefront Switch. Adv. Opt. Mater. 2019, 7, 1900171. [Google Scholar] [CrossRef]
- Moitra, P.; Wang, Y.; Liang, X.; Lu, L.; Poh, A.; Mass, T.W.W.; Simpson, R.E.; Kuznetsov, A.I.; Paniagua-Dominguez, R. Programmable Wavefront Control in the Visible Spectrum Using Low-Loss Chalcogenide Phase-Change Metasurfaces. Adv. Mater. 2022, 2205367. [Google Scholar] [CrossRef]
- Liu, T.; Han, Z.; Duan, J.; Xiao, S. Phase-Change Metasurfaces for Dynamic Image Display and Information Encryption. Phys. Rev. Appl. 2022, 18, 044078. [Google Scholar] [CrossRef]
- Ding, F.; Zhong, S.; Bozhevolnyi, S.I. Vanadium Dioxide Integrated Metasurfaces with Switchable Functionalities at Terahertz Frequencies. Adv. Opt. Mater. 2018, 6, 1701204. [Google Scholar] [CrossRef]
- Li, X.; Tang, S.; Ding, F.; Zhong, S.; Yang, Y.; Jiang, T.; Zhou, J. Switchable Multifunctional Terahertz Metasurfaces Employing Vanadium Dioxide. Sci. Rep. 2019, 9, 5454. [Google Scholar] [CrossRef] [PubMed]
- Abdollahramezani, S.; Hemmatyar, O.; Taghinejad, M.; Taghinejad, H.; Krasnok, A.; Eftekhar, A.A.; Teichrib, C.; Deshmukh, S.; El-Sayed, M.; Pop, E.; et al. Electrically Driven Programmable Phase-Change Meta-Switch Reaching 80% Efficiency. arXiv 2021, arXiv:2104.10381. [Google Scholar]
- Zhang, Y.; Fowler, C.; Liang, J.; Azhar, B.; Shalaginov, M.Y.; Deckoff-Jones, S.; An, S.; Chou, J.B.; Roberts, C.M.; Liberman, V.; et al. Electrically Reconfigurable Non-Volatile Metasurface Using Low-Loss Optical Phase-Change Material. Nat. Nanotechnol. 2021, 16, 661–666. [Google Scholar] [CrossRef]
- Wang, Y.; Landreman, P.; Schoen, D.; Okabe, K.; Marshall, A.; Celano, U.; Wong, H.-S.P.; Park, J.; Brongersma, M.L. Electrical Tuning of Phase-Change Antennas and Metasurfaces. Nat. Nanotechnol. 2021, 16, 667–672. [Google Scholar] [CrossRef]
- Abdollahramezani, S.; Hemmatyar, O.; Taghinejad, M.; Taghinejad, H.; Kiarashinejad, Y.; Zandehshahvar, M.; Fan, T.; Deshmukh, S.; Eftekhar, A.A.; Cai, W.; et al. Dynamic Hybrid Metasurfaces. Nano Lett. 2021, 21, 1238–1245. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Pu, M.; Zhang, F.; Guo, Y.; He, Q.; Ma, X.; Huang, Y.; Li, X.; Yu, H.; Luo, X. Plasmonic Metasurfaces for Switchable Photonic Spin–Orbit Interactions Based on Phase Change Materials. Adv. Sci. 2018, 5, 1800835. [Google Scholar] [CrossRef] [PubMed]
- Shalaginov, M.Y.; An, S.; Zhang, Y.; Yang, F.; Su, P.; Liberman, V.; Chou, J.B.; Roberts, C.M.; Kang, M.; Rios, C.; et al. Reconfigurable All-Dielectric Metalens with Diffraction-Limited Performance. Nat. Commun. 2021, 12, 1225. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Plum, E.; Li, H.; Duan, S.; Li, S.; Xu, Q.; Zhang, X.; Zhang, C.; Zou, C.; Jin, B.; et al. Switchable Chiral Mirrors. Adv. Opt. Mater. 2020, 8, 2000247. [Google Scholar] [CrossRef]
- Carrillo, S.G.-C.; Trimby, L.; Au, Y.-Y.; Nagareddy, V.K.; Rodriguez-Hernandez, G.; Hosseini, P.; Ríos, C.; Bhaskaran, H.; Wright, C.D. A Nonvolatile Phase-Change Metamaterial Color Display. Adv. Opt. Mater. 2019, 7, 1801782. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3, ISBN 0-12-544423-0. [Google Scholar]
- Zhou, C.; Xie, Z.; Zhang, B.; Lei, T.; Li, Z.; Du, L.; Yuan, X. Reconfigurable Dielectric Metasurface for Active Wavefront Modulation Based on a Phase-Change Material Metamolecule Design. Opt. Express 2020, 28, 38241–38251. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, J.B.; Li, J.; Li, H.; Du, Q.; Yadav, A.; Zhou, S.; Shalaginov, M.Y.; Fang, Z.; Zhong, H.; et al. Broadband Transparent Optical Phase Change Materials for High-Performance Nonvolatile Photonics. Nat. Commun. 2019, 10, 4279. [Google Scholar] [CrossRef]
- Zhang, F.; Pu, M.; Luo, J.; Yu, H.; Luo, X. Symmetry Breaking of Photonic Spin-Orbit Interactions in Metasurfaces. Opto-Electron. Eng. 2017, 44, 319–325. [Google Scholar] [CrossRef]
- Qin, F.; Liu, B.; Zhu, L.; Lei, J.; Fang, W.; Hu, D.; Zhu, Y.; Ma, W.; Wang, B.; Shi, T.; et al. π-Phase Modulated Monolayer Supercritical Lens. Nat. Commun. 2021, 12, 32. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Shi, Z.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Zaidi, A.; Capasso, F. Achromatic Metalens over 60 Nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xiao, T.; Xie, Z.; Zheng, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; Müller-Buschbaum, P.; Li, L. Single-Layered Reflective Metasurface Achieving Simultaneous Spin-Selective Perfect Absorption and Efficient Wavefront Manipulation. Adv. Opt. Mater. 2021, 9, 2001663. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary Optics for Achromatic Generation of Perfect Optical Angular Momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).