Abstract
High-performance megapixel focal plane arrays with small pixels have been widely used in modern optical remote sensing, astronomical, and surveillance instruments. In the prediction models applied in the traditional instrument performance analysis, the image of a point source is assumed to fall on the center of a detector pixel. A geometrical image of a point source in the realistic optical system may actually fall on any position on the detector pixel because the sensor’s line of sight includes pointing errors and jitter. This traditional assumption may lead to an optimistic error, estimated at between 10% and 20%. We present the critical factors that impact the performance estimate in a realistic instrument design based on the prediction for the noise-equivalent power (NEP). They are the optical centroid efficiency (OCE) and the ensquared energy, or more precisely, the energy on the rectangular detector pixel (EOD). We performed the simulation studies for imaging with an optical system with and without a generalized rectangular central obscuration.
1. Discrete Pixels
The advances in IR sensor technology are arising to a large degree due to the improvements in focal plane array (FPA) technologies. These include an increase in FPA size, reduced detector pixel dimensions, low dark current, low readout noise, and high responsivity. A larger FPA covers a wider footprint in the object space, while a smaller pixel may lead to a reduction in the object-space footprint. For example, the Teledyne H2RG FPA, integrated into the James Webb Space Telescope (JWST), features a 2048 by 2048-pixel array with an 18 µm pixel pitch (distance between pixel centers) [1]. Raytheon produced a 2048 × 2048 detector array with a 20 µm-pixel pitch for the UK Visible and Infrared Survey Telescope for Astronomy (VISTA) [2]. The analysis presented here applies to the instruments operating from the UV to the microwaves. The sensor figures of merit were originally developed consistently using radiometric concepts for the IR part of the electromagnetic spectrum, so we rely and build our theory on those.
Modern instrument design procedures continue to rely on parameters such as enclosed energy and the noise-equivalent power (NEP) for their performance assessment and prediction. In Figure 1, we illustrate how the previously important quantity encircled energy increases as a function of the radius of the enclosing circle. We can also read the approximate amount of energy that would be incident, or enclosed, within a (circular) pixel equal to the radial distance r.
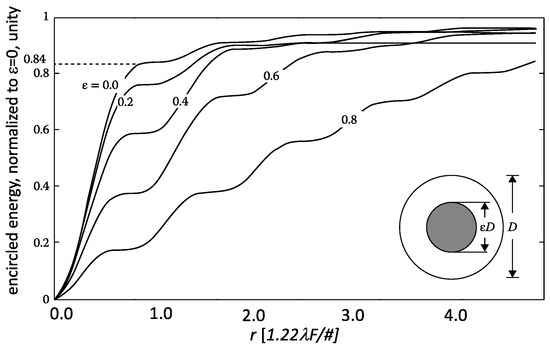
Figure 1.
The normalized integrated, encircled energy as a function of radius r of the enclosing circle for an ideal, diffraction-limited optical system with a circular aperture. The obscuration ratio ε is a parameter (ratio of radii), varying from 0 (no obscuration) to 0.8 in increments of 0.2. The degree of compactness of the central spot may be recognized from the average slope of these curves for radial values less than 1. About 84% of the energy is enclosed within the first dark ring of a diffraction-limited optical system without the central obscuration. All the curves also flatten to zero slope for radial distances that correspond to the zero-rings, due to the absence of radiation there.
In Section 2, we introduce the concept of the energy on detector (EOD) to consider a rectangular pixelated image plane. We also account for the fact that the EOD is diminished when the pixel axis and optical system axis do not coincide, the real situation in most instruments. This leads us to introduce the optical centroiding efficiency (OCE). In Section 3, we develop a theoretical model to represent the imaging of a point source onto an arbitrary point on a detector pixel, to evaluate the NEP more realistically. We describe the relationship of the point spread function, psf, to both the EOD and the OCE. In the following section, the imaging theory is developed for the case when the optical system and the detector pixel are misaligned. In Section 4, the simulation methodology is described in detail. Next, we analyze the performance of an optical system with and without central obscuration. Finally in Section 6, we discuss the significance of using the OCE to predict the future performance of an instrument during its conceptual design stage. The conclusions are summarized in Section 7.
2. Energy Interception by Discrete Pixels
2.1. Energy on Detector (EOD)
The concept of the EOD became important when rectangular pixels were introduced, their dimensions became ever smaller, and their dimensions started to define the instrument resolution. Figure 2a presents the image that the optical system with a circular aperture delivers onto the focal plane, where an array of sensing elements detect the incident radiation. The inset shows the corresponding grayscale intensity, assuming low exposure. The first bright ring is barely visible. Theoretically, there is zero intensity in the first minimum, measured from the central peak.
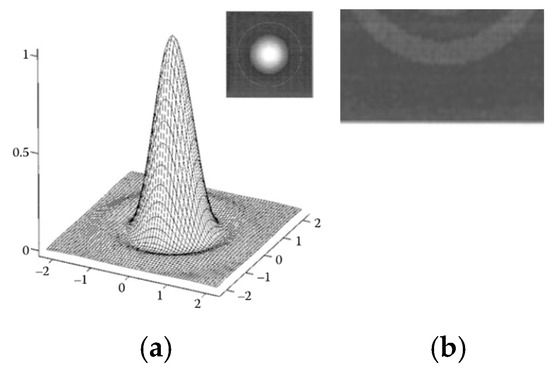
Figure 2.
(a) Image by an optical system of a point object at infinity, with the central spot often referred to as the Airy disc; (b) Rayleigh resolution distance is equal to the Airy disc radius.
This zero defines the first dark ring, or the radius of the resolution spot, according to the Rayleigh criterion, as illustrated in Figure 2b. In the 1980s, during the early periods of the design of the Mars orbiter, we required four pixels per resolution distance of the optical system to ensure the shape recognition of 1 m rocks or holes. Due to the 1 m diameter rover wheels, 1 m diameter holes were considered most detrimental, because the vehicle could become stuck inside. A hole would, then, bring its exploration to an end [3,4,5]. The orbiter was tasked to find a suitable lander landing site in the middle of an initial Mars Rover exploration area. At that time, we were optimistically designing an autonomous rover with optical navigation system for autonomous navigation on its surface.
Figure 3 illustrates schematically how the pixel dimension relative to the size of the Airy disc affects the amount of energy that is incident on the detector pixel. The radius of the Airy disc is dependent on the optical system, rA = 1.22 λF/#. The wavelength is denoted by λ, and the instrument is characterized by its ratio f/D = F/#. D is the aperture diameter, f is the focal distance, and F/# (sometimes also f/#) is the f-number. The pixel size is equal to the Airy disc diameter in the third illustration from the left. The two pixels on its left are larger by 20% and 40% than the diameter of the Airy disc. Both also include two point-sources positioned at the Rayleigh resolution limit. In this case, the pixel dimension acts to define the instrument resolution. The pixel on the furthest right would resolve the two point-sources at the Rayleigh’s resolution limit, but only if it were correctly centered.

Figure 3.
A schematic illustration of how the pixel dimension relative to the size of the Airy disc affects the amount of energy that is incident on and absorbed by the detector pixel.
We first modified the concept of energy enclosed within a circle, due to the existence of rectangular pixels. We then introduced a modified term due to the random position of the image centroid on the pixel. The EOD is a multiplicative correction factor that was invoked in the system design to account for the spread of an image of a point source over several detector pixels. The EOD may be formally defined as the fraction of energy incident on the signal-carrying detector pixel over the total energy within the image. This definition implicitly assumes that the centroid of the image of the point source is located at the pixel center. The pixel area is 4dxdy for the pixel dimensions of 2dx by 2dy.
Here, psf(x,y) is the point spread function of the optical system. In theory, it is unitless, but in practice, it is measured in units of [watts/cm2] or [#photons/(cm2 s)] [6,7,8]. We note that the (degree of) coherence of the object point source is not of interest. The source coherence may only change the form of the psf(x,y) function to some degree, but not the theoretical development presented here. For the image centered at the origin (0,0), the psf(x,y) attains the maximum value at x = y = 0 in this EOD formulation. The denominator is the total energy in the image of a point source. In practice, the total energy only includes the summation of energy incident on the few neighboring pixels.
In Figure 4, we see two images of point sources at infinity incident on the pixel distribution in the focal plane. In part (b), we see a pixel that is nearly centered on the optical axis, while in part (b), we show the displacement of the optical axis to the pixel corner. The image that is of approximately of the same size as the pixel (upper right, darker pinkish color) does not necessarily fall on a single pixel. The image centroid may be located anywhere on the specific pixel with equal probability. Even a significant fraction of its image, or energy, may be incident on the neighboring pixels.

Figure 4.
(a) The image of a point source is in general not aligned with a pixel center. (b) When in the extreme, limiting case, the image falls on the corner of four pixels, the detected signal in upper right pixel is equal to the noise in three neighboring pixels. In fact, there is no image detected against the noise, or possibly a broadly blurred image.
The pixel size is the most important parameter that determines the amount of the energy on detector, followed by the aperture configuration, and the aberrations that include any manufacturing and assembly errors. We consider a general aperture, incorporating an ideal circular aperture of diameter D with a rectangular obscuration, 0.27 D × 0.46 D, where D is the diameter of the entrance pupil. Figure 5a presents the aperture geometry, while part (b) shows the diffraction pattern in the image plane. The rectangular obscuration results in an asymmetrical psf. Such an obscuration has the effect of moving the energy out in an asymmetric fashion. The primary consequence of having an optical system with an obscured aperture is a decreased EOD.
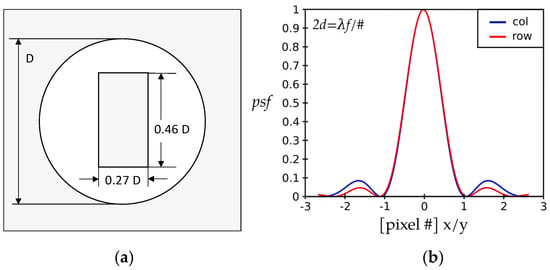
Figure 5.
(a) Transmission profile of a circular pupil featuring a general rectangular central obscuration. Gray indicates zero-transmission. The size of the obscuration rectangle is 0.27 D × 0.46 D, where D is the diameter of the entrance pupil. (b) Point spread function, psf, of the circular pupil with the internal central obscuration shown in part (a). Different profiles are obtained along the x- and y-dimensions because the rectangular obscuration is asymmetrical.
The energy EOD, and, by derivation, the NEP and other figures of merit, were traditionally calculated under the assumption that the image of a point source on the optical axis, or the image centroid, is located exactly at the center of a detector pixel. This assumption would imply that the center of the central pixel of a large FPA is aligned within nanometers with the instrument optical axis. In the true and realistic operational environments, there exists too much image jitter for this assumption to be valid.
2.2. Optical Centroiding Efficiency (OCE)
The image of a point source is, in general, not aligned with a pixel center. In an extreme case, the image may fall on the corner of four pixels, as in Figure 4b. The energy in the signal-carrying upper-right pixel is equal to the noise in three neighboring pixels. In fact, there is no image detected against the noise.
The probability of finding the image centroid in the pixel center (that itself is located on the optical axis) is negligibly small. In the first approximation, we may reasonably assume that the position of the image centroid is uniformly distributed over the pixel area, defined as the product of the pitch along the two perpendicular directions. A correction analysis, hopefully leading to a single correction factor, is needed to formulate realistic design concepts applicable to the actual operational conditions. This is precisely what we endeavor to achieve here.
For a modern space/ground remote sensing instrument or a telescope with a large FPA, it is practically impossible to image a remote point source at the very center of a detector pixel, due to the image jitter and randomness in the line of sight. Toward a more realistic instrument modeling, we introduced a parameter, related to the EOD, that we call the optical centroiding efficiency (OCE). This statistical quantity tells us how much the EOD changes on average when the image centroid is displaced to a position on the pixel at (±Δdx, ±Δdy) where these two quantities lie between 0 and dx, dy, respectively.
3. Imaging Theory When Optical and Detector Axes Are Arbitrarily Displaced
3.1. Image Radiometry of a Point Source
The power collected from a distant point source by the aperture of the optical system in the image (the focal) plane, EP, is most easily obtained from the power transfer equation [9,10]. This formulation considers a continuous detection process, such as the film used in the past, prior to the introduction of the digital sensors.
Here, ΦP is the irradiance at the instrument aperture [watts/cm2] or [#photons/(cm2 s)]. As is the sensor/instrument aperture area [cm2]; τ is the instrument optical transmission factor, including any aperture obscuration or obstruction.
When the image of a point object in the object space is spread over several neighboring detector pixels in the image space, only the central pixel contributes to the image formation. The radiation that falls on the neighboring pixels represents the energy lost to the image-forming pixel, while it is added as the optical noise to the neighboring pixels [11]. This formulation includes the consideration that the pixels have a rectangular shape.
Next, we consider the absorption of the energy by a signal-carrying pixel. We may write ΦP in Equation (2) as a product of relative power φP and the EOD, introduced in Equation (1).
Using this expression, Equation (2) becomes
This power, referred colloquially to as energy, has traditionally been referred to as “encircled”, when the integration limit is the radial distance from the origin, or “enclosed” energy [12,13,14,15,16,17,18,19,20,21]. The maximum energy on a rectangular pixel, or the EOD, is obtained when the image centroid coincides with the center of the detector pixel. We denote this energy as the energy-on-detector pixel Ed(dx, dy).
An optical system afflicted with coma is an obvious case of an instrument in which the image centroid is displaced from its geometric image. In systems without coma, however, the image centroid and the center of the geometric image coincide.
The modern astronomical, space, or ground remote sensing instruments and telescopes, equipped with a large FPA, feature the state-of-the-art line-of-sight and pointing-control systems. Nevertheless, in a realistic environment with many sources of random motion, the image of a point source does not necessarily come to focus on the center of a desired detector pixel. This model was reasonable in the past, prior to pixelated detection schemes. The practitioners accept, to some degree, the unavoidable randomness in the pixel position [22,23,24].
The possibility of the displacement of the optical axis to an off axis point on the pixel may be described as a probability. We call this probability the optical centroiding efficiency, the OCE. We insert it as a correction factor into Equation (5) next to the EOD to obtain an accurate estimate of the radiative power transfer from a point source onto a detector pixel in a modern focal plane architecture.
The need for such a correction factor has occasionally been accepted implicitly in earlier publications, employing a somewhat different terminology. We ascribe this unintentional historical oversight to the difficulty associated with its estimate for conditions of random environmental disturbances. The product EOD × OCE must be included in important radiometric concepts, such as the NEP and the figures of merit derived from it.
A realistic formula for the NEP of the point-source imaging sensor may then be reformulated, recalling its definition [25].
Here, σ is the detector noise in [counts] and R is the sensor responsivity in [counts/W] or [counts/(#photon s)]; C denotes counts.
3.2. Instrument Characteristic Function
The instrument characteristic function, or a point response function, prf, of a linear system is the convolution of the individual point response functions of the constituent subsystems [6]. The prf(x,y) of an optical instrument is the 2-D convolution of the psf(x,y), the point spread function of the optical system (the imaging system of the camera or the telescope), with the detector response function drf(x,y).
The computer-assisted design, analysis, and optimization of optical systems has progressed to such an advanced degree that that psf(x,y) may be considered known. The magnitude of its Fourier transform, the modulation transfer function, is employed as one of the basic figures of merit for its performance evaluation. For the rectangular pixel, the detector (considered spatial here) response function, drf(x,y), has the usual form,
We may also consider drf(x,y) as the pixel aperture function. We use 2dx by 2dy as pixel dimensions. This function is sometimes denoted as rect(x,y). It has the property that its one-dimensional Fourier transform is a sinc(x) = sinx/x. The pixel center is, in general, not aligned with the axis of the optical system; the pixel center is displaced randomly, in direction and magnitude, from the optical axis of the image-forming system. The image centroid falls on point (Δdx, Δdy). We consider that the coordinates of the detector-pixel center define the origin of the coordinate system, because the detector-pixel geometry introduces a fixed reference in the image detection and readout.
Using Equation (8) and displaced psf(x−Δdx, y−Δdy), we obtain the instrument point response function, prf, or the instrument function,
As a reference, the psf(x,y) of a perfect optical system with a circular aperture is a Bessel function, presented in Figure 2a. Using the definition of convolution, we find
We could limit the spatial extend of the PSF (the Fourier Transform of psf) to 10-pixel sizes, meaning that the integration limits are equal to +/−10dx, +/−10dy (see also Figure 1).
The rect-function of the pixel dimensions just defines the integration limits to smaller values.
The instrument function is, then, the psf, displaced by the optical axis displacement, integrated for each value of (v,w), over the area of overlap of the psf function and the pixel extent. Its maximum value, for a given psf(x,y) of the optical system and the detector sides, is found when their coordinate axes coincide, that is, when Δdx, Δdy are zero.
The peak value of the prf(x,y), the instrument response function, is the EOD of the point source, found when Δdx, Δdy are zero. Thus, recalling Equation (1) for the energy on detector, the EOD, we modify Equation (8), resulting in the normalized prfn(x,y). We denote the pixel area, 4dxdy, with Ad.
The EODd(x,y) is the ensquared energy, that is, the energy enclosed within a pixel of dimensions 2dx by 2dy when the image centroid is not coincident with the pixel center. In this equation (Δdx, Δdy) are the coordinates of the image centroid. Inserting the decentering in Equation (1), we have
This is the energy on the detector pixel that is misaligned by (Δdx,Δdy) with respect to the optical axis. The OCE is, then, a single number that is defined as the ratio of the energy-on-detector pixel that is misaligned by (Δdx,Δdy) with respect to the optical axis, averaged over all possible misalignments, to the ensquared energy on the aligned detector pixel.
We treat the numerator of Equation (15) statistically, because of the lack of knowledge. By averaging over all possible displacements of the optical axis from the pixel center, we find the most likely value for the OCE(dx,dy).
The EODd(dx,dy;Δdx,Δdy) is given in Equation (15) and the EOD(dx,dy) in Equation (1). The OCE(dx,dy) is a statistical variable that depends only on the relationship between the pixel dimensions and the point spread function through EODd(dx,dy;Δdx,Δdy) and EOD(dx,dy).
The OCE(dx,dy) is, therefore, defined as the normalized EOD(dx,dy) average over a detector area, given the equal probability that the image centroid falls anywhere on the detector pixel. It may be computed when we know the psf(x,y) of the optical system and the detector pixel size, 2dx and 2dy. We are interested in the product of the OCE and the EOD because it enters the figures of merit of radiometric systems, as in Equation (7).
4. Modeling and Methods
Both the EOD and OCE depend on the point spread function psf(x,y) of the optical system. The psf(x,y) may be interpreted as the irradiance distribution of the image of a distant point source, normalized to 1 at the origin. In an imaging optical system, it may be found according to the wave diffraction theory of aberrations [26].
Here, λ is the wavelength of the radiation emitted by the point source and i is (−1)1/2. D denotes the aperture diameter. Both ξ and η coordinates are assumed to have non-zero values in the image plane within the range [(−dx,+dx), (−dy,+dy)]. According to the formal analysis, the limits of integration range from minus infinity to plus infinity while the image is formed in the far field. R is the image distance. Furthermore, by the definition of the f-number, F/#, (λR/D) = λF/#, the dimensions in the image plane may be normalized by the system (λF/#)-product.
The pupil function P(ξ,η) describes the pupil transmission characteristics. It is zero outside of the projected aperture and at the obstruction. Inside, it may be expressed as a wavefront aberration function W(x,ɳ) [27,28].
Here, A(ξ,η) and W(ξ,η) are the amplitude and the phase of the wavefront aberration function, respectively. For a perfect optical system with circular aperture and no aberration, the diffraction generates an image as a Bessel function of the first order. Its square, or normalized irradiance, is also known as the Airy function (see Figure 2a).
We used a simple and straightforward approach to compute both the EOD(dx,dy) and the OCE(dx,dy), presented schematically in Figure 6. We set up a lens in CodeV and calculated psf(x,y) directly. We then exported psf(x,y) to MatLab, where the EOD was verified one more time to ensure the consistency of numerical and ray-trace results. The OCE was obtained with MatLab, employing the formulas here derived. We modeled the detector pixel as a square with a dimension of 2d. For the sake of due diligence, part of our work was also numerically evaluated (using Equations in Figure 6) with Mathcad. Both approaches agreed.
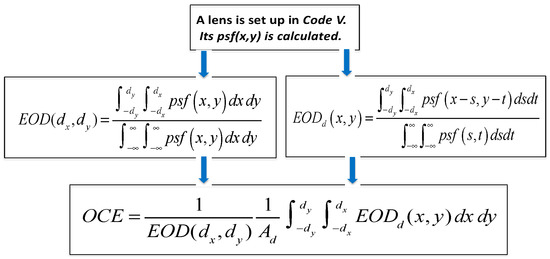
Figure 6.
Block diagram to determine the EOD and OCE, using CodeV or some other lens design program to calculate the optical system psf(x,y).
Next, we describe a study as an illustration of the process, related to the pixel dimensions. We discuss the determination of the OCE for an optical system with and without a generalized rectangular obscuration. The difficulties and the repetition inherent to a statistical analysis indicate why the concepts of energy on detector and optical centroiding efficiency have not been implemented previously. The implementation through the numerical evaluations are quite time consuming.
5. Effects of Pixel Size and Central Obscuration
We start this analysis with the detector size effects for an ideal optical system with and without a central obscuration. We examine the cases of a circular aperture with and without a rectangular central obscuration.
5.1. Aperture Configuration: No Central Obscuration
We analyzed two aperture types: an ideal circular aperture of diameter D and an ideal circular aperture with a rectangular central obscuration. The obscuration size was 0.27 D × 0.46 D, where D is the diameter of the entrance pupil (see Figure 5a).
We first analyzed the case of unobstructed aperture. We present its OCE as a function of detector size from 1.67 λF/# to 15 λF/# in Figure 7. We recall that the radius of the Airy disc was 1.22 λF/#. Thus, we started with the pixel size that did not quite enclose the central peak of the psf(x,y) or the Airy disc, even when the image of the point source fell on the center of the pixel. For the larger detector sizes, the radius of the image of the central disc was increasingly smaller than the pixel dimensions. This figure shows that the OCE increased with the pixel size.
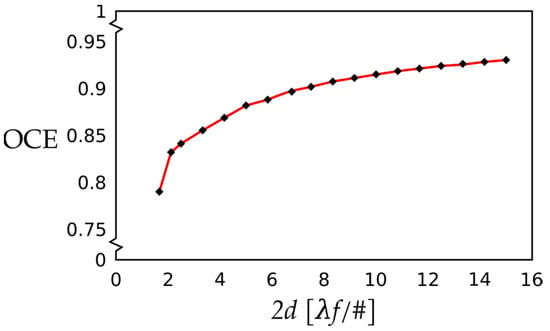
Figure 7.
Optical centroid efficiency vs. detector pixel size in units of [λF/#] for a perfect optical system with a circular aperture, without a central obscuration.
From the block diagram presented on Figure 6, we noted that the construction of the OCE requires that the EOD(dx,dy) and EODd(dx,dy) be first determined. Therefore, we first calculated the prf(x,y). Figure 8 presents the instrument point response function, prf(x,y), vs. pixel number for two orthogonal directions and two different pixel sizes, 2d = 3.33 λF/# in (a), and 2d = 13.33 λF/# in (b).
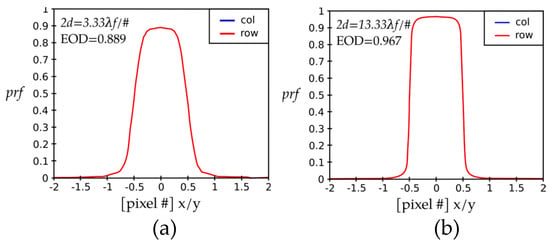
Figure 8.
Two prf-s vs. pixel number shown for two orthogonal directions, x and y (in the inset denoted as red, rows, and blue, columns): (a) 2d = 3.33 λF/# and (b) 2d = 13.33 λF/#. Pixel coordinates along both dimensions are, in both cases, normalized to the pixel size. The general features of the curves for the small (left) and large (right) pixel sizes are quite similar, except that the peak for the smaller pixel (3.33 λF/#) is decreased by about 4% with respect to the peak of the large pixel. Additionally, the top of the profile for the smaller pixel size (left) is more rounded and narrower than that of the large pixel (right).
We next analyze a small detector pixel with a dimension of 3.33 λF/# to present our methodology and to illustrate the salient steps.
5.1.1. Case 1: Small Pixel, No Central Obscuration
When the detector size was small, 3.33 λF/#, the pixel comfortably enclosed the complete image of the point source. The diameter of the Airy disc (2.44 λF/#) was equal to about 2/3 of the pixel side. The convolution of the detector area with the Airy function started to produce ripples on both sides of the maximum of the prf-profile. More energy was distributed outside of the reference detector pixel, resulting in a reduced OCE. We present this case in Figure 8a, exhibiting the prf(x,y) cross-section as a function of pixel number for a 3.33 λF/#-pixel size. Rows and columns are superimposed because the optical system is rotationally symmetric.
We note that the peak portion looks like a flat top with rounded edges, with a peak value (that is, EOD) of 0.889. The curve is broadened at the base. The OCE for this case was calculated by convolution and averaging to be 0.855. The values (3.33 λF/#, 0.855) are entered as a single point in Figure 7. By neglecting the effects of the OCE, we overestimated the instrument performance. The product of EOD by OCE was 0.760.
Next, we analyze the case of the detector pixel with dimension of 13.33 λF/# to illustrate the effect of the pixel size.
5.1.2. Case 2: Large Pixel, No Central Obscuration
Figure 8b presents a prf(x,y) vs. pixel number for two orthogonal directions, x (red, row) and y (blue, column) for 13.33 λF/# pixel size. The curves along the horizontal and vertical direction overlap because we analyzed a rotationally symmetric circular aperture and an ideal, diffraction-limited system. The detector physical extent ranges from −0.5 to +0.5 along the x- and y-axis. The pixel size of 13.33 λF/# is approximately 5 times the diameter of the Airy disc; thus, the image of a point source is contained completely inside this pixel. The pixel-side dimension on the abscissa is normalized to 1.0 (in units of λF/#). The peak of the curve is centered at the origin because the square pixel intercepted the highest amount of radiation when the image was centered at the origin. Furthermore, because the pixel size is so much larger than the Airy disc diameter, the peak is nearly flat. This means that the image may be appreciably decentered over the pixel surface, nearly to the edge, before the prf changes.
The peak value of prf is the EOD. From Figure 8b, we read that EOD(dx,dy) was 0.967 for the 13.33 λF/#-pixel size. The psf of the optical system was convolved with the detector pixel response function (drf) to find EODd(dx,dy). Next, the OCE value was calculated by integrating the prf(x,y) over the detector area (−0.5 < x < 0.5, −0.5 < y < 0.5). We calculated a value of 0.926 for this OCE. The product of the EOD by OCE (0.967 × 0.926) was 0.895.
The size of the Airy disc, or more precisely, the diameter of the first dark ring, was 2.44 λF/#. For a relatively large detector size of 13.33 λF/#, the resulting prf(x,y) presented a rather flat response similar to a hat, except for the slightly rounded corners, as seen in Figure 8b. These values (13.33 λF/#, 0.926) are entered as a single point in Figure 7. By neglecting the effects of the OCE, we overestimated the instrument performance.
In addition to the pixel size, the pupil geometry also plays an important role in the amount of radiation collected at the image pixel for a point object at infinity.
5.2. Aperture Configuration: Circular, Incorporating Rectangular Central Obscuration
The optical system features a rectangular central obscuration of Figure 5a. The obscuration size was 0.27 D × 0.46 D, where D is the diameter of the entrance pupil. The rectangular central obscuration breaks the circular symmetry, resulting in an increased relative intensity level in the first ring and decreased diameter of the Airy disc [27]. Figure 5b presents the point spread function, psf(x,y), as a function of pixel number, in units of [λF/#], for two orthogonal directions, x (rows, red) and y (columns, blue).
Case 3: Small Pixel, Round Aperture with a Central Rectangular Obscuration
The pupil geometry-driven diffraction patterns incident on the pixel resulted in a rise in additional features in the shape of the OCE and the EOD curves. This may be observed in the OCE vs. detector size curves generated for the special case of an optical system with the central obscuration, exhibited in Figure 9. We modeled the case where the diameter of the first zero–zero ring was equal to 2 pixels (in units of λF/#). We observed a small negative spike in the small pixel-size regime, at about 3.4 λF/#. Afterwards, the curve resumed a trend, like that presented in Figure 7. With nearly 60 percent obstruction by area, this curve was expected to behave similarly to the lowest one in Figure 1. However, the rectangular pixel and rectangular obstruction were somewhat in resonance to produce a pronounced peak, followed by an unexpected dip in the small pixel-size regime.
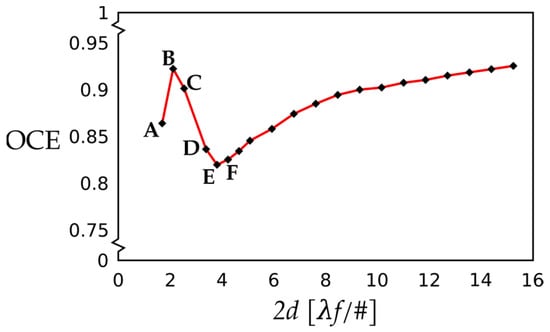
Figure 9.
The OCE as a function of pixel size in [λF/#] for an optical system with a central rectangular obscuration (see Figure 5a). We observed a sharp increase in the OCE value toward the first peak to about 0.93 at about 2.05 pixels (Point B), followed by a sharp dip to about 0.82 (Point E) at about 4 pixels. Only from this, the lowest point on the curve, its shape starts to increase in a monotonical fashion.
We investigated further the first six data points in the unusual spike region where the detector size ranged from 1.67 λF/# to 4.23 λF/#. We followed the same analysis steps as we did in Cases 1 and 2. We plotted the corresponding prf(x,y) cross-section graphs for the six key points indicated in Figure 9 as parts (a) through (f) in Figure 10.
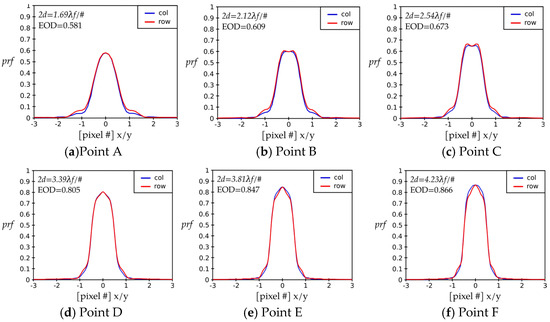
Figure 10.
Cross-sections of the prf as a function of two orthogonal directions, x and y, or rows and columns, for the points labeled in Figure 9. We modeled the case where the diameter of the first zero in the ideal diffraction pattern was equal to 2 pixels (in λF/# units) with the rectangular obscuration of Figure 4a. We observed that the EOD value increased with increasing detector pixel size. EOD is the value of the prf at the pixel center. Concurrently, the shape of the prf(x,y) became modified with increasing detector size from that with explicit support at the base to that with a thin base and without features there.
The pixel size was equal to the diameter of the Airy disc just before Point C. When the pixel size was smaller than the disk diameter, the increase in the pixel size resulted in an increased energy on detector. Moving the beam center around the detector surface area did not affect the amount of collected energy, because the Airy function is relatively flat at the central part. Therefore, the overestimation in the collected energy for this region is quite significant.
6. Discussion
Even when a sensor is equipped with a high-quality line-of-sight control, the centroid of the image of a point source falls somewhere between the center and the edge of a detector pixel for most realistic cases. This results in a decreased signal-carrying energy on detector.
6.1. Signal-Carrying Energy on Detector
We demonstrated that each point on the prf curve is the value of the energy on detector at that point when the image centroid of a point source comes into focus at that point. If we simply applied the calculated value of the EOD (of 0.967) to characterize the performance of the FPA with a detector pitch of, for instance, 13.33 λF/#, this would imply that the centroid of each point source is always imaged at the pixel center. This assumption would generate an overly optimistic performance prediction for this FPA sensor because some energy is spilled on the neighboring pixels when the image of a point source is imaged at another position on the detector pixel. The more the image centroid is displaced from the pixel center, the more energy is spilled on the neighboring pixels and, correspondingly, less energy is contributed to the image formation.
Thus, a properly determined energy on detector used in the development of the detector and system figures of merit would have the peak EOD value modified by the factor of OCE which accounts for all possible misalignments between the optical system axis and the pixel axis. Including the calculated OCE of 0.926, the product of EOD by OCE is 0.895. This is a more realistic figure of merit of the sensor performance. By neglecting the effects misalignment, and therefore those of the OCE, we overestimate the instrument performance by about 10% in the optical system with a circular aperture without a central obscuration.
In summary, comparing both sides of Figure 8, we may form the first significant conclusion for a diffraction-limited case with no central obscuration. As the detector pixel size increases relative to the image size, the EOD increases together with the associated OCE. By considering that the image of a point source falls on the pixel center, at least 10% energy is overestimated in performance measures.
6.2. Small, Medium, and Large Pixels to Collect Signal-Carrying Energy
We performed an illustrative study of the OCE vs. detector pixel size for a circular aperture with and without the rectangular central obscuration, displayed in Figure 11. We treated three regions of interest separately.
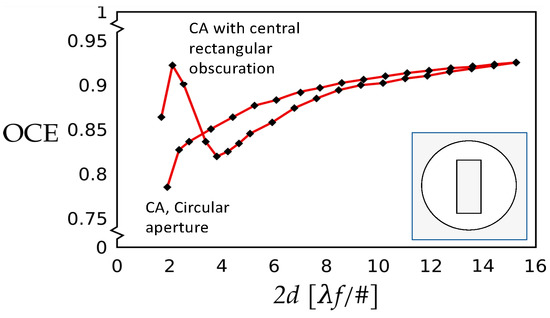
Figure 11.
The OCE as a function of pixel size in [λF/#] for an optical system with and without a central rectangular obscuration. A sharp increase in the OCE value toward the first peak at about 2.05 pixels is followed by a sharp dip at about 4 pixels only for the case of the circular aperture with a central obscuration. The OCE curve for a circular aperture without a central obscuration increases in a monotonical fashion. CA denotes a circular aperture.
We first consider the case without the central obscuration. When the pixel size (2d) is smaller than the psf diameter, used in applications of shape recognition and object height contouring, the EOD increases together with the associated OCE. Additionally, the EOD increases according to the traditional concept of the enclosed energy. The OCE, however, increases at a much faster rate than the EOD, because psf is nearly constant over the pixel up to the pixel edge.
For the intermediate regions of pixels being equal to two to four central spots, the energy on detector still increases, but less rapidly than in the small pixel regime. The OCT increases in this region because the energy on detector is still relatively large at the pixel edge.
When the detector pixel size becomes larger than four central spots, the EOD increases start to moderate according to the traditional concept of the enclosed energy. The OCE increases slow down with the increase in the detector pixel size, because at large distances, there is increasingly small increment in detected energy. At the edge of a relatively large pixel, the psf is already small, resulting in a large fraction of the pixel area where the image may not be completely detected to produce a large OCE, approaching its limiting value of nearly 0.90.
The situation is appreciably different in the case of optical systems with a sizable central obscuration. They are characterized as having a smaller spot diameter, and more energy is spread into outer rings than those with a circular aperture without central obscuration. Thus, such a system could be required to have somewhat larger pixels to collect a slightly spread-out spot.
In the region where the pixel size is smaller than the central spot diameter, the EOD for a system with a large central obscuration increases with the pixel size more slowly than for a clear system. We already observed this phenomenon in the enclosed energy graphs in Figure 1. The OCE, however, increases very rapidly when the central spot is smaller than the pixel. The value of the sensor point response function prf at the pixel edge is still high just because the pixel is smaller than the central spot. Table 1 summarizes the point numbers, the pixel size, the EOD from Figure 9, the OCE values from Figure 10, and their product.

Table 1.
The EOD, the OCE, and their product for small and medium pixel sizes and a circular aperture with a rectangular obscuration.
When the pixel size is equal to about two to four spot diameters, the psr value at the pixel edge stars becoming increasingly smaller, close to zero. The EOD still increases with the detector pixel size because energy is spread out to higher-order rings nearly linearly (see Figure 1, bottom curve). The outer pixel regions, however, start to make a decreased contribution to the overall OCE, because the prf value there is low. In this region, we observe a pronounced decrease in the OCE as a function of the pixel size.
For pixel sizes equal to or larger than about four bright spots, the OCE starts to increase at a somewhat faster rate than in the case of the clear aperture. In this region, the EOD also increases at a rate that depends on the amount of obscuration. Yet, the side lobes have a lot of energy, so increasing the pixel dimension also results in a steady increase in the OCE values.
The energy on detector always increases with the detector size because a larger area of the detector always intercepts more energy.
Based on this analysis, we may conclude that the OCE is a meaningful quantity in the case when the detector pixel size is sufficiently large that it collects a significant fraction of energy in the image of a point source. In the case of a large obscuration with a transmission loss of about 0.6, the smallest reasonable value for EOD is about 0.85. This means that in diffraction-limited cases, the concept of the OCE is applicable and relevant for cases with relatively small central obscurations.
The OCE analysis does not apply to the cases where large amount of energy is spread out from the central spot, or where the detector is smaller than the central spot diameter.
The size of the pixel, which is smaller than the diameter of the Airy disc, corresponds to the case when imaging that requires high topographic details is performed, as in the Mars landing survey, and where the amount of incident energy is not an issue. Thus, one would one expect to analyze the displacement of the pixel and the optical system axes for such cases.
7. Summary and Conclusions
We introduced novel concepts and rationale for more appropriate terminology to describe the image detection process in modern digital instruments. The first one is the energy on detector (EOD), that replaces the old concept of energy enclosed inside a circle to assist with the performance measures of the pixelated sensors. We further argued that the image of a point source at infinity neither usually nor generally falls in the center of a pixel. Rather, in modern instruments, the axis of an optical system intersects a pixel at any point on the pixel surface. Considering that this point is unknown, we proposed as the second novel concept the optical centroiding efficiency (OCE). It is found by convolving the point spread function (psf) of the optical system with the detector responsivity function for all possible positions on the pixel. The product of these two quantities (EOD × OCE) is proposed as a more realistic quantity to assess the sensor figures of merit.
Using the linear system theory in the instrument analysis, we developed a theory to evaluate the EOD and the OCE. We implemented it numerically on the CodeV and MatLab.
We performed two studies to illustrate the usefulness of these new concepts. (i) The OCE vs. detector pixel size for an ideal circular aperture. (ii) The OCE vs. detector pixel size for a circular aperture with a rectangular central obscuration. Based on this analysis, we may conclude that the OCE as a design parameter is a meaningful quantity in the case when the detector pixel size is sufficiently large that it collects a significant fraction of energy in the image of a point source. In the case of a large obscuration with a transmission loss of about 0.6, the smallest reasonable value for the EOD is about 0.85.
The OCE is proposed as the meaningful concept in the system performance assessment and in the development of figures of merit when the resolution of optical system is matched to the pixel size.
In the future, we want to extend this study to aberrations. We also plan to apply this theory to other telescopes and remote sensing instruments.
Author Contributions
All authors contributed equally to this M.S. Conceptualization, Y.W.; Investigation, R.M. and Y.W.; Methodology, R.M. and M.S.; Visualization, Y.W., M.S. and B.B.-M.; Writing—original draft, M.S. and Y.W.; Writing—review and editing, M.S. and B.B.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are included in this study.
Acknowledgments
This paper is based on a presentation prepared for the “1st International Conference–Advances in 3OM: Opto-Mechatronics, Opto-Mechanics, and Optical Metrology,” 13–16 December 2021, Timisoara, Romania.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rauscher, B.J.; Fox, O.; Ferruit, P.; Ferruit, R.J.; Waczynski, A.; Wen, Y.; Xia-Serafino, W.; Xia-Serafino, B.; Alexander, D.; Brambora, C.; et al. Detectors for the James Webb Space Telescope Near-Infrared Spectrograph I: Readout Mode, Noise Model, and Calibration Considerations. arXiv 2007, arXiv:0706.2344. [Google Scholar] [CrossRef]
- Sutherland, W.; Emerson, J.; Dalton, G.; Atad-Ettedgui, E.; Beard, S.; Bennett, B.; Bezawada, N.; Born, A.; Caldwell, M.; Clark, P.; et al. The Visible and Infrared Survey Telescope for Astronomy (VISTA): Design, technical overview, and performance. Astron. Astrophys. 2015, 575, A25. [Google Scholar] [CrossRef]
- Scholl, M.S.; Wang, Y.; Randolph, J.E.; Ayon, J.A. Site certification imaging sensor for Mars exploration. Opt. Eng. 1991, 30, 590–597. [Google Scholar] [CrossRef]
- Scholl, M.S.; Padila, G.; Wang, Y. Design of a high resolution telescope for an Imaging sensor to characterize a (Martian) landing-site. Opt. Eng. 1995, 34, 3222–3228. [Google Scholar] [CrossRef]
- Scholl, M.S.; Padila, G. Push-broom reconnaissance camera with time expansion for a (Martian) landing-site certification. Opt. Eng. 1997, 36, 566–573. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: San Francisco, CA, USA, 1968; p. 141. [Google Scholar]
- Gaskill, J.D. Linear Systems, Fourier Transforms, and Optics; John Wiley & Sons: New York, NY, USA, 1978; p. 449. [Google Scholar]
- Strojnik, M. Point spread function of (multiple) Bracewell interferometric configuration(s) and the nulling hypothesis in planet detection. J. Appl. Remote Sens. 2014, 8, 084981. [Google Scholar] [CrossRef]
- Wolfe, W.L. Radiometric terms. In The Infrared Handbook, rev. ed.; IRIA, Ed.; ERIM for Office of Naval Research: Ann Arbor, MI, USA, 1993. [Google Scholar]
- Wolfe, W.L. Introduction to Infrared System Design; SPIE: Bellingham, WA, USA, 1996; Volume TT24, p. 17. [Google Scholar]
- Strojnik, M.; Scholl, M.K. Radiometry. In Advanced Optical Instruments and Techniques; Malacara, D., Thompso, B.N., Eds.; CRC Press: New York, NY, USA, 2018; pp. 459–717. ISBN 9781498720670. [Google Scholar]
- Kingslake, R. Lens Design Fundamentals; Academic Press: New York, NY, USA, 1978; p. 153. [Google Scholar]
- Fisher, R.; Tadic-Galeb, B. Optical System Design; McGraw-Hill: New York, NY, USA, 2000; p. 7. [Google Scholar]
- Smith, W. Modern Optical Engineering, 4th ed.; McGraw Hill: New York, NY, USA, 2008; p. 191. [Google Scholar]
- Hecht, E. Optics, 4th ed.; Addison Wesley: San Francisco, CA, USA, 2002; p. 470. [Google Scholar]
- Mahajan, V. Aberration Theory Made Simple; SPIE: Bellingham, WA, USA, 1991; Volume TT6, p. 71. [Google Scholar]
- Beyer, L.M.; Cobb, S.H.; Clune, L.C. Ensquared power for obscured circular pupils with off-center imaging. Appl. Opt. 1991, 30, 3569. [Google Scholar] [CrossRef] [PubMed]
- Harvey, J.E.; Ftaclas, C. Diffraction effects of telescope secondary mirror spiders on varies image-quality criteria. Appl. Opt. 1995, 34, 6337. [Google Scholar] [CrossRef] [PubMed]
- Barhydt, H. Effect of F/number and other parameters on performance of nearly BLIP search and surveillance systems. Opt. Eng. 1978, 17, SR-28. [Google Scholar]
- Barhydt, H. Figures of Merit for Infrared Sensors; SPIE: Bellingham, WA, USA, 1979; Volume 197, p. 64. [Google Scholar]
- Lloyd, J.M. Fundamentals of electro-optical imaging systems analysis. Electro-optical systems design, analysis, and testing. In The Infrared & Electro-Optical Systems Handbook; Accetta, J.S., Shumaker, D.L., Dudzik, M., Eds.; ERIM: Ann Arbor, MI, USA; SPIE: Bellingham, WA, USA, 1993; Volume 4, p. 18. [Google Scholar]
- Holst, G. Electro-Optical Imaging System Performance, 3rd ed.; SPIE: Bellingham, WA, USA, 2002; p. 204. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge U. Press: Cambridge, UK, 1999; p. 443. [Google Scholar]
- Hudson, R.D. Infrared System Engineering; Wiley & Son: New York, NY, USA, 1969; pp. 270–429. [Google Scholar]
- Lloyd, J.M. Thermal Imaging Systems; Plenum Press: New York, NY, USA, 1975; pp. 11–166. [Google Scholar]
- Stoltzmann, D.E. The perfect point spread function. In Applied Optics and Optical Engineering; Shannon, R.R., Wyant, J.C., Eds.; Academic Press: New York, NY, USA, 1983; Volume IX, pp. 111–148. [Google Scholar]
- Wyant, J.C.; Creath, K. Basic wavefront aberration theory for optical metrology. In Applied Optics and Optical Engineering; Shannon, R.R., Wyant, J.C., Eds.; Academic Press: New York, NY, USA, 1992; Volume XI, pp. 1–53. [Google Scholar]
- Welford, W.T. Aberrations of the Symmetrical Optical System; Academic Press: London, UK, 1974; p. 22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).