Design of a Broadband Fiber Optic Mode Coupler for Multimode Optical Coherence Tomography
Abstract
1. Introduction
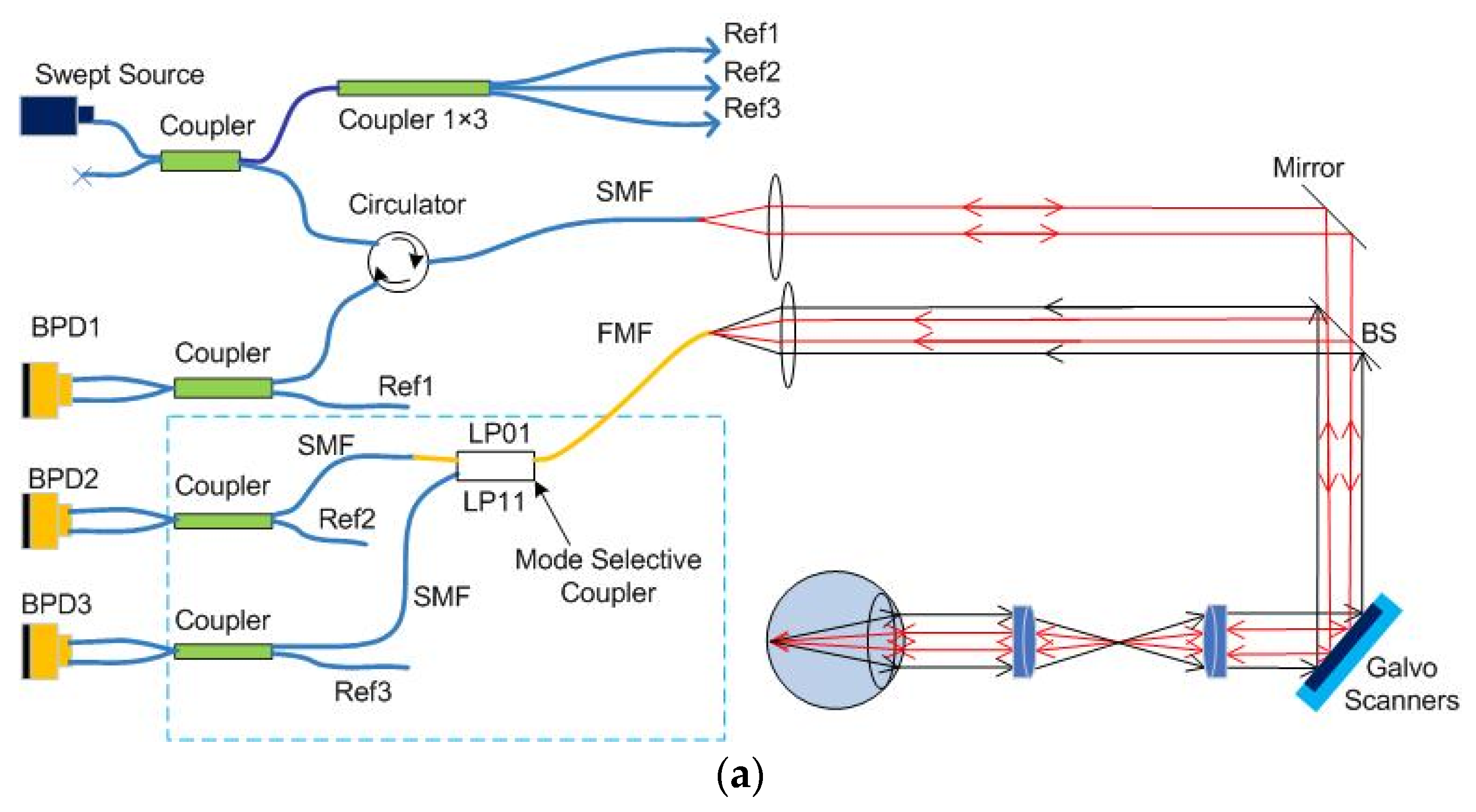
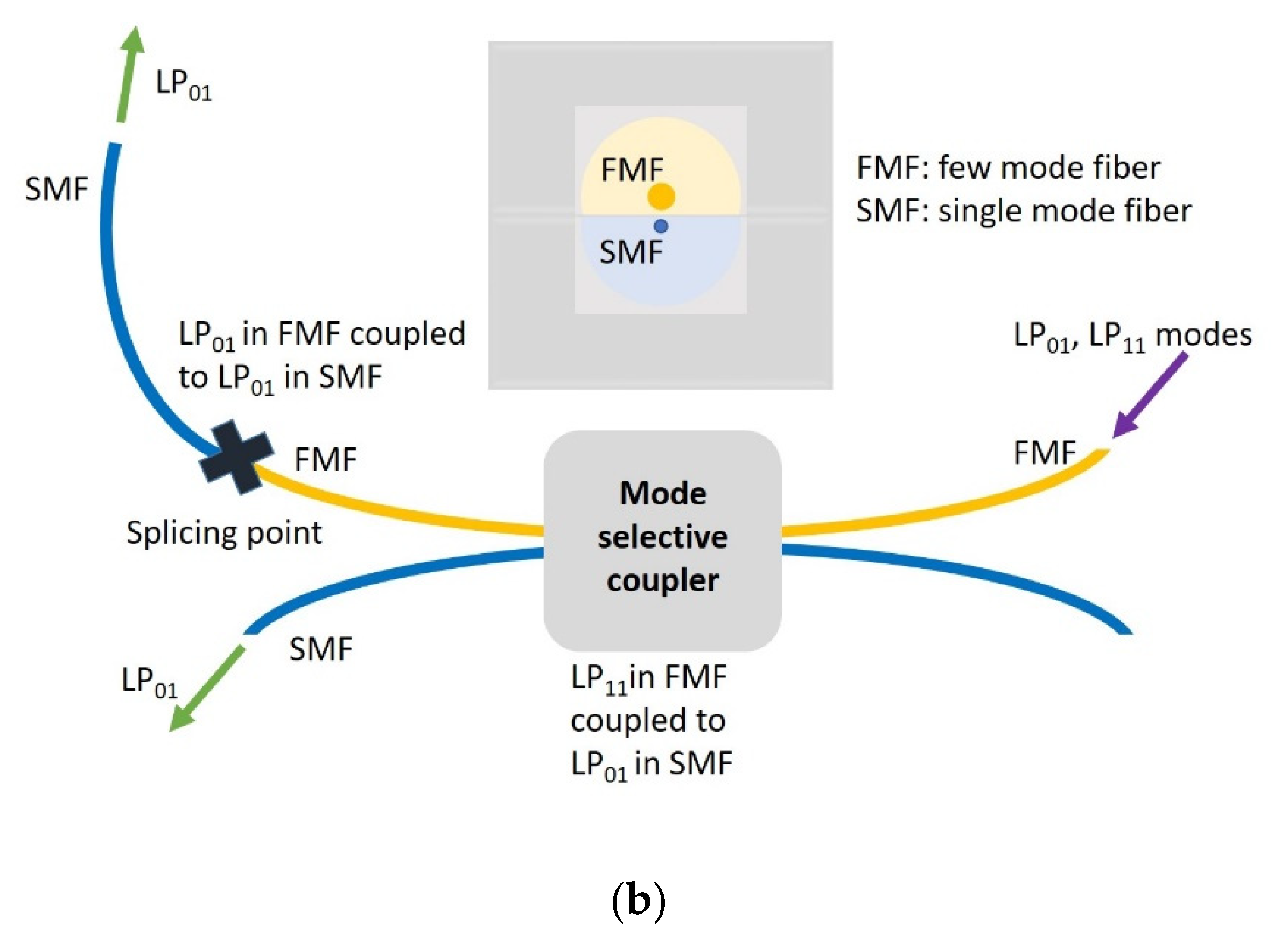
2. Operating Principle of the Proposed Multimode OCT System and the Broadband Fiber Optic Mode Coupler
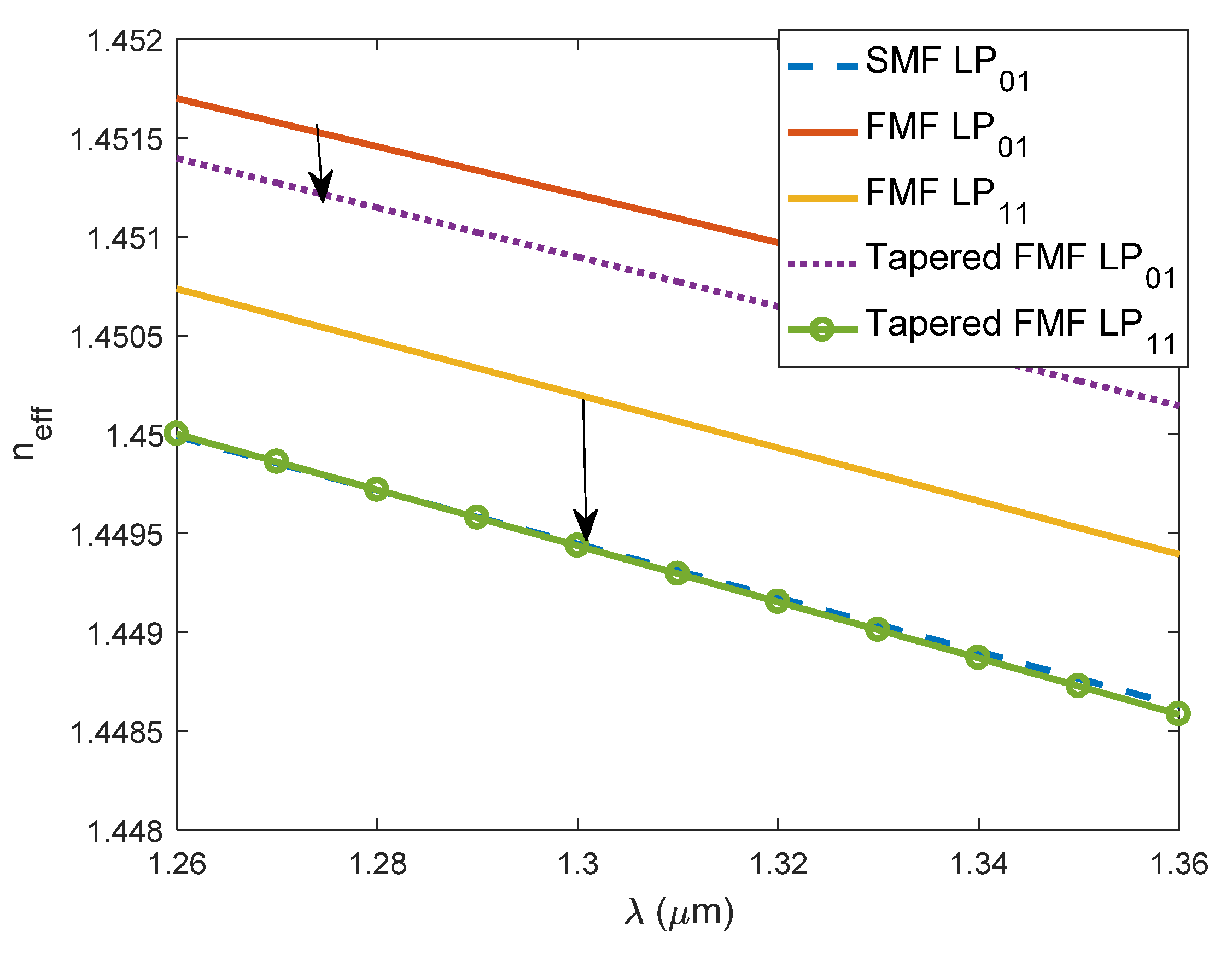
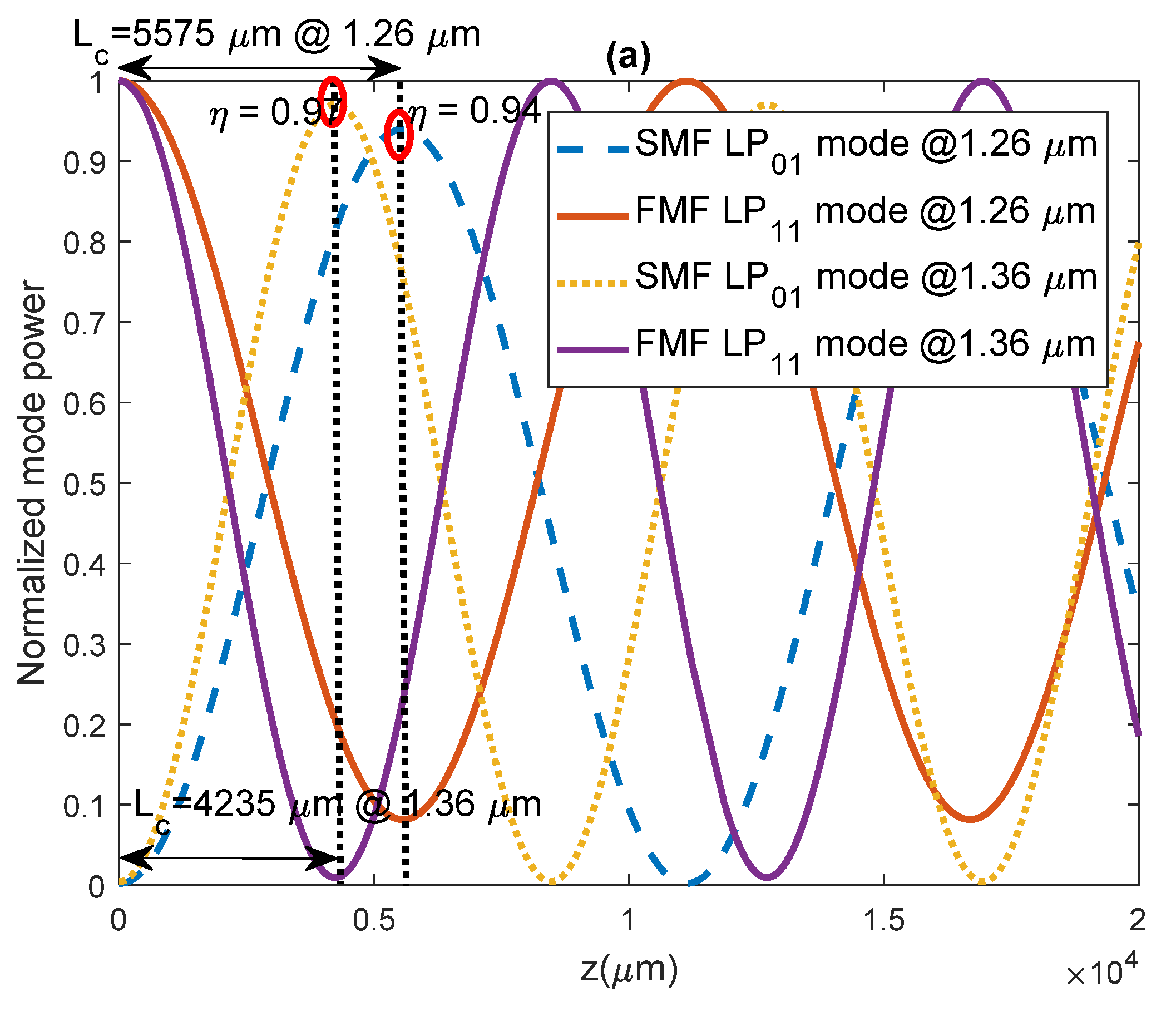
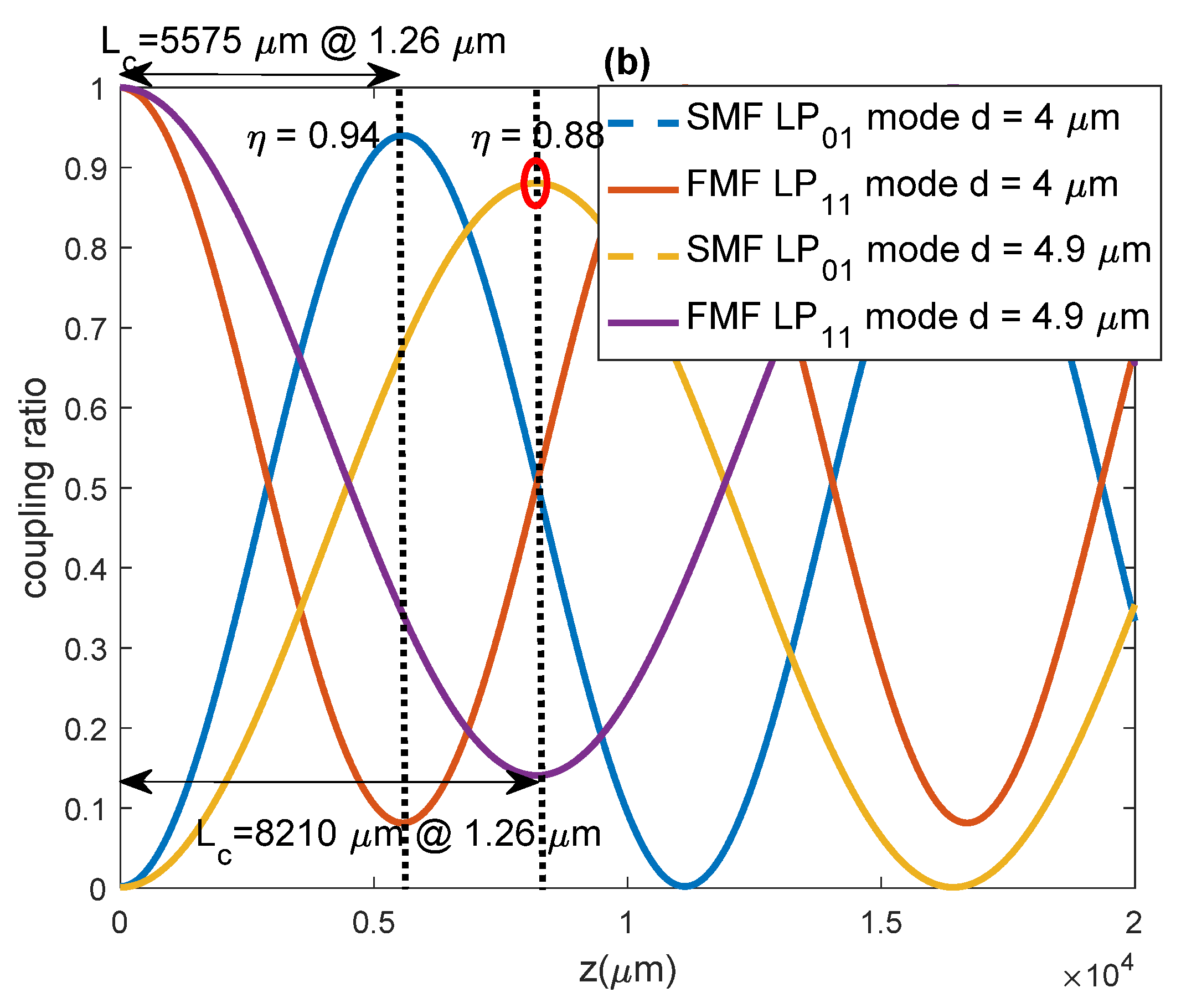
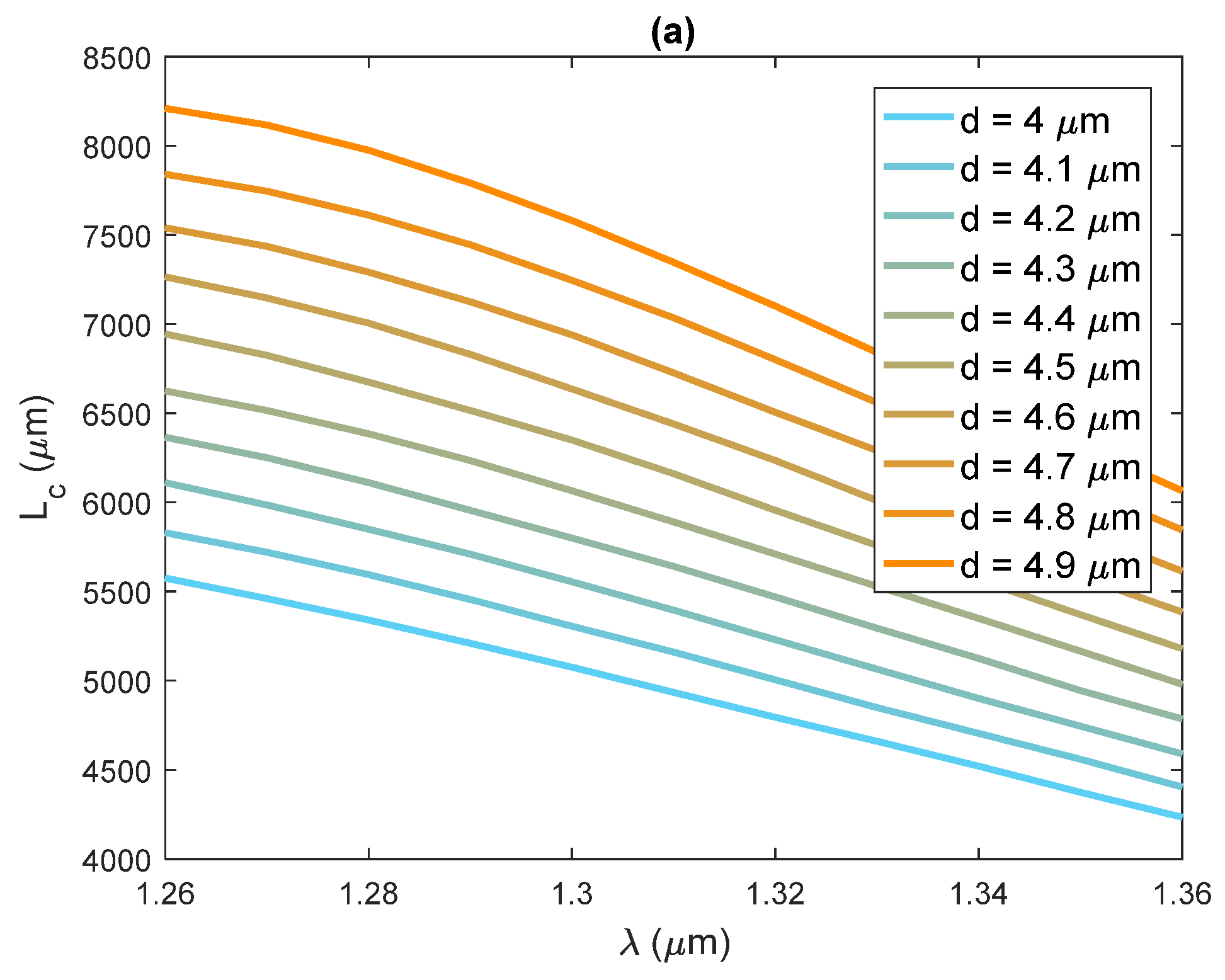
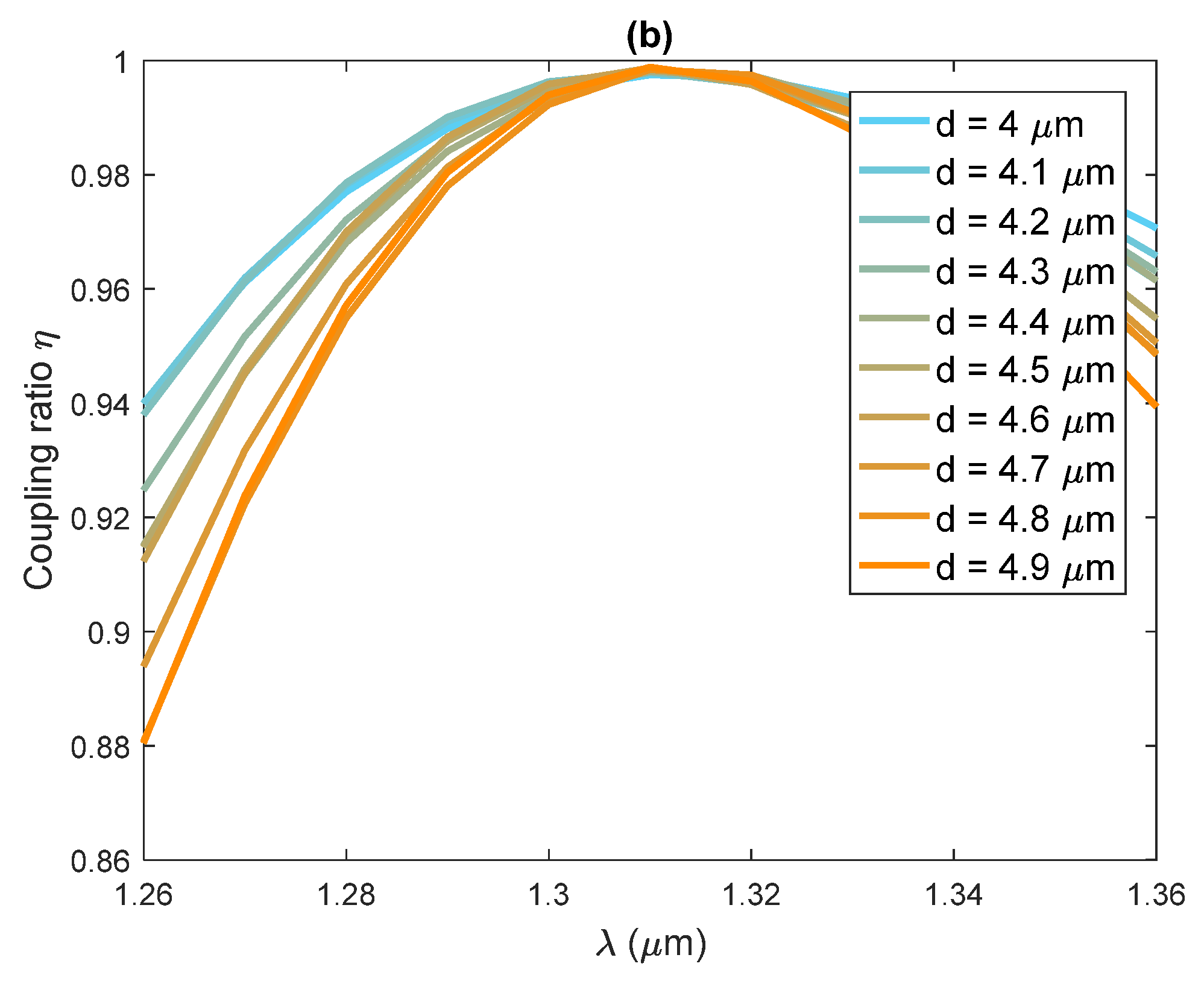
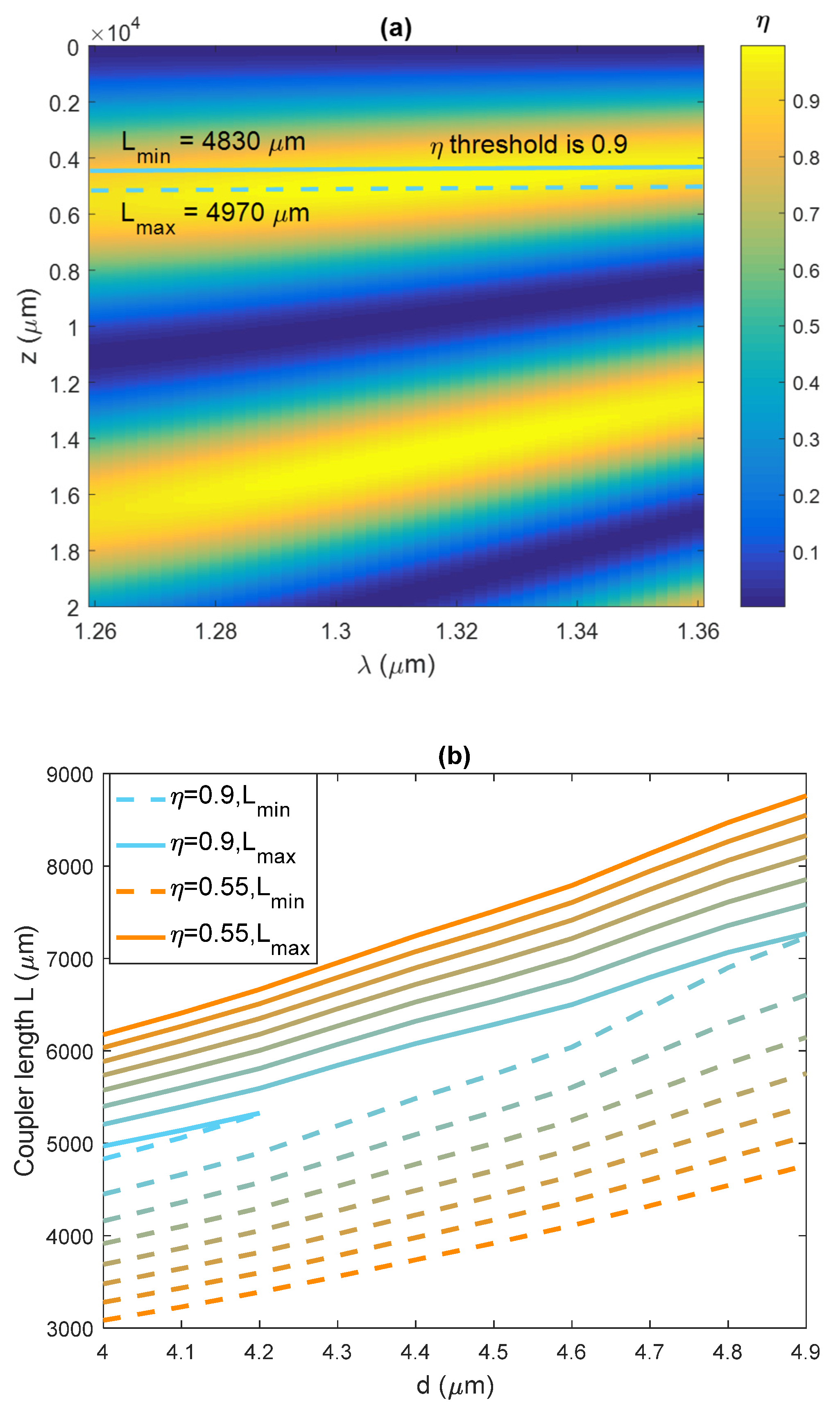
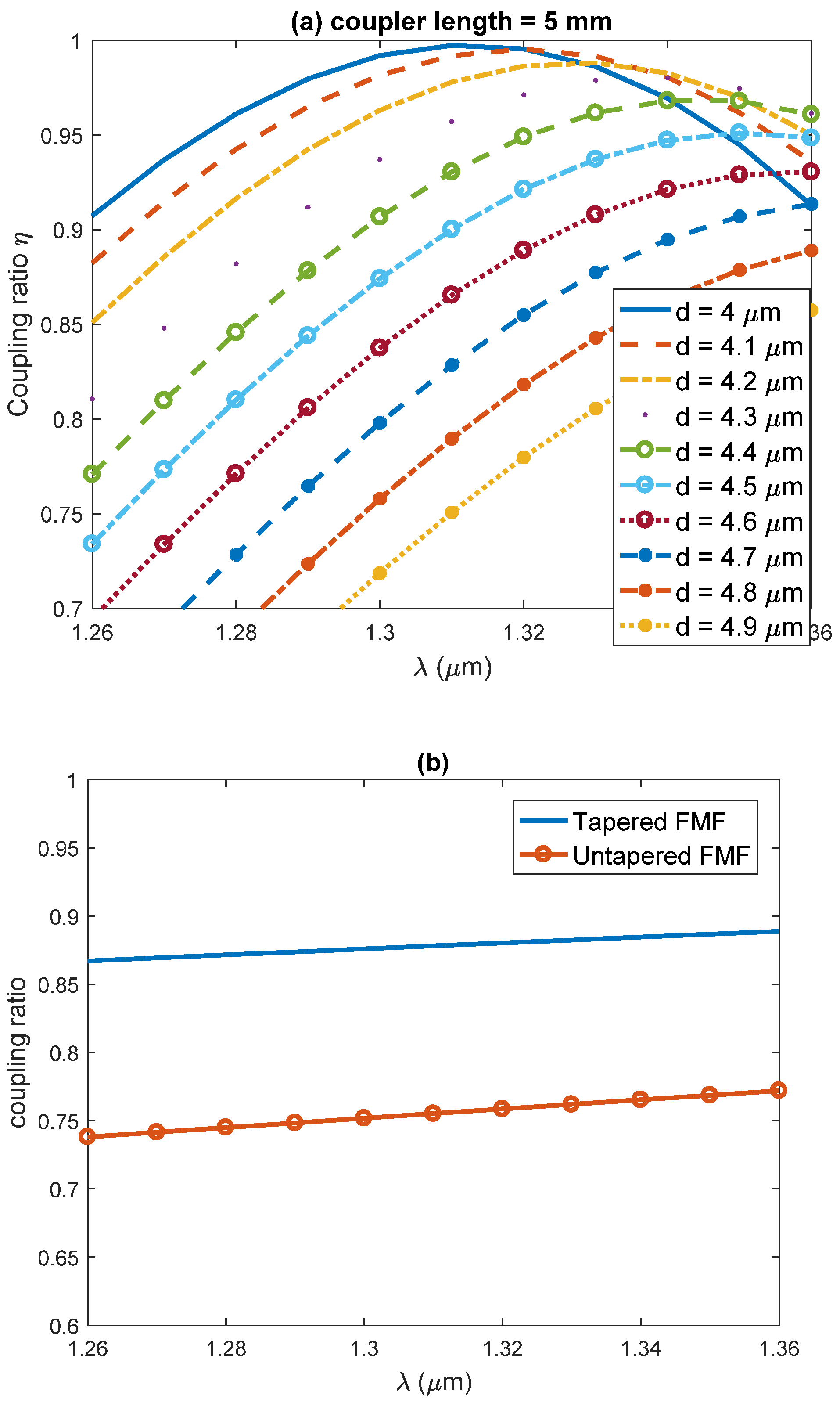
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical coherence tomography. science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R.A. Optical coherence tomography today: Speed, contrast, and multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef]
- Vakoc, B.J.; Lanning, R.M.; Tyrrell, J.A.; Padera, T.P.; Bartlett, L.A.; Stylianopoulos, T.; Munn, L.L.; Tearney, G.J.; Fukumura, D.; Jain, R.K.; et al. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat. Med. 2009, 15, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.-F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based handheld scanning probe with pre-shaped input signals for distortion-free images in Gabor-domain optical coherence microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.K. Signal degradation by multiple scattering in optical coherence tomography of dense tissue: A Monte Carlo study towards optical clearing of biotissues. Phys. Med. Biol. 2002, 47, 2281–2299. [Google Scholar] [CrossRef]
- Park, H.-Y.L.; Lee, N.Y.; Choi, J.A.; Park, C.K. Measurement of scleral thickness using swept-source optical coherence tomography in patients with open-angle glaucoma and myopia. Am. J. Ophthalmol. 2014, 157, 876–885. [Google Scholar] [CrossRef] [PubMed]
- Ikuno, Y.; Nouchi, T.; Yasuno, Y. Scleral and Choroidal Thickness in Normal Subjects Measured by High-Penetration Optical Coherence Tomography With Long Wavelength. Investig. Ophthalmol. Vis. Sci. 2010, 51, 1634. [Google Scholar]
- Willemse, J.; Gräfe, M.G.O.; Verbraak, F.D.; Boer, J.F.d. In Vivo 3D Determination of Peripapillary Scleral and Retinal Layer Architecture Using Polarization-Sensitive Optical Coherence Tomography. Transl. Vis. Sci. Technol. 2020, 9, 21. [Google Scholar] [CrossRef]
- Spaide, R.F.; Fujimoto, J.G.; Waheed, N.K.; Sadda, S.R.; Staurenghi, G. Optical coherence tomography angiography. Prog. Retin. Eye Res. 2018, 64, 1–55. [Google Scholar] [CrossRef]
- Yoshida, S.; Tanaka, S.; Hirata, M.; Mouri, R.; Kaneko, I.; Oka, S.; Yoshihara, M.; Chayama, K. Optical biopsy of GI lesions by reflectance-type laser-scanning confocal microscopy. Gastrointest. Endosc. 2007, 66, 144–149. [Google Scholar] [CrossRef]
- Bezerra, H.G.; Costa, M.A.; Guagliumi, G.; Rollins, A.M.; Simon, D.I. Intracoronary Optical Coherence Tomography: A Comprehensive Review. JACC Cardiovasc. Interv. 2009, 2, 1035–1046. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Gardecki, J.A.; Nadkarni, S.K.; Toussaint, J.D.; Yagi, Y.; Bouma, B.E.; Tearney, G.J. Imaging the subcellular structure of human coronary atherosclerosis using micro–optical coherence tomography. Nat. Med. 2011, 17, 1010–1014. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.C.; Ahsen, O.O.; Liang, K.; Wang, Z.; Figueiredo, M.; Giacomelli, M.G.; Potsaid, B.; Huang, Q.; Mashimo, H.; Fujimoto, J.G. Endoscopic optical coherence tomography angiography microvascular features associated with dysplasia in Barrett’s esophagus (with video). Gastrointest. Endosc. 2017, 86, 476–484.e3. [Google Scholar] [CrossRef]
- White, B.R.; Pierce, M.C.; Nassif, N.; Cense, B.; Park, B.H.; Tearney, G.J.; Bouma, B.E.; Chen, T.C.; de Boer, J.F. In vivo dynamic human retinal blood flow imaging using ultra-high-speed spectral domain optical Doppler tomography. Opt. Express 2003, 11, 3490–3497. [Google Scholar] [CrossRef]
- Leitgeb, R.; Hitzenberger, C.K.; Fercher, A.F. Performance of fourier domain vs. time domain optical coherence tomography. Opt. Express 2003, 11, 889–894. [Google Scholar] [CrossRef] [PubMed]
- You, J.-W.; Chen, T.C.; Mujat, M.; Hyle Park, B.; de Boer, J.F. Pulsed illumination spectral-domain optical coherence tomography for human retinal imaging. Opt. Express 2006, 14, 6739–6748. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.H.; Tearney, G.J.; Bouma, B.E.; Park, B.H.; de Boer, J.F. High-speed spectral-domain optical coherence tomography at 1.3 µm wavelength. Opt. Express 2003, 11, 3598–3604. [Google Scholar] [CrossRef]
- Nassif, N.; Cense, B.; Hyle Park, B.; Yun, S.H.; Chen, T.C.; Bouma, B.E.; Tearney, G.J.; de Boer, J.F. In vivo human retinal imaging by ultrahigh-speed spectral domain optical coherence tomography. Opt. Lett. 2004, 29, 480–482. [Google Scholar] [CrossRef]
- Eugui, P.; Lichtenegger, A.; Augustin, M.; Harper, D.J.; Fialová, S.; Wartak, A.; Hitzenberger, C.K.; Baumann, B. Few-Mode Fiber Detection for Tissue Characterization in Optical Coherence Tomography. In Proceedings of the Optical Coherence Imaging Techniques and Imaging in Scattering Media II, Munich Germany, 25–29 June 2017; Wojtkowski, M., Ed.; [Google Scholar]
- Eugui, P.; Lichtenegger, A.; Augustin, M.; Harper, D.J.; Muck, M.; Roetzer, T.; Wartak, A.; Konegger, T.; Widhalm, G.; Hitzenberger, C.K.; et al. Beyond backscattering: Optical neuroimaging by BRAD. Biomed. Opt. Express 2018, 9, 2476–2494. [Google Scholar] [CrossRef]
- Sivry-Houle, M.P.d.; Beaudoin, S.B.; Brais-Brunet, S.; Dehaes, M.; Godbout, N.; Boudoux, C. All-fiber few-mode optical coherence tomography using a modally-specific photonic lantern. Biomed. Opt. Express 2021, 12, 5704–5719. [Google Scholar] [CrossRef]
- Chang, S.H.; Moon, S.-R.; Chen, H.; Ryf, R.; Fontaine, N.K.; Park, K.J.; Kim, K.; Lee, J.K. All-fiber 6-mode multiplexers based on fiber mode selective couplers. Opt. Express 2017, 25, 5734–5741. [Google Scholar] [CrossRef]
- Corral, J.L.; Garcia-Rodriguez, D.; Llorente, R. Mode-Selective Couplers for Two-Mode Transmission at 850 nm in Standard SMF. IEEE Photonics Technol. Lett. 2016, 28, 425–428. [Google Scholar] [CrossRef]
- Li, A.; Chen, X.; Amin, A.A.; Shieh, W. Fused Fiber Mode Couplers for Few-Mode Transmission. IEEE Photonics Technol. Lett. 2012, 24, 1953–1956. [Google Scholar]
- Bremer, K.; Schlangen, S.; Böhm, S.; Wellmann, F.; Steinke, M.; Neumann, J.; Roth, B.; Overmeyer, L. Investigation of grating assisted mode-selective few-mode fused fiber couplers. In Proceedings of the 2019 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference, Munich Germany, 23–27 June 2019. [Google Scholar]
- Park, K.J.; Song, K.Y.; Kim, Y.K.; Lee, J.H.; Kim, B.Y. Broadband mode division multiplexer using all-fiber mode selective couplers. Opt. Express 2016, 24, 3543–3549. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.J.J.; Liu, L.; Dong, H.; Zhang, H. Design of a Tapered Few-Mode Fiber based Broadband Mode Coupler for Multimode OCT. In Proceedings of the Imaging and Applied Optics Congress 2022 (3D, AOA, COSI, ISA, pcAOP), Vancouver, BC, Canada, 11–15 July 2022. [Google Scholar]
- Malitson, H. Interspecimen Comparison of the Refractive Index of Fused Silica*,†. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Okamoto, K. Fundamentals of Optical Waveguides; Academic press: Cambridge, MA, USA, 2010. [Google Scholar]
- Hu, D.J.J.; Shum, P.P.; Lim, J.L.; Cui, Y.; Milenko, K.; Wang, Y.; Wolinski, T. A Compact and Temperature-Sensitive Directional Coupler Based on Photonic Crystal Fiber Filled With Liquid Crystal 6CHBT. IEEE Photonics J. 2012, 4, 2010–2016. [Google Scholar] [CrossRef]
- Xu, Z.; Lim, J.; Hu, D.J.J.; Sun, Q.; Wong, R.Y.-N.; Li, K.; Jiang, M.; Shum, P.P. Investigation of temperature sensing characteristics in selectively infiltrated photonic crystal fiber. Opt. Express 2016, 24, 1699–1707. [Google Scholar] [CrossRef]
| Fiber Parameters | SMF | FMF |
|---|---|---|
| Core diameter (untapered) | 8 μm | 19 μm |
| Refractive index of the cladding | Sellmeier Equation for silica | Sellmeier Equation for silica |
| Numerical aperture (NA) | 0.12 | 0.12 |
| Tapering ratio | 1 | 0.7–0.9 |
| SMF core to FMF core separation | 4–4.9 μm | |
| Wavelength | 1.26–1.36 μm | |
| Coupler length | Up to 20 mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, D.J.J.; Liu, L.; Dong, H.; Zhang, H. Design of a Broadband Fiber Optic Mode Coupler for Multimode Optical Coherence Tomography. Photonics 2023, 10, 162. https://doi.org/10.3390/photonics10020162
Hu DJJ, Liu L, Dong H, Zhang H. Design of a Broadband Fiber Optic Mode Coupler for Multimode Optical Coherence Tomography. Photonics. 2023; 10(2):162. https://doi.org/10.3390/photonics10020162
Chicago/Turabian StyleHu, Dora Juan Juan, Linbo Liu, Hui Dong, and Hailiang Zhang. 2023. "Design of a Broadband Fiber Optic Mode Coupler for Multimode Optical Coherence Tomography" Photonics 10, no. 2: 162. https://doi.org/10.3390/photonics10020162
APA StyleHu, D. J. J., Liu, L., Dong, H., & Zhang, H. (2023). Design of a Broadband Fiber Optic Mode Coupler for Multimode Optical Coherence Tomography. Photonics, 10(2), 162. https://doi.org/10.3390/photonics10020162





