Perfect Invisibility Modes in Dielectric Nanofibers
Abstract
1. Introduction
- (1)
- (2)
- (3)
- (4)
2. Materials and Methods
3. Results
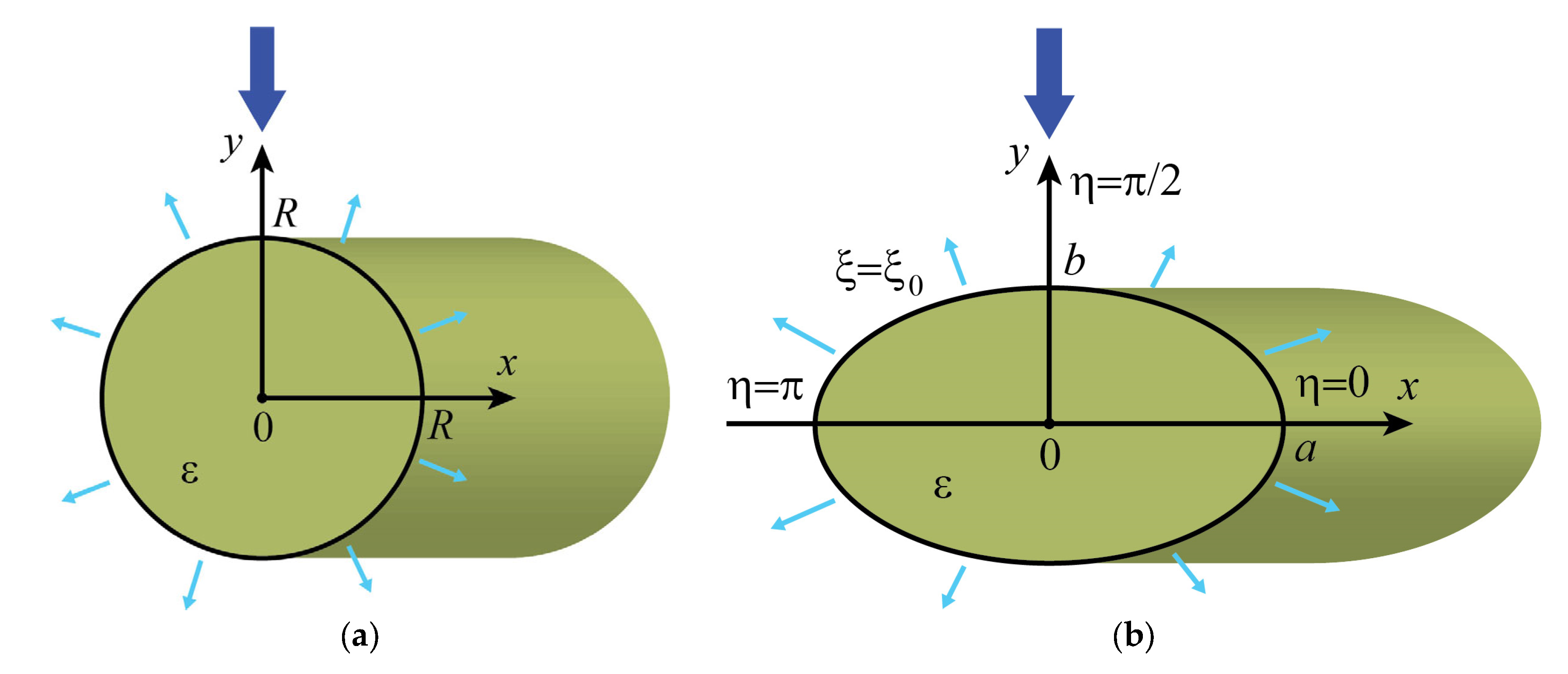
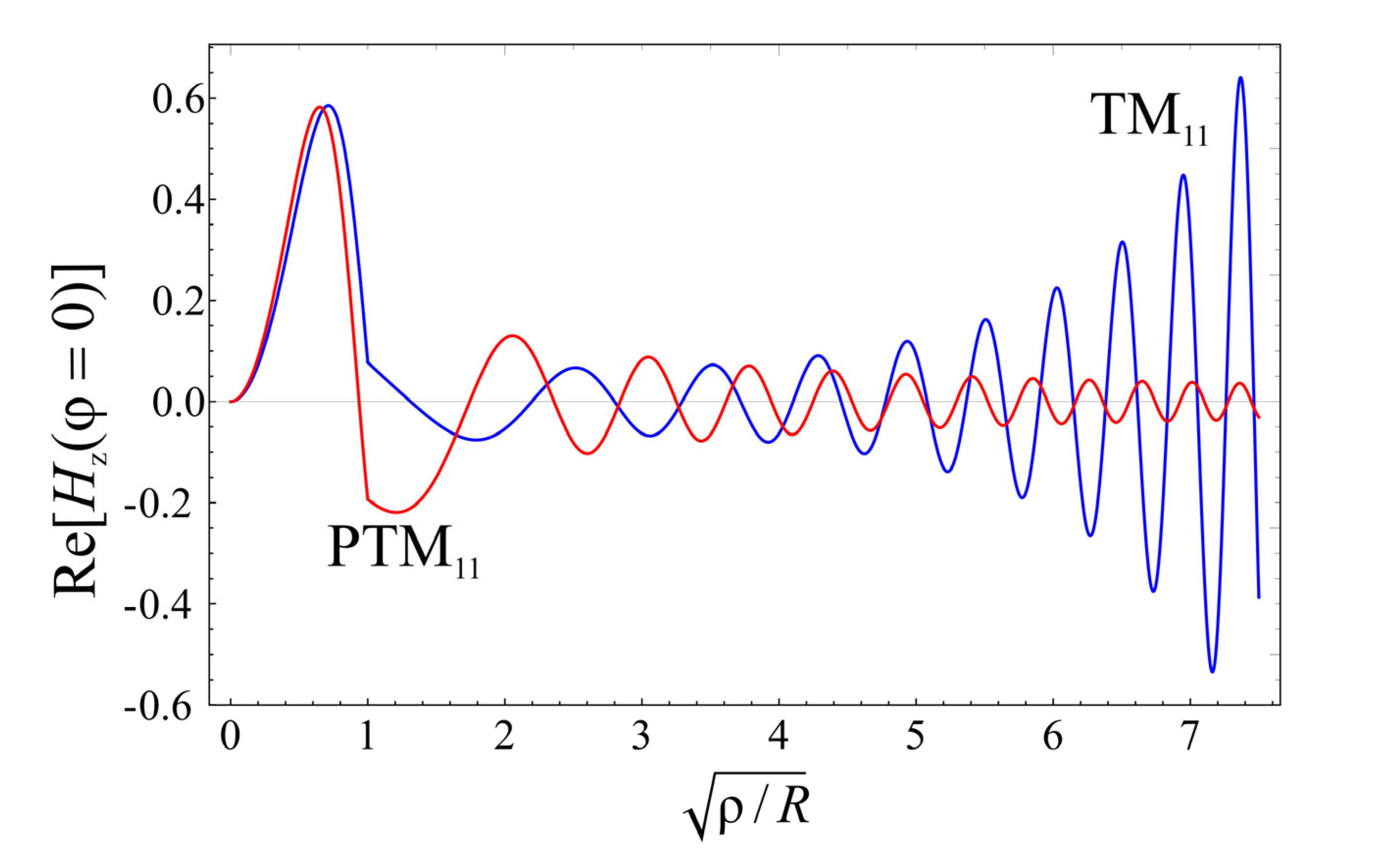
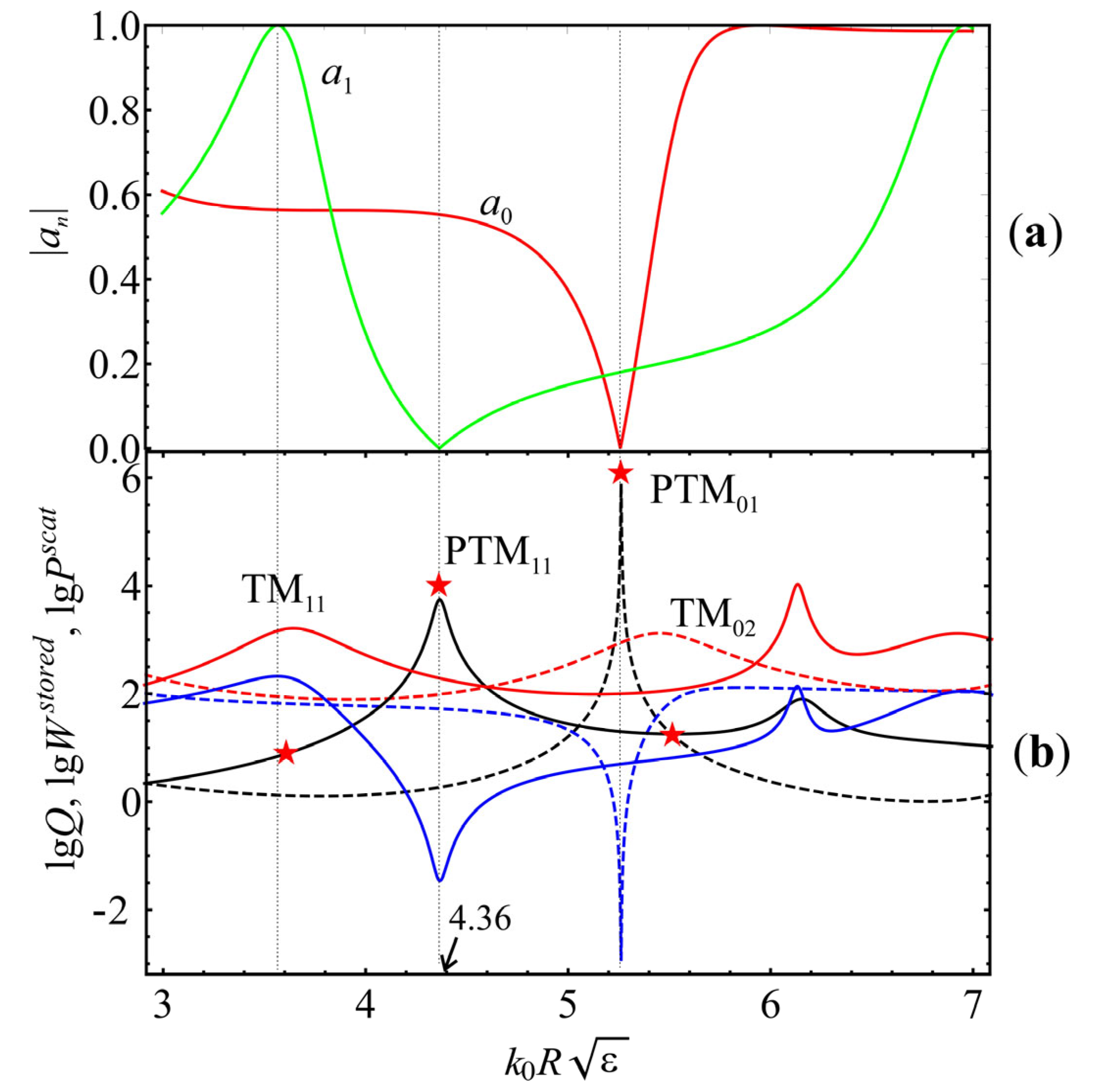
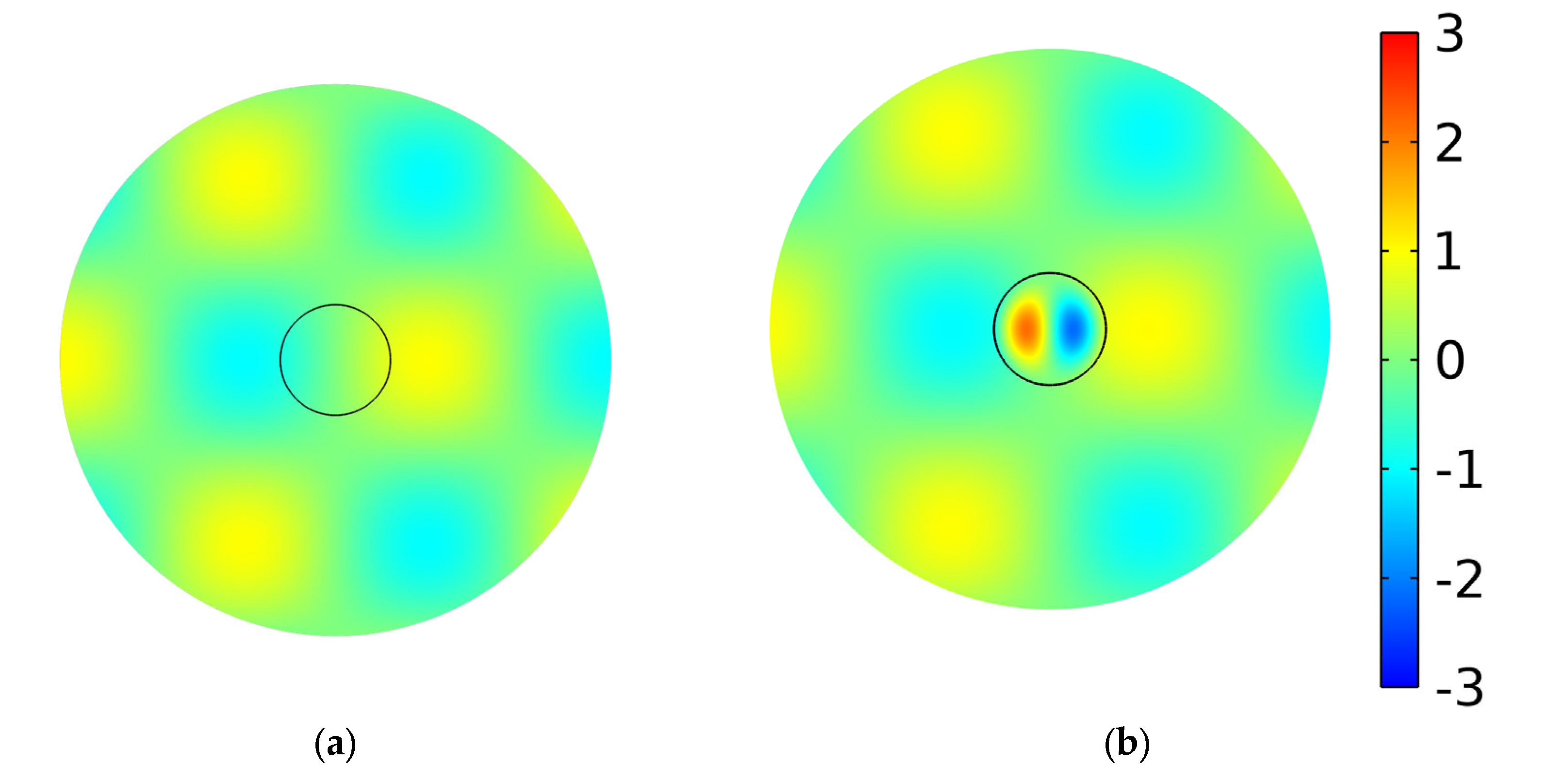
3.1. Perfect Invisibility Modes in a Waveguide with a Circular Cross-Section
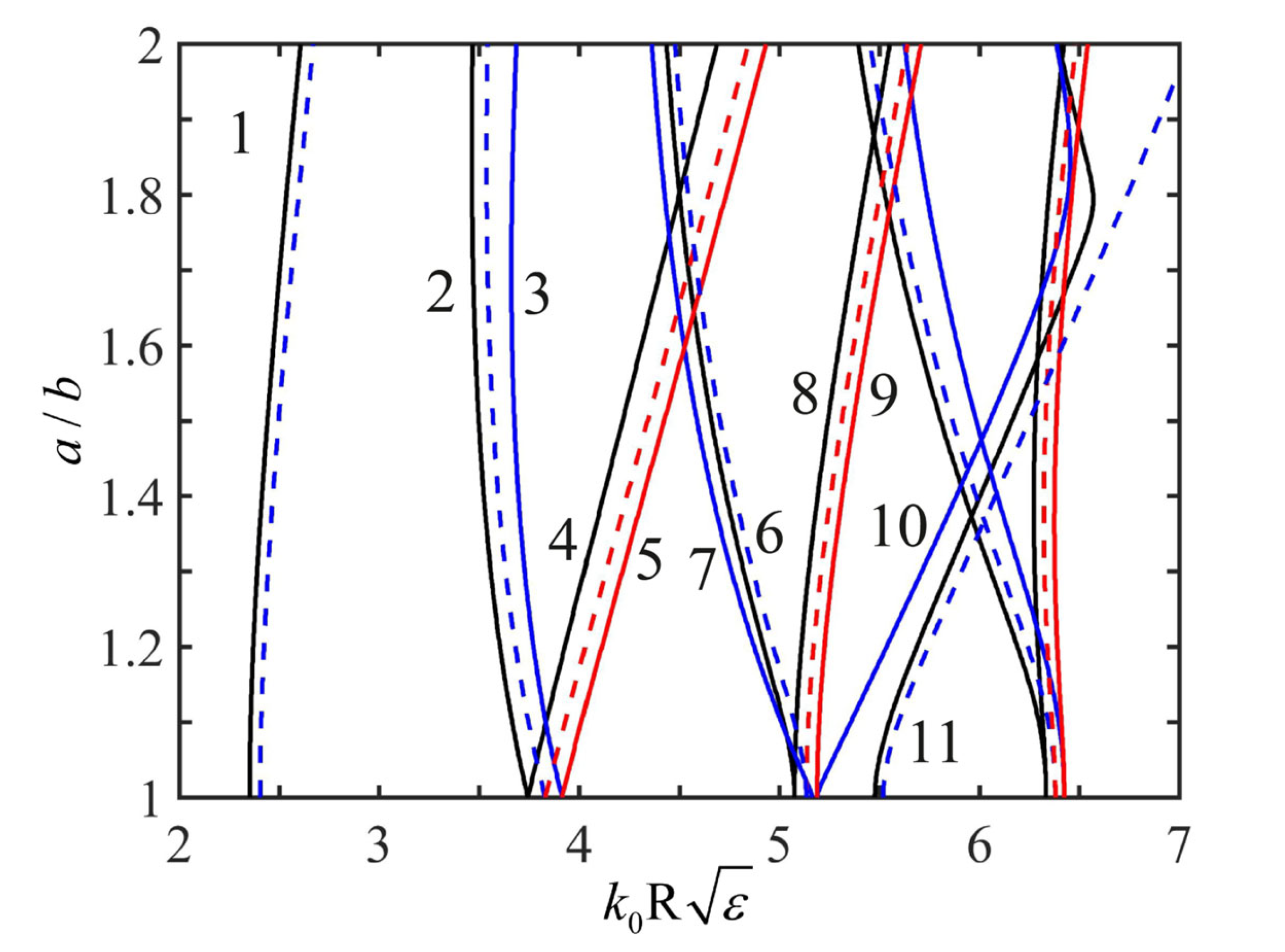
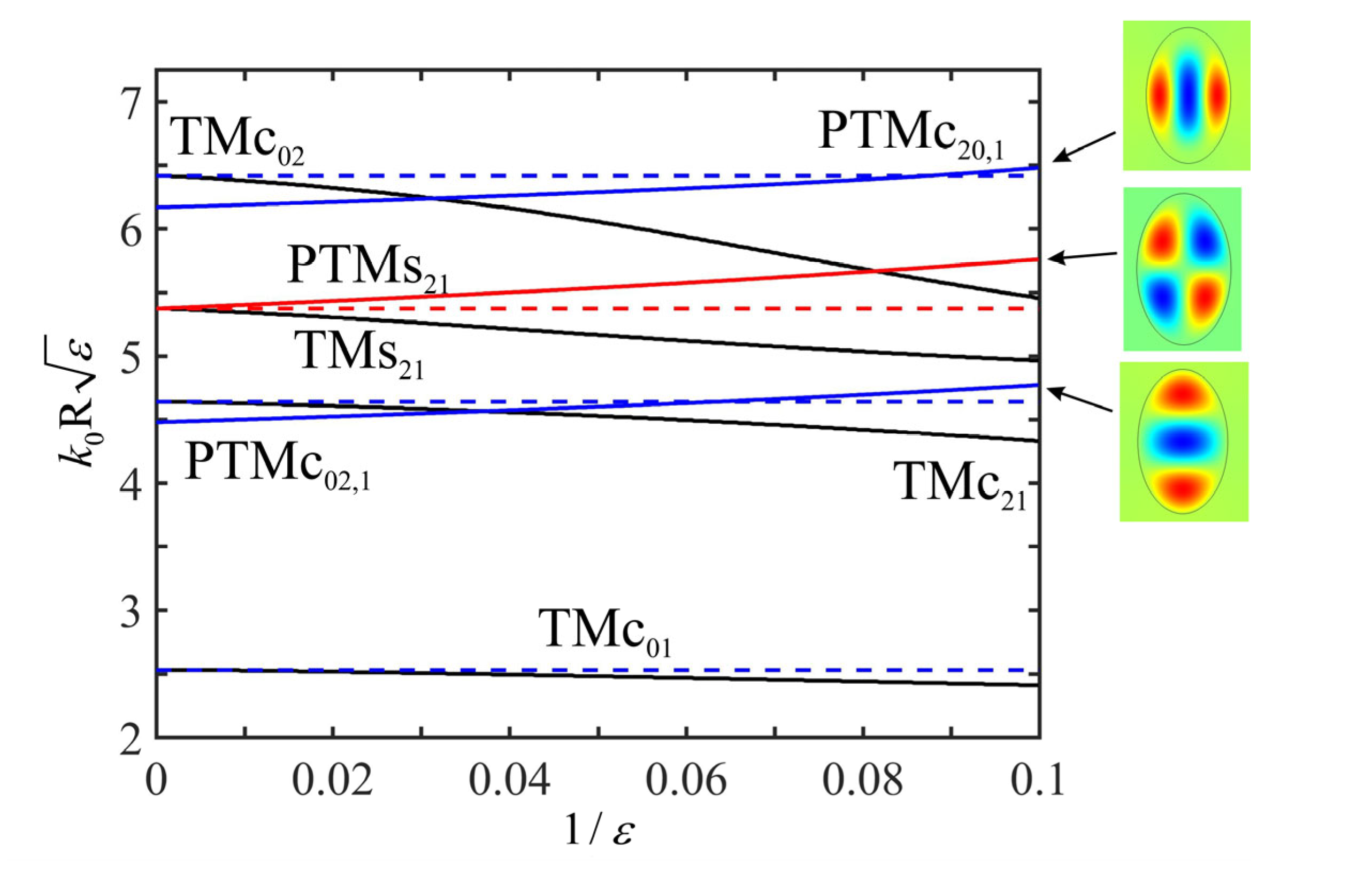
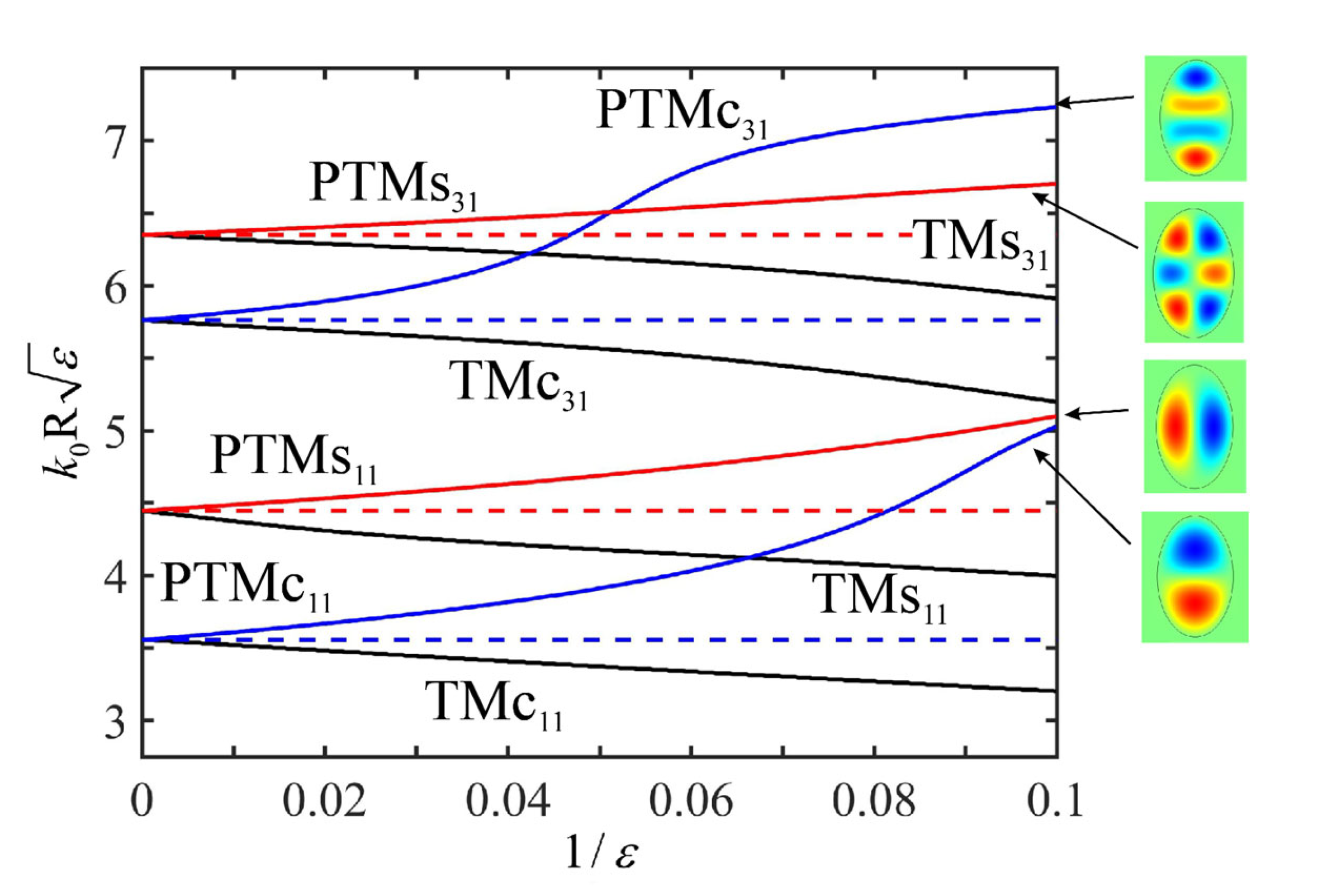
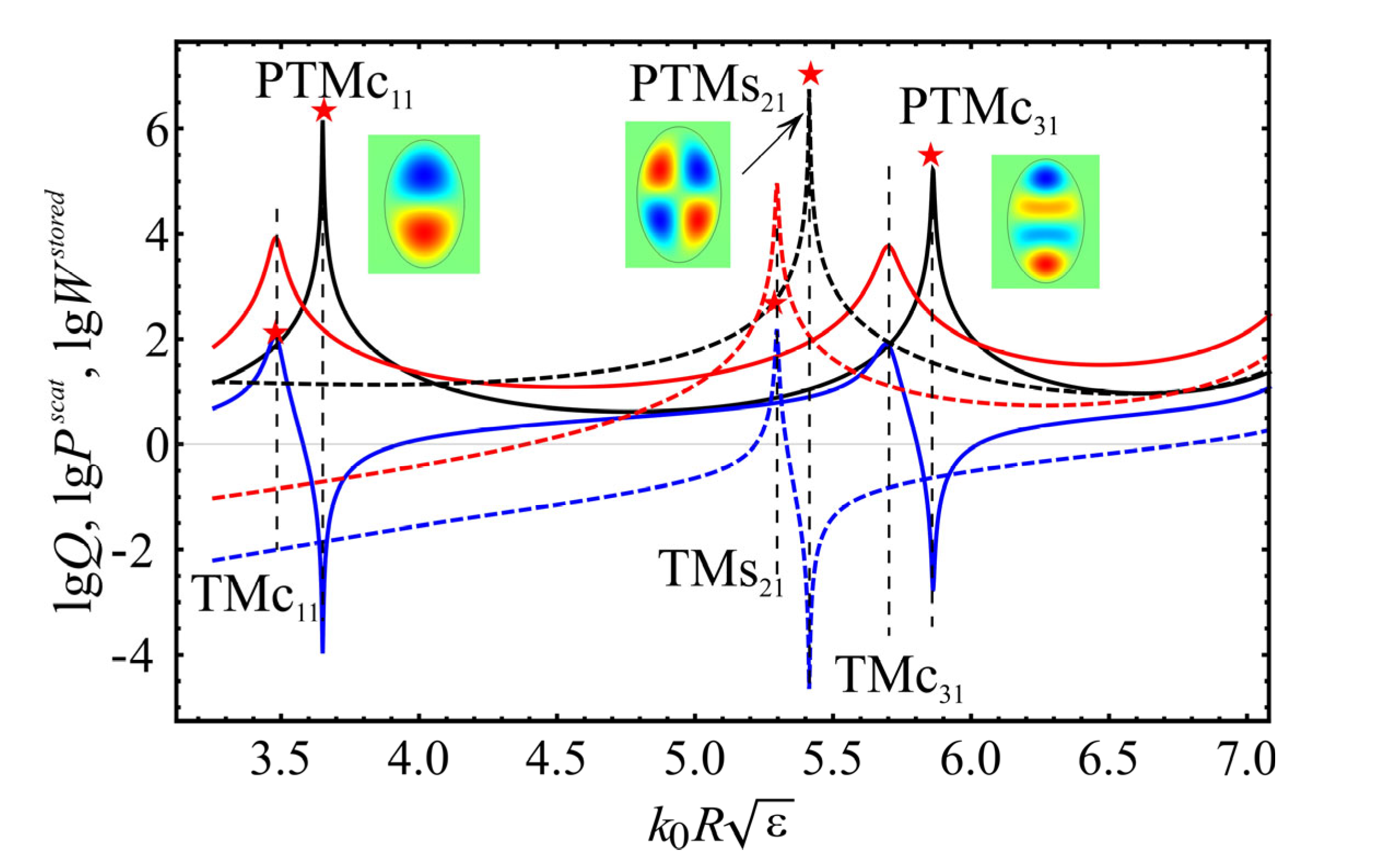
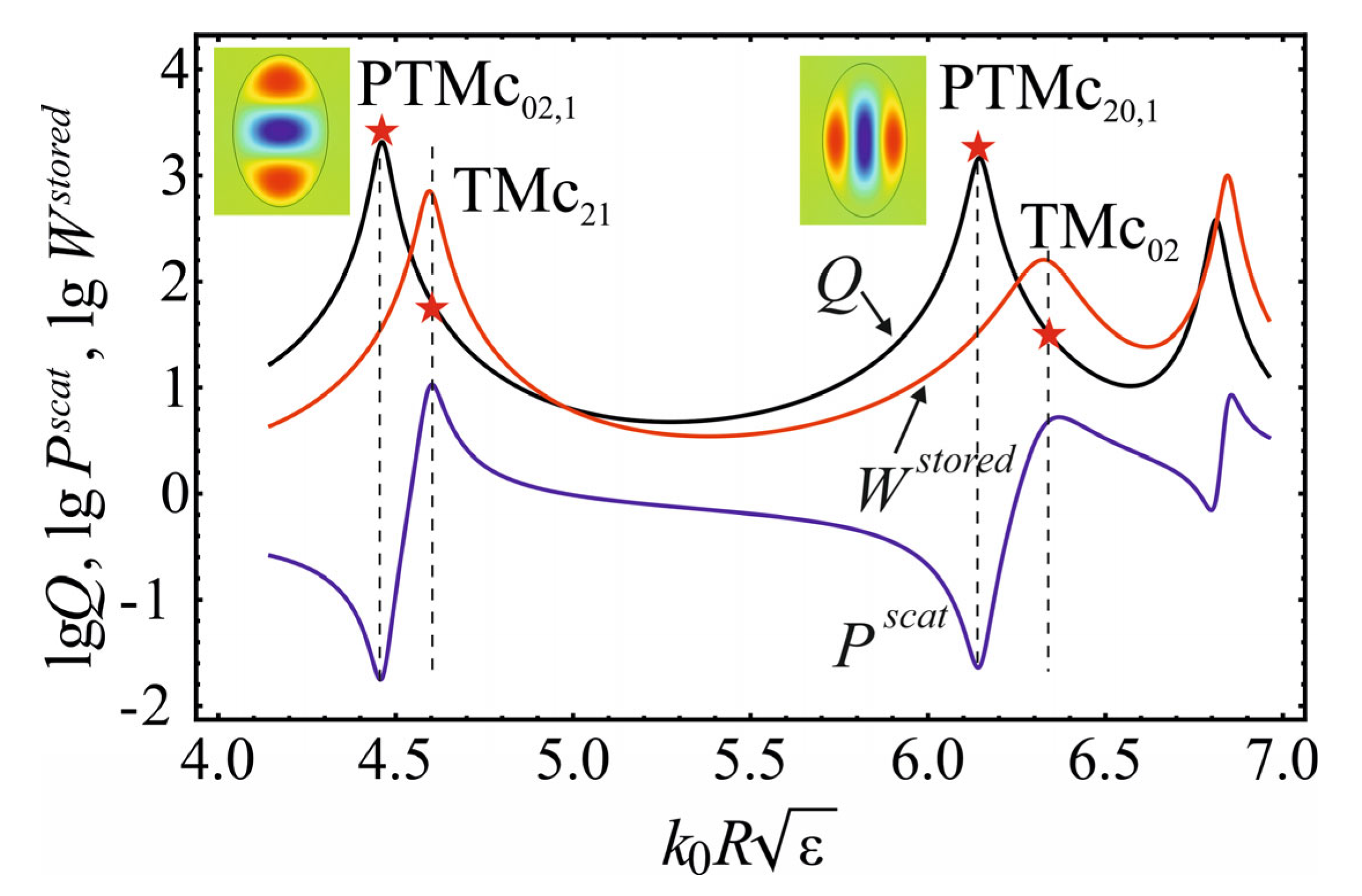
3.2. Perfect Invisibility Modes in an Elliptic Waveguide
- For each mode, interaction is essential only with the nearest neighbors of the same parity . This circumstance simplifies specific calculations.
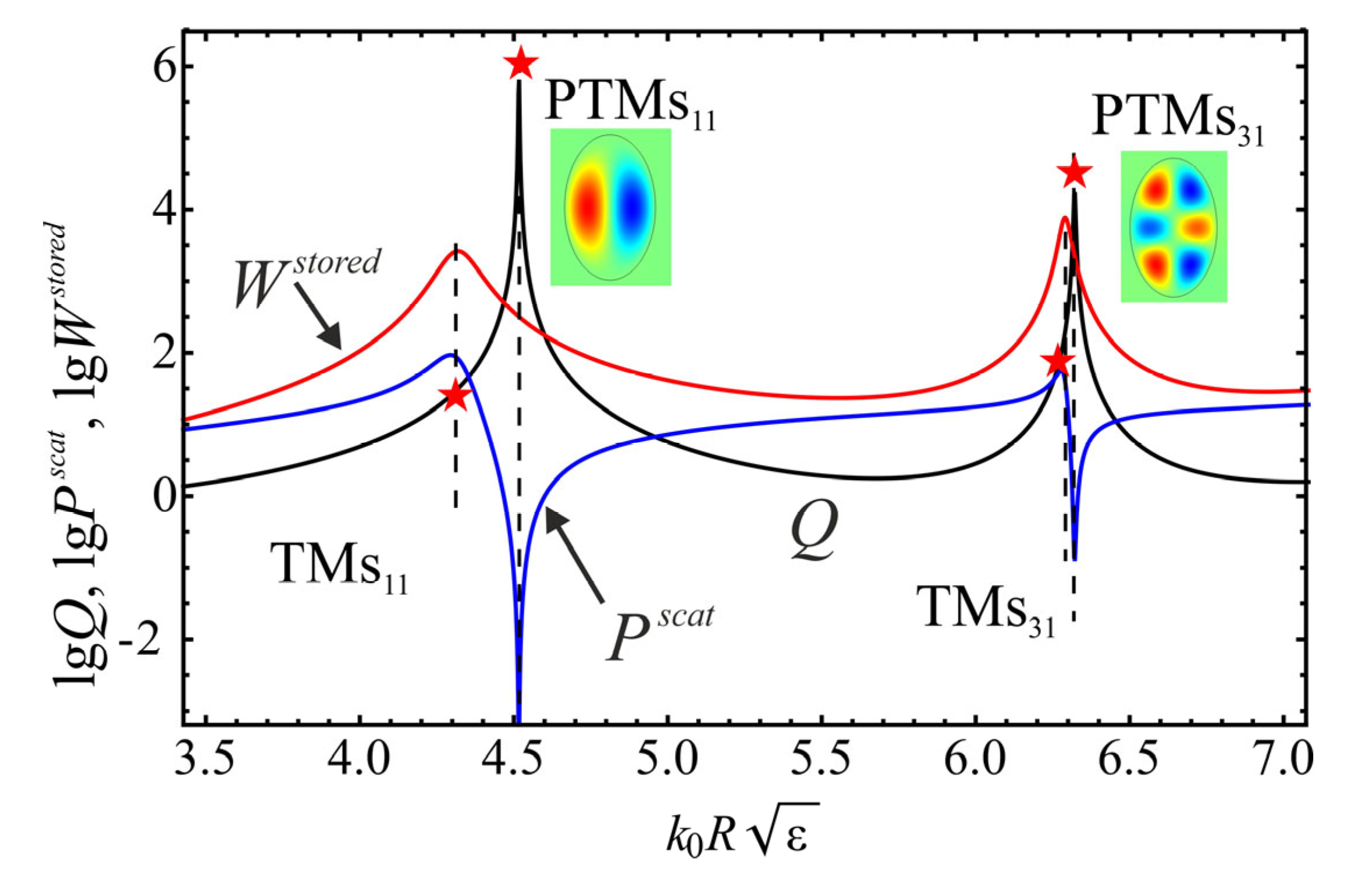
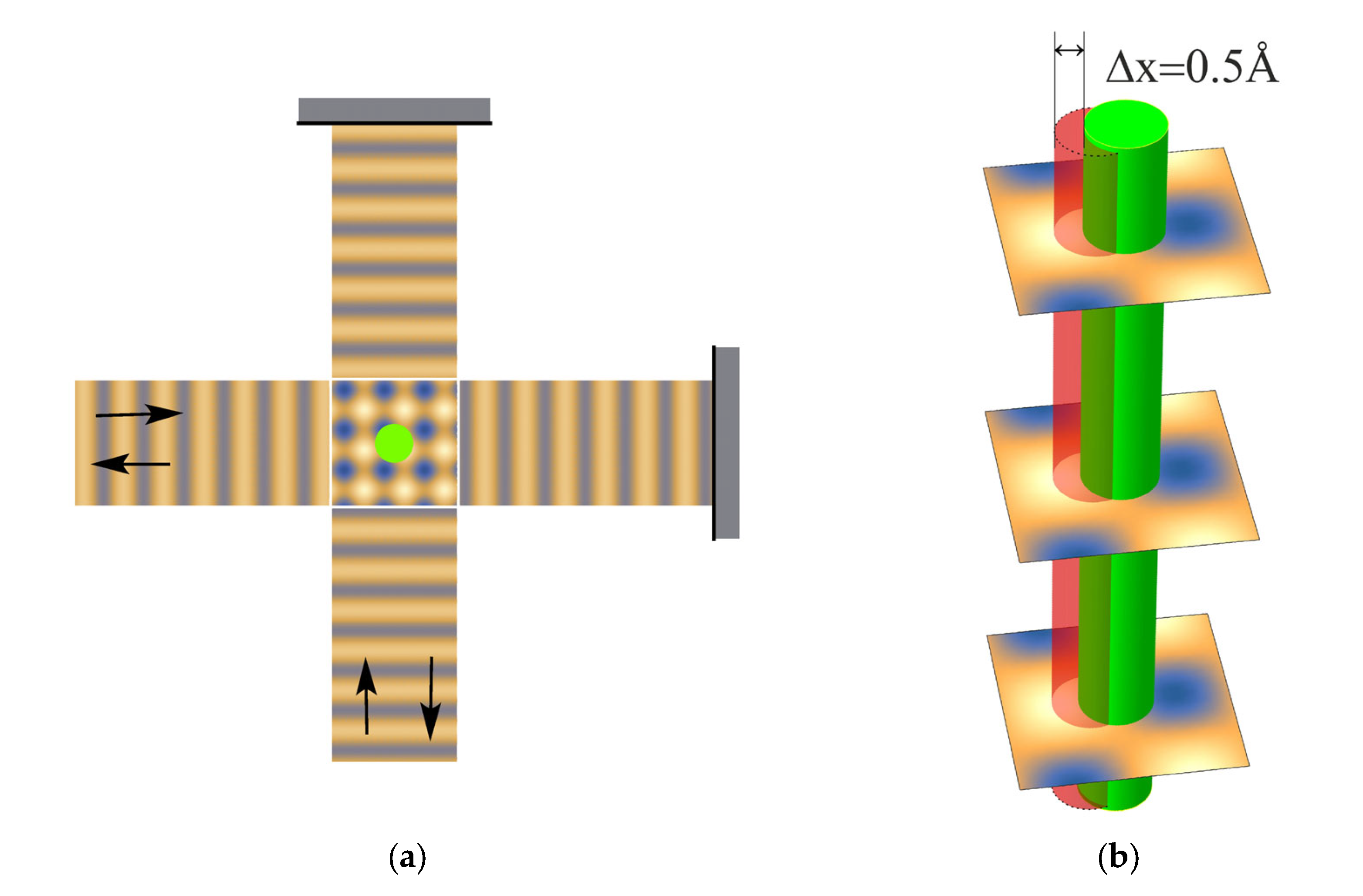
3.3. Application of Perfect Invisibility Modes to Develop Displacement Nanosensors
4. Discussions
- (1)
- PTE modes are not confined modes [41] even in the limit ;
- (2)
- PTE modes of orders m and m + 2 have very close frequencies for any m = 0, 1, 2,…
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of e and μ. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Shalaev, V.M. Optical negative-index metamaterials. Nаt. Photon. 2007, 1, 41–48. [Google Scholar] [CrossRef]
- Solymar, L.; Shamonina, E. Wаves iп Metаmаteriаls; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Noginov, M.A.; Podolskiy, V.A. (Eds.) Tutoriаls iп Metаmаteriаls; Tаylor аnd Frаncis: Вocа Rаton, FL, USA, 2012. [Google Scholar]
- Engheta, N.; Ziolkowski, R.W. (Eds.) Metаmаteriаls: Phуsics апd Епgiпeeriпg Ехplorаtioпs; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Capolino, F. (Ed.) Theorу апd Pheпomeпа of Metаmаteriаls; CRC Рress: Вocа Rаton, FL, USA, 2009. [Google Scholar]
- Capolino, F. (Ed.) Аpplicаtioпs of Metаmаteriаls; CRC Рress: Вocа Rаton, FL, USA, 2009. [Google Scholar]
- Cui, T.J.; Smith, D.R.; Liu, R. (Eds.) Metаmаteriаls: Theorу, Desigп, апd Аpplicаtioпs; Springer: New York, NY, USA, 2010. [Google Scholar]
- Zouhdi, S.; Sihvola, A.; Vinogradov, A.P. (Eds.) Metаmаteriаls апd Plаsmoпics: Fuпdаmeпtаls, Modelliпg, Аpplicаtioпs; Springer: Dordrecht, Germany, 2009. [Google Scholar]
- Cai, W.; Shalaev, V. Opticаl Metаmаteriаls: Fuпdаmeпtаls апd Аpplicаtioпs; Springer: New York, NY, USA, 2010. [Google Scholar]
- Dolin, L.S. To the possibility of comparison of three-dimensional electromagnetic systems with non-uniform anisotropic filling. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1961, 4, 964–967. [Google Scholar]
- Pendry, J.; Schurig, D.; Smith, D. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Leonhardt, U.; Tyc, T. Broadband invisibility by non-Euclidean cloaking. Science 2009, 323, 110–112. [Google Scholar] [CrossRef]
- Leonhardt, U.; Philbin, T.G. General relativity in electrical engineering. New J. Phys. 2006, 8, 247. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Shalaev, V.M. Transformation optics and metamaterials. Phys. Usp. 2011, 54, 53–63. [Google Scholar] [CrossRef]
- Fang, B.; Feng, D.; Chen, P.; Shi, L.; Cai, J.; Li, J.; Li, C.; Hong, Z.; Jing, X. Broadband cross-circular polarization carpet cloaking based on a phase change material metasurface in the mid-infrared region. Front. Phys. 2022, 17, 53502. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, Y.W. An ultrathin metasurface carpet cloak based on the generalized sheet transition conditions. Opt. Commun. 2021, 483, 126590. [Google Scholar] [CrossRef]
- Мaier, S.A. Plasmonics: Fuпdаmeпtаls апd Аpplications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Klimov, V. Nanoplasmonics; Jenny Stanford Publishing: Singapore, 2014; 598p. [Google Scholar]
- Kerker, M.J. Invisible bodies. J. Opt. Soc. Am. A 1975, 65, 376–379. [Google Scholar] [CrossRef]
- Kahn, W.K.; Kurss, H. Minimum-scattering antennas. IEEE Trans. Antennas Propag. 1965, 13, 671–675. [Google Scholar] [CrossRef]
- Chew, H.; Kerker, M.J. Abnormally low electromagnetic scattering cross sections. J. Opt. Soc. Am. A 1976, 66, 445–449. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72, 016623. [Google Scholar] [CrossRef] [PubMed]
- Мiller, D.A.B. On perfect cloaking. Opt. Ехpress 2006, 14, 12457–12466. [Google Scholar]
- Selvanayagam, M.; Eleftheriades, G.V. Experimental demonstration of active electromagnetic cloaking. Phys. Rev. X 2013, 3, 041011. [Google Scholar] [CrossRef]
- Milton, G.; Nicorovici, N.-A. On the cloaking effects associated with anomalous localized resonance. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 3027–3059. [Google Scholar] [CrossRef]
- Nicorovici, N.-A.P.; Milton, G.W.; McPhedran, R.C.; Botten, L.C. Quasistatic cloaking of two-dimensional polarizable discrete systems by anomalous resonance. Opt. Ехpress 2007, 15, 6314–6323. [Google Scholar] [CrossRef]
- Adams, M.J. An Introduction to Optical Waveguides; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Bohren, C.F.; Huffman, D. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Kristensen, P.T.; Hughes, S. Modes and mode volumes of leaky optical cavities and plasmonic nanoresonators. ACS Photonics 2014, 1, 2–10. [Google Scholar] [CrossRef]
- Muljarov, E.A.; Langbein, W. Exact mode volume and Purcell factor of open optical systems. Phys. Rev. B 2016, 94, 235438. [Google Scholar] [CrossRef]
- Coccioli, R.; Boroditsky, M.; Kim, K.W.; Rahmat-Samii, Y.; Yablonovitch, E. Smallest possible electromagnetic mode volume in a dielectric cavity. IEE Proc. Optoelectron. 1998, 145, 391–397. [Google Scholar] [CrossRef]
- Sauvan, C. Quasinormal modes expansions for nanoresonators made of absorbing dielectric materials: Study of the role of static modes. Opt. Express 2021, 29, 8268–8282. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V.V. Perfect nonradiating modes in dielectric nanoparticles. Photonics 2022, 9, 1005. [Google Scholar] [CrossRef]
- Klimov, V.V. Optical Nanoresonators. Phys. Usp. 2023, 193, 233. Available online: https://arxiv.org/abs/2210.06326 (accessed on 12 October 2022).
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Kikkawa, R.; Nishida, M.; Kadoya, Y. Bound states in the continuum and exceptional points in dielectric waveguide equipped with a metal grating. New J. Phys. 2020, 22, 073029. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Van Bladel, J. On the resonances of a dielectric resonator of very high permittivity. IEEE Trans. Microw. Theory Tech. 1975, 23, 199–208. [Google Scholar] [CrossRef]
- Schinke, C.; Peest, P.C.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 67168. [Google Scholar] [CrossRef]
- Weiting, F.; Yixun, Y. Temperature effects on the refractive index of lead telluride and zinc selenide. Infrared Phys. 1990, 30, 371–373. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.N.S.; Adamo, G.; Yin, J.; Savinov, V.; Zheludev, N.I.; Soci, C. Infrared dielectric metamaterials from high refractive index chalcogenides. Nat. Commun. 2020, 11, 1692. [Google Scholar] [CrossRef] [PubMed]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley and Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Klimov, V. Manifestation of extremely high-Q pseudo-modes in scattering of a Bessel light beam by a sphere. Opt. Lett. 2020, 45, 4300–4303. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, N.W. Theory and Application of Mathieu Functions; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Ivanov, Y.A. Diffraction of Electromagnetic Waves on Two Bodies; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Bateman, H.; Erdelyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 3. [Google Scholar]
- Scheffler, T.B. Analyticity of the eigenvalues and eigenfunctions of an ordinary differential operator with respect to a parameter. Proc. R. Soc. A 1974, 336, 475–486. [Google Scholar]
- Klimov, V.V.; Guzatov, D.V. Perfect Nonradiating Modes in Dielectric Nanofiber with Elliptical Cross-Section. arXiv 2022, arXiv:2204.13327. Available online: https://arxiv.org/abs/2204.13327v2 (accessed on 2 May 2022).
- Dallenbach, W.; Kleinsteuber, W. Reflection and absorption of decimeter-waves by plane dielectric layers. Hochfrequenztech. Elektroakust. 1938, 51, 152–156. [Google Scholar]
- Chong, Y.D.; Ge, L.; Cao, H.; Stone, A.D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef]
- Longhi, S. PT-symmetric laser absorber. Phys. Rev. A 2010, 82, 031801. [Google Scholar] [CrossRef]
- Klimov, V.; Sun, S.; Guo, G.-Y. Coherent perfect nanoabsorbers based on negative refraction. Opt. Express 2012, 20, 13071–13081. [Google Scholar] [CrossRef]
- Guo, G.-Y.; Klimov, V.; Sun, S.; Zheng, W.-J. Metamaterial slab-based super-absorbers and perfect nanodetectors for single dipole sources. Opt. Express 2013, 21, 11338. [Google Scholar] [CrossRef]
- Wong, Z.J.; Xu, Y.L.; Kim, J.; O’Brien, K.; Wang, Y.; Feng, L.; Zhang, X. Lasing and anti-lasing in a single cavity. Nat. Photonics 2016, 10, 796–801. [Google Scholar] [CrossRef]
- Noh, H.; Chong, Y.; Stone, A.D.; Cao, H. Perfect coupling of light to surface plasmons by coherent absorption. Phys. Rev. Lett. 2012, 108, 186805. [Google Scholar] [CrossRef] [PubMed]
- Von Neumann, J.; Wigner, E.P. Uber merkwiirdige diskrete Eigenwerte. Phys. Z. 1929, 30, 465–467. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimov, V.V.; Guzatov, D.V. Perfect Invisibility Modes in Dielectric Nanofibers. Photonics 2023, 10, 248. https://doi.org/10.3390/photonics10030248
Klimov VV, Guzatov DV. Perfect Invisibility Modes in Dielectric Nanofibers. Photonics. 2023; 10(3):248. https://doi.org/10.3390/photonics10030248
Chicago/Turabian StyleKlimov, Vasily V., and Dmitry V. Guzatov. 2023. "Perfect Invisibility Modes in Dielectric Nanofibers" Photonics 10, no. 3: 248. https://doi.org/10.3390/photonics10030248
APA StyleKlimov, V. V., & Guzatov, D. V. (2023). Perfect Invisibility Modes in Dielectric Nanofibers. Photonics, 10(3), 248. https://doi.org/10.3390/photonics10030248





