1. Introduction
Optical solitons are fundamental molecules that traverse intercontinental distances with optical fibers. These soliton dynamics have proven to be an engineering marvel for telecommunication industry. Today, the world is completely paralyzed without Internet activity. Therefore, it is the wired global connection with underground and undersea cables that needs to be addressed to boost up performance enhancement. Thus, it is imperative to address soliton dynamics numerically to supplement the reported analytical results from a visual standpoint.
One of the latest concepts that have been introduced during 2019 is highly dispersive (HD) optical solitons [
1,
2,
3,
4,
5]. It is out of extreme necessity, this concept was conceived. When chromatic dispersion (CD) is negligibly small, it is imperative to supplement it with higher order dispersion terms so that the necessary balance between dispersion and self-phase modulation (SPM) is sustained. Therefore, the additional dispersion effects are from inter-modal dispersion (IMD), third-order dispersion (3OD), fourth-order dispersion (4OD), fifth-order dispersion (5OD) and sixth-order dispersion (6OD). It must be noted that soliton dynamics is studied with monomode fibers while IMD is typically considered in the context of multi-mode fibers. However, to address the problem from a numerical perspective, these technical details of telecommunications industry are overlooked.
The next feature of HD solitons that is going to be addressed is the absence of SPM. If SPM is discarded due to its low count, it should be complemented by additional nonlinear effects in order to preserve the delicate balance between dispersion and nonlinearity required for solitons to persist. This effect comes from self-steepening and nonlinear dispersion terms. The necessary balance thus persists and consequently HD solitons without SPM turns out to be a reality! Thus, the governing model that will be addressed using Laplace-Adomian decomposition method (LADM) is with six linear dispersive effects and three terms that provide the necessary nonlinear effect along with a linear temporal evolution. The LADM analysis is written following a brief introduction to the governing model in this paragraph.
Description of the Governing Model
In the absence of SPM, the dimensionless formulation of the governing nonlinear Schrödinger’s equation (NLSE) with higher order dispersion terms is expressed as follows [
1,
2]:
where
stands for the complex-valued wave profile, where
x and
t are respectively spatial and temporal variables. The first term signifies linear temporal evolution and
. Moreover
,
,
,
,
and
are coefficients of IMD, GVD, 3OD, 4OD, 5OD and 6OD respectively. Nonlinear terms include the
coefficient, which represents the influence of self-steepening, and the
and
coefficients, which represent the influence of nonlinear dispersions.
It must be noted that the concept of highly dispersive optical solitons is a very theoretical concept that is not yet implemented in any laboratory let alone any manufactured materials. The concept is yet to be implemented and optical fibers with such properties are yet to be manufactured. There are, however, a few issues that naturally arise with such higher order dispersions. These are the shedding of energy and consequently the slowdown of the soliton velocity. This is from the heavy-duty radiation that is formed with such dispersive effects. These effects are therefore ignored and the focus is on the core soliton regime with bound states that arise from the inverse scattering transform.
2. Highly Dispersive Soliton Solutions for the Governing Model (1.1)
The dark highly dispersive optical soliton solution to (
1) were recently obtained in [
3] using the mathematical technique known as Jacobi’s elliptic function expansion and these in their general form are given by
where
A,
B,
,
,
and
are all real parameters whereas the relationship between some of them is given by
and the soliton speed is related to the model parameters by the following equality
Relatively recently, the bright highly dispersive optical soliton solution to (
1) was also achieved in [
3] using the same mathematical technique mentioned above and these in their general form are given by
where
A,
B,
,
,
and
are all real parameters and they are related to the model by means of the relations given by the Equations (
3) and (
4).
Other research involving highly dispersive solitons using algebraic techniques and special functions are found in [
4,
5]. In addition, the authors in [
6,
7] successfully handle the same topic with semi-analytical approaches comparable to our own.
3. Application of Laplace Transform Combined with Adomian Decomposition Method
This section discusses the general approach for numerically treating (
1) with provided initial conditions for darks and brights solitons. The method we are going to describe and use is the well-known Adomian decomposition method combined with the Laplace transform (LADM), which was originally established in [
8,
9].
The standard form of the generalized NLSE equation Equation (
1) in an operator form is
with initial condition
where the operators
,
and
symbolize the nonlinear term, respectively. The operational notation
symbolize the linear differential operator, whereas
simply denotes time-dependent derivative.
The technique is based on a series of functions to obtain at the solution
q of the problem, which can be written as follows:
and the nonlinear term series
Each
is a polynomial called to as an Adomian polynomial. Then the nonlinear terms
,
, and
, can be split into an series of Adomian polynomials provided by:
and
,
, and
are Adomian polynomials corresponding to the nonlinear terms
,
and
respectively. These can be calculated by the formulas shown in [
10], that is,
Applying these formulas to the expressions given by Equations (
10)–(
12) we obtain that the first few Adomian polynomials are given by
Accordingly, the Adomian polynomials
into which the nonlinear part
is decomposed turn out to be:
so also for additional Adomian polynomials.
When the Laplace transform is applied to both sides of Equation (
6), we obtain
and using initial condition, which will be derived from the profiles for highly dispersive solitons and considering that
, we obtian
Substituting Equations (
8) and (
16) into Equation (
18), it gives
Applying the characteristic linearity property of the Laplace transform in Equation (
19), we obtain
Matching both sides of Equation (
19), we obtain the Laplace transform of each of the components of the solution, that is
for every
, the recursive relations are given by
Finally, the components
,
,
, ⋯, are then determined recursively by using inverse Laplace transform:
where
is referred to as the zeroth component. An
-components truncated series solution is thus obtained as
The series solution (
24) may be utilized numerically. For further information on the convergence of the suggested approach, see [
11,
12].
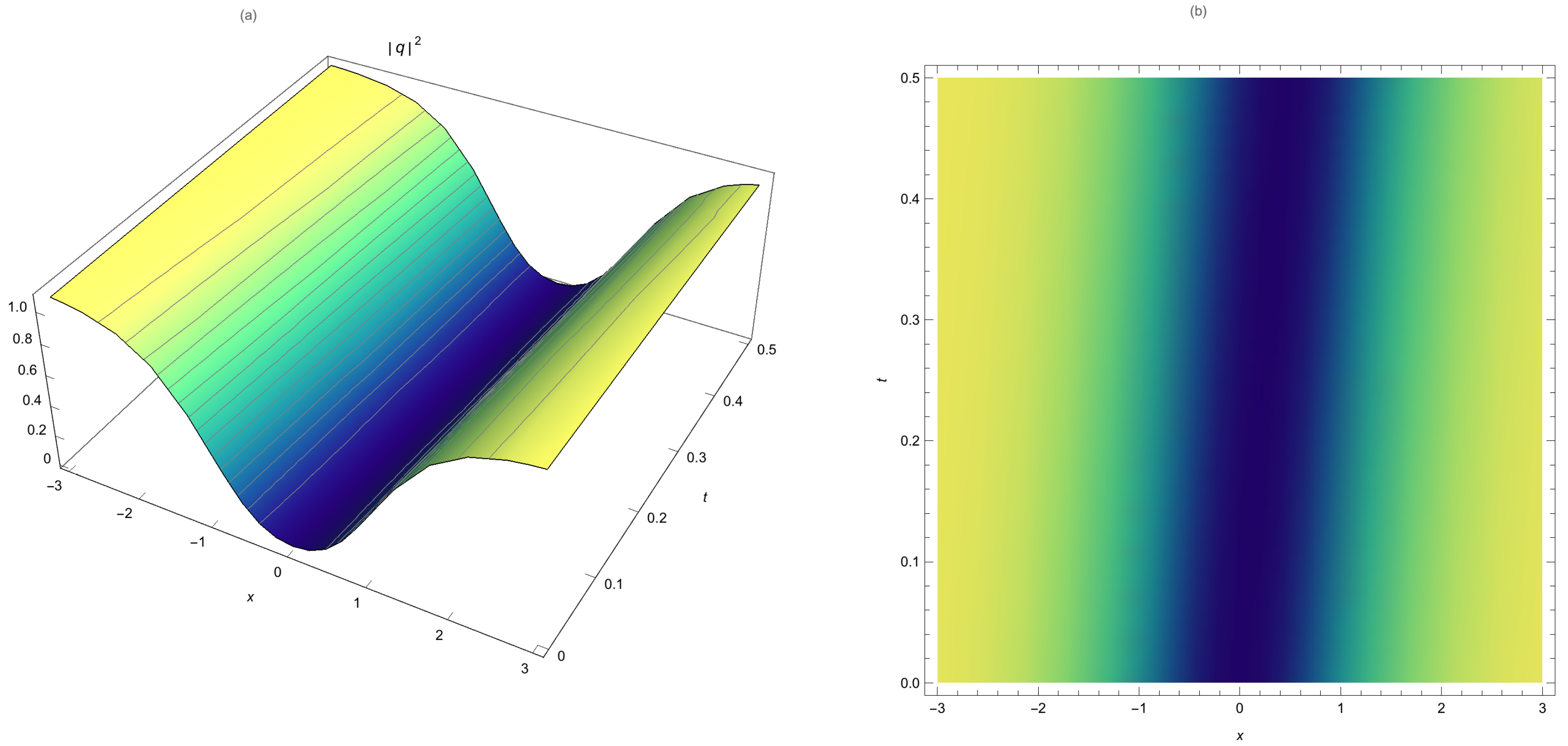
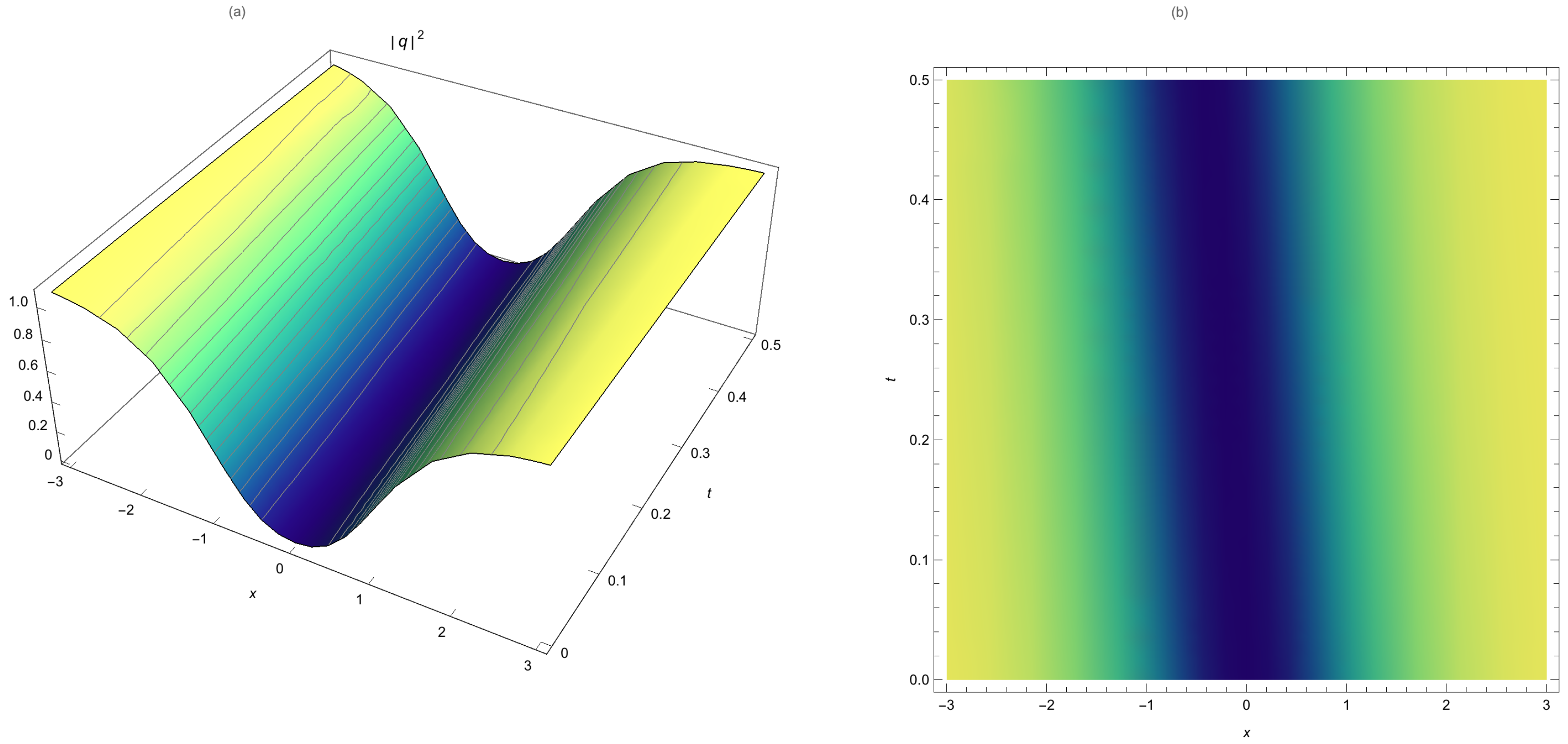
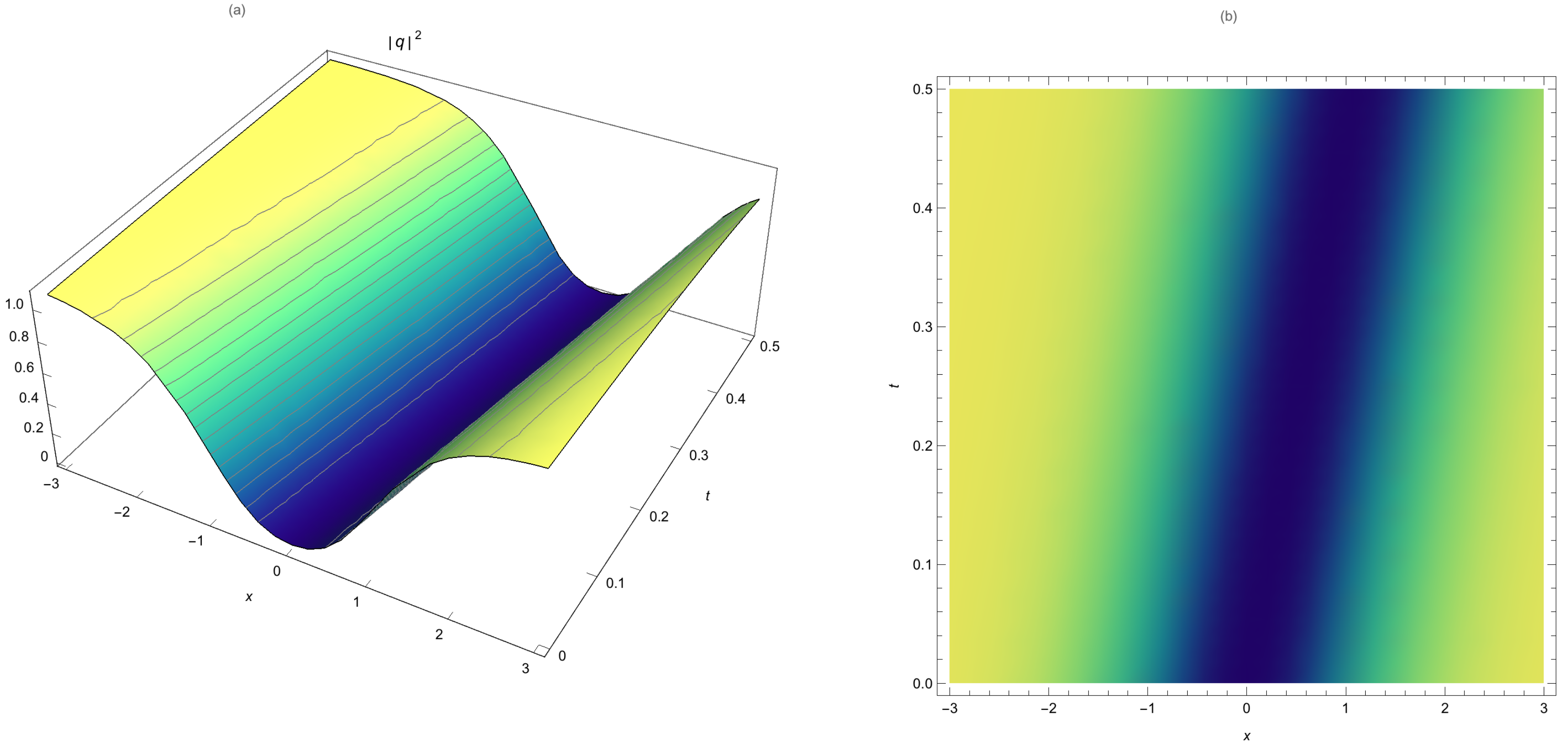
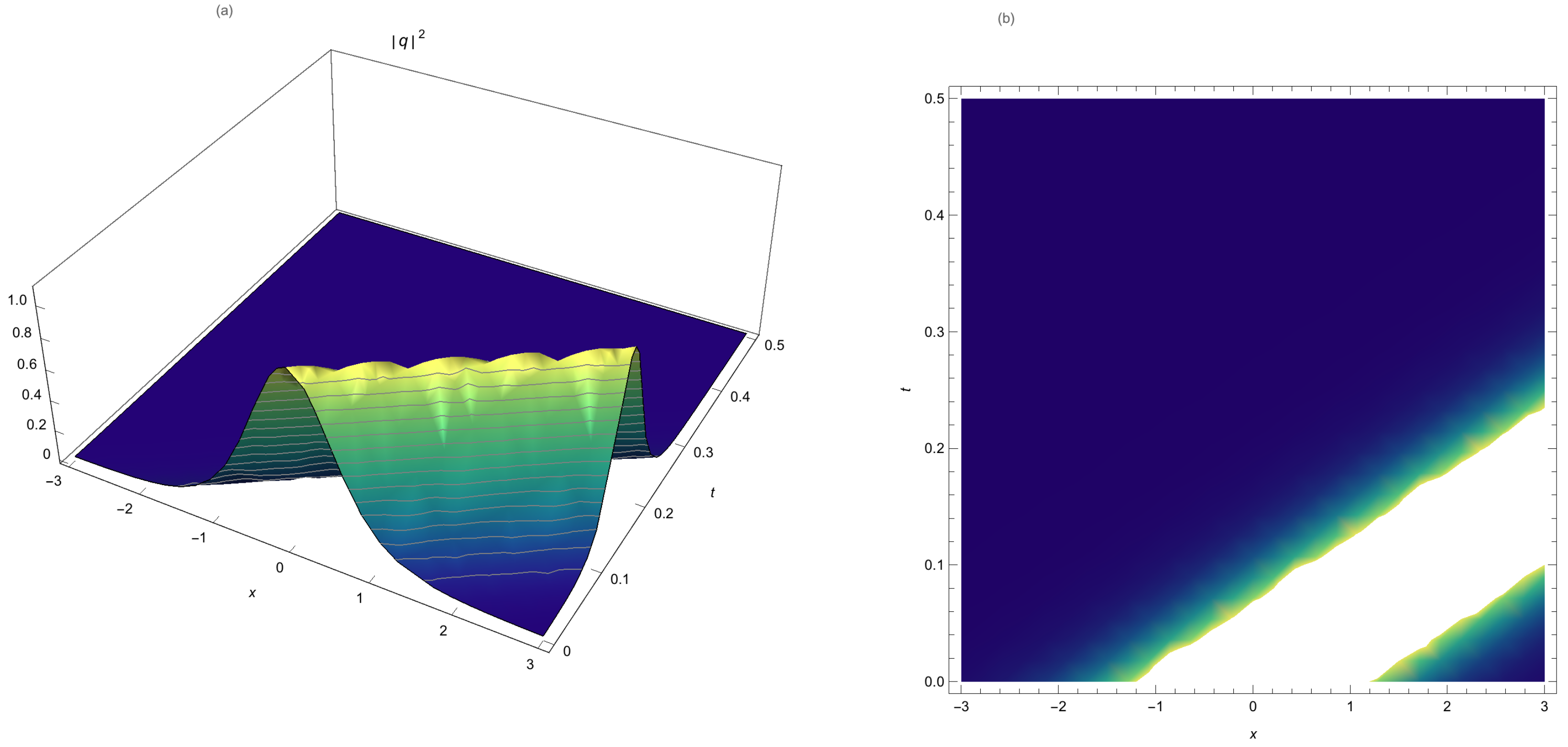
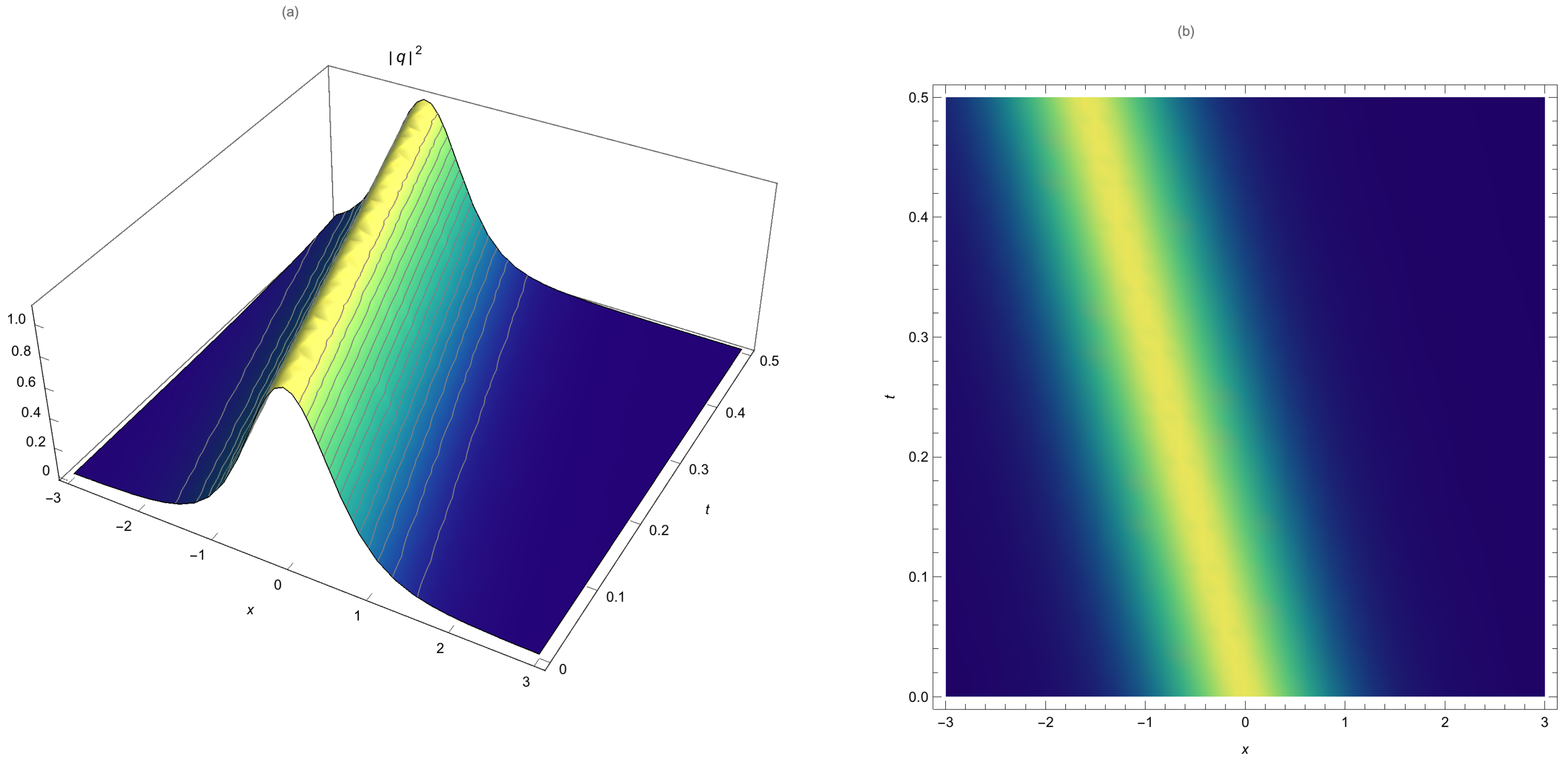
Numeral examples are given in the next section to demonstrate the suggested method’s algorithm’s high accuracy, ease of implementation, and efficacy.
5. Conclusions
This paper studied bright and dark HD solitons that are governed by NLSE with no SPM. The nonlinearity effects stem from self-steepening and nonlinear dispersions. The integration algorithm was provided by LADM that has portrayed a stunning numerical perspective to HD solitons. The absolute error measure for this numerical study is impressively small. The results are thus going to be of great value to telecommunications industry particularly in the context of fiber-optic dynamics.
This research will be expanded in the future to include birefringent fibers as well as dispersion-flattened fibers that would give an expanded view in the context of differential group delay with HD solitons in absence of SPM. Such investigation is now being conducted, and its findings will be communicated.