Abstract
The modulation bandwidth in the direct modulation of a laser diode is limited by relaxation oscillation. To achieve an even higher frequency response, photon–photon resonance has been investigated to extend this modulation bandwidth. Thus far, several reports have demonstrated a higher modulation performance being achieved when utilizing PPR; however, to our knowledge, the PPR control scheme has not been comprehensively discussed. In this paper, we discuss the theory of PPR in regard to the PPR frequency, intensity, and width control scheme. We propose to utilize waveguide configuration, specifically an active multimode interferometer, for optimization. The simulation results offer an approximately 8 GHz improvement in the frequency response.
1. Introduction
It is forecasted that the interconnection speed in supercomputers will exceed 1 Tbps in the near future [1]. For this reason, optical interconnection has been already deployed in supercomputers [2,3,4]. A similar performance to that of supercomputers will be required in personal computers (PCs) within a few decades, according to past research [5]. Optical interconnection, therefore, may be also introduced into mobile devices, including PCs, smartphones, and others. For these applications, a directly modulated laser diode (DML) is one candidate, with the merits of a small footprint and relatively low energy consumption [6].
The DML’s modulation bandwidth is restricted, in principle, by the so-called relaxation oscillation frequency (or, in other words, the carrier photon resonance (CPR) frequency). Here, we write this frequency as . It is well known that damping occurs in the frequency response in regions with a higher frequency than . Consequently, the response degrades by less than −3 dB at around (typically a slightly higher frequency than ). Because of this damping, a response at a much higher frequency is not available, which prevents potential high-speed direct modulation.
One possible means to overcome the restriction of relaxation oscillation is to utilize photon–photon resonance (PPR) [7,8,9,10,11,12,13,14], which is known to display a higher-frequency resonance compared to CPR. Thus far, all the theoretical works focused on laser diodes (LDs) have reported that PPR phenomena appear with the existence of an additional oscillation path, besides the main oscillation path, in an LD cavity [15,16,17,18,19,20,21,22,23,24]. PPR at 45 GHz was calculated in a DBR laser with a complex cavity [20]. A coupled cavity injection grating laser [21] was proposed to extend the modulation bandwidth to 37 GHz. An active multimode interferometer (MMI) laser diode (LD) with multiple PPRs at 24 GHz and 60 GHz was reported [19]. A DFB+R laser exhibited a bandwidth over 65 GHz [22]. A novel dual DFB laser increased the modulation bandwidth to 57.6 GHz [23]. Furthermore, a bandwidth of 108 GHz was reported in a DFB laser combined with a DBR structure [24]. This is because another resonance peak, in addition to , improves the damping at higher frequencies than . Therefore, the so-called −3 dB bandwidth is extended compared to the case without PPR. Compared to other reports on PPR in DBR and DFB lasers, there are two advantages of the active MMI laser. The first is that there are no grating structures, which eases the fabrication. The second is that the active MMI LD configuration offers the potential to exploit multiple PPRs. To achieve a higher-frequency response without −3 dB degradation in the bandwidth in an active MMI LD, one important point is to optimize the peak position, width, and height (i.e., using a control scheme for the PPR peak). However, it seems that the investigation of the control scheme is not sufficient. In this paper, we propose a control scheme for the PPR peak in terms of the frequency position, peak intensity height, and width, using an active MMI laser diode configuration. Based on a theoretical analysis, coupling efficiency is a key parameter of PPR phenomena. Previously, PPR control with coupling efficiency in VCSEL lasers was reported by changing the aperture between two sections [25]. In this work, we utilize a unique active MMI LD that enables the tuning of the coupling efficiency. In this active MMI LD, two spatial lasing modes are employed. The unique active MMI LD configuration enables two different lasing paths sharing the same output port. In addition, the proposed active MMI LD consists of separated identical waveguides. By considering the length balance of the output port waveguide and the separated identical waveguides, the coupling efficiency is designed as the optimum portion. As a result, we demonstrate a substantial improvement of 8 GHz in the frequency response when the coupling ratio is set at 75%.
2. PPR Numerical Model in Proposed Active MMI LD
It has been reported that PPR phenomena are related to the interaction between multiple longitudinal lasing modes in LD [15,16,17,18,19,20,21,22,23,24,25]. To generate multiple lasing modes, multiple cavities assembled in one device are required. For the purpose of achieving and controlling the PPR phenomenon, we propose utilizing a unique, mode-selectable active MMI configuration in this paper. This is because this configuration enables a common output port, whereas it secures different lasing paths independently in a single laser diode, which is explained as follows. Figure 1 illustrates the waveguide configuration of this active MMI LD. It is divided into three sections. Section 1 is a separated identical waveguide in LHS. Section 2 is the MMI section, which lies in the middle as the main pumping area. Section 3 is the output waveguide section, which is connected to the RHS of the MMI section. Section 3 is the modulation region. Cleaved waveguide facets are present in Section 1 and Section 3. Facet reflection is used in this design. All the sections in the active MMI LD are active areas. An active MMI high-power laser was reported previously [26] and the direct-monitored light field had a mostly decentral profile, in contrast to the case of hole burning attributed to filamentation. Hence, we assume that the gain is relatively uniform in this paper. In this configuration, one route supports the lateral fundamental order oscillation mode for one wavelength, and the other one is the lateral first-order oscillation mode at a different wavelength [27]. In this case, the two different routes merge to form a single output.
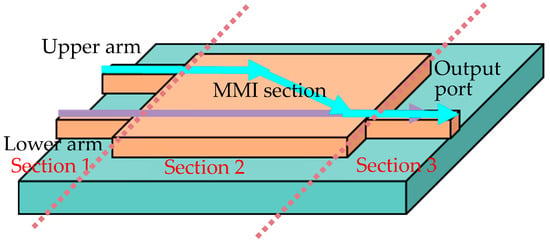
Figure 1.
The structure of the 1 × 2 active MMI laser.
As explained above, this configuration supports two distinct oscillation modes and, consequently, two different lasing wavelengths. In the case of two different lasing wavelengths, it is known that the following rate equation is exploitable. Using the following equations, it is possible to analyze PPR phenomena in the proposed active MMI configuration. All four rate equations are derived from electro-magnetic wave theory in lasers [28,29,30,31,32,33,34,35,36,37,38]. Unlike the traditional one [39], two lasing modes are included in the rate equation. One is referred to as the main lasing mode and the other is referred to as the sub-lasing mode.
The four differential equations for the PPR phenomena are summarized in the following (1)–(4) (The detail of the rate equations are explained in the Appendix A):
and are the photon numbers of the main lasing mode and sub-lasing mode. , , , and are the carrier number, threshold carrier number, transparency carrier number, and linewidth enhancement factor, respectively. are the gain coefficients of the main lasing mode and sub-lasing mode. and are the photon lifetimes of the two lasing modes. In the lasing condition, . is the carrier lifetime. and are the phase terms in the electrical field of the main lasing mode and sub-lasing mode. is the frequency difference of the main lasing mode and sub-lasing mode. is the current injection. is the coupling efficiency. All parameters used in this paper are listed in Table 1. has been historically defined as follows [33,34,35,36,37]:
is the group velocity of light. and are the effective refractive index and total length of the laser diode (All the value are listed in Table 1).

Table 1.
Parameters of rate equation with PPR [40,41].
The differences from the conventional rate equation are listed as follows.
- (1)
- Equation (2): This equation is the derivative of the photon density for the sub-lasing mode, in addition to the one for the main lasing mode (Equation (1)).
- (2)
- As indicated, it involves a co-related term between the main and sub-lasing modes as a second term related to the coupling efficiency, . Note that, in Equation (1), this co-related term is neglected as the main lasing mode is strongly associated, rather than a sub-mode laser, in a laser cavity. Equation (3): This equation considers that this phase term relates to the co-relation in longitudinal mode.
- (3)
- To ensure that corresponds to the coupling efficiency between the main and sub-lasing modes, we introduce a coupling ratio in [27], which satisfies . is defined as the optical profile overlap of the lateral mode between the two lasing modes. In this situation, the coupling efficiency in the active MMI LD is:
- (4)
- affects PPR phenomena directly. The coupling efficiency is defined as the propagation of two lasers along the entire cavity to couple. The two lasing modes in the active MMI LD are not always present together, as visible in Section 1. As the 1 × N active MMI configuration may offer the possibility to control itself, we verify the effect of in the following.
Using the rate equations (Equations (1)–(4)), it is possible to analyze the PPR phenomenon in the proposed active MMI configuration. The modulation response of the laser diode with PPR is calculated by applying the small-signal response approach [26]. Similarly to the conventional small-signal analysis, the small-modulated current, carrier number, and photon number (main lasing mode and sub-lasing mode) are assumed in the analysis, and the frequency response in the laser output is obtained (Parameters are listed in Table 2).

Table 2.
Parameters of transfer function in active MMI LD.
The modulation response derived from the four rate equations suggests that the PPR phenomenon is affected by the coupling efficiency. Figure 2 shows the modulation response as a parameter of the coupling ratio. Here, we use the condition of relaxation oscillation frequency (or CPR: carrier photon resonance frequency) fCPR = 12 GHz, and an intrinsic PPR frequency of 34 GHz with = 1. Due to the damping problem between CPR and PPR, the modulation bandwidth only reaches a value of 22 GHz. As decreases from 1 to 0.6, the PPR tends to be shifted to a lower frequency from 34 GHz to 22 GHz. The width of the PPR tends to become narrower, which has a negative impact on the modulation bandwidth improvement. Despite this width narrowing effect, the peak height of PPR increases to 0.7. This peak height increase is effective in improving the extension of the modulation bandwidth . It is necessary to ensure that the peak height does not increase continuously as increases.
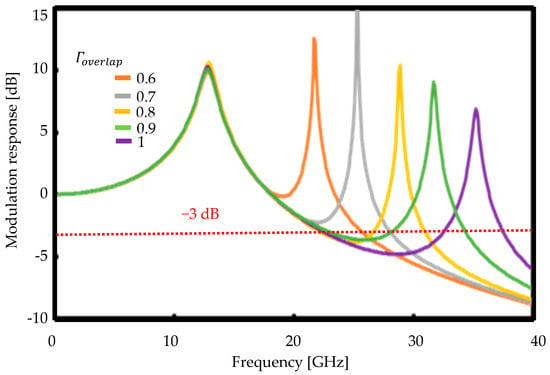
Figure 2.
Simulation of modulation response with PPR across different coupling ratio from 0.6 to 1.
From the discussion above, the PPR phenomenon appears to be significantly affected by the coupling ratio. In other words, targeted PPR can be engineered by optimizing the coupling ratio. The optimal exists between 0.7 and 0.8. The active MMI LD has the potential to improve the control coupling efficiency by changing the configuration.
3. Active MMI Configuration for the Control of PPR and Discussion
As explained in Section 2, related to the coupling efficiency is a key parameter in the PPR phenomenon. In this section, we show how to adjust by modifying the active MMI LD’s geometry.
Figure 3a shows the waveguide configuration of the 1 × 2 active MMI LD involving different lasing paths in a cavity for each spatial mode. In Section 1, when the upper arm and lower arm are both designed as fundamental mode waveguides, the two different lasing paths do not share the same output port. As the BPM simulation results show in Figure 3b,c, each path for the fundamental mode is designed as cross-propagation in Section 2. The coupling area for the two fundamental modes is only the MMI area. The coupling efficiency and its variation are small. With the aim of solving this problem, different lateral modes are utilized. As shown in Figure 3d, the first-order mode propagates in the bar direction in Section 3. Thus, two different lasing paths exist, whereas the output port is shared. As shown in Figure 3b–d, despite the presence of optical leakages in the absent upper output section, the majority of the incident light will be confined within the single waveguide in Section 3. The optical loss is less than 1 dB. Consequently, the impact on modulation is anticipated to remain minimal.
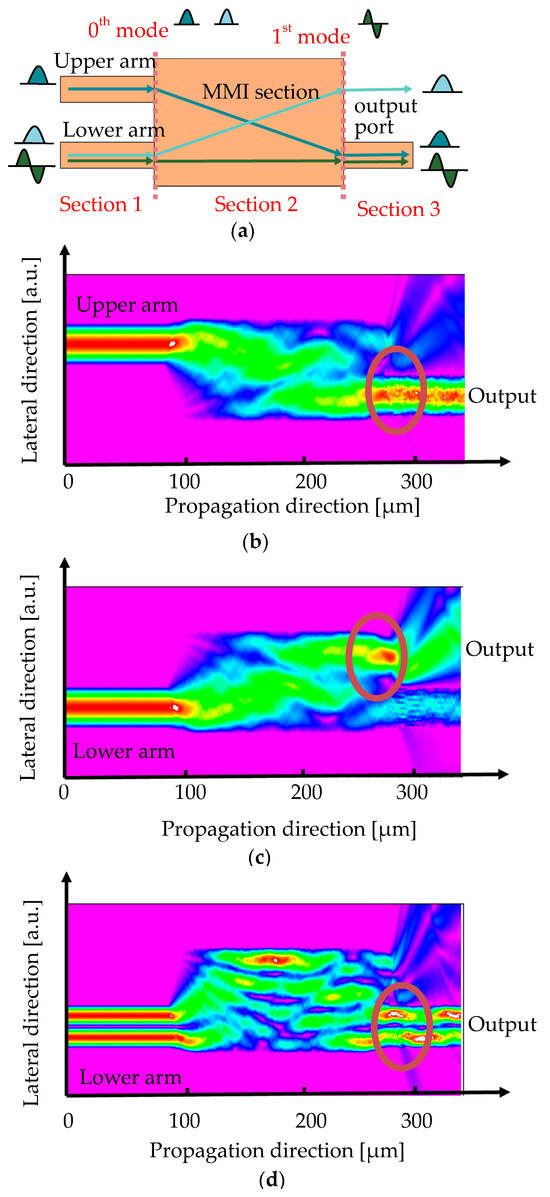
Figure 3.
Propagation paths of different lateral modes in 1 × 2 active MMI laser: (a) scheme propagation route of fundamental and first mode in 1 × 2 active MMI LD; (b) BPM simulation of fundamental mode propagation through the upper arm; (c) BPM simulation of fundamental mode propagation through the lower arm; and (d) BPM simulation of first-order mode propagation through the lower arm.
Considering that the lasing paths of the two lasing modes are different in the 1 × 2 active MMI LD, the coupling efficiency of the two lasing modes in each section has to be discussed. When two space modes are lasing in Section 1, the two lasing modes are separated from each other. In Section 2 and Section 3, the two lasing modes overlap. This overlap is close to 1 in Section 3, whereas the lateral optical field overlap of the two lasing modes is less than 1 in Section 2. The expression of in the active MMI LD is
In this expression, , , , and are, respectively, the optical field overlap of the two modes in the MMI section (Section 2), the length of Section 2, the length of Section 3, and the total length of the whole active MMI LD. This definition suggests that is affected by the proportion of the three regions. Thus, the parameter has to be determined.
The optical field overlap of the two lasing modes in Section 2 is calculated to confirm . In the calculation process, we set the length of Section 1 at 90 μm and the length of Section 3 at 50 μm. The wavelength value in the simulation process is set to 1550 nm. The simulation results of the fundamental mode and first-order mode in Figure 3c,d suggest that the optical field overlap of the two lasing modes varies along the propagation direction. Moreover, Figure 4a illustrates the optical profile of two lateral modes in the middle of Section 2. As indicated in the figure, the optical profiles of the two lasing modes do not entirely overlap. To calculate , from Figure 4b, we divide the MMI area into slices along the propagation direction. Hence, the overlap of the two lasing modes in each slice is calculated. is obtained. The result shows that is around 0.74 when the MMI area length changes from 150 μm to 300 μm.
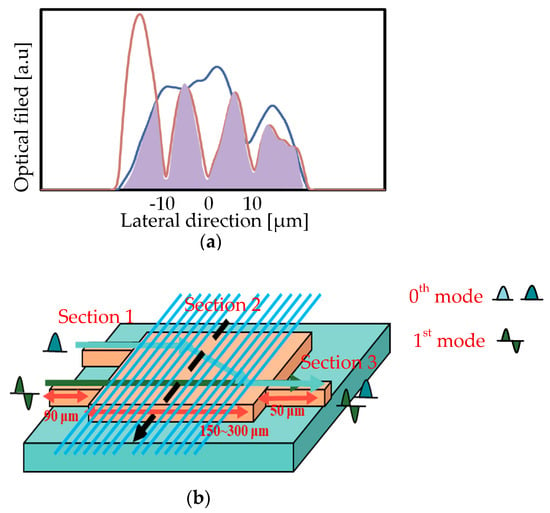
Figure 4.
(a) Optical field overlap of two lasing modes in 1 × 2 active MMI LD in the middle of Section 2; and (b) scheme of two lasing modes’ propagation in 1 × 2active MMI LD.
Based on the discussion above, the is determined by the proportion in the active MMI LD configuration. The length of the MMI area is set at 240 μm. The relationship between the length of the arm part and is depicted in Figure 5. can be set from 0.5 to 0.8.
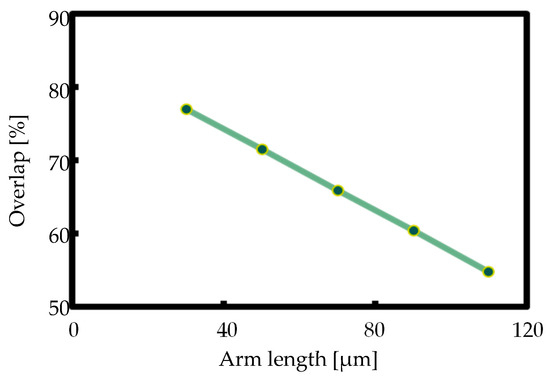
Figure 5.
with different arm lengths (@ 360 μm of total active MMI LD length and 240 μm of MMI area).
It is necessary to point out that, when utilizing different lateral modes in the active MMI LD, the coupling efficiency is tunable. Multimode light, however, is not commonly used as a light source for optical interconnection due to the dispersion loss in long-distance transmission. An active MMI LD is considered as the optical light source for interconnection in supercomputers or mobile devices. This implies that this device can be applied in short-distance cases for which dispersion loss would not be a serious problem.
Based on the theoretical analysis discussed in Section 2, a wider frequency response may occur for 0.7. We verified the response in detail. We found that 0.75 was the optimal value in this case. Figure 6 shows the calculated frequency response of the 0.75 case. An 8 GHz improvement was successfully achieved in the modulation bandwidth. The control of is enabled through the proportions of the three parts of the active MMI LD. at 0.75 is obtained by setting Section 1, Section 2, and Section 3 at 30 μm, 220 μm, and 110 μm, respectively. It is possible that modifying the lengths of Section 1 and Section 3 will impact the free spectral range (FSR) of the Fabry–Perot resonance, which, in turn, influences the CPR and the PPR. In our specific design, the overall cavity length and the length of the primary MMI section remain unchanged. Consequently, the proportion of Section 1 and Section 2 is the focal point of our design efforts. Given that the primary MMI section and the total cavity length remain unaltered, the FSR of the Fabry–Perot resonance will also remain unaffected.
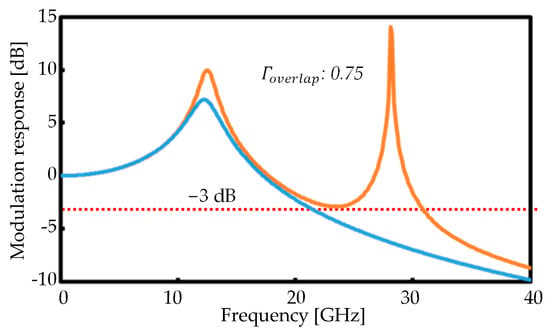
Figure 6.
Calculated modulation response with/without PPR.
Although the modulation bandwidth extension is confirmed by the existence of PPR, it is worth noting that the PPR intensity stands at approximately 14 dB, which is regarded as a detrimental factor affecting large signal modulation. In order to address this issue, it is important to devise a control scheme to manage the intensity. In the PPR model proposed in Section 2, the PPR phenomenon is treated as a synchronization phenomenon. Based on synchronization theory [27], it is strongly related to the initial phase of two oscillations. The simulation results, which depict the characterization of the PPR at 0.75 under varying initial phase differences, are presented in Figure 7. When the initial phase difference is −14.95π/30, the peak in PPR is observed at 14 dB. The intensity of PPR is reduced with the change in the initial phase difference ranging from −14.95π/30 to −14.75π/30. When the initial phase difference is −14.75π/30, the intensity of the PPR is 0 dB. The fluctuation in the PPR intensity suggests that the PPR phenomenon may not manifest under certain circumstances, primarily due to the absence of optimal tuning in the initial phase difference between the two lasing modes. As 0.75, an 8 GHz improvement with a lower PPR intensity is confirmed, as shown in Figure 7. To tune the initial phase, it is imperative to implement separate current injections for each waveguide within Section 1 of this active MMI LD. The initial phase is then adjusted when operating the current value.
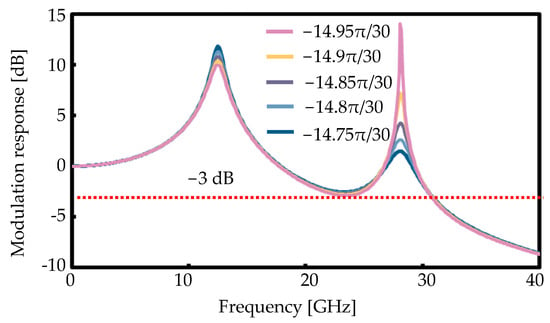
Figure 7.
Calculated modulation response with different initial phase values (@ : 0.75).
4. Discussion
A notable enhancement of 8 GHz in the modulation bandwidth is confirmed when the fCPR is set at 12 GHz. It is necessary to point out that the optimum design for different fCPR is different. The location of fCPR is the main determinant of the optimized value of the coupling efficiency. The reason that fCPR is set at 12 GHz is that, in the former experiments, for an active MMI laser around 400 µm, the highest fCPR is located at around 10 GHz. If fCPR is located at 15 GHz, the optimized value changes. In Figure 8, the simulation results show that, with a higher fCPR, a higher fPPR is preferred to extend the modulation bandwidth. The optimal value in this case is around = 0.85. Based on the simulation results, it is suggested that, in the design process, different values need to be considered.
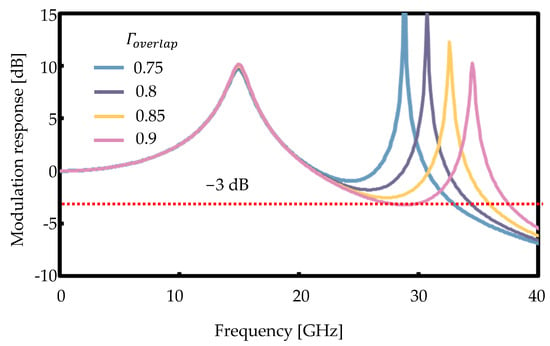
Figure 8.
Simulation of modulation response with PPR across different coupling ratio from 0.75 to 0.9.
While we successfully enhanced the modulation response, it is important to note that our simulations were conducted under the conditions of the effective refractive index with no lasing operation. The effective refractive index, however, varies with the current injection because of the so-called carrier plasma effect [42]. In the semiconductor field, when a laser is lasing, the carrier density inside the active MMI laser diode accumulates from 0 to its threshold carrier density [40]. Changes in the effective refractive index can significantly influence the propagation paths of lasing modes, leading to alterations in the overlap between these modes. Therefore, it is crucial to consider the impact of variations in the effective refractive index resulting from the accumulation of the carrier density.
When a laser composed of InGaAsP is lasing at 1.55 µm, the increase in the carrier density results in a reduction in the refractive index. The difference in effective refractive index would be lower than 0.1 [43]. As shown in Table 1, the refractive index of our device is 3.24. We conducted calculations to determine the overlap between two light sources across a range of effective refractive indices, spanning from 3.14 to 3.34. The calculation results are shown in Figure 9.
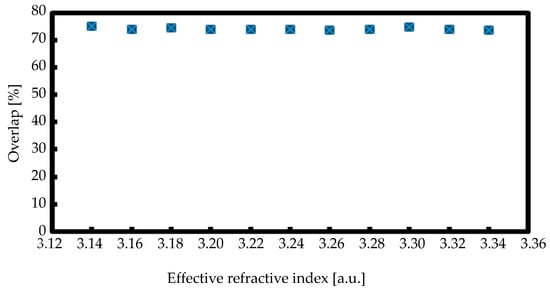
Figure 9.
Overlap ratio of two lights with refractive index (@ 360 μm of total active MMI LD length and 220 μm of MMI area).
Based on the simulation results shown in Figure 9, the stability of the overlap is confirmed. Although the overlap between the two lights changed with different effective refractive indices, it remained within the range of 0.74–0.75. This result suggests that the active MMI laser diode is able to operate stably, even in the presence of variations in the effective refractive index induced by the accumulation of the carrier density.
In addition to the carrier plasma effect, temperature is a factor that needs to be taken into consideration, as rising temperatures lead to a narrower bandgap, consequently resulting in an increase in the refractive index. During experimental procedures, it is essential to employ a temperature controller in order to maintain and stabilize the operating conditions at room temperature. This ensures that temperature-related effects are controlled and minimized. The real temperature inside the active MMI LD, however, is still different from the setting temperature [44]. The Varshni relation [45] for the temperature dependence of semiconductor bandgaps is:
where and are fitting parameters characteristic of a given material [46]. Gupta and Ravindra [47] express the refractive index and energy bandgap as:
Using Equations (16) and (17), at room temperature, the refractive index variation in the active MMI LD is far less than 0.1 when the temperature rises from 290 K to 310 K. As indicated by the simulation result shown in Figure 9, the desired coupling ratio is maintained.
Finally, the fabrication tolerance is discussed. The single output port in Section 3 of the active MMI LD configuration relies on the self-image phenomenon in the MMI section, which is significantly affected by the width of the MMI section [26]. With a fabrication error, the overlap between the two modes and the optical loss will be affected, which can impact the laser performance. Therefore, the optical loss and the overlap variation with the width difference are calculated, and the results are shown in Figure 10. The optical loss of the optimum active MMI LD is 0.78 dB. It rises with the increase in the width difference. When the width difference is within ±150 nm, the optical loss is below 1 dB. Regarding the overlap, with the width difference of ±150 nm, the overlap is stabilized within the range from 72% to 74%. Given that the overlap and the optical loss at a width difference of ±150 nm remain minimal, the fabrication tolerance of the active MMI LD is ±150 nm.
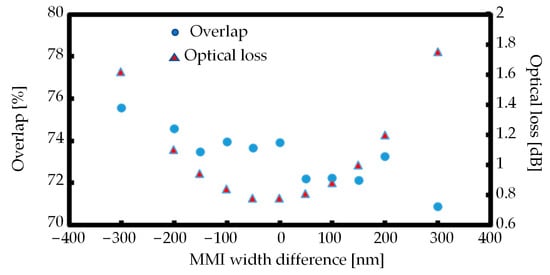
Figure 10.
Overlap ratio and optical loss with different MMI widths.
In this work, the control scheme of PPR in a 1 × 2 active MMI LD is discussed. This is a promising method as it offers the potential for broader applicability to active MMI LD structures supporting more sub-modes. When minimizing the length of the LD, a larger modulation bandwidth is expected.
5. Conclusions
In this work, we proposed an active MMI LD configuration to achieve the ideal overlap between the main mode and sub-mode of a laser. The optimized modulation response was obtained when was 0.75, and the design of an active MMI laser was also proposed. We plan to verify this with experiments and exploit a similar scheme for the control of multiple PPR peaks, thereby aiming for even greater modulation response capabilities.
Author Contributions
Conceptualization, H.X. and K.H.; methodology, H.X.; software, H.X.; investigation, Y.K.; writing—original draft preparation, H.X.; writing—review and editing, K.H and H.J.; supervision, administration, and funding acquisition, K.H and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Japanese Society for the Promotion of Science (#19H02201 and #22H01556).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Two lasing modes are included in the rate equations. One is referred to as the main lasing mode . The other is referred to as the sub-lasing mode .
For the main lasing mode, its electric field is:
is the field magnitude and is a phase term that is defined as:
where is the angular frequency and is the initial phase.
Regarding the sub-lasing mode, the electric field is:
is the field magnitude. is given in Equation (4):
where is the angular frequency and is the linewidth confinement. is the time-dependent phase factor of the sub-lasing mode [28]. Here, we introduce the time derivative of the electric field, which was derived in reference [22,23,24].
Here, is the gain coefficient of the sub-lasing mode, is the coupling efficiency, and is the frequency difference of the main lasing mode and sub-lasing mode, defined as:
We utilize the following relation, particularly in the sub-lasing mode using an electric field:
where is the conjugate complex of , and is the photon number. The time derivate of Equation (A7) is then:
Here, we utilize the time derivative of indicated in Equation (A9):
Substituting (A5) and (A9) into (A8), we obtain the following rate equation for the sub-lasing mode (the details are shown in the Appendix A):
In addition to the differential equation of , here, we derive the differential equation of : the phase factor for the sub-lasing mode. We again utilize Equation (A7). The time derivatives of and are rewritten as follows:
Then, the equation for is derived by multiplying and , leading to Equations (A11) and (A12):
The differential equation regarding photon density is:
The differential equation regarding the phase term is:
Subtracting Equation (A22) from Equation (A20), the equation is:
References
- Rumley, S.; Bahadori, M.; Polster, R.; Hammond, S.D.; Calhoun, D.M.; Wen, K.; Rodrigues, A.; Bergman, K. Optical interconnects for extreme scale computing systems. Parallel Comput. 2017, 64, 65–80. [Google Scholar] [CrossRef]
- Faanes, G.; Bataineh, A.; Roweth, D.; Court, T.; Froese, E.; Alverson, B.; Johnson, T.; Kopnick, J.; Higgins, M.; Reinhard, J. Cray Cascade: A scalable HPC system based on a Dragonfly network. In Proceedings of the SC’12: Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; pp. 1–9. [Google Scholar]
- Ajima, Y.; Kawashima, T.; Okamoto, T.; Shida, N.; Hirai, K.; Shimizu, T.; Hiramoto, S.; Ikeda, Y.; Yoshikawa, T.; Uchida, K.; et al. The Tofu Interconnect D. In Proceedings of the 2018 IEEE International Conference on Cluster Computing (CLUSTER), Belfast, UK, 10–13 September 2018; pp. 646–654. [Google Scholar]
- Alverson, R.; Roweth, D.; Kaplan, L. The Gemini System Interconnect. In Proceedings of the 2010 18th IEEE Symposium on High Performance Interconnects, Mountain View, CA, USA, 18–20 August 2010; pp. 83–87. [Google Scholar]
- Kilper, D.; Bergman, K.; Chan, V.W.; Monga, I.; Porter, G.; Rauschenbach, K. Optical Networks Come of Age. Opt. Photonics News 2014, 25, 50–57. [Google Scholar] [CrossRef]
- Matsui, Y. Direct modulated laser technology: Past, present, and future. In Datacenter Connectivity Technologies: Principles and Practice; River Publisher: Gistrup, Demark, 2018; pp. 87–90. [Google Scholar]
- Radziunas, M.; Glitzky, A.; Bandelow, U.; Wolfrum, M.; Troppenz, U.; Kreissl, J.; Rehbein, W. Improving the modulation bandwidth in semiconductor lasers by passive feedback. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 136–142. [Google Scholar] [CrossRef]
- Vallone, M.; Bardella, P.; Montrosset, I. Enhanced modulation bandwidth in complex cavity injection grating lasers. IEEE J. Quantum Electron. 2011, 47, 1269–1276. [Google Scholar] [CrossRef]
- Nowell, M.C.; Carroll, J.E.; Plumb, R.G.S.; Marcenac, D.D.; Robertson, M.J.; Wickes, H.; Zhang, L.M. Low-chirp and enhanced-resonant frequency by direct push-pull modulation of DFB lasers. IEEE J. Sel. Top. Quant. Electron. 1995, 1, 433–441. [Google Scholar] [CrossRef]
- Kaiser, W.; Bach, L.; Reithmaier, J.P.; Forchel, A. High-speed coupled-cavity injection grating lasers with tailored modulation transfer functions. IEEE Photonics Technol. Lett. 2004, 16, 1997–1999. [Google Scholar] [CrossRef]
- Gerschütz, F.; Fischer, M.; Koeth, J.; Krestnikov, I.; Kovsh, A.; Schilling, C.; Kaiser, W.; Höfling, S.; Forchel, A. 1.3 µm Quantum Dot Laser in coupled-cavity-injection-grating design with bandwidth of 20 GHz under direct modulation. Opt. Express 2008, 16, 5596–5601. [Google Scholar] [CrossRef]
- Bach, L.; Kaiser, W.; Reithmaier, J.; Forchel, A.; Gioannini, M.; Feies, V.; Montrosset, I. 22-GHz modulation bandwidth of long cavity DBR laser by using a weakly laterally coupled grating fabricated by focused ion beam lithography. IEEE Photonics Technol. Lett. 2004, 16, 18–20. [Google Scholar] [CrossRef]
- de Valicourt, G.; Levaufre, G.; Pointurier, Y.; Le Liepvre, A.; Antona, J.C.; Jany, C.; Accard, A.; Lelarge, F.; Make, D.; Duan, G.H. Direct modulation of hybrid-integrated InP/Si transmitters for short and long reach access network. J. Light. Technol. 2015, 33, 1608–1616. [Google Scholar] [CrossRef]
- Troppenz, U.; Kreissl, J.; Moehrle, M.; Bornholdt, C.; Rehbein, W.; Sartorius, B.; Woods, I.; Schell, M. 40 Gbit/s directly modulated lasers: Physics and application. In Proceedings of the Novel In-Plane Semiconductor Lasers, San Francisco, CA, USA, 25–28 January 2011; Volume 7953, pp. 98–107. [Google Scholar]
- Hong, B.; Kitano, T.; Mori, T.; Jiang, H.; Hamamoto, K. Bandwidth enhancement scheme demonstration on direct modulation active-MMI laser diode using multiple photon photon resonance. Appl. Phys. Lett. 2017, 111, 221105. [Google Scholar] [CrossRef]
- Reithmaier, J.P.; Kaiser, W.; Bach, L.; Forchel, A.; Feies, V.; Gioannini, M.; Montrosset, I.; Berg, T.W.; Tromborg, B. Modulation speed enhancement by coupling to higher order resonances: A road towards 40 GHz bandwidth lasers on InP. In Proceedings of the International Conference on Indium Phosphide and Related Materials, Glasgow, UK, 8–12 May 2005; pp. 118–123. [Google Scholar]
- Dumitrescu, M.; Telkkälä, J.; Karinen, J.; Viheriälä, J.; Laakso, A.; Afzal, S.; Reithmaier, J.P.; Kamp, M.; Melanen, P.; Uusimaa, P.; et al. High-speed directly-modulated lasers with photon-photon resonance. In Proceedings of the IPRM 2011–23rd International Conference on Indium Phosphide and Related Materials, Berlin, Germany, 22–26 May 2011; pp. 1–4. [Google Scholar]
- Hong, B.; Mori, T.; Jiang, H.; Hamamoto, K. Mode selective active multimode interferometer laser diode with over 40 GHz direct modulation bandwidth. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. Th3B-4. [Google Scholar]
- Murakami, S.; Hong, B.; Jiang, H.; Hamamoto, K. Observation of 60 GHz and 20 GHz Multiple Photon-Photon Resonances Using Active Multimode Interferometer Laser Diodes. In Proceedings of the 2019 24th Microoptics Conference (MOC), Toyama, Japan, 17–20 November 2019; pp. 304–305. [Google Scholar]
- Bardella, P.; Chow, W.W.; Montrosset, I. Design and analysis of enhanced modulation response in integrated coupled cavities DBR lasers using photon-photon resonance. Photonics 2016, 3, 4. [Google Scholar] [CrossRef]
- Bach, L.; Kaiser, W.; Reithmaier, J.P.; Forchel, A.; Berg, T.W.; Tromborg, B. Enhanced direct-modulated bandwidth of 37 GHz by a multi-section laser with a coupled-cavity-injection-grating design. Electron. Lett. 2003, 39, 1592–1593. [Google Scholar] [CrossRef]
- Matsui, Y.; Schatz, R.; Che, D.; Khan, F.; Kwakernaak, M.; Sudo, T. Low-chirp isolator-free 65-GHz-bandwidth directly modulated lasers. Nat. Photonics 2021, 15, 59–63. [Google Scholar] [CrossRef]
- Rajeswari, G.V.; Moehrle, M.; Ehrensack, F.; Troppenz, U.; Sigmund, A.; Schell, M. Novel > 57 GHz bandwidth O-band InGaAlAs MQW RW DFB. In Proceedings of the Novel In-Plane Semi Lasers XXII, San Francisco, CA, USA, 31 January–2 February 2023; Volume 3, pp. 34–39. [Google Scholar]
- Yamaoka, S.; Diamantopoulos, N.P.; Nishi, H.; Nakao, R.; Fujii, T.; Takeda, K.; Hiraki, T.; Tsurugaya, T.; Kanazawa, S.; Tanobe, H.; et al. Directly modulated membrane lasers with 108 GHz bandwidth on a high-thermal-conductivity silicon carbide substrate. Nat. Photonics 2021, 15, 28–35. [Google Scholar] [CrossRef]
- Ahmed, M.; Bakry, A.; Alghamdi, M.S.; Dalir, H.; Koyama, F. Enhancing the modulation bandwidth of VCSELs to the millimeter-waveband using strong transverse slow-light feedback. Opt. Express 2015, 23, 15365–15371. [Google Scholar] [CrossRef]
- Hamamoto, K.; Jiang, H. Active MMI devices: Concept, proof, and recent progress. J. Phys. D Appl. Phys. 2015, 48, 383001. [Google Scholar] [CrossRef]
- Jiang, H.; Bastawrous, H.A.; Hagio, T.; Matsuo, S.; Hamamoto, K. Low hysteresis threshold current (39 mA) active multimode-interferometer. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1258–1263. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization, A Universal Concept in Nonlinear Sciences, 1st ed.; Cambridge University Press: New York, NY, USA, 2001; pp. 53–56. [Google Scholar]
- Murakami, A.; Kawashima, K.; Atsuki, K. Cavity resonance shift and bandwidth enhancement in semiconductor lasers with strong light injection. IEEE J. Quantum Electron. 2003, 39, 1196–1204. [Google Scholar] [CrossRef]
- Lang, R. Injection locking properties of a semiconductor laser. IEEE J. Quantum Electron. 1982, 18, 976–983. [Google Scholar] [CrossRef]
- Lau, E.K.; Sung, H.K.; Wu, M.C. Frequency response enhancement of optical injection-locked lasers. IEEE J. Quantum Electron. 2007, 44, 90–99. [Google Scholar] [CrossRef]
- Lau, E.K.; Wong, L.J.; Wu, M.C. Enhanced modulation characteristics of optical injection-locked lasers: A tutorial. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 618–633. [Google Scholar] [CrossRef]
- Lau, E.K.; Sung, H.K.; Wu, M.C. Scaling of resonance frequency for strong injection-locked lasers. Opt. Lett. 2007, 32, 3373–3375. [Google Scholar] [CrossRef] [PubMed]
- Simpson, T.B.; Liu, J.M.; Gavrielides, A. Bandwidth enhancement and broadband noise reduction in injection-locked semiconductor lasers. IEEE Photonics Technol. Lett. 1995, 7, 709–711. [Google Scholar] [CrossRef]
- Mogensen, F.; Olesen, H.; Jacobsen, G. Locking conditions and stability properties for a semiconductor laser with external light injection. IEEE J. Quantum Electron. 1985, 21, 784–793. [Google Scholar] [CrossRef]
- Liu, Z.; Slavík, R. Optical injection locking: From principle to applications. J. Light. Technol. 2020, 38, 43–59. [Google Scholar] [CrossRef]
- Henry, C.; Olsson, N.; Dutta, N. Locking range and stability of injection locked 1.54 µm InGaAsP semiconductor lasers. IEEE J. Quantum Electron. 1985, 21, 1152–1156. [Google Scholar] [CrossRef]
- Xiao, H.; Shoda, K.; Koudu, K.; Jiang, H.; Hamamoto, K. Affection analysis of frequency response with photon-photon-resonance (PPR) to directly modulated 40 Gbps signal. In Proceedings of the 2021 26th Microoptics Conference (MOC), Hamamatsu, Japan, 26–29 September 2021; pp. 1–2. [Google Scholar]
- Siegman, A.E. LASERS, 1st ed.; University Science Books US: Sausalito, CA, USA, 1986; pp. 187–211. [Google Scholar]
- Coldren, L.A.; Corzine, S.W.; Mashanovitch, M.L. Diode Lasers and Photonic Integrated Circuits, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 260–279. [Google Scholar]
- Suematsu, Y.; Adams, A.R. Handbook of Semiconductor Lasers and Photonic Integrated Circuits, 1st ed.; Ohmsha Press: Tokyo, Japan, 1994; pp. 262–273. [Google Scholar]
- Manning, J.; Olshansky, R.; Su, C. The carrier-induced index change in AlGaAs and 1.3 μm InGaAsP diode lasers. IEEE J. Quantum Electron. 1983, QE-19, 1525–1530. [Google Scholar] [CrossRef]
- Bennett, B.R.; Soref, R.A.; Del Alamo, J.A. Carrier-induced change in refractive index of InP, GaAs and InGaAsP. IEEE J. Quantum Electron. 1990, 26, 113–122. [Google Scholar] [CrossRef]
- Zang, Z.; Mukai, K.; Navaretti, P.; Duelk, M.; Velez, C.; Hamamoto, K. Thermal resistance reduction in high power superluminescent diodes by using active multi-mode interferometer. Appl. Phys. Lett. 2012, 100, 031108. [Google Scholar] [CrossRef]
- Varshni, Y.P. Comparative study of potential energy functions for diatomic molecules. Rev. Mod. Phys. 1957, 29, 664–682. [Google Scholar] [CrossRef]
- Varshni, Y.P. Temperature dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Gupta, V.P.; Ravindra, N.M. Comments on the moss formula. Phys Status Solidi (b) 1980, 100, 715–719. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).