Metasurface Enhanced Upconversion Efficiency for High-Performance Pixel-Less Thermal Imaging
Abstract
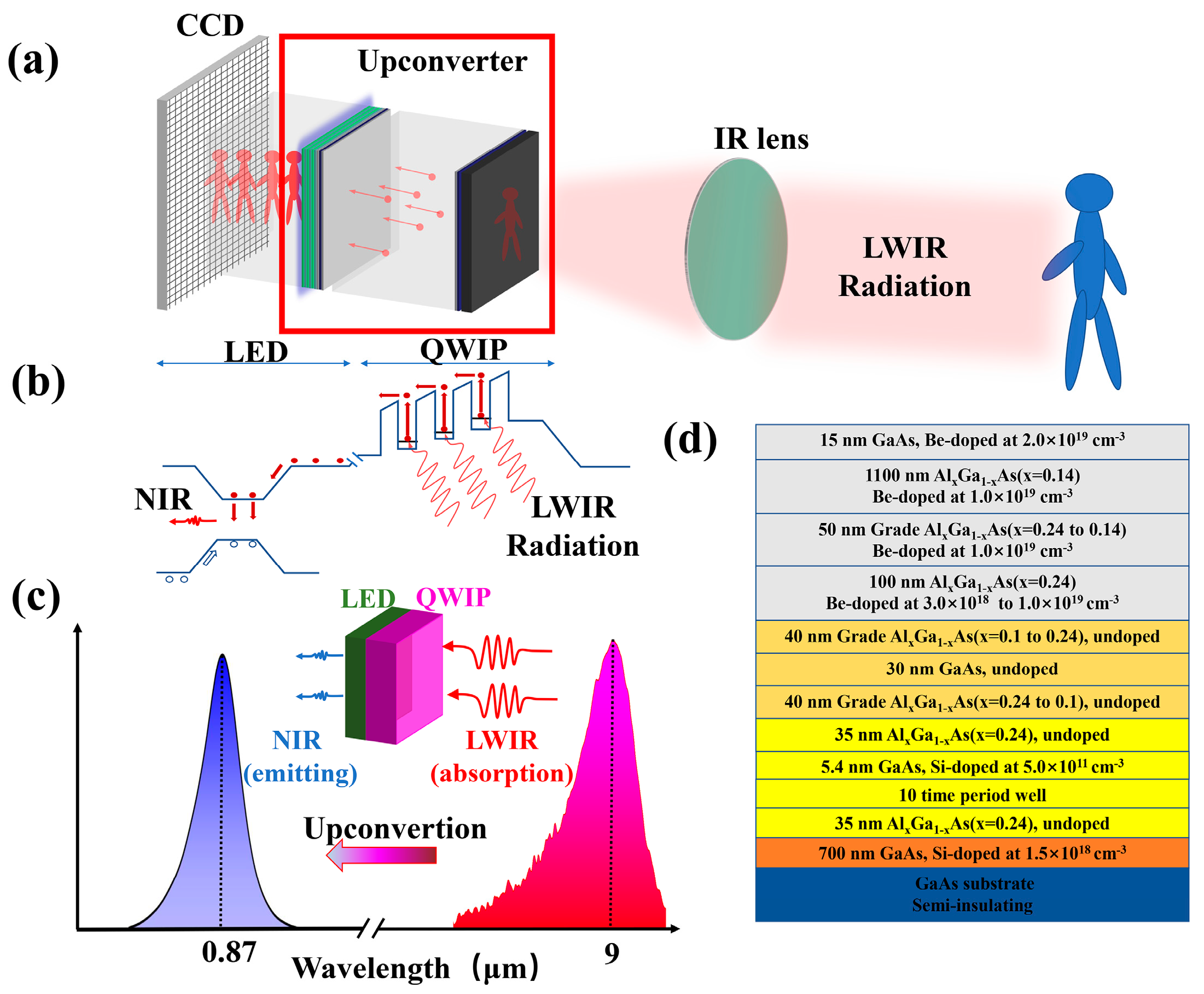
1. Introduction
2. Principle of Pixel-Less Thermal Imaging
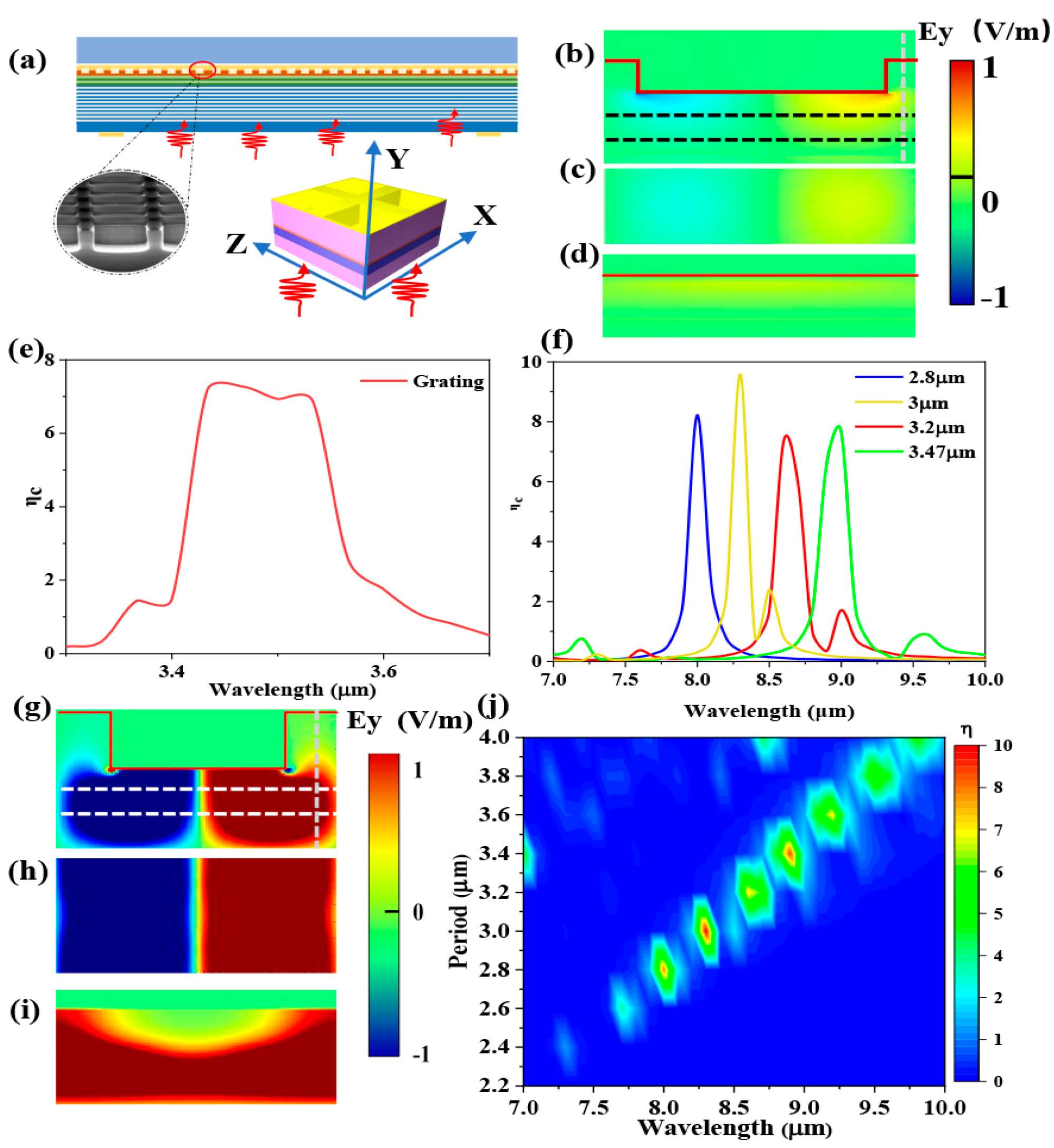
3. 45° Edge-Coupled Upconverter
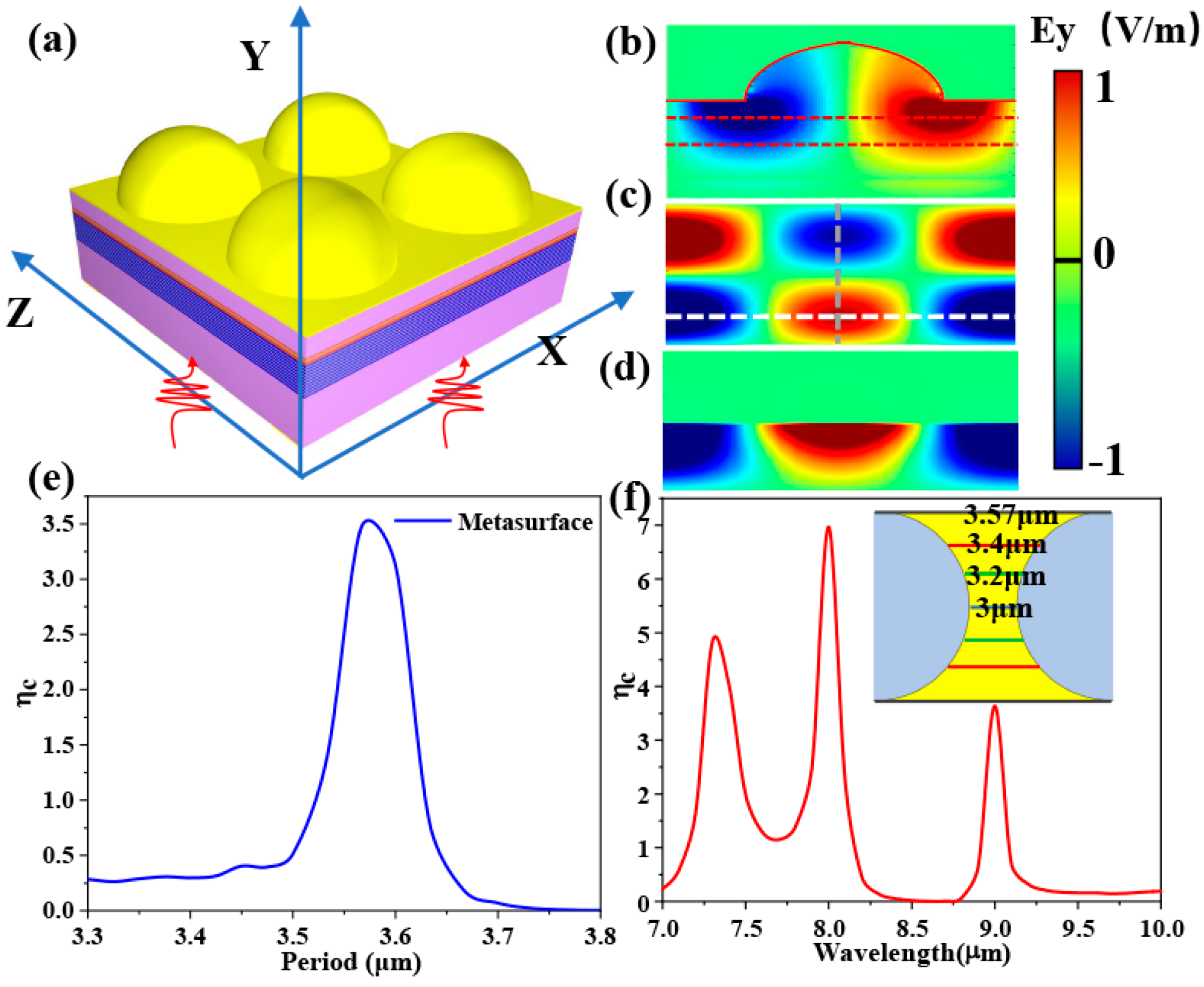
4. Metasurface Enhanced Upconverter
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
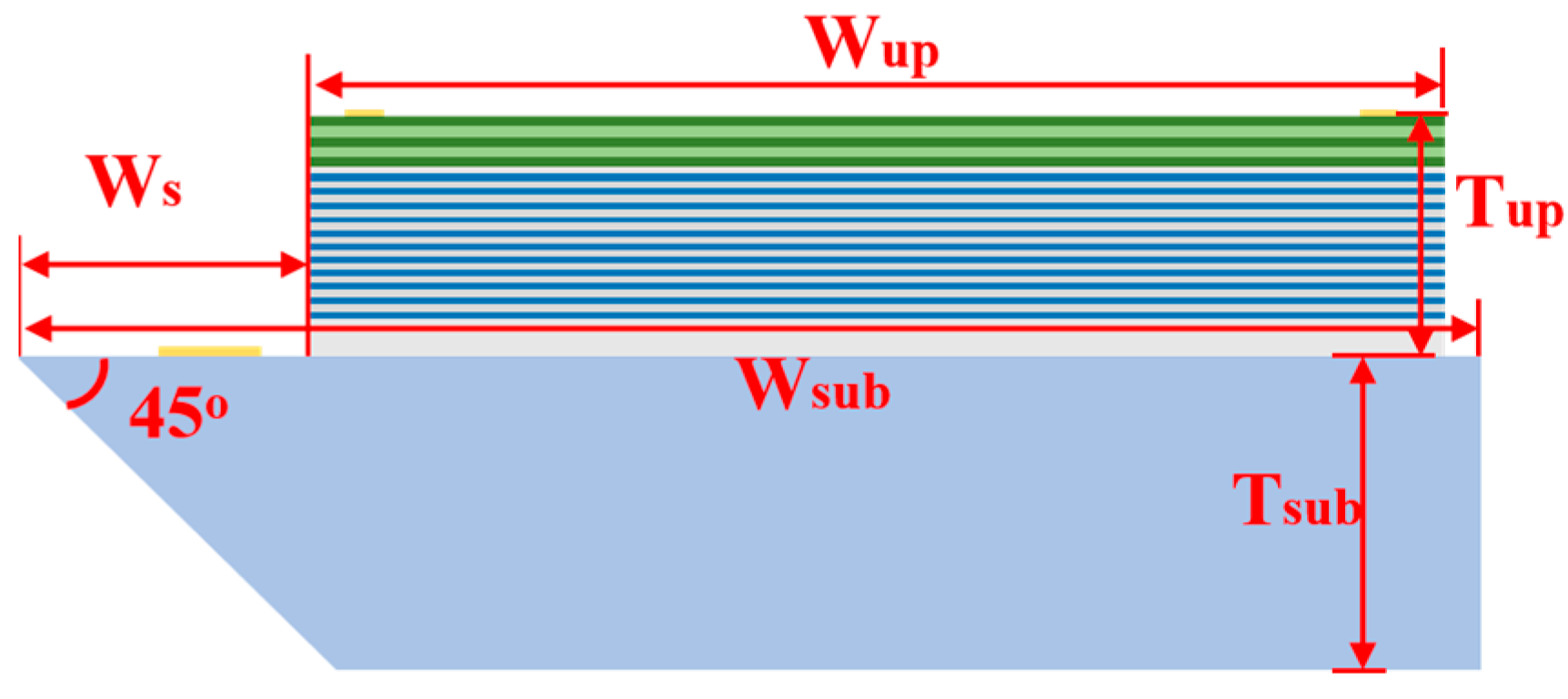
| Value | Unit | |
|---|---|---|
| Wup | 36 | μm |
| Wsub | 40 | μm |
| Ws | 3 | μm |
| Tup | 1364 | nm |
| Tsub | 38 | μm |

| Value | Unit | |
|---|---|---|
| Wetch | 2080 | nm |
| W | 720 | nm |
| Hetch | 1000 | nm |
| Htotal | 2479 | nm |
| TAu | 30 | nm |
| P | 2800 | nm |

| Value | Unit | |
|---|---|---|
| Pmeta | 3.57 | μm |
| Rsphere | 1 | μm |
| Htop | 1.165 | μm |
| Htotal | 1.479 | μm |
Appendix B
| Material | Composition | Thickness (nm) | Dopant | Concentration (cm−3) | Name of Layer |
|---|---|---|---|---|---|
| AlxGa1−xAs | x varying from 0.24 to 0.14 | 50 | Be | 1 × 1019 | LED |
| AlxGa1−xAs | x = 0.24 | 100 | Be | from 3 × 1018 to 1 × 1019 | |
| AlxGa1−xAs | x varying from 0.1 to 0.24 | 40 | |||
| GaAs | 30 | ||||
| AlxGa1−xAs | x varying from 0.24 to 0.1 | 40 | |||
| GaAs | 5.4 | Si | 5 × 1011 | 10-period QWIP | |
| AlxGa1−xAs | x = 0.24 | 35 | |||
| GaAs | 700 | Si | 1.5 × 1018 | Bottom contact | |
| GaAs | 380,000 | Substrate |
| Material | Composition | Thickness (nm) | Dopant | Concentration (cm−3) | Name of Layer |
|---|---|---|---|---|---|
| Au | 30 | Metal contact | |||
| GaAs | 15 | Be | 2 × 1019 | Top contact | |
| AlxGa1−xAs | x = 0.14 | 1100 | Be | 1 × 1019 | LED |
| AlxGa1−xAs | x varying from 0.24 to 0.14 | 50 | Be | 1 × 1019 | |
| AlxGa1−xAs | x = 0.24 | 100 | Be | from 3 × 1018 to 1 × 1019 | |
| AlxGa1−xAs | x varying from 0.1 to 0.24 | 40 | |||
| GaAs | 30 | ||||
| AlxGa1−xAs | x varying from 0.24 to 0.1 | 40 | |||
| GaAs | 5.4 | Si | 5 × 1011 | 10-period QWIP | |
| AlxGa1−xAs | x = 0.24 | 35 | |||
| GaAs | 700 | Si | 1.5 × 1018 | Bottom contact |
Appendix C
| Simulation Setting | 45° | 2D Grating | Metasurface |
|---|---|---|---|
| Dimensions | 2D simulation | 3D simulation | 3D simulation |
| Boundary conditions (x) | PML | Periodic | Periodic |
| Boundary conditions (y) | PML | PML | PML |
| Boundary conditions (z) | Periodic | Periodic | |
| Simulation of LED | 3D simulation | 3D simulation | 3D simulation |
| Type of incident light | Plane wave | Plane wave | Plane wave |
| Wavelength of incident | 9 μm | 9 μm | 9 μm |
| Emitting wavelength | 870 nm | 870 nm | 870 nm |
| Type of LED | Dipole | Dipole | Dipole |
Appendix D
References
- Mizaikoff, B. Mid-IR fiber-optic sensors. Anal. Chem. 2003, 75, 258A–267A. [Google Scholar] [CrossRef]
- Gunapala, S.D.; Bandara, S.V.; Liu, J.K.; Luong, E.M.; Stetson, N.; Shott, C.A.; Bock, J.J.; Rafol, S.B.; McKelvey, M.J. Long-wavelength 256/spl times/256 GaAs/AlGaAs quantum well infrared photodetector (QWIP) palm-size camera. IEEE Trans. Electron Devices 2000, 47, 326–332. [Google Scholar] [CrossRef]
- Yuffa, A.J.; Gurton, K.P.; Videen, G. Three-dimensional facial recognition using passive long-wavelength infrared polarimetric imaging. Appl. Opt. 2014, 53, 8514–8521. [Google Scholar] [CrossRef] [PubMed]
- Gunapala, S.D.; Bandara, S.V.; Bock, J.J.; Ressler, M.E.; Liu, J.K.; Mumolo, J.M.; Rafol, S.B.; David, Z.T.; Werner, M.W. Large-format long-wavelength GaAs/AlGaAs multiquantum well infrared detector arrays for astronomy. Photodetect. Mater. Devices 2001, 4288, 278–285. [Google Scholar]
- Netinant, P.; Vasprasert, P.; Rukhiran, M. Evaluations of effective on LWIR micro thermal camera IoT and digital thermometer for human body temperatures. In Proceedings of the 5th International Conference on E-Commerce, E-Business and E-Government, Rome, Italy, 28–30 April 2021. [Google Scholar]
- Slussarenko, S.; Pryde, G.J. Photonic quantum information processing: A concise review. Appl. Phys. Rev. 2019, 6, 041303. [Google Scholar] [CrossRef]
- Reine, M.B. HgCdTe photodiodes for IR detection: A review. Photodetectors Mater. Devices VI 2001, 4288, 266–277. [Google Scholar]
- Klipstein, P.C.; Avnon, E.; Azulai, D.; Benny, Y.; Fraenkel, R.; Glozman, A.; Hoiman, E.; Klin, O.; Krasovitsky, L.; Langof, L.; et al. Type II superlattice technology for LWIR detectors. Infrared Technol. Appl. XLII 2016, 9819, 216–225. [Google Scholar]
- Arslan, Y.; Çolakoglu, T.; Torunoglu, G.; Aktas, O.; Besikci, C. Enhanced performance QWIP FPAs. Infrared Phys. Technol. 2013, 59, 108–111. [Google Scholar] [CrossRef]
- Bois, P.; Guériaux, V.; de l’Isle, N.B.; Manissadjian, A.; Facoetti, H.; Marcadet, X.; Costard, E.; Nedelcu, A. QWIP status and future trends at Thales. Quantum Sens. Nanophotonic Devices IX 2012, 8268, 566–576. [Google Scholar]
- Nielsen, M.P.; Pusch, A.; Sazzad, M.H.; Pearce, P.M.; Reece, P.J.; Ekins-Daukes, N.J. Thermoradiative power conversion from HgCdTe photodiodes and their current–voltage characteristics. ACS Photonics 2022, 9, 1535–1540. [Google Scholar] [CrossRef]
- Li, Q.; Xie, R.; Wang, F.; Liu, S.; Zhang, K.; Zhang, T.; Gu, Y.; Guo, J.; He, T.; Wang, Y.; et al. SRH suppressed PGI design for very long-wavelength infrared HgCdTe photodiodes. Opt. Express 2022, 30, 16509–16517. [Google Scholar] [CrossRef] [PubMed]
- Rogalski, A.; Martyniuk, P.; Kopytko, M. Type-II superlattice photodetectors versus HgCdTe photodiodes. Prog. Quantum Electron. 2019, 68, 100228. [Google Scholar] [CrossRef]
- Rogalski, A. Toward third generation HgCdTe infrared detectors. J. Alloys Compd. 2004, 371, 53–57. [Google Scholar] [CrossRef]
- Smith, J.S.; Chiu, L.C.; Margalit, S.; Yariv, A.; Cho, A.Y. A new infrared detector using electron emission from multiple quantum wells. J. Vac. Sci. Technol. B Microelectron Process. Phenom. 1983, 1, 376–378. [Google Scholar] [CrossRef][Green Version]
- Goldberg, A.; Choi, K.K.; Cho, E.; McQuiston, B. Laboratory and field performance of megapixel QWIP focal plane arrays. Infrared Phys. Technol. 2005, 47, 91–105. [Google Scholar] [CrossRef]
- Bahrehmand, M.; Gacemi, D.; Vasanelli, A.; Li, L.; Davies, A.G.; Linfield, E.; Sirtori, C.; Todorov, Y. Auto-Calibrated Charge-Sensitive Infrared Phototransistor at 9.3 µm. Sensors 2023, 23, 3635. [Google Scholar] [CrossRef]
- Schneider, H.; Liu, H.C. Quantum Well Infrared Photodetectors, 3rd ed.; Springer Nature: Berlin, Germany, 2007; pp. 13–41. [Google Scholar]
- Liu, H.C.; Dudek, R.; Shen, A.; Dupont, E.; Song, C.Y.; Wasilewski, Z.R.; Buchanan, M. High absorption (>90%) quantum-well infrared photodetectors. Appl. Phys. Lett. 2001, 79, 4237–4239. [Google Scholar] [CrossRef]
- Palaferri, D.; Todorov, Y.; Bigioli, A.; Mottaghizadeh, A.; Gacemi, D.; Calabrese, A.; Vasanelli, A.; Li, L.; Davies, A.G.; Linfield, E.H.; et al. Room-temperature nine-µm-wavelength photodetectors and GHz-frequency heterodyne receivers. Nature 2018, 556, 85–88. [Google Scholar] [CrossRef]
- Olson, B.V.; Murray, L.M.; Prineas, J.P.; Flatté, M.E.; Olesberg, J.T.; Boggess, T.F. All-optical measurement of vertical charge carrier transport in mid-wave infrared InAs/GaSb type-II superlattices. Appl. Phys. Lett. 2013, 102, 202101. [Google Scholar] [CrossRef]
- Jiang, D.; Xiang, W.; Guo, F.; Hao, H.; Han, X.; Li, X.C.; Wang, G.; Xu, Y.; Yu, Q.; Niu, Z. Very high quantum efficiency in InAs/GaSb superlattice for very long wavelength detection with cutoff of 21 μm. Appl. Phys. Lett. 2016, 108, 121110. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Z.; Xu, J.; Dong, F.; Wang, F.; Bai, Z.; Zhou, Y.; Xuliang, C.; Li, H.; Ding, R.; et al. Fabrication and characterization of InAs/GaSb type-II superlattice long-wavelength infrared detectors aiming high temperature sensitivity. J. Light. Technol. 2020, 38, 6129–6134. [Google Scholar] [CrossRef]
- Huang, Y.; Ryou, J.-H.; Dupuis, R.; D’Costa, V.; Steenbergen, E.; Fan, J.; Zhang, Y.-H.; Petschke, A.; Mandl, M.; Chuang, S.-L. Epitaxial growth and characterization of InAs/GaSb and InAs/InAsSb type-II superlattices on GaSb substrates by metalorganic chemical vapor deposition for long wavelength infrared photodetectors. J. Cryst. Growth 2011, 314, 92–96. [Google Scholar] [CrossRef]
- Jiang, J.; Tsao, S.; O’Sullivan, T.; Razeghi, M.; Brown, G.J. Fabrication of indium bumps for hybrid infrared focal plane array applications. Infrared Phys. Technol. 2004, 45, 143–151. [Google Scholar] [CrossRef]
- Luo, H.; Ban, D.; Liu, H.C.; Poole, P.J.; Buchanan, M. Pixel-less imaging device using optical up-converter. IEEE Electron Device Lett. 2004, 25, 129–131. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, J.; Wasilewski, Z.R.; Buchanan, M. Integrated quantum well intersub-band photodetector and light emitting diode. Electron. Lett. 1995, 31, 832–833. [Google Scholar] [CrossRef]
- Liu, H.C.; Dupont, E.; Byloos, M.; Buchanan, M.; Song, C.Y.; Wasilewski, Z.R. QWIP-LED pixel-less thermal imaging device. Int. J. High Speed Electron. Syst. 2002, 12, 891–905. [Google Scholar] [CrossRef]
- Dupont, E.; Byloos, M.; Gao, M.; Buchanan, M.; Song, C.Y.; Wasilewski, Z.R.; Liu, H.C. Pixel-less thermal imaging with integrated quantum-well infrared photodetector and light-emitting diode. IEEE Photonics Technol. Lett. 2002, 14, 182–184. [Google Scholar] [CrossRef]
- Dupont, E.; Byloos, M.; Oogarah, T.; Buchanan, M.; Liu, H.C. Optimization of quantum-well infrared detectors integrated with light-emitting diodes. Infrared Phys. Technol. 2005, 47, 132–143. [Google Scholar] [CrossRef]
- Magnan, P. Detection of visible photons in CCD and CMOS: A comparative view. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 504, 199–212. [Google Scholar] [CrossRef]
- Choi, K.K. Electromagnetic modeling of edge-coupled quantum well infrared photodetectors. J. Appl. Phys. 2012, 111, 124507. [Google Scholar] [CrossRef]
- Li, L.; Bai, P.; Zhang, Y.; Shen, W.; Cao, J. Optical field simulation of edge-coupled terahertz quantum well photodetectors. AIP Adv. 2018, 8, 035214. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Q.; Luo, S.; Ye, F.; Cui, H.; Cui, T. Touch Programmable Metasurface for Various Electromagnetic Manipulations and Encryptions. Small 2022, 18, e2203871. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-optical controlled-NOT logic gate achieving directional asymmetric transmission based on metasurface doublet. Opto-Electron. Adv. 2023, 6, 220073. [Google Scholar] [CrossRef]
- Lian, X.R.; Wang, K.; Bai, X.Q.; Bai, P.; Li, X.H.; Huang, S.H.; Song, W.J.; Shen, W.Z.; Xu, G.Y.; Zhang, Y.H. E-shaped patch antenna for GaAs-based broadband THz detectors. J. Phys. D Appl. Phys. 2022, 55, 475101. [Google Scholar] [CrossRef]
- Dang, T.H.; Cavallo, M.; Khalili, A.; Dabard, C.; Bossavit, E.; Zhang, H.; Ledos, N.; Prado, Y.; Lafosse, X.; Abadie, C.; et al. Multiresonant Grating to Replace Transparent Conductive Oxide Electrode for Bias Selected Filtering of Infrared Photoresponse. Nano Lett. 2023, 18, 8539–8546. [Google Scholar] [CrossRef] [PubMed]
- Ban, D.; Luo, H.; Liu, H.C.; Wasilewski, Z.R.; SpringThorpe, A.J.; Glew, R.; Buchanan, M. Optimized GaAs/AlGaAs light-emitting diodes and high efficiency wafer-fused optical up-conversion devices. J. Appl. Phys. 2004, 9, 5243–5248. [Google Scholar] [CrossRef]
- Lee, H.W.; Lin, B.S. Improvement of illumination uniformity for LED flat panel light by using micro-secondary lens array. Opt. Express 2012, 20, A788–A798. [Google Scholar] [PubMed]
- Eun-Hyun, P. Microlens for efficient coupling between LED and Optical Fiber. IEEE Photonics Technol. Lett. 1999, 11, 439–441. [Google Scholar] [CrossRef]
- Bai, P.; Zhang, Y.; Shen, W.; Yang, N.; Chu, W. Optimization of the Cryogenic Light-Emitting Diodes for High-Performance Broadband Terahertz Upconversion Imaging. Front. Phys. 2021, 9, 774524. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, X.G.; Cao, J.C.; Liu, H.C. Near field and cavity effects on coupling efficiency of one-dimensional metal grating for terahertz quantum well photodetectors. J. Appl. Phys. 2011, 109, 073110. [Google Scholar] [CrossRef]
- Durschlag, M.S.; De Temple, T.A. Infrared optical characterization of GaAs/AlxGa1−xAs submicron heterostructures. Solid State Commun. 1981, 40, 307–310. [Google Scholar] [CrossRef]


| Device | 45° | 2D Grating | Optimized 2D Grating | Hybrid Metasurface |
|---|---|---|---|---|
| ηc | 0.2069 | 0.0486 | 7.6815 | 3.6356 |
| LEE870nm (%) | 1.3673 | 0.1727 | 0.1569 | 4.4120 |
| ηup | 0.2829 | 0.0084 | 1.2052 | 16.0403 |
| Integration time (s) | 0.1782 | 6 | 0.0418 | 0.0032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, J.; Han, S.; Cai, J.; Bai, P.; Yang, N.; Chu, W.; Wang, H.; Li, J.; Xie, Y.; et al. Metasurface Enhanced Upconversion Efficiency for High-Performance Pixel-Less Thermal Imaging. Photonics 2023, 10, 1301. https://doi.org/10.3390/photonics10121301
Wang Y, Zhang J, Han S, Cai J, Bai P, Yang N, Chu W, Wang H, Li J, Xie Y, et al. Metasurface Enhanced Upconversion Efficiency for High-Performance Pixel-Less Thermal Imaging. Photonics. 2023; 10(12):1301. https://doi.org/10.3390/photonics10121301
Chicago/Turabian StyleWang, Yi, Jing Zhang, Shangjie Han, Jiaxuan Cai, Peng Bai, Ning Yang, Weidong Chu, Hanbin Wang, Jiaying Li, Yan Xie, and et al. 2023. "Metasurface Enhanced Upconversion Efficiency for High-Performance Pixel-Less Thermal Imaging" Photonics 10, no. 12: 1301. https://doi.org/10.3390/photonics10121301
APA StyleWang, Y., Zhang, J., Han, S., Cai, J., Bai, P., Yang, N., Chu, W., Wang, H., Li, J., Xie, Y., Chen, M., Wang, Y., & Zhao, Z. (2023). Metasurface Enhanced Upconversion Efficiency for High-Performance Pixel-Less Thermal Imaging. Photonics, 10(12), 1301. https://doi.org/10.3390/photonics10121301





