Exceptional Points in a Non-Markovian Anti-Parity-Time Symmetric System
Abstract
:1. Introduction
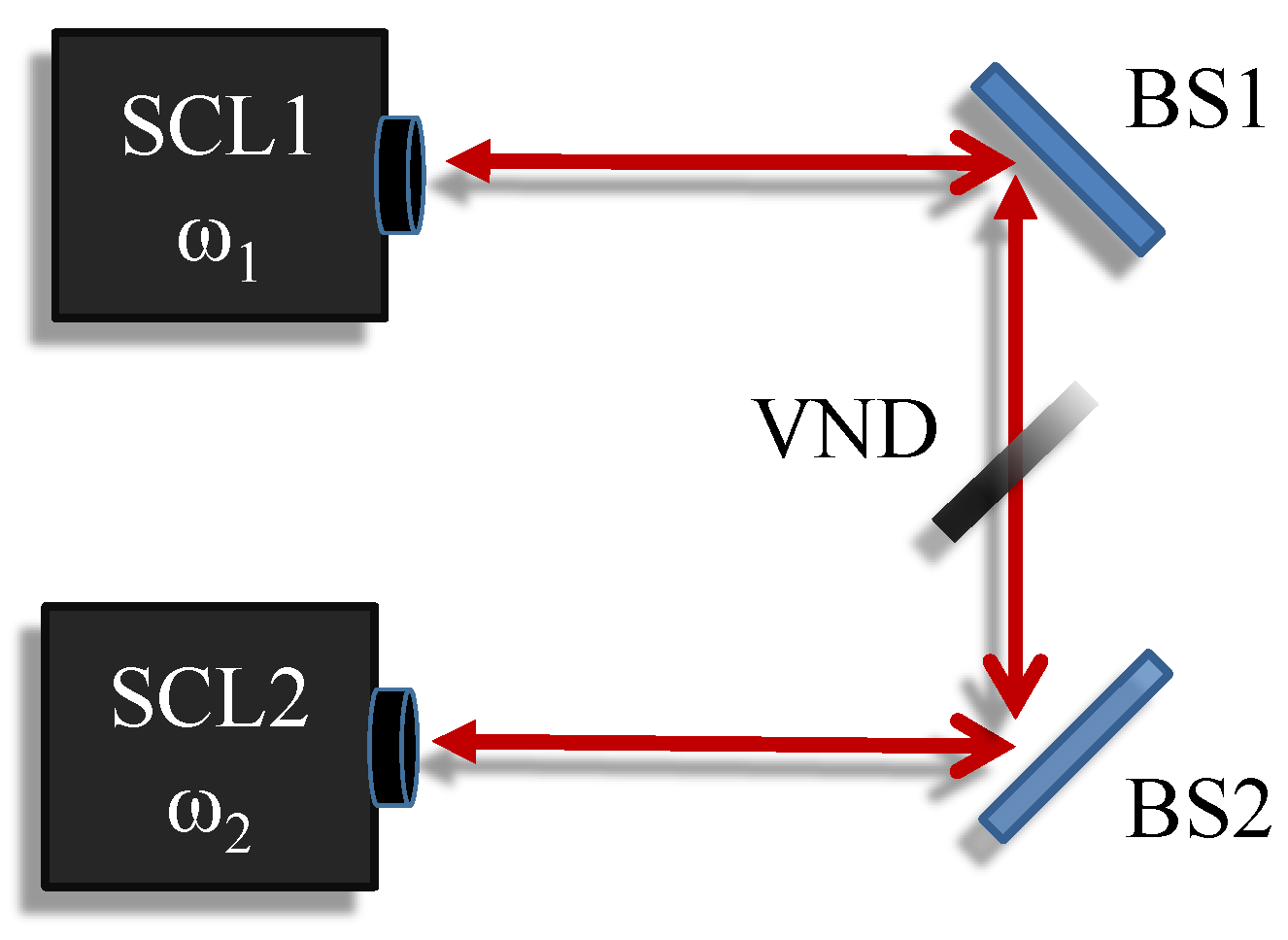
2. Model
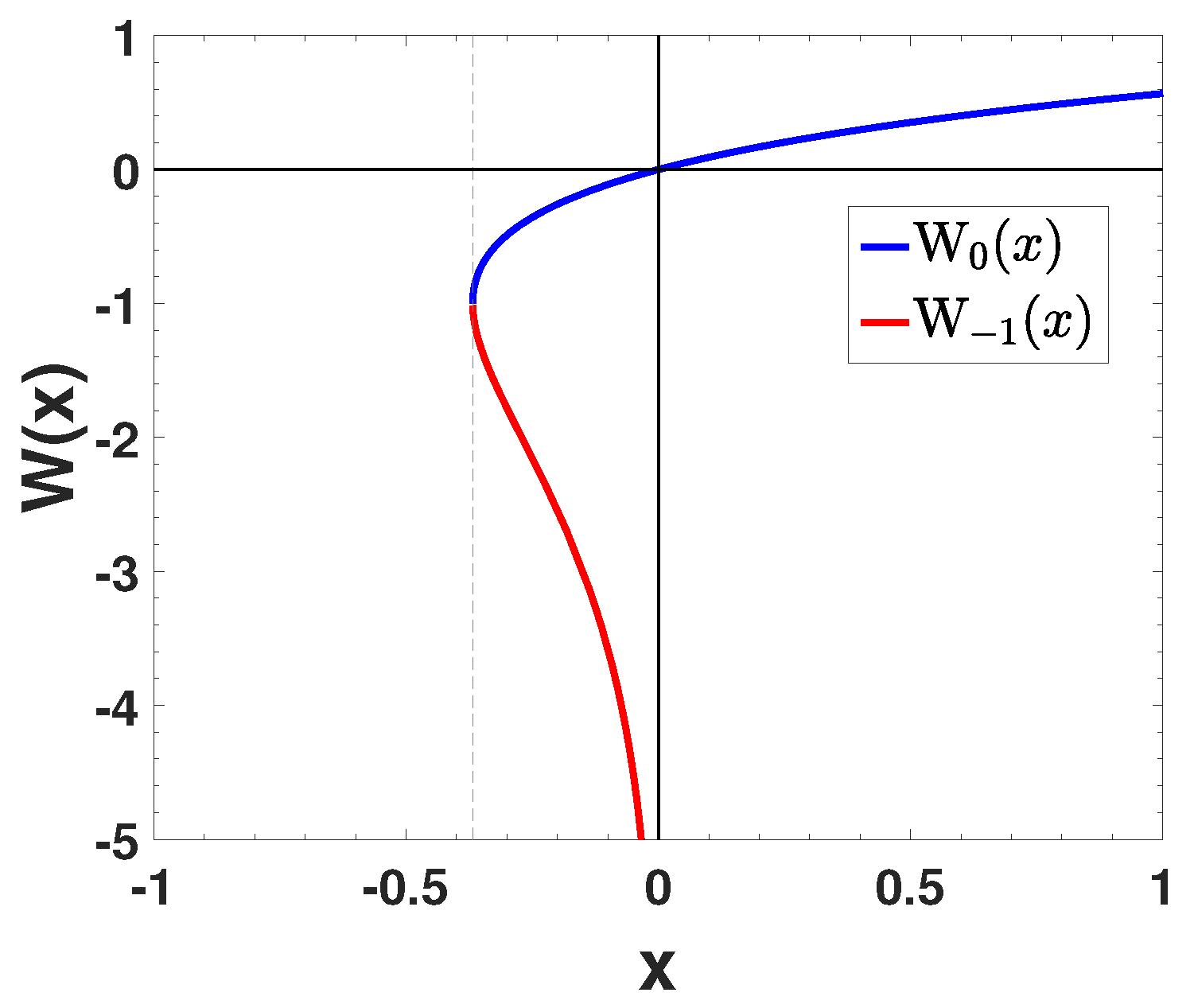
3. Analytic Results
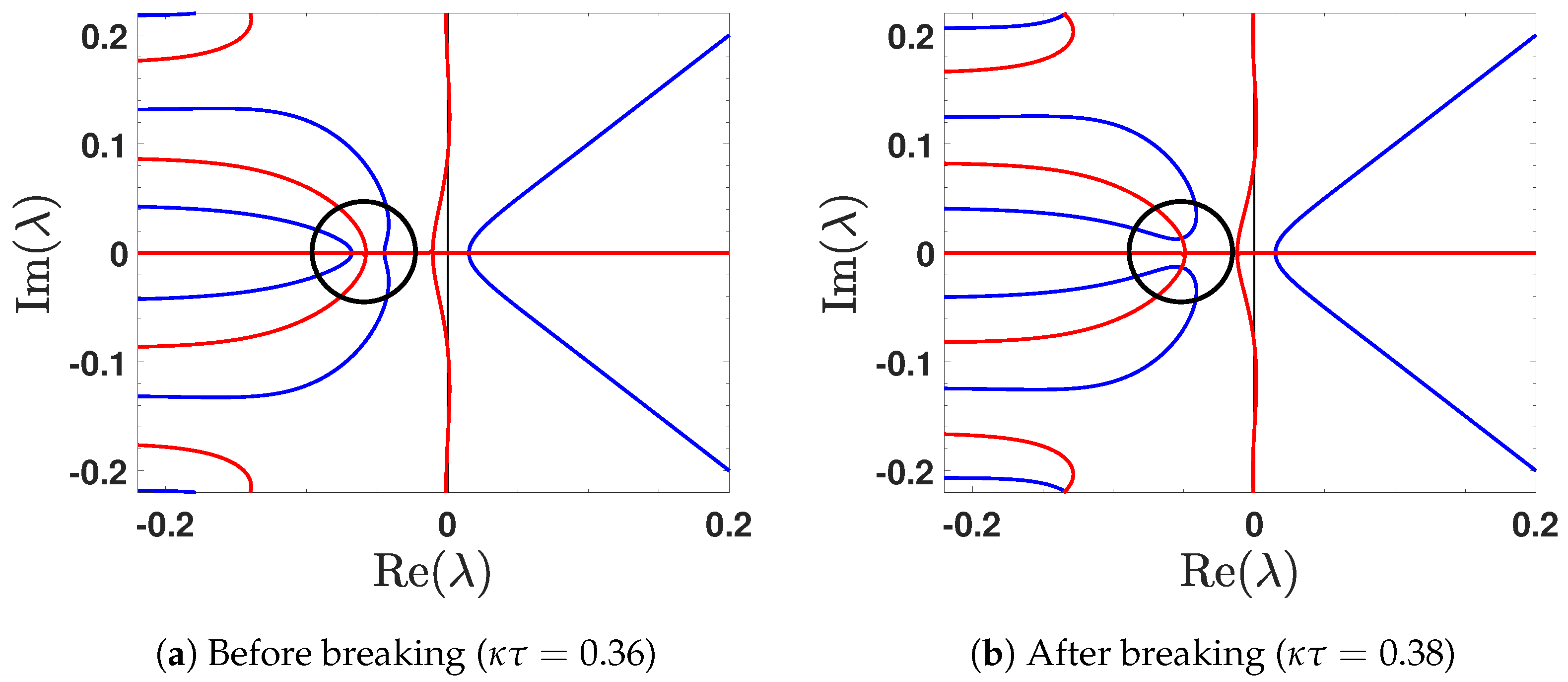
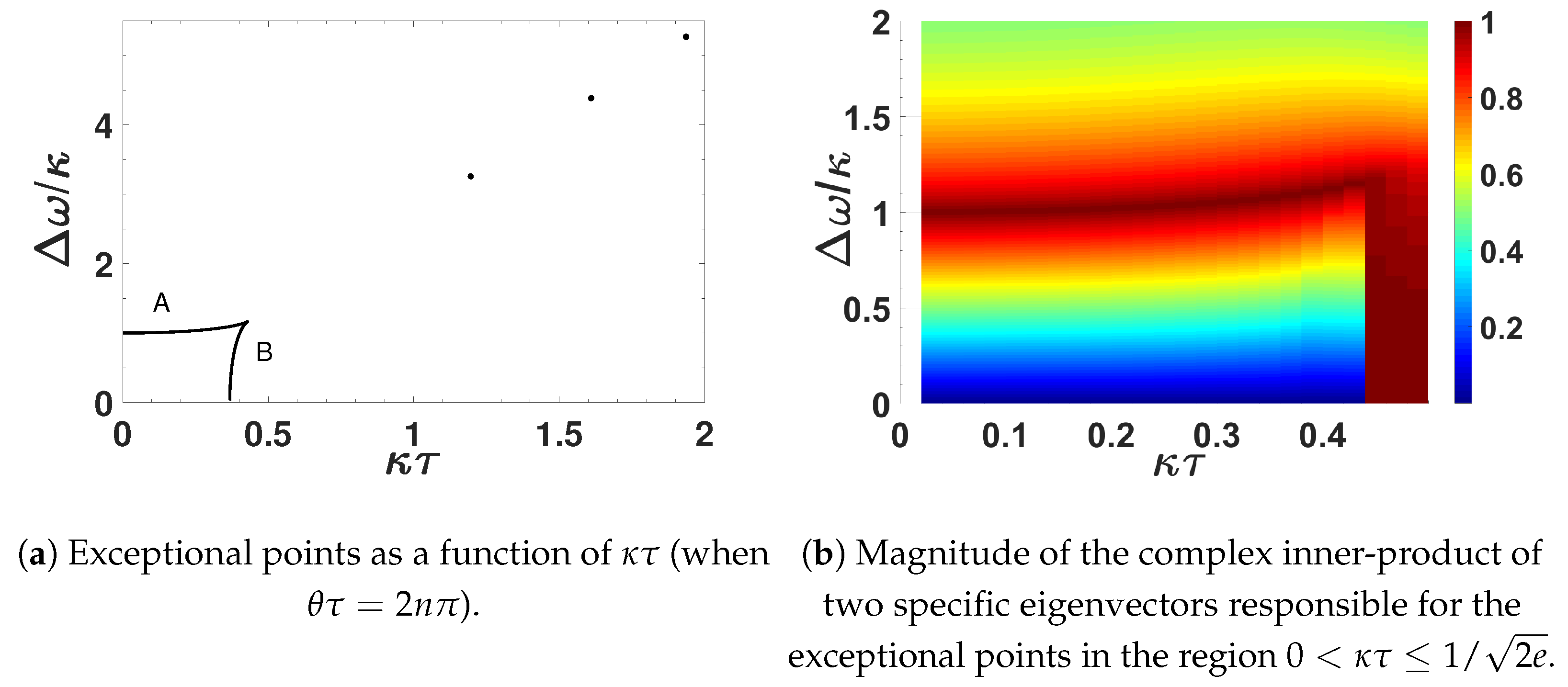
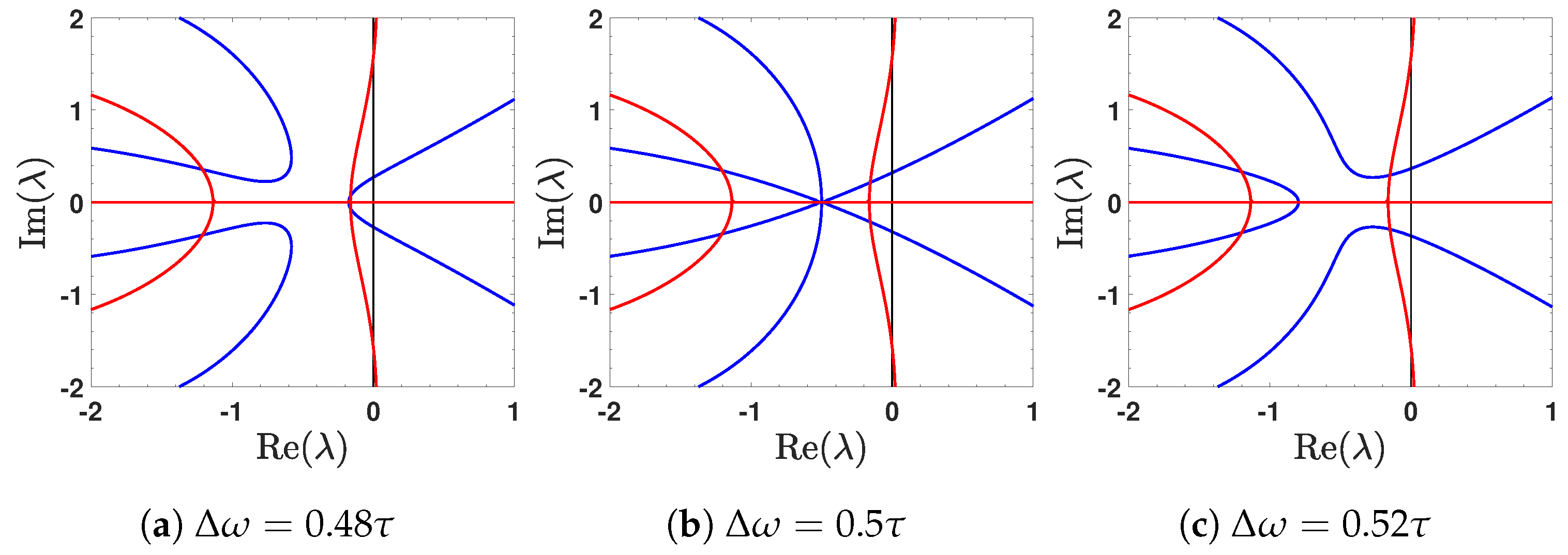
3.1. Second-Order EPs
3.2. Higher-Order EPs
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real spectra in non-hermitian hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M.; Hook, D.W.; Meisinger, P.M.; Wang, Q.H. Complex extension of quantum mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef]
- Schindler, J.; Li, A.; Zheng, M.C.; Ellis, F.M.; Kottos, T. Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A 2011, 84, 040101. [Google Scholar] [CrossRef]
- Bittner, S.; Dietz, B.; Gunther, U.; Harney, H.L.; Miski-Oglu, M.; Richter, A.; Schafer, F. PT symmetry and spontaneous symmetry breaking in a microwave billiard. Phys. Rev. Lett. 2012, 108, 024101. [Google Scholar] [CrossRef]
- Bender, C.M.; Berntson, B.K.; Parker, D.; Samuel, E. Observation of PT phase transition in a simple mechanical system. Am. J. Phys. 2013, 81, 173–179. [Google Scholar] [CrossRef]
- Fleury, R.; Sounas, D.; Alù, A. An invisible acoustic sensor based on parity-time symmetry. Nat. Commun. 2015, 6, 5905. [Google Scholar] [CrossRef]
- Hang, C.; Huang, G.; Konotop, V.V. PT symmetry with a system of three-level atoms. Phys. Rev. Lett. 2013, 110, 083604. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Sheng, J.; Yang, L.; Miri, M.A.; Christodoulides, D.N.; He, B.; Zhang, Y.; Xiao, M. Observation of parity-time symmetry in optically induced atomic lattices. Phys. Rev. Lett. 2016, 117, 123601. [Google Scholar] [CrossRef]
- Peng, P.; Cao, W.; Shen, C.; Qu, W.; Wen, J.; Jiang, L.; Xiao, Y. Anti-parity–time symmetry with flying atoms. Nat. Phys. 2016, 12, 1139–1145. [Google Scholar] [CrossRef]
- Wimmer, M.; Regensburger, A.; Miri, M.A.; Bersch, C.; Christodoulides, D.N.; Peschel, U. Observation of optical solutions in PT-symmetric lattices. Nat. Commun. 2015, 6, 7782. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Onanga, F.A.; Harter, A.K. Time-invariant pt product and phase locking in pt-symmetric lattice models. Phys. Rev. A 2018, 97, 012128. [Google Scholar] [CrossRef]
- Ge, L.; Chong, Y.D.; Rotter, S.; Tureci, H.E.; Stone, A.D. Unconventional modes in lasers with spatially varying gain and loss. Phys. Rev. A 2011, 84, 023820. [Google Scholar] [CrossRef]
- Zheng, M.C.; Christodoulides, D.N.; Fleischmann, R.; Kottos, T. PT optical lattices and universality in beam dynamics. Phys. Rev. A 2010, 82, 010103. [Google Scholar] [CrossRef]
- Alexeeva, N.V.; Barashenkov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Optical solitons in PT-symmetric nonlinear couplers with gain and loss. Phys. Rev. A 2012, 85, 063837. [Google Scholar] [CrossRef]
- Ramezani, H.; Schindler, J.; Ellis, F.M.; Gunther, U.; Kottos, T. Bypassing the bandwidth theorem with PT symmetry. Phys. Rev. A 2012, 85, 062122. [Google Scholar] [CrossRef]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Qu, K. Spontaneous generation of photons in transmission of quantum fields in PT-symmetric optical systems. Phys. Rev. A 2012, 85, 031802. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Dadap, J.I.; Osgood, R.M. Optical parametric amplifcation via non-Hermitian phase matching. Opt. Lett. 2015, 40, 5086–5089. [Google Scholar] [CrossRef]
- Ruzicka, F.; Agarwal, K.S.; Joglekar, Y.N.; Xiao, Y. Conserved quantities, exceptional points, and antilinear symmetries in non-hermitian systems. arXiv 2021, arXiv:2104.11265. [Google Scholar] [CrossRef]
- Jian, Y.; Mei, Y.; Zuo, Y.; Zhai, Y.; Li, J.; Wen, J.; Du, S. Anti-Parity-Time Symmetric Optical Four-Wave Mixing in Cold Atoms. Phys. Rev. Lett. 2019, 123, 193604. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Hahn, C.; Yoon, J.W.; Song, S.H. Observation of an anti-PT-symmetric exceptional point and energy-difference conserving dynamics in electrical circuit resonators. Nat. Commun. 2018, 9, 2182. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Peng, Y.-G.; Han, L.; Miri, M.-A.; Li, W.; Xiao, M.; Zhu, X.-F.; Zhao, J.; Alu, A.; Fan, S.; et al. Anti-parity-time symmetry in diffusive systems. Science 2019, 364, 170–173. [Google Scholar] [CrossRef]
- Wen, J.; Qin, G.; Zheng, C.; Wei, S.; Kong, X.; Xin, T. Observation of information flow in the anti-PT-symmetric system with nuclear spin. npj Quantum Inf. 2020, 6, 28. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many Body Problem; Springer: New York, NY, USA, 1980. [Google Scholar]
- Lipkin, H.J.; Meshkov, N.; Glick, N. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl. Phys. A 1965, 62, 188. [Google Scholar] [CrossRef]
- Dembowski, C.; Graf, H.D.; Harney, H.L.; Heine, A.; Heiss, W.D.; Rehfeld, H.; Richter, A. Experimental observation of the topilogical structure of exceptional points. Phys. Rev. Lett. 2001, 86, 787. [Google Scholar] [CrossRef]
- Parto, M.; Liu, Y.; Bahari, B.; Khajavikhan, M.; Christodoulides, D. Non-Hermitian and topological photonics: Optics at an exceptional point. Nanophotonics 2021, 10, 403–423. [Google Scholar] [CrossRef]
- Miri, M.A.; Alu, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef]
- Ozdemir, S.K.; Rotter, S.; Nori, F.; Yang, L. Parity-time symmetry and exceptional points in photonics. Nat. Mater. 2019, 18, 783–798. [Google Scholar] [CrossRef]
- Doppler, J.; Mailybaev, A.M.; Bohm, J.; Kuhl, U.; Girschik, A.; Libisch, F.; Milburn, T.J.; Rabl, P.; Moiseyev, N.; Rotter, S. Dynamically Encircling an Exceptional Point for Asymmetric Mode Switching. Nature 2016, 537, 76–79. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Miri, M.A.; Hassan, A.U.; Hayenga, W.E.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric coupled microring lasers operating around an exceptional point. Opt. Lett. 2015, 40, 4955–4958. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.W.; Choi, Y.; Hahn, C.; Kim, G.; Song, S.H.; Yang, K.Y.; Lee, J.Y.; Kim, Y.; Lee, C.S.; Shin, J.K.; et al. Time-asymmetric loop around an exceptional point over the full optical communications band. Nature 2018, 562, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Peng, B.; Ozdemir, S.K.; Liu, Y.; Jing, H.; Lu, X.; Liu, Y.; Yang, L.; Nori, F. Giant nonlinearity via breaking parity-time symmetry: A route to low-threshold phonon diodes. Phys. Rev. B 2015, 92, 115407. [Google Scholar] [CrossRef]
- Lü, H.; Ozdemir, S.K.; Kuang, L.-M.; Nori, F.; Jing, H. Exceptional points in random-defect phonon lasers. Phys. Rev. Appl. 2017, 8, 044020. [Google Scholar] [CrossRef]
- Cerjan, A.; Raman, A.; Fan, S. Exceptional contours and band structuredesign in parity-time symmetric photonic crystals. Phys. Rev. Lett. 2016, 116, 203902. [Google Scholar] [CrossRef]
- Ding, K.; Zhang, Z.Q.; Chan, C.T. Coalescence of exceptional points and phase diagrams for one-dimensional PT-symmetric photonic crystals. Phys. Rev. B 2015, 92, 235310. [Google Scholar] [CrossRef]
- Heiss, W.D. Exceptional points of non-Herimitian operators. J. Phys. A 2004, 37, 6. [Google Scholar] [CrossRef]
- Liu, H.; Sun, D.; Zhang, C.; Groesbeck, M.; Mclaughlin, R.; Vardeny, Z.V. Observation of exceptional points in magnonic parity-time symmetric devices. Sci. Adv. 2019, 5, 9144. [Google Scholar] [CrossRef]
- Sakhdari, M.; Hajizadegan, M.; Zhong, Q.; Christodoulides, D.N.; El-Ganainy, R.; Chen, P.Y. Experimental observation of parity-time symmetry breaking near divergent exceptional points. Phys. Rev. Lett. 2019, 123, 193901. [Google Scholar] [CrossRef]
- Brandstetter, M.; Liertzer, M.; Deutsch, C.; Klang, P.; Schoberl, J.; Tureci, H.E.; Strasser, G.; Unterrainer, K.; Rotter, S. Reversing the pump dependence of a laser at an exceptional point. Nat. Commun. 2014, 5, 4034. [Google Scholar] [CrossRef]
- Liertzer, M.; Li, G.; Cerjan, A.; Stone, A.D.; Türeci, H.E.; Rotter, S. Pump-induced exceptional points in lasers. Phys. Rev. Lett. 2012, 108, 173901. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia, H.; El-Ganainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced Sensitivity at Higher-Order Exceptional Points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Ozdemir, S.K.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional Points Enhance Sensing in an Optical Microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Wiersig, J. Enhancing the sensitivity of frequency and energy splitting detection by using exceptional points: Application to microcavity sensors for single-particle detection. Phys. Rev. Lett. 2014, 112, 203901. [Google Scholar] [CrossRef]
- Wilkey, A.; Suelzer, J.; Joglekar, Y.N.; Vemuri, G. Theoretical and experimental characterization of non-Markovian anti-parity-time systems. Commun. Phys. 2023, 6, 308. [Google Scholar] [CrossRef]
- Soriano, M.C.; Garcia-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductor lasers. Rev. Mod. Phys. 2013, 85, 421. [Google Scholar] [CrossRef]
- Wilkey, A.; Suelzer, J.; Joglekar, Y.N.; Vemuri, G. Non-hermitian dynamics in delay-coupled semiconductor lasers. Proc. SPIE 2019, 11081, XI110810G. [Google Scholar]
- Mulet, J.; Masoller, C.; Mirasso, C.R. Modeling bidirectionally coupled single-mode semiconductor lasers. Phys. Rev. A 2002, 65, 063815. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Wilkey, A.; Vemuri, G. Lambert function methods for laser dynamics with time-delayed feedback. Acta Polytech. 2017, 57, 399–403. [Google Scholar] [CrossRef]
- Wilkey, A.; Suelzer, J.S.; Joglekar, Y.; Vemuri, G. Parity-time symmetry in bidirectionally coupled semiconductor lasers. Photonics 2019, 6, 122. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math 1996, 5, 329–359. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilkey, A.; Joglekar, Y.N.; Vemuri, G. Exceptional Points in a Non-Markovian Anti-Parity-Time Symmetric System. Photonics 2023, 10, 1299. https://doi.org/10.3390/photonics10121299
Wilkey A, Joglekar YN, Vemuri G. Exceptional Points in a Non-Markovian Anti-Parity-Time Symmetric System. Photonics. 2023; 10(12):1299. https://doi.org/10.3390/photonics10121299
Chicago/Turabian StyleWilkey, Andrew, Yogesh N. Joglekar, and Gautam Vemuri. 2023. "Exceptional Points in a Non-Markovian Anti-Parity-Time Symmetric System" Photonics 10, no. 12: 1299. https://doi.org/10.3390/photonics10121299
APA StyleWilkey, A., Joglekar, Y. N., & Vemuri, G. (2023). Exceptional Points in a Non-Markovian Anti-Parity-Time Symmetric System. Photonics, 10(12), 1299. https://doi.org/10.3390/photonics10121299






