Abstract
We investigate a simple paraxial vector beam, which is a coaxial superposition of two single-ringed Laguerre–Gaussian (LG) beams, linearly polarized along the horizontal axis, with topological charges (TC) n and −n, and of two LG beams, linearly polarized along the vertical axis, with the TCs m and −m. In the initial plane, such a vector beam has zero spin angular momentum (SAM). Upon propagation in free space, such a propagation-invariant beam has still zero SAM at several distances from the waist plane (initial plane). However, we show that at all other distances, the SAM becomes nonzero. The intensity distribution in the cross-section of such a beam has 2m (if m > n) lobes, the maxima of which reside on a circle of a certain radius. The SAM distribution has also several lobes, from 2m till 2(m + n), the centers of which reside on a circle with a radius smaller than that of the maximal-intensity circle. The SAM sign alternates differently: one lobe has a positive SAM, while two neighbor lobes on the circle have a negative SAM, or two neighbor pairs of lobes can have a positive and negative SAM. When passing through a plane with zero SAM, positive and negative SAM lobes are swapped. The maximal SAM value is achieved at a distance smaller than or equal to the Rayleigh distance.
1. Introduction
As we have demonstrated in [1], in the tight focus of a two-index cylindrical vector beam, the spin Hall effect arises. Therefore, we can suppose that a similar 3D spin Hall effect can also arise in a similar paraxial vector beam, for instance, a propagation-invariant beam obtained as a superposition of Laguerre–Gaussian beams. Previously, the possibility of the 3D spin Hall effect in vector paraxial beams was discovered in [2,3]. As was shown in [2], the spin Hall effect arises in a vector Gaussian beam with several polarization singularities (V-points), i.e., points with indefinite polarization, embedded in the waist plane and residing evenly on a circle of a certain radius. In [3], a vector beam that has an infinite number of the polarization singularities residing on a straight line in the cross-section of the Gaussian beam was studied. It was also shown that upon the propagation of such a paraxial beam in free space, the 3D spin Hall effect arises. Under the spin Hall effect, we understand a phenomenon where a vector beam has inhomogeneous linear polarization in the initial plane (waist plane), but, upon beam propagation, only a finite number of planes exists where the polarization singularities are reconstructed and polarization is inhomogeneous linear, but in all the other transverse planes, there are areas with spin of different sign, i.e., areas where the spin angular momentum (SAM) has a different sign or the third Stokes parameter changes its sign. Thus, due to the beam diffraction in free space, initial inhomogeneous linear polarization becomes inhomogeneous elliptic and the areas with left and right elliptic polarization are separated in the transverse beam section.
Earlier, the spin Hall effect was investigated in microresonators [4], metamaterials [5], dielectric gratings [6], as well as in free space under tight focusing conditions [7]. In [8], the tight focusing of a radially polarized light field was studied. The spin Hall effect in the focus of a radially polarized optical vortex [9] was studied in [10]. In [11], the 3D SAM distribution was investigated in the tight focus of an optical vortex with linear polarization. Tight focusing of an azimuthally polarized optical vortex was studied in [12]. In [13], angular momentum (AM) was studied in the tight focus of hybrid cylindrical vector beams. The orbital motion of microparticles trapped in the tight focus of circularly and radially polarized optical vortices was considered in [14]. In [15], spin-orbital conversion was observed in nonparaxial beams with hybrid polarization. Such hybridly polarized beams in the tight focus were considered in [16]. In [17], the tight focusing of circularly polarized Bessel beams was studied, whereas tight focusing of the high-order Poincaré beams was investigated in [18]. Finally, in [19], spin-orbital conversion after a spherical lens was studied.
In this work, we consider a paraxial vector beam, which is propagation-invariant, i.e., its intensity distribution upon free-space propagation changes only in scale, both theoretically and numerically. For such a beam, we derive the longitudinal component of the SAM vector at an arbitrary distance from the initial plane. It is demonstrated that such a beam has zero SAM in the initial plane, and, at several distances from the waist, the SAM becomes zero again. However, at all the other distances from the waist, the SAM is nonzero. At these distances, the cross-section of the beam has several areas where the SAM is of a different sign, i.e., photons in these areas have spins of opposite signs, which is a manifestation of the spin Hall effect. We note that earlier, the spin Hall effect was studied in uniaxial crystals [20].
2. Field Components and Intensity Distribution of the Two-Index Vector Laguerre–Gaussian Beams
We consider here an initial paraxial vector light field given by
In Equation (1), (r, φ) are the polar coordinates in the beam section. If α = 0 and β = –π/2, such a field reduces to a field with a generalized radial polarization of the order (n, m). If α = π/2 and β = 0, such a field reduces to a field with a generalized azimuthal polarization.
Upon free space propagation, the field acquires the following field components:
where , R, and ζ are, respectively, the beam radius, wavefront curvature, and the Gouy phase at a distance z:
and is the Rayleigh distance, k = 2π/λ is the wavenumber, and λ is the wavelength. We consider a paraxial monochromatic light field, and its longitudinal component Ez can be neglected. Therefore, transverse components of the SAM vector of such a field are also negligible since they are proportional to the longitudinal field component Ez. The tight focusing of a beam, similar to the beam from Equation (2), the longitudinal component of which can no longer be neglected, was studied earlier in our work [1].
The intensity distribution in such a light field reads as
The total power per unit length of such a field is equal to
with δ0,m being the Kronecker delta.
3. Spin Angular Momentum Density of the Two-Index Vector Beams
For nonparaxial vector light fields, all three components of the SAM density vector are significant. For instance, it is the transverse spin density that is responsible for generating the tight focus “optical wheels” [21] or polarization Möbius stripe [22]. However, for the paraxial light fields studied in the current work, only the longitudinal component of the SAM vector is nonzero. The longitudinal components of the spin angular momentum density (Sz) can be obtained by using the following general formula:
For the considered light field (2), it is equal to
It is seen that the SAM density does not change its distribution on propagation in space but changes its value and sign. It is also seen from Equation (7) that the full spin density, i.e., integral of Sz over the whole beam section, is equal to zero at any value z. This is explainable since the integral of cos(x) over the polar angle φ from 0 to 2π is zero. Thus, the full longitudinal spin is conserved upon the propagation of the beam (2).
The SAM density in Equation (7) is the absolute value, but for determining the polarization ellipticity, this value should be compared with the intensity. For instance, circular polarization (C-points) occur in points where Sz = ±I, or Ey = ±iEx. The latter condition leads to the following equation:
It has the solution only if , i.e., C-points can occur only in the following planes:
with p being an integer number.
It is seen that if n = m + 1, then the C-points can be only in far field, z → ∞.
In the planes given by the condition , coordinates of the C-points can be found by solving the equation
Since the notable intensity is concentrated near the rings with the radii w(m/2)1/2 and w(n/2)1/2, then r > w (if n and m exceed 2) and thus the C-points should be located at the polar angles such that .
At certain planes, the SAM density turns to zero, i.e., there are planes with linear polarization:
with p being an arbitrary integer number.
As indicated in Equation (11), if m and n are of the same parity, then there are |m − n|/2 planes (including the initial plane z = 0) with linear polarization. In the far field, (i.e., p = |m − n|/2), polarization is also linear. Thus, between these planes, there are |m − n|/2 planes with locally maximal SAM density.
If m and n have different parity, then there are |m − n + 1|/2 planes (including the initial plane z = 0) with linear polarization. Between these planes, there are |m − n + 1|/2 planes with locally maximal SAM density.
Solving an equation ∂Sz/∂r = 0, we obtain that in each transverse plane, maximal SAM density occurs on a circle with the radius given by
This radius is between the radii of maximal intensity of the components Ex and Ey, which are equal, respectively, to
Below, we consider some partial cases.
If n = 2m, α = 0, β = −π/2 then the SAM density reads as
The cosine turns to zero at φ = φ1 = (π/2 + πp)/m, whereas the sine turns to zero at φ = φ2 = (πp)/m. At φ = φ1, the SAM density does not change its sign, whereas at φ = φ2, it changes the sign. Thus, the SAM density distribution has a petal shape, where the petals of one sign are present in pairs.
If n = 3m, β = 3α, then the SAM density is given by
At , Sz = 0, but it does not change sign.
At , Sz = 0, and it changes sign.
Thus, the SAM density distribution has a petal shape with zero values at the angles φ1 and φ2. Since at φ = φ1, the SAM density does not change its sign, the petals of one sign are present in pairs, whereas the petals of the opposite sign are present in singles.
For other choices of the indices n and m, the distribution of lobes with the spin of different signs is different. Some possible distributions of areas with left and right elliptic polarization in the section of the beam (2) are obtained by numerical simulation and are shown in the next section.
4. Numerical Simulation
Figure 1 illustrates the intensity and SAM density distributions of the light field (2) when m = 2, n = 3, α = 0, and β = −π/2. In this case, the cosines in Equation (7) turn to zero for different polar angles and thus the SAM density should contain 2(m + n) = 10 zero lines. Figure 1 confirms this. The distributions were obtained by theoretical Formula (2) and compared with the Fresnel transform
implemented numerically as the convolution using fast Fourier transform. The obtained images were visually indistinguishable. The polarization ellipses were obtained by M.V. Berry’s formulae [23]:
where A and B are the semiaxes vectors of the polarization ellipse.
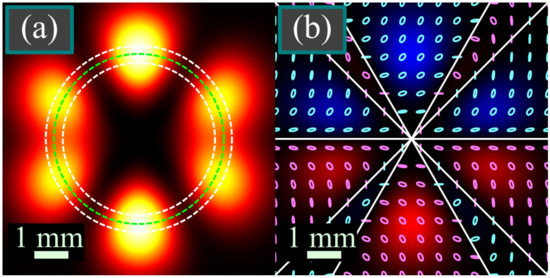
Figure 1.
Intensity (a) and SAM density (b) distributions of the light field (2) at a distance z = 2z0 for the following computation parameters: wavelength λ = 0.532 μm, waist radius of the Gaussian envelope w0 = 1 mm, beam orders m = 2 and n = 3, and initial phases α = 0, β = −π/2. Scale mark in each figure denotes 1 mm. Black and yellow color (a) denote zero and maximal intensity. Blue and red color (b) denote positive and negative SAM density. Pink and cyan ellipses (b) denote right- and left-handed elliptic polarization. White lines (b) denote lines with zero SAM density. Dashed circles (a) illustrate the circles with maximal SAM density (green circle) and with maximal intensity of the components Ex and Ey (white circles) obtained using Equations (12) and (13).
Now, we consider the degenerate cases when the zeros of the cosines in Equation (7) coincide.
Figure 2 illustrates the intensity and SAM density distributions of the light field (2) in several transverse planes when n = 2m, α = 0, and β = –π/2.
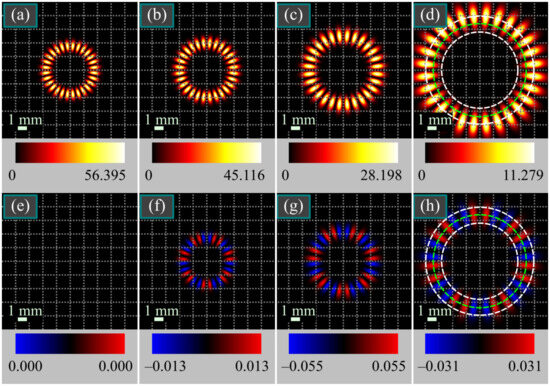
Figure 2.
Intensity (a–d) and SAM density (e–h) distributions of the light field (2) in several transverse planes for the following computation parameters: wavelength λ = 0.532 μm, waist radius of the Gaussian envelope w0 = 1 mm, beams orders m = 7 and n = 14, initial phases α = 0, β = −π/2, and propagation distances z = 0 (a,e), z = z0/2 (b,f), z = z0 (b,f), and z = 2z0 (b,f). The scale mark in each figure denotes 1 mm. Dashed circles (d,h) illustrate the circles with maximal SAM density (green circle) and with the maximal intensity of the components Ex and Ey (white circles) obtained using Equations (12) and (13). Numbers near the color bar under each figure denote minimal and maximal values.
Figure 2 confirms that the SAM density distribution has a petal shape and that the petals of one sign are present in pairs (blue and red pairs in Figure 2f–h).
We note that the energies of the Ex and Ey field components are different and equal, respectively, to and . Therefore, regarding the intensity distributions, only one field component is notable whereas the other is insignificant. Indeed, since in this case n = 2m and m = 7, the energies ratio is Wx/Wy = 7·10−6. Nevertheless, these components interact and the weak component affects the SAM density distribution. It is seen in Figure 2d that the ring of the maximal intensity of the Ex-component is outside the area of notable intensity (inner white ring in Figure 2d,h), but the Ex-component affects the radius of the maximal-SAM ring (green middle ring in Figure 2d,h).
According to Equation (11), zero SAM density should be in the following planes: z = 0, z = z0 tan(π/7) ≈ 0.48z0, z = z0 tan(2π/7) ≈ 1.25z0, and z = z0 tan(3π/7) ≈ 4.38z0. That is why the petal colors in Figure 2f and Figure 2g (z = z0/2 and z = z0) are the same, whereas in Figure 2h (z = 2z0) they are inverted.
Figure 3 shows the intensity and SAM density distributions of the light field (2) in several transverse planes when n = 3m and α = β = 0.
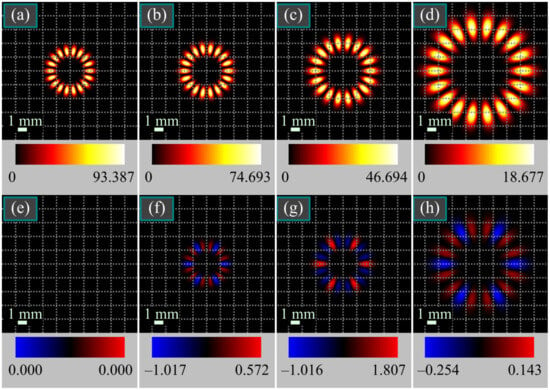
Figure 3.
Intensity (a–d) and SAM density (e–h) distributions of the light field (2) in several transverse planes for the following computation parameters: wavelength λ = 0.532 μm, waist radius of the Gaussian envelope w0 = 1 mm, beams orders m = 3 and n = 9, initial phases α = β = 0, and propagation distances z = 0 (a,e), z = z0/2 (b,f), z = z0 (b,f), and z = 2z0 (b,f). Scale mark in each figure denotes 1 mm. Numbers near the color bar under each figure denote minimal and maximal values.
Figure 3 confirms that the SAM density consists of petals, and the petals of one sign are present in pairs, whereas the petals of the opposite sign are present in singles.
According to Equation (11), zero SAM density should be in the following planes: z = 0, z = z0 tan(π/6) ≈ 0.58z0, and z = z0 tan(π/3) ≈ 1.73z0. These distances explain why the petals in Figure 3g (z = z0) are inverted compared to petals in Figure 3f (z = z0/2), and the petals in Figure 3h (z = 2z0) are inverted compared to petals in Figure 3g (z = z0).
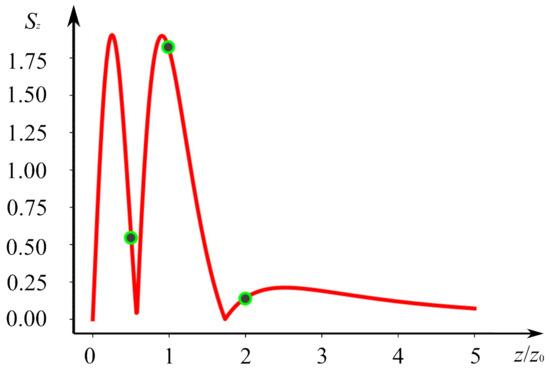
Figure 4 depicts the dependence of the maximal SAM density in each transverse plane on the propagation distance for the light field from Figure 3.
If the index n is high, but the index m is low, the intensity distribution of the component Ey significantly overwhelms that of the component Ex. Thus, for two close values m, the intensity distributions should look the same, but the SAM density distributions should be different. Figure 5 shows the intensity and SAM density distributions of the light field (2) in the plane z = 2z0 when n = 14, m = 6 (Figure 5a,b), m = 7 (Figure 5c,d), and α = β = 0.
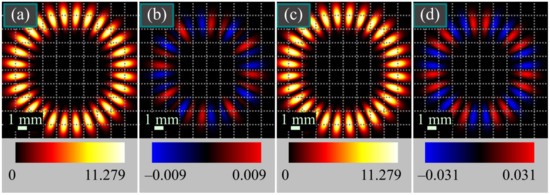
Figure 5.
Intensity (a,c) and SAM density (b,d) distributions of the light field (2) for the following computation parameters: wavelength λ = 0.532 μm, waist radius of the Gaussian envelope w0 = 1 mm, beams orders m = 6 and n = 14 (a,b), m = 7 and n = 14 (c,d), initial phases α = 0, β = −π/2, and propagation distance z = 2z0. Scale mark in each figure denotes 1 mm. Numbers near the color bar under each figure denote minimal and maximal values.
It is seen that, indeed, despite identical intensity distributions, SAM density distributions are qualitatively different. Thus, such beams can be used for hidden data transmission. If the incoming optical beam is identified by its intensity distribution, then it is not seen how it changes the third Stokes parameter, used for encoding the hidden data.
5. Discussion
There are a lot of works reporting on the spin Hall effect in various devices, like microresonators [4], metamaterials [5], or dielectric gratings [6]. The current work is our third work (after [2,3]) investigating the spin Hall effect in free space and without tight focusing conditions. In contrast to [2,3], there is no need to generate multiple spatially separated polarization singularities. Instead, one singularity in the beam center should be generated, but it should have a different order in the horizontal and vertical field components. We have not conducted an experiment yet, since generating such beams requires, after splitting the incoming light field into orthogonally polarized fields, either combining two different-order fork gratings on a spatial light modulator, or encoding two amplitude-phase distributions into phase-only elements using a technique like those described in [24,25]. However, the studied beams are easy to identify by using polarization analyzers and then by simply counting the lobes with right and left elliptic polarization.
6. Conclusions
In this work, we have demonstrated theoretically and by numerical simulation that when a vector propagation-invariant beam with two different indices propagates in free space, there are several planes, transverse to the optical axis, including the initial plane, where the spin density is zero. In the whole space between these planes, the spin Hall effect arises, i.e., there are several areas in the beam section, the count of which depends on the beam indices, where the spin is of different signs. Thus, the polarization state changes over the beam section from left circular and elliptic polarization to right circular and elliptic polarization, and, what is interesting, the intensity distribution in the beam section is not changed upon propagation, whereas the polarization state in each point is changed. This is because different transverse components of the electric field strength vectors Ex and Ey have different Gouy phases, and at different distances from the beam waist, the difference between the Gouy phases makes a different contribution to the spin angular momentum distribution. The beams studied here can be used for hidden data transmission in wireless telecommunication systems, if the data are transmitted by changing the polarization state without modifying the intensity distribution [26,27,28]. In addition, the investigated beams can be used as optical traps for several microparticles [29] or as pumping beams for pumping disc lasers based on whispering gallery modes, or for other perspective lasers [30].
Author Contributions
Conceptualization, V.V.K.; methodology, V.V.K. and A.A.K.; software, A.A.K.; validation, V.V.K.; formal analysis, V.V.K.; investigation, V.V.K. and A.A.K.; resources, V.V.K.; data curation, A.A.K.; writing—original draft preparation, V.V.K.; writing—review and editing, V.V.K.; visualization, A.A.K.; supervision, V.V.K.; project administration, V.V.K.; funding acquisition, V.V.K. and A.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Russian Science Foundation grant no. 22-12-00137 (in terms of theory) and within the framework of the State assignment of the Federal Scientific Research Center “Crystallography and Photonics” of the Russian Academy of Sciences (in terms of modeling).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kovalev, A.A.; Kotlyar, V.V. Spin Hall effect of double-index cylindrical vector beams in a tight focus. Micromachines 2023, 14, 494. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Stafeev, S.S. Spin Hall effect in the paraxial light beams with multiple polarization singularities. Micromachines 2023, 14, 777. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Nalimov, A.G. Spin Hall effect in paraxial vectorial light beams with an infinite number of polarization singularities. Micromachines 2023, 14, 1470. [Google Scholar] [CrossRef]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical spin Hall effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Lee, D.; Kim, T.H.; Yang, Y.; Park, H.J.; Rho, J. Observation of enhanced optical spin Hall effect in a vertical hyperbolic metamaterial. ACS Photonics 2019, 6, 2530–2536. [Google Scholar] [CrossRef]
- Kim, M.; Lee, D.; Ko, B.; Rho, J. Diffraction-induced enhancement of optical spin Hall effect in a dielectric grating. APL Photonics 2020, 5, 066106. [Google Scholar] [CrossRef]
- Stafeev, S.S.; Nalimov, A.G.; Kovalev, A.A.; Zaitsev, V.D.; Kotlyar, V.V. Circular polarization near the tight focus of linearly polarized light. Photonics 2022, 9, 196. [Google Scholar] [CrossRef]
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Han, L.; Liu, S.; Li, P.; Zhang, Y.; Cheng, H.; Zhao, J. Catalystlike effect of orbital angular momentum on the conversion of transverse to three-dimensional spin states within tightly focused radially polarized beams. Phys. Rev. A 2018, 97, 053802. [Google Scholar] [CrossRef]
- Li, H.; Ma, C.; Wang, J.; Tang, M.; Li, X. Spin-orbit Hall effect in the tight focusing of a radially polarized vortex beam. Opt. Express 2021, 29, 39419–39427. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, B.; Zhu, Z.; Rui, G.; He, J.; Cui, Y.; Gu, B. Understanding of transverse spin angular momentum in tightly focused linearly polarized vortex beams. Opt. Express 2022, 30, 5121–5130. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Cai, Y.; Yan, S.; Liang, Y.; Zhang, P.; Yao, B. Orbit-induced localized spin angular momentum in strong focusing of optical vectorial vortex beams. Phys. Rev. A 2018, 97, 053842. [Google Scholar] [CrossRef]
- Meng, P.; Man, Z.; Konijnenberg, A.P.; Urbach, H.P. Angular momentum properties of hybrid cylindrical vector vortex beams in tightly focused optical systems. Opt. Express 2019, 27, 35336–35348. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yan, S.; Yao, B.; Liang, Y.; Zhang, P. Spinning and orbiting motion of particles in vortex beams with circular or radial polarizations. Opt. Express 2016, 24, 20604–20612. [Google Scholar] [CrossRef]
- Chen, R.P.; Chew, K.H.; Dai, C.Q.; Zhou, G. Optical spin-to-orbital angular momentum conversion in the near field of a highly nonparaxial optical field with hybrid states of polarization. Phys. Rev. A 2017, 96, 053862. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Z.; Pu, J. Tight focusing properties of hybridly polarized vector beams. J. Opt. Soc. Am. A 2012, 29, 1099–1104. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhang, G.L.; Wang, Q.; Wang, M.; Tu, C.; Li, Y.; Wang, H.T. Spin-to-orbital angular momentum conversion via light intensity gradient. Optica 2021, 8, 1231–1236. [Google Scholar] [CrossRef]
- Yu, P.; Liu, Y.; Wang, Z.; Li, Y.; Gong, L. Interplay between spin and orbital angular momenta in tightly focused higher-order Poincaré sphere beams. Ann. Phys. 2020, 532, 2000110. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodríguez-Herrera, O.G.; Lara, D.; Dainty, C. Spin-to-orbital angular momentum conversion in focusing, scattering, and imaging systems. Opt. Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef]
- Fadeyeva, T.A.; Rubass, A.F.; Volyar, A.V. Transverse shift of a high-order paraxial vortex-beam induced by a homogeneous anisotropic medium. Phys. Rev. A 2009, 79, 053815. [Google Scholar] [CrossRef]
- Aiello, A.; Banzer, P.; Neugebauer, M.; Leuchs, G. From transverse angular momentum to photonic wheels. Nature Photon. 2015, 9, 789–795. [Google Scholar] [CrossRef]
- Bauer, T.; Banzer, P.; Karimi, E.; Orlov, S.; Rubano, A.; Marrucci, L.; Leuchs, G. Observation of optical polarization Möbius strips. Science 2015, 347, 964–966. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Index formulae for singular lines of polarization. J. Opt. A Pure Appl. Opt. 2004, 6, 675. [Google Scholar] [CrossRef]
- Goorden, S.A.; Bertolotti, J.; Mosk, A.P. Superpixel-based spatial amplitude and phase modulation using a digital micromirror device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Mínguez-Vega, G.; Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef]
- Ran, W.; Ren, Z.; Wang, P.; Yan, Y.; Zhao, K.; Li, L.; Li, Z.; Wang, L.; Yang, J.; Wei, Z.; et al. Integrated polarization-sensitive amplification system for digital information transmission. Nat. Commun. 2021, 12, 6476. [Google Scholar] [CrossRef]
- Ding, S.; Li, R.; Luo, Y.; Dang, A. Polarization coherent optical communications with adaptive polarization control over atmospheric turbulence. J. Opt. Soc. Am. A 2018, 35, 1204–1211. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Dang, A. Performance of wireless optical communication systems under polarization effects over atmospheric turbulence. Opt. Commun. 2018, 416, 207–213. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photon. 2021, 3, 034001. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M. Highlighting photonics: Looking into the next decade. eLight 2021, 1, 2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).