Abstract
Microwave photonic (MWP) signal processors, which process microwave signals based on photonic technologies, bring advantages intrinsic to photonics such as low loss, large processing bandwidth, and strong immunity to electromagnetic interference. Optical microcombs can offer a large number of wavelength channels and compact device footprints, which make them powerful multi-wavelength sources for MWP signal processors to realize a variety of processing functions. In this paper, we experimentally demonstrate the capability of microcomb-based MWP signal processors to handle diverse input signal waveforms. In addition, we quantify the processing accuracy for different input signal waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. Finally, we analyse the factors contributing to the difference in the processing accuracy among the different input waveforms, and our theoretical analysis well elucidates the experimental results. These results provide guidance for microcomb-based MWP signal processors when processing microwave signals of various waveforms.
1. Introduction
Microwave signal processors have found wide applications in telecommunication and radar systems [1,2,3,4]. Traditional microwave signal processors relying on electronic devices exhibit significant loss and strong crosstalk when handling high-frequency microwave signals, which make them suffer from limited operation bandwidths. To overcome this restriction, microwave photonic (MWP) signal processors that perform signal processing functions based on MWP technologies have attracted great interest [3,4,5,6].
A variety of MWP signal processors have been demonstrated by exploiting different optical filtering modules to process microwave signals that are modulated onto a single optical carrier [7,8,9,10,11,12,13,14,15,16,17]. Although these approaches perform well regarding achieving specific processing functions, they face limitations in their reconfigurability to realize diverse processing functions based on a single system. On the contrary, in MWP signal processors implemented based on the transversal filter structure [18], input microwave signals are modulated onto multiple optical carriers with adjustable time delays and tap weights before summing via photodetection. This enables high reconfigurability to achieve various processing functions without changing any hardware [2,18].
For MWP signal processors implemented by the transversal filter systems, a large number of taps, or the wavelength channels provided by multi-wavelength optical sources, are required to improve their performance. Compared to other multi-wavelength optical sources, such as discrete laser arrays [19,20,21], fibre Bragg grating arrays [22,23,24], laser frequency combs generated by electro-optic (EO) modulation [25,26,27], and mode-locked fibre lasers [28,29], optical microcombs can provide significantly increased numbers of wavelength channels by using compact micro-scale resonators [30,31], which is critical for improving the processing accuracy of MWP transversal signal processors. They also have the ability to offer broad Nyquist zones, which allow for large processing bandwidths [4,32,33]. With these advantages, a variety of signal processing functions have been successfully demonstrated using microcomb-based MWP signal processors, such as differentiation [34], integration [35], Hilbert transform [36], arbitrary waveform generation [37], and convolutional processing [38,39]. In addition to applications in microwave photonics, optical microcombs have also found wide applications in communications [40,41,42], logic operation [43], and sensing [44,45].
Although a range of signal processing functions have been realized, they only used Gaussian input waveforms for demonstrations, while the ability to handle various input signal waveforms is essential for practical applications. In this paper, we experimentally demonstrate the capability of microcomb-based MWP signal processors for dealing with various input signal waveforms. We investigate the processing accuracy of different input waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. We also perform theoretical analysis and discuss the reasons for the difference in the processing accuracy among the different input waveforms. These results offer a valuable guide for microcomb-based MWP signal processors to handle microwave signals with different waveforms.
2. Microcomb-Based MWP Signal Processors
MWP signal processors based on the transversal filter are implemented based on MWP technologies, which can overcome the electrical bandwidth bottleneck by providing a substantially increased processing bandwidth. An MWP transversal signal processor has high reconfigurability in terms of its spectral transfer function, which can be expressed as [4]
where ω is the angular frequency of the input microwave signal to be processed, M is the tap number, an (n = 0, 1, 2, …, M − 1) is the tap coefficient of the nth tap, and ΔT is the time delay between adjacent taps. By properly designing the various tap coefficients an (n = 0, 1, 2, …, M − 1), different signal processing functions can be realized by using a single system without changing the hardware.
Optical microcombs enable MWP transversal systems to have small size, weight, and power consumption (SWaP) [30,31,46,47], and excellent compatibility with monolithic integration, making them powerful alternatives to conventional multi-wavelength optical sources. Figure 1 shows the schematic of a microcomb-based MWP signal processor. An optical microcomb is used to generate multiple wavelength channels that act as discrete taps for the transversal signal processor. The generated optical microcomb is spectrally shaped according to the designed tap coefficients an (n = 0, 1, 2, …, M − 1). Next, all of the wavelength channels of the shaped optical microcomb are imprinted with the input microwave signal via an electro-optic modulator (EOM), leading to the generation of multiple microwave replicas. Following this, the modulated optical signals transmit through a dispersive medium to introduce time delays ∆T, which progressively separate the microwave replicas. Finally, the delayed replicas are summed upon photodetection via a photodetector.
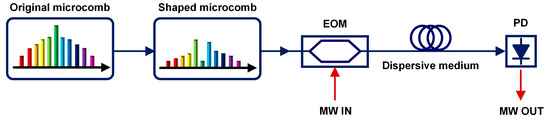
Figure 1.
Schematic diagram of a microcomb-based microwave photonic (MWP) signal processor. EOM: electro-optic modulator. MW: microwave. PD: photodetector.
In principle, the microcomb-based MWP signal processor in Figure 1 can work with different types of optical microcombs, such as single soliton [48,49,50], dark soliton [51,52], and soliton crystal [53,54]. Before spectral shaping is used to achieve the desired tap coefficients, the initial comb with non-uniform power distributions in the comb lines can be amplified and pre-shaped to obtain a uniform power distribution. Therefore, the initial spectral shape of optical microcomb is not an essential factor for the realization of MWP transversal signal processors. It is also worth mentioning that as the optical microcomb primarily functions as a multi-wavelength source for the transversal signal processor, it can operate under relatively incoherent conditions. However, in many practical applications, high-coherence optical combs are still preferred. Optical microcombs operating under different states, including different types of solitons, as well as incoherent and especially chaotic states [49], can introduce additional noise and instability, thus leading to a decrease in the processing accuracy [30,46,47].
The operation bandwidth of the microcomb-based MWP transversal signal processor in Figure 1 is determined by both the comb spacing and time delay between adjacent wavelength channels. Generally, it remains constant unless there are changes to the hardware within the system, such as using an MRR with a different free spectral range (FSR) or employing a dispersion medium with a different length or dispersion parameter. According to the Nyquist sampling theorem, the sampling rate of a continuous-time bandwidth-limited signal needs to exceed twice its maximum frequency component to avoid aliasing. This constraint sets an upper threshold for the bandwidth of the input microwave signal to be processed, which should not surpass half of the microcomb’s comb spacing. On the other hand, the bandwidth of the input microwave signal should not exceed half of the FSR of the RF spectral response (FSRRF), i.e., 1/2 · FSRRF = 1/(2∆T). This sets another limitation for the maximum bandwidth of the input microwave signal. In our work, we focus on the influence of different temporal waveforms of input microwave signals on the processing accuracy of the signal processors. Detailed discussion on the influence of the input signal bandwidth on the processing accuracy can be found in Ref. [30].
3. Experimental Results
In our experimental demonstration, we implemented the microcomb-based MWP signal processors based on the setup shown in Figure 2, which consisted of a microcomb generation module and a transversal signal processing module. In the microcomb generation module, the optical microcomb was generated by a microring resonator (MRR) made from high-index doped silica glass [55]. The high-index doped silica glass offers attractive material properties for microcomb generation, including ultra-low linear loss (~0.06 dB/cm), a moderate nonlinear parameter (~233 W−1·km−1), and a negligible nonlinear loss even at extremely high intensities (~25 GW·cm−2) [55]. The MRR had a quality factor of ~1.5 × 106. A continuous-wave (CW) light was amplified to ~32.1 dBm by an erbium-doped fibre amplifier (EDFA) and used to pump the MRR. The polarization of the CW pump was adjusted to TE polarization, which aligned with the TE-polarized resonance of the MRR at ~1551.23 nm. When the pump power of the CW laser was sufficiently high and its wavelength was swept across the MRR’s resonance at ~1551.23 nm, optical parametric oscillation occurred, resulting in the generation of a palm-like soliton crystal microcomb [56], as shown in Figure 3a. The MRR was designed to have a radius of ~592 μm, which corresponded to a comb spacing of ~0.4 nm or ~49 GHz. In our experimental demonstration, 20 comb lines were employed as discrete taps. The initially generated microcomb exhibited non-uniform power distributions among the comb lines, and so it was shaped by the first waveshaper (WS1, Finisar) to flatten the comb lines. This was carried out to achieve a higher signal-to-noise ratio and reduce the required loss control range for the second waveshaper in the transversal signal processing module, which further shaped the comb lines according to the designed tap coefficients.
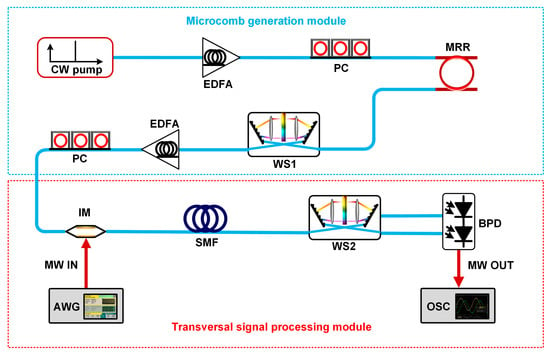
Figure 2.
Experimental schematic of a microcomb-based MWP signal processor. CW pump: continuous-wave pump. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. WS: wave shaper. IM: intensity modulator. MW: microwave. BPD: balanced photodetector. SMF: single-mode fibre. AWG: arbitrary waveform generator. OSC: oscilloscope.
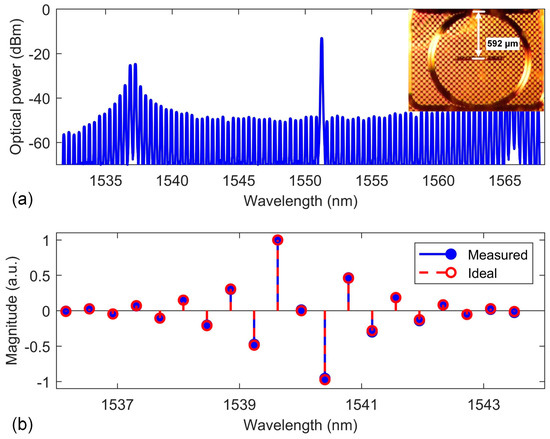
Figure 3.
(a) Optical spectrum of soliton crystal microcomb generated by an MRR made from high-index doped silica glass. Inset shows a microscope image of the MRR. (b) Ideal and measured tap coefficients after optical spectral shaping.
In the transversal signal processing module, the shaped microcomb was modulated by the input microwave signal via an intensity modulator (IM) (iXblue). The input microwave signal was multicast onto different wavelength channels, resulting in the generation of multiple microwave replicas. Next, the microwave replicas were transmitted through a spool of single mode fibre (SMF), which served as the dispersive medium that introduced a time delay between adjacent wavelength channels, i.e., ∆T in Equation (1). The time delay ∆T can be further expressed as [4]
where L is the fibre length, D2 is the second-order dispersion parameter, and ∆λ is the comb spacing. In our experiments, these parameters were L = ~5.124 km, D2 = ~17.4 ps/nm/km, and ∆λ = ~0.4 nm, which resulted in a time delay ∆T = ~35.7 ps.
After passing the dispersive medium, the comb lines were spectrally shaped by the second waveshaper (WS2, Finisar) according to the designed tap coefficients an (n = 0, 1, 2, …, M − 1). Finally, the delayed microwave replicas were summed upon photodetection via a balanced photodetector (BPD, Finisar). The BPD separated the wavelength channels into two categories according to the sign of tap coefficients, achieving both positive and negative tap coefficients.
We took the first-order differentiation as an example to investigate the influence of different input signal waveforms on the processing accuracy of microcomb-based MWP signal processors. The spectral transfer function of the first-order differentiation can be described by [3]
where j = , and ω is the angular frequency. The ideal tap coefficients were calculated by performing an inverse Fourier transform of Equation (3), and the results are shown in Figure 3b. For comparison, the measured tap coefficients after spectral shaping of the comb lines are also shown. As can be seen, the measured tap coefficients closely matched with the ideal tap coefficients, indicating the achievement of effective spectral shaping.
We selected five different temporal waveforms for the input microwave signal, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. The input microwave signals were generated by an arbitrary waveform generator (AWG, Keysight). As mentioned in Section 2, to prevent aliasing, the sampling rate of the input microwave signal needs to exceed twice its maximum frequency component. Thus, the bandwidth of the input microwave signal to be processed should not surpass half of the microcomb’s comb spacing, i.e., ~24.5 GHz. In addition, the FSR of the RF spectral response (FSRRF) of the differentiator was 1/∆T = ~28 GHz. Therefore, the bandwidth of the input microwave signal should not exceed 28/2 =~14 GHz. Considering these factors, in our experiments, we employed input microwave signals with a full width at half maximum (FWHM) of ~0.2 ns (Figure 4a) and the primary frequency components resided within 14 GHz.
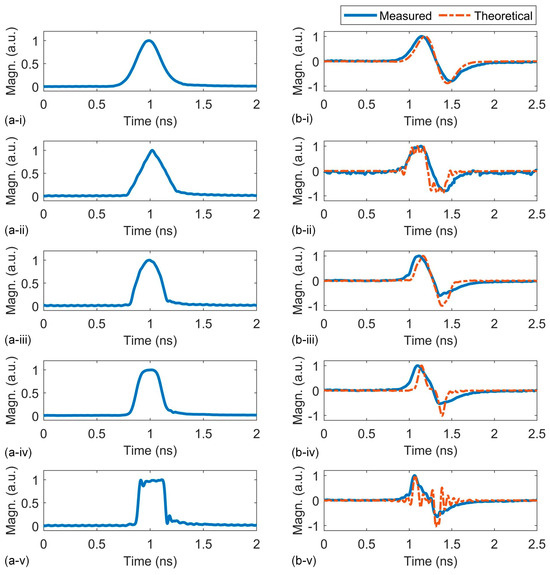
Figure 4.
(a) Measured input microwave signal waveforms of (i) Gaussian, (ii) triangle, (iii) parabolic, (iv) super Gaussian, and (v) nearly square waveforms with full width at half maximum (FWHM) of ~0.2 ns. (b) Measured output waveforms from the MWP signal processor that performs first-order differentiation. The theoretical output results are also shown for comparison.
The signal processing results are shown in Figure 4b, which were measured by a high-speed real-time oscilloscope (OSC, Keysight). The theoretical outputs are also shown for comparison, which were calculated based on Equations (1)–(3). To facilitate a fair comparison, we used the recorded waveforms generated by the AWG as the input signal waveforms to calculate the theoretical outputs. As can be seen, all the measured outputs match with their corresponding theoretical outputs. Nevertheless, different input waveforms exhibit differences in the discrepancies between them. The Gaussian input waveform shows the lowest discrepancies, whereas the nearly square waveform displays the highest.
To quantify the processing accuracy of the processing results, the concept of root mean square error (RMSE) is introduced, which is defined as [30]
where Y1, Y2, …, Yk are the values of theoretical processing results; y1, y2, …, yk are the values of measured output waveforms.
Figure 5a shows the RMSEs between the measured output waveforms and the theoretical processing results for different input signal waveforms. The Gaussian and nearly square waveforms have the lowest and highest RMSE values, showing agreement with the results in Figure 4b.
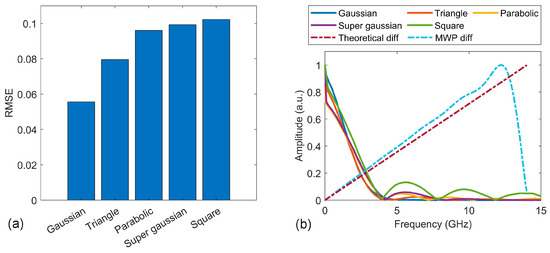
Figure 5.
(a) RMSEs between theoretical differentiation results and the processor’s output waveforms for different input microwave signal waveforms in Figure 4. (b) Amplitude frequency response of theoretical differentiation and the processor, together with the amplitude spectra of different input microwave signals including with Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms.
To analyse the reason for the differences in the processing accuracy for different waveforms, we further plot the amplitude frequency response of the processor and a theoretical differentiator in Figure 5b, together with the spectra of input signals with different waveforms. It can be seen that the deviations between the response of the transversal signal processor and the theoretical differentiator become more significant in the high-frequency range. On the other hand, the nearly square waveform contains greater high-frequency components than other waveforms, resulting in a reduction in its processing accuracy. In contrast, the Gaussian waveform has the least high-frequency components, enabling the highest level of processing accuracy.
4. Discussion
Based on the experimental results in Section 3, it can be seen that the processing accuracy varies for different input signal waveforms, even when performing the same processing function. The processing accuracy improves when there is better overlap between the high-intensity frequency components of the input signal and the low-error region of the MWP processor’s response spectrum.
In our system, uncertainties and noise are introduced by several sources due to the imperfect response of practical devices [57]. These sources can be classified into two categories, relying on whether amplitude or phase errors are introduced to the taps. The sources for amplitude errors include the amplitude noise of microcombs, chirp of EOM, high-order dispersion of SMF, shaping errors of waveshapers, intensity noise of PD, and limited response bandwidth and uneven transmission response of EOM and PD. The sources of phase errors include the phase noise of microcombs, high-order dispersion of SMF, and shot noise of PD.
To reduce the amplitude and phase noises of microcombs, mode-locking approaches, such as power kicking [58], self-injection locking [59], forward and backward tuning [60], filter-driven four-wave mixing (FWM) [61], two-colour pumping [62], integrated heaters [51], EO modulation [63], and self-referencing [64], can be employed to achieve microcombs with high coherence and stability [3,4]. Recently, some mode-locking approaches such as filter-driven FWM and self-injection locking have experienced significant improvement [61,65]. Some advanced mode-locking approaches have also been proposed, such as nonlinear dynamics engineering [66], cryogenic cooling [67], and auxiliary laser heating [68]. There are two main directions that are crucial for future improvement in practical applications. One involves achieving easily operated mode-locking without complex procedures [66] or self-emergence microcombs [69], the other is realizing mode-locking systems on a single chip, where, for example, significant advances have been achieved through the integration of actuators for the piezoelectric control of microcombs [70].
Introducing feedback control can effectively alleviate processing errors induced by slowly varying noises, such as the uneven gain or transmission response and shaping errors [3,30]. A feedback control loop can be adopted to calibrate the tap coefficients set for the second waveshaper in Figure 2, where the powers of comb lines are detected and then compared with the desired tap coefficients, yielding error signals for calibration. To further reduce the processing errors, two-stage feedback control can be introduced. One feedback loop can be employed in the microcomb generation module to achieve a uniform power distribution of the comb lines. This allows for uniform wavelength channel link gain and can also reduce the loss control range for spectral shaping in the transversal signal processing module. To minimize the intensity noise, multiple iterations along the entire feedback loop can be conducted. To reduce the phase noise, calibration can be achieved by using the phase-modulating capabilities of the waveshaper to compensate for the discrepancies between the measured and ideal phase response.
The photodetector in Figure 2 induces both intensity and phase noise. The intensity noise can be largely cancelled out by employing a BPD based on a balanced detection scheme. The phase noise arises from the shot noise, which causes random power fluctuations in the output microwave signal. The shot noise restricts the lowest achievable phase noise floor, and can be mitigated by using highly sensitive PDs [71].
Comb multiplexing technologies [72] hold promise in supplying additional discrete wavelength channels for the MWP transversal signal processors, which is beneficial for improving their processing accuracy. However, the augmentation of wavelength channels would also lead to a reduction in the channel spacing or processing bandwidth for the MWP transversal signal processors. Consequently, there is a trade-off that needs to be taken into account in practical applications [30,46,47].
For on-chip microcomb-based MWP signal processors, to improve the processing accuracy, feedback control is also required. Self-calibrating photonic integrated circuits have been proposed recently [73,74], where the calibration of impulse response was realized by introducing an optical reference path to establish a Kramers–Kronig relationship, followed by the computation of amplitude and phase errors. Apart from feedback control, there are some other ways to further alleviate the uncertainties and noise in the system. The chirp of silicon EOM can be minimized through the adoption of push–pull configurations and a p-n depletion mode structure [75], together with proper bias point calibration methods [76]. Gradient-descent control and calibration procedures can be employed to mitigate the shaping errors of integrated optical spectral shapers [76]. Integrated optical delay elements can introduce additional loss, especially when waveguides with high propagation loss are used. The incorporation of adiabatic Euler bends can be beneficial for achieving low-loss and low-crosstalk waveguide bends [77]. In addition, to enable large-scale integration, a wavelength-addressable serial integration scheme can be employed [78].
5. Conclusions
In summary, we experimentally demonstrate that microcomb-based MWP signal processors are capable of processing microwave signals with different temporal waveforms. We characterize the processing accuracy for different input signal waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. We find that the difference in the processing accuracy for various input waveforms mainly results from the difference in their frequency components, as well as their overlap with the processor’s frequency response that exhibits different degrees of deviation from the ideal response. These results provide a useful guidance for microcomb-based MWP signal processors to process microwave signals with various waveforms.
Author Contributions
Conceptualization, methodology, J.W. and Y.L.; Experiments, Y.L. and Y.S.; Integrated devices, S.T.C., B.E.L. and R.M.; Experimental instruments, G.R., B.C., X.X. and A.M.; writing—original draft preparation, Y.L. and Y.S.; writing—review and editing, J.W. and D.J.M.; supervision, J.W., A.M. and D.J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the funded ARC Centre of Excellence in Optical Microcombs for Breakthrough Science (grant number CE230100006), in part by the Australian Research Council Discovery Projects Programs (grant numbers DP150104327, DP190102773, and DP190101576), and in part by the Early Career Researcher-Swinburne University Postgraduate Research Award program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors declare that the data supporting the findings of this study are available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photonics 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Wu, J.Y.; Xu, X.Y.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. RF Photonics: An Optical Microcombs’ Perspective. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 20. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, J.; Tan, M.; Xu, X.; Li, Y.; Morandotti, R.; Mitchell, A.; Moss, D.J. Applications of optical microcombs. Adv. Opt. Photonics 2023, 15, 86. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated microwave photonics. Nat. Photonics 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Capmany, J.; Mora, J.; Gasulla, I.; Sancho, J.; Lloret, J.; Sales, S. Microwave Photonic Signal Processing. J. Light. Technol. 2013, 31, 571–586. [Google Scholar] [CrossRef]
- Liu, W.; Li, M.; Guzzon, R.S.; Norberg, E.J.; Parker, J.S.; Lu, M.; Coldren, L.A.; Yao, J. A fully reconfigurable photonic integrated signal processor. Nat. Photonics 2016, 10, 190–195. [Google Scholar] [CrossRef]
- Ferrera, M.; Park, Y.; Razzari, L.; Little, B.E.; Chu, S.T.; Morandotti, R.; Moss, D.J.; Azaña, J. On-chip CMOS-compatible all-optical integrator. Nat. Commun. 2010, 1, 29. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, W. Fully reconfigurable waveguide Bragg gratings for programmable photonic signal processing. J. Light. Technol. 2019, 38, 202–214. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. Photonic integrated field-programmable disk array signal processor. Nat. Commun. 2020, 11, 406. [Google Scholar] [CrossRef]
- Berger, N.K.; Levit, B.; Fischer, B.; Kulishov, M.; Plant, D.V.; Azaña, J. Temporal differentiation of optical signals using a phase-shifted fiber Bragg grating. Opt. Express 2007, 15, 371–381. [Google Scholar] [CrossRef]
- Rutkowska, K.A.; Duchesne, D.; Strain, M.J.; Morandotti, R.; Sorel, M.; Azaña, J. Ultrafast all-optical temporal differentiators based on CMOS-compatible integrated-waveguide Bragg gratings. Opt. Express 2011, 19, 19514–19522. [Google Scholar] [CrossRef]
- Liu, F.; Wang, T.; Qiang, L.; Ye, T.; Zhang, Z.; Qiu, M.; Su, Y. Compact optical temporal differentiator based on silicon microring resonator. Opt. Express 2008, 16, 15880–15886. [Google Scholar] [CrossRef]
- Wu, J.; Cao, P.; Hu, X.; Jiang, X.; Pan, T.; Yang, Y.; Qiu, C.; Tremblay, C.; Su, Y. Compact tunable silicon photonic differential-equation solver for general linear time-invariant systems. Opt. Express 2014, 22, 26254–26264. [Google Scholar] [CrossRef]
- Wu, J.; Liu, B.; Peng, J.; Mao, J.; Jiang, X.; Qiu, C.; Tremblay, C.; Su, Y. On-Chip Tunable Second-Order Differential-Equation Solver Based on a Silicon Photonic Mode-Split Microresonator. J. Light. Technol. 2015, 33, 3542–3549. [Google Scholar] [CrossRef]
- Zheng, A.; Dong, J.; Zhou, L.; Xiao, X.; Yang, Q.; Zhang, X.; Chen, J. Fractional-order photonic differentiator using an on-chip microring resonator. Opt. Lett. 2014, 39, 6355. [Google Scholar] [CrossRef]
- Zheng, A.; Yang, T.; Xiao, X.; Yang, Q.; Zhang, X.; Dong, J. Tunable fractional-order differentiator using an electrically tuned silicon-on-isolator Mach-Zehnder interferometer. Opt. Express 2014, 22, 18232–18237. [Google Scholar] [CrossRef]
- Capmany, J.; Ortega, B.; Pastor, D.; Sales, S. Discrete-time optical processing of microwave signals. J. Light. Technol. 2005, 23, 702–723. [Google Scholar] [CrossRef]
- Mansoori, S.; Mitchell, A. RF transversal filter using an AOTF. IEEE Photonics Technol. Lett. 2004, 16, 879–881. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, J. Photonic true-time delay beamforming using a switch-controlled wavelength-dependent recirculating loop. J. Light. Technol. 2016, 34, 3923–3929. [Google Scholar] [CrossRef]
- Zhang, L.; Li, M.; Shi, N.; Zhu, X.; Sun, S.; Tang, J.; Li, W.; Zhu, N. Photonic true time delay beamforming technique with ultra-fast beam scanning. Opt. Express 2017, 25, 14524–14532. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Zhang, W.; Williams, J. High-performance microwave transversal filter using fiber Bragg grating arrays. IEEE Photonics Technol. Lett. 2000, 12, 1183–1185. [Google Scholar] [CrossRef]
- Hunter, D.B.; Minasian, R.A.; Krug, P.A. Tunable optical transversal filter based on chirped gratings. Electron. Lett. 1995, 31, 2205–2207. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Yang, J. Wideband true-time-delay unit for phased array beamforming using discrete-chirped fiber grating prism. Opt. Commun. 2002, 207, 177–187. [Google Scholar] [CrossRef]
- Supradeepa, V.R.; Long, C.M.; Wu, R.; Ferdous, F.; Hamidi, E.; Leaird, D.E.; Weiner, A.M. Comb-based radiofrequency photonic filters with rapid tunability and high selectivity. Nat. Photonics 2012, 6, 186–194. [Google Scholar] [CrossRef]
- Hamidi, E.; Leaird, D.E.; Weiner, A.M. Tunable Programmable Microwave Photonic Filters Based on an Optical Frequency Comb. IEEE Trans. Microw. Theory Tech. 2010, 58, 3269–3278. [Google Scholar] [CrossRef]
- Metcalf, A.J.; Kim, H.J.; Leaird, D.E.; Jaramillo Villegas, J.A.; McKinzie, K.A.; Lal, V.; Hosseini, A.; Hoefler, G.E.; Kish, F.; Weiner, A.M. Integrated line-by-line optical pulse shaper for high-fidelity and rapidly reconfigurable RF-filtering. Opt. Express 2016, 24, 23925–23940. [Google Scholar] [CrossRef]
- Ortigosa-Blanch, A.; Mora, J.; Capmany, J.; Ortega, B.; Pastor, D. Tunable radio-frequency photonic filter based on an actively mode-locked fiber laser. Opt. Lett. 2006, 31, 709–711. [Google Scholar] [CrossRef]
- Maram, R.; Onori, D.; Azaña, J.; Chen, L.R. Discretely programmable microwave photonic filter based on temporal Talbot effects. Opt. Express 2019, 27, 14381–14391. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, J.; Li, Y.; Tan, M.; Xu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Quantifying the Accuracy of Microcomb-Based Photonic RF Transversal Signal Processors. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–17. [Google Scholar] [CrossRef]
- Lin, G.; Liu, F.; Coillet, A.; Gomila, D.; Menyuk, C.R.; Chembo, Y.K. Subharmonic instabilities in Kerr microcombs. Opt. Lett. 2023, 48, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; et al. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Microcomb-Based Photonic RF Signal Processing. IEEE Photonics Technol. Lett. 2019, 31, 1854–1857. [Google Scholar] [CrossRef]
- Xu, X.; Wu, J.; Shoeiby, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source. APL Phontonics 2017, 2, 096104. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Boes, A.; Corcoran, B.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF and Microwave Integrator Based on a Transversal Filter With Soliton Crystal Microcombs. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 3582–3586. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Microwave and RF Photonic Fractional Hilbert Transformer Based on a 50 GHz Kerr Micro-Comb. J. Light. Technol. 2019, 37, 6097–6104. [Google Scholar] [CrossRef]
- Wang, B.; Yang, Z.; Sun, S.; Yi, X. Radio-frequency line-by-line Fourier synthesis based on optical soliton microcombs. Photonics Res. 2022, 10, 932. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef]
- Zhou, Z.; Ou, X.; Fang, Y.; Alkhazraji, E.; Xu, R.; Wan, Y.; Bowers, J.E. Prospects and applications of on-chip lasers. eLight 2023, 3, 1. [Google Scholar] [CrossRef]
- Corcoran, B.; Tan, M.; Xu, X.; Boes, A.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Ultra-dense optical data transmission over standard fibre with a single chip source. Nat. Commun. 2020, 11, 7. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; An, N.; Lu, Z.; Wang, Y.; Chang, B.; Tan, T.; Guo, X.; Xu, X.; He, J.; Xia, H.; et al. Nonlinear co-generation of graphene plasmons for optoelectronic logic operations. Nat. Commun. 2022, 13, 3138. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.; Yuan, Z.; Zhang, H.; Yan, G.; Zhou, S.; An, N.; Peng, B.; Soavi, G.; Rao, Y.; Yao, B. Multispecies and individual gas molecule detection using Stokes solitons in a graphene over-modal microresonator. Nat. Commun. 2021, 12, 6716. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, J.; Kang, G.; Gao, J.; Qu, Z.; Wan, S.; Dong, C.; Pan, Y.; Qu, J. Soliton microcomb-assisted microring photonic thermometer with ultra-high resolution and broad range. Photonics Res. 2023, 11, A44–A53. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, J.; Li, Y.; Xu, X.; Ren, G.; Tan, M.; Chu, S.K.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Optimizing the performance of microcomb based microwave photonic transversal signal processors. J. Light. Technol. 2023, 41, 1–15. [Google Scholar]
- Li, Y.; Sun, Y.; Wu, J.; Ren, G.; Morandotti, R.; Tan, M.; Xu, X.; Mitchell, A.; Moss, D.J. Performance analysis of microwave photonic spectral filters based on optical microcombs. Opt. Lasers Eng. 2023, in press.
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Wang, W.Q.; Wang, L.R.; Zhang, W.F. Advances in soliton microcomb generation. Adv. Photonics 2020, 2, 034001. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, B.; Li, Z.; Liang, Y.-P.; Qin, C.-Y.; Wang, C.; Xia, H.-D.; Tan, T.; Yao, B.-C. Coherent optical frequency combs: From principles to applications. J. Electron. Sci. Technol. 2022, 20, 100157. [Google Scholar] [CrossRef]
- Xue, X.; Xuan, Y.; Liu, Y.; Wang, P.H.; Chen, S.; Wang, J.; Leaird, D.E.; Qi, M.; Weiner, A.M. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators. Nat. Photonics 2015, 9, 594–600. [Google Scholar] [CrossRef]
- Liu, M.; Huang, H.; Lu, Z.; Wang, Y.; Cai, Y.; Zhao, W. Dynamics of dark breathers and Raman-Kerr frequency combs influenced by high-order dispersion. Opt. Express 2021, 29, 18095–18107. [Google Scholar] [CrossRef] [PubMed]
- Cole, D.C.; Lamb, E.S.; Del’Haye, P.; Diddams, S.A.; Papp, S.B. Soliton crystals in Kerr resonators. Nat. Photonics 2017, 11, 671–676. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, H.; Wang, W.; Yao, L.; Wang, Y.; Yu, Y.; Little, B.E.; Chu, S.T.; Gong, Q.; Zhao, W.; et al. Synthesized soliton crystals. Nat. Commun. 2021, 12, 3179. [Google Scholar] [CrossRef]
- Razzari, L.; Duchesne, D.; Ferrera, M.; Morandotti, R.; Chu, S.; Little, B.E.; Moss, D.J. CMOS-compatible integrated optical hyper-parametric oscillator. Nat. Photonics 2010, 4, 41–45. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Advanced Adaptive Photonic RF Filters with 80 Taps Based on an Integrated Optical Micro-Comb Source. J. Light. Technol. 2019, 37, 1288–1295. [Google Scholar] [CrossRef]
- Salzenstein, P.; Pavlyuchenko, E. Uncertainty evaluation on a 10.52 GHz (5 dBm) optoelectronic oscillator phase noise performance. Micromachines 2021, 12, 474. [Google Scholar] [CrossRef]
- Yi, X.; Yang, Q.F.; Yang, K.Y.; Suh, M.G.; Vahala, K. Soliton frequency comb at microwave rates in a high-Q silica microresonator. Optica 2015, 2, 1078–1085. [Google Scholar] [CrossRef]
- Del’Haye, P.; Beha, K.; Papp, S.B.; Diddams, S.A. Self-Injection Locking and Phase-Locked States in Microresonator-Based Optical Frequency Combs. Phys. Rev. Lett. 2014, 112, 043905. [Google Scholar] [CrossRef]
- Guo, H.; Karpov, M.; Lucas, E.; Kordts, A.; Pfeiffer, M.H.; Brasch, V.; Lihachev, G.; Lobanov, V.E.; Gorodetsky, M.L.; Kippenberg, T.J. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. 2017, 13, 94–102. [Google Scholar] [CrossRef]
- Bao, H.; Cooper, A.; Rowley, M.; Di Lauro, L.; Totero Gongora, J.S.; Chu, S.T.; Little, B.E.; Oppo, G.-L.; Morandotti, R.; Moss, D.J.; et al. Laser cavity-soliton microcombs. Nat. Photonics 2019, 13, 384–389. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Yu, N. Generation of optical combs in a whispering gallery mode resonator from a bichromatic pump. Phys. Rev. A 2009, 79, 041805. [Google Scholar] [CrossRef]
- Del’Haye, P.; Papp, S.B.; Diddams, S.A. Hybrid Electro-Optically Modulated Microcombs. Phys. Rev. Lett. 2012, 109, 263901. [Google Scholar] [CrossRef] [PubMed]
- Del’Haye, P.; Coillet, A.; Fortier, T.; Beha, K.; Cole, D.C.; Yang, K.Y.; Lee, H.; Vahala, K.J.; Papp, S.B.; Diddams, S.A. Phase-coherent microwave-to-optical link with a self-referenced microcomb. Nat. Photonics 2016, 10, 516–520. [Google Scholar] [CrossRef]
- Voloshin, A.S.; Kondratiev, N.M.; Lihachev, G.V.; Liu, J.; Lobanov, V.E.; Dmitriev, N.Y.; Weng, W.; Kippenberg, T.J.; Bilenko, I.A. Dynamics of soliton self-injection locking in optical microresonators. Nat. Commun. 2021, 12, 235. [Google Scholar] [CrossRef]
- Shen, B.; Chang, L.; Liu, J.; Wang, H.; Yang, Q.; Xiang, C.; Wang, R.; He, J.; Liu, T.; Xie, W.; et al. Integrated turnkey soliton microcombs. Nature 2020, 582, 365–369. [Google Scholar] [CrossRef]
- Moille, G.; Chang, L.; Xie, W.; Rao, A.; Lu, X.; Davanço, M.; Bowers, J.E.; Srinivasan, K. Dissipative Kerr Solitons in a III-V Microresonator. Laser Photon. Rev. 2020, 14, 2000022. [Google Scholar] [CrossRef]
- Zhou, H.; Geng, Y.; Cui, W.; Huang, S.W.; Zhou, Q.; Qiu, K.; Wei Wong, C. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities. Light Sci. Appl. 2019, 8, 50. [Google Scholar] [CrossRef]
- Rowley, M.; Hanzard, P.-H.; Cutrona, A.; Bao, H.; Chu, S.T.; Little, B.E.; Morandotti, R.; Moss, D.J.; Oppo, G.L.; Totero Gongora, J.S.; et al. Self-emergence of robust solitons in a microcavity. Nature 2022, 608, 303–309. [Google Scholar] [CrossRef]
- Liu, J.; Tian, H.; Lucas, E.; Raja, A.S.; Lihachev, G.; Wang, R.N.; He, J.; Liu, T.; Anderson, M.H.; Weng, W.; et al. Monolithic piezoelectric control of soliton microcombs. Nature 2020, 583, 385–390. [Google Scholar] [CrossRef]
- Miao, J.; Zhang, F. Recent progress on highly sensitive perovskite photodetectors. J. Mater. Chem. C 2019, 7, 1741–1791. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, T.; Chen, H.-J.; Yu, Y.; Wang, W.; Chang, B.; Liang, Y.; Guo, Y.; Zhou, H.; Xia, H.; et al. Soliton Microcombs Multiplexing Using Intracavity-Stimulated Brillouin Lasers. Phys. Rev. Lett. 2023, 130, 153802. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Ren, G.; Feleppa, T.; Liu, X.; Boes, A.; Mitchell, A.; Lowery, A.J. Self-calibrating programmable photonic integrated circuits. Nat. Photonics 2022, 16, 595–602. [Google Scholar] [CrossRef]
- Xu, X.; Ren, G.; Dubey, A.; Feleppa, T.; Liu, X.; Boes, A.; Mitchell, A.; Lowery, A.J. Phase retrieval of programmable photonic integrated circuits based on an on-chip fractional-delay reference path. Optica 2022, 9, 1401. [Google Scholar] [CrossRef]
- Sinatkas, G.; Christopoulos, T.; Tsilipakos, O.; Kriezis, E.E. Electro-optic modulation in integrated photonics. J. Appl. Phys. 2021, 130, 010901. [Google Scholar] [CrossRef]
- Bai, B.; Yang, Q.; Shu, H.; Chang, L.; Yang, F.; Shen, B.; Tao, Z.; Wang, J.; Xu, S.; Xie, W.; et al. Microcomb-based integrated photonic processing unit. Nat. Commun. 2023, 14, 66. [Google Scholar] [CrossRef]
- Ji, X.; Liu, J.; He, J.; Wang, R.N.; Qiu, Z.; Riemensberger, J.; Kippenberg, T.J. Compact, spatial-mode-interaction-free, ultralow-loss, nonlinear photonic integrated circuits. Commun. Phys. 2022, 5, 84. [Google Scholar] [CrossRef]
- Kuramochi, E.; Nozaki, K.; Shinya, A.; Takeda, K.; Sato, T.; Matsuo, S.; Taniyama, H.; Sumikura, H.; Notomi, M. Large-scale integration of wavelength-addressable all-optical memories on a photonic crystal chip. Nat. Photonics 2014, 8, 474–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).