Topological Edge States on Different Domain Walls of Two Opposed Helical Waveguide Arrays
Abstract
:1. Introduction
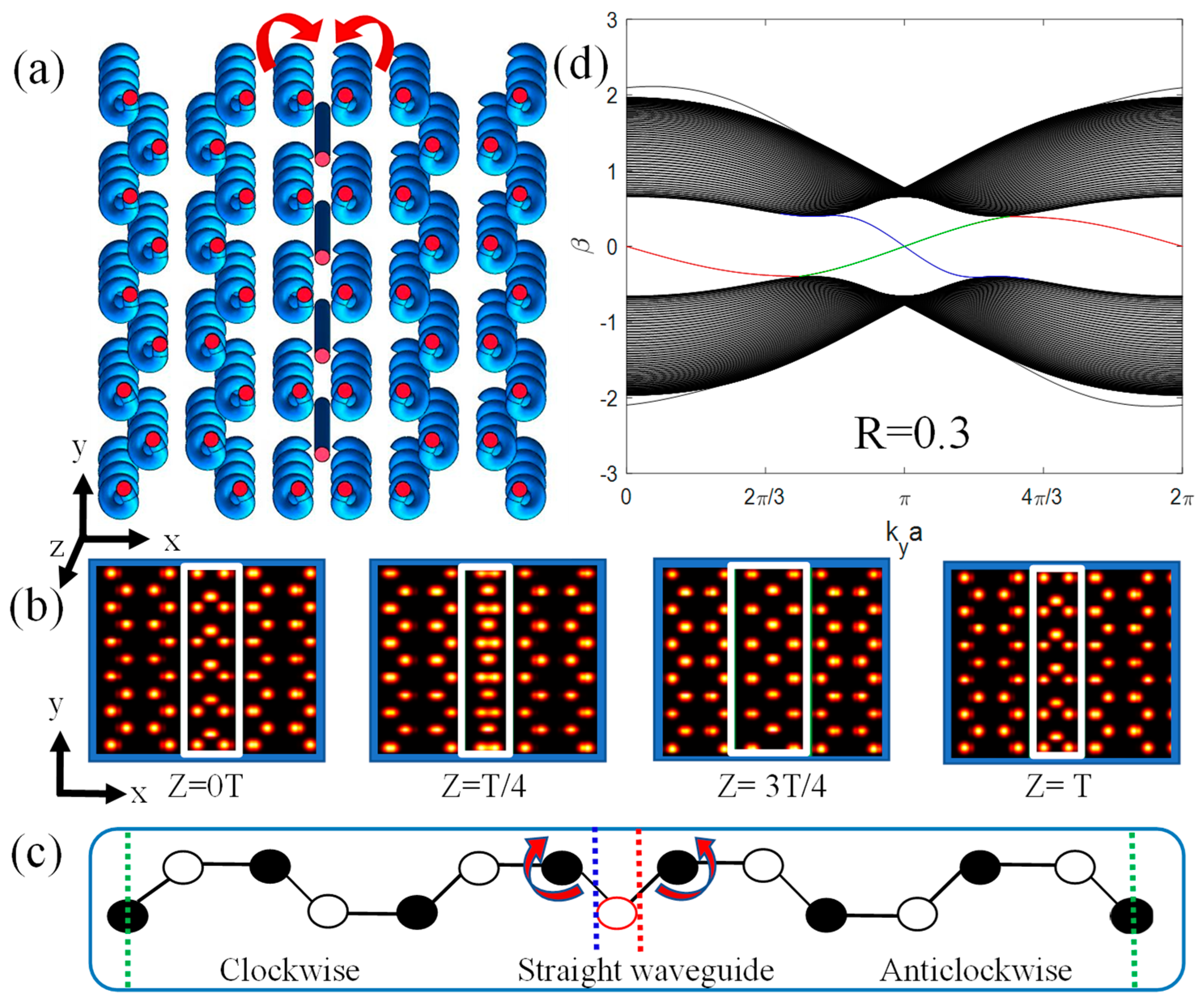
2. Model and Method
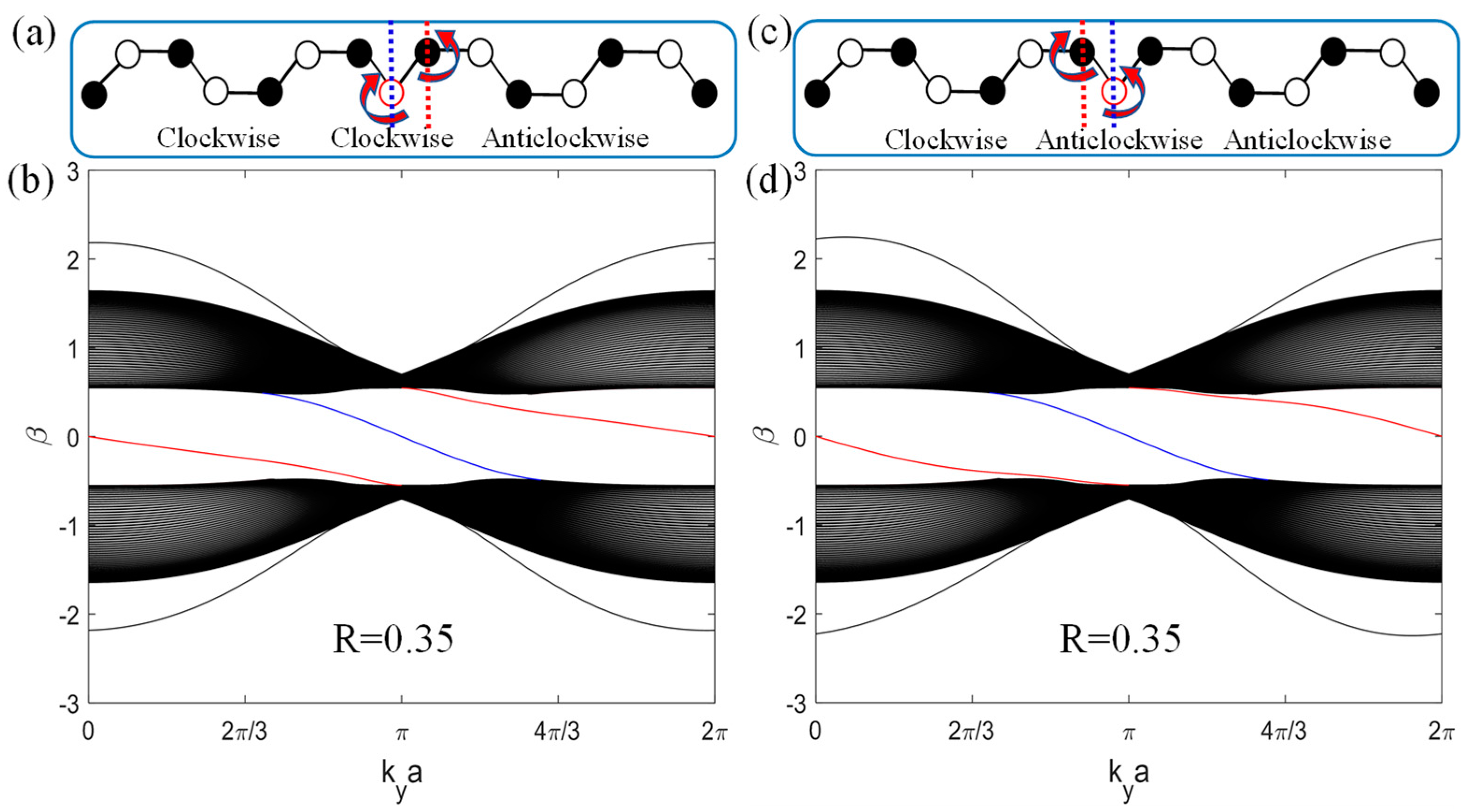
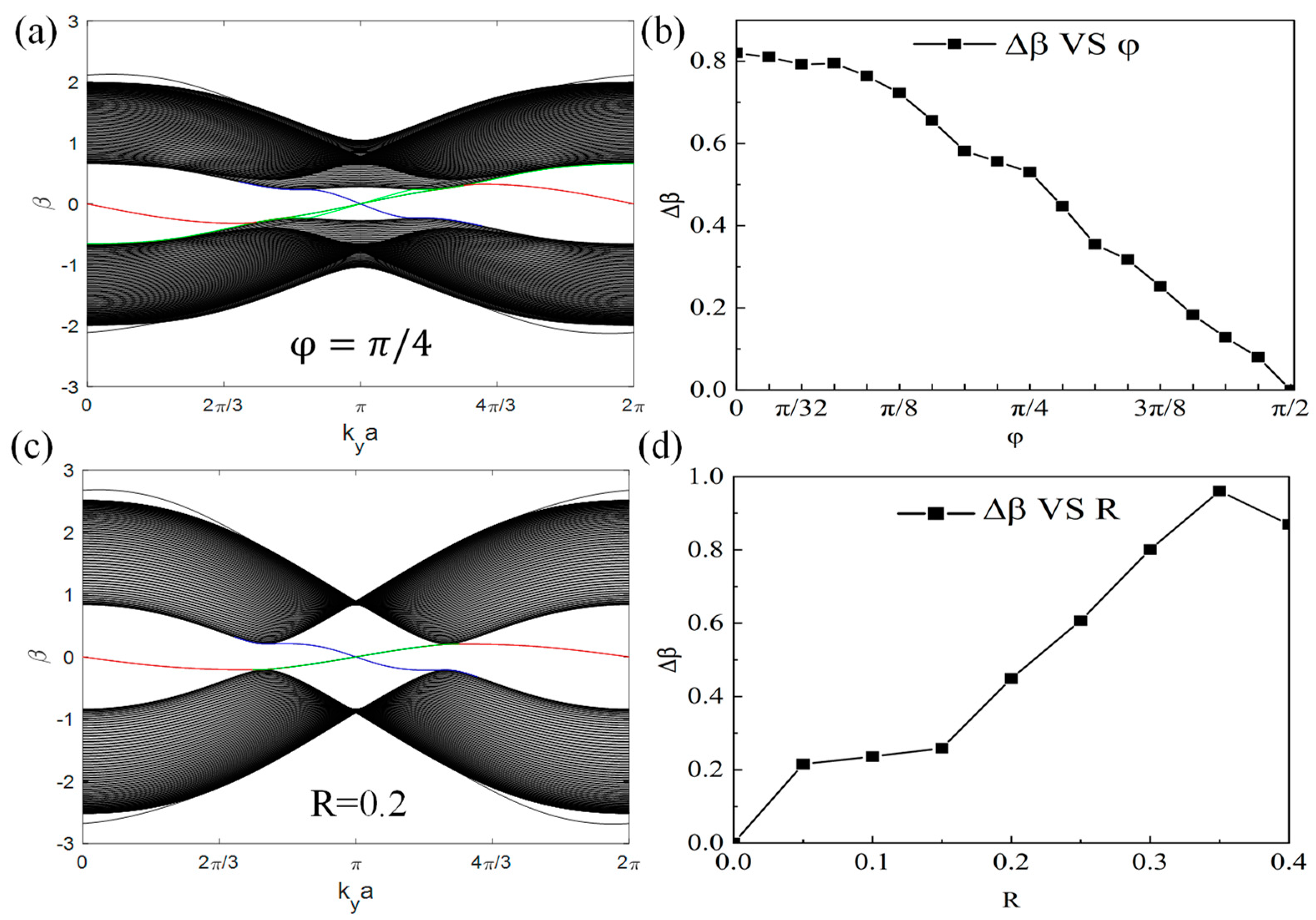
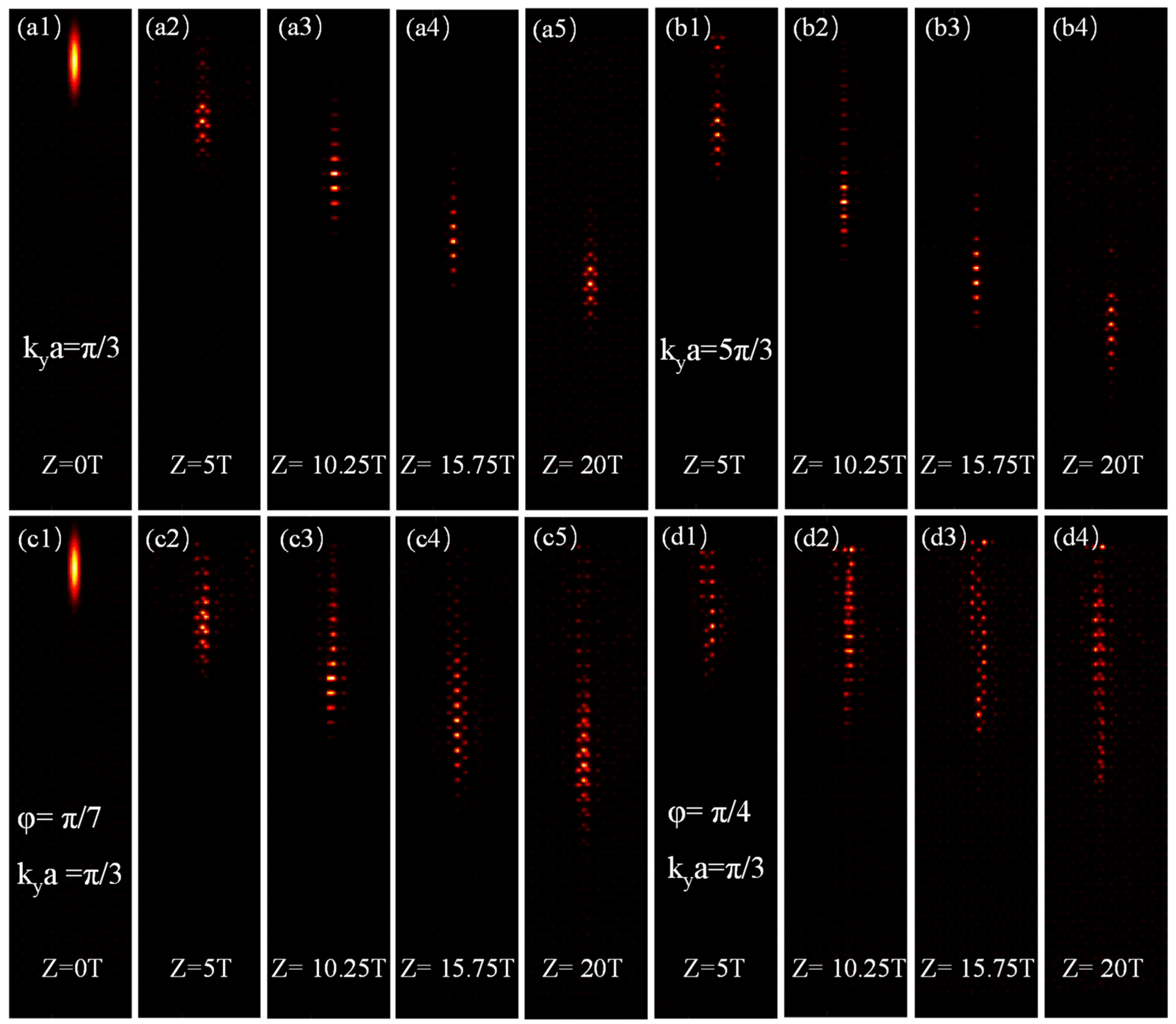
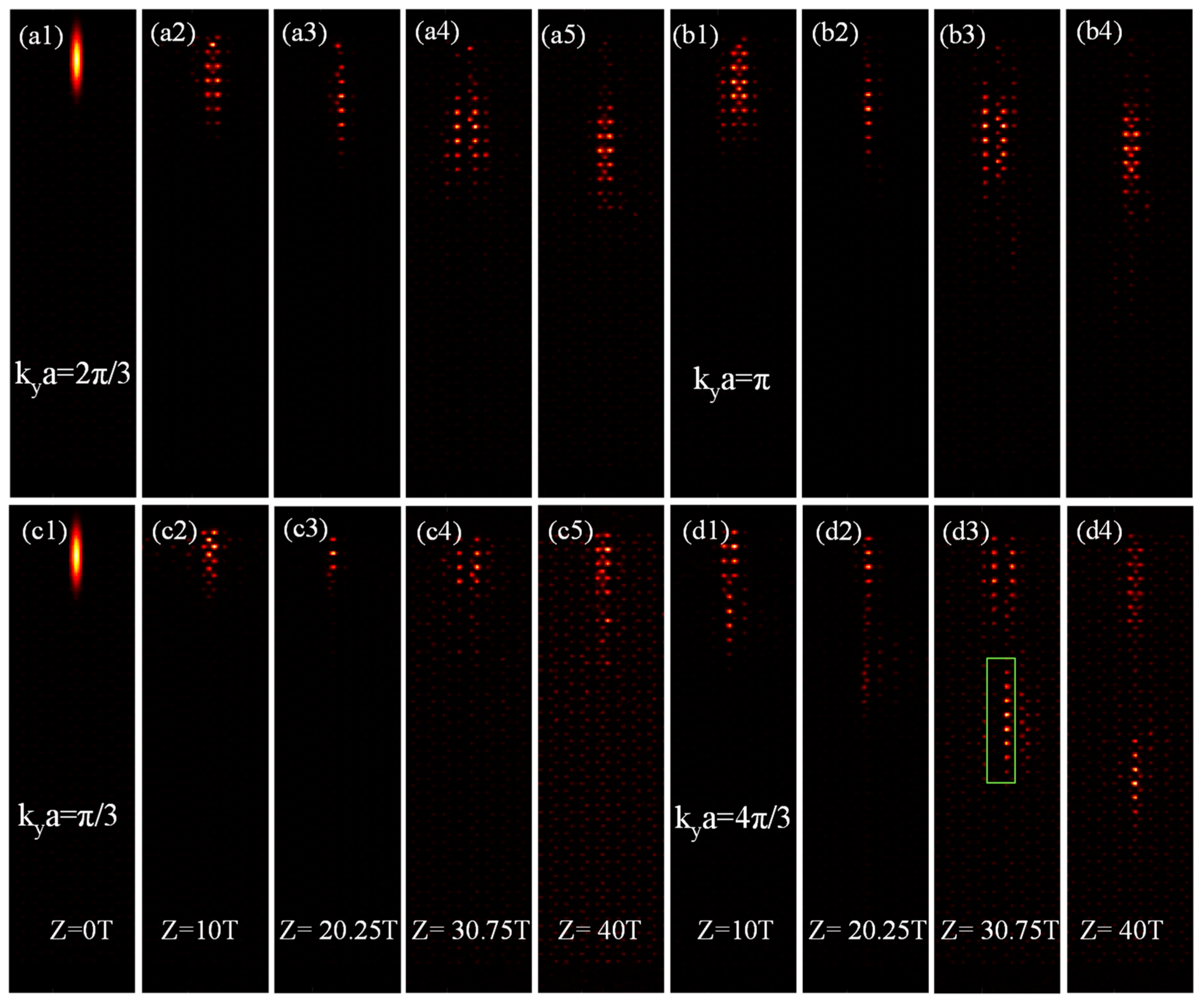
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Li, J.T.; Yue, Z.; Zheng, C.L.; Wang, G.C.; Liu, J.Y.; Xu, H.; Song, C.Y.; Yang, F.; Li, H.; et al. Structured Vector Field Manipulation of Terahertz Wave along the Propagation Direction Based on Dielectric Metasurfaces. Laser Photonics Rev. 2022, 16, 2200325. [Google Scholar] [CrossRef]
- Reserbat-Plantey, A.; Epstein, I.; Torre, I.; Costa, A.T.; Goncalves, P.A.D.; Mortensen, N.A.; Polini, M.; Song, J.C.W.; Peres, N.M.R.; Koppens, F.H.L. Quantum Nanophotonics in Two-Dimensional Materials. ACS Photonics 2021, 8, 85–101. [Google Scholar] [CrossRef]
- Tang, G.J.; He, X.T.; Shi, F.L.; Liu, J.W.; Chen, X.D.; Dong, J.W. Topological Photonic Crystals: Physics, Designs, and Applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Li, C.; Hu, X.Y.; Yang, H.; Gong, Q.J. Unidirectional transmission in 1D nonlinear photonic crystal based on topological phase reversal by optical nonlinearity. AIP Adv. 2017, 7, 025203. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Hu, X.Y.; Ao, Y.T.; Zhao, Y.F.; Gong, Q.H. Applications of Topological Photonics in Integrated Photonic Devices. Adv. Opt. Mater. 2017, 5, 1700357. [Google Scholar] [CrossRef]
- Bonnell, D.A.; Basov, D.N.; Bode, M.; Diebold, U.; Kalinin, S.V.; Madhavan, V.; Novotny, L.; Salmeron, M.; Schwarz, U.D.; Weiss, P.S. Imaging physical phenomena with local probes: From electrons to photons. Rev. Mod. Phys. 2012, 84, 1343. [Google Scholar] [CrossRef]
- Prabha, K.R.; Kavitha, V.; Robinson, S.; Jayabharathan, J.K.; Balamurugan, P. Two-dimensional photonic crystal-based half adder: A review. J. Opt. 2022, 51, 415–436. [Google Scholar] [CrossRef]
- Liu, R.X.; Cai, Z.Y.; Zhang, Q.S.; Yuan, H.; Zhang, G.L.; Yang, D. Colorimetric two-dimensional photonic crystal biosensors for label-free detection of hydrogen peroxide. Sens. Actuators B Chem. 2022, 354, 131236. [Google Scholar] [CrossRef]
- Balaji, V.R.; Murugan, M.; Robinson, S.; Hegde, G. A Novel Hybrid Channel DWDM Demultiplexer Using Two Dimensional Photonic Crystals Meeting ITU Standards. Silicon 2022, 14, 617–628. [Google Scholar] [CrossRef]
- Latha, K.; Arunkumar, R.; Prabha, K.R.; Robinson, S. Performance analysis of all optical 4*2 and 8*3 encoder using two dimensional photonic crystals waveguides. Silicon 2021, 14, 3245–3258. [Google Scholar] [CrossRef]
- Markel, V.A.; Schoebinger, M.; Hollaus, K. A fast method to compute dispersion diagrams of three-dimensional photonic crystals with rectangular geometry. Comput. Phys. Commun. 2022, 279, 108441. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Xue, P.; Valenzuela, C.; Chen, Y.; Yang, X.; Wang, L.; Feng, W. Three-Dimensional Electrochromic Soft Photonic Crystals Based on MXene-Integrated Blue Phase Liquid Crystals for Bioinspired Visible and Infrared Camouflage. Angew. Chem. Int. Ed. 2022, 134, e202211030. [Google Scholar] [CrossRef]
- Deng, W.M.; Chen, Z.M.; Li, M.Y.; Guo, C.H.; Tian, Z.T.; Sun, K.X.; Chen, X.D.; Chen, W.J.; Dong, J.W. Ideal nodal rings of one-dimensional photonic crystals in the visible region. Light Sci. Appl. 2022, 11, 134. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Liu, D.J.; Teo, H.T.; Wang, Q.; Xue, H.R.; Zhang, B.L. Higher-order Dirac semimetal in a photonic crystal. Phys. Rev. B 2022, 105, L060101. [Google Scholar] [CrossRef]
- Qiu, Y.; Yang, Y.; Valenzuela, C.; Zhang, X.; Yang, M.; Xue, P.; Ma, J.; Liu, Z.; Wang, L.; Feng, W. Near-Infrared Light-Driven Three-Dimensional Soft Photonic Crystals Loaded with Upconversion Nanoparticles. Adv. Opt. Mater. 2022, 10, 2102475. [Google Scholar] [CrossRef]
- Rabus, D.G.; Sada, C.; Rabus, D.G.; Sada, C. Ring resonators: Theory and modeling. In Integrated Ring Resonators: A Compendium; Springer: Cham, Switzerland, 2020; pp. 3–46. [Google Scholar] [CrossRef]
- Steglich, P.; Hulsemann, M.; Dietzel, B.; Mai, A. Optical Biosensors Based on Silicon-On-Insulator Ring Resonators: A Review. Molecules 2019, 24, 519. [Google Scholar] [CrossRef]
- Taishi, B.Y.; Yang, Y.T.; Wu, X.Q.; Xu, J.C.; Huang, S.G. Dual-band 3D electrically small antenna based on split ring resonators. Adv. Compos. Hybrid Mater. 2022, 5, 350–355. [Google Scholar] [CrossRef]
- Moradi, M.; Mohammadi, M.; Olyaee, S.; Seifouri, M. Design and Simulation of a Fast All-Optical Modulator Based on Photonic Crystal Using Ring Resonators. Silicon 2022, 14, 765–771. [Google Scholar] [CrossRef]
- Zhu, C.; Zhuang, Y. Microwave photonic fiber ring resonator. Sensors 2022, 22, 3771. [Google Scholar] [CrossRef]
- Lee, D.; So, S.; Hu, G.; Kim, M.; Badloe, T.; Cho, H.; Kim, J.; Kim, H.; Qiu, C.-W.; Rho, J. Hyperbolic metamaterials: Fusing artificial structures to natural 2D materials. eLight 2022, 2, 1. [Google Scholar] [CrossRef]
- Indukuri, S.R.K.C.; Frydendahl, C.; Sharma, N.; Mazurski, N.; Paltiel, Y.; Levy, U. Enhanced Chiral Sensing at the Few-Molecule Level Using Negative Index Metamaterial Plasmonic Nanocuvettes. ACS Nano 2022, 16, 17289–17297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Leng, Q.; Kan, Y.S.; Ge, J.; Wu, S. Asymmetric transmission of linearly polarized waves based on chiral metamaterials. Opt. Commun. 2022, 517, 128321. [Google Scholar] [CrossRef]
- Su, Z.P.; Wang, Y.K. Anisotropic Photonics Topological Transition in Hyperbolic Metamaterials Based on Black Phosphorus. Nanomaterials 2020, 10, 1694. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.W.; Wu, X.; Sun, Y.; Jiang, H.T.; Ding, Y.Q.; Li, Y.H.; Zhang, Y.W.; Chen, H. Anomalous broadband Floquet topological metasurface with pure site rings. Adv. Photonics Nexus 2023, 2, 016006. [Google Scholar] [CrossRef]
- Li, L.Q.; Kong, W.J.; Chen, F. Femtosecond laser-inscribed optical waveguides in dielectric crystals: A concise review and recent advances. Adv. Photonics 2022, 4, 024002. [Google Scholar] [CrossRef]
- Zhang, K.V.; Boehm, G.; Belkin, M.A. Mid-infrared microring resonators and optical waveguides on an InP platform. Appl. Phys. Lett. 2022, 120, 061106. [Google Scholar] [CrossRef]
- Chen, T.; Dang, Z.; Ding, Z.; Liu, Z.; Zhang, Z. Multibit NOT logic gate enabled by a function programmable optical waveguide. Opt. Lett. 2022, 47, 3519–3522. [Google Scholar] [CrossRef]
- Leal, A.; Avellar, L.; Biazi, V.; Soares, M.S.; Frizera, A.; Marques, C. Multifunctional flexible optical waveguide sensor: On the bioinspiration for ultrasensitive sensors development. Opto-Electron. Adv. 2022, 5, 210098. [Google Scholar] [CrossRef]
- Zhu, T.Q.; Zhang, J.T.; Zhang, H.F. Investigation of photonic band gap properties of one-dimensional magnetized plasma spherical photonic crystals. Waves Random Complex Media 2023. [Google Scholar] [CrossRef]
- Wang, X.X.; Guo, Z.W.; Song, J.; Jiang, H.T.; Chen, H.; Hu, X. Unique Huygens-Fresnel electromagnetic transportation of chiral Dirac wavelet in topological photonic crystal. Nat. Commun. 2023, 14, 304010. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Li, J.; Jiang, H.W.; Li, N.; Wang, J.S.; Xu, J.P.; Zhu, C.J.; Yang, Y.P. Coherent interaction of a quantum emitter and the edge states in two-dimensional optical topological insulators. Phys. Rev. A 2022, 105, 053703. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.H.; Hannes, H.; Liu, J.; Lu, C.Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Kim, M.; Jacob, Z.; Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci. Appl. 2020, 9, 130. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Hu, S.J.; Eggert, S.; Fleischhauer, M.; Pelster, A.; Zhang, X.F. Floquet-induced superfluidity with periodically modulated interactions of two-species hardcore bosons in a one-dimensional optical lattice. Phys. Rev. Res. 2020, 2, 013275. [Google Scholar] [CrossRef]
- Fang, K.J.; Yu, Z.F.; Fan, S.H. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Yang, Z.J.; Lustig, E.; Lumer, Y.; Segev, M. Photonic Floquet topological insulators in a fractal lattice. Light Sci. Appl. 2020, 9, 128. [Google Scholar] [CrossRef]
- Pasek, M.; Chong, Y.D. Network models of photonic Floquet topological insulators. Phys. Rev. B 2014, 89, 075113. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Price, H.; Chong, Y.D.; Khanikaev, A.; Schomerus, H.; Maczewsky, L.J.; Kremer, M.; Heinrich, M.; Szameit, A.; Zilberberg, O.; Yang, Y.H.; et al. Roadmap on topological photonics. J. Phys. Photonics 2022, 4, 032501. [Google Scholar] [CrossRef]
- Barone, S.; Narcowich, M.; Narcowich, F. Floquet theory and applications. Phys. Rev. A 1977, 15, 1109. [Google Scholar] [CrossRef]
- Neves, A. Floquet’s Theorem and Stability of Periodic Solitary Waves. J. Dyn. Differ. Equ. 2009, 21, 555–565. [Google Scholar] [CrossRef]
- Dai, C.M.; Shi, Z.C.; Yi, X.X. Floquet theorem with open systems and its applications. Phys. Rev. A 2016, 93, 032121. [Google Scholar] [CrossRef]
- Bazhan, N.; Malomed, B.; Yakimenko, A. Josephson oscillations of edge quasi-solitons in a photonic-topological coupler. Opt. Lett. 2021, 46, 6067–6070. [Google Scholar] [CrossRef] [PubMed]
- Lustig, E.; Weimann, S.; Plotnik, Y.; Lumer, Y.; Bandres, M.A.; Szameit, A.; Segev, M. Photonic topological insulator in synthetic dimensions. Nature 2019, 567, 356–360. [Google Scholar] [CrossRef] [PubMed]
- Luo, M. Floquet engineering of two dimensional photonic waveguide arrays with π or ±2π/3 corner states. Opt. Commun. 2023, 534, 129333. [Google Scholar] [CrossRef]
- Zhong, H.; Kartashov, Y.V.; Li, Y.D.; Zhang, Y.Q. π-mode solitons in photonic Floquet lattices. Phys. Rev. A 2023, 107, L021502. [Google Scholar] [CrossRef]
- Ivanov, S.K.; Kartashov, Y.V.; Maczewsky, L.J.; Szameit, A.; Konotop, V.V. Bragg solitons in topological Floquet insulators. Opt. Lett. 2020, 45, 2271–2274. [Google Scholar] [CrossRef]
- Ivanov, S.K.; Kartashov, Y.V.; Szameit, A.; Torner, L.; Konotop, V.V. Vector Topological Edge Solitons in Floquet Insulators. ACS Photonics 2020, 7, 735–745. [Google Scholar] [CrossRef]
- Shi, Z.W.; Zuo, M.W.; Li, H.G. Edge states supported by different boundaries of two helical lattices with opposite helicity. Results Phys. 2021, 24, 104191. [Google Scholar] [CrossRef]
- Shi, Z.W.; Zuo, M.W.; Li, H.G.; Preece, D.; Zhang, Y.Q.; Chen, Z.G. Topological Edge States and Solitons on a Dynamically Tunable Domain Wall of Two Opposing Helical Waveguide Arrays. ACS Photonics 2021, 8, 1077–1084. [Google Scholar] [CrossRef]
- Zhong, H.; Li, Y.D.; Song, D.H.; Kartashov, Y.V.; Zhang, Y.Q.; Zhang, Y.P.; Chen, Z.G. Topological Valley Hall Edge State Lasing. Laser Photonics Rev. 2020, 14, 2000001. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Ningyuan, J.; Owens, C.; Sommer, A.; Schuster, D.; Simon, J. Time- and Site-Resolved Dynamics in a Topological Circuit. Phys. Rev. X 2015, 5, 021031. [Google Scholar] [CrossRef]
- He, C.; Ni, X.; Ge, H.; Sun, X.C.; Chen, Y.B.; Lu, M.H.; Liu, X.P.; Chen, Y.F. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 2016, 12, 1124–1129. [Google Scholar] [CrossRef]
- Yan, M.; Lu, J.Y.; Li, F.; Deng, W.Y.; Huang, X.Q.; Ma, J.H.; Liu, Z.Y. On-chip valley topological materials for elastic wave manipulation. Nat. Mater. 2018, 17, 993–998. [Google Scholar] [CrossRef]
- Wang, Y.T.; Luan, P.G.; Zhang, S. Coriolis force induced topological order for classical mechanical vibrations. New J. Phys. 2015, 17, 073031. [Google Scholar] [CrossRef]
- Martin, I.; Blanter, Y.M.; Morpurgo, A.F. Topological confinement in bilayer graphene. Phys. Rev. Lett. 2008, 100, 036804. [Google Scholar] [CrossRef]
- Jung, J.; Zhang, F.; Qiao, Z.H.; MacDonald, A.H. Valley-Hall kink and edge states in multilayer graphene. Phys. Rev. B 2011, 84, 075418. [Google Scholar] [CrossRef]
- Lu, J.Y.; Qiu, C.Y.; Ke, M.Z.; Liu, Z.Y. Valley Vortex States in Sonic Crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Cole, J.T. Topological insulators in longitudinally driven waveguides: Lieb and Kagome lattices. Phys. Rev. A 2019, 99, 033821. [Google Scholar] [CrossRef]
- Bisharat, D.J.; Davis, R.J.; Zhou, Y.; Bandaru, P.R.; Sievenpiper, D.F. Photonic Topological Insulators: A Beginner’s Introduction. IEEE Antennas Propag. Mag. 2021, 63, 112–124. [Google Scholar] [CrossRef]
- Orazbayev, B.; Fleury, R. Quantitative robustness analysis of topological edge modes in C6 and valley-Hall metamaterial waveguides. Nanophotonics 2019, 8, 1433–1441. [Google Scholar] [CrossRef]
- Kohmoto, M.; Hasegawa, Y. Zero modes and edge states of the honeycomb lattice. Phys. Rev. B 2007, 76, 205402. [Google Scholar] [CrossRef]
- Su, W.-P.; Schrieffer, J.R.; Heeger, A.J. Solitons in polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.S.; Li, Y.M.; Lou, W.K.; Chang, K. Pure magnon valley currents in a patterned ferromagnetic thin film. Phys. Rev. B 2023, 107, 104426. [Google Scholar] [CrossRef]
- Huang, A.H.; Ke, S.S.; Guan, J.H.; Lou, W.K. Tight-binding model and quantum transport with disorder for 1T’transition metal dichalcogenides. J. Appl. Phys. 2023, 134, 084302. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Shi, Z.; Ji, X.; Zhang, Y.; Li, H.; Deng, Y.; Xie, K. Topological Edge States on Different Domain Walls of Two Opposed Helical Waveguide Arrays. Photonics 2023, 10, 1220. https://doi.org/10.3390/photonics10111220
Wang J, Shi Z, Ji X, Zhang Y, Li H, Deng Y, Xie K. Topological Edge States on Different Domain Walls of Two Opposed Helical Waveguide Arrays. Photonics. 2023; 10(11):1220. https://doi.org/10.3390/photonics10111220
Chicago/Turabian StyleWang, Junying, Zhiwei Shi, Xifeng Ji, Yajing Zhang, Huagang Li, Yaohua Deng, and Kang Xie. 2023. "Topological Edge States on Different Domain Walls of Two Opposed Helical Waveguide Arrays" Photonics 10, no. 11: 1220. https://doi.org/10.3390/photonics10111220
APA StyleWang, J., Shi, Z., Ji, X., Zhang, Y., Li, H., Deng, Y., & Xie, K. (2023). Topological Edge States on Different Domain Walls of Two Opposed Helical Waveguide Arrays. Photonics, 10(11), 1220. https://doi.org/10.3390/photonics10111220




