Measurement-Based Control of Quantum Entanglement and Steering in a Distant Magnomechanical System
Abstract
:1. Introduction
2. System and Equations
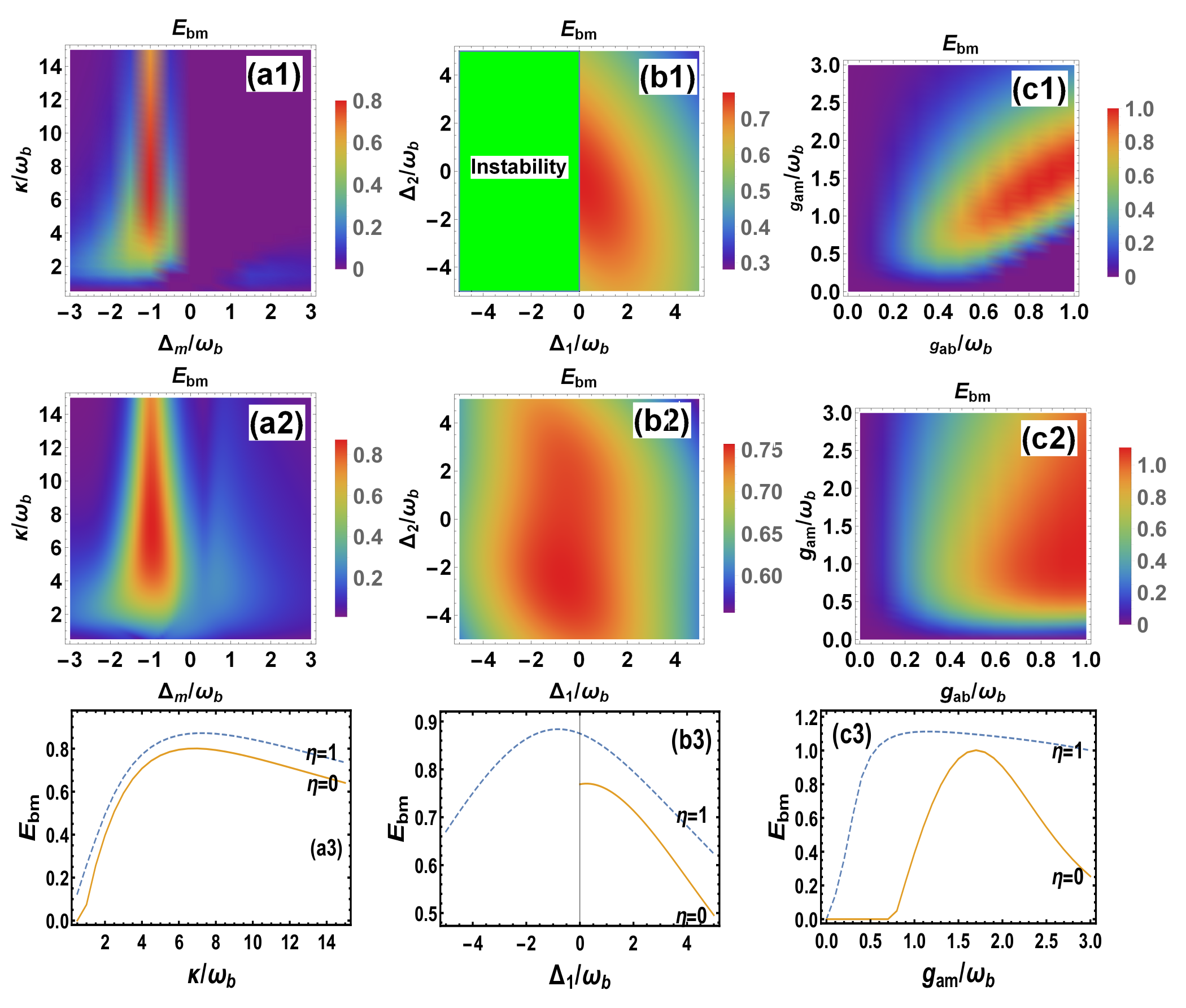
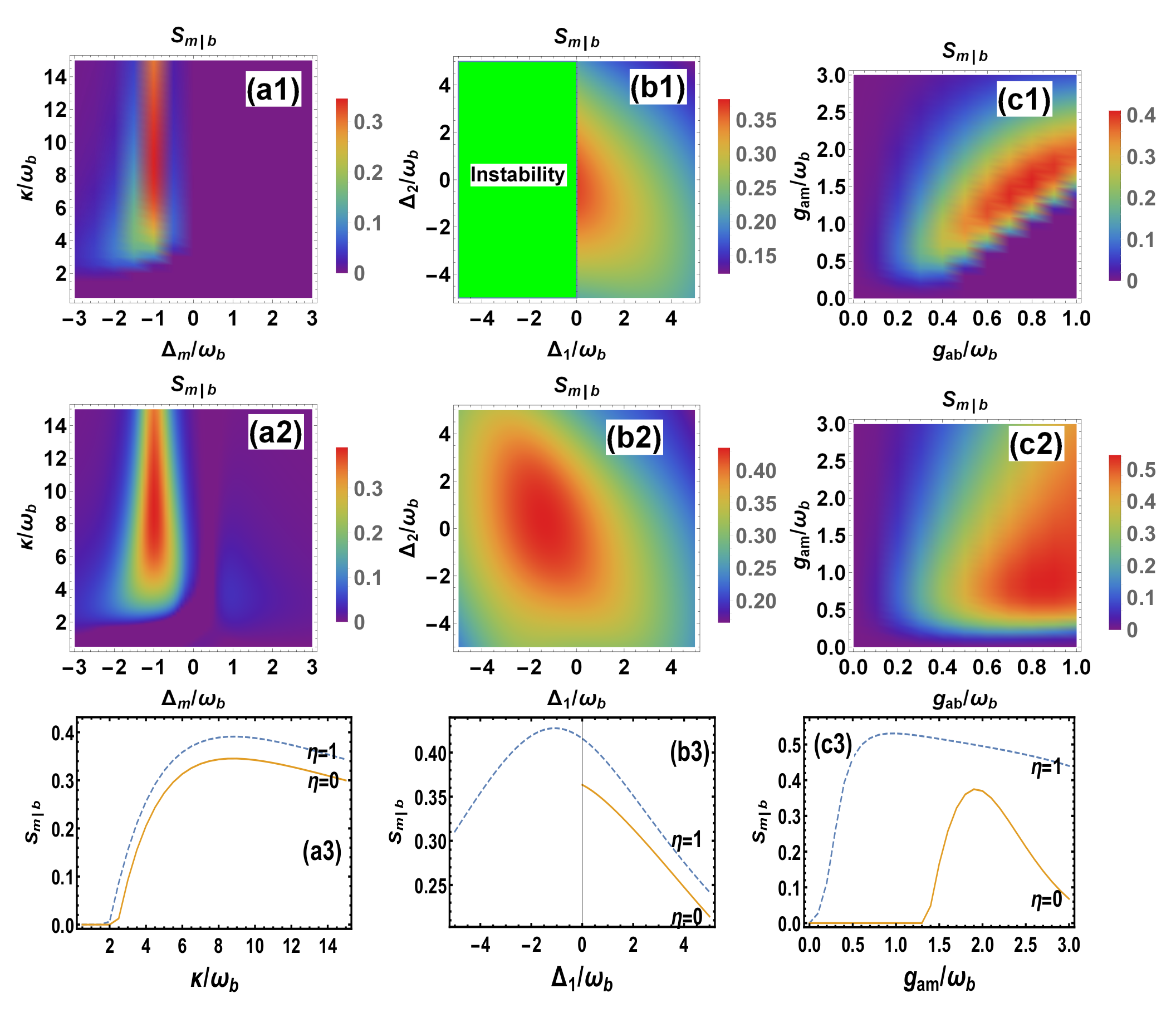
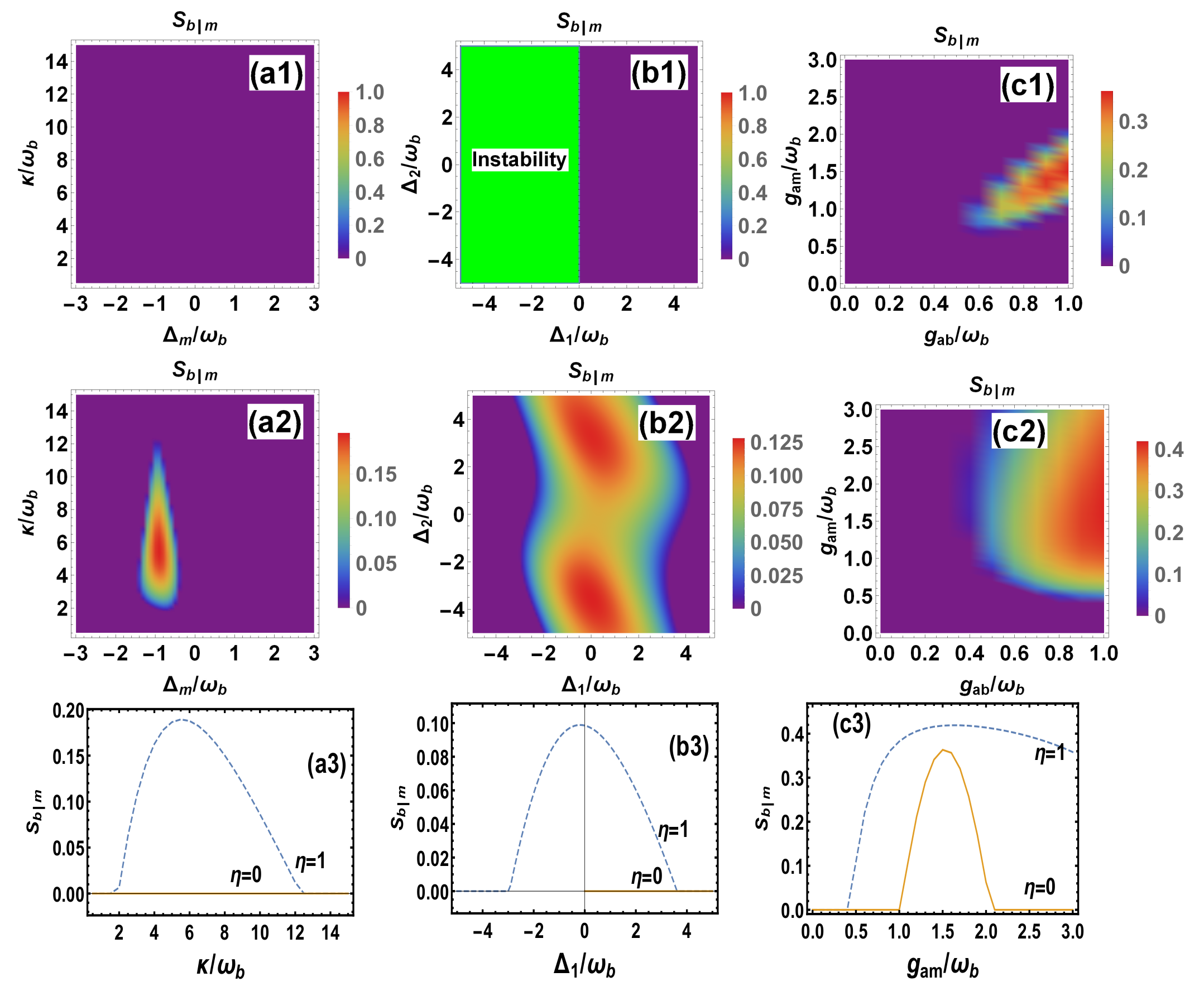
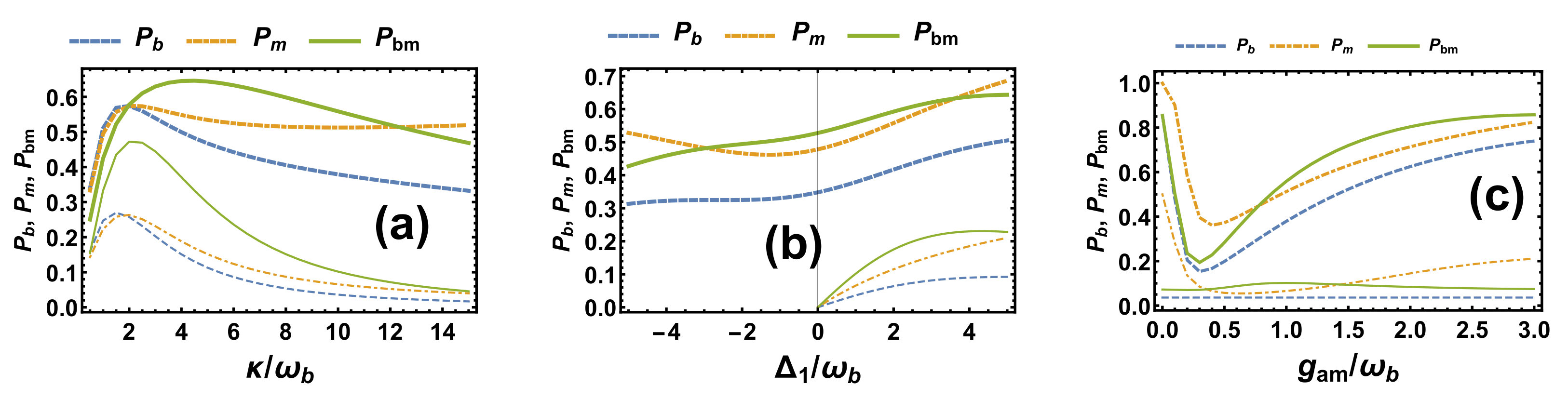
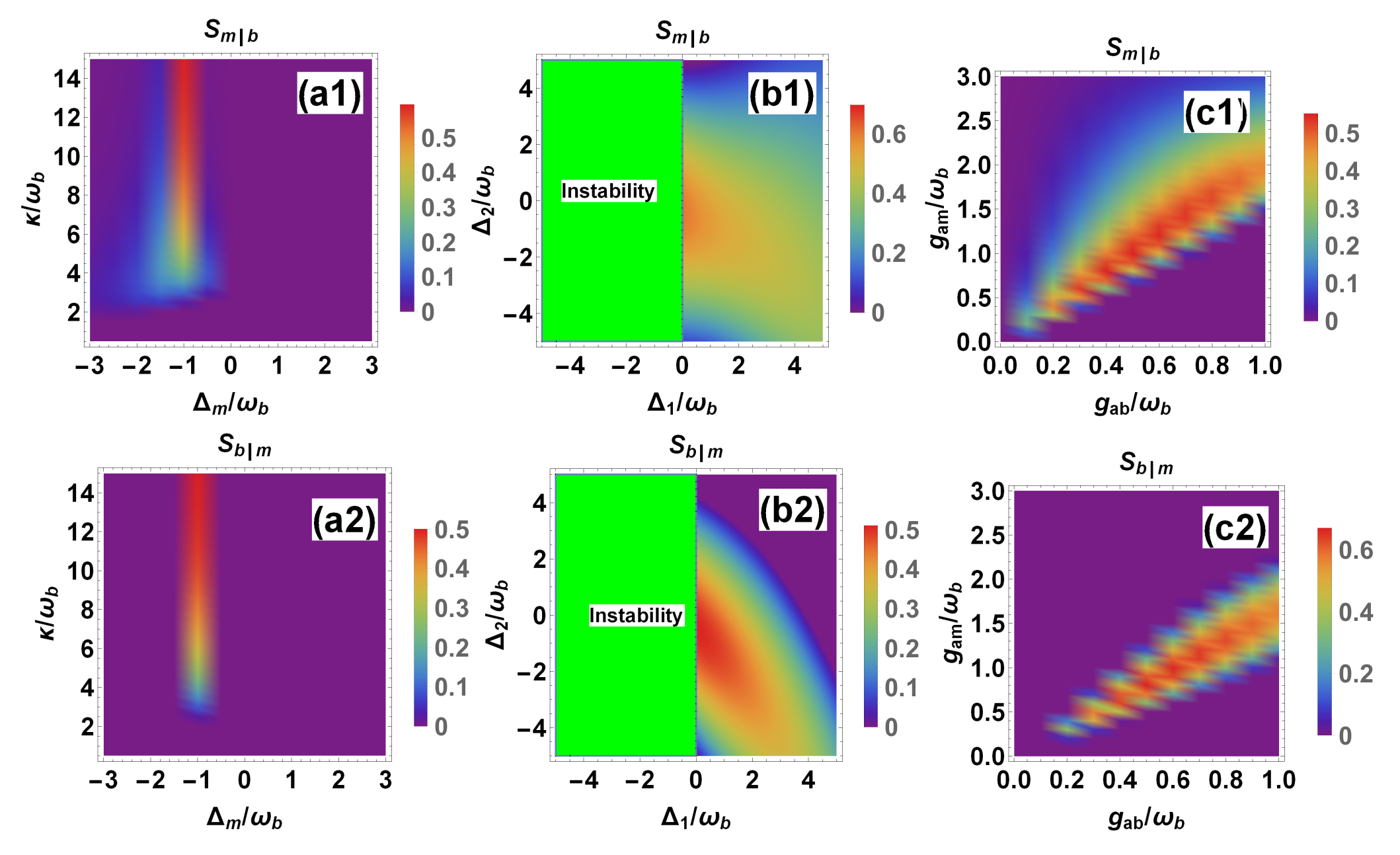
3. Conditional Entanglement and Steering via Measurement
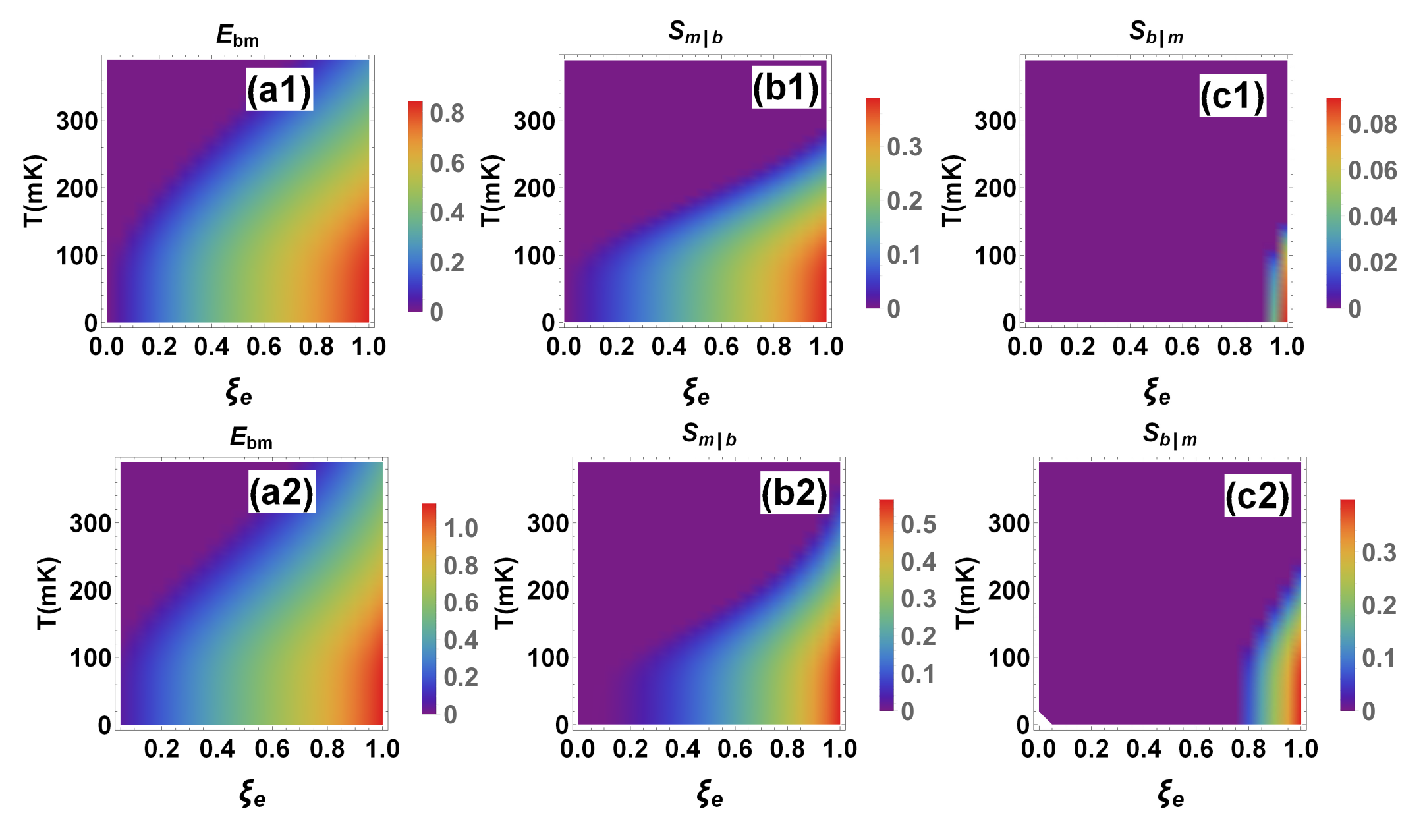
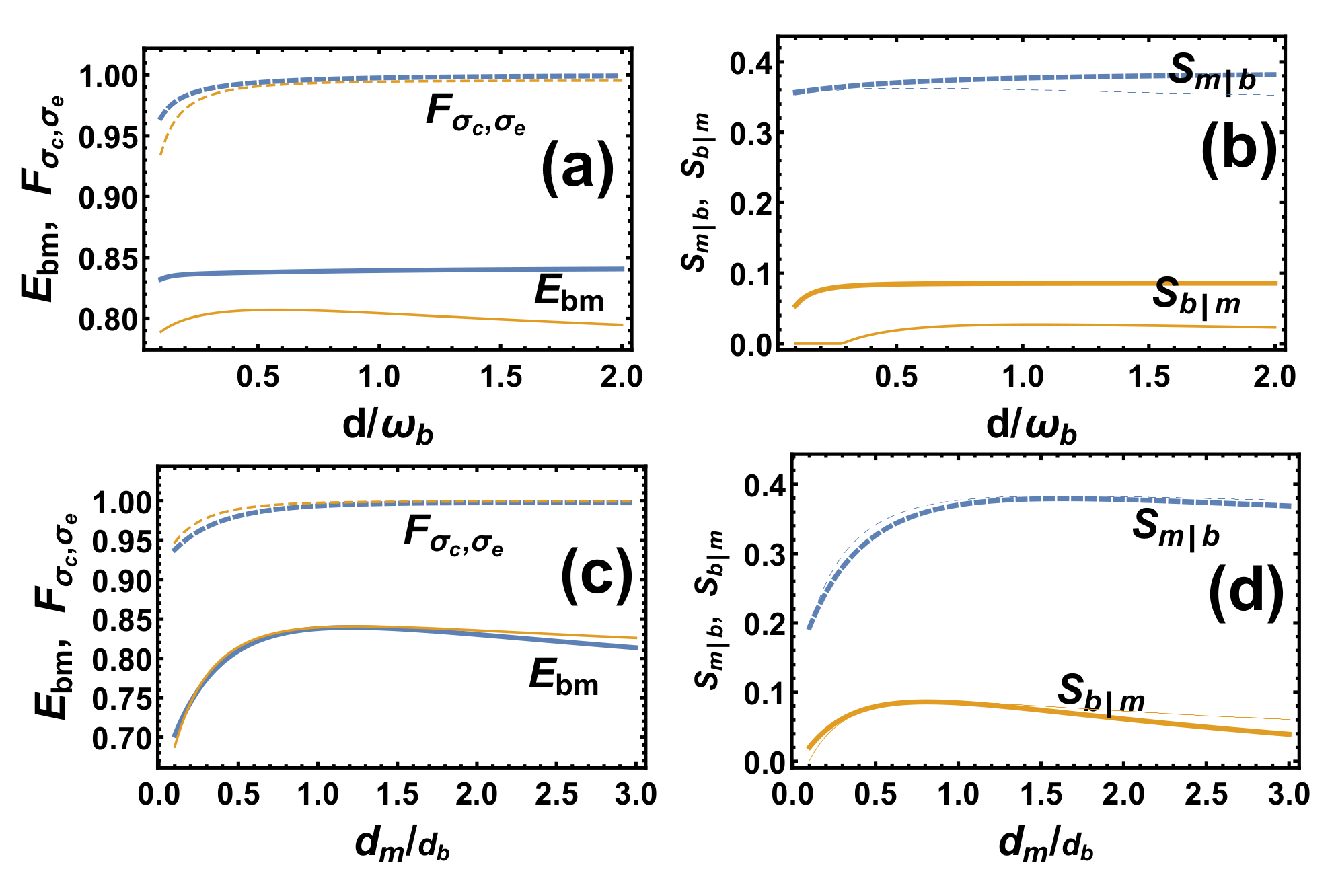
4. Unconditional Entanglement and Steering via Indirect Feedback
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meystre, P. A short walk through quantum optomechanics. Ann. Phys. 2013, 525, 215. [Google Scholar] [CrossRef]
- Poot, M.; van der Zant, H.S.J. Mechanical systems in the quantum regime. Phys. Rep. 2012, 511, 273. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Xuereb, A.; Gröblacher, S.; Paternostro, M.; Regal, C.A.; Weig, E. Optomechanics for quantum technologies. Nat. Phys. 2022, 18, 15. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef]
- Caves, C.M.; Thorne, K.S.; Drever, R.W.P.; Sandberg, V.D.; Zimmermann, M. On the measurement of a weak classical force coupled to a quantum-mechanical oscillator. I. Issues of principle. Rev. Mod. Phys. 1980, 52, 341. [Google Scholar] [CrossRef]
- Metcalfe, M. Applications of cavity optomechanics. Appl. Phys. Rev. 2014, 1, 031105. [Google Scholar] [CrossRef]
- Li, B.-B.; Ou, L.; Lei, Y.; Liu, Y.-C. Cavity optomechanical sensing. Nanophotonics 2021, 10, 2799. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Naderi, M.H. Ultraprecision quantum sensing and measurement based on nonlinear hybrid optomechanical systems containing ultracold atoms or atomic Bose-Einstein condensate. AVS Quantum Sci. 2021, 3, 024701. [Google Scholar] [CrossRef]
- Rips, S.; Hartmann, M.J. Quantum Information Processing with Nanomechanical Qubits. Phys. Rev. Lett. 2013, 110, 120503. [Google Scholar] [CrossRef] [PubMed]
- Muschik, C.A.; Krauter, H.; Hammerer, K.; Polzik, E.S. Quantum information at the interface of light with atomic ensembles and micromechanical oscillators. Quantum Inf. Process. 2011, 10, 839. [Google Scholar] [CrossRef]
- Wollman, E.E.; Lei, C.U.; Weinstein, A.J.; Suh, J.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. QUANTUM MECHANICS. Quantum squeezing of motion in a mechanical resonator. Science 2015, 349, 952. [Google Scholar] [CrossRef] [PubMed]
- Pirkkalainen, J.M.; Damskägg, E.; Brandt, M.; Massel, F.; Sillanpää, M.A. Squeezing of Quantum Noise of Motion in a Micromechanical Resonator. Phys. Rev. Lett. 2015, 115, 243601. [Google Scholar] [CrossRef]
- Ockeloen-Korppi, C.F.; Damskägg, E.; Pirkkalainen, J.M.; Asjad, M.; Clerk, A.A.; Massel, F.; Woolley, M.J.; Sillanpää, M.A. Stabilized entanglement of massive mechanical oscillators. Nature 2018, 556, 478. [Google Scholar] [CrossRef]
- Kotler, S.; Peterson, G.A.; Shojaee, E.; Lecocq, F.; Cicak, K.; Kwiatkowski, A.; Geller, S.; Glancy, S.; Knill, E.; Simmonds, R.W.; et al. Direct observation of deterministic macroscopic entanglement. Science 2021, 372, 622. [Google Scholar] [CrossRef]
- Palomaki, T.A.; Teufel, J.D.; Simmonds, R.W.; Lehnert, K.W. Entangling mechanical motion with microwave fields. Science 2013, 342, 710. [Google Scholar] [CrossRef]
- Ho, M.; Oudot, E.; Bancal, J.; Sangouard, N. Witnessing Optomechanical Entanglement with Photon Counting. Phys. Rev. Lett. 2018, 121, 023602. [Google Scholar] [CrossRef]
- Riedinger, R.; Hong, S.; Norte, R.A.; Slater, J.A.; Shang, J.; Krause, A.G.; Anant, V.; Aspelmeyer, M.; Gröblacher, S. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 2016, 530, 313. [Google Scholar] [CrossRef]
- Hong, S.; Riedinger, R.; Marinkovic, I.; Wallucks, A.; Hofer, S.G.; Norte, R.A.; Aspelmeyer, M.; Gröblacher, S. Hanbury Brown and Twiss interferometry of single phonons from an optomechanical resonator. Science 2017, 358, 203–206. [Google Scholar] [CrossRef]
- Marinkovic, I.; Wallucks, A.; Riedinger, R.; Hong, S.; Aspelmeyer, M.; Gröblacher, S. An optomechanical Bell test. arXiv 2018, arXiv:1806.10615. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 2018, 563, 53. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Mason, D.; Chen, J.; Schliesser, A. Observing and Verifying the Quantum Trajectory of a Mechanical Resonator. Phys. Rev. Lett. 2019, 123, 163601. [Google Scholar] [CrossRef] [PubMed]
- Mason, D.; Chen, J.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745. [Google Scholar] [CrossRef]
- Rossi, M.; Mancino, L.; Landi, G.T.; Paternostro, M.; Schliesser, A.; Belenchia, A. Experimental Assessment of Entropy Production in a Continuously Measured Mechanical Resonator. Phys. Rev. Lett. 2020, 125, 080601. [Google Scholar] [CrossRef]
- Tebbenjohanns, F.; Mattana, M.L.; Rossi, M.; Frimmer, M.; Novotny, L. Quantum control of a nanoparticle optically levitated in cryogenic free space. Nature 2021, 595, 378. [Google Scholar] [CrossRef]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373. [Google Scholar] [CrossRef]
- Tan, H.; Zhan, H. Strong mechanical squeezing and optomechanical steering via continuous monitoring in optomechanical systems. Phys. Rev. A 2019, 100, 023843. [Google Scholar] [CrossRef]
- Brunelli, M.; Malz, D.; Nunnenkamp, A. Conditional Dynamics of Optomechanical Two-Tone Backaction-Evading Measurements. Phys. Rev. Lett. 2019, 123, 093602. [Google Scholar] [CrossRef]
- Quirion, D.L.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 2022, 965, 1. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Piotr Wolski, S.; Tabuchi, Y.; Kono, S.; Usami, K.; Nakamura, Y. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 2020, 367, 425. [Google Scholar] [CrossRef]
- Xu, D.; Gu, X.-K.; Li, H.-K.; Weng, Y.-C.; Wang, Y.-P.; Li, J.; Wang, H.; Zhu, S.-Y.; You, J.Q. Quantum Control of a Single Magnon in a Macroscopic Spin System. Phys. Rev. Lett. 2023, 130, 193603. [Google Scholar] [CrossRef]
- Xu, D.; Gu, X.-K.; Weng, Y.-C.; Li, H.-K.; Wang, Y.-P.; Zhu, S.-Y.; You, J.Q. Deterministic generation and tomography of a macroscopic Bell state between a millimeter-sized spin system and a superconducting qubit. arXiv 2023, arXiv:2306.09677. [Google Scholar]
- Potts, C.A.; Varga, E.; Bittencourt, V.A.S.V.; Viola Kusminskiy, S.; Davis, J.P. Dynamical Backaction Magnomechanics. Phys. Rev. X 2021, 11, 031053. [Google Scholar] [CrossRef]
- Shen, R.-C.; Li, J.; Fan, Z.-Y.; Wang, Y.-P.; You, J.Q. Mechanical Bistability in Kerr-modified Cavity Magnomechanics. Phys. Rev. Lett. 2022, 129, 123601. [Google Scholar] [CrossRef]
- Zhang, Z.; Scully, M.O.; Agarwal, G.S. Quantum entanglement between two magnon modes via Kerr nonlinearity driven far from equilibrium. Phys. Rev. Res. 2019, 1, 023021. [Google Scholar] [CrossRef]
- Zhan, H.; Sun, L.; Tan, H. Chirality-induced one-way quantum steering between two waveguide-mediated ferrimagnetic microspheres. Phys. Rev. B 2022, 106, 104432. [Google Scholar] [CrossRef]
- Ren, Y.; Xie, J.; Li, X.; Ma, S.; Li, F. Long-range generation of a magnon-magnon entangled state. Phys. Rev. B 2022, 105, 094422. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Xiong, H.; Wu, Y. Magnon blockade in a hybrid ferromagnet-superconductor quantum system. Phys. Rev. B 2019, 100, 134421. [Google Scholar] [CrossRef]
- Xie, H.; He, L.-W.; Shang, X.; Lin, G.-W.; Lin, X.-M. Nonreciprocal photon blockade in cavity optomagnonics. Phys. Rev. A 2022, 106, 053707. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Zheng, S.; Ficek, Z.; He, Q.Y.; Yung, M.-H. Steady Bell State Generation via Magnon-Photon Coupling. Phys. Rev. Lett. 2020, 124, 053602. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, S.-Y.; Agarwal, G.S. Magnon-Photon-Phonon Entanglement in Cavity Magnomechanics. Phys. Rev. Lett. 2018, 121, 203601. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, S.-Y.; Agarwal, G.S. Squeezed states of magnons and phonons in cavity magnomechanics. Phys. Rev. A 2019, 99, 021801. [Google Scholar] [CrossRef]
- Yu, M.; Shen, H.; Li, J. Magnetostrictively Induced Stationary Entanglement between Two Microwave Fields. Phys. Rev. Lett. 2020, 124, 213604. [Google Scholar] [CrossRef]
- Sun, F.-X.; Zheng, S.-S.; Xiao, Y.; Gong, Q.; He, Q.; Xia, K. Remote Generation of Magnon Schrödinger Cat State via Magnon-Photon Entanglement. Phys. Rev. Lett. 2021, 127, 087203. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Li, Y.-Q. Optomagnonic frequency combs. Photon. Res. 2022, 12, 2786. [Google Scholar] [CrossRef]
- Xiong, H. Magnonic frequency combs based on the resonantly enhanced magnetostrictive effect. Fund. Res. 2023, 3, 8. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Wang, B.; Xiong, H.; Wu, Y. Magnon-induced high-order sideband generation. Opt. Lett. 2018, 43, 3698. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023. [Google Scholar] [CrossRef]
- Simon, C. Towards a global quantum network. Nat. Photon. 2017, 11, 678. [Google Scholar] [CrossRef]
- Thomas, R.A.; Parniak, M.; ØStfeldt, C.; Moller, C.B.; Bærentsen, C.; Tsaturyan, Y.; Schliesser, A.; Appel, J.; Zeuthen, E.; Polzik, E.S. Entanglement between distant macroscopic mechanical and spin systems. Nat. Phys. 2021, 17, 228. [Google Scholar] [CrossRef]
- Roch, N.; Schwartz, M.E.; Motzoi, F.; Macklin, C.; Vijay, R.; Eddins, A.W.; Korotkov, A.N.; Whaley, K.B.; Sarovar, M.; Siddiqi, I. Observation of Measurement-Induced Entanglement and Quantum Trajectories of Remote Superconducting Qubits. Phys. Rev. Lett. 2014, 112, 170501. [Google Scholar] [CrossRef] [PubMed]
- Chantasri, A.; Kimchi-Schwartz, M.E.; Roch, N.; Siddiqi, I.; Jordan, A.N. Quantum Trajectories and Their Statistics for Remotely Entangled Quantum Bits. Phys. Rev. X 2016, 6, 041052. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zhang, J.; Liu, Y.-X.; Wu, R.-B.; Jacobs, K.; Nori, F. Quantum feedback: Theory, experiments, and applications. Phys. Rep. 2017, 679, 1. [Google Scholar] [CrossRef]
- Plenio, M.B. Logarithmic Negativity: A Full Entanglement Monotone That is not Convex. Phys. Rev. Lett. 2005, 95, 090503. [Google Scholar] [CrossRef] [PubMed]
- Kogias, I.; Lee, A.R.; Ragy, S.; Adesso, G. Quantification of Gaussian Quantum Steering. Phys. Rev. Lett. 2015, 114, 060403. [Google Scholar] [CrossRef]
- Tan, H.; Li, J. Einstein-Podolsky-Rosen entanglement and asymmetric steering between distant macroscopic mechanical and magnonic systems. Phys. Rev. Res. 2021, 3, 013192. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Hybridizing Ferromagnetic Magnons and Microwave Photons in the Quantum Limit. Phys. Rev. Lett. 2014, 113, 083603. [Google Scholar] [CrossRef]
- Peterson, G.A.; Kotler, S.; Lecocq, F.; Cicak, K.; Jin, X.Y.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Ultrastrong Parametric Coupling between a Superconducting Cavity and a Mechanical Resonator. Phys. Rev. Lett. 2019, 123, 247701. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, X.-Q.; Wang, Y.-P.; Li, T.-F.; You, J.Q. Observation of the exceptional point in cavity magnon-polaritons. Nat. Commun. 2017, 8, 1368. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-P.; Zhang, G.-Q.; Zhang, D.; Li, T.-F.; Hu, C.-M.; You, J.Q. Bistability of Cavity Magnon Polaritons. Phys. Rev. Lett. 2018, 120, 057202. [Google Scholar] [CrossRef] [PubMed]
- Poggio, M.; Degen, C.L.; Mamin, H.J.; Rugar, D. Feedback Cooling of a Cantilever’s Fundamental Mode below 5 mK. Phys. Rev. Lett. 2007, 99, 017201. [Google Scholar] [CrossRef] [PubMed]
- Schäfermeier, C.; Kerdoncuff, H.; Hoff, U.B.; Fu, H.; Huck, A.; Bilek, J.; Harris, G.I.; Bowen, W.P.; Gehring, T.; Andersen, U.L. Quantum enhanced feedback cooling of a mechanical oscillator using nonclassical light. Nat. Commun. 2016, 7, 13628. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Fong, K.Y.; Poot, M.; Tang, H.X. Cascaded optical transparency in multimode-cavity optomechanical systems. Nat. Commun. 2015, 6, 5850. [Google Scholar] [CrossRef]
- Banchi, L.; Braunstein, S.L.; Pirandola, S. Quantum Fidelity for Arbitrary Gaussian States. Phys. Rev. Lett. 2015, 115, 260501. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, H. Measurement-Based Control of Quantum Entanglement and Steering in a Distant Magnomechanical System. Photonics 2023, 10, 1081. https://doi.org/10.3390/photonics10101081
Tan H. Measurement-Based Control of Quantum Entanglement and Steering in a Distant Magnomechanical System. Photonics. 2023; 10(10):1081. https://doi.org/10.3390/photonics10101081
Chicago/Turabian StyleTan, Huatang. 2023. "Measurement-Based Control of Quantum Entanglement and Steering in a Distant Magnomechanical System" Photonics 10, no. 10: 1081. https://doi.org/10.3390/photonics10101081
APA StyleTan, H. (2023). Measurement-Based Control of Quantum Entanglement and Steering in a Distant Magnomechanical System. Photonics, 10(10), 1081. https://doi.org/10.3390/photonics10101081



