Broadband Terahertz Metal-Wire Signal Processors: A Review
Abstract
1. Introduction
2. THz Guiding Properties of Metal-Wire Waveguides
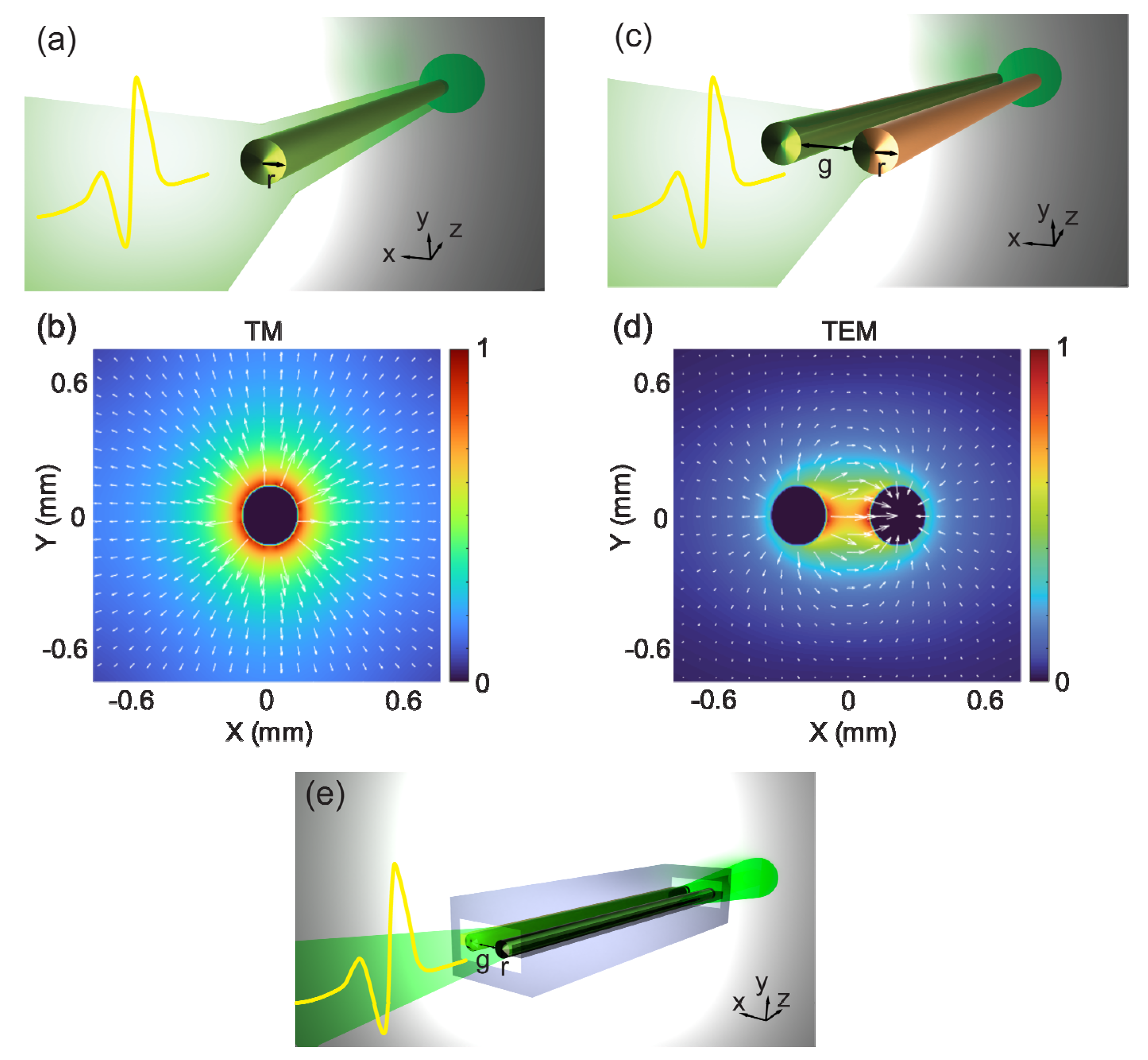
3. Broadband THz Metal-Wire Signal Processors
3.1. Inserting Standalone Components
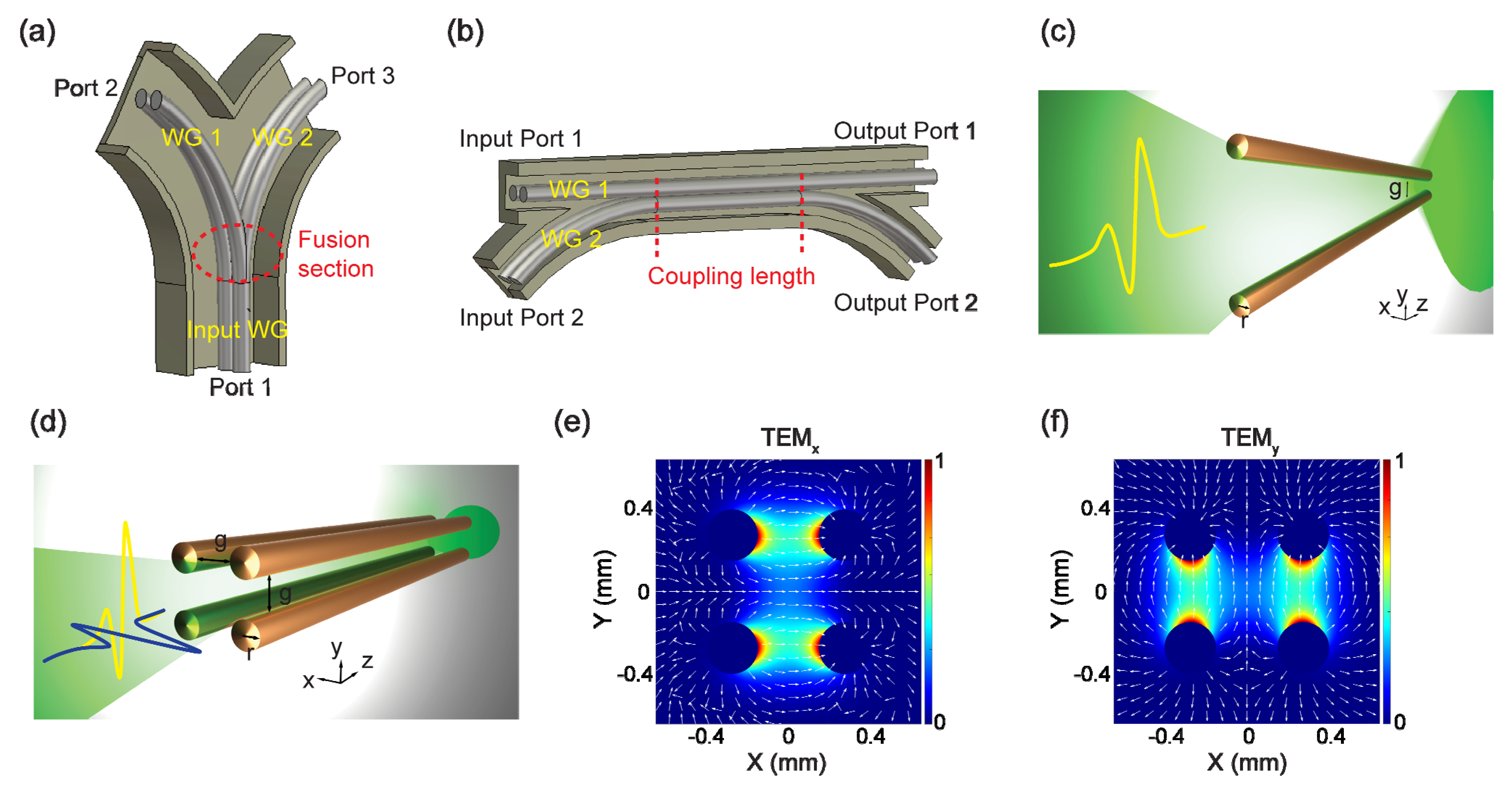
3.2. Varying Waveguide Geometries/Topologies
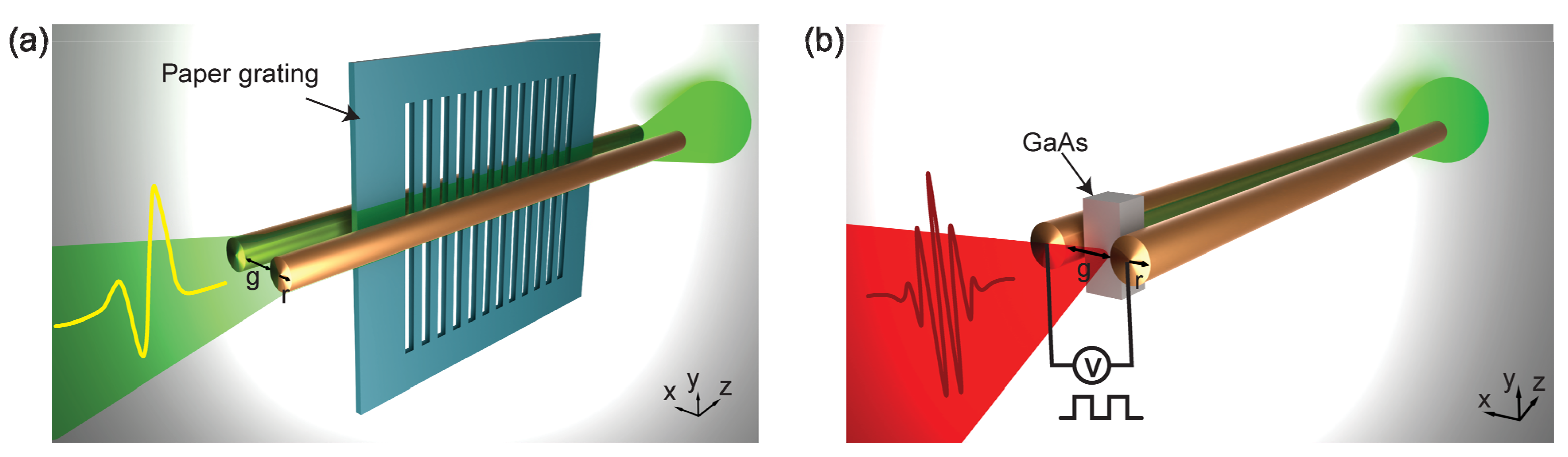
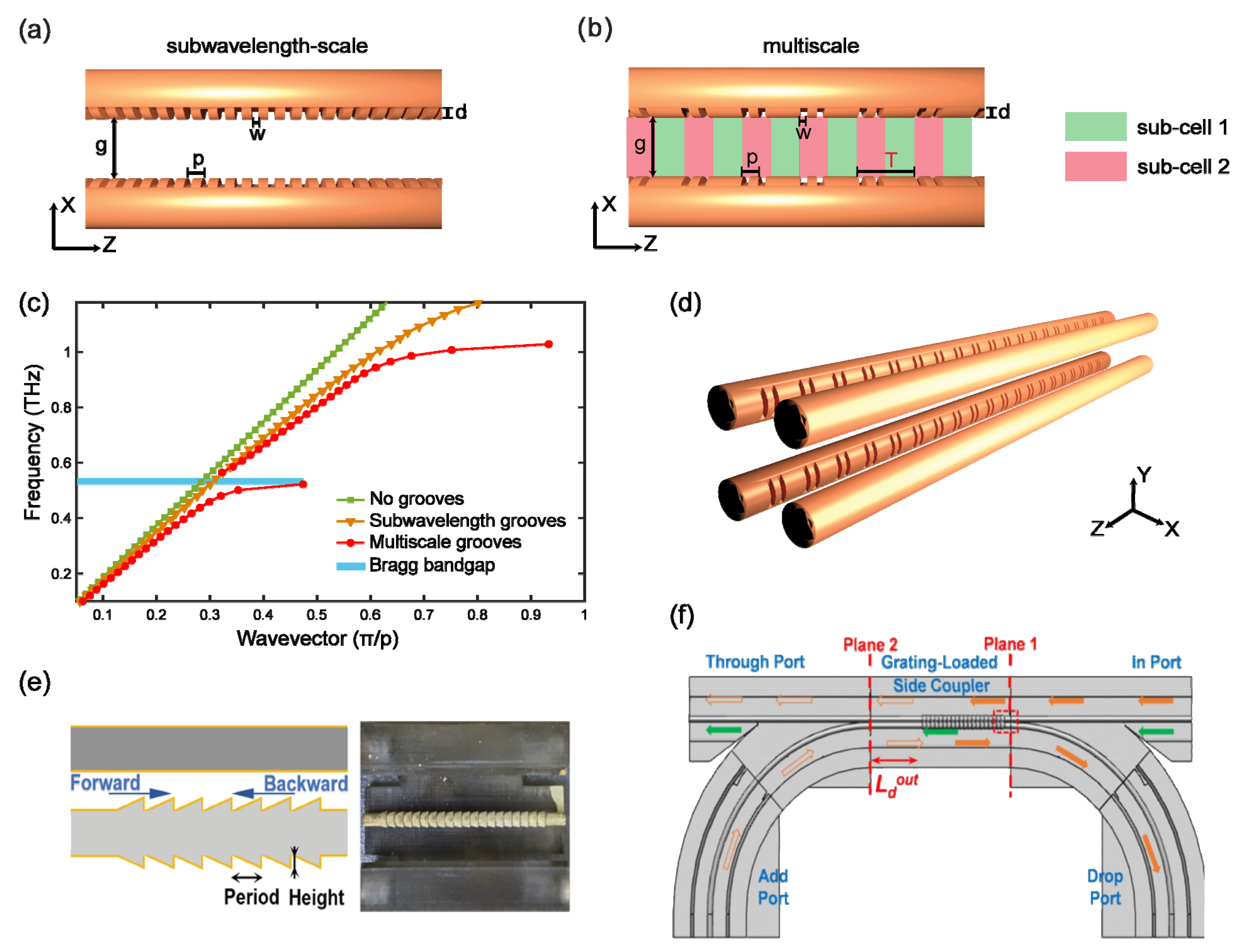
3.3. Engineering the Metal-Wire Surfaces
4. Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M. What Should 6G Be ? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Calvanese Strinati, E.; Barbarossa, S.; Gonzalez-Jimenez, J.L.; Ktenas, D.; Cassiau, N.; Maret, L.; Dehos, C. 6G: The Next Frontier: From Holographic Messaging to Artificial Intelligence Using Subterahertz and Visible Light Communication. IEEE Veh. Technol. Mag. 2019, 14, 42–50. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in Terahertz Communications Accelerated by Photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Atakaramians, S.; Afshar, V.S.; Monro, T.M.; Abbott, D. Terahertz Dielectric Waveguides. Adv. Opt. Photonics 2013, 5, 169. [Google Scholar] [CrossRef]
- Weidenbach, M.; Jahn, D.; Rehn, A.; Busch, S.F.; Beltrán-Mejía, F.; Balzer, J.C.; Koch, M. 3D Printed Dielectric Rectangular Waveguides, Splitters and Couplers for 120 GHz. Opt. Express 2016, 24, 28968. [Google Scholar] [CrossRef]
- Cruz, A.; Cordeiro, C.; Franco, M. 3D Printed Hollow-Core Terahertz Fibers. Fibers 2018, 6, 43. [Google Scholar] [CrossRef]
- Khan, M.T.A.; Li, H.; Duong, N.N.M.; Blanco-Redondo, A.; Atakaramians, S. 3D-Printed Terahertz Topological Waveguides. Adv. Mater. Technol. 2021, 6, 2100252. [Google Scholar] [CrossRef]
- Nallappan, K.; Cao, Y.; Xu, G.; Guerboukha, H.; Nerguizian, C.; Skorobogatiy, M. Dispersion-Limited versus Power-Limited Terahertz Communication Links Using Solid Core Subwavelength Dielectric Fibers. Photonics Res. 2020, 8, 1757. [Google Scholar] [CrossRef]
- Ma, T.; Nallapan, K.; Guerboukha, H.; Skorobogatiy, M. Analog Signal Processing in the Terahertz Communication Links Using Waveguide Bragg Gratings: Example of Dispersion Compensation. Opt. Express 2017, 25, 11009. [Google Scholar] [CrossRef]
- Atakaramians, S.; Afshar, V.S.; Ebendorff-Heidepriem, H.; Nagel, M.; Fischer, B.M.; Abbott, D.; Monro, T.M. THz Porous Fibers: Design, Fabrication and Experimental Characterization. Opt. Express 2009, 17, 14053. [Google Scholar] [CrossRef]
- Ung, B.; Mazhorova, A.; Dupuis, A.; Rozé, M.; Skorobogatiy, M. Polymer Microstructured Optical Fibers for Terahertz Wave Guiding. Opt. Express 2011, 19, B848. [Google Scholar] [CrossRef]
- Bao, H.; Nielsen, K.; Rasmussen, H.K.; Jepsen, P.U.; Bang, O. Fabrication and Characterization of Porous-Core Honeycomb Bandgap THz Fibers. Opt. Express 2012, 20, 29507. [Google Scholar] [CrossRef]
- Faisal, M.; Shariful Islam, M. Extremely High Birefringent Terahertz Fiber Using a Suspended Elliptic Core with Slotted Airholes. Appl. Opt. 2018, 57, 3340. [Google Scholar] [CrossRef]
- Islam, M.S.; Cordeiro, C.M.B.; Franco, M.A.R.; Sultana, J.; Cruz, A.L.S.; Abbott, D. Terahertz Optical Fibers [Invited]. Opt. Express 2020, 28, 16089. [Google Scholar] [CrossRef]
- Gallot, G.; Jamison, S.P.; McGowan, R.W.; Grischkowsky, D. Terahertz Waveguides. J. Opt. Soc. Am. B 2000, 17, 851. [Google Scholar] [CrossRef]
- Navarro-Cía, M.; Wu, J.; Liu, H.; Mitrofanov, O. Generation of Radially-Polarized Terahertz Pulses for Coupling into Coaxial Waveguides. Sci. Rep. 2016, 6, 38926. [Google Scholar] [CrossRef]
- Mendis, R.; Grischkowsky, D. Undistorted Guided-Wave Propagation of Subpicosecond Terahertz Pulses. Opt. Lett. 2001, 26, 846. [Google Scholar] [CrossRef]
- Pahlevaninezhad, H.; Darcie, T.E.; Heshmat, B. Two-Wire Waveguide for Terahertz. Opt. Express 2010, 18, 7415. [Google Scholar] [CrossRef]
- Markov, A.; Guerboukha, H.; Skorobogatiy, M. Hybrid Metal Wire–Dielectric Terahertz Waveguides: Challenges and Opportunities [Invited]. J. Opt. Soc. Am. B 2014, 31, 2587. [Google Scholar] [CrossRef]
- Li, H.; Atakaramians, S.; Lwin, R.; Tang, X.; Yu, Z.; Argyros, A.; Kuhlmey, B.T. Flexible Single-Mode Hollow-Core Terahertz Fiber with Metamaterial Cladding. Optica 2016, 3, 941. [Google Scholar] [CrossRef]
- Sengupta, K.; Nagatsuma, T.; Mittleman, D.M. Terahertz Integrated Electronic and Hybrid Electronic–Photonic Systems. Nat. Electron. 2018, 1, 622–635. [Google Scholar] [CrossRef]
- Reichel, K.S.; Mendis, R.; Mittleman, D.M. A Broadband Terahertz Waveguide T-Junction Variable Power Splitter. Sci. Rep. 2016, 6, 28925. [Google Scholar] [CrossRef] [PubMed]
- Reichel, K.S.; Lozada-Smith, N.; Joshipura, I.D.; Ma, J.; Shrestha, R.; Mendis, R.; Dickey, M.D.; Mittleman, D.M. Electrically Reconfigurable Terahertz Signal Processing Devices Using Liquid Metal Components. Nat. Commun. 2018, 9, 4202. [Google Scholar] [CrossRef]
- Karl, N.J.; McKinney, R.W.; Monnai, Y.; Mendis, R.; Mittleman, D.M. Frequency-Division Multiplexing in the Terahertz Range Using a Leaky-Wave Antenna. Nat. Photonics 2015, 9, 717–720. [Google Scholar] [CrossRef]
- Mbonye, M.; Mendis, R.; Mittleman, D.M. A Terahertz Two-Wire Waveguide with Low Bending Loss. Appl. Phys. Lett. 2009, 95, 1–4. [Google Scholar] [CrossRef]
- Shrestha, R.; Kerpez, K.; Hwang, C.S.; Mohseni, M.; Cioffi, J.M.; Mittleman, D.M. A Wire Waveguide Channel for Terabit-per-Second Links. Appl. Phys. Lett. 2020, 116, 131102. [Google Scholar] [CrossRef]
- Wang, K.; Mittleman, D.M. Metal Wires for Terahertz Wave Guiding. Nature 2004, 432, 376–379. [Google Scholar] [CrossRef]
- Maier, S.A.; Andrews, S.R.; Martín-Moreno, L.; García-Vidal, F.J. Terahertz Surface Plasmon-Polariton Propagation and Focusing on Periodically Corrugated Metal Wires. Phys. Rev. Lett. 2006, 97, 176805. [Google Scholar] [CrossRef]
- Astley, V.; Scheiman, J.; Mendis, R.; Mittleman, D.M. Bending and Coupling Losses in Terahertz Wire Waveguides. Opt. Lett. 2010, 35, 553. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Mittleman, D.M. Dispersion of Surface Plasmon Polaritons on Metal Wires in the Terahertz Frequency Range. Phys. Rev. Lett. 2006, 96, 157401. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Nahata, A. Coupling of Terahertz Pulses onto a Single Metal Wire Waveguide Using Milled Grooves. Opt. Express 2005, 13, 7028. [Google Scholar] [CrossRef]
- Mridha, M.K.; Mazhorova, A.; Clerici, M.; Al-Naib, I.; Daneau, M.; Ropagnol, X.; Peccianti, M.; Reimer, C.; Ferrera, M.; Razzari, L.; et al. Active Terahertz Two-Wire Waveguides. Opt. Express 2014, 22, 22340. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-S. Principles of Terahertz Science and Technology; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-09539-4. [Google Scholar]
- Markov, A.; Skorobogatiy, M. Two-Wire Terahertz Fibers with Porous Dielectric Support. Opt. Express 2013, 21, 12728. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Nallappan, K.; Guerboukha, H.; Xu, G.; Skorobogatiy, M. Additive Manufacturing of Highly Reconfigurable Plasmonic Circuits for Terahertz Communications. Optica 2020, 7, 1112. [Google Scholar] [CrossRef]
- Yan, G.; Markov, A.; Chinifooroshan, Y.; Tripathi, S.M.; Bock, W.J.; Skorobogatiy, M. Low-Loss Terahertz Waveguide Bragg Grating Using a Two-Wire Waveguide and a Paper Grating. Opt. Lett. 2013, 38, 3089. [Google Scholar] [CrossRef]
- Cao, Y.; Nallappan, K.; Xu, G.; Skorobogatiy, M. Add Drop Multiplexers for Terahertz Communications Using Two-Wire Waveguide-Based Plasmonic Circuits. Nat. Commun. 2022, 13, 4090. [Google Scholar] [CrossRef]
- Balistreri, G.; Tomasino, A.; Dong, J.; Yurtsever, A.; Stivala, S.; Azaña, J.; Morandotti, R. Time-Domain Integration of Broadband Terahertz Pulses in a Tapered Two-Wire Waveguide. Laser Photon. Rev. 2021, 15, 2100051. [Google Scholar] [CrossRef]
- Dong, J.; Tomasino, A.; Balistreri, G.; You, P.; Vorobiov, A.; Charette, É.; Le Drogoff, B.; Chaker, M.; Yurtsever, A.; Stivala, S.; et al. Versatile Metal-Wire Waveguides for Broadband Terahertz Signal Processing and Multiplexing. Nat. Commun. 2022, 13, 741. [Google Scholar] [CrossRef]
- Shen, L.; Chen, X.; Zhong, Y.; Agarwal, K. Effect of Absorption on Terahertz Surface Plasmon Polaritons Propagating along Periodically Corrugated Metal Wires. Phys. Rev. B 2008, 77, 075408. [Google Scholar] [CrossRef]
- Meng, Y.; Xiang, H.; Zhang, R.-Y.; Wu, X.; Han, D.; Chan, C.T.; Wen, W. Topological Interface States in Multiscale Spoof-Insulator-Spoof Waveguides. Opt. Lett. 2016, 41, 3698. [Google Scholar] [CrossRef]
- Fu, Z.; Gan, Q.; Ding, Y.J.; Bartoli, F.J. From Waveguiding to Spatial Localization of THz Waves within a Plasmonic Metallic Grating. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 486–490. [Google Scholar] [CrossRef]
- Gan, Q.; Fu, Z.; Ding, Y.J.; Bartoli, F.J. Ultrawide-Bandwidth Slow-Light System Based on THz Plasmonic Graded Metallic Grating Structures. Phys. Rev. Lett. 2008, 100, 256803. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.-X.; Zhai, X.; Wang, L.-L.; Wen, S.-C. Plasmonically Induced Transparency in Double-Layered Graphene Nanoribbons. Photonics Res. 2018, 6, 692. [Google Scholar] [CrossRef]
- Gopalan, P.; Sensale-Rodriguez, B. 2D Materials for Terahertz Modulation. Adv. Opt. Mater. 2020, 8, 1900550. [Google Scholar] [CrossRef]
- He, W.; Tong, M.; Xu, Z.; Hu, Y.; Cheng, X.; Jiang, T. Ultrafast All-Optical Terahertz Modulation Based on an Inverse-Designed Metasurface. Photonics Res. 2021, 9, 1099. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Topological Analog Signal Processing. Nat. Commun. 2019, 10, 2058. [Google Scholar] [CrossRef]
- Mengu, D.; Sakib Rahman, M.S.; Luo, Y.; Li, J.; Kulce, O.; Ozcan, A. At the Intersection of Optics and Deep Learning: Statistical Inference, Computing, and Inverse Design. Adv. Opt. Photonics 2022, 14, 209. [Google Scholar] [CrossRef]
| Cu | Ag | Au | Al | Stainless Steel 1 | |
|---|---|---|---|---|---|
| 59.6 | 63.0 | 45.2 | 37.8 | 1.45 | |
| 65.2 | 63.4 | 74.9 | 81.9 | 418 |
| Reference | Method | fc | Q-Factor |
|---|---|---|---|
| Yan et al. [38] | Laser cutting on papers | 0.637 THz | 142 |
| Cao et al. [37] | Hot stamping + metal deposition | 0.14 THz | 4.4 |
| Cao et al. [39] | 3D printing + metal deposition | 0.14 THz | 7.8 |
| Dong et al. [41] | Directly engraving wire surfaces | 0.53 THz | 479.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghazialsharif, M.; Dong, J.; Abbes, A.; Morandotti, R. Broadband Terahertz Metal-Wire Signal Processors: A Review. Photonics 2023, 10, 48. https://doi.org/10.3390/photonics10010048
Ghazialsharif M, Dong J, Abbes A, Morandotti R. Broadband Terahertz Metal-Wire Signal Processors: A Review. Photonics. 2023; 10(1):48. https://doi.org/10.3390/photonics10010048
Chicago/Turabian StyleGhazialsharif, Mohammad, Junliang Dong, Alaeddine Abbes, and Roberto Morandotti. 2023. "Broadband Terahertz Metal-Wire Signal Processors: A Review" Photonics 10, no. 1: 48. https://doi.org/10.3390/photonics10010048
APA StyleGhazialsharif, M., Dong, J., Abbes, A., & Morandotti, R. (2023). Broadband Terahertz Metal-Wire Signal Processors: A Review. Photonics, 10(1), 48. https://doi.org/10.3390/photonics10010048





