Next Article in Journal / Special Issue
Near-Perfect Narrow-Band Tunable Graphene Absorber with a Dual-Layer Asymmetric Meta-Grating
Previous Article in Journal
Flexible, Stretchable, Tunable, and Switchable DFB Laser
Previous Article in Special Issue
Investigation of InGaN-Based Green Micro-Photonic-Crystal- Light-Emitting-Diodes with Bottom, Nanoporous, Distributed Bragg Reflectors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 10
Issue 1
10.3390/photonics10010013
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Investigation of Optical-Switching Mechanism Using Guided Mode Resonances

by
Atiq Ur Rehman
1,
Yousuf Khan
1,*,
Muhammad Irfan
1 and
Muhammad A. Butt
2
1
Nanophotonics Research Group, Department of Electronic Engineering, Balochistan University of Information Technology, Engineering and Management Sciences, Quetta 87300, Pakistan
2
Institute of Microelectronics and Optoelectronics, Warsaw University of Technology, Koszykowa 75, 00-662 Warsaw, Poland
*
Author to whom correspondence should be addressed.
Photonics 2023, 10(1), 13; https://doi.org/10.3390/photonics10010013
Submission received: 26 November 2022 / Revised: 19 December 2022 / Accepted: 20 December 2022 / Published: 23 December 2022
(This article belongs to the Special Issue Photonic Crystals: Physics and Devices)
Browse Figures
Versions Notes

Abstract

:
Recently, photonic crystals have paved the way to control photonic signals. Therefore, this research numerically investigated the design of the optical switch using the guided-mode resonances in photonic crystals operating in a communication window around 1.55 μm. The design of the device is based on a dielectric slab waveguide to make it compatible with optical waveguides in photonic circuits. Moreover, two signals are used and are termed as the data signal and control signal. The data signal is coupled into the optical waveguide using an out-of-the-plane vertical coupling mechanism, whereas the control signal is index-guided into the optical waveguide to amplify the data signal. The switching parameters of the optical switch are adjusted by changing the number of the photonic crystal periods and implementing a varying radius PhC-cavity within the middle of the PhC-lattice, where the optical characteristics in terms of resonant wavelength, reflection peaks, linewidth, and quality factor of the data signal can be adjusted. The numerical simulations are carried out in open-source finite difference time domain-based software. Congruently, 7% optical amplification is achieved in the data signal with a wavelength shift of 0.011 μm and a quality factor of 12.64. The amplification of the data signal can be utilized to implement an optical switching mechanism. The device is easy to implement and has great potential to be used in programmable photonics and optical integrated circuits.

1. Introduction

Electronic technology has reached its climax at the current time and the utmost efforts are being made to further increase its performance in terms of operating speed, power efficiency and the reduction in heating effects. For this purpose, different mechanisms are used, such as increasing the number of transistors, reducing the die size, grouping different semiconductor materials and improving the interconnections. However, on-chip heat production and the loss of information during long-haul communication is still a persistent problem [1]. Therefore, the introduction of an alternate technology is the need of the hour to address the rising issues of the already developed silicon technology. Considering the above-mentioned issues, a good alternative can be optical technology, which is still in its infancy stage [2]. Other than long-haul communication, the research in optical technology has undergone a boost in the past decade, especially relating to the design of the optical components i.e., switches, logic gates, modulators, decoders, and other essential components used in the design of the optical integrated circuits [3]. Additionally, different phenomena from the optical fields are brought together for the designing purposes of these components in the form of optical interference [4], Guided-mode resonances (GMR) (also known as the Fano-resonances) [5], Kerr effect [6], and many more. Similarly, diverse time domain mathematical approaches, i.e., Finite Difference Time Domain (FDTD) [7], Coupling method [8], Finite Integral Time Domain (FITD) [9], Plane Wave Expansion (PWE) [10], along with frequency domain methods such as the Finite Elements Method (FEM) [11], Method of Moments [12], Transfer Matric Method (TMM) [13] and Fast Multi-pole Method (FMM) [14], are being used to design these components. Mainly dielectrics and semiconductors have been utilized for the design of optical components, which in turn can be modified into different forms to achieve various functionalities, such as optical waveguides [15], directional couplers [16] and Photonic Crystals (PhCs) [17]. By definition, PhCs are dielectric material-based nanostructures that are capable of controlling light at the wavelength scale. PhCs exist in nature on the bodies of insects and feathers of a different species of birds [18] and can be designed and fabricated artificially to design different optical events and components [19]. Considering the optical integrated circuits, the optical switching phenomena is of utmost interest to replicate the function of electronic switching components, i.e., the transistor. Several investigations are reported to implement optical switching mechanisms involving diverse combinations of the optical waveguides [20], PhCs-based ring resonators [21], cross-waveguide geometry [22], optical pumping [23], quantum dots [24], Opto-electro hybrid devices [25], thermo-optic interferometric configurations [26] and combination of active-transparent materials [27]. However, these devices are complex to implement and fabricate in large quantities, such as in the fields of biomedical sensors, communication systems and optical integrated devices.
Moreover, there are numerous approaches designed to perform the phenomenon of optical switching efficiently, as imitated in ref. [22], using a 2-Dimensional (2D) cross-waveguide PhCs-based structure and a control signal to amplify or de-amplify a given data signal using the concepts of couple-mode theory and FDTD. The usage of the PhCs on the layers of the porous silicon (Si) to shift the photonic band gap edge [28] and its realization for optical switching by removing a diagonal of the PhCs from its lattice, is studied in ref. [29], along with the formation of a cross-waveguide-like structure. Thus, by putting a single rod within the intersection of these diagonals, the optical switching action is implemented. An approach of using the guiding layer and the GMR phenomena combined with optical switching is realized in ref. [30], a structure comprising of the PhCs-based cavities using the data signal and a pump signal of different intensities, which is investigated in ref. [31] using the PhCs-based couplers and directional couplers in refs. [32,33]; utilizing granular sub-base (GSB) materials to enhance the optical properties is imitated in ref. [34] and through ultra-broadband Mach-Zehnder in ref. [35] for a similar purpose. A 2D PhCs-based frustrated total internal reflection-based optical-switching is reported in ref. [36], with qualities of the metasurfaces along the plasmon-induced Enhancement of Index of Refraction (EIR) in ref. [37] to control the amplitude of the incident signals with the help of coherent absorption [38] for all-optical switching action. The nanowires of group III-V with the implementation of the PhCs-based cavity are considered in ref. [39] and designing parameters for the switching gain in ref. [40], bringing in the concepts of the active and transparent materials together. The short-length optical fiber is investigated in [41] to achieve the phenomenon, using its multi-mode properties in the presence of the soliton [42] and a weak pulse using a polarizer with 45° tilted fiber gratings [43]. A single optical emitter is studied in [44], where a weak source signal is amplified or de-amplified by using a second gate source, which is responsible for the rate of the propulsion in the optical emitter according to its varying intensities, performing the electro-optical integration [45] and the optical buffering to reduce the delays in the long-haul communication systems [46]. Additionally, a novel design of the optical switch based on GMR is investigated in ref. [47], inducing a 2D PhCs-based cavity at the start of the optical membrane in dielectric structures, to amplify or de-amplify the given data signal with the help of a control signal using the FDTD approach [48]. Correspondingly, the field of PhC-based logic gates have seen a peak in recent time, where vast research is dedicated to the design of optical modulators [49], couplers [50], multiplexers [51], and logic gates i.e., NOT [52], OR [53], AND [54] and universal logic gates i.e., NOR [55], NAND [56], XOR [57], XNOR [58] and their usage in the optical integrated circuits. However, no such investigation is performed, using a dual source to implement the all-optical switching action in the 2D PhC structures using the phenomena of GMR with a PhC-cavity in the middle of the PhC-lattice. However, the study in ref. [48] has a close resemblance with the ongoing research, which is compared in the discussion section of the research.
Therefore, this research numerically investigates all-optical switching in the near-infrared region (NIR) for communication systems using low-index contrast dielectric materials. The structure is implemented in the 2D FDTD domain using the phenomenon of interference between GMR modes and index-guided modes inside the slab waveguide. The phenomenon of GMR works by a phase-matching mechanism between the free-space modes in the incident light and the guided modes inside the structure to cause the resonances. The data signal is coupled into the PhC slab waveguide structure using the out-of-plane incidence and it is amplified or de-amplified using an index-guiding source termed the control signal. Additionally, a PhC-cavity is implemented within the middle of the PhC-lattice, which helps to tune the GMR modes and optimize the mechanism of the optical switching by varying its radius ( r c ).
The conceptual diagram of the proposed optical switch design is shown in Figure 1a, presenting an innovative, compact, cost-effective, and easy-to-fabricate device. The device shows good suitability to be used in broad-spectral ranges due to the low absorption of dielectric materials and a stable solid layer design. In contrast to this, semiconductor material-based optical devices [59,60,61,62] have their limitations, such as high material cost and higher absorption in most of the spectral ranges, making them difficult to use and fabricate in densely populated optical integrated circuits. The proposed use of the presented optical switching device in a photonic logic circuit is shown in Figure 1b, requiring rigorous switching and amplification actions. They also find applications in data communication, fiber-optics networks, quantum computing, industrial networks, optical sensors, filters, and medical and measurement technologies.

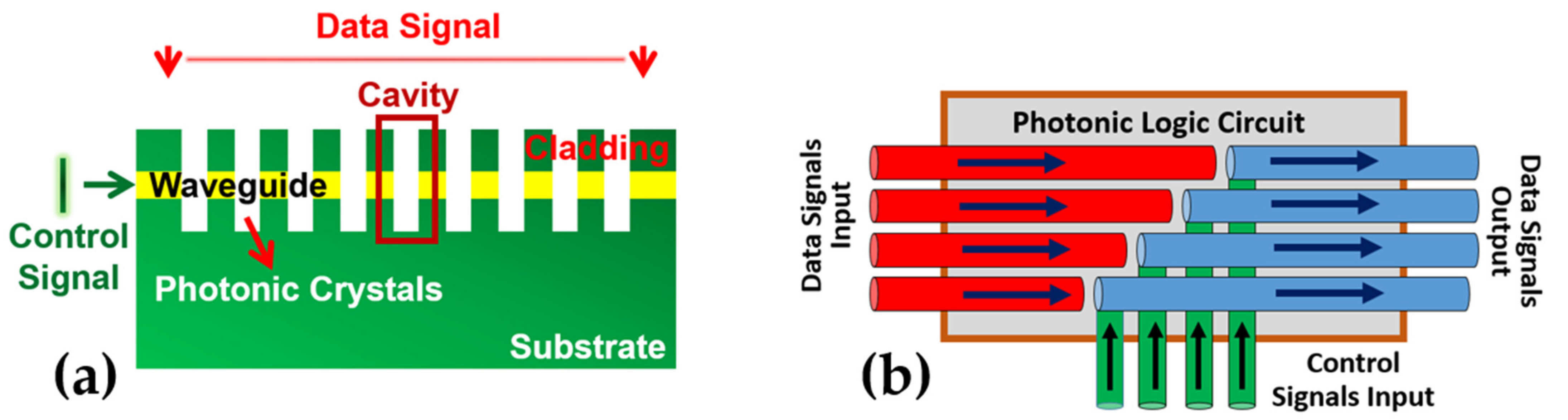
2. Simulation Approach

The design of the optical switch is investigated in 2D simulation using an open-source software platform known as the MIT Electromagnetic Equation Propagation (MEEP) [63], based on the FDTD technique [64]. At the start of the simulation, the structure is converted into a finite arrangement of grids, also known as the YEE grid [65]. The electromagnetic field propagation is calculated via Maxwell’s equations-based algorithm. Moreover, FDTD allows solving a broad range of frequencies using a short Gaussian pulse providing both near-field and far-field results requiring less computational resources and time as compared with the frequency domain [66,67].

3. Designing Parameters

To enable the operation of the device in the NIR communication window around 1.55   μ m , the lattice constant of the device was chosen to be ( a = 1   μ m ) and to make the design scalable to different wavelength ranges, other designing parameters are mentioned in the form of the lattice constant. The optimized values of the structural parameters along with their symbols are given in Table 1, where the depth ( d ) of the PhC-elements and PhC-cavity is kept constant at 1.8   a .
The design of the proposed device is depicted in Figure 2, where the material of the optical waveguide is based on Niobium pentaoxide (Nb2O5), having a refractive index of n w = 2.2 , and it is deposited on a substrate based on Silicon dioxide (SiO2), with a refractive index of n s = 1.5 and a SiO2-based cladding layer on top of the waveguide. The materials and the refractive index values are taken as references from the experimental works presented in [5,19,48].
A Gaussian time profile source is used for the data signal placed at a distance of 2.7 a from the waveguide. While a similar profile source acting as the control signal is coupled into the waveguide from the lateral side of the device, using a user-defined number of frequencies ( n f ) for both sources i.e., n f = 550 , during the calculation. Similarly, the flux-monitoring layers, i.e., the reflection and transmission monitoring layers are placed at a distance of 0.8 a above and below the waveguide. The field decay monitoring point is kept with a user-defined position of 1.2 a to terminate the process and conclude it using the Perfectly Matched Layers (PML) at the boundaries of the structure to absorb the unwanted EM radiations both in x and z directions [67] to save time and computational resources. The PhC-elements used in the structure are selected to be cylindrical-in-shape. However, as the 2D-FDTD domain is used during this study, these PhC-elements appear to be rectangular in a cross-sectional view. Moreover, for good-quality simulation results, the grid size should be smaller than the smallest wavelength in the EM spectrums of both sources. Therefore, this work uses a resolution of 20 for all of the simulations with a smoothing factor of 0.05 , which is lesser than the ω 30 equaling a grid size of 0.052 , ensuring the precision of the results.

4. Results

Different structural parameters were investigated to reach the optimized spectral results for transmission and reflection response of the device and tune them around a resonant wavelength, i.e., 1.55   μ m . The investigated structural parameters include the thickness of the waveguide ( w d ) , the cladding layer, the radius ( r ) and depth ( d ) of the PhC-elements, and the radius of the PhC-cavity ( r c ). Moreover, the spectral response is investigated for a range of values for r c from 0.060 a − 0.350 a . Similarly, the properties of the data signal and control signal are also optimized in terms of resonant wavelength, bandwidth, size, and position.
Initially, the investigation is carried out using just the data signal to get the optimum structural parameters. The spectral parameters such as reflection, linewidth, quality factor, finesse, and FSR obtained for 9 to 15 PhC-periods ( N ) are listed in Table 2 and detailed investigations regarding data signal can be found in previous work of the group [48].
It can be seen from the data trends that when the N is increased, the coupling of energy into the periodic structure is increased and the reflection peaks rise with an overall increase in the value of the Finesse ( F ) and the quality factor. Furthermore, a decrease in the linewidth of the resonant modes occurs, which improves the optical filtering characteristics and selectivity of the structures. Thus, it is preferable to have a high value of N , in the case of the single source, i.e., the data signal. However, having a higher value of N , while using both sources simultaneously (data signal and control signal), reduces the influence of the control signal on the output of the data signal. This is due to the fact that a higher value of N improves the optical filtering characteristics of the structure and increases its energy confinement properties. Moreover, this value of N acts analogous to the depletion region of the electronic transistor, i.e., when the depletion is large enough, it acts as an open switch, applying a base signal; the depletion region narrow-downs and the transistor acts as a closed switch, and, as a result, the value of N is limited to 15 in this research to overcome its adverse effects. Therefore, the unity factor cannot be achieved in the output of the structures, as the propagation losses of the control signal due to gratings remains a common problem and are added to the absorption losses of the materials.

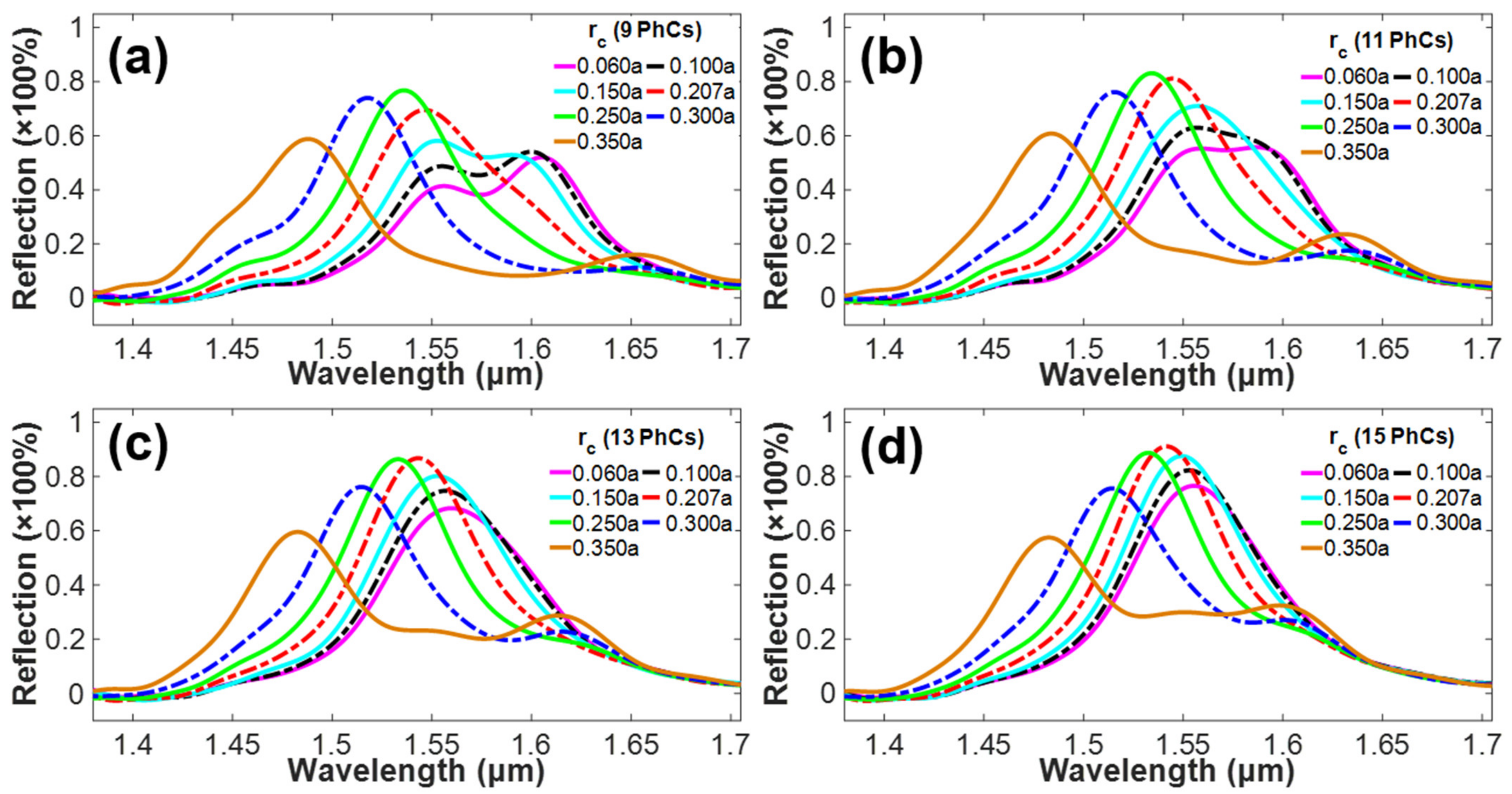
4.1. Effects of Variation in the Radius of the PhC-Cavity Using the Data Signal

To investigate the effects of variation in the r c located in the middle of the PhC-lattice on the quality of the data signal, the values of N is varied from N = 9 ,   11 ,   13 , and 15   . While r c is varied from 0.060 a − 0.0350 a , in all the arrangements for which the reflection spectra are shown in Figure 3.
Varying the r c from 0.060 a − 0.350 a shifts the resonant wavelength from a longer wavelength towards a shorter wavelength and vice versa using the data source. Similarly, besides shifting, the reflection peaks tend to increase from r c = 0.06 a − 0.250 a and decreases onwards from r c = 0.250 a − 0.350 a . This is attributed to a drop in the fill factor resulting in a decrease in the effective refractive index of the waveguide and the coupling of the energy as a whole. Therefore, the quality of the reflection spectra is maximum when r c = 0.250 a in arrangements comprising of the N = 9 and 11 PhC-elements. Similarly, in arrangements comprising of N = 13 and 15 PhC-elements, the quality of the spectra is maximum, when r c equals to the r of the PhC-elements, i.e., r = 0.207 a . Figure 3a depicts the structure where N = 9 PhC-elements with reduced reflection peaks and coupling of energy. Figure 3b imitates structure with N = 11 PhC-elements, representing an increase in the reflection spectra, the coupling of energy and well-defined GMR modes with a decrease in the second-order modes at a longer wavelength. Figure 3c displays a structure comprising of N = 13 PhC-elements, with an overall increase in the peaks of the reflection spectra. Figure 3d shows the arrangement of an N = 15 PhC-elements-based structure, where the reflection peaks are nearer to the unity factor and the guided modes are well-defined. Moreover, in arrangements where N = 9 and 11 , some non-Fano shapes appear at smaller values of the r c   i.e., 0.060a, 0.100a, and 0.150a of the PhC-cavity, which is due to a change in the effective refractive index and reduction in the coupling of energy into the optical waveguide, thus changing the shape of asymmetric Fano modes to more symmetric Lorentz modes [5]. Therefore, the implementation of the PhC-cavity in the middle of the PhC-lattice and variation in its r c , produces profound effects on the output and the resonant wavelength of the structures beneficial in the design of numeral optical devices and integrated circuits.

4.2. Effects of Variation in the Number of PhC-Elements and Radius of PhC-Cavity for Data Signal

Here, we observe the variation in spectral properties of the device for r c in the structures comprising of N = 9 ,   11 ,   13 , and 15 PhC-elements using the data source as shown in Figure 4. Therefore, Figure 4a presents the change in resonant wavelength and reflection peaks, as the value of the N is increased, the peaks of the reflection spectra increase showing an increase in the coupling of energy and well-defined GMR modes into the optical structure and decreases with an increase in the values of r c of the PhC-cavity, presenting overall loss of energy and GMR modes. Figure 4b imitates the change in the linewidth against the variation in the r c of the PhC-cavity, reflecting the highest value of the linewidth in the structure comprising of N = 9 PhC-element showing lower filtering characteristics and coupling of the GMR modes. Similarly, the lowest value of the linewidth is achieved in N = 15 PhC-elements-based arrangement. Congruently, at a value of r c = 0.250 a , the linewidth remains almost similar in all of the structures. Onwards from r c = 0.250 a , the value of the linewidth remains higher in structures comprising a higher value of N in the following sequence, i.e., 15 ,   13 ,   11 , and 9 PhC-elements. Moreover, a non-homogenous behavior is investigated in linewidth of the structures, which is due to a change in the effective refractive index of the optical structure due to the implementation of the PhC-cavity and the changing value of the N   in the PhC-elements. Figure 4c investigates the change in reflection peaks against the r c of the PhC-cavity in all of the four PhC-elements-based structures. Thus, it replicates a drop in the reflection peaks with a reduced coupling of energy as the value of the r c increases, i.e., r c = 0.060 a − 0.350 a . This is because as the value of the r c increases, there is a drop in the fill factor, which in turn results in a drop in the effective refractive index of the waveguide. Additionally, the values of the reflection peaks are almost similar at higher values of r c i.e., 0.300 a and 0.350 a . Figure 4d displays the EM radiations in the structures containing a PhC-cavity of r c = 0.060 a and 0.0350 a based on N = 11 PhC-elements, showing resonant cavity modes.

4.3. Quality Factor Analysis for Variation in the Number of PhC-Elements and Radius of PhC-Cavity for Data Signal

The quality factor is an important aspect of the investigation, which will determine the appropriate structure to achieve a higher value of optical filtering and selectivity based on the value of N and r c of the PhC-cavity. The detailed analysis is presented in Figure 5. Therefore, the quality factor retains a higher value in the arrangement comprising of N = 15 PhC-elements, which is due to the high coupling of energy and enhanced localized-GMR modes and a lower value in an arrangement containing N = 9 PhC-elements due to a decrease in the fill factor and effective refractive index of the optical structure. Moreover, the quality factor increases as the r c of the PhC-cavity is increased from 0.06 a − 0.207 a and decreases onwards from 0.207 a − 0.350 a . Similarly, the r c of the PhC-cavity with the lowest value of quality factor is achieved in r c = 0.06 a , and highest in r c = 0.207 a in structures comprising of N = 11 ,   13 , and 15 PhC-elements and in r c = 0.150 a in N = 9 PhC-elements-based structure.

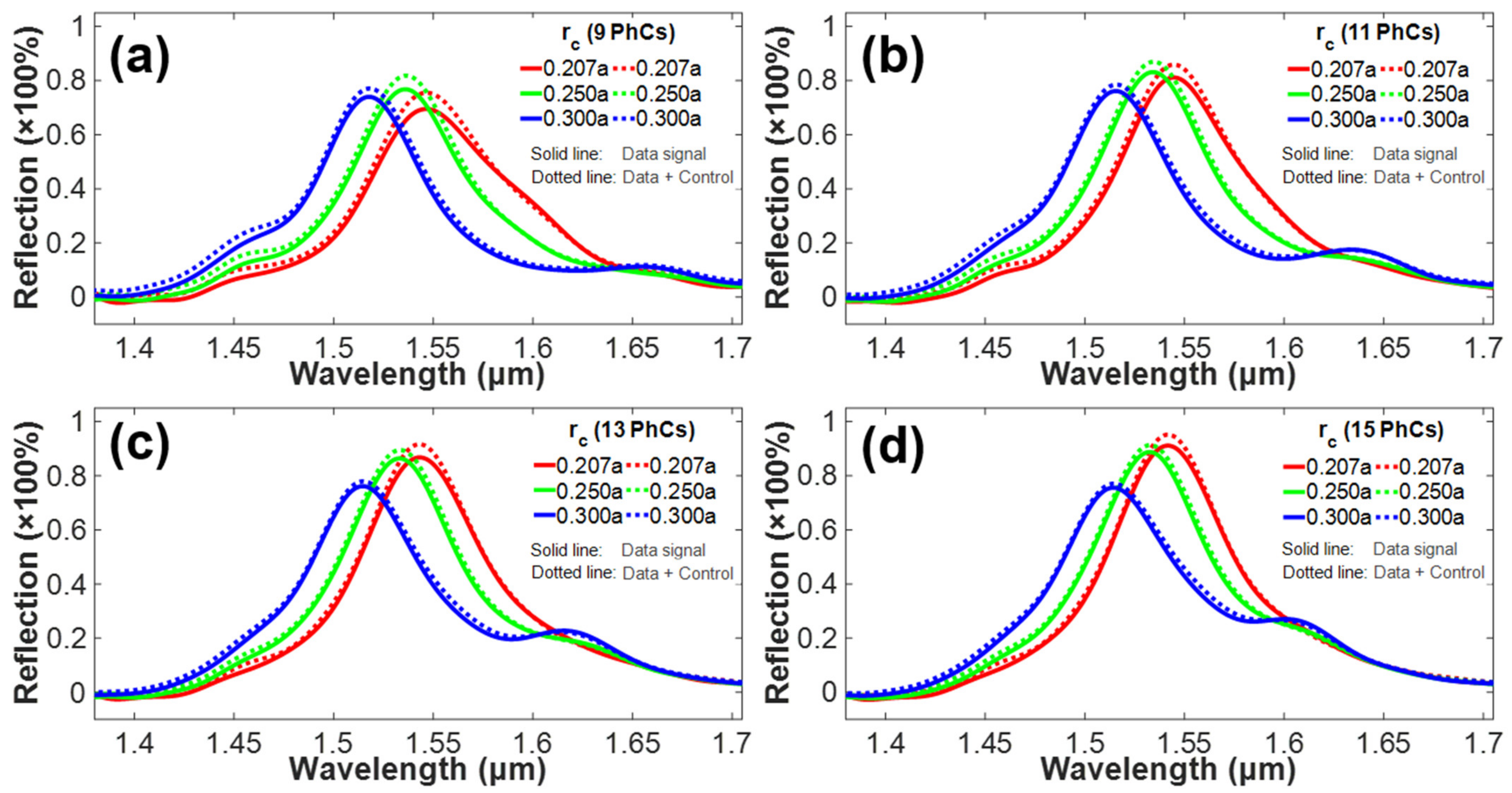
4.4. Investigation of Optical Switching Action in Different PhC-Elements-Based Structures Using Both Signals (Data and Control)

To investigate the phenomena of optical switching, the control signal is implemented along with the data signal. Moreover, to determine the designing parameters in such a way, that the control signal helps to perform the phenomena of the interference and produce an ambient amount of optical amplification. Therefore, Figure 6 visualizes the output reflection spectra of the structures comprising N = 9 ,   11 ,   13 , and 15 PhC-elements, respectively. The output spectra of the data signal are denoted by a (solid) line, while the (dotted) line depicts the spectra when both the data signal and the control signal are turned on simultaneously.
To perform the optical switching, three values of the r c of the PhC-cavity, i.e., 0.207 a ,   0.250 a , and 0.300 a are selected based on their high reflection peaks and coupling of energy in all of the four PhC-elements-based structures. Therefore, the implementation of the control signal and change in the r c amplifies the data signal and shifts the resonant wavelength and GMR modes with the highest peaks of the reflection spectra achieved in a PhC-cavity of r c = 0.250 a in structures of N = 9 and 11 and r c = 0.207 a in structures of N = 13 and 15 PhC-elements, respectively. Figure 6a shows the arrangement of N = 9 PhC-elements, representing a lower value of coupling of energy and wider linewidth with lower quality of the resonant modes. However, with a lower value of N , i.e., 9 PhC-elements, the amount of amplification produced by the control signal is maximum. Figure 6b represents a structure of N = 11 PhC elements, where the value of the reflection peaks and coupling of energy is increased with narrow linewidth as compared with a 9 PhC-elements-based structure with a maximum value of optical amplification produced in r c = 0.207 a and 0.250 a . Figure 6c depicts N = 13 PhC-elements-based structure, with an increase in the value of the reflection peaks, well-defined GMR modes and a narrower linewidth due to more ratio of coupling of the energy into the optical structure. However, the effect produced by the control signal gradually decreased in this case. Figure 6d displays a structure comprising of N = 15 PhC-elements, where the normalized value of the reflection peaks is close to the unity factor. Moreover, this Figure reflects distinct GMR modes and a narrower linewidth, which increases the quality of filtering and selectivity of the optical signals. However, to implement the mechanism of the optical switching, the change produced by the control signal is minimum in this case as compared with all of the above-mentioned structures. Therefore, the arrangements based on N = 9 and 11 PhC-elements with r c = 0.207 a and 0.250 a are appropriate for the design of the optical switch.

4.5. Analysis of Reflection Peaks against Variation in the Number of PhC Elements for Optical Switching Action

To investigate the effects of the control signal on the output of the data signal and make the phenomenon of the optical amplification ambient, the reflection peaks against variation in the r c of the PhC-cavity are shown in Figure 7a–d, using the four PhC-elements-based arrangements. Moreover, three values of the r c are selected, i.e., r c = 0.207 a ,   0.250 a , and 0.300 a represented by different colors, where (solid) circles are used to show the reflection spectra of the data signal, while (hollow) circles are used for the output of the data signal when the control signal is implemented along it. Therefore, comparing the four arrangements, a greater value of optical amplification is achieved in a structure comprising of N = 9 PhC-elements with a value of r c = 0.207 a with a reduced coupling of energy. Whereas, increasing the value of N , the coupling of energy increases, however adversely affects the value of the optical amplification with the lowest value achieved in a structure containing N = 15 PhC-elements and in a PhC-cavity, i.e., r c = 0.300 a   in all of the PhC-elements-based structures.

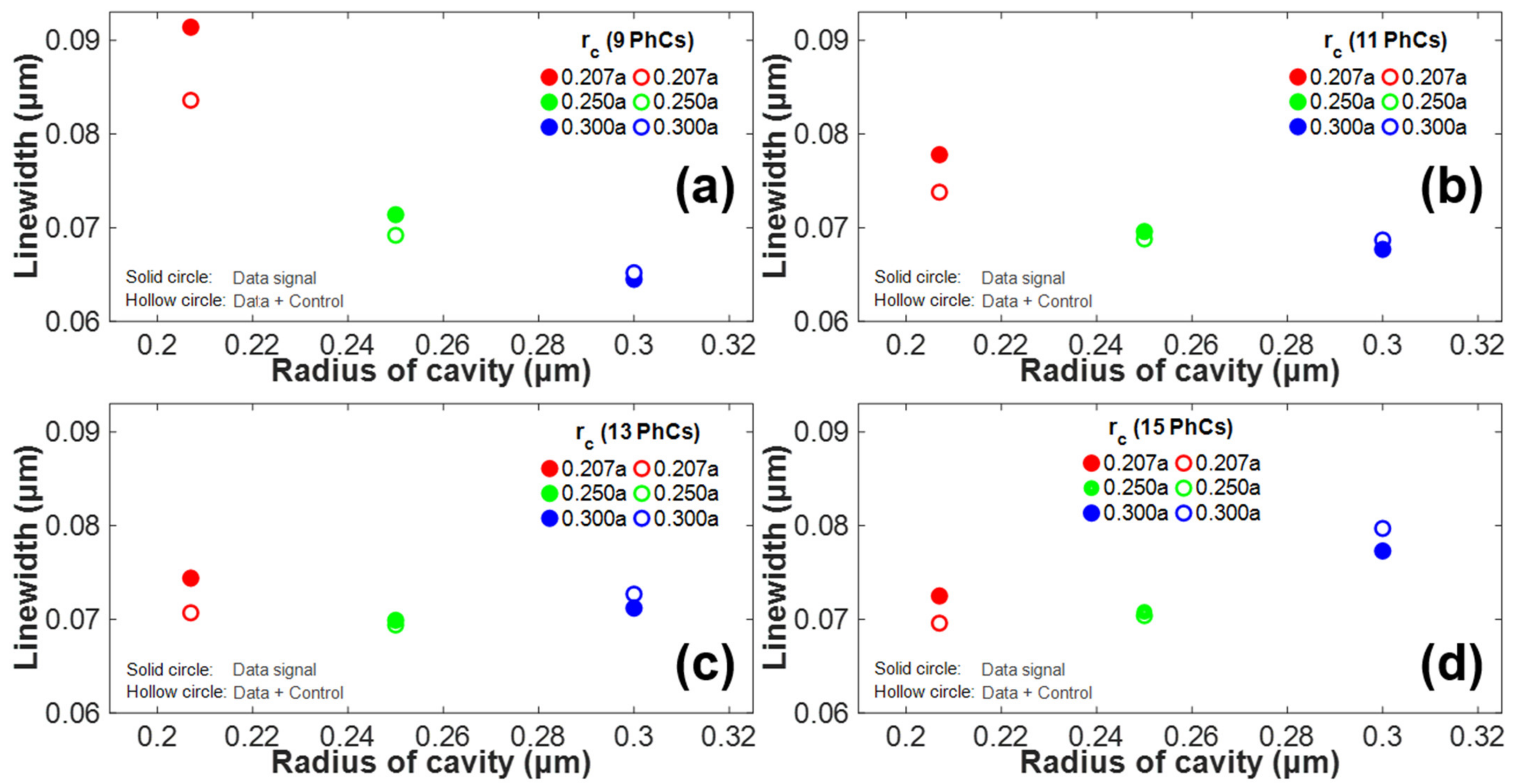
4.6. Analysis of Linewidth against Variation in the Number of PhC Elements for Optical Switching Action

The change in linewidth is observed by varying the value of N in all of the four PhC-elements-based arrangements using the data signal only. The same phenomenon is applied to observe the change in linewidth by applying a control signal along the data signal, as shown in Figure 8a–d. Thus, it can be seen that in the arrangement comprising of N = 9 PhC-elements, the linewidth is wider using a data signal (solid) circle, which in turn decreases the optical filtering by the structure. However, implementing the control signal (hollow) circle narrow downs this linewidth, thus increasing the optical characteristics of the structure with the highest change produced by the control signal in a PhC-cavity of r c = 0.207 a followed by r c = 0.250 a . Correspondingly, increasing the value of N , the linewidth of the structure increases with a data signal. However, by implementing the control signal, the change brought in linewidth decreases as shown. Congruently, as an important aspect of all the PhC-elements-based structures, the linewidth of the structure increases by implementing the control signal in PhC-cavity of r c = 0.300 a . Thus, for better optical characteristics in terms of higher coupling energy, narrow linewidth and resonant modes, a higher value of N , i.e., 15 PhC-elements is better. However, for optical amplification and switching action, a lower value of N , i.e., 9 PhC-elements, is preferred.

4.7. Analysis of Quality Factor against Variation in the Number of PhC Elements and Radius of PhC-Cavity for Optical Switching Action

To better understand the quality factor and its behavior when the control signal (hollow) circle is implemented along the data signal (solid) circle as depicted in Figure 9a–d, investigating the change in quality factor against the variation in the r c of PhC-cavity. Thus, it can be seen that the optical characteristics in terms of filtering and selectivity of the resonant modes increases, when the control signal is implemented. Therefore, the highest quality factor is achieved in an arrangement comprising of N = 15 PhC-elements with r c = 0.207 a and lowest in N = 9 PhC-elements with r c = 0.207 a . Moreover, the maximum change achieved in the quality factor using the control signal is in the arrangement containing N = 9 PhC-elements at r c = 0.207 a , and minimum change is observed in the structure containing N = 15 PhC-elements at r c = 0.300 a .
Table 3 presents a detailed overview of the spectral characteristics in terms of resonant wavelength, reflectance, linewidth, and quality factor of all the investigated structures in this research based on the value of N of the PhC-elements, r c of PhC-cavity, using one source i.e., data signal and then two sources (data + control) simultaneously. Therefore, this table helps to determine a specific structure according to the needs and requirements of the device and its usage in optical integrated circuits.

5. Discussion

A comparative analysis of this work with reported similar ideas is given in this section to investigate the optical amplification and switching mechanism. In ref. [68], different concentrations of the Ar+ ions are used within the PhC-cavity to create dislocation loops, which in turn induces the recombination of the carriers and as a result achieves the qualities of the optical switching. To achieve, a higher optical amplification of the optical signal, a structure based on the properties of the PhCs-line-defect model is investigated in ref. [69]. Therefore, using the injection current, variation in the length of the device, cladding layer, depth of the air-hole and interaction of the incident wave with the PhCs determine the design of the optical amplifier with notable optical gain using a 3-Dimensional (3D) FDTD approach. Another study is given in ref. [70], using 1-Dimensional (1D) PhC acting as the quantum dot (QD) and three-laser sources to achieve specific levels of the transmitted and reflected pulses using a weak-probe source. In ref. [71], two PhC-based line defects are used for input and output signals and graphene rods surrounded by the Si rods, forming the shape of a ring-resonator. Thus, when an input signal is applied, it changes the refractive index of the Si rods, which changes the effective index of the ring resonator and as a result, the phenomenon of optical switching is achieved. Moreover, graphene rods are used to enhance the light-material interaction and in turn decreases the threshold intensity for the switching mechanism. Similarly, using a PhC-based cavity within the middle of the PhC-lattice and a line defect is investigated in ref. [72] for the design of the optical switch, using a diamond-shaped rod across the PhC-cavity. Henceforth, by changing the refractive index across the PhC-cavity, the phenomenon of optical switching is efficiently achieved. Differently, styled PhC-cavities in the form of varying sizes, nano-beams, line defects and the number of the unit-cells are presented in ref. [73].
However, the investigated structure in ref. [48] closely resembles the structural design of this research in terms of the designed model and referenced values for materials of the substrate and waveguide. Similarly, the values of r c = 0.060 a − 0.350 a for the PhC-cavity are equivalent, except the position of the PhC-cavity investigated in ref. [48] is at the start of the PhC-lattice, while it is in the middle of the PhC-lattice in this research. Moreover, helps to tune the GMR modes and enhance the coupling of energy into the optical membrane. Therefore, this investigation presents a compact, easy-to-implement, and fabricate, designing approach, using a control signal to enhance and de-enhance the data signal as opposed to previously presented arrangements, which are bulky, hard to implement and fabricate as a whole.

6. Proposed Fabrication

The fabrication of the PhC-based-structure proposed in this work can be performed using conventional methods widely used in the photonics industry. For the deposition of the SiO2 base, either the Plasma Enhanced Chemical Vapor Deposition (PECVD) or Ion-Beam Sputter Deposition (IBSD) method can be used based on their merits [74,75]. As a next step, the thin layer of Nb2O5 can be deposited over the silica base using IBSD [5] or by employing the spin coating technique (SCT) [76], that results in a uniform layering of the material with lesser physical defects. As a final stage, the holes to form PhCs can be milled by using focused ion-beam (FIB) technology [77,78,79]. FIB is a tried and tested technique in carving PhC holes in 2D and 3D structures and is precise to the nanometer scale [80]. Moreover, in refs. [66,67], the structure comprising the PhC-based-waveguide slab is already fabricated and used in the design of optical filtering and sensing applications. 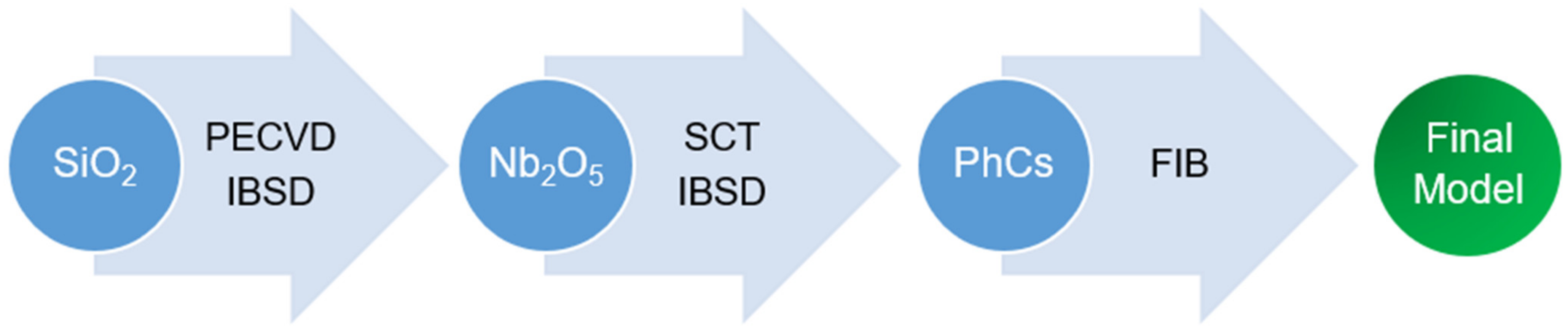Figure 10 illustrates the stepwise cycle of the proposed fabrication.

7. Conclusions

In this paper, a compact design of the optical switch using the GMR phenomenon is investigated using two light sources termed data signal and control signal. Moreover, the data signal is coupled into the optical waveguide using an out-of-plane GMR mechanism, while the control signal is index-guided into the structure, helping in the amplification of the output of the data signal to achieve the effects of the optical switching. Similarly, the number of the PhC-elements in the structure is varied with a change in the radius of the PhC-cavity, to optimize the spectral properties of the data signal and optical switching. The number of the PhC-elements is varied from 9 to 1 5 , with a change in the radius of PhC-cavity from 0.207 a to 0.300 a to tune the GMR modes and its optical filtering characteristics in terms of the resonant wavelength, reflection peaks, linewidth, and quality factor of the data signal and then along the control signal simultaneously in the output spectra. Therefore, a PhC-cavity of radius 0.207 a and 0.250 a provided the best values of amplification in all of the PhC-elements-based structures. However, it is observed that a larger number of PhC-elements in the structure, i.e., 13 and 15 , yield a higher percentage of reflection peaks, coupling of energy, narrow linewidth, and higher quality factor but lower switching effects. While a lesser number of the PhC-elements i.e., 9 and 11 , produces less pronounced reflection peaks, wider linewidth, and a moderate quality factor, however, better optical amplification and switching mechanism can be well observed. Therefore, the structure comprising 11 PhC-elements with a radius of PhC-cavity as 0.207 a and 0.250 a is selected for the design of the optical switch. In terms of optical switching, a maximum amplification of 5 – 7 % with a 0.011   μ m shift in resonant wavelength and a quality factor of 12.64 is achieved. Therefore, the proposed device is suitable to be used in all types of optical amplification and switching scenarios, such as in optical sensors, filters, logic gates, and integrated circuits.

Author Contributions

Conceptualization, A.U.R., Y.K., M.I. and M.A.B.; methodology, A.U.R., Y.K. and M.A.B.; software, A.U.R., Y.K. and M.I.; validation, A.U.R., Y.K., M.I. and M.A.B.; formal analysis, A.U.R., Y.K., M.I. and M.A.B.; investigation, A.U.R., Y.K., M.I. and M.A.B.; resources, A.U.R., Y.K. and M.A.B.; data curation, A.U.R., Y.K. and M.A.B.; writing—original draft preparation, A.U.R., Y.K. and M.I.; writing—review and editing, A.U.R., Y.K., M.I. and M.A.B.; visualization, A.U.R., Y.K. and M.A.B.; supervision, Y.K. and M.A.B.; project administration, A.U.R., Y.K. and M.A.B.; funding acquisition, Y.K. and M.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to pay gratitude to Nanophotonics Research Group (BUITEMS), Quetta, and Parveen Ghoutie for their support and appreciation.

Conflicts of Interest

The authors declare no conflict of interest and agreed to the current version of the manuscript.

References

  1. Yu, T.-P.; Lee, Y.-L.; Li, Y.-W.; Mao, S.-W. The study of cooling mechanism design for high-power communication module with experimental verification. Appl. Sci. 2021, 11, 5188. [Google Scholar] [CrossRef]
  2. Miller, D.A.B. Are optical transistors the logical next step? Nat. Photonics 2010, 4, 3–5. [Google Scholar] [CrossRef]
  3. Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Advancement in silicon integrated photonics technologies for sensing applications in near-infrared and mid-infrared region: A review. Photonics 2022, 9, 331. [Google Scholar] [CrossRef]
  4. Mohebzadeh-Bahabady, A.; Olyaee, S. All-Optical NOT and XOR Logic gates using photonic crystal nano-resonator and based on an interference effect. IET Optoelectron. 2018, 12, 191–195. [Google Scholar] [CrossRef]
  5. Khan, Y.; Rehman, A.U.; Batool, B.A.; Noor, M.; Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Fabrication and investigation of spectral properties of a dielectric slab waveguide photonic crystal based fano-filter. Crystals 2022, 12, 226. [Google Scholar] [CrossRef]
  6. Shen, T.-Z.; Hong, S.-H.; Song, J.-K. Electro-optical switching of graphene oxide liquid crystals with an extremely large kerr coefficient. Nat. Mater. 2014, 13, 394–399. [Google Scholar] [CrossRef]
  7. Decleer, P.; Van Londersele, A.; Rogier, H.; Ginste, D.V. An alternating-direction hybrid implicit-explicit finite-difference time-domain method for the schrödinger equation. J. Comput. Appl. Math. 2022, 403, 113881. [Google Scholar] [CrossRef]
  8. Guerra, G.; Mousavi, S.M.A.; Taranta, A.; Fokoua, E.N.; Santagius, M. Unified coupled-mode theory for geometric and material perturbations in optical waveguides. J. Light Technol. 2022, 40, 4714–4727. [Google Scholar] [CrossRef]
  9. Dong, M.; Chen, L.; Jiang, L.; Li, P.; Bagci, H. Explicit time-domain finite-element boundary integral method for analysis of electromagnetic scattering. IEEE Trans. Antennas Propag. 2022, 70, 6089–6094. [Google Scholar] [CrossRef]
  10. Goswami, K.; Mondal, H.; Sen, M. Optimized design of multiple bends for maximum power transfer in optical waveguide. Optik 2022, 265, 169448. [Google Scholar] [CrossRef]
  11. Li, B.; Sun, H.; Zhang, H.; Li, Y.; Zang, J.; Cao, X.; Zhu, X.; Zhao, X.; Zhang, Z. Refractive index sensor based on the fano resonance in metal–insulator–metal waveguides coupled with a whistle-shaped Cavity. Micromachines 2022, 13, 1592. [Google Scholar] [CrossRef]
  12. Bass, S.F.; Palmer, A.M.; Schab, K.R.; Kerby-Patel, K.C.; Ruyle, J.E. Conversion matrix method of moments for time-varying electromagnetic analysis. IEEE Trans. Antennas Propag. 2022, 70, 6763–6774. [Google Scholar] [CrossRef]
  13. Xu, J.; Mai, W.; Werner, D.H. Generalized Temporal Transfer Matrix Method: A systematic approach to solving electromagnetic wave scattering in temporally stratified structures. Nanophotonics 2022, 11, 1309–1320. [Google Scholar] [CrossRef]
  14. Mastorakis, E.; Papakanellos, P.J.; Anastassiu, H.T.; Tsitsas, N.L. Analysis of electromagnetic scattering from large arrays of cylinders via a hybrid of the method of auxiliary sources (MAS) with the fast multipole method (FMM). Mathematics 2022, 10, 3211. [Google Scholar] [CrossRef]
  15. Han, J.; Wu, X.; Ge, X.; Xie, Y.; Song, G.; Liu, L.; Yi, Y. Highly sensitive liquid m-z waveguide sensor based on polymer suspended slot waveguide structure. Polymers 2022, 14, 3967. [Google Scholar] [CrossRef]
  16. Bhandari, B.; Lee, S.S. Reconfigurable fiber-to-waveguide coupling module enabled by phase-change material incorporated switchable directional couplers. Nat. Sci. Rep. 2022, 12, 1–10. [Google Scholar] [CrossRef]
  17. Asano, T.; Noda, S. Photonic crystal devices in silicon photonics. Proc. IEEE 2018, 106, 2183–2195. [Google Scholar] [CrossRef]
  18. Vigneron, J.P.; Simonis, P. Natural photonic crystals. Phys. B 2012, 407, 4032–4036. [Google Scholar] [CrossRef]
  19. Ahmed, U.; Khan, Y.; Ehsan, M.K.; Amirzada, M.R.; Ullah, N.; Khatri, A.R.; Ur Rehman, A.; Butt, M.A. Investigation of spectral properties of dbr-based photonic crystal structure for optical filter application. Crystals 2022, 12, 409. [Google Scholar] [CrossRef]
  20. Yang, H.; Kuan, Y.; Xiang, T.; Zhu, Y.; Cai, X.; Liu, L. Broadband polarization-insensitive optical switch on silicon-on-insulator platform. Opt. Express 2018, 26, 14340-5. [Google Scholar] [CrossRef]
  21. Ouahab, I.; Naoum, R. A novel all optical 4×2 encoder switch based on photonic crystal ring resonators. Optik 2016, 127, 7835–7841. [Google Scholar] [CrossRef]
  22. Yanik, M.F.; Fan, S. All-optical transistor action with bistable switching in a photonic crystal cross-waveguide geometry. Opt. Lett. 2003, 28, 2506–2508. [Google Scholar] [CrossRef] [PubMed]
  23. Khani, S.; Danaie, M.; Rezaei, P. Compact and low-oower all-optical surface plasmon switches with isolated pump and data waveguides and a rectangular cavity containing nano-silver strips. Superlattices Microstruct. 2020, 141, 106481. [Google Scholar] [CrossRef]
  24. Nguyen, H.A.; Grange, T.; Malik, N.S.; Dupuy, E.; Tumanov, D.; de Assis, P.L.; Yeo, I.; Fratini, F.; Gregersen, N.; Auffèves, A.; et al. Ultra-Low Power Optical Transistor using a Single Quantum Dot Embedded in a Photonic Wire. In Proceedings of the Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 25–29 June 2017. [Google Scholar]
  25. Ma, L.L.; Li, C.; Sun, L.; Song, Z.; Lu, Y.; Li, B. Submicrosecond electro-optical switching of one-dimensional soft photonic crystals. Photonics Res. 2022, 10, 786–792. [Google Scholar] [CrossRef]
  26. Brunetti, G.; Marocco, G.; Di Benedetto, A.; Giorgio, A.; Armenise, M.N.; Ciminelli, C. Design of a large bandwidth 2 × 2 interferometric switching cell based on a sub-wavelength grating. J. Opt. 2021, 23, 085801. [Google Scholar] [CrossRef]
  27. Huang, Y.; Ho, S.-T. Photonic Transistors based on Gain and Absorption Manipulation of Optical Interference. In Proceedings of the IEEE: Photonics in Switching, San Francisco, CA, USA, 19–22 August 2007. [Google Scholar]
  28. Afonina, S.; Maslennikov, E.D.; Zabotnov, S.V.; Golovan, L.A. All-Optical Switching in Photonic Crystals Based on Porous Silicon. In Proceedings of the SPIE: Photonic Crystal Materials and Devices IX, Brussels, Belgium, 14 May 2010. [Google Scholar]
  29. Wang, H.Z.; Zhou, W.M.; Zheng, J.P. A 2D rods-in-air square-lattice photonic crystal optical switch. Optik 2010, 121, 1988–1993. [Google Scholar] [CrossRef]
  30. Kang, X.-B.; Li, H.-D.; Wien, L.-W. A scheme for high-quality nonlinear all-optical switches. Opt. Int. J. Light Electron Opt. 2017, 134, 21–27. [Google Scholar] [CrossRef]
  31. Rao, W.; Song, Y.; Liu, M.; Jin, C. All-optical switch based on photonic crystal microcavity with multi-resonant modes. Optik 2010, 121, 1934–1936. [Google Scholar] [CrossRef]
  32. Cuesta-Soto, F.; Martínez, A.; Garcia, J.; Ramos, F.; Sanchis, P.; Blasco, J.; Martí, J. All-optical switching structure based on a photonic crystal directional coupler. Opt. Express 2004, 12, 1–7. [Google Scholar] [CrossRef]
  33. Locatelli, A.; Modotto, D.; Paloschi, D.; De Angelis, C. All optical switching in ultrashort photonic crystal couplers. Opt. Commun. 2004, 237, 97–102. [Google Scholar] [CrossRef]
  34. Parra, J.; Navarro-Arenas, J.; Kovylina, M.; Sanchis, P. Impact of GST thickness on GST-loaded silicon waveguides for optimal optical switching. Sci. Rep. 2022, 12, 1–9. [Google Scholar] [CrossRef]
  35. Van Campenhout, J.; Green, W.M.; Assefa, S.; Vlasov, Y.A. Low-power, 2×2 silicon electro-optic switch with 110-nm bandwidth for broadband reconfigurable optical networks. Opt. Express 2009, 17, 24020–24029. [Google Scholar] [CrossRef]
  36. Goodarzi, A.; Ghanaatshoar, M. Coherent all-optical transistor based on frustrated total internal reflection. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
  37. Dhama, R.; Panahpour, A.; Pihlava, T.; Ghindani, D.; Caglayan, H. All-optical switching based on plasmon-induced enhancement of index of refraction. Nat. Commun. 2022, 13, 1–9. [Google Scholar] [CrossRef]
  38. Wang, T.; Tang, J.; Chen, M.; Xiong, J.; Wang, H.; Xu, J.; Yuan, L. Ultrafast metamaterial all-optical switching based on coherent modulation. Opt. Express 2022, 30, 9284–9297. [Google Scholar] [CrossRef]
  39. Takiguchi, M.; Takemura, N.; Tateno, K.; Nozaki, K.; Sasaki, S.; Sergent, S.; Notomi, M. All-Optical Switching Using a III-V Nanowire Integrated Si Photonic Crystal Nanocavity. In Proceedings of the IEEE Photonics Conference (IPC), San Antonio, TX, USA, 29 September–3 October 2019. [Google Scholar]
  40. Krishnamurthy, V.; Chen, Y.; Ho, S.-T. Photonic transistor design principles for switching gain ≥2. J. Light Technol. 2013, 31, 2086–2098. [Google Scholar] [CrossRef]
  41. Mishra, V.; Haldar, R.; Mondal, P.; Varshney, S.K. Efficient all-optical transistor action in shortlength multimode optical fibers. J. Light Technol. 2018, 36, 2582–2588. [Google Scholar] [CrossRef]
  42. Hui, Z.; Bu, X.; Wang, Y.; Han, D.; Gong, J.; Li, L.; Yan, S. Bi2O2Te nanosheets saturable absorber-based passive mode-locked fiber laser: From soliton molecules to harmonic soliton. Adv. Opt. Mater. 2022, 10, 2201812. [Google Scholar] [CrossRef]
  43. Lin, Y.; Huang, Z.; Huang, Q.; Dai, L.; Song, Q.; Yan, Z.; Zhang, L. Pump-controlled wavelength switchable dissipative soliton mode-locked yb-doped fiber laser using a 45° tilted fiber grating. Opt. Int. J. Light Electron Opt. 2020, 222, 1–6. [Google Scholar] [CrossRef]
  44. Hwang, J.; Pototschnig, M.; Lettow, R.; Zumofen, G.; Renn, A.; Götzinger, S.; Sandoghdar, V. A single-molecule optical transistor. Nat. Lett. 2009, 460, 76–80. [Google Scholar] [CrossRef]
  45. Winoto, A.; Qiu, J.; Wu, D.; Feng, M. Transistor laser–integrated photonics for optical logic. IEEE Nanotechnology. Mag. 2019, 13, 27–34. [Google Scholar] [CrossRef]
  46. Ng, W.H.; Podoliak, N.; Horak, P.; Wu, J.; Liu, H.; Stewart, W.J.; Kenyon, A.J. Design and fabrication of suspended indium phosphide waveguides for mems-actuated optical buffering. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 1–7. [Google Scholar] [CrossRef]
  47. Rehman, A.U.; Khan, Y.; Fomchenkov, S.; Butt, M.A. Investigation of Optical Amplification Action in Dielectric Photonic Crystals Cavity Based Structure. In Proceedings of the IEEE: VIII International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 23–27 May 2022. [Google Scholar]
  48. Rehman, A.U.; Khan, Y.; Irfan, M.; Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. A novel design of optical switch based on guided mode resonances in dielectric photonic crystal structures. Photonics 2022, 9, 580. [Google Scholar] [CrossRef]
  49. Zhang, J.; Pan, B.; Liu, W.; Dai, D.; Shi, Y. Ultra-compact electro-optic modulator based on etchless lithium niobate photonic crystal nanobeam cavity. Opt. Express 2022, 30, 20839–20846. [Google Scholar] [CrossRef] [PubMed]
  50. Gayathri, M.; Alagesan, T.; Yogesh, N. Cavity confinement in defect-based honeycomb photonic crystals and the design of waveguide–cavity fano-coupler for dielectric loss sensing. Opt. Commun. 2022, 508, 127757. [Google Scholar] [CrossRef]
  51. Jile, H. Application of nonlinear ring resonators for realizing all-optical digital multiplexers. Photonics Nanostructures Fundam. Appl. 2021, 45, 100920. [Google Scholar] [CrossRef]
  52. Kumar, S.; Sen, M. Integrable all-optical not gate using nonlinear photonic crystal mzi for photonic integrated circuit. J. Opt. Soc. Am. B 2022, 37, 359–369. [Google Scholar] [CrossRef]
  53. Kabilan, A.P.; Christina, X.S.; Caroline, P.E. Photonic Crystal Based All Optical OR and XO Logic Gates. In Proceedings of the IEEE: Second International Conference on Computing, Communication and Networking Technologies, Karur, India, 29–31 July 2010. [Google Scholar]
  54. Rani, P.; Kalra, Y.; Sinha, R.K. Realization of AND gate in y shaped photonic crystal waveguide. Opt. Commun. 2013, 298–299, 227–231. [Google Scholar] [CrossRef]
  55. Moradi, M.; Danaie, M.; Orouji, A.A. All-optical nor and not logic gates based on ring resonator-based plasmonic nanostructures. Optik 2022, 258, 168905. [Google Scholar] [CrossRef]
  56. Heydarian, K.; Nosratpour, A.; Razaghi, M. Design and analysis of an all-optical nand logic gate using a photonic crystal semiconductor optical amplifier based on the mach–zehnder optical amplifier. Photonics Nanostructures Fundam. Appl. 2022, 49, 100992. [Google Scholar] [CrossRef]
  57. Heydarian, K.; Nosratpour, A.; Razaghi, M. design and simulation of the all-optical xor logic gate by xpm mechanism using photonic crystal semiconductor optical amplifier based on mach–zehnder interferometer. J. Nonlinear Opt. Phys. Mater. 2022, 31, 2250013. [Google Scholar] [CrossRef]
  58. Jasim, M.A.; Aldalbahi, A. design of XOR photonic gate using highly nonlinear fiber. Electronics 2019, 8, 215. [Google Scholar] [CrossRef] [Green Version]
  59. Georgel, R.; Grygoryev, K.; Sorensen, S.; Lu, H.; Andersson-Engels, S.; Burke, R.; O’Hare, D. Silicon Photomultiplier—A high dynamic range, high sensitivity sensor for bio-photonics applications. Biosensors 2022, 12, 793. [Google Scholar] [CrossRef]
  60. Peng, Z.; Feng, J.; Yuan, H.; Cheng, W.; Wang, Y.; Ren, X.; Cheng, H.; Zang, S.; Shuai, Y.; Liu, H.; et al. A non-volatile tunable ultra-compact silicon photonic logic gate. Nanomaterials 2022, 12, 1121. [Google Scholar] [CrossRef]
  61. Ha, Y.; Guo, Y.; Pu, M.; Xu, M.; Li, X.; Ma, X.; Zou, F.; Luo, X. Meta-optics-empowered switchable integrated mode converter based on the adjoint method. Nanomaterials 2022, 12, 3395. [Google Scholar] [CrossRef]
  62. Parandin, F.; Olyaee, S.; Kamarian, R.; Jomour, M. Design and simulation of linear all-optical comparator based on square-lattice photonic crystals. Photonics 2022, 9, 459. [Google Scholar] [CrossRef]
  63. MEEP Documentation MkDocs. Available online: https://meep.readthedocs.io/en/latest/ (accessed on 1 October 2022).
  64. Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. A flexible free-software package for electromagnetic simulations by the fdtd method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
  65. Yee, K.S. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
  66. Khan, Y.; Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. numerical study of fabrication-related effects of the structural-profile on the performance of a dielectric photonic crystal-based fluid sensor. Materials 2022, 15, 3277. [Google Scholar] [CrossRef]
  67. Khan, Y. Design and Numerical Simulation of Dielectric Photonic Crystal Devices and Investigation of an Optical Characterization Method. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2017. [Google Scholar]
  68. Tanabe, T.; Nishiguchi, K.; Shinya, A.; Kuramochi, E.; Inokawa, H.; Notomi, M.; Itabashi, S. All-optical switching using ion-implanted silicon photonic crystal nanocavities. Appl. Phys. Lett. 2007, 90, 031115. [Google Scholar] [CrossRef]
  69. Nosratpour, A.; Razagh, M.; Darvish, G. Computational study of pulse propagation in photonic crystal semiconductor optical amplifier. J. Nanophotonics 2018, 12, 036015. [Google Scholar]
  70. Sahrai, M.; Abbasabadi, M. All-optical switch based on doped graphene quantum dots in a defect layer of a one-dimensional photonic crystal. Appl. Opt. 2017, 57, 521–526. [Google Scholar] [CrossRef] [PubMed]
  71. Jalali Azizpour, M.R.; Soroosh, M.; Dalvand, N.; Seifi-Kavian, Y. All-optical ultra-fast graphene-photonic crystal switch. Crystals 2019, 9, 461. [Google Scholar] [CrossRef] [Green Version]
  72. Rebhi, S.; Najjar, M. Hourglass nonlinear photonic crystal cavity for ultra-fast all-optical switching. Optik 2019, 180, 858–865. [Google Scholar] [CrossRef]
  73. Saldutti, M.; Xiong, M.; Dimopoulos, E.; Yu, Y.; Gioannini, M.; Mørk, J. Modal properties of photonic crystal cavities and applications to lasers. Nanomaterials 2021, 11, 3030. [Google Scholar] [CrossRef]
  74. Okada, H.; Baba, M.; Furukawa, M.; Yamane, K.; Sekiguchi, H.; Wakahara, A. Formation of SiO2 film by chemical vapor deposition enhanced by atomic species extracted from a surface-wave generated plasma. AIP Conf. Proc. 2017, 1807, 020006. [Google Scholar]
  75. Nomura, K.; Ogawa, H. SiO2 thin films deposited by reactive ion-beam sputtering under ultraviolet light irradiation. J. Appl. Phys. 1992, 71, 1469. [Google Scholar] [CrossRef]
  76. Abood, M.K.; Wahid, M.H.A.; Salim, E.T.; Saimon, J.A. Niobium Pentoxide thin films employ simple colloidal suspension at low preparation temperature. In Proceedings of the EPJ Web of Conferences, Dubna, Russia, 3–7 July 2017. [Google Scholar]
  77. Micco, A.; Ricciardi, A.; Pisco, M.; La Ferrara, V.; Cusano, A. Optical fiber tip templating using direct focused ion beam milling. Nat. Sci. Rep. 2015, 5, 1–10. [Google Scholar] [CrossRef] [Green Version]
  78. Li, W.; van Baren, J.; Berges, A.; Bekyarova, E.; Lui, C.H.; Bardeen, C.J. Organic Microcrystals Using Focused Ion Beam Milling. Cryst. Growth Des. 2020, 20, 1583–1589. [Google Scholar] [CrossRef]
  79. Juodkazis, S.; Rosa, L.; Bauerdick, S.; Peto, L.; El-Ganainy, R.; John, S. Sculpturing of photonic crystals by ion beam lithography: Towards complete photonic bandgap at visible wavelengths. Opt. Express 2011, 19, 5802–5810. [Google Scholar] [CrossRef]
  80. Manoccio, M.; Esposito, M.; Passaseo, A.; Cuscunà, M.; Tasco, V. Focused ion beam processing for 3D chiral photonics nanostructures. Micromachines 2021, 12, 6. [Google Scholar] [CrossRef]
Photonics 10 00013 g001 550
Figure 1. (a) Design of the proposed optical switching device. (b) Implementation of the proposed optical switching mechanism in photonic logic circuits.
Figure 1. (a) Design of the proposed optical switching device. (b) Implementation of the proposed optical switching mechanism in photonic logic circuits.
Photonics 10 00013 g001
Photonics 10 00013 g002 550
Figure 2. Numerical design of the optical switch showing the details of the structural and simulation parameters.
Figure 2. Numerical design of the optical switch showing the details of the structural and simulation parameters.
Photonics 10 00013 g002
Photonics 10 00013 g003 550
Figure 3. Reflection spectra of the structures based on the number of the PhC-elements with a varying radius of PhC-cavity. (a) 9 PhC-elements. (b) 11 PhC-elements. (c) 13 PhC-elements. (d) 15 PhC-elements.
Figure 3. Reflection spectra of the structures based on the number of the PhC-elements with a varying radius of PhC-cavity. (a) 9 PhC-elements. (b) 11 PhC-elements. (c) 13 PhC-elements. (d) 15 PhC-elements.
Photonics 10 00013 g003
Photonics 10 00013 g004 550
Figure 4. Spectral analysis of the PhC-elements-based structures and EM field distribution based on the number of the PhC-elements (a) Reflection vs wavelength (b) Linewidth vs radius of PhC-cavity (c) Reflection vs radius of PhC-cavity (d) EM field distribution.
Figure 4. Spectral analysis of the PhC-elements-based structures and EM field distribution based on the number of the PhC-elements (a) Reflection vs wavelength (b) Linewidth vs radius of PhC-cavity (c) Reflection vs radius of PhC-cavity (d) EM field distribution.
Photonics 10 00013 g004
Photonics 10 00013 g005 550
Figure 5. Analysis of quality factor vs change in radius of the PhC-cavity based on the number of PhC-elements.
Figure 5. Analysis of quality factor vs change in radius of the PhC-cavity based on the number of PhC-elements.
Photonics 10 00013 g005
Photonics 10 00013 g006 550
Figure 6. Output reflection spectra signifying the phenomenon of the optical amplification and switching using the control signal along the data signal (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Figure 6. Output reflection spectra signifying the phenomenon of the optical amplification and switching using the control signal along the data signal (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Photonics 10 00013 g006
Photonics 10 00013 g007 550
Figure 7. Spectral analysis of the effects of the optical amplification and switching mechanism in terms of reflection peaks vs radius of PhC-cavity (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Figure 7. Spectral analysis of the effects of the optical amplification and switching mechanism in terms of reflection peaks vs radius of PhC-cavity (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Photonics 10 00013 g007
Photonics 10 00013 g008 550
Figure 8. The analysis of the effects of the optical amplification and switching mechanism on the linewidth of the PhC-elements-based structures (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Figure 8. The analysis of the effects of the optical amplification and switching mechanism on the linewidth of the PhC-elements-based structures (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Photonics 10 00013 g008
Photonics 10 00013 g009 550
Figure 9. Spectral analysis of the effects of the optical amplification and switching mechanism in terms of a quality factor vs radius of PhC-cavity (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Figure 9. Spectral analysis of the effects of the optical amplification and switching mechanism in terms of a quality factor vs radius of PhC-cavity (a) 9 PhC-elements (b) 11 PhC-elements (c) 13 PhC-elements (d) 15 PhC-elements.
Photonics 10 00013 g009
Photonics 10 00013 g010 550
Figure 10. A stepwise cycle of the proposed fabrication.
Figure 10. A stepwise cycle of the proposed fabrication.
Photonics 10 00013 g010
Table
Table 1. List of the design parameters used in the proposed optical switching device.
Table 1. List of the design parameters used in the proposed optical switching device.
ParametersSymbolValue
Lattice constanta1 μ m
Radius of PhC-elementsr0.207a
Radius of PhC-cavityrc0.060a–0.350a
Wavelength-Varying
Resonant wavelength-1.55 μ m
Refractive index of the substrate n s 1.5
Refractive index of the waveguide n w 2.2
Thickness of waveguide w d 0.44a
Thickness of cladding-0.68a
Thickness of PML PML3.0a
Padding on either sidePadding4.0a
Field decay monitoring point value- 1   e − 3
Table
Table 2. Details of the resonance characteristics for data signal for the different number of PhC elements.
Table 2. Details of the resonance characteristics for data signal for the different number of PhC elements.
Number of PhCs-PeriodsSingle Source (Data Signal)
Reflectance %FinesseLinewidth (µm)FSR (µm)Quality Factor
09 PhC-elements606.080.0730.4447.6
11 PhC-elements708.7630.070.61310.43
13 PhC-elements719.1290.0660.60311.66
15 PhC-elements7913.2980.0610.81112.57
Table
Table 3. Presenting detailed change in terms of resonant wavelength, reflectance, linewidth, and quality factor using one source (data) and then dual sources (data + control) to acknowledge the phenomenon of optical switching.
Table 3. Presenting detailed change in terms of resonant wavelength, reflectance, linewidth, and quality factor using one source (data) and then dual sources (data + control) to acknowledge the phenomenon of optical switching.
Radius of PhC-cavity
(9 PhCs)		Resonant wavelength (μm)Reflectance
(×100%)		Linewidth
(μm)		Quality factor
-
One sourceDual sourcesOne sourceDual sourcesOne sourceDual sourcesOne sourceDual sources
0.207 (μm)1.5461.5460.69500.75500.09140.08367.6009.030
0.250 (μm)1.5361.5360.76790.81830.07140.069210.7511.83
0.350 (μm)1.5171.5180.73980.77080.06450.065211.4711.93
Radius of PhC-cavity
(11 PhCs)		Resonant wavelength (μm)Reflectance
(×100%)		Linewidth
(μm)		Quality factor
-
One sourceDual sourcesOne sourceDual sourcesOne sourceDual sourcesOne sourceDual sources
0.207 (μm)1.5451.5450.81140.85900.07780.073810.4311.64
0.250 (μm)1.5341.5340.83140.86950.06960.068811.9512.64
0.350 (μm)1.5161.5160.76140.78510.06770.068711.2511.43
Radius of PhC-cavity
(13 PhCs)		Resonant wavelength (μm)Reflectance
(×100%)		Linewidth
(μm)		Quality factor
-
One sourceDual sourcesOne sourceDual sourcesOne sourceDual sourcesOne sourceDual sources
0.207 (μm)1.5431.5430.86780.91650.07440.070711.6612.96
0.250 (μm)1.5331.5330.86390.89490.06990.069412.3612.90
0.350 (μm)1.5151.5150.76140.77940.07120.072710.7010.72
Radius of PhC-cavity
(15 PhCs)		Resonant wavelength (μm)Reflectance
(×100%)		Linewidth
(μm)		Quality factor
-
One sourceDual sourcesOne sourceDual sourcesOne sourceDual sourcesOne sourceDual sources
0.207 (μm)1.5421.5420.91120.95180.07250.069612.5713.68
0.250 (μm)1.5331.5330.88760.91310.07080.070412.5412.97
0.350 (μm)1.5141.5150.75580.77080.07730.07979.8009.700
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rehman, A.U.; Khan, Y.; Irfan, M.; Butt, M.A. Investigation of Optical-Switching Mechanism Using Guided Mode Resonances. Photonics 2023, 10, 13. https://doi.org/10.3390/photonics10010013

AMA Style

Rehman AU, Khan Y, Irfan M, Butt MA. Investigation of Optical-Switching Mechanism Using Guided Mode Resonances. Photonics. 2023; 10(1):13. https://doi.org/10.3390/photonics10010013

Chicago/Turabian Style

Rehman, Atiq Ur, Yousuf Khan, Muhammad Irfan, and Muhammad A. Butt. 2023. "Investigation of Optical-Switching Mechanism Using Guided Mode Resonances" Photonics 10, no. 1: 13. https://doi.org/10.3390/photonics10010013

APA Style

Rehman, A. U., Khan, Y., Irfan, M., & Butt, M. A. (2023). Investigation of Optical-Switching Mechanism Using Guided Mode Resonances. Photonics, 10(1), 13. https://doi.org/10.3390/photonics10010013

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop