Study on Screening Mechanism and Numerical Simulation for Crashed Concrete Particles by Using DEM
Abstract
:1. Introduction
2. Basic Theory
2.1. The Elastoplastic Collision Model of Two Particles and Rigid Plate
2.2. The Restitution Process between Particles and Screen Surface
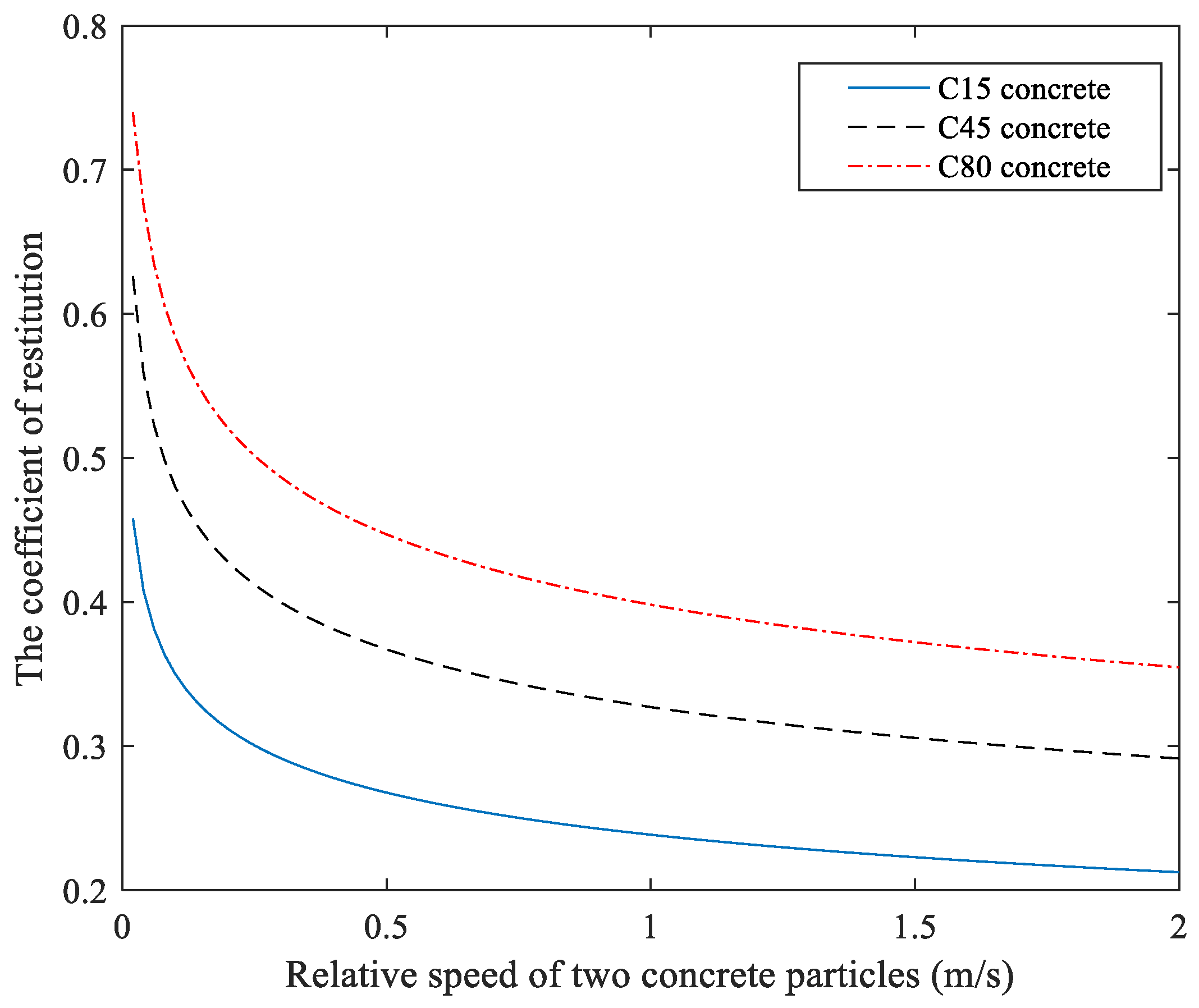
2.3. Calculation of Coefficient of Restitution for Concrete Particles
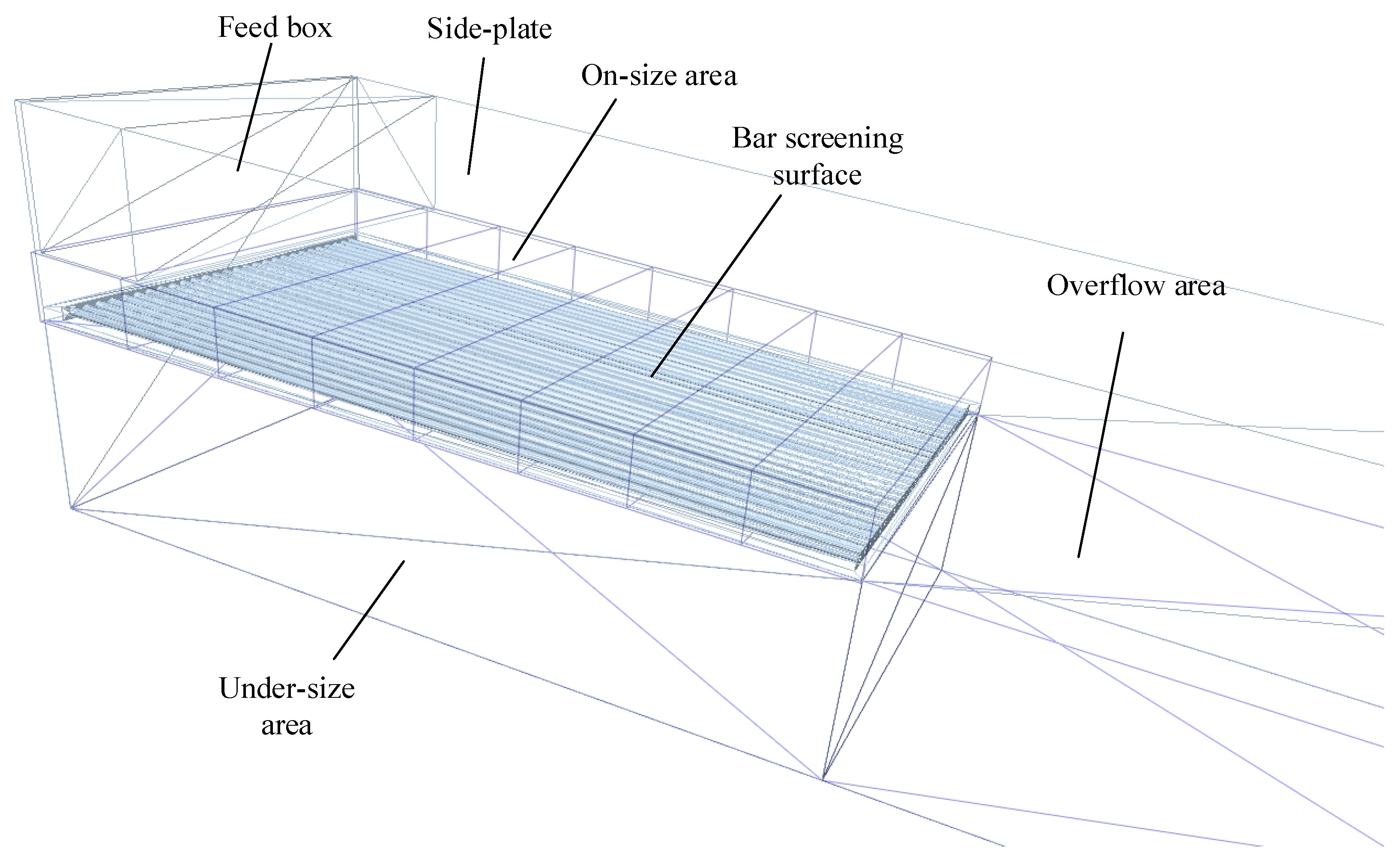
3. Simulation Conditions
4. Results and Discussion
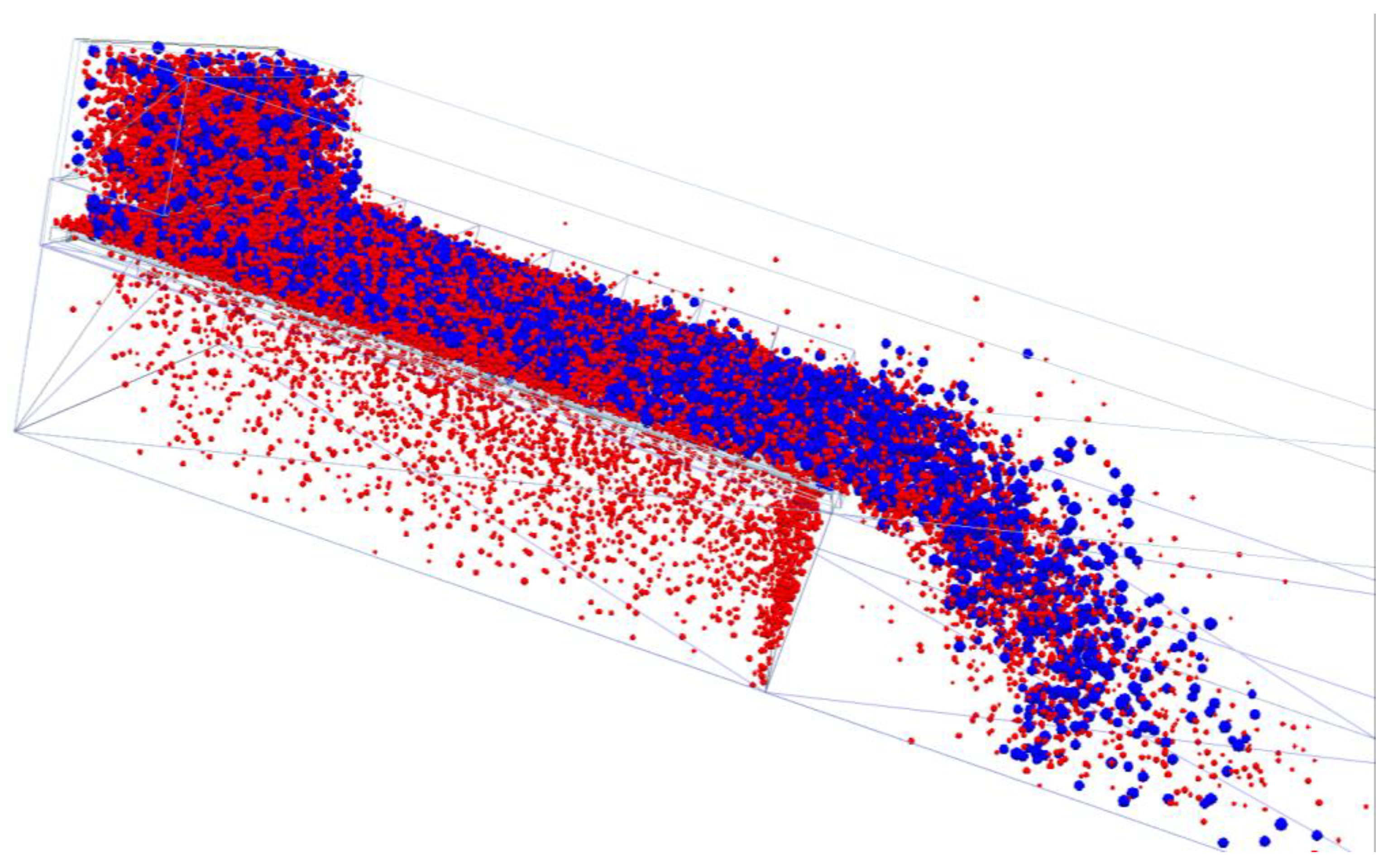
4.1. The Simulation Analysis for a Typical Screening Process
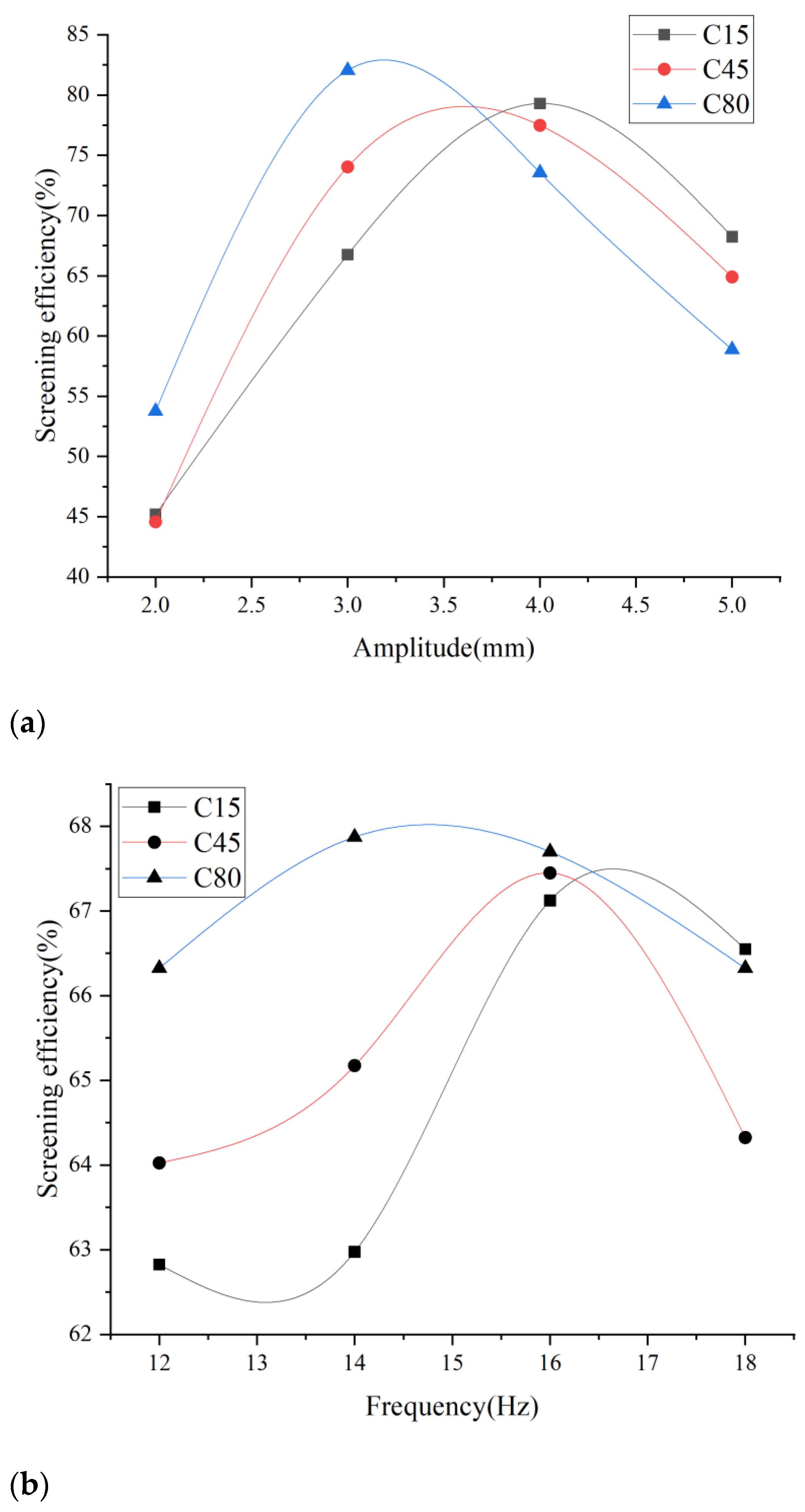
4.2. Optimal Parameters for Different Concretes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akhtar, A.; Sarmah, A.K. Construction and demolition waste generation and properties of recycled aggregate concrete: A global perspective. J. Clean Prod. 2018, 186, 262–281. [Google Scholar] [CrossRef]
- Topçu, I.B. Physical and mechanical properties of concretes produced with waste concrete. Cem. Concr. Res. 1997, 27, 1817–1823. [Google Scholar] [CrossRef]
- Guo, L.; Guan, Z.; Guo, L.; Shen, W.; Xue, Z.; Chen, P.; Li, M. Effects of Recycled Aggregate Content on Pervious Concrete Performance. J. Renew. Mater. 2020, 8, 1711–1727. [Google Scholar] [CrossRef]
- Evangelista, L.; Brito, J.D. Mechanical behaviour of concrete made with fine recycled concrete aggregates. Cement Concrete Compos. 2007, 29, 397–401. [Google Scholar] [CrossRef]
- Sérifou, M.; Sbartaï, Z.M.; Yotte, S.; Boffoué, M.O.; Emeruwa, E.; Bos, F. A Study of Concrete Made with Fine and Coarse Aggregates Recycled from Fresh Concrete Waste. J. Constr. Eng. 2013, 2013, 317182. [Google Scholar] [CrossRef] [Green Version]
- Ly, B.T.; Far, H. Investigation on properties of coarse reclaimed aggregates and their effects on concrete strength and workability. Struct Concr. 2019, 20, 1622–1630. [Google Scholar] [CrossRef]
- Kou, S.C.; Zhan, B.J.; Poon, C.S. Properties of partition wall blocks prepared with fresh concrete wastes. Constr Build. Mater. 2012, 36, 566–571. [Google Scholar] [CrossRef]
- Zhang, L.W.; Sojobi, A.O.; Liew, K.M. Sustainable CFRP-reinforced recycled concrete for cleaner eco-friendly construction. J. Clean Prod. 2019, 233, 56–75. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, J.; Singh, A. Crack Propagation and Failure Characteristics of Modeled Concrete with Natural and Brick Aggregates. J. Renew. Mater. 2021, 9, 19. [Google Scholar] [CrossRef]
- Duan, Z.; Han, N.; Singh, A.; Xiao, J. Multi-Scale Investigation on Concrete Prepared with Recycled Aggregates from Different Parent Concrete. J. Renew. Mater. 2020, 8, 1375–1390. [Google Scholar] [CrossRef]
- Gholampour, A.; Mansouri, I.; Kisi, O.; Ozbakkaloglu, T. Evaluation of mechanical properties of concretes containing coarse recycled concrete aggregates using multivariate adaptive regression splines (MARS), M5 model tree (M5Tree), and least squares support vector regression (LSSVR) models. Neural Comput. Appl. 2020, 32, 295–308. [Google Scholar] [CrossRef]
- Ho, H.J.; Iizuka, A.; Shibata, E. Chemical recycling and use of various types of concrete waste: A review. J. Clean Prod. 2021, 284, 124785. [Google Scholar] [CrossRef]
- Guerra, B.C.; Leite, F.; Faust, K.M. 4D-BIM to enhance construction waste reuse and recycle planning: Case studies on concrete and drywall waste streams. Waste Manag. 2020, 116, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Mi, R.J.; Pan, G.H.; Liew, K.M.; Kuang, T. Utilizing recycled aggregate concrete in sustainable construction for a required compressive strength ratio. J. Clean Prod. 2020, 276, 124249. [Google Scholar] [CrossRef]
- Xia, B.; Ding, T.; Xiao, J.Z. Life cycle assessment of concrete structures with reuse and recycling strategies: A novel framework and case study. Waste Manag. 2020, 105, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Welsh-Huggins, S.J.; Liel, A.B.; Cook, S.M. Reduce, Reuse, Resilient? Life-Cycle Seismic and Environmental Performance of Buildings with Alternative Concretes. J. Infrastruct. Syst. 2020, 26, 04019033. [Google Scholar] [CrossRef]
- Collivignarelli, C.; Sorlini, S. Reuse of municipal solid wastes incineration fly ashes in concrete mixtures. Waste Manag. 2002, 22, 909–912. [Google Scholar] [CrossRef]
- Hamdi, A.; Abdelaziz, G.; Farhan, K.Z. Scope of reusing waste shredded tires in concrete and cementitious composite materials: A review. J. Build. Eng. 2021, 35, 102014. [Google Scholar] [CrossRef]
- Wu, H.; Liu, C.; Shi, S.; Chen, K. Experimental Research on the Physical and Mechanical Properties of Concretewith Recycled Plastic Aggregates. J. Renew. Mater. 2020, 8, 727–738. [Google Scholar] [CrossRef]
- Dosho, Y. Development of a sustainable concrete waste recycling system—Application of recycled aggregate concrete produced by aggregate replacing method. J. Adv. Concr. Technol. 2007, 5, 27–42. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.X.; Zhang, Y.X. Recycling fresh concrete waste: A review. Struct Concr. 2018, 19, 1939–1955. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, L.; Jiang, H.; Wen, P.; Zhao, L.; Zhao, Y.; Duan, C.; Luo, Z.; Wang, Z.; Liu, C.; et al. Kinematics of elastic screen surface and elimination mechanism of plugging during dry deep screening of moist coal. Powder Technol. 2019, 346, 452–461. [Google Scholar] [CrossRef]
- Peng, L.; Wang, Z.; Ma, W.; Chen, X.; Zhao, Y.; Liu, C. Dynamic influence of screening coals on a vibrating screen. Fuel 2018, 216, 484–493. [Google Scholar] [CrossRef]
- Jiang, H.; Qiao, J.; Zhou, Z.; Zhao, Y.; Yang, Y.; Duan, C.; Luo, Z.; Cai, L.; Wang, S.; Pan, M. Time evolution of kinematic characteristics of variable-amplitude equal-thickness screen and material distribution during screening process. Powder Technol. 2018, 336, 350–359. [Google Scholar] [CrossRef]
- Wang, W.N.; Duan, C.L.; Jiang, H.S.; Yu, S.J.; Zhou, Z.G.; Qiao, J.P.; Zhao, Y.M.; Pan, M. Mechanism of overcoming plugging and optimization of parameters for rigid-flexible coupled elastic screening of moist fine coal. Powder Technol. 2020, 376, 113–125. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Harzanagh, A.A.; Orhan, E.C.; Ergun, S.L. Discrete.e element modelling of vibrating screens. Min. Eng. 2018, 121, 107–121. [Google Scholar] [CrossRef]
- Zhao, L.L.; Zhao, Y.M.; Bao, C.Y.; Hou, Q.F.; Yu, A.B. Optimisation of a circularly vibrating screen based on DEM simulation and Taguchi orthogonal experimental design. Powder Technol. 2017, 310, 307–317. [Google Scholar] [CrossRef]
- Li, C.Z.; Honeyands, T.; O’Dea, D.; Moreno-Atanasio, R. DEM study on size segregation and voidage distribution in green bed formed on iron ore sinter strand. Powder Technol. 2019, 356, 778–789. [Google Scholar] [CrossRef]
- Jimenez-Herrera, N.; Barrios, G.K.P.; Tavares, L.M. Comparison of breakage models in DEM in simulating impact on particle beds. Adv. Powder Technol. 2018, 29, 692–706. [Google Scholar] [CrossRef]
- George, G.F.F. Hertz’s Miscellaneous Papers. Nature 1896, 55, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface Energy and the Contact of Elastic Solids. Proc. Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]




| C15 | C45 | C80 | |
|---|---|---|---|
| Density | 2360 | 2410 | 2440 |
| Poisson’s ratio | 0.17 | 0.17 | 0.17 |
| Elastic modulus (GPa) | 22 | 33.5 | 38 |
| Compressive strength | 15 | 45 | 80 |
| Parameters | Value | |
|---|---|---|
| Screen length (mm) | 600 | |
| Screen width (mm) | 300 | |
| Bar gap (mm) | 5 | |
| Bar diameter (mm) | 5 | |
| Particle size range (mm) | 3–5 | 5–10 |
| Mass of feeding materials for each particle size range in an experiment (kg/s) | 3.5 | 3.5 |
| Total feeding rate (kg/s) | 7 | |
| Inclination angle of the deck α (°) | 15, 20, 25, 30 | |
| Vibration frequency f (Hz) | 12, 14, 16, 18 | |
| Vibration amplitude A (mm) | 2, 3, 4, 5 | |
| Vibration motion | Circular | |
| Parameters | Value | ||
|---|---|---|---|
| C15 | C45 | C80 | |
| Coefficient of restitution for particle to particle | 0.2385 | 0.3271 | 0.3982 |
| Coefficient of static friction | 0.5 | 0.5 | 0.5 |
| Coefficient of rolling friction | 0.01 | 0.01 | 0.01 |
| Coefficient of restitution for particle to screening surface | 0.2125 | 0.2915 | 0.3548 |
| Coefficient of static friction | 0.4 | 0.4 | 0.4 |
| Coefficient of rolling friction | 0.01 | 0.01 | 0.01 |
| Case Number | Amplitude | Frequency | Inclination Angle | Screening Efficiency (%) | ||
|---|---|---|---|---|---|---|
| C15 | C45 | C80 | ||||
| 1 | 2 | 12 | 15 | 36.8 | 38.1 | 44.7 |
| 2 | 2 | 14 | 18 | 40.2 | 44.3 | 52.7 |
| 3 | 2 | 16 | 21 | 49.1 | 52.7 | 57.4 |
| 4 | 2 | 18 | 24 | 54.7 | 43.2 | 60.2 |
| 5 | 3 | 12 | 18 | 58.4 | 66.5 | 78.2 |
| 6 | 3 | 14 | 15 | 65.5 | 70.9 | 82.2 |
| 7 | 3 | 16 | 24 | 72.5 | 78.2 | 84.1 |
| 8 | 3 | 18 | 21 | 70.6 | 80.5 | 83.7 |
| 9 | 4 | 12 | 21 | 78.9 | 80.2 | 77.2 |
| 10 | 4 | 14 | 24 | 78.2 | 79.7 | 75.3 |
| 11 | 4 | 16 | 15 | 81.6 | 76.8 | 73.5 |
| 12 | 4 | 18 | 18 | 78.5 | 73.2 | 68.2 |
| 13 | 5 | 12 | 24 | 77.2 | 71.3 | 65.2 |
| 14 | 5 | 14 | 21 | 68 | 65.8 | 61.3 |
| 15 | 5 | 16 | 18 | 65.3 | 62.1 | 55.8 |
| 16 | 5 | 18 | 15 | 62.4 | 60.4 | 53.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, D.; Liu, C. Study on Screening Mechanism and Numerical Simulation for Crashed Concrete Particles by Using DEM. Separations 2022, 9, 153. https://doi.org/10.3390/separations9060153
He D, Liu C. Study on Screening Mechanism and Numerical Simulation for Crashed Concrete Particles by Using DEM. Separations. 2022; 9(6):153. https://doi.org/10.3390/separations9060153
Chicago/Turabian StyleHe, Deyi, and Chusheng Liu. 2022. "Study on Screening Mechanism and Numerical Simulation for Crashed Concrete Particles by Using DEM" Separations 9, no. 6: 153. https://doi.org/10.3390/separations9060153
APA StyleHe, D., & Liu, C. (2022). Study on Screening Mechanism and Numerical Simulation for Crashed Concrete Particles by Using DEM. Separations, 9(6), 153. https://doi.org/10.3390/separations9060153






