Modeling and Optimization of Membrane Process for Salinity Gradient Energy Production
Abstract
1. Introduction
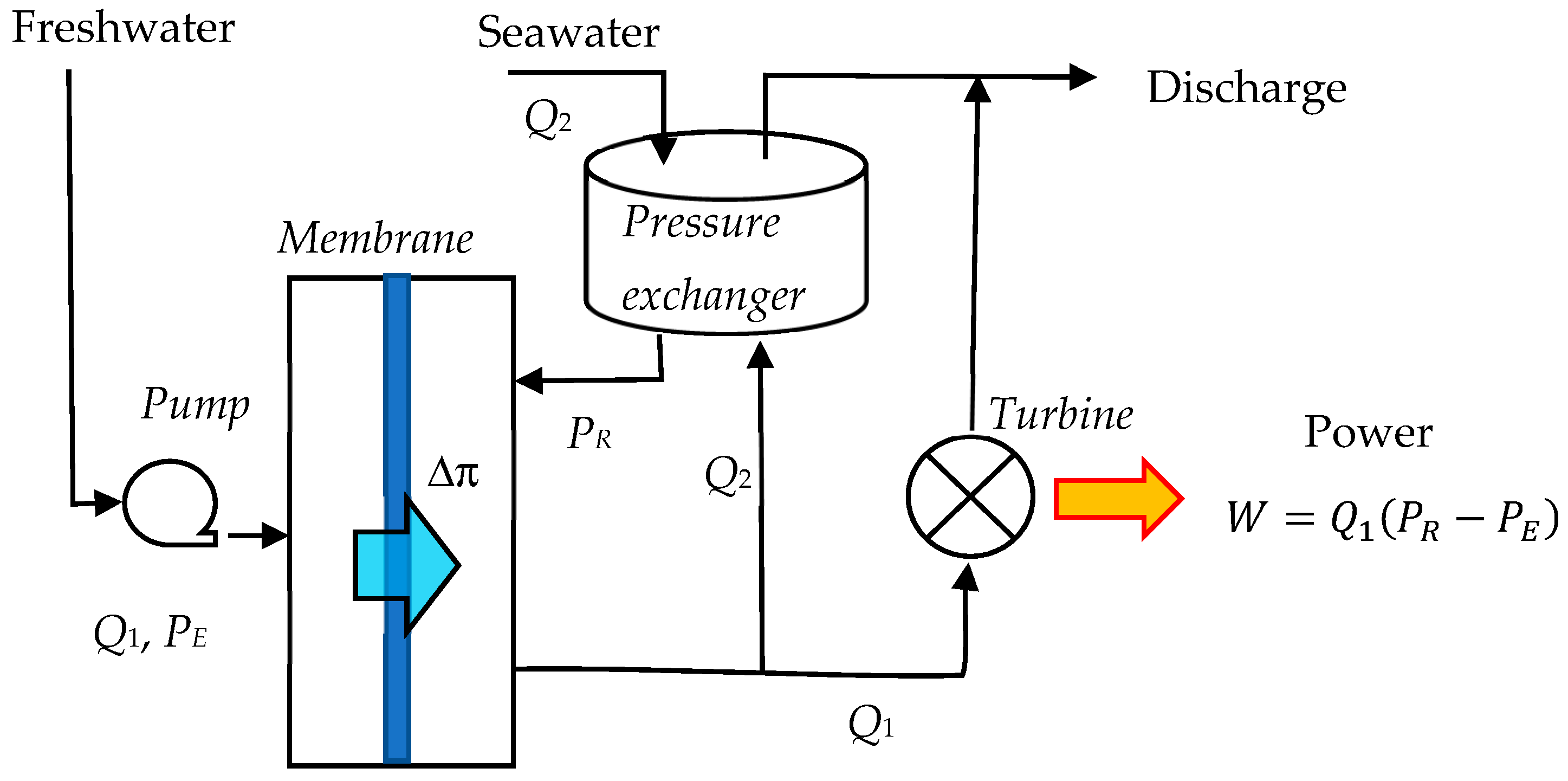
2. Power Production Calculation
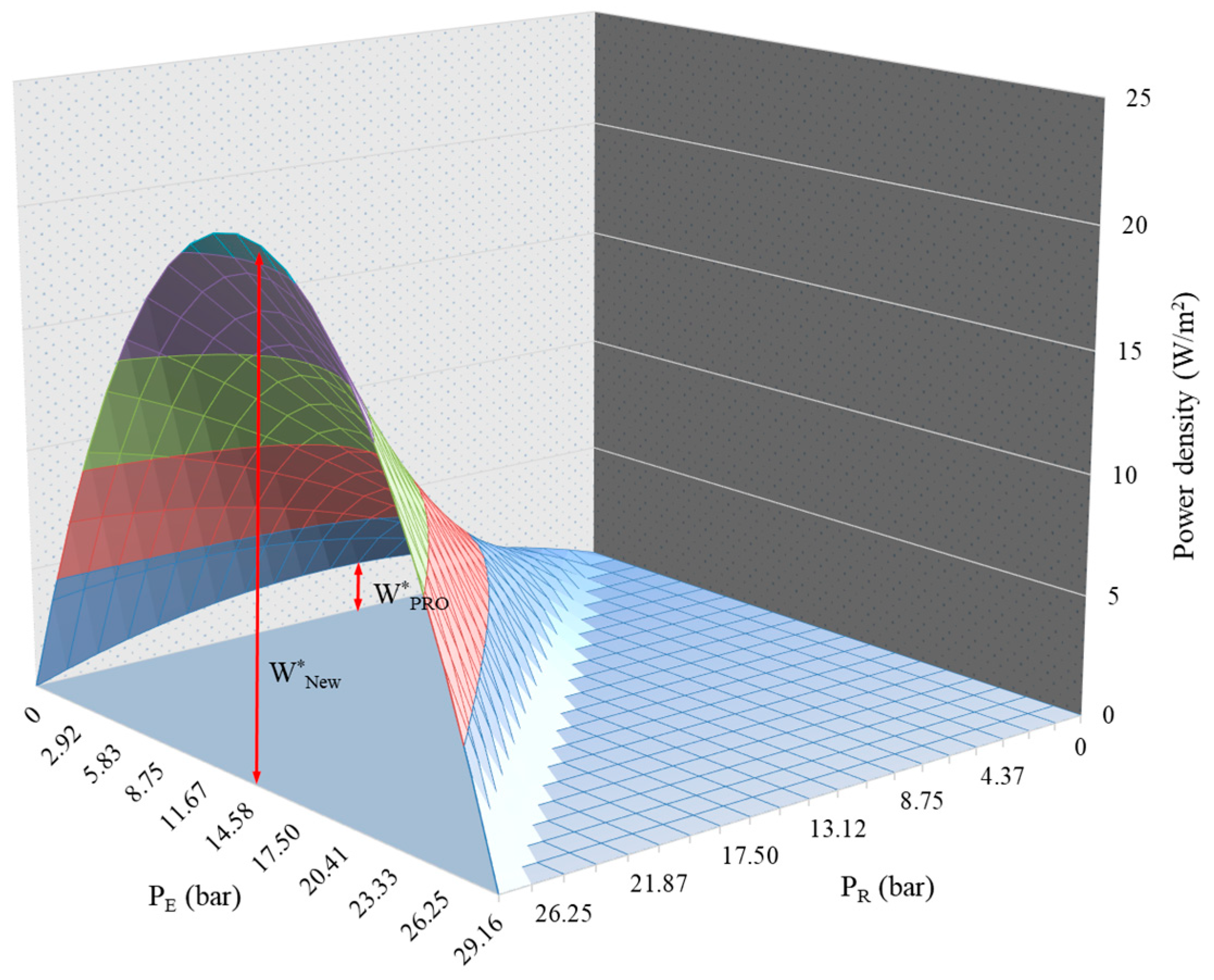
3. Process Optimization
4. Simulations and Discussion
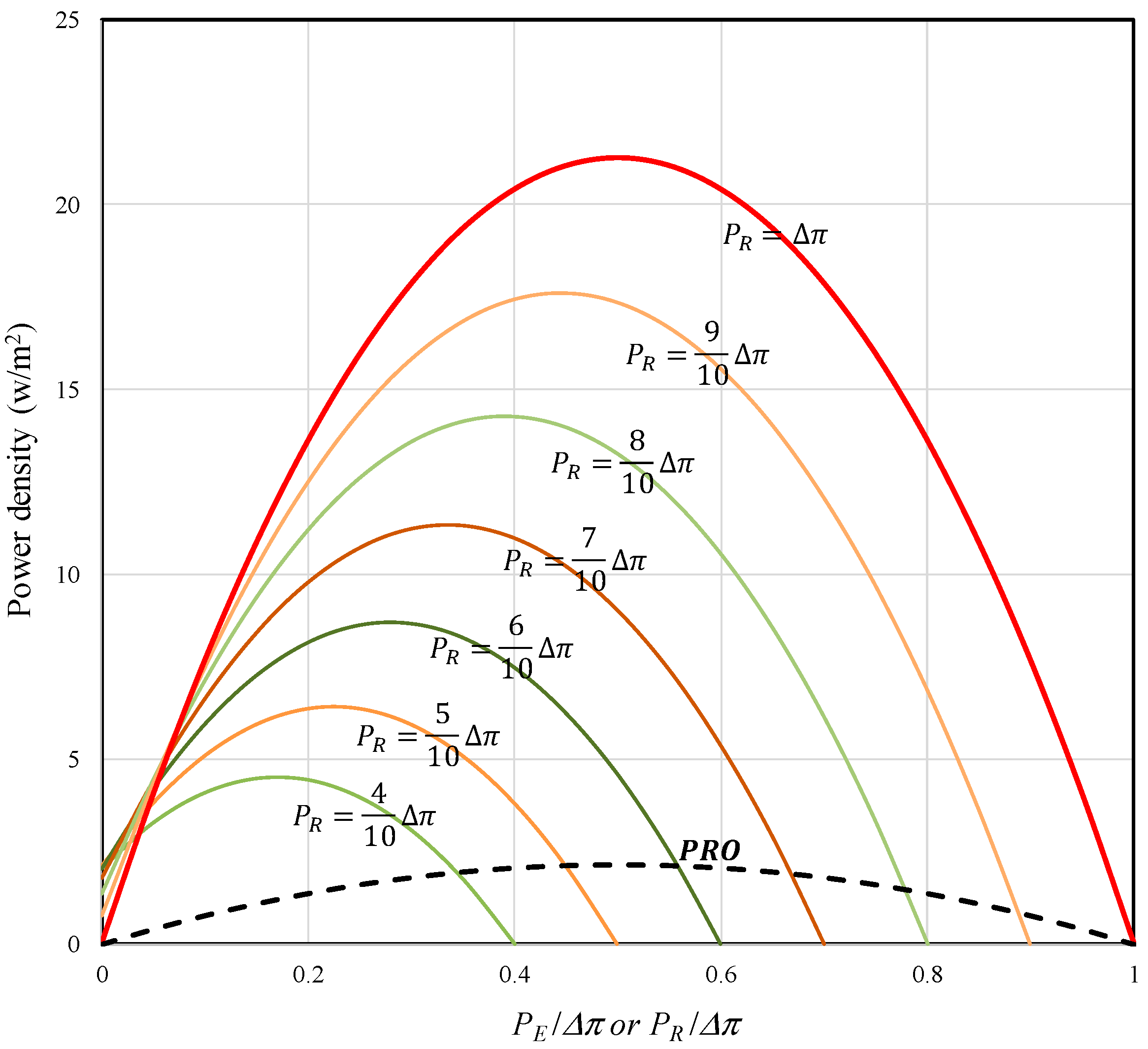
4.1. High Power Density of Membrane
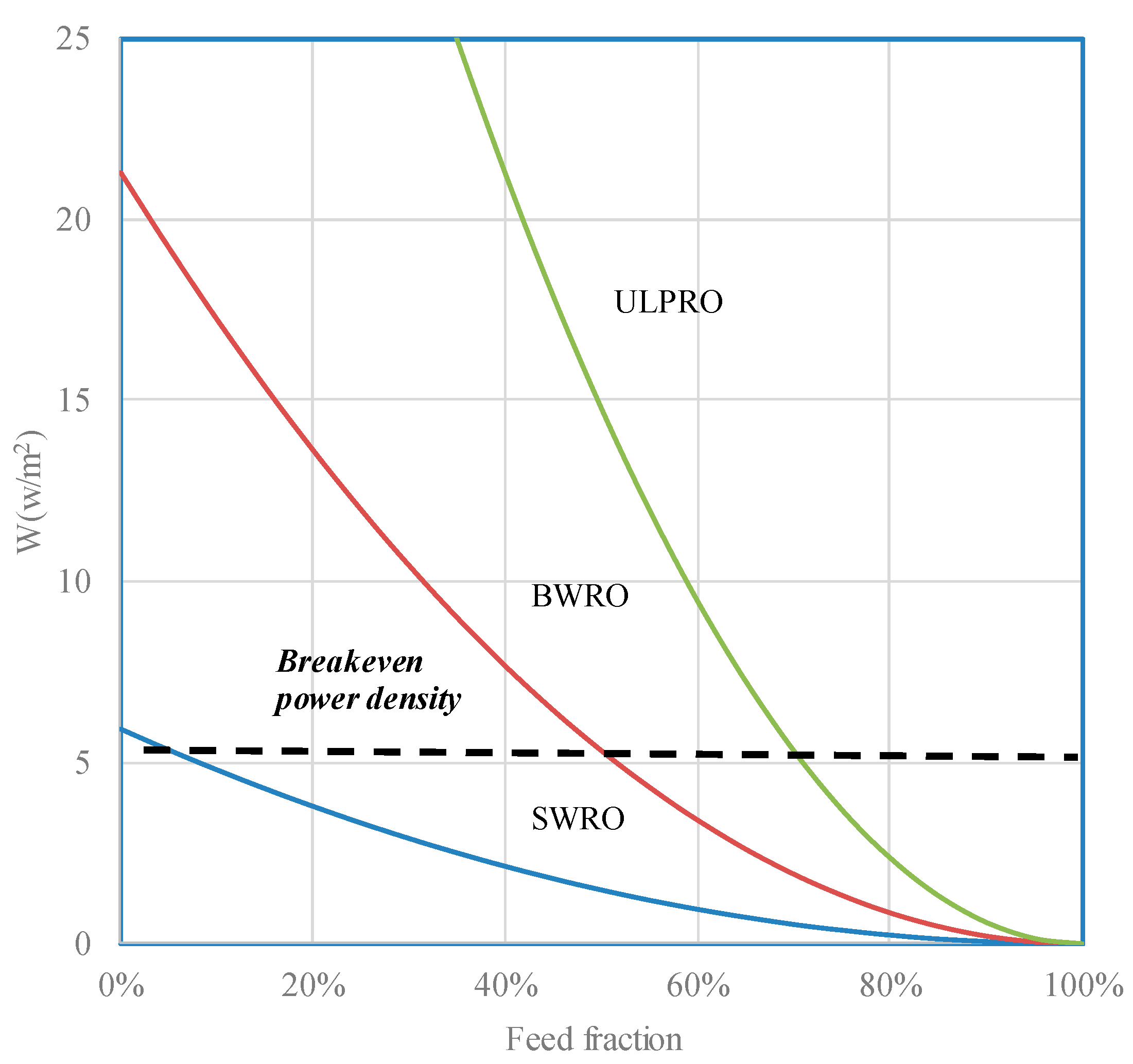
4.2. Assessments of the Currently Available Membranes
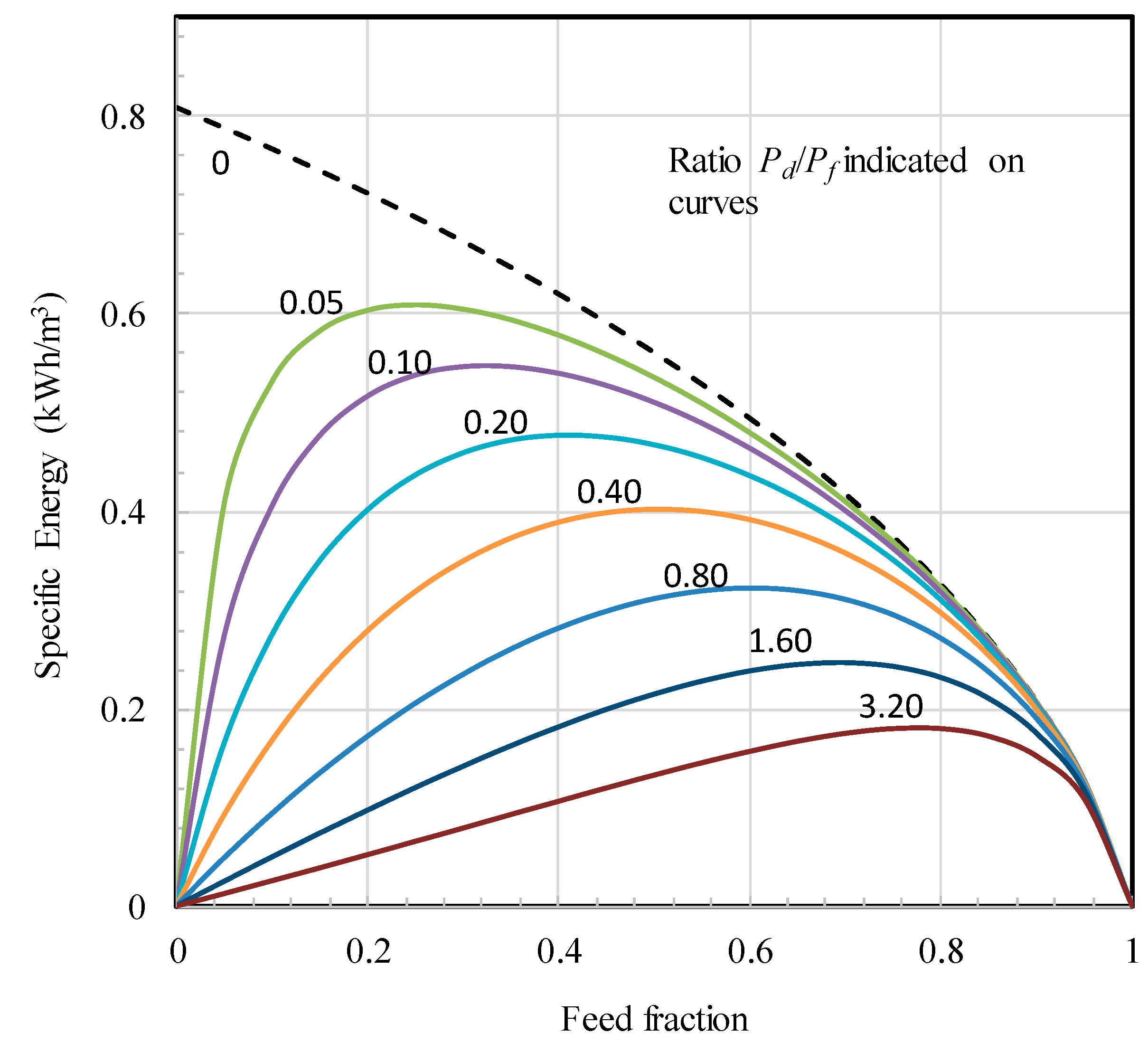
4.3. Specific Energy
5. Conclusions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Hamiche, A.M.; Stambouli, A.B.; Flazi, S. A review of the water-energy nexus. Renew. Sustain. Energy Rev. 2016, 65, 319–331. [Google Scholar] [CrossRef]
- DOE. Water Energy Nexus Executive Summary. Available online: https://www.energy.gov/downloads/water-energy-nexus-challenges-and-opportunities (accessed on 6 June 2019).
- Wick, G.L.; Isaacs, J.D. Salt domes: Is there more energy available from their salt than from their oil? Science 1978, 199, 1436–1437. [Google Scholar] [CrossRef] [PubMed]
- Mehta, G.D.; Loeb, S. Internal polarization in the porous substructure of a semipermeable membrane under pressure-retarded osmosis. J. Membr. Sci. 1978, 4, 261–265. [Google Scholar] [CrossRef]
- Lee, K.L.; Baker, R.W.; Lonsdale, H.K. Membranes for power generation by pressure-retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Dandeno, J.B. Osmotic theories, with special reference to van’t Hoff’s law. Bull. Torrey Bot. Club 1909, 36, 283–298. [Google Scholar] [CrossRef]
- Kahlenberg, L. On the nature of the process of osmosis and osmotic pressure with observations concerning dialysis. J. Phys. Chem. 1906, 10, 141–209. [Google Scholar] [CrossRef]
- Yates, F.E. Osmosis: A transport of confusion. Am. J. Physiol. 1978, 235, R1. [Google Scholar] [CrossRef]
- Post, J.W.; Veerman, J.; Hamelers, H.V.M.; Euverink, G.J.W.; Metz, S.J.; Nymeijer, K.; Buisman, C.J.N. Salinity-gradient power: Evaluation of pressure-retarded osmosis and reverse electrodialysis. J. Membr. Sci. 2007, 288, 218–230. [Google Scholar] [CrossRef]
- Straub, P.; Deshmukh, A.; Elimelech, M. Pressure-retarded osmosis for power generation from salinity gradients: Is it viable? Energy Environ. Sci. 2016, 9, 31–48. [Google Scholar] [CrossRef]
- Altaee, A.; Zhou, J.; Alanezi, A.A.; Zaragoza, G. Pressure retarded osmosis process for power generation: Feasibility, energy balance and controlling parameters. Appl. Energy 2017, 206, 303–311. [Google Scholar] [CrossRef]
- She, Q.; Jin, X.; Tang, C.Y. Osmotic power production from salinity gradient resource by pressure retarded osmosis: Effects of operating conditions and reverse solute diffusion. J. Membr. Sci. 2012, 401–402, 262–273. [Google Scholar] [CrossRef]
- Altaee, A.; Sharif, A. Pressure retarded osmosis: Advancement in the process applications for power generation and desalination. Desalination 2015, 356, 31–46. [Google Scholar] [CrossRef]
- Gerstandt, K.; Peinemann, K.V.; Skilhagen, S.E.; Thorsen, T.; Holt, T. Membrane processes in energy supply for an osmotic power plant. Desalination 2008, 224, 64–70. [Google Scholar] [CrossRef]
- Han, G.; Zhang, S.; Li, X.; Chung, T.S. High performance thin film composite pressure retarded osmosis (PRO) membranes for renewable salinity-gradient energy generation. J. Membr. Sci. 2013, 440, 108–121. [Google Scholar] [CrossRef]
- Patel, S. Statkraft Shelves Osmotic Power Project. Available online: https://www.powermag.com/statkraft-shelves-osmotic-power-project/ (accessed on 9 September 2019).
- Zhang, H.; Wang, J.; Rainwater, K.; Song, L. Metastable state of water and performance of osmotically driven membrane processes. Membranes 2019, 9, 43. [Google Scholar] [CrossRef]
- Gao, N.; Wang, J.; Song, L. Independence of hydraulic pressures on the feed and draw solutions in the osmotically driven membrane processes. J. Membr. Sci. 2019, 586, 1–6. [Google Scholar] [CrossRef]
- Blandin, G.; Myat, D.T.; Verliefde, A.R.D.; Le-Clech, P. Pressure assisted osmosis using nanofiltration membranes (PAO-NF): Towards higher efficiency osmotic processes. J. Membr. Sci. 2017, 533, 250–260. [Google Scholar] [CrossRef]
- Kim, B.; Gwak, G.; Hong, S. Analysis of enhancing water flux and reducing reverse solute flux in pressure assisted forward osmosis process. Desalination 2017, 421, 61–71. [Google Scholar] [CrossRef]
- Klayson, C.; Cath, T.Y.; Deoyydt, T.; Vankelecom, I.F.J. Forward and pressure retarded osmosis: Potential solutions for global challenges in energy and water supply. Chem. Soc. Rev. 2013, 42, 6959–6989. [Google Scholar] [CrossRef]
- Shaffer, D.L.; Werber, J.R.; Jaramillo, H.; Lin, S.; Elimelech, M. Forward osmosis: Where are we now? Desalination 2015, 356, 271–284. [Google Scholar] [CrossRef]
- Lin, S.; Straub, A.P.; Elimelech, M. Thermodynamic limits of extractable energy by pressure retarded osmosis. Energy Environ. Sci. 2014, 7, 2706–2714. [Google Scholar] [CrossRef]
- Straub, A.P.; Lin, S.; Elimelech, M. Module-Scale Analysis of Pressure Retarded Osmosis: Performance Limitations and Implications for Full-Scale Operation. Environ. Sci. Technol. 2014, 48, 12435–12444. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Yang, W.; Rainwater, K.; Song, L. Limiting extractable energy from pressure retarded osmosis with different pretreatment costs for feed and draw solutions. J. Membr. Sci. 2017, 544, 208–212. [Google Scholar] [CrossRef]
- O’Toole, G.; Jones, L.; Coutinho, C. River-to-sea pressure retarded osmosis: Resource utilization in a full-scale facility. Desalination 2016, 389, 39–51. [Google Scholar] [CrossRef]
| Water Flux J (µm/s) | Structural Parameter S (mm) | |||
|---|---|---|---|---|
| 10.00 | 5.00 | 1.00 | 0.50 | |
| 2.00 | 6.76 × 10−6 | 2.60 × 10−3 | 3.04 × 10−1 | 5.51 × 10−1 |
| 3.00 | 1.76 × 10−8 | 1.33 × 10−4 | 1.68 × 10−1 | 4.09 × 10−1 |
| 4.00 | 4.57 × 10−11 | 6.76 × 10−6 | 9.25 × 10−2 | 3.04 × 10−1 |
| 5.00 | 1.19 × 10−13 | 3.45 × 10−7 | 5.10 × 10−2 | 2.26 × 10−1 |
| 6.00 | 3.09 × 10−16 | 1.76 × 10−8 | 2.81 × 10−2 | 1.68 × 10−1 |
| Membrane | SWRO | BWRO | ULPRO |
|---|---|---|---|
| Permeability, | 1.0 | 3.6 | 10 |
| Power density, W/m2 | 5.91 | 21.26 | 59.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L. Modeling and Optimization of Membrane Process for Salinity Gradient Energy Production. Separations 2021, 8, 64. https://doi.org/10.3390/separations8050064
Song L. Modeling and Optimization of Membrane Process for Salinity Gradient Energy Production. Separations. 2021; 8(5):64. https://doi.org/10.3390/separations8050064
Chicago/Turabian StyleSong, Lianfa. 2021. "Modeling and Optimization of Membrane Process for Salinity Gradient Energy Production" Separations 8, no. 5: 64. https://doi.org/10.3390/separations8050064
APA StyleSong, L. (2021). Modeling and Optimization of Membrane Process for Salinity Gradient Energy Production. Separations, 8(5), 64. https://doi.org/10.3390/separations8050064





