Abstract
Reverse electrodialysis is a promising membrane technology to generate energy from controlled mixing of water streams of different salinities. Electrical potentials generate on the ion exchange membranes (IEMs) when selective transport of cations and anions across the membranes driven by concentration difference. The accurate determination of the potentials developed on the IEMs is critical to fairly assess the feasibility of the technology. The Nernst–Planck–Poisson (NPP) equations for IEMs (the membranes with fixed charge) were solved numerically with the boundary updating scheme. The validity of this numerical method was verified by the identical values of Donnan potential obtained with the well-established analytical methods. The suitability and applicability of the classic Teorell–Meyer–Siever (TMS) model were assessed by comparison to the simulation results from the numerical method.
1. Introduction
Salinity gradient energy (SGE) is a type of clean and renewable energy embodied in water streams of different salinities [1,2]. The amount of SGE is estimated at about 2.6 terawatts globally or approximately 20% of the current worldwide energy consumption rate [3]. Pressure retarded osmosis (PRO) and reverse electrodialysis (RED) are currently under investigation as two promising technologies to harvest SGE [3,4,5,6]. In PRO process, a semipermeable membrane is employed to separate two solutions of different salt concentration. Driven by osmotic pressure, water transports from low concentration side to high concentration side and builds up a hydraulic pressure there. The controlled release of the pressurized water from the high concentration side can generate energy by turning a hydro turbine. The working principle, process features, and technical and economic feasibilities of PRO have been extensively studied.
RED, which is the other promising technology that can be used to harvest SGE, is also a membrane-based process. Instead of semipermeable membranes, ion exchange membranes (IEMs) are used in RED processes [7,8,9,10,11]. IEMs are permselective membranes due to the fixed charges on membrane materials. There are two types of IEMs according to the fixed charges carried by the membranes. Cation exchange membranes (CEMs) carry negative fixed charges and only allow cations to pass while anion exchange membranes (AEMs) carry positive fixed charges and only allow anion to pass. When a CEM and an AEM are arranged on two sides of a concentrated flow, sandwiched with two diluted flows, cations and anions in the concentrated flow would move through membranes to opposite directions. As a result, electrical potentials develop on the membranes. Electrical energy can be produced when the potentials are applied to an external load.
Development of potential on IEMs is a very complex phenomenon that is affected by many factors, such as properties of IEMs, diffusivities of various ions, and configuration of the RED cells. Although it is well established that membrane potential is governed by the Poisson equation coupled with the Nernst–Planck equation for concentration distributions of ions along the membrane thickness, seeking a rigorous solution of the Nernst–Planck–Poisson (NPP) equations remains a serious challenge in the field. The commonly used Nernst equation [5,6] and Teorell–Meyer–Siever (TMS) model [12,13,14] for the potential on IEMs are at best approximations or surrogates for the true membrane potential because both models are obtained with suspicious simplifications and assumptions [15,16].
An optional method for the membrane potential is to directly seek numerical solutions of the NPP equations without the commonly used simplifications and assumptions [17,18,19,20]. However, new challenge emerges that the potentials and ion concentrations at the membrane surfaces cannot be assigned a priori in the rigorous formulation of the problem [21,22]. Inappropriately imposed boundary conditions were often used in the numerical solutions in previous studies until we recently developed a boundary updating scheme to handle this challenge successfully [23]. With this scheme, the NPP equations for a membrane of no-fixed charge was rigorously solved for the first time under the true boundary conditions.
The main objective of this article is to apply the boundary updating scheme to determine the potential developed on the membranes with fixed charges. Numerical solutions of the NPP equations for IEMs with various charge density were obtained and the suitability and accuracy of the numerical method were discussed. The impact of charge density of IEMs on the total potential and potential components were studied. Finally, the classic TMS model was compared and assessed for its applicability and limitations with the numerical method.
2. Governing Equations and Numerical Methods
2.1. Governing Equations
The problem under consideration is to determine the membrane potential at steady state on an IEM as schematically shown in Figure 1. The IEM of fixed charge density X separates two solutions of a monovalent salt with concentrations Cb0 and CbL, respectively. There is a transition layer between the membrane surface and the bulk solution on each side of the membrane. While electroneutrality is always maintained in the bulk solutions, charge is usually unbalanced in the transition layers because the attraction of counter-ions and repulsion of co-ions by the charge on the membrane. As a result, both ion concentrations and potential on the membrane surfaces differ from those in the bulk solutions, as schematically described by the lines for concentrations and potential in Figure 1. There is only a concentration profile for one ion in the figure for the sake of clarity. The concentration profile for the other ion would be different in the transition layers and on the membrane.
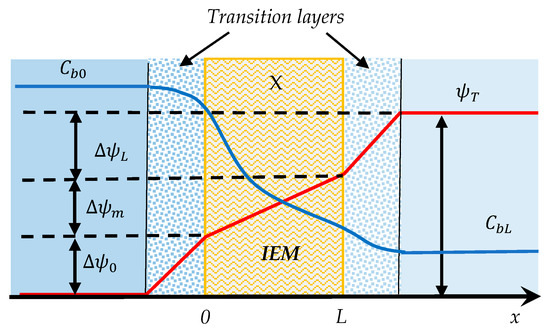
Figure 1.
Schematic of ion transport across an IEM that separates two solutions of different electrolyte concentration. The profiles of salt concentration and potential are schematically presented.
The ion concentrations on a membrane are governed by the Nernst–Planck Equation (1):
where Ci is the concentration of ion i, Di is the diffusion coefficient of ion i, x is the spatial coordinate perpendicular to the membrane, zi is the valance of ion i, F is the Faraday constant, R is the gas constant, and is the potential. Convection term was not considered in Equation (1) because no water flow across the membrane was assumed. The potential on the membrane is then governed by Poisson equation:
where is the permittivity of the membrane material, and X is the fixed charge density. Please be reminded that the variable X can take a positive value for AEMs or a negative value for CEMs.
The boundary conditions for the NPP equations in the problem depicted in Figure 1 cannot be specified a priori. There is a dilemma between the boundary conditions and the final solutions of the equations. The ion concentrations and potential on the membrane surfaces are strongly dependent on the free charge developed on the membrane. However, the free charge on the membrane can only be known after the equations have been solved with the specified boundary conditions. We will handle this dilemma with the boundary updating scheme described below.
2.2. Boundary Updating Scheme
The boundary updating scheme was initially developed in one of our previous papers [23]. For convenience of readers, a more concise description of the method is provided here. The scheme starts with a state of the membrane for which the boundary conditions can be easily specified. For example, there is no potential on a neutral membrane (referring to the bulk solutions) and the ion concentrations at the membrane surfaces are equal to the bulk solutions, i.e.:
where and are the concentrations of ion i on the left surface and right surface of the membrane, respectively, and are the concentrations of ion i in the bulk solutions on the left and right sides of the membrane, respectively, and is the potential on the left surface of the membrane, and is the derivative of membrane potential at the right surface of the membrane. Ion concentrations on the membrane surfaces are equal to the bulk concentrations because there are not electrical forces on the neutral membrane to repel co-ions and to attract counter-ions.
The governing Equations (1) and (2) with the boundary conditions Equations (3)–(6) completely define the membrane transport problem and can be solved with common numerical methods. The Crank–Nicolson method and central difference method are used for the Nernst–Planck equation and Poisson equation, respectively. From the numerical solutions, the ion fluxes at the two boundaries can be determined:
where is the flux of ion i. The derivatives of concentration and potential at two membrane surfaces are calculated from the numerical solutions.
The cumulative net charges in the two transition layers can be calculated with:
and
where Q0 and QL are the cumulative charges in the transient layers on left and right sides of the membrane, respectively, and are the cumulative charges at the previous time step in the conresping transient layers, respectively, and is timestep size. At the first timestep, and for the initially neutral membrane.
The boundary conditions at any timestep are updated with the cumulative charges in the transition layers by:
where and are the Debye lengths in the solutions on the left and right sides of the membrane, which are calculated by:
The numerical solution of the NPP equations can be obtained for the next timestep with the updated boundary conditions. The above procedure is repeated with the newly obtained numerical solution to update the boundary conditions for the next timestep until the steady state is reached, which is indicated by the null current condition:
With boundary updating scheme, the concentration boundary conditions are always consistent with potential boundary conditions at any time step. Therefore, the true solution of NPP equations at the steady state is guaranteed.
2.3. Calculation of Membrane Potentials
With the numerical solution at the steady state, the ion fluxes can be calculated by:
The total membrane potential can be calculated with:
where is the total potential of the membrane, is the potential difference across the membrane thickness, and and are the potential differences across the transition layers on the two sides of the membrane, respectively. The potential difference across the membrane thickness is available from the numerical solution of the Poisson equation. The two potential differences across the transition layers can be calculated from the cumulated charges in the layers with:
3. Simulations and Discussion
A C++ program for the numerical procedure described above was developed on Visual Studio 2019 for calculation of the potential on IEMs under various conditions. All simulations reported below were done at a PC with CPU of Intel i7-9700 at 3.00 Ghz, on which a numerical solution can be obtained in a few seconds. Unless other specified, the parameters listed in Table 1 were used in the simulations.

Table 1.
Default parameter values used in numerical simulations.
3.1. The Effectiveness of Boundary Updating Schemne
The numerical solution of NPP equations for parameters given in Table 1 is presented in Figure 2. The membrane in this case is an AEM because of the positive fixed charge on it. The numerical solution for a membrane of no-fixed-charge for the same parameters is also shown in the figure. Figure 2a shows that concentrations of both cations and anions at the membrane surfaces (boundaries) differ significantly from the bulk concentrations, which are 10 mol/m3 and 5 mol/m3, respectively, in the solutions on the left and right sides of the membrane. The different cation and anion concentrations at the membrane surfaces are an essential feature of ion transport across the membranes, which is especially true for IEMs. The boundary updating scheme is particularly effective for the IEMs because of the bigger differences between cation and anion concentrations at the surfaces than those for the membranes of no-fixed-charge.
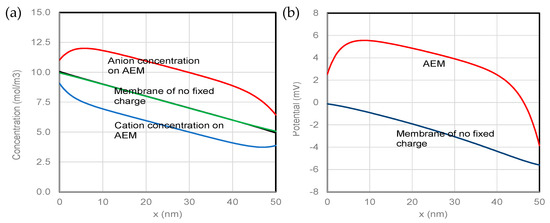
Figure 2.
(a) Concentration distributions and (b) potential distributions across the membrane thickness.
The anion concentration is higher than the cation concentration throughout the entire membrane thickness because of the positive fixed charge on the AEM. The electroneutrality can only be roughly maintained in a middle section of the membrane thickness, i.e., the difference between anion concentration and cation concentration is nearly equal to the fixed positive charge of the AEM. The lower anion concentrations and higher cation concentrations (unbalanced charges) in the regions near the membrane surfaces are the results of ion transfer between the membrane and solutions. The distributions of ions for the membrane of no-fixed-charge are relatively simple. Concentrations of anions and cations are equal through almost the entire membrane thickness with exceptions in two narrow regions near the membrane surfaces. The concentration differences cannot be clearly seen for the membrane of no-fixed-charge in the figure. Interested readers can find more details about the distributions of ion concentrations on the membrane of no-fixed-charge in one of our previous papers [23].
The corresponding potential distributions are presented in Figure 2b. The potential on the membrane of no-fixed-charge decreases monotonically from the left surface to the right surface. The potential on the AEM behaves more complexly than that on the membrane of no-fixed-charge. The middle section of potential on the AEM declines with a rate like that on the membrane of no-fixed- charge. This behavior of potential is obviously due to the differential diffusion of ions with different mobilities. A jump in an initial region and a drop in a final region of the potential on the AEM can be attributed to the repulsion of cations and the attraction of anions by the fixed positive charge on the AEM, i.e., the Donnan effect of the fixed charge on the membrane. The potentials at the membrane surfaces were again determined by the boundary updating scheme, which are consistent with the ion concentrations at the membrane surfaces. Such rigorous numerical solutions of NPP equations with the well-defined consistent boundary conditions have not been obtained before with any methods other than the boundary updating scheme.
3.2. Impact of the Charge Density of IEMs
Potential distributions along the membrane thickness for IEMs with different charge densities are presented in Figure 3. The thick line in the middle presents the potential profile on the membrane of no-fixed-charge. The potentials for AEMs are all above the line for the uncharged membrane while those for CEMs are below. This feature can be attributed to the Donnan effect of the fixed charge on the IEMs. The parallel middle sections of all the potential lines decline from the left to the right reflect impact of the differential diffusion of cations and anions on the potential profiles.
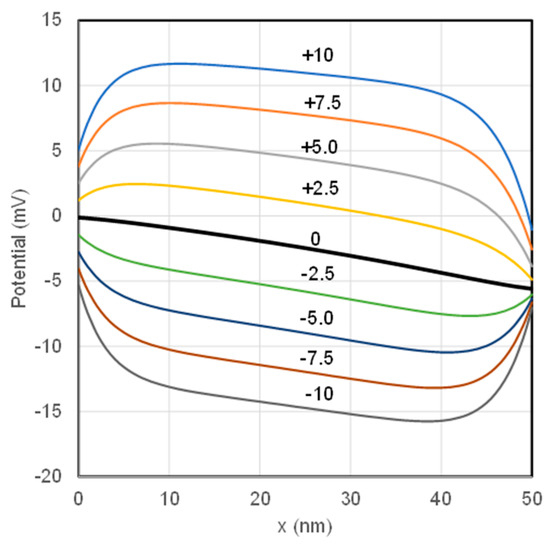
Figure 3.
Potential distributions across the membrane thickness for membranes with different fixed charge. The charge density is indicated on the lines.
Another useful feature of the boundary updating scheme is that the potential differences across the transition layers are determined simultaneously with the numerical solution of the NPP equations. The potential differences across the two transition layers and across the membrane calculated with parameters in Table 1 are presented in Figure 4, together with the total membrane potential. The potential difference on the membrane Δϕm varies in a range of ~5 mV under the simulation conditions. The potential difference across the left transition layer Δϕ0 varies in a range that is more than doubled the range for the membrane potential (~10 mV). The potential difference across the right transition layer ΔϕL varies in a range of about 25 mV. Under the simulation conditions, the potential differences in the transition layers are primarily controlled by Donnan potential. The larger absolute value of the potential difference in the right transition layer is reasonable because Donnan potential of the same fixed charge density is greater in the solution of lower concentration. The total potential difference of the membrane ΔϕT decreases monotonically throughout the entire range of charge density.
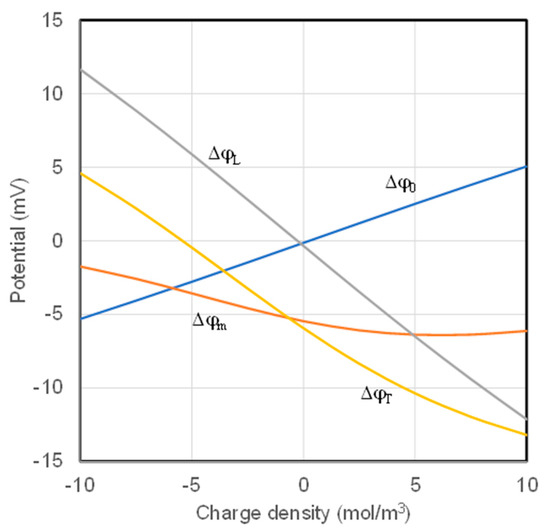
Figure 4.
Total membrane potential and potential components.
Ion fluxes at various charge densities are listed in Table 2 with the corresponding membrane potentials and total potentials. The impact of the charge density on flux is much more moderate than on the potentials. Ion flux changes less than 50% in magnitude for the range of charge density used in the simulations. It clearly demonstrates that the ion flux through the membrane is largely determined by the concentration difference across the membrane with relatively minor impact of charge density on the membrane. This observation is reasonable because concentration difference across the membrane is the original driving force for ion transport. The fixed charge density on the membrane can only modify the ratio of cation and anion concentrations inside the membrane.

Table 2.
Ion fluxes and potentials at different charge density.
Ion flux increases as the charge density decreases in CEMs and maximizes at charge density of −5 mol/m3. Ion flux then declines as charge density further decrease to zero in CEMs and as charge density increase in AEMs. In this example, because cations have smaller mobility than the anions, the appropriate increase in cation concentration would improve ion flux due to the zero current condition at steady state. The positive fixed charge in the AEMs will reduce cation concentration and therefore further reduce the capacity of ion transport. On the other hand, the negative fixed charge of the membrane can increase cation concentration in the CEMs so that the capacity of ion transport can be increased. Of course, the anion concentration would be reduced in the CEMs at the same time. Because of the larger mobility of anions, the impact of the reduced anion concentration in a certain range on ion flux would be over-compensated by the benefit of the increased cation concentration. Beyond this range, anion would become the limiting factor for ion transport. Further decrease in anion concentration would reduce the ion flux.
3.3. Comparison of Donnan Potentials Determinded Analytically and Numerically
As a demonstration of the boundary updating scheme, Donnan potential was calculated by solving the NPP equations with solutions of equal concentrations on both sides of an AEM. Concentrations Cb0 = CbL = 10 mol/m3 and X = 10 mol/m3 were used in the simulation. The distributions of ion concentrations and potential at the steady state from a numerical solution is presented in Figure 5. Anion concentration is higher than cation concentration throughout the membrane thickness. In a middle section of membrane thickness (~10–40 nm), electroneutrality is roughly satisfied because difference between anions and cations is about equal to the fixed charge density on the membrane. The results also show that there are some ion exchanges between the initially neutral membrane and solutions. As a result, lower anion concentration and higher cation concentration compared to those in the middle section were observed in regions near the membrane surfaces. The unbalanced charges in these regions are the cause for the Donnan potential. The boundary updating scheme is capable to catch this subtle feature of the numerical solution for the NPP equations. Potential distribution is also presented in Figure 5 for the AEM. The potential increases inward from the membrane surfaces on the membrane. The value of the plateau on the potential curve is the Donnan potential, which is 12.36 mV in this case.
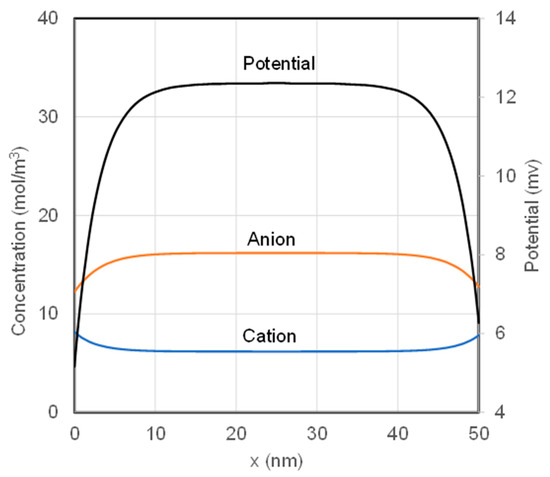
Figure 5.
Distributions of cation and anion concentrations and potential for equal solution concentration on both sides of an AEM.
Donnan potential for a membrane of a fixed change density X in contact with solution of a monovalent salt can be calculated analytically by [14,24]:
where is the Donnan potential and C is the salt concentration in the solution. Equation (21) was derived with the electroneutrality assumption of the membrane. Donnan potentials determined both numerically with our method and analytically with Equation (21) are listed in Table 3. It is a good surprise to find that the two methods yield Donnan potentials that are identical up to 3 effective digits! It is convincing evidence that the numerical method for membrane potential is very accurate. At the same time, it also shows that the use of electroneutrality assumption to reach the analytical expression for Donnan potential is acceptable though it is unphysical fundamentally.

Table 3.
Analytically and numerically calculated Donnan potentials.
3.4. The Applicability and Accuracy of TMS Model
Membrane potential on an IEM with monovalent salt solutions of different concentration on two sides of the membrane can be calculated analytically with the classic TMS model [14]:
where is the mobility coefficient that is defined as:
where and are the diffusion coefficients of cations and anions, respectively. The potentials on an AEM calculated analytically with Equation (22) for varying charge density are presented (as dots) in Figure 6. In the calculation, concentrations Cb0 = 10 mol/m3 and CbL = 1 mol/m3 were employed on two sides of the membrane. The numerically calculated membrane potentials under the same conditions are also presented (as lines) in Figure 6. The mobility coefficients are indicated on the graphs. The results for a CEM would produce similar graphs as Figure 6 but with the mobility coefficients flipped on the figure.
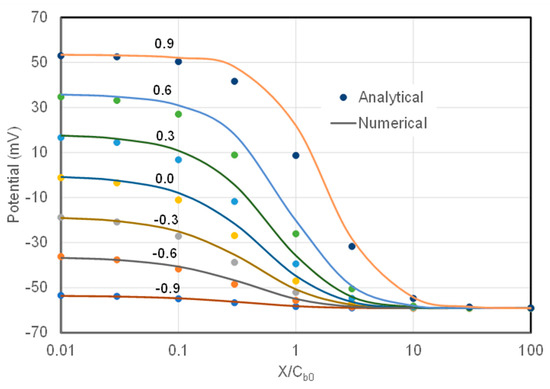
Figure 6.
Membrane potentials on an AEM calculated analytically (symbols) and numerically (lines) as a function of ratio of the fixed charge density to salt concentration on the right side of the membrane. The mobility coefficients are indicated on the graphs.
Figure 6 shows that the membrane potentials from TMS model agree well with the numerically calculated values when the ratio of X/Cb0 is smaller than 0.03 or greater than 30. However, there are significant discrepancies between the two values in the range of 0.03 < X/Cb0 < 30. The TMS potentials are systematically lower than the true membrane potentials, with the biggest discrepancy at X/Cb0 = 1. For example, the TMS potential (8.71 mV) is only about 40% of the numerical potential (22.0 mV) for mobility coefficient of 0.9 at X/Cb0 = 1.
TMS model is not a rigorous solution of the NPP equations because it is simply impossible. The assumptions and simplifications [12,13] used to reach the analytical solution would certainly cause some deviations from the true solution of the equations. On the other hand, the numerical potentials can be taken as the true values because no assumptions and simplifications are made in the solution seeking process. Furthermore, the TMS model can be only used for limited cases where only two types of ions of equal charges exist in solutions while the numerical method can be applied to the general cases with multiple ions of various charges.
4. Conclusions
The potential of an IEM in RED can be rigorously calculated with the boundary updating scheme. The validity and accuracy of the numerical method is strongly supported by the identical Donnan potentials calculated with the well-established analytical method and the numerical method presented in this study. It is demonstrated that the classic TMS model tends to underestimate the membrane potentials systematically for IEMs with fixed charge density in the intermediate range.
Author Contributions
Conceptualization, L.S.; investigation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, L.S.; supervision, L.S.; project administration, L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Bureau of Reclamation, grant number R17AC00140.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mehta, G.D.; Loeb, S. Internal polarization in the porous substructure of a semipermeable membrane under pressure-retarded osmosis. J. Membr. Sci. 1978, 4, 261–265. [Google Scholar] [CrossRef]
- Lee, K.L.; Baker, R.W.; Lonsdale, H.K. Membranes for power generation by pressure-retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Post, J.W.; Veerman, J.; Hamelers, H.V.M.; Euverink, G.J.W.; Metz, S.J.; Nymeijer, K.; Buisman, C.J.N. Salinity-gradient power: Evaluation of pressure-retarded osmosis and reverse electrodialysis. J. Membr. Sci. 2007, 288, 218–230. [Google Scholar] [CrossRef]
- Straub, P.; Deshmukh, A.; Elimelech, M. Pressure-retarded osmosis for power generation from salinity gradients: Is it viable? Energy Environ. Sci. 2016, 9, 31–48. [Google Scholar] [CrossRef]
- Yip, N.Y.; Vermaas, D.A.; Nijmeijer, K.; Elimelech, M. Thermodynamic, energy efficiency, and power density analysis of reverse electrodialysis power generation with natural salinity gradients. Environ. Sci. Technol. 2014, 48, 4925–4936. [Google Scholar] [CrossRef] [PubMed]
- Długołecki, P.; Nymeijer, K.; Metz, S.; Wessling, M. Current status of ion exchange membranes for power generation from salinity gradients. J. Membr. Sci. 2008, 319, 214–222. [Google Scholar] [CrossRef]
- Lacey, R.E. Energy by reverse electrodialysis. Ocean Eng. 1980, 7, 1–47. [Google Scholar] [CrossRef]
- Tedesco, M.; Hamelers, H.V.M.; Biesheuvel, P.M. Nernst-Planck transport theory for (reverse) electrodialysis: I. Effect of co-ion transport through the membranes. J. Membr. Sci. 2016, 510, 370–381. [Google Scholar] [CrossRef]
- Kim, H.; Choi, J.; Jeong, N.; Jung, Y.-G.; Kim, H.; Kim, D.; Yang, S. Correlations between properties of pore-filling ion exchange membranes and performance of a reverse electrodialysis stack for high power density. Membranes 2021, 11, 609. [Google Scholar] [CrossRef]
- Jang, H.; Kang, Y.; Han, J.-Y.; Jang, K.; Kim, C.M.; Kim, I.S. Developments and future prospects of reverse electrodialysis for salinity gradient power generation: Influence of ion exchange membranes and electrodes. Desalination 2020, 491, 114540. [Google Scholar] [CrossRef]
- Zaffora, A.; Culcasi, A.; Gurreri, L.; Cosenza, A.; Tamburini, A.; Santamaria, M.; Micale, G. Energy harvesting by waste acid/base neutralization via bipolar membrane reverse electrodialysis. Energies 2020, 13, 5510. [Google Scholar] [CrossRef]
- Teorell, T. An attempt to formulate a quantitative theory of membrane permeability. Proc. Soc. Exp. Biol. Med. 1935, 33, 282–285. [Google Scholar] [CrossRef]
- Westermann-Clark, G.B.; Christoforou, C. The exclusion-diffusion potential in charged porous membranes. J. Electroanal. Chem. Interfacial Electrochem. 1986, 198, 213–231. [Google Scholar] [CrossRef]
- Galama, A.H.; Post, J.W.; Hamelers, H.V.M.; Nikonenko, V.V.; Biesheuvel, P.M. On the origin of the membrane potential arising across densely charged ion exchange membranes: How well does the Teorell-Meyer-Sievers theory work? J. Membr. Sci. Res. 2016, 2, 128–140. [Google Scholar]
- Hodgkin, A.L.; Katz, B. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 1949, 108, 37–77. [Google Scholar] [CrossRef]
- Feldberg, S.W. On the dilemma of the use of the electroneutrality constraint in electrochemical calculations. Electrochem. Commun. 2000, 2, 453–456. [Google Scholar] [CrossRef]
- Syganow, A.; Von Kitzing, E. (In)validity of the constant field and constant currents assumptions in theories of ion transport. Biophys. J. 1999, 76, 768–781. [Google Scholar] [CrossRef][Green Version]
- Kato, M. Numerical analysis of the Nernst-Planck-Poisson system. J. Theor. Biol. 1995, 177, 299–304. [Google Scholar] [CrossRef]
- Blank, M. The surface compartment model: A theory of ion transport focused on ionic processes in the electrical double layers at membrane protein surfaces. Biochim. Biophys. Acta 1987, 906, 277–294. [Google Scholar] [CrossRef]
- Buck, R.P. Kinetics of bulk and interfacial ionic motion: Microscopic bases and limits for the Nernst-Planck equation applied to membrane systems. J. Membr. Sci. 1984, 17, 1–62. [Google Scholar] [CrossRef]
- Filipek, R.; Szyszkiewicz-Warzecha, K.; Bożek, B.; Danielewski, M.; Lewenstam, A. Diffusion transport in electrochemical systems: A new approach to determining of the membrane potential at steady state. Defect Diffus. Forum 2009, 283–286, 487–493. [Google Scholar] [CrossRef]
- Perrama, J.W.; Stiles, P.J. On the nature of liquid junction and membrane potentials. Phys. Chem. Chem. Phys. 2006, 8, 4200–4213. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Song, L. On rigorous definition of ion transport process and accurate determination of membrane potential at steady state. AIChE J. 2019, 65, e16715. [Google Scholar] [CrossRef]
- Sten-Knudsen, O. Biological Membranes: Theory of Transport, Potentials and Electric Impulses; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).