Abstract
It is necessary to determine the limit of detection when validating any analytical method. For methods with a linear response, a simple and low labor-consuming procedure is to use the linear regression parameters obtained in the calibration to estimate the blank standard deviation from the residual standard deviation (sres), or the intercept standard deviation (sb0). In this study, multiple experimental calibrations are evaluated, applying both ordinary and weighted least squares. Moreover, the analyses of replicated blank matrices, spiked at 2–5 times the lowest calculated limit values with the two regression methods, are performed to obtain the standard deviation of the blank. The limits of detection obtained with ordinary least squares, weighted least squares, the signal-to-noise ratio, and replicate blank measurements are then compared. Ordinary least squares, which is the simplest and most commonly applied calibration regression methodology, always overestimate the values of the standard deviations at the lower levels of calibration ranges. As a result, the detection limits are up to one order of magnitude greater than those obtained with the other approaches studied, which all gave similar limits.
1. Introduction
The limit of detection (LOD) is a fundamental parameter of method validation that defines the limitations of an analytical method. According to the IUPAC, the LOD, expressed as either the concentration or the quantity, is derived from the smallest measure, yLOD, that can be detected with a reasonable certainty for a given analytical procedure [1,2]. Despite the simplicity of this definition, the LOD is a troublesome concept from a practical point of view. This is due to the different approaches that can be applied to calculate this parameter with “reasonable certainty” [2,3,4,5,6,7,8,9,10], which leads to differences that can reach several orders of magnitude depending on the approach used [11,12,13]. For this reason, validation guidelines leave the analyst free to choose, but suggest that the method used for determining the LOD should be documented and supported, and that an appropriate number or samples should be analyzed at the limit to validate the level [10].
Some industrial guidelines, such as those of the International Council for Harmonisation (ICH) [4], allow the determination of LODs simply by visual inspection. This procedure is based on preparing samples with known concentrations of the analyte and establishing the level at which the analyte can be reliably detected (e.g., by successive dilution until the analyte is no longer detected visually). The main drawbacks of this approach are that it is subjective, it is not based on any statistical assessment, and when compared with other approaches, the smaller values are usually obtained by visual inspection [7].
In chromatographic methods, the use of the signal-to-noise (S/N) ratio is probably the most widespread procedure applied to assess LODs [3,7,8,10,14]. This approach requires working at the minimal attenuation of the chromatographic signal, and the S/N is determined by comparing the analytical signals at known low concentrations with those of a blank sample. The noise is taken as an estimate of the blank standard deviation, and a concentration that gives a peak with an S/N equal to two or three is taken as the LOD. However, the measurement of the noise is not always trivial, and it is often subjective and highly variable. Nowadays, instrumentation software of chromatographic instruments allows this value to be auto-integrated, measuring the baseline at a pre-fixed time interval near the analyte peak.
The hypothesis testing approach to detection limit decisions introduced by Currie [11] has gradually become accepted since the term “detected with reasonable certainty” in the LOD definition implies the need for statistics. The IUPAC [1,2,12] and ISO [15] put emphasis on the use of statistics and indicate that the LOD depends on the variability of the method at the blank level (σbl) and on two risk values: α (probability of false positives, type I error) and β (false negatives, type II error or power). This procedure requires the determination of two analytical parameters: the standard deviation of the blank, and the slope of a regression function (i.e., analytical sensitivity) [5].
The value of σbl can only be estimated when blank measurement gives a signal, which is not the common situation in chromatographic methods. To solve this problem, the analysis of matrix blanks fortified at a level close to the LOD (usually <5 times the LOD) is accepted by many validation guidelines for the estimation of σbl [4,5,16]. This procedure is labor intensive, as ≥20 blank measurements [7,12] are required to calculate a value of the standard deviation of the blank (sbl) that can be taken as a good estimator of σbl. However, from a practical point of view a minimum of seven [6] or ten blank analyses [7,16] are typically used.
In order to simplify the experimental requirements needed to determine σbl, the Hubaux-Vos approach has been proposed when the instrument response is linearly related to the concentration [17]. This approach indicates that σbl can be estimated from the linear calibration curve, either by the regression residual standard deviation (sres) or the standard deviation of the y-intercept (sb0). To fulfil the requirements of this approach, the error distribution of all standards used in the calibration must be constant (homoscedasticity). This procedure is also accepted by ISO [18].
Despite the large number of studies discussing the requirements to calculate the LOD of a chromatographic method from a theoretical point of view, there is still considerable variation in the methods used in routine laboratories to determine this fundamental parameter. A large amount of work performing many replicate assays and calibrations is required to obtain good estimates of the detection limits. As a result, these procedures are not the most appropriate for routine laboratories.
The aim of this study was to assess whether one of the simplest approaches to calculating limits of detection from a practical point of view—estimating σbl from the standard deviations obtained applying ordinary least squares to analytical calibrations—enables useful LODs to be obtained for routine work.
2. Experimental and Statistical Calculations
Twenty different experimental analytical calibrations using gas chromatography with flame ionization detector GC-FID (n = 6), gas chromatography with mass spectrometry GC-MS (n = 3), high performance liquid chromatography with ultra-violet detection HPLC-UV (n = 8) and capillary zone electrophoresis with ultra-violet detection, CZE-UV (n = 3) were evaluated (see Supplementary Materials for specific information about each method). In all cases, a minimum of six standards evenly distributed along the calibration range were used. The signal for each calibration level was obtained as the mean value of seven replicates prepared for each standard, which were prepared and measured (once each) on different days. This allowed an estimation of σ at each calibration level to be obtained.
Linearity for all calibration curves was evaluated applying the lack-of-fit (LOF) [19] and Mandel’s [20] tests, whereas the homogeneity (homoscedasticity) of the variances in each calibration was evaluated using the Levene test [21,22]. SPSS 15.0 for Windows (SPSS Inc., Chicago, IL, USA), was used for the regression (both with ordinary least squares, OLS, and weighted least squares, WLS) and statistical analyses, and p < 0.05 was considered as significant. The weighting factor (wi) as inverse of si2 was applied in the WLS regressions [14,23]. Other empirical wi such as 1/xi2 and 1/yi2 were also evaluated.
Once the LODs were calculated using the Hubaux-Vos approach for the OLS and WLS calibrations, two fortified matrix blanks at levels equivalent to the calculated LOD for each regression method were prepared and analyzed to assess the S/N ratio. For the determination of the standard deviation of the blank (sbl), a minimum of seven replicates of a blank matrix were obtained for each method and spiked at a level between 2–5 times the smallest LOD value calculated through OLS and WLS regressions. The LODs from the standard deviation of the fortified blanks were also determined.
3. Statistical Considerations
According to Currie [11], if we consider both type I and type II errors, the value of the signal corresponding to the LOD (yLOD) is given by the following equation:
where μbl is the signal of the “true” blank mean (which is usually zero in chromatography in absence of bias in the procedure), z1−α and z1−β are the z-values of the one-sided standardized normal distribution at given significance levels α and β, σbl is the standard deviation at the blank level when the component is not present in the sample, and σLOD is the standard deviation at the LOD level.
When μbl = 0, and assuming normal distribution for the blank and LOD signals and a constant dispersion between blank and LOD range (i.e., σbl = σLOD), Equation (1) can be rewritten as:
IUPAC and ISO recommend fixing confidence levels α = β at 0.05 [1,2,14]; therefore z1−α = z1−β = 1.645:
When the response calibration function is linear, this measurement is converted to concentration as:
where b1 is the slope of the linear regression function.
In practice, σbl is unknown and has to be estimated from the standard deviation of a limited number of blank measurements (sbl). Therefore, the z1−α value should be replaced by the one-tailed Student’s t for ν degrees of freedom and α = 0.05 (t(1−α,ν)) [1,3,11]:
which means that in experimental measurements the constant value (2t(1−α,ν)) multiplying sbl should range from 3.89 (for 7 blank replicates) to 3.67 (n = 10).
Some guidelines, such as the US-EPA [6], only consider the type I error, but require α = 0.01 (99% significance) and n ≥ 7. In this situation, t(0.99,ν) ranges from 3.14 (n = 7) and 2.82 (n = 10).
In general, the 2 t-value is rounded to three for practical applications and results in the common value of yLOD = 3 sbl that is usually applied in many studies. It should be taken into account that 3 sbl corresponds either to α = 0.00135 and β = 0.50 [24], which means that there is no control of false negative errors, or to α = 0.05 and β = 0.16 (84% power) [10], which may be considered as an acceptable β level, but is higher than the recommended β = 0.05 (95% power) by ISO and IUPAC. In general, it is accepted that yLOD ≥ 3 sbl, but the use of yLOD = 2 sbl, as proposed by some studies, should not be applied for estimating LODs as this value corresponds to the critical level (Lc) and would result in a concentration level where, assuming a normal distribution, there is only a 50% probability of the analyte being detected [3,11,12,13,25].
4. Results
Before performing the regression analyses, the linearity was checked for each calibration curve. Initially, 22 calibrations were evaluated, but Mandel’s test [20] yielded F-values that were higher than the tabulated values at 95% and 99% confidence for two HPLC-UV calibrations. This indicates that the variance explained by the addition of a quadratic factor to the linear model was statistically significant and does not correspond to random errors. These two calibrations were not considered in the study as they cannot be considered linear (Figure S1 in Supplementary Materials).
The linearity of the 20 selected calibrations was confirmed through the LOF test [19], which gave p > 0.10 for each method (Table 1, Table 2, Table 3 and Table 4), and Mandel’s test [20]. Therefore, the instrumental response can be considered linear in the ranges evaluated and the use of linear regression functions was adequate. The Levene test for homogeneity of variances [21,22] showed that the calibrations evaluated yielded non-constant variances (p < 0.01), confirming heteroscedasticity (Figure 1, Table 1, Table 2, Table 3 and Table 4).

Table 1.
Regression parameters obtained with different GC-FID methods. All calibrations were performed with a minimum of -six calibrations standards evenly distributed along the working range. The signal value for each calibration was determined as the mean value obtained for at least seven replicates prepared and measured in different days. sres = regression residual standard deviation; b0 = y-intercept; sb0 = y-intercept standard deviation; b1 = slope of the calibration function; sb1 = slope standard deviation; sbl = standard deviation of the blank.

Table 2.
Regression parameters obtained with GC-MS methods. Experimental conditions as indicated in Table 1.

Table 3.
Regression parameters obtained with HPLC-UV methods. Experimental conditions as indicated in Table 1.

Table 4.
Regression parameters obtained with CZE-UV methods. Experimental conditions as indicated in Table 1.
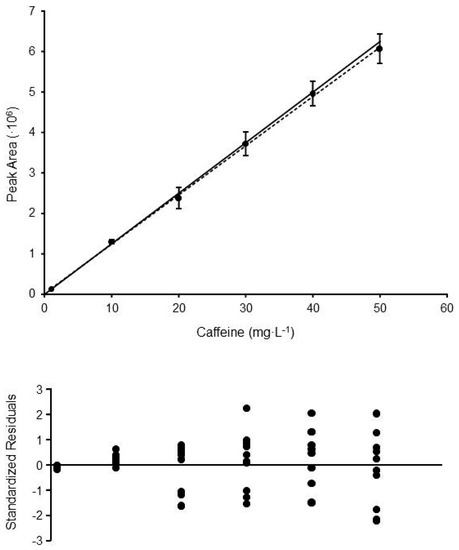
Figure 1.
Calibration curve and standardized residuals plot obtained for the method HPLC-UV#3 (determination of caffeine in coffee samples). Each calibration point is the mean of 8–10 replicate standards prepared and measured in different days. The error bars show the standard deviations obtained at each level. Solid line shows the linear trend obtained applying OLS (y = 121,810x + 224,242; R2 = 0.99926), whereas the dashed line corresponds to the linear trend obtained by WLS (y = 124,904x + 1678; R2 = 0.99896).
The statistical evaluation of the linear regression parameters (Table 1, Table 2, Table 3 and Table 4) showed that all the slopes (b1) obtained were significant (p < 0.001 for the null hypothesis b1 = 0) for both OLS and WLS regressions. The y-intercept values (b0) did not differ significantly from zero (p > 0.05 for the null hypothesis b0 = 0) for OLS regression functions. However, ten calibrations (50%) did not yield intercepts equivalent to zero with WLS regression. It is important to point out that the b0 value of the linear function must not be significantly different from the mean blank signal, which means that b0 must not differ statistically from zero for chromatographic methods with no bias.
In the present study, none of the analyses of blank matrices for any of the methods evaluated yielded detectable signals, suggesting that the WLS calculations introduced some bias at low concentration levels in the ten calibrations where the y-intercept was not equivalent to zero. Taking these considerations into account, Equation (4) was applied for the calculation of LOD values with OLS calculations and those WLS with no bias, whereas it was substituted in the WLS calibrations where b0 was found to differ from zero by:
Two standard deviation parameters (sb0 and sres) are usually accepted as estimates of σbl when linear calibrations are applied for the determination of LODs [5,8,10]. In the case of WLS, the calculated sres is significantly rounded to near unity due to the inverse variance weighting scheme [26,27] (Table 1, Table 2, Table 3 and Table 4) and cannot be used directly as an estimate of σbl, with sb0 being the only estimator for this regression model. For OLS regressions with appropriate determination coefficients for quantitative purposes and ≥6 calibration standards, it is common to find that sb0 < sres [5,8,28,29], which also happened with the calibrations analyzed in the present study. Therefore, sb0 has been chosen to make the comparison between OLS and WLS regressions. In most calibrations (n = 16), LODs determined with OLS were significantly higher than those obtained with WLS (from 1.4–15 times higher, Table 5). In four GC-FID calibrations, LOD values calculated by OLS and WLS were equivalent.

Table 5.
Limits of detection determined with the different approaches.
In those calibrations where different LOD values were obtained by applying OLS and WLS regressions, spiked blanks at the two calculated LOD values were analyzed. In all cases, it was found that fortified blanks prepared at the LOD level determined by OLS gave signals with S/N > 8, whereas the fortified blanks prepared at the levels calculated with the WLS regression were always detectable with S/N ≥ 3 (Figure 2).
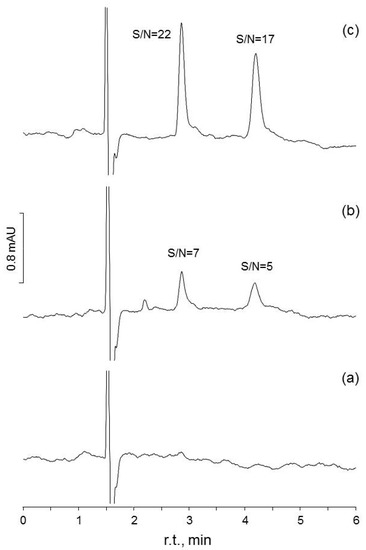
Figure 2.
Chromatograms obtained to assess S/N for two of the methods evaluated in the present study (HPLC-UV #1, #2: determination of theobromine and caffeine in tea beverages): (a) chromatogram for a matrix blank; (b) the same blank spiked at 0.04 mg·L−1, a level close to the LOD value determined by WLS; (c) chromatogram for the blank spiked at 0.30 mg·L−1, close to the LOD level calculated by OLS.
Finally, 7–10 replicates of spiked blank matrices prepared at levels 2–5 times greater than those determined by WLS were analyzed and the measured sbl was used as a new estimate of σbl. All LOD values obtained from sbl were equivalent to those obtained by WLS regression (Table 5).
5. Discussion
To estimate σbl from the linear calibration curve applying the Hubaux-Vos approach, the error distribution of all standards used in the calibration must be constant (homoscedasticity) [8,13,17]. However, despite the fact that many researchers often do not take it into account, heteroscedasticity is more frequent than might be expected in experimental sciences. Many analytical methods yield non-constant variances over the calibration range [8,26,27,30,31,32,33,34], as was the case with the calibrations evaluated in the present study (Figure 1). In these conditions, the absolute errors of the instrument tend to be proportional to the concentrations, and the relative standard deviation is the constant parameter across the curve instead of the standard deviation [33,35,36,37,38].
Different studies have demonstrated that since homoscedasticity is a necessary condition to apply the Hubaux-Vos approach, the use of OLS to assess limits of detection should be limited to calibrations where experimental levels are chosen in a small range, around and up to ten times the LOD [7,8,14,34,39]. Moreover, those guidelines that accept the estimation of LOD via the calibration approach require the calibration to be performed in the range of the detection limit [4,7], with the most concentrated standard not exceeding ten times the level of the LOD [7]. Unfortunately, this procedure limits the use of the calibration function obtained, as the working range is very restricted.
Despite this basic requirement, it is common to find many studies in which OLS is applied to estimate σbl without considering whether or not the calibration presents heteroscedasticity [28,29,40,41,42,43,44]. Unfortunately, OLS assumes constant variance over the whole calibration range and the standard deviations calculated by OLS can differ greatly from the true standard deviation, particularly at low concentration levels [35,36,37,45]. Moreover, as indicated by Meites et al. [46], in experimental calibrations where the independent variable can also be subject to random measurement errors, OLS always lead to biased estimates of the intercept. As can be seen in the results obtained in the present study, sb0 values were always higher when OLS regression was applied, leading to an overestimation of LOD values (Table 5). This was corroborated by the fact that when fortified blanks were prepared at the LOD level estimated by OLS regression, the signals obtained gave S/N > 8 (as auto-integrated by the software of the instruments, Figure 2c); and fortified blanks prepared below this limit gave chromatograms with clearly identified peaks (S/N ≥ 3) (Figure 2b). Moreover, in many of the calibrations evaluated the value of the signal obtained for the first standard and the S/N confirmed that this standard gave a signal clearly above the LOD, but its concentration was below the LOD determined on applying OLS.
The use of WLS regression has been proposed as a good alternative to OLS in linear calibrations, as it can manage heteroscedasticity [8,26,27,30]. It should be considered that OLS and WLS regression models consider that the independent variable is free of error. Therefore, biased estimates of the intercept are always to be anticipated in analytical calibrations, but sometimes this error is too small to have any experimental significance [46]. It has been reported that WLS does not alter significantly the slope estimate obtained by OLS, whereas the intercept is moderately affected [26,27]. In this study, differences for the slopes calculated by OLS and WLS regressions were <5%, a difference that for practical applications can be considered as equivalent. In the case of y-intercepts, the differences were >10% (up to 1300%), which do have experimental significance.
Previous studies have found that the variances obtained at low concentrations with WLS are significantly reduced when compared to OLS, and that precision loss with OLS calculations can be as high as one order of magnitude in the lower range of the calibration curves [32,35,36,37]. The results obtained in the present study show that in 17 calibrations sb0 values determined by WLS were significantly smaller (2–23 times, p < 0.05, Fisher F-test) than by OLS (Table 1, Table 2, Table 3 and Table 4), which agrees with the results obtained by other studies comparing OLS and WLS with experimental calibrations involving heteroscedastic data [8,26,27,47].
The standard deviations of the blanks determined through the analysis of matrix blanks spiked at 2–5 times the LOD levels calculated by WLS (n = 7–10, Table 1, Table 2, Table 3 and Table 4) confirmed that the LODs obtained with the sbl approach were equivalent to the LODs determined by WLS (Table 5). In general, the limits determined with OLS were up to one order of magnitude higher than those obtained with WLS, S/N and fortified blank measurements.
One of the main drawbacks of WLS is the need to analyze a large number of replicate standards at each level to obtain the weighting factors (wi = 1/si2). Taking into account that standard deviation is usually proportional to the concentration [33,35,36,37,38], different experimental approaches have been proposed to avoid the requirement of replicate measurements at each calibration level [33,35,38,48]. Therefore, different empirical weighting factors, such as 1/xi1/2, 1/xi, 1/xi2, 1/yi1/2, 1/yi and 1/yi2, have been proposed, from which 1/xi2 and 1/yi2 seem to yield the best results. The WLS regressions were evaluated applying these two empirical weighting factors and the corresponding regression parameters, and their standard deviations were used to determine the LODs (Table 5). It was observed that, in general, there were no significant differences between the LODs determined by WLS independently of the weighting factor used. Only in two calibrations were the LODs determined applying both 1/xi2 and 1/yi2 weights significantly smaller than those obtained by 1/si2 or sbl.
6. Conclusions
For routine applications, the working range of a calibration needs to cover several orders of magnitude, which results in heteroscedastic data being obtained in experimental sciences. In these conditions, the use of OLS, which is the simplest and most applied regression method for linear calibrations, leads to an overestimation of the real standard deviation at the blank level. Therefore, the calculated sb0 through OLS is not a good estimate of σbl (sb0 can be up to one order of magnitude higher than the real σbl).
The results obtained in the present study show WLS to be the most adequate regression function in determining LODs when the Hubaux-Vos approach is applied with linear chromatographic methods. When WLS regression is used in the determination of the regression parameters, the deviation in the variance at the blank level is significantly reduced. The LODs obtained with this regression function tend to be equivalent to those calculated by the most common and accepted methodologies, such as the S/N, and by performing a large number of analyses of fortified blank samples to calculate the sbl.
The WLS procedure is not the most appropriate in laboratory routine as it requires a large number of replicate analyses to be performed at each calibration level. It is known that the experimental requirements needed to perform WLS can be reduced by using empirical weighting factors such as 1/xi2 and 1/yi2. In the present study, it has been found that, in general, the use of these empirical weighting factors allows equivalent LODs to those determined by 1/si2 to be obtained.
Despite the limitations of OLS in determining LODs, the limits calculated by OLS can be accepted as conservative estimates. It has been demonstrated that the limits obtained with OLS are always higher than those obtained by other procedures and are often just above the quantification limit. In many non-research laboratories, the minimum required performance limit (MRPL) is the minimum concentration that laboratories must be able to reliably detect and identify for routine and daily operations. In situations where LODs determined by OLS are below the MRPL, the limit obtained is sufficient to confirm the ability of the laboratory to reach the MRPL.
Supplementary Materials
The following are available online at http://www.mdpi.com/2297-8739/5/4/49/s1, Figure S1: Calibration curves and residual plot obtained for an HPLC-UV method for the analysis of theobromine in chocolate samples.
Funding
This research received no external funding.
Acknowledgments
This study has been supported by the University of Girona (MPCUdG2016/100). The author would like to thank A. Hughes for his help in the writing and proof reading of the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Currie, L.A. Nomenclature in evaluation of analytical methods including detection and quantification capabilities. Pure Appl. Chem. 1995, 67, 1699–1723. [Google Scholar] [CrossRef]
- International Union of Pure and Applied Chemistry. IUPAC Compendium of Chemical Terminology—The Gold Book; IUPAC. Available online: https://goldbook.iupac.org (accessed on 8 March 2018).
- Heyden, Y.V.; Boqué, R. The limit of detection. LCGC Eur. 2009, 22, 82–85. [Google Scholar]
- International Conference on Harmonisation (ICH). Q2(R1): Validation of Analytical Procedures—Text and Methodology. ICH Harmonised Tripartite Guideline. 1994/1996. Available online: http://www.ich.org/products/guidelines/quality/quality-single/article/validation-of-analytical-procedures-text-and-methodology.html (accessed on 31 July 2018).
- Shabir, G.A. Validation of high-performance liquid chromatography methods for pharmaceutical analysis: Understanding the differences and similarities between validation requirements of the US Food and Drug Administration, the US Pharmacopeia and the International Conference on Harmonization. J. Chromatogr. A 2003, 987, 57–66. [Google Scholar] [CrossRef] [PubMed]
- US-EPA. 40 CFR Appendix B to Part 136—Definition and Procedure for the Determination of the Method Detection Limit; Revision 2, EPA 821-R-16-006; US Environmental Protection Agency: Washington, DC, USA, 2016. Available online: https://www.gpo.gov/fdsys/granule/CFR-2011-title40-vol23/CFR-2011-title40-vol23-part136-appB/content-detail.html (accessed on 31 July 2018).
- Wenzl, T.; Haedrich, J.; Schaechtele, A.; Robouch, P.; Stroka, J. Guidance Document on the Estimation of LOD and LOQ for Measurements in the Field of Contaminants in Feed and Food; EUR 28099; Publications Office of the European Union: Luxembourg, 2016; ISBN 978-92-79-61768-3. [Google Scholar]
- Vial, J.; Jardy, A. Experimental comparison of the different approaches to estimate LOD and LOQ of an HPLC method. Anal. Chem. 1999, 71, 2672–2677. [Google Scholar] [CrossRef]
- Shrivastava, A.; Gupta, V.B. Methods for the determination of limit of detection and limit of quantification of the analytical methods. Chron. Young Sci. 2011, 2, 21–25. [Google Scholar] [CrossRef]
- Araujo, P. Key aspects of analytical method validation and linearity evaluation. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 2009, 877, 2224–2234. [Google Scholar] [CrossRef] [PubMed]
- Currie, L.A. Limits for qualitative detection and quantitative determination: Application to radiochemistry. Anal. Chem. 1968, 40, 586–593. [Google Scholar] [CrossRef]
- Long, G.L.; Winefordner, J.D. Limit of detection: A closer look at the IUPAC definition. Anal. Chem. 1983, 55, 712A–724A. [Google Scholar] [CrossRef]
- Bernal, E. Limit of detection and limit of quantification: Determination in gas chromatograpy. In Advances in Gas Chromatography; Guo, X., Ed.; IntechOpen: Rijeka, Croatia, 2014; pp. 57–81. ISBN 978-953-51-1227-3. Available online: https://www.intechopen.com/books/advances-in-gas-chromatography (accessed on 8 March 2018).
- Desimoni, E.; Brunetti, B. About estimating the limit of detection by the signal to noise approach. Pharm. Anal. Acta 2015, 6, 1000355. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Capability of Detection, Part 1: Terms and Definitions; ISO 11843-1; ISO: Geneve, Switzerland, 1997. [Google Scholar]
- Magnusson, B.; Ornemark, U. (Eds.) EURACHEM Guide: The Fitness for Purpose of Analytical Methods—A Laboratory Guide to Method Validation and Related Topics, 2nd ed.; LCG: Teddington, UK, 2014; ISBN 978-91-87461-59-0. [Google Scholar]
- Hubaux, A.; Vos, G. Decision and detection limits for linear calibration curves. Anal. Chem. 1970, 42, 849–855. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Capability of Detection. Part 2: Methodology in the Linear Calibration Case; ISO 11843-2; ISO: Geneve, Switzerland, 2000. [Google Scholar]
- Massart, D.L.; Vandeginste, B.G.M.; Buydens, L.M.C.; De Jong, S.; Lewi, P.H.; Smeyers-Verbeke, J. Handbook of Chemometrics and Qualimetrics: Part A; Elsevier: Amsterdam, The Netherlands, 1997; ISBN 0-444-89724-0. [Google Scholar]
- Mandel, J. The Statistical Analysis of Experimental Data; Dover Pub. Inc.: New York, NY, USA, 1964; ISBN 978-0486646664. [Google Scholar]
- Levene, H. Robust test for equality of variances. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Olkin, I., Ghurye, S.G., Hoedffding, W., Madow, W.G., Mann, H.B., Eds.; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. ISBN 978-0804705967. [Google Scholar]
- Brown, M.B.; Forsythe, A.B. Robust test for the equality of variances. J. Am. Stat. Assoc. 1974, 69, 364–367. [Google Scholar] [CrossRef]
- Jacquez, J.A.; Norusis, M. Sampling experiments on the estimation of parameters in heteroscedastic linear regression. Biometrics 1973, 29, 771–780. [Google Scholar] [CrossRef]
- Miller, J.N.; Miller, J.C. Statistics and Chemometrics for Analytical Chemistry, 6th ed.; Prentice Hall: Harlow, UK, 2010; ISBN 978-0273730422. [Google Scholar]
- Voigtman, E. Limits of Detection in Chemical Analysis; Wiley: Hoboken, NJ, USA, 2017; ISBN 978-1119188971. [Google Scholar]
- Oppenheimer, L.; Capizzi, T.P.; Weppelman, R.M.; Mehta, H. Determining the lowest limit of reliable assay measurement. Anal. Chem. 1983, 55, 638–643. [Google Scholar] [CrossRef]
- Zorn, M.E.; Gibbons, R.D.; Sonzogni, W.C. Weigthed least-squares approach to calculating limits of detection and quantification by modeling variability as a function of concentration. Anal. Chem. 1997, 69, 3069–3075. [Google Scholar] [CrossRef] [PubMed]
- Sanagi, M.M.; Ling, S.L.; Nasir, Z.; Wan Ibrahim, W.A.; Naim, A.A. Comparison of signal-to-noise, blank determination, and linear regression methods for the estimation of detection and quantification limits of volatile organic compounds by gas chromatography. J. AOAC Int. 2009, 92, 1833–1838. [Google Scholar] [PubMed]
- Ismail, R.; Lee, H.Y.; Mahyudin, N.A.; Bakar, F.A. Linearity study on detection and quantification limits for the determination of avermectins using linear regression. J. Food Drug Anal. 2014, 22, 407–412. [Google Scholar] [CrossRef] [PubMed]
- Zorn, M.E.; Gibbons, R.D.; Sonzogni, W.C. Evaluation of approximate methods for calculating the limit of detection and quantification. Environ. Sci. Technol. 1999, 33, 2291–2295. [Google Scholar] [CrossRef]
- Desimoni, E.; Brunetti, B. About estimating the limit of detection of heteroscedastic analytical systems. Anal. Chim. Acta 2009, 655, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, J.M. Ordinary least squares with laboratory calibrations: A practical way to show students that this fitting model may easily yield biased results when used indiscriminately. World J. Anal. Chem. 2017, 5, 1–8. [Google Scholar] [CrossRef]
- Raposo, F. Evaluation of analytical calibration based on least-square linear regression for instrumental techniques: A tutorial review. TRAC Trends Anal. Chem. 2016, 77, 167–185. [Google Scholar] [CrossRef]
- Uhrovcik, J. Strategy for determination of LOD and LOQ values—Some basic aspects. Talanta 2014, 119, 178–180. [Google Scholar] [CrossRef] [PubMed]
- Almeida, A.M.; Castel-Branco, M.M.; Falcao, A.C. Linear regression for calibration revisited: Weighting schemes for bioanalytical methods. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 2002, 774, 215–222. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Weighted least-squares in calibration: What difference does it make? Analyst 2007, 132, 536–543. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.C.; Zhang, E.; Dong, H.; Tellinghuisen, J. Weighted least squares in calibration: Estimating data variance functions in high-performance liquid chromatography. J. Chromatogr. A 2008, 1206, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Liu, G.; Wang, J.; Aubry, A.F.; Arnold, M.E. Selecting the correct weighting factor for linear and quadratic calibration curves with least-square regression algorithm in bioanalytical LC-MS/MS assays and impacts of using incorrect weighting factors on curve stability, data quality, and assay performance. Anal. Chem. 2014, 86, 8959–8966. [Google Scholar] [CrossRef] [PubMed]
- Mulholland, M.; Hibbert, D.B. Linearity and the limitations of least squares calibration. J. Chromatogr. A 1997, 762, 73–82. [Google Scholar] [CrossRef]
- Vanatta, L.E.; Coleman, D.E. Calculation of detection limits for a single-laboratory ion-chromatographic method to determine parts-per-trillion ions in ultrapure water. J. Chromatogr. A 1997, 770, 105–114. [Google Scholar] [CrossRef]
- Luo, W.; Li, H.; Zhang, Y.; Ang, C.Y.W. Determination of formaldehyde in blood plasma by high-performance liquid chromatography with fluorescence detection. J. Chromatogr. B Biomed. Sci. Appl. 2001, 753, 253–257. [Google Scholar] [CrossRef]
- Ribani, M.; Collins, C.H.; Bottoli, C.B.G. Validation of chromatographic methods: Evaluation of detection and quantification limits in the determination of impurities in omeprazol. J. Chromatogr. A 2007, 1156, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Proestos, C.; Sereli, D.; Komaitis, M. Determination of phenolic compounds in aromatic plants by RP-HPLC and GC-MS. Food Chem. 2006, 95, 44–52. [Google Scholar] [CrossRef]
- Muranaka, L.S.; Giorgiano, T.E.; Takita, M.A.; Forim, M.R.; Silva, L.F.C.; Coletta-Filho, H.D.; Machado, M.A.; de Souza, A.A. N-Acetylcysteine in agriculture, a novel use for an old molecule: Focus on controlling the plant-pathogen Xylella fastidiosa. PLoS ONE 2013, 8, e72937. [Google Scholar] [CrossRef] [PubMed]
- Zabell, A.P.R.; Lytle, F.E.; Julina, R.K. A proposal to improve calibration and outlier detection in high-throughput mass spectrometry. Clin. Mass Spectrom. 2016, 2, 25–33. [Google Scholar] [CrossRef]
- Meites, L.; Smit, H.C.; Kateman, G. The effects of errors in measuring the independent variable in least-squares regression analysis. Anal. Chim. Acta 1984, 164, 287–291. [Google Scholar] [CrossRef]
- Gibbons, R.D.; Jarke, F.H.; Stoub, K.P. Detection limits for linear calibration curves with increasing variance and multiple future detection decisions. In Waste Testing and Quality Assurance: Third Volume; STP 1075; ASTM Publication Code Number 04-010750-56; Friedman, D., Ed.; ASTM: Philadelphia, PA, USA, 1991; pp. 377–390. ISBN 978-0-8031-1294-0. [Google Scholar]
- Kiser, M.M.; Dolan, J.W. Selecting the best curve fit. LCGC Eur. 2004, 17, 138–143. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).